Переводной экзамен по геометрии за 8 класс
Билеты по геометрии для переводного экзамена в 8 классе
(учебник Геометрия 7 – 9 Л. С. Атанасян.)
Каждый билет содержит 4 вопроса. В первом вопросе предлагается сформулировать и доказать теорему. Во втором вопросе даётся одно из следующих заданий: дать определение понятия, указать его основные свойства или привести примеры, описать этапы построения геометрических фигур. Третий и четвертый вопросы — практические, они содержат задачи за курс 8 класса. Задачи к билетам необходимо решить в тетради. К каждой задаче выполнить рисунок и необходимые пояснения. На экзамен надо принести эту тетрадь с решением и необходимые инструменты: линейка, карандаш, циркуль, ручка. Все билеты надо выучить, уметь ответить у доски и быть готовым к дополнительным вопросам.
Билет №1.
1.Параллелограмм. Свойства параллелограмма. Доказать, что диагонали параллелограмма точкой пересечения делятся пополам.
2.Определение синуса острого угла прямоугольного треугольника. Чему равны значения синуса для углов 300 , 450 , 600?
3. В выпуклом пятиугольнике длины сторон относятся как 5: 7: 8 : 9: 10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
4. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билет №2.
1.Параллелограмм. Признаки параллелограмма (доказать один из признаков).
2.Определение косинуса острого угла прямоугольного треугольника. Чему равны значения косинуса для углов 300 , 450 , 600?
3. В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
4. Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Билет №3.
1.Прямоугольник. Свойства прямоугольника. Доказать, что диагонали прямоугольника равны.
2.Определение тангенса острого угла прямоугольного треугольника. Чему равны значения тангенса для углов 300 , 450 , 600?
3. В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4. Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
Билет №4.
1.Ромб. Свойства ромба. Доказать, что диагонали ромба взаимно перпендикулярны.
2.Определение подобных треугольников. Признаки подобия треугольников.
3.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
4. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
Билет №5.
1.Квадрат. Свойства квадрата. Доказать, что если в ромбе диагонали равны, то ромб является квадратом.
2.Центральный угол. Свойство центрального угла.
3. Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
4. В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
Билет №6.
1.Доказать теорему о вычислении площади параллелограмма.
2. Вписанная окружность, центр вписанной окружности. Свойство сторон четырёхугольника, описанного около окружности.
3.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
4. Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
Билет №7.
1.Доказать теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника?
2. Описанная окружность, центр описанной окружности. Свойство углов четырёхугольника, вписанного в окружность.
3. Основания прямоугольной трапеции равны 10см и 22см, а большая боковая сторона15см. Найти площадь трапеции.
4. Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
Билет №8.
1.Доказать теорему о вычислении площади трапеции.
2.Вписанный угол. Следствия, вытекающие из теоремы о вписанном угле.
3. Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
4. Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
Билет №9.
1.Доказать теорему Пифагора.
2.Биссектриса угла. Свойство биссектрисы угла.
3. Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
4. Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
Билет №10.
1.Определение средней линии треугольника. Доказать теорему о средней линии треугольника.
2.Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку.
3. АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
4. Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
Билет №11.
1.Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники. Сформулировать утверждения о пропорциональных отрезках в прямоугольном треугольнике.
2.Сформулировать теорему обратную теореме Пифагора.
3. Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
4. Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
Билет №12.
1.Касательная к окружности, точка касания прямой к окружности. Доказать теорему о свойстве касательной.
2.Дать определение подобных треугольников. Теорема об отношении площадей подобных треугольников.
3. В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
4. Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
Билет №13.
1.Доказать, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют углы с прямой, проходящей через эту точку и центр окружности.
2.Сформулировать свойство медиан треугольника пересекающихся в одной точке.
3. Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
4. Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
Билет №14.
1.Вписанный угол. Теорема о вписанном угле.
2.Трапеция. Виды трапеции. Свойства равнобокой трапеции.
3. Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
4. Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см,
ДС =4см. Найти основание АС и высоту АД.
Билет №15.
1.Доказать теорему об отрезках пересекающихся хорд.
2.Теорема Фалеса. Деление отрезка на п-равных отрезков.
3. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
4. АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
Задачи к билетам
1.В выпуклом пятиугольнике длины сторон относятся как 5:7:8:9:10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
2.В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
3.В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
5.Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
6.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
7.Основания равнобедренной трапеции равны 10см и 24см, а большее основание 15см. Найти площадь трапеции.
8.Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
9.Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
10.АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
11.Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
12.В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
13.Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
14.Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
15.АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
16. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
Задачи к билетам
1.АВСД – ромб, угол АВС равен 1400 . Найти углы треугольника СОД, где точка О – пересечение диагоналей.
2.Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см. Найти основание АС и высоту АД.
3.Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
4.Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
5.Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
6.Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
7.Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
8.Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
9.Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
10.Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
11.В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
12.Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
13.Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
14.Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
15.В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билеты и задачи переводного
экзамена по геометрии в 8 классе
Билет 1
1. Описанный
четырехугольник. Свойство описанного четырехугольника.
2.
Трапеция.
Виды трапеций. Свойства равнобедренной трапеции. Доказательство одного из них.
3. В ромбе АВСD
проведена диагональ АС. Найдите угол АВС, если известно, что угол АСD
равен 35°.
Билет 2
1. Центральный и
вписанный уголы. Теоремы о вписанных углах.
2.
Параллелограмм.
Определение. Свойства.
3. Гипотенуза
прямоугольного треугольника равна 20 см, а один из катетов 16 см. Найдите
площадь треугольника.
Билет 3
1. Определение
подобных треугольников. Признаки подобия.
2.
Теорема
о площади треугольника. Площадь прямоугольного треугольника.
3. Диагонали ромба
равны 10 и 12 см.
Найдите
его
площадь
и периметр.
Билет 4
1. Вписанный
четырехугольник. Свойство вписанного четырехугольника.
2.
Прямоугольник.
Свойства прямоугольника. Доказательство характеристического свойства.
3. У прямоугольного
треугольника катеты равны 5 и 12. Найдите высоту, проведенную к гипотенузе.
Билет 5
1. Определение
синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Основное тригонометрическое тождество.
2.
Ромб.
Свойства ромба. Доказательство характеристического свойства.
3. Боковая сторона
равнобедренного треугольника равна 17
см, а основание равно 16 см. Найдите площадь треугольника.
Билет 6
1. Выпуклые,
невыпуклые многоугольники. Теорема о сумме углов выпуклого многоугольника.
2. Площадь
параллелограмма.
3. Найдите сторону
равностороннего треугольника, если его высота равна 3.
Билет 7
1. Метрические
соотношения в прямоугольном треугольнике.
2. Площадь ромба.
3. Найдите углы
выпуклого четырехугольника, если они пропорциональны числам 1,2,4,5.
Билет 8
1. Теорема Фалеса.
Теорема о пропорциональных отрезках.
2.
Площадь
трапеции.
3. Центральный
угол АОВ на 300 больше
вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
Билет 9
1. Треугольник.
Классификация треугольников.
2. Свойство
биссектрисы треугольника.
3. Один
из углов ромба на 400 больше
другого. Найти углы ромба.
Билет 10
1. Параллельные
прямые. Признаки параллельности прямых.
2. Свойство
вписанного угла.
3. Сумма трёх углов
параллелограмма равна 254о. Найдите углы параллелограмма.
Билет 11
1. Смежные и
вертикальные углы. Теоремы о вертикальных и смежных углах.
2. Свойство
пересекающихся хорд.
3. Гипотенуза
прямоугольного треугольника равна 20 см, а один из катетов 16 см. Найти площадь
треугольника.
Билет 12
1. Прямоугольный
треугольник. Свойства прямоугольных треугольников.
2. Свойство
касательной и секущей к окружности.
3.
Найти
периметр прямоугольника, если его площадь 40 см2, а одна из сторон
на 3 см больше другой.
Задачи второй части
1.
В
параллелограмме АВСD высота, опущенная на сторону СD, делит её пополам и образует со стороной ВС угол 300,
АВ = 12 см. Найти периметр параллелограмма.
2.
В
равнобедренной трапеции АВСD диагональ AC перпендикулярна боковой стороне, угол D равен 60°. Основание АD = 20 см., ВС = 12 см. Найти периметр трапеции.
3.
Периметр
треугольника равен 40 см, две его стороны равны 15 см и 9 см. Найти отрезки, на
которые биссектриса треугольника делит его третью сторону.
4.
Стороны
параллелограмма равны 6 см и 7 см, угол между ними 600 . Найти высоты параллелограмма.
5.
АВ и ВС
отрезки касательных, проведённых к окружности с центром О радиуса 6 см. Найти
периметр четырёхугольника АВСО, если угол АВС равен 600 .
6.
Одна из
диагоналей ромба на 4см больше другой, а площадь ромба равна 96 см2 . Найти сторону ромба.
7.
Основания
прямоугольной трапеции равны 10 см и 22 см, а большая боковая сторона15 см.
Найти площадь трапеции.
8.
Площадь
прямоугольного треугольника равна 24 см2 ,
а один из его катетов равен 6см. Найти длину средней линии, параллельной
гипотенузе.
9.
Точка касания окружности,
вписанной в равнобедренный треугольник, делит одну из боковых сторон на
отрезки, равные 3 см и 4 см., считая от основания. Найдите периметр
треугольника.
10.
Диагонали
трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите
АВ, если ОВ=4 см, OD=10 см, DC=25 см.
11.
В окружность вписан равнобедренный треугольник АВС с основанием
ВС. Найти углы треугольника, если дуга ВС равна 1020.
12.
Найдите
периметр параллелограмма, если биссектриса одного из его углов делит сторону
параллелограмма на отрезки 7 см и 14 см.
Укажите номера верных утверждений:
1) Прямая является касательной к окружности, если она имеет одну общую точку с окружностью.
2 )Треугольники, имеющие равные площади, равны.
3) Диагонали ромба равны, взаимно перпендикулярны и являются биссектрисами его углов.
4) Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
5) Если в четырёхугольнике две противоположные стороны равны и параллельны, то он является параллелограммом.
6) Тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.
7) В четырёхугольник можно вписать окружность, если суммы противоположных сторон его равны.

Укажите номера верных утверждений:
1) Точка пересечения медиан является центром описанной около треугольника окружности.
2) Площадь прямоугольного треугольника равна произведению катетов
3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
4) Если 3 стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
5) Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
6) Касательная к окружности перпендикулярна к любому радиусу этой окружности.
7) Около четырёхугольника можно описать окружность, если суммы противоположных углов его равны 1800.

Укажите номера верных утверждений:
1) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
2 ) Площадь ромба равна половине произведения его диагоналей.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
4) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
5) Центральный угол равен половине вписанного угла, опирающегося на ту же дугу.
6) Диагонали квадрата равны, пересекаются под прямым углом и делят углы квадрата пополам.
7) В прямоугольном треугольнике квадрат одной стороны равен сумме квадратов двух других сторон.

-
Угол при основании р/б трапеции равен 470. Тогда остальные углы трапеции будут равны:

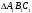
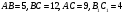
3.
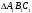
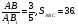
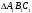
4.
Периметр параллелограмма равен 54см., одна сторона на 1см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 35см., а острый угол – 600.
6. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание.
7. В 
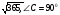
8. Боковые стороны трапеции, описанной около окружности равны 16см и 3см. Найдите среднюю линию трапеции.
9. Угол А четырехугольника АВСD, вписанного в окружность, равен 400. Найдите 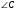
10. АС и BD – диаметры окружности с центром в точке О. 
11. ΔАВС – пр/уг. ∠С=900. АВ=10см, cos∠A=0,4. Найти ВС и АС.
12.Найти площадь прямоугольной трапеции с основаниями 5 см, 9см и углом 600.
13.Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 6см, а боковая сторона 5см.
1.Углы при основании трапеции равны 670 и 540. Тогда остальные углы трапеции будут равны:
2. 
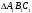
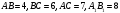
3. 
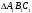
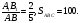
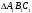
4.
Периметр параллелограмма равен 68 см., одна сторона на 5 см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 19см., а острый угол – 600.
6. Средняя линия трапеции равна 23, а меньшее основание равно 15. Найдите большее основание.
7. В 
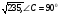
8. Боковые стороны трапеции, описанной около окружности равны 7см и 4см. Найдите среднюю линию трапеции.
9. Угол С четырехугольника АВСD, вписанного в окружность, равен 460. Найдите ∠А этого четырехугольника.
10. АС и BD – диаметры окружности с центром в точке О. 
11. ΔАВС – пр/уг. ∠С=900. АВ=15см, sin∠A=0,6. Найти ВС и АС.
12.Найти площадь равнобедренной трапеции с основаниями 8см и 12см и углом 600.
13. Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 16см, а боковая сторона 10см
1.Углы при основании трапеции равны 710 и 340. Тогда остальные углы трапеции будут равны:
2.
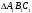

3.

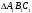
Площадь
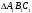
4.
Периметр параллелограмма равен 100см., одна сторона на 8см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 12 см., а острый угол – 600.
6. Средняя линия трапеции равна 13, а большее основание равно 25. Найдите меньшее основание.
7. В 
. Найдите радиус окружности описанной около этого треугольника.
8. Боковые стороны трапеции, описанной около окружности равны 9см и 5см. Найдите среднюю линию трапеции.
9. Угол D четырехугольника АВСD, вписанного в окружность, равен 540. Найдите ∠В этого четырехугольника.
10. АС и BD – диаметры окружности с центром в точке О. . Найдите ∠ ВCО, ∠АОВ.
11. ΔАВС – пр/уг. ∠С=900. АC=10см, tg∠A=2. Найти ВС и АВ.
12. Найти площадь равнобедренной трапеции, если меньшее основание 6см, боковая сторона 4см, острый угол 600.
13. Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 10см, а боковая сторона 13см
Муниципальное бюджетное образовательное учреждение
дополнительного образования детей дом детского творчества
г. Зверева Ростовской области.
Муниципальное бюджетное образовательное учреждение
средняя образовательная школа №1
г.Зверева Ростовской области.
Билеты к устному экзамену по геометрии 8 класс
Работа педагога дополнительного
образования МБОУ ДОД ДДТ,
учителя математики МБОУ СОШ №1
Куца Фёдора Ивановича
г. Зверево
2014 г.
Билет №1.
1. Сформулируйте определение выпуклого многоугольника ( периметр, диагональ). Сформулируйте теорему о сумме углов выпуклого многоугольника.
2.Признаки подобия треугольников. Доказать один признак на выбор обучающегося.
3. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°;
Билет №2.
1.Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
2.Площадь прямоугольника (формулировка и доказательство).
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника
Билет №3
1.Параллелограмм. Определение. Свойства.
2.Теорема об окружности, вписанной в треугольник.
3. Стороны прямоугольника равны 3 см и 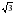
Билет № 4.
1.Четырехугольник. Сумма углов четырёхугольника.
2.Свойство касательной к окружности (формулировка и доказательство).
3. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Билет № 5.
1.Свойства площадей.
2.Теорема о средней линии треугольника (формулировка и доказательство).
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Билет № 6
1.Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
2.Свойство отрезков касательных, проведенных из одной точки (формулировка и доказательство).
3. Подобны ли треугольники ABC и МКР если:
АВ=3 см, ВС=5 см, СА=7 см, МК=4,5 см, КР=7,5 см, РМ = 10,5 см.
Билет № 7
1.Прямоугольник. Свойства прямоугольника. Квадрат.
2.Теорема о вписанном угле (формулировка и доказательство).
3. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите: АВ, если ОВ=4 см, OD=10 см, DC=25 см.
Билет № 8
1.Ромб. Свойства ромба. Квадрат.
2.Свойство биссектрисы угла (формулировка и доказательство).
3. Площади двух подобных треугольников равны 75 и 300. Одна из сторон второго треугольника равна 9 . Найдите сходственную ей сторону первого треугольника.
Билет № 9
1.Квадрат. Свойства квадрата.
2.Свойство серединного перпендикуляра к отрезку (доказательство).
3. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Билет № 10.
1.Подобные треугольники. Определение. Коэффициент подобия.
2.Свойства прямоугольника.
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см. а больший угол равен 135°.
Билет № 11.
1.Медиана треугольника. Определение. Свойство точки пересечения медиан треугольника.
2.Площадь параллелограмма (формулировка и доказательство).
3. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная к большей стороне, равна 2,4 см. Найдите высоту, проведенную к меньшей из данных сторон.
Билет № 12.
1.Пропорциональные отрезки в прямоугольном треугольнике.
2.Теорема об окружности, описанной около треугольника (формулировка и доказательство).
3. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями равен
Билет № 13.
1. Свойство описанного четырехугольника.
2.Свойства ромба (формулировка и доказательство).
3. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1,2,4,5.
Билет № 14.
1. Свойство вписанного четырехугольника.
2. Площадь треугольника (формулировка и доказательство).
3. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Билет № 15.
1. Центральный угол. Вписанный угол.
2.Площадь трапеции (формулировка и доказательство).
3. Найдите площадь равнобедренного треугольника, если его основание равно 10см, а боковая сторона
равна 13см.
Билет № 16.
1.Значения синуса, косинуса и тангенса для углов 30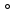
2.Теорема, обратная теореме Пифагора (формулировка и доказательство).
3.Катеты прямоугольного треугольника равны 6 и 8см., гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе.
Билет № 17
1.Описанная окружность. Центр окружности, описанной около треугольника.
2.Свойства параллелограмма (формулировка и доказательство).
3. Найдите площадь трапеции с основаниями AD и BC, если АD=12см, ВС=6см, СD=5см, АС=13см.
Билет № 18
1.Вписанная окружность. Центр окружности, вписанной в треугольник.
2. Теорема Пифагора (формулировка и доказательство). Пифагоровы треугольники.
3. Найдите площадь параллелограмма, если АD =12см, ВD=5см, АВ=13см.
.
Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
-
Определение четырёхугольника. Виды четырёхугольников.
-
Доказать теорему Фалеса.
-
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет №2.
-
Параллелограмм. Определение. Свойства параллелограмма.
-
Доказать теорему о средней линии треугольника.
-
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №3.
-
Квадрат. Определение. Свойства.
-
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
-
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №4.
-
Пропорциональность отрезков в прямоугольном треугольнике.
-
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
-
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
-
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
-
Ромб. Доказательство теоремы о диагоналях ромба.
-
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Билет № 6.
-
Касательная к окружности. Свойства.
-
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
-
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
-
В треугольнике АВС
=90
,cosВ=
, АВ=45
Найдите АС.
Билет № 7.
-
Площадь четырехугольников: параллелограмма, трапеции
-
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
-
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
-
В треугольнике АВС
=90
,ВС=
21, АВ=5. Найдите sinВ.
Билет №8.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Докажите свойство противолежащих сторон и углов параллелограмма.
-
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
-
В треугольнике АВС
=90
,АВ=13, АС=5. Найдите tgА.
Билет №9.
-
Признаки параллельности прямых.
-
Докажите теорему об отношении площадей треугольников.
-
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
-
В треугольнике АВС
=90
,cosВ=
, АВ=25
Найдите АС.
Билет №10.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
-
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
-
В треугольнике АВС
=90
,АВ=15, АС=12. Найдите tgА.
Билет №11.
-
Вписанный и центральный углы, дуга окружности.
-
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
-
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
-
В треугольнике АВС
=90
,АВ=20, АС=12. Найдите sinА
Билет №12.
-
Признаки равенства треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет № 13.
-
Понятие площади многоугольника. Свойства площадей.
-
Докажите теорему Пифагора.
-
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №14.
-
Формулы для вычисления площади параллелограмма.
-
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
-
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №15.
-
Признаки равенства прямоугольных треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
-
Треугольник. Свойства равнобедренного треугольника.
-
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
-
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
Итоговое тестирование по геометрии, 8 класс
2 вариант
1. АВСД – параллелограмм. Угол В равен 70°. Чему равен угол Д?
а) 70° б)110° в) 35°
2. Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его
периметр?
Ответ:___________
3. В параллелограмме МNКР угол N равен 150°. Чему равен угол М?
Ответ:___________
4. В квадрате АВСД диагональ АС = 16 см. Найти длину ВО (O – точка
пересечения диагоналей)
а) 16 см б) 24 см в) 8 см
5. Величина одного из углов прямоугольной трапеции равна 120°. Найдите
острый угол этой трапеции.
а) 30° б) 60 ° в) 45°
6. Один из углов параллелограмма равен 36° . Найдите остальные его углы.
а) 36° , 144° , 144° б) 36° , 36° , 144 ° в) 36° , 72°, 144°
7. Меньшая сторона прямоугольника АВСД равна 18 см. О — точка
пересечения диагоналей. АОД = 120°. Определите длину диагонали.
а) 36 см б) 18 см в) 9 см
8. В четырехугольнике АВСД ВАС =40° , ВСА = САД = 50°, АСД = 70° .
Определите его вид.
а) параллелограмм б) прямоугольник в) трапеция
г) ромб д) произвольный четырехугольник
9. В прямоугольнике АВСД биссектриса угла Д делит сторону ВС на отрезки
ВК и СК. Найдите длину стороны ДС, если ВК = 6 см, а периметр
прямоугольника равен 48 см.
Ответ:_____________
10. Какие из следующих утверждений верны?
1) Если дуга окружности составляет , то центральный угол,
опирающийся на эту дугу, равен .


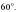
 =90
=90 ,
,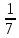 , АС=4
, АС=4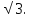 Найдите АВ.
Найдите АВ.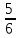 , АС=5
, АС=5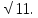 Найдите АВ.
Найдите АВ.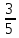 , АВ=5
, АВ=5 Найдите АС.
Найдите АС. 21, АВ=5. Найдите
21, АВ=5. Найдите 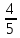 , АВ=25
, АВ=25