Билеты по геометрии для переводного
экзамена в 8классе
(учебник Геометрия 7 – 9 Л.С.Атанасян.)
Каждый билет
содержит 4 вопроса.
В первом вопросе
предлагается сформулировать и доказать теорему.
Во втором вопросе
даётся одно из следующих заданий: дать определение понятия, указать его
основные свойства или привести примеры, описать этапы построения геометрических
фигур.
Третий вопрос —
практический, он содержит задачу первого уровня сложности. Четвёртый вопрос –
практический, он содержит задачу второго уровня сложности.
Билет №1.
1.Параллелограмм.
Свойства параллелограмма. Доказать, что диагонали параллелограмма точкой
пересечения делятся пополам.
2.Определение
синуса острого угла прямоугольного треугольника. Чему равны значения синуса для
углов 300 , 450 , 600 ?
3. В выпуклом
пятиугольнике длины сторон относятся как 5 : 7 : 8 : 9: 10, а его периметр
равен 117 см. Найти наибольшую сторону пятиугольника.
4. В трапеции АВСД
с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы
ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен
600.
Билет №2.
1.Параллелограмм.
Признаки параллелограмма (доказать один из признаков ).
2.Определение
косинуса острого угла прямоугольного треугольника. Чему равны значения косинуса
для углов 300 , 450 , 600 ?
3. В
параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и
образует со стороной ВС угол 300, АВ = 12см. Найти периметр
параллелограмма.
4. Дан
треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника,
вершинами которого являются середины сторон данного треугольника.
Билет №3.
1.Прямоугольник.
Свойства прямоугольника. Доказать, что диагонали прямоугольника равны.
2.Определение
тангенса острого угла прямоугольного треугольника. Чему равны значения тангенса
для углов 300 , 450 , 600 ?
3. В
равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол
А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4. Центральный
угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ.
Найти каждый из этих углов.
Билет №4.
1.Ромб. Свойства
ромба. Доказать, что диагонали ромба взаимно перпендикулярны.
2.Определение
подобных треугольников. Признаки подобия треугольников.
3.В ромбе АВСД
биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в
точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
4. Через концы
хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в
точке С. Найти угол АСВ.
Билет №5.
1.Квадрат.
Свойства квадрата. Доказать, что если в ромбе диагонали равны, то ромб является
квадратом.
2.Центральный
угол. Свойство центрального угла.
3. Высота ВД
треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь
треугольника равна 55см» . Найти длину ВД.
4. В окружность
вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника,
если дуга ВС равна 1020.
Билет №6.
1.Доказать теорему
о вычислении площади параллелограмма.
2. Вписанная
окружность, центр вписанной окружности. Свойство сторон четырёхугольника,
описанного около окружности.
3.В треугольнике
АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти
площадь треугольника.
4. Найти сторону
равностороннего треугольника, если радиус описанной окружности около него
окружности равен 10см.
Билет №7.
1.Доказать теорему
о вычислении площади треугольника. Как вычислить площадь прямоугольного
треугольника?
2. Описанная
окружность, центр описанной окружности. Свойство углов четырёхугольника,
вписанного в окружность.
3. Основания
равнобедренной трапеции равны 10см и 24см, а большее основание 15см. Найти
площадь трапеции.
4. Трапеция ВСНМ с
основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760
, и определите вид трапеции.
Билет №8.
1.Доказать теорему
о вычислении площади трапеции.
2.Вписанный угол.
Следствия, вытекающие из теоремы о вписанном угле.
3. Периметр
треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на
которые биссектриса треугольника делит его третью сторону.
4. Найти площадь
прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен
600.
Билет №9.
1.Доказать теорему
Пифагора.
2.Биссектриса
угла. Свойство биссектрисы угла.
3. Стороны
параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты
параллелограмма.
4. Площадь
прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти
все стороны трапеции, если одно из оснований больше другого на 6см.
Билет №10.
1.Определение
средней линии треугольника. Доказать теорему о средней линии треугольника.
2.Серединный
перпендикуляр. Свойство серединного перпендикуляра к отрезку.
3. АВ и ВС отрезки
касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр
четырёхугольника АВСО, если угол АВС равен 600 .
4. Смежные стороны
параллелограмма равны 32см и 26см., а один из его углов равен 1500 .
Найти площадь параллелограмма.
Билет №11.
1.Доказать, что
высота прямоугольного треугольника , проведённая из вершины прямого угла,
разделяет треугольник на подобные треугольники. Сформулировать утверждения о пропорциональных
отрезках в прямоугольном треугольнике.
2.Сформулирлвать
теорему обратную теореме Пифагора.
3. Хорды АВ и СД
пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2
раза больше длины ВЕ.
4. Одна из
диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 .
Найти сторону ромба.
Билет №12.
1.Касательная к
окружности, точка касания прямой к окружности. Доказать теорему о свойстве
касательной.
2.Дать определение
подобных треугольников. Теорема об отношении площадей подобных треугольников.
3. В
равнобедренном треугольнике основание равно 20см. а угол между боковыми
сторонами равен 1200 . Найти высоту, проведённую к основанию.
4. Площадь
прямоугольного треугольника равна 24см2 , а один из его катетов
равен 6см. Найти длину средней линии, параллельной другому катету.
Билет №13.
1.Доказать, что
отрезки касательных к окружности, проведённые из одной точки, равны и
составляют углы с прямой, проходящей через эту точку и центр окружности.
2.Сформулировать
свойство медиан треугольника пересекающихся в одной точке.
3. Один из углов
ромба на 400 больше другого. Найти углы треугольника ВОС, если О –
точка пересечения диагоналей.
4. Найти площадь
равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона
равна 10см.
Билет №14.
1.Вписанный угол.
Теорема о вписанном угле.
2.Трапеция. Виды
трапеции. Свойства равнобокой трапеции.
3. Найти площадь
равнобедренного треугольника, если его основание равно 30см, боковая сторона
равна 17см.
4. Треугольник АВС
– равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см.Найти
основание АС и высоту АД.
Билет №15.
1.Доказать теорему
об отрезках пересекающихся хорд.
2.Теорема Фалеса.
Деление отрезка на п-равных отрезков.
3. АМ и ВК –
медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его
периметр, если АВ =14см, ВС = 12см, АС = 18см.
Задачи к билетам.1.уровень.
1.В
выпуклом пятиугольнике длины сторон относятся как 5 : 7 : 8 : 9: 10, а его
периметр равен 117 см. Найти наибольшую сторону пятиугольника.
2.В
параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и
образует со стороной ВС угол 300, АВ = 12см. Найти периметр
параллелограмма.
3.В равнобедренной
трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600
, АД = 24см., ВС = 12см. Найти периметр трапеции.
4.В ромбе АВСД
биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в
точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
5.Высота ВД
треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь
треугольника равна 55см» . Найти длину ВД.
6.В треугольнике
АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти
площадь треугольника.
7.Основания равнобедренной
трапеции равны 10см и 24см, а большее основание 15см. Найти площадь трапеции.
8.Периметр
треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на
которые биссектриса треугольника делит его третью сторону.
9.Стороны параллелограмма
равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
10.АВ и ВС отрезки
касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр
четырёхугольника АВСО, если угол АВС равен 600 .
11.Хорды АВ и СД
пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2
раза больше длины ВЕ.
12.В
равнобедренном треугольнике основание равно 20см. а угол между боковыми
сторонами равен 1200 . Найти высоту, проведённую к основанию.
13.Один из углов
ромба на 400 больше другого. Найти углы треугольника ВОС, если О –
точка пересечения диагоналей.
14.Найти площадь
равнобедренного треугольника, если его основание равно 30см, боковая сторона
равна 17см.
15.АМ и ВК –
медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его
периметр, если АВ =14см, ВС = 12см, АС = 18см.
2.уровень.
1.АВСД – ромб,
угол АВС равен 1400 . Найти углы треугольника СОД, где точка О –
пересечение диагоналей.
2.Треугольник АВС
– равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см.Найти
основание АС и высоту АД.
3.Найти площадь
равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона
равна 10см.
4.Площадь
прямоугольного треугольника равна 24см2 , а один из его катетов
равен 6см. Найти длину средней линии, параллельной другому катету.
5.Одна из
диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 .
Найти сторону ромба.
6.Смежные стороны
параллелограмма равны 32см и 26см., а один из его углов равен 1500 .
Найти площадь параллелограмма.
7.Площадь
прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти
все стороны трапеции, если одно из оснований больше другого на 6см.
8.Найти площадь
прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
9.Трапеция ВСНМ с
основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760
, и определите вид трапеции.
10.Найти сторону
равностороннего треугольника, если радиус описанной окружности около него
окружности равен 10см.
11.В окружность
вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника,
если дуга ВС равна 1020.
12.Центральный
угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ.
Найти каждый из этих углов.
13.Через концы
хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в
точке С. Найти угол АСВ.
14.Дан
треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника,
вершинами которого являются середины сторон данного треугольника.
15.В трапеции АВСД
с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы
ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен
600.
Укажите номера верных утверждений:
1) Прямая является касательной к окружности, если она имеет одну общую точку с окружностью.
2 )Треугольники, имеющие равные площади, равны.
3) Диагонали ромба равны, взаимно перпендикулярны и являются биссектрисами его углов.
4) Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
5) Если в четырёхугольнике две противоположные стороны равны и параллельны, то он является параллелограммом.
6) Тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.
7) В четырёхугольник можно вписать окружность, если суммы противоположных сторон его равны.

Укажите номера верных утверждений:
1) Точка пересечения медиан является центром описанной около треугольника окружности.
2) Площадь прямоугольного треугольника равна произведению катетов
3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
4) Если 3 стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
5) Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
6) Касательная к окружности перпендикулярна к любому радиусу этой окружности.
7) Около четырёхугольника можно описать окружность, если суммы противоположных углов его равны 1800.

Укажите номера верных утверждений:
1) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
2 ) Площадь ромба равна половине произведения его диагоналей.
3) Отношение площадей подобных треугольников равно коэффициенту подобия.
4) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
5) Центральный угол равен половине вписанного угла, опирающегося на ту же дугу.
6) Диагонали квадрата равны, пересекаются под прямым углом и делят углы квадрата пополам.
7) В прямоугольном треугольнике квадрат одной стороны равен сумме квадратов двух других сторон.

-
Угол при основании р/б трапеции равен 470. Тогда остальные углы трапеции будут равны:

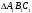
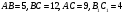
3.
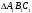
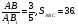
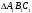
4.
Периметр параллелограмма равен 54см., одна сторона на 1см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 35см., а острый угол – 600.
6. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание.
7. В 
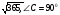
8. Боковые стороны трапеции, описанной около окружности равны 16см и 3см. Найдите среднюю линию трапеции.
9. Угол А четырехугольника АВСD, вписанного в окружность, равен 400. Найдите 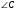
10. АС и BD – диаметры окружности с центром в точке О. 
11. ΔАВС – пр/уг. ∠С=900. АВ=10см, cos∠A=0,4. Найти ВС и АС.
12.Найти площадь прямоугольной трапеции с основаниями 5 см, 9см и углом 600.
13.Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 6см, а боковая сторона 5см.
1.Углы при основании трапеции равны 670 и 540. Тогда остальные углы трапеции будут равны:
2. 
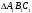
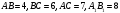
3. 
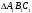
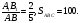
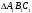
4.
Периметр параллелограмма равен 68 см., одна сторона на 5 см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 19см., а острый угол – 600.
6. Средняя линия трапеции равна 23, а меньшее основание равно 15. Найдите большее основание.
7. В 
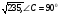
8. Боковые стороны трапеции, описанной около окружности равны 7см и 4см. Найдите среднюю линию трапеции.
9. Угол С четырехугольника АВСD, вписанного в окружность, равен 460. Найдите ∠А этого четырехугольника.
10. АС и BD – диаметры окружности с центром в точке О. 
11. ΔАВС – пр/уг. ∠С=900. АВ=15см, sin∠A=0,6. Найти ВС и АС.
12.Найти площадь равнобедренной трапеции с основаниями 8см и 12см и углом 600.
13. Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 16см, а боковая сторона 10см
1.Углы при основании трапеции равны 710 и 340. Тогда остальные углы трапеции будут равны:
2.
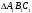

3.

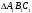
Площадь
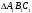
4.
Периметр параллелограмма равен 100см., одна сторона на 8см. больше другой. Найдите меньшую сторону.
5. Найдите меньшую диагональ ромба, стороны которого равны 12 см., а острый угол – 600.
6. Средняя линия трапеции равна 13, а большее основание равно 25. Найдите меньшее основание.
7. В 
. Найдите радиус окружности описанной около этого треугольника.
8. Боковые стороны трапеции, описанной около окружности равны 9см и 5см. Найдите среднюю линию трапеции.
9. Угол D четырехугольника АВСD, вписанного в окружность, равен 540. Найдите ∠В этого четырехугольника.
10. АС и BD – диаметры окружности с центром в точке О. . Найдите ∠ ВCО, ∠АОВ.
11. ΔАВС – пр/уг. ∠С=900. АC=10см, tg∠A=2. Найти ВС и АВ.
12. Найти площадь равнобедренной трапеции, если меньшее основание 6см, боковая сторона 4см, острый угол 600.
13. Найти площадь, радиусы вписанной и описанной окружностей равнобедренного треугольника, если его основание 10см, а боковая сторона 13см
Итоговое тестирование по геометрии, 8 класс
2 вариант
1. АВСД – параллелограмм. Угол В равен 70°. Чему равен угол Д?
а) 70° б)110° в) 35°
2. Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его
периметр?
Ответ:___________
3. В параллелограмме МNКР угол N равен 150°. Чему равен угол М?
Ответ:___________
4. В квадрате АВСД диагональ АС = 16 см. Найти длину ВО (O – точка
пересечения диагоналей)
а) 16 см б) 24 см в) 8 см
5. Величина одного из углов прямоугольной трапеции равна 120°. Найдите
острый угол этой трапеции.
а) 30° б) 60 ° в) 45°
6. Один из углов параллелограмма равен 36° . Найдите остальные его углы.
а) 36° , 144° , 144° б) 36° , 36° , 144 ° в) 36° , 72°, 144°
7. Меньшая сторона прямоугольника АВСД равна 18 см. О — точка
пересечения диагоналей. АОД = 120°. Определите длину диагонали.
а) 36 см б) 18 см в) 9 см
8. В четырехугольнике АВСД ВАС =40° , ВСА = САД = 50°, АСД = 70° .
Определите его вид.
а) параллелограмм б) прямоугольник в) трапеция
г) ромб д) произвольный четырехугольник
9. В прямоугольнике АВСД биссектриса угла Д делит сторону ВС на отрезки
ВК и СК. Найдите длину стороны ДС, если ВК = 6 см, а периметр
прямоугольника равен 48 см.
Ответ:_____________
10. Какие из следующих утверждений верны?
1) Если дуга окружности составляет , то центральный угол,
опирающийся на эту дугу, равен .
Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
-
Определение четырёхугольника. Виды четырёхугольников.
-
Доказать теорему Фалеса.
-
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет №2.
-
Параллелограмм. Определение. Свойства параллелограмма.
-
Доказать теорему о средней линии треугольника.
-
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №3.
-
Квадрат. Определение. Свойства.
-
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
-
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №4.
-
Пропорциональность отрезков в прямоугольном треугольнике.
-
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
-
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
-
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
-
Ромб. Доказательство теоремы о диагоналях ромба.
-
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Билет № 6.
-
Касательная к окружности. Свойства.
-
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
-
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
-
В треугольнике АВС
=90
,cosВ=
, АВ=45
Найдите АС.
Билет № 7.
-
Площадь четырехугольников: параллелограмма, трапеции
-
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
-
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
-
В треугольнике АВС
=90
,ВС=
21, АВ=5. Найдите sinВ.
Билет №8.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Докажите свойство противолежащих сторон и углов параллелограмма.
-
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
-
В треугольнике АВС
=90
,АВ=13, АС=5. Найдите tgА.
Билет №9.
-
Признаки параллельности прямых.
-
Докажите теорему об отношении площадей треугольников.
-
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
-
В треугольнике АВС
=90
,cosВ=
, АВ=25
Найдите АС.
Билет №10.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
-
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
-
В треугольнике АВС
=90
,АВ=15, АС=12. Найдите tgА.
Билет №11.
-
Вписанный и центральный углы, дуга окружности.
-
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
-
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
-
В треугольнике АВС
=90
,АВ=20, АС=12. Найдите sinА
Билет №12.
-
Признаки равенства треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет № 13.
-
Понятие площади многоугольника. Свойства площадей.
-
Докажите теорему Пифагора.
-
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №14.
-
Формулы для вычисления площади параллелограмма.
-
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
-
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №15.
-
Признаки равенства прямоугольных треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
-
Треугольник. Свойства равнобедренного треугольника.
-
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
-
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
Подборка по базе: кроссворд геометрия.docx, ҚМЖ 7В геометрия 31.01.23.docx, 7 ГЕОМЕТриЯ БЖБ 2 Токсан ҮШБҰРЫШТАР.docx, ІІ тоқсан геометрия 7 сынып ТЖБ талдауы .doc, Итоговый тест по физике для 7 класса к учебнику А.В.Перышкина по, 2-тоқсан. 7-сынып геометрия бжб-1-1.docx, Текст учебников-5.pdf, 10 сынып БЖБ Геометрия ЖМБ.docx, 03.03.2023 ж. 7 сынып БЖБ геометрия.docx, СЕТИ И ТЕЛЕКОММУНИКАЦИИ. Учебник и практикум для вузов1.pdf
Переводной экзамен по геометрии за 8 класс
Билеты по геометрии для переводного экзамена в 8 классе
(учебник Геометрия 7 – 9 Л. С. Атанасян.)
Каждый билет содержит 4 вопроса. В первом вопросе предлагается сформулировать и доказать теорему. Во втором вопросе даётся одно из следующих заданий: дать определение понятия, указать его основные свойства или привести примеры, описать этапы построения геометрических фигур. Третий и четвертый вопросы — практические, они содержат задачи за курс 8 класса. Задачи к билетам необходимо решить в тетради. К каждой задаче выполнить рисунок и необходимые пояснения. На экзамен надо принести эту тетрадь с решением и необходимые инструменты: линейка, карандаш, циркуль, ручка. Все билеты надо выучить, уметь ответить у доски и быть готовым к дополнительным вопросам.
Билет №1.
1.Параллелограмм. Свойства параллелограмма. Доказать, что диагонали параллелограмма точкой пересечения делятся пополам.
2.Определение синуса острого угла прямоугольного треугольника. Чему равны значения синуса для углов 300 , 450 , 600?
3. В выпуклом пятиугольнике длины сторон относятся как 5: 7: 8 : 9: 10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
4. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билет №2.
1.Параллелограмм. Признаки параллелограмма (доказать один из признаков).
2.Определение косинуса острого угла прямоугольного треугольника. Чему равны значения косинуса для углов 300 , 450 , 600?
3. В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
4. Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Билет №3.
1.Прямоугольник. Свойства прямоугольника. Доказать, что диагонали прямоугольника равны.
2.Определение тангенса острого угла прямоугольного треугольника. Чему равны значения тангенса для углов 300 , 450 , 600?
3. В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4. Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
Билет №4.
1.Ромб. Свойства ромба. Доказать, что диагонали ромба взаимно перпендикулярны.
2.Определение подобных треугольников. Признаки подобия треугольников.
3.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
4. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
Билет №5.
1.Квадрат. Свойства квадрата. Доказать, что если в ромбе диагонали равны, то ромб является квадратом.
2.Центральный угол. Свойство центрального угла.
3. Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
4. В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
Билет №6.
1.Доказать теорему о вычислении площади параллелограмма.
2. Вписанная окружность, центр вписанной окружности. Свойство сторон четырёхугольника, описанного около окружности.
3.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
4. Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
Билет №7.
1.Доказать теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника?
2. Описанная окружность, центр описанной окружности. Свойство углов четырёхугольника, вписанного в окружность.
3. Основания прямоугольной трапеции равны 10см и 22см, а большая боковая сторона15см. Найти площадь трапеции.
4. Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
Билет №8.
1.Доказать теорему о вычислении площади трапеции.
2.Вписанный угол. Следствия, вытекающие из теоремы о вписанном угле.
3. Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
4. Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
Билет №9.
1.Доказать теорему Пифагора.
2.Биссектриса угла. Свойство биссектрисы угла.
3. Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
4. Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
Билет №10.
1.Определение средней линии треугольника. Доказать теорему о средней линии треугольника.
2.Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку.
3. АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
4. Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
Билет №11.
1.Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники. Сформулировать утверждения о пропорциональных отрезках в прямоугольном треугольнике.
2.Сформулировать теорему обратную теореме Пифагора.
3. Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
4. Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
Билет №12.
1.Касательная к окружности, точка касания прямой к окружности. Доказать теорему о свойстве касательной.
2.Дать определение подобных треугольников. Теорема об отношении площадей подобных треугольников.
3. В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
4. Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
Билет №13.
1.Доказать, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют углы с прямой, проходящей через эту точку и центр окружности.
2.Сформулировать свойство медиан треугольника пересекающихся в одной точке.
3. Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
4. Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
Билет №14.
1.Вписанный угол. Теорема о вписанном угле.
2.Трапеция. Виды трапеции. Свойства равнобокой трапеции.
3. Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
4. Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см,
ДС =4см. Найти основание АС и высоту АД.
Билет №15.
1.Доказать теорему об отрезках пересекающихся хорд.
2.Теорема Фалеса. Деление отрезка на п-равных отрезков.
3. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
4. АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
Задачи к билетам
1.В выпуклом пятиугольнике длины сторон относятся как 5:7:8:9:10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
2.В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
3.В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
5.Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
6.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
7.Основания равнобедренной трапеции равны 10см и 24см, а большее основание 15см. Найти площадь трапеции.
8.Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
9.Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
10.АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
11.Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
12.В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
13.Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
14.Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
15.АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
16. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
Задачи к билетам
1.АВСД – ромб, угол АВС равен 1400 . Найти углы треугольника СОД, где точка О – пересечение диагоналей.
2.Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см. Найти основание АС и высоту АД.
3.Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
4.Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
5.Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
6.Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
7.Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
8.Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
9.Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
10.Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
11.В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
12.Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
13.Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
14.Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
15.В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Геометрия 8 Контрольные работы Атанасян — контрольные работы по геометрии в 8 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Атанасян 8. Поурочные планы
Геометрия 8. Самостоятельные работы
Геометрия 8 класс. Контрольные работы
по учебнику Атанасяна
ГЛАВА V. ЧЕТЫРЕХУГОЛЬНИКИ
К-1. Контрольная работа по геометрии с ответами «Четырехугольники»:
К-1 Уровень 1 (легкий)
К-1 Уровень 2 (средний)
К-1 Уровень 3 (сложный)
ГЛАВА VI. ПЛОЩАДЬ
К-2. Контрольная работа по геометрии с ответами «Площадь»:
К-2 Уровень 1 (легкий)
К-2 Уровень 2 (средний)
К-2 Уровень 3 (сложный)
ГЛАВА VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
К-3. Контрольная работа по геометрии с ответами «Признаки подобия треугольников»:
К-3 Уровень 1 (легкий)
К-3 Уровень 2 (средний)
К-3 Уровень 3 (сложный)
К-4. Контрольная работа по геометрии с ответами «Применение теории подобия к решению задач. Соотношения между сторонами и углами прямоугольного треугольника».
К-4 Уровень 1 (легкий)
К-4 Уровень 2 (средний)
К-4 Уровень 3 (сложный)
ГЛАВА VIII. ОКРУЖНОСТЬ
К-5. Контрольная работа по геометрии с ответами «Окружность».
К-5 Уровень 1 (легкий)
К-5 Уровень 2 (средний)
К-5 Уровень 3 (сложный)
ПОВТОРЕНИЕ за 8 класс
К-6 «Итоговая контрольная работа» за курс 8 класса с ответами.
Контрольная работа № 6
ПОЯСНЕНИЯ
По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.
Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи). Итоговая работа — 2 варианта одного уровня сложности.
Атанасян 8. Поурочные планы
Геометрия 8. Самостоятельные работы
Смотрите также: ВСЕ КОНТРОЛЬНЫЕ РАБОТЫ в 8 классе
Вы смотрели: Геометрия 8 Контрольные работы Атанасян — контрольные работы по геометрии в 8 классе с ответами и решениями по УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».
Другие контрольные работы от других авторов и УМК:
УМК МЕРЗЛЯК: Дидактические материалы 8 класс (7 контрольных по 2 варианта)
УМК АТАНАСЯН: Мельникова. Контрольные работы в 8 классе (5 КР)
УМК АТАНАСЯН: Геометрия 8 класс УЧЕБНИК (задачи из учебника с ответами)
УМК ПОГОРЕЛОВ: Гусев. Дидактические материалы: Контрольные работы
УМК БУТУЗОВ: Дидактические материалы: контрольные работы и матем. диктанты
К любому УМК: Гаврилова, КИМ: контрольные работы. 8 класс
Контрольные работы по геометрии в 8 классе с ответами и решениями (4 варианта) к учебнику Л.С. Атанасяна и др. Дидактические материалы для учителей, школьников и родителей. В учебных целях использованы цитаты из пособия «Геометрия 8 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др.» (авт. Н.Б. Мельникова). При постоянном использовании контрольных работ по геометрии в 8 классе рекомендуем купить книгу: Наталия Мельникова: Геометрия. 8 класс. Контрольные работы к учебнику Л.С. Атанасяна и др. ФГОС. Ответы Геометрия 8 Атанасян (Мельникова) адресованы родителям.
Контрольная работа № 1. Четырехугольники (свойства и признаки параллелограмма, прямоугольника, ромба, квадрата; трапеция; осевая и центральная симметрии).
К-1. Вариант 0 К-1. Вариант 1 К-1. Вариант 2 К-1. Вариант 3 К-1. Вариант 4
Контрольная работа № 2. Теорема Пифагора. Площадь (теорема Пифагора; площадь параллелограмма, треугольника, трапеции)
К-2. Вариант 0 К-2. Вариант 1 К-2. Вариант 2 К-2. Вариант 3 К-2. Вариант 4
Контрольная работа № 3. Подобные треугольники (признаки подобия треугольников; средняя линия треугольника; синус, косинус, тангенс острого угла прямоугольного треугольника).
К-3. Вариант 0 К-3. Вариант 1 К-3. Вариант 2 К-3. Вариант 3 К-3. Вариант 4
Контрольная работа № 4. Окружность (касательная к окружности; центральные и вписанные углы; вписанная и описанная окружности).
К-4. Вариант 0 К-4. Вариант 1 К-4. Вариант 2 К-4. Вариант 3 К-4. Вариант 4
Контрольная работа № 5. Итоговая контрольная работа за курс 8 класса (площадь параллелограмма, треугольника, трапеции; синус, косинус, тангенс острого угла прямоугольного треугольника; средняя линия треугольника; касательная к окружности; признаки подобия треугольников).
К-5. Вариант 0 К-5. Вариант 1 К-5. Вариант 2 К-5. Вариант 3 К-5. Вариант 4
Каждая контрольная работа направлена на проверку усвоения материала главы учебника. Указанные ниже проверяемые элементы знаний отражают только тот материал, который изучался в данной теме. При этом, естественно, задачи тематической контрольной работы могут проверять также и усвоение сведений, изучавшихся в предыдущих темах.
Каждая работа состоит из трех частей, соответствующих форме предлагаемых заданий.
В Часть 1 включаются задания с выбором ответа. Учащимся нужно выбрать из предложенных вариантов либо верное утверждение, либо нужный рисунок. При этом верных ответов может быть несколько, и учащимся необходимо записать номера ответов, которые, по их мнению, верны. Заметим, что, вообще говоря, в заданиях с выбором ответа применяются два подхода. При первом подходе среди предлагаемых вариантов ответа имеется только один правильный. При втором — верных ответов может быть несколько, и результатом решения задачи является не один номер, а все номера верных ответов. При этом задание считается выполненным верно, если указаны номера всех верных ответов. (Иногда такое задание оценивается несколькими баллами и возможны варианты оценивания в зависимости от числа правильно выбранных ответов.)
В Часть 2 входят вычислительные задачи, которые необходимо решить и записать число, которое получилось в результате вычислений.
При выполнении частей 1 и 2 контрольной работы учащиеся не записывают ни обоснования, ни вычисления, нужные для решения задач. Все записи или рисунки учащиеся, в случае необходимости, могут делать в черновике. Черновик не сдается учителю и не влияет на оценку за выполнение работы.
В Части 3 имеются и задачи на доказательство, и задачи на вычисление геометрических величин. Решение этих задач должно быть оформлено письменно, как в традиционной контрольной работе. Следует иметь в виду, что при записи решения вычислительных задач, так же как и при решении задач на доказательство, необходимо приводить обоснования с использованием изученных геометрических фактов.
Последняя задача в каждом варианте, отмеченная звездочкой, предназначена для наиболее подготовленных учащихся, успевающих достаточно быстро выполнить все предыдущие задания. В зависимости от уровня подготовленности класса эту задачу можно считать дополнительной, и оценивать ее решение отдельно.
Перед проведением первой контрольной работы необходимо подробно проинструктировать учащихся о том, как они должны оформить решение задач. Полезно привести пример, показывающий, как должны выглядеть ответы на задачи частей 1 и 2. Следует напомнить эти инструкции и при проведении каждой последующей контрольной работы.
Дифференцированный подход к учащимся осуществляется за счет того, что в работах представлены задания разного уровня, которые, как правило, расположены по мере возрастания уровня сложности. Номера заданий обязательного уровня, посильных для менее подготовленных учащихся, отмечены кружком. Такие задания представлены во всех трех частях работы.
Следует заметить, что при традиционном письменном оформлении решения задач, предлагаемое в контрольных работах количество задач было бы нереально решить за один урок. Однако, нужно иметь в виду, что задания с выбором ответа и с кратким ответом не требуют времени на оформление решения и очень часто ответы на них могут быть получены устно. Поэтому основные затраты времени будут связаны с решением задач части 3.
Вы смотрели: Геометрия 8 Атанасян (Мельникова): Контрольные работы по геометрии в 8 классе с ответами и решениями (4 варианта) к учебнику Л.С. Атанасяна и др. В учебных целях использованы цитаты из пособия «Геометрия 8 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др.» (авт. Н.Б. Мельникова). Дидактические материалы для учителей, школьников и родителей.
Смотрите также Решебник к учебнику «Геометрия 8 класс Атанасян» (решения и ответы):
ГДЗ Геометрия 8 Атанасян


 =90
=90 ,
,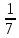 , АС=4
, АС=4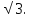 Найдите АВ.
Найдите АВ.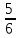 , АС=5
, АС=5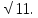 Найдите АВ.
Найдите АВ.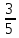 , АВ=5
, АВ=5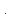 Найдите АС.
Найдите АС.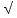 21, АВ=5. Найдите
21, АВ=5. Найдите 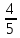 , АВ=25
, АВ=25