Переводной экзамен 10 класс математика в форме егэ

Переводной экзамен за курс 10 класса

по предмету «математика»

вариант 1

1.  Найдите зна­че­ние
вы­ра­же­ния 

2.  Найдите зна­че­ние
вы­ра­же­ния 

3.  В ма­га­зи­не
вся ме­бель продаётся в разо­бран­ном виде. По­ку­па­тель может за­ка­зать сбор­ку
ме­бе­ли на дому, сто­и­мость ко­то­рой со­став­ля­ет 5 % от сто­и­мо­сти куп­лен­ной
мебели. Шкаф стоит 4200 рублей. Во сколь­ко руб­лей обойдётся по­куп­ка этого
шкафа вме­сте со сборкой?

4.  Площадь тре­уголь­ни­ка
со сто­ро­на­ми   и  можно
найти по фор­му­ле Ге­ро­на ,
где .
Най­ди­те пло­щадь тре­уголь­ни­ка со сто­ро­на­ми 7, 15, 20.

5.  Найдите зна­че­ние
вы­ра­же­ния: 

6.  В об­мен­ном
пунк­те 1 грив­на стоит 3 рубля 70 копеек. От­ды­ха­ю­щие об­ме­ня­ли
рубли на грив­ны и ку­пи­ли 3 кг по­ми­до­ров по цене 4 грив­ны за
1 кг. Во сколь­ко руб­лей обо­шлась им эта покупка? Ответ округ­ли­те до
це­ло­го числа.

 7. Найдите корень
уравнения: .

8. Дачный уча­сток имеет
форму прямоугольника, сто­ро­ны ко­то­ро­го равны 50м и 30м. Дом, рас­по­ло­жен­ный
на участке, на плане также имеет форму прямоугольника, сто­ро­ны ко­то­ро­го
равны 8 м и 10 м. Най­ди­те пло­щадь остав­шей­ся части участка, не за­ня­той
домом. Ответ дайте в квад­рат­ных метрах.

9.  Установите
соответствие между величинами и их возможными значениями:

к
каждому элементу первого столбца подберите соответствующий элемент

из
второго столбца.

ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А)площадь
территории России                                  1)364 кв. м

Б) площадь
поверхности тумбочки                           2)0,2 кв. м

В) площадь
почтовой марки                                      3) 17,1 млн. кв. км

Г) площадь
баскетбольной площадки                      4) 6,8 кв. см

В таблице
под каждой буквой укажите соответствующий номер.

10.  На семинар
приехали 3 учёных из Норвегии, 3 из России и 4 из Испании. Каждый учёный
подготовил один доклад. Порядок докладов определяется случайным образом.
Найдите вероятность того, что восьмым окажется доклад учёного из России.

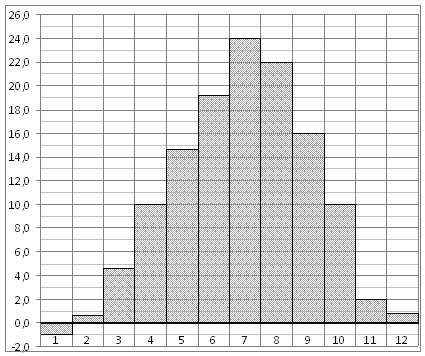
11.  На рисунке жирными
точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по
19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали —
температура в градусах Цельсия. Для наглядности жирные точки соединены линией.
Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах
Цельсия.

  12.  Путешественник
из Моск­вы хочет по­се­тить четыре го­ро­да Золотого коль­ца России: Владимир,
Ярославль, Суз­даль и Ро­стов Великий. Ту­ра­гент­ство предлагает марш­ру­ты с
по­се­ще­ни­ем некоторых го­ро­дов Золотого кольца. Све­де­ния о сто­и­мо­сти
билетов и марш­ру­тах представлены в таблице.

 Какие марш­ру­ты должен вы­брать путешественник, чтобы по­бы­вать
во всех четырёх го­ро­дах и за­тра­тить менее 5000 рублей?

В от­ве­те укажите какой-нибудь
один набор но­ме­ров маршрутов без пробелов, за­пя­тых и дру­гих дополнительных
символов.

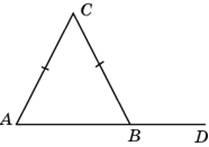
13.  На прямой АВ
взята точка М. луч MD – биссектриса угла СМВ. Известно, что угол DMC равен 55°.
Найдите величину угла СМА. Ответ дайте в градусах.

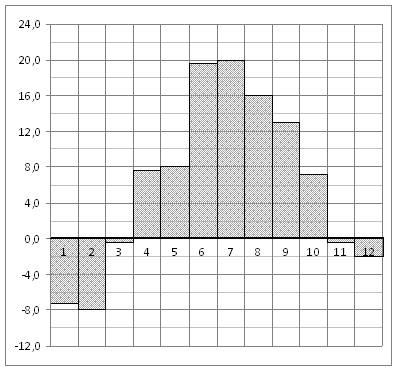
14. На рисунке
изображена сравнительная диаграмма  ежемесячной рождаемости мальчиков и девочек
в городском роддоме в течение 2013 года. По горизонтали указывается  месяцы, а
по вертикали  — количество родившихся.

Пользуясь       диаграммой,
поставьте         в соответствие          каждому         из указанных периодов
времени характеристику рождаемости в этот период.

ПЕРИОДЫ
ВРЕМЕНИ                ХАРАКТЕРИЧТИКИ РОЖДАЕМОСТИ

А) 1-й
квартал года           1) в каждом месяце мальчиков рождалось  больше, чем
девочек                                                  

Б) 2-ой
квартал года          2) рождаемость
девочек была наименьшей за весь год

В) 3-ий
квартал года 3) в каждом месяце девочек рождалось больше, чем              
мальчиков

Г) 4-й
квартал года             4) рождаемость девочек почти не изменялась в течение
этого периода

В таблице под
каждой буквой укажите соответствующий номер

15.  В
выпуклом четырехугольнике ABCD
известно, что AB=BC,
AD=СD,
угол В равен 77°, угол D равен 141°.
Найдите угол А. ответ дайте в градусах.

16. Катеты прямоугольного треугольника равны 6
и 8. Найдите наибольшую среднюю линию треугольника

 17. На прямой
отмечены числа m и n.

Каждому из четырех
чисел в левом столбце соответствует отрезок, которому оно принадлежит. Установите
соответствие между числами левого столбца и отрезками из правого столбца.

Впишите
в приведенную таблицу под каждой буквой соответствующую цифру.

18. Какие из
приведённых ниже утвер­жде­ний рав­но­силь­ны утвер­жде­нию «Если Вы ― слон,
значит, Вы ни­че­го не забываете»?

       (1) Если Вы ни­че­го не забываете, значит, Вы ― слон.

(2) Если Вы ― не слон,
значит, Вы все забываете.

(3) Если Вы ― не слон,
значит, Вы что-то забываете.

(4) Если Вы что-то
забываете, значит, Вы ― не слон.

 В от­ве­те ука­жи­те но­ме­ра вы­бран­ных Вами утвер­жде­ний
без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных символов.

19.  Приведите при­мер
трёхзначного числа, сумма цифр ко­то­ро­го равна 20, а сумма квад­ра­тов цифр
де­лит­ся на 3, но не де­лит­ся на 9.

20.  Саша пригласил Петю в гости, сказав, что живет в седьмом
подъезде в квартире №333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил,
что дом девятиэтажный. На каком этаже живет Саша?(На каждом этаже число квартир
одинаково, номера квартир в доме начинаются с единицы.)

Переводной экзамен за курс 10 класса

по предмету «математика»

вариант 2

1.  Найдите зна­че­ние вы­ра­же­ния .

2.  Найдите значение выражения 

3.  В сентябре 1 кг слив стоил 60 рублей. В октябре сливы
подорожали на 25%. Сколько рублей стоил 1 кг слив после подорожания в
октябре?

 4.  Площадь тре­уголь­ни­ка со сто­ро­на­ми    можно найти по фор­му­ле Ге­ро­на ,
где .
Най­ди­те пло­щадь тре­уголь­ни­ка со сто­ро­на­ми   .

5.  Найдите зна­че­ние вы­ра­же­ния 

6.  Стоимость проездного билета на месяц составляет 1150 рублей, а
стоимость билета на одну поездку — 40 рублей. Аня купила проездной и сделала за
месяц 37 поездок. На сколько рублей больше она бы потратила, если бы каждый раз
покупала билет на одну поездку?

7.  Найдите корень уравнения: .

8. 
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров.
Хозяин планирует обнести его забором и разделить таким же забором на две части,
одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.

9.  Установите со­от­вет­ствие между ве­ли­чи­на­ми и их воз­мож­ны­ми
значениями: к каж­до­му эле­мен­ту пер­во­го столб­ца под­бе­ри­те со­от­вет­ству­ю­щий
эле­мент из вто­ро­го столбца.

В таб­ли­це под каж­дой
буквой, со­от­вет­ству­ю­щей величине, ука­жи­те номер её воз­мож­но­го значения.

10.  Конкурс
исполнителей проводится в 5 дней. Всего заявлено 60 выступлений по одному от
каждой страны, участвующей в конкурсе. Исполнитель из России участвует в
конкурсе. Все выступления поровну распределены между конкурсными днями. Порядок
выступлений определяется жеребьёвкой. Какова вероятность, что выступление
исполнителя из России состоится в третий день конкурса?

11.  На диаграмме
показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря
2009 года. По горизонтали указывается номер часа, по вертикали — количество
посетителей сайта за данный час. Определите по диаграмме, за какой час в данный
день на сайте РИА Новости побывало максимальное количество посетителей.

12.  Турист, при­быв­ший в Санкт-Петербург, хочет по­се­тить че­ты­ре
музея: Эрмитаж, Рус­ский музей, Пет­ро­пав­лов­скую кре­пость и Иса­а­ки­ев­ский
собор. Экс­кур­си­он­ные кассы пред­ла­га­ют марш­ру­ты с по­се­ще­ни­ем од­но­го
или не­сколь­ких объектов. Све­де­ния о сто­и­мо­сти би­ле­тов и со­ста­ве марш­ру­тов
пред­став­ле­ны в таблице.

Какие
марш­ру­ты дол­жен вы­брать турист, чтобы по­се­тить все че­ты­ре музея и за­тра­тить
на все би­ле­ты наи­мень­шую сумму? В от­ве­те ука­жи­те ровно один набор но­ме­ров
марш­ру­тов без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных символов.

Номера указывайте в порядке
возрастания.

13. На
окружности радиуса 3 взята точка С. АВ – диаметр окружности, АС=. Найдите
ВС.

14.  На рисунке точками показано
атмосферное давление в некотором городе на протяжении трёх суток с 4 по 6
апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00, в 6:00, в
12:00 и в 18:00. По горизонтали указываются время суток и дата, по вертикали —
давление в миллиметрах ртутного столба. Для наглядности точки соединены
линиями.

Пользуясь
рисунком, поставьте в соответствие каждому из указанных периодов времени
характеристику атмосферного давления в этом городе в течение этого периода.

Запишите в ответ
цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

15. В
треугольнике АВС известно, что АВ=ВС=25, АС=14. Найдите длину медианы ВМ.

16.  Стороны параллелограмма равны 8 и
16. Высота, опущенная на меньшую сторону, равна 12. Найдите длину высоты,
опущенной на большую сторону параллелограмма.

17. На координатной прямой отмечены число m и
точки A, B, C и D.

В каждой точке соответствует одно из чисел в правом столбце.
Установите соответствие между указанными точками и числами.

В таблице для каждой точки укажите номер соответвующего числа.

18.  В офисе фирмы ком­пью­те­ры ра­бо­та­ют толь­ко от се­те­во­го
электропитания. Если ком­пью­те­ры работают, то элек­три­че­ство в офисе есть.
Вы­бе­ри­те утверждения, ко­то­рые не­по­сред­ствен­но сле­ду­ют из этих
данных.

1) Если
в офисе нет электричества, то ком­пью­те­ры не работают.

2) Если
в офисе есть электричество, то ком­пью­те­ры работают.

3) Если
ком­пью­те­ры не работают, зна­чит в офисе нет электричества.

4) Если
в офисе нет электричества, то не ра­бо­та­ет ком­пью­тер директора.

 В от­ве­те ука­жи­те но­ме­ра
вы­бран­ных утвер­жде­ний без пробелов, за­пя­тых и дру­гих до­пол­ни­тель­ных
символов.

19.  Найдите трех­знач­ное на­ту­раль­ное число, боль­шее 500, ко­то­рое
при де­ле­нии на 4, на 5 и на 6 дает в остат­ке 2, и в за­пи­си ко­то­ро­го
есть толь­ко две раз­лич­ные цифры. В от­ве­те ука­жи­те какое-нибудь одно
такое число.

20. 
Улитка за день залезает вверх по дереву на 2 м, а за ночь ползает на 1 м.
высота дерева 9 м. за сколько дней улитка доползет до вершины дерева?

Инструкция по выполнению работы

На выполнение переводной работы по математике 10 класс дается 90 минут. Работа состоит из 12 заданий. Задания 1–10 базового уровня сложности с кратким ответом по материалу курса математики. Задания 1–10 считаются выполненными, если учащийся дал верный ответ в виде целого числа или конечной десятичной дроби. Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Желаем успеха!

Вариант 1

Ответом на задания 1-10 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Единицы измерений писать не нужно.

1. Цена на элек­три­че­ский чай­ник была по­вы­ше­на на 21% и со­ста­ви­ла 3025 руб­лей. Сколь­ко руб­лей стоил чай­ник до по­вы­ше­ния цены?

2. На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки меди в 10 стра­нах мира (в ты­ся­чах тонн) за 2006 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке меди за­ни­ма­ли США, де­ся­тое место — Ка­зах­стан. Какое место за­ни­ма­ла Ин­до­не­зия?

3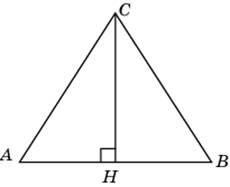. Най­ди­те , если и .

4. В тре­уголь­ни­ке , , вы­со­та равна . Най­ди­те угол . Ответ дайте в гра­ду­сах.

5. Най­ди­те ко­рень урав­не­ния:

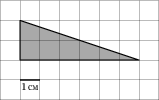
6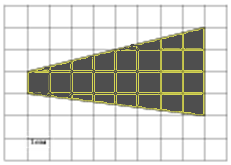. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

7. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 10 чер­ных, 2 жел­тых и 8 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет зе­ле­ное такси.

8. Най­ди­те ко­рень урав­не­ния.

9. Решите неравенство 25. В ответе укажите наибольшее целое решение.

10.Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 60 км, од­но­вре­мен­но вы­еха­ли ав­то­мо­би­лист и ве­ло­си­пе­дист. Из­вест­но, что в час ав­то­мо­би­лист про­ез­жа­ет на 110 км боль­ше, чем ве­ло­си­пе­дист. Опре­де­ли­те ско­рость ве­ло­си­пе­ди­ста, если из­вест­но, что он при­был в пункт В на 5,5 часов позже ав­то­мо­би­ли­ста. Ответ дайте в км/ч.

Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ.

11. а) Решите уравнение = cos (

б) Найдите все корни этого уравнения, принадлежащие отрезку

12. Решить систему неравенств

Инструкция по выполнению работы

На выполнение переводной работы по математике 10 класс дается 90 минут. Работа состоит из 12 заданий. Задания 1–10 базового уровня сложности с кратким ответом по материалу курса математики. Задания 1–10 считаются выполненными, если учащийся дал верный ответ в виде целого числа или конечной десятичной дроби. Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Желаем успеха!

Вариант 2

Ответом на задания 1-10 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Единицы измерений писать не нужно.

1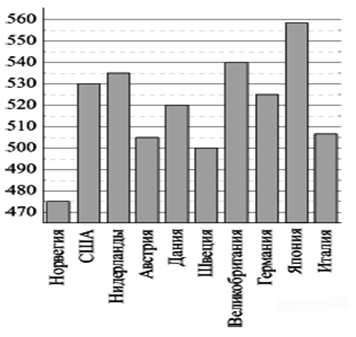. Опто­вая цена учеб­ни­ка 220 руб­лей. Роз­нич­ная цена на 20% выше опто­вой. Какое наи­боль­шее число таких учеб­ни­ков можно ку­пить по роз­нич­ной цене на 9000 руб­лей?

2. На диа­грам­ме по­ка­зан сред­ний балл участ­ни­ков 10 стран в те­сти­ро­ва­нии уча­щих­ся 4-го клас­са, по ма­те­ма­ти­ке в 2007 году (по 1000-балль­ной шкале). По дан­ным диа­грам­мы най­ди­те число стран, в ко­то­рых сред­ний балл ниже, чем в Ни­дер­лан­дах.

3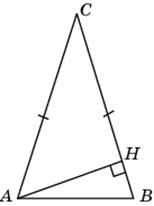. Най­ди­те , если и

4. В тре­уголь­ни­ке ABC , вы­со­та AH равна 33. Най­ди­те угол C. Ответ дайте в гра­ду­сах.

5. Най­ди­те ко­рень урав­не­ния:

6. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

7. На та­рел­ке 16 пи­рож­ков: 7 с рыбой, 5 с ва­ре­ньем и 4 с виш­ней. Юля на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что он ока­жет­ся с виш­ней.

8. Най­ди­те ко­рень урав­не­ния.

9. Решите неравенство 81. В ответе укажите наибольшее целое решение.

10. Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 50 км, од­но­вре­мен­но вы­еха­ли ав­то­мо­би­лист и ве­ло­си­пе­дист. Из­вест­но, что в час ав­то­мо­би­лист про­ез­жа­ет на 45 км боль­ше, чем ве­ло­си­пе­дист. Опре­де­ли­те ско­рость ве­ло­си­пе­ди­ста, если из­вест­но, что он при­был в пункт В на 2 часа 30 минут позже ав­то­мо­би­ли­ста. Ответ дайте в км/ч.

Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ.

11. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

12. Решить систему неравенств

Инструкция по выполнению работы

На выполнение переводной работы по математике 10 класс дается 90 минут. Работа состоит из 12 заданий. Задания 1–10 базового уровня сложности с кратким ответом по материалу курса математики. Задания 1–10 считаются выполненными, если учащийся дал верный ответ в виде целого числа или конечной десятичной дроби. Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Желаем успеха!

Вариант 3

Ответом на задания 1-10 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Единицы измерений писать не нужно.

1. Налог на до­хо­ды со­став­ля­ет от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 11500 руб­лей. Сколь­ко руб­лей он по­лу­чит после вы­че­та на­ло­га на до­хо­ды?

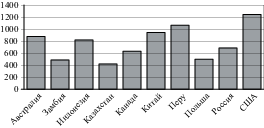
2. На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки цинка (в ты­ся­чах тонн) в 11 стра­нах мира за 2009 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке цинка за­ни­ма­ло Ма­рок­ко, один­на­дца­тое место — Бол­га­рия. Какое место за­ни­ма­ла Гре­ция?

3. Най­ди­те , еслии .

4. В тре­уголь­ни­ке ABC , , вы­со­та CH равна . Най­ди­те угол C. Ответ дайте в гра­ду­сах.

5. Най­ди­те ко­рень урав­не­ния:

6. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

7. Ро­ди­тель­ский ко­ми­тет за­ку­пил 40 паз­лов для по­дар­ков детям на окон­ча­ние учеб­но­го года, из них 14 с ви­да­ми при­ро­ды и 26 с ис­то­ри­че­ски­ми до­сто­при­ме­ча­тель­но­стя­ми. По­дар­ки рас­пре­де­ля­ют­ся слу­чай­ным об­ра­зом. Най­ди­те ве­ро­ят­ность того, что Пете до­ста­нет­ся пазл с видом при­ро­ды.

8 . Най­ди­те ко­рень урав­не­ния.

9 Решите неравенство 64. В ответе укажите наименьшее целое решение.

10. Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 40 км, од­но­вре­мен­но вы­еха­ли ав­то­мо­би­лист и ве­ло­си­пе­дист. Из­вест­но, что в час ав­то­мо­би­лист про­ез­жа­ет на 70 км боль­ше, чем ве­ло­си­пе­дист. Опре­де­ли­те ско­рость ве­ло­си­пе­ди­ста, если из­вест­но, что он при­был в пункт В на 3,5 часа позже ав­то­мо­би­ли­ста. Ответ дайте в км/ч.

Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ.

11. а) Решите уравнение = cos (

б) Найдите все корни этого уравнения, принадлежащие отрезку

12. Решить систему неравенств

Инструкция по выполнению работы

На выполнение переводной работы по математике 10 класс дается 90 минут. Работа состоит из 12 заданий. Задания 1–10 базового уровня сложности с кратким ответом по материалу курса математики. Задания 1–10 считаются выполненными, если учащийся дал верный ответ в виде целого числа или конечной десятичной дроби. Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ. Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Желаем успеха!

Вариант 4

Ответом на задания 1-10 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Единицы измерений писать не нужно.

1. В школе 92 уче­ни­ка изу­ча­ло фран­цуз­ский язык, что со­став­ля­ет 23% от числа всех уче­ни­ков. Сколь­ко уче­ни­ков учит­ся в школе?

2. На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки цинка (в ты­ся­чах тонн) в 11 стра­нах мира за 2009 год. Среди пред­став­лен­ных стран пер­вое место по вы­плав­ке цинка за­ни­ма­ли США, один­на­дца­тое место — Иран. Какое место за­ни­ма­ла Ка­на­да?

3. Най­ди­те , если и .

4. В тре­уголь­ни­ке ABC , , вы­со­та CH равна . Най­ди­те угол C. Ответ дайте в гра­ду­сах.

5. Най­ди­те ко­рень урав­не­ния:

6. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

7. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 3 белых, 11 синих и 6 серых. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­це. Най­ди­те ве­ро­ят­ность того, что к ней при­е­дет белое такси.

8 . Най­ди­те ко­рень урав­не­ния.

9 Решите неравенство 27. В ответе укажите наименьшее целое решение.

10. Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 30 км, од­но­вре­мен­но вы­еха­ли ав­то­мо­би­лист и ве­ло­си­пе­дист. Из­вест­но, что в час ав­то­мо­би­лист про­ез­жа­ет на 65 км боль­ше, чем ве­ло­си­пе­дист. Опре­де­ли­те ско­рость ве­ло­си­пе­ди­ста, если из­вест­но, что он при­был в пункт В на 2 часа 36 минут позже ав­то­мо­би­ли­ста. Ответ дайте в км/ч.

Задание 11-12 – повышенного уровня сложности. При их выполнении надо записать полное решение и записать ответ.

11. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

12. Решить систему неравенств

«Утверждаю»

Директор Школы___________Р.Р. Богапов

Приказ № _____от_____2017 г

Материал

Для проведения итогового контроля по математике в 10 класс

Рассмотрен и согласован на заседании МО учителей математик
 

Пояснительная записка

к экзаменационному материалу по

математике

для учащихся 10 класса.

 Цель экзамена: проверка уровня предметной компетентности учащихся 10 класса

по математике за курс 10 класса в рамках проведения промежуточной аттестации.

Требования, предъявляемые к знаниям и умениям учащихся на экзамене:

выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма,;

применять понятия, связанные с делимостью целых чисел, при решении математических задач;

проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

решать уравнения, неравенства, используя свойства функций и их графические представления;

решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения и неравенства;

доказывать несложные неравенства;

решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;

решать задачи по теории вероятности, используя теоремы о вероятности события;

интерпретировать данные диаграммы;

вычислять площадь и периметр геометрических фигур;

находит неизвестные элементы стереометрических фигур по данным задачи, используя теоремы и свойства стереометрии.

Форма экзамена: письменно, по контрольно-измерительным материалам.

Количество вариантов 2.

Структура экзаменационной работы:

Каждый вариант экзаменационной работы содержит 2 части.

1 часть содержит 9 заданий по алгебре и началам анализа и 5 задания по геометрии базового уровня сложности. Эти задания направлены на проверку усвоения основных свойств, понятий, владения основными алгоритмами, умения решать простейшие уравнения.

2 часть содержит 4 задания по алгебре и началам анализа и 1 задание по геометрии повышенного и высокого уровня сложности. При выполнении этих заданий проверяется умение учащихся применять знания в несколько измененной ситуации. В заданиях второй части учащиеся должны записать решения и обосновать их.

Содержание тестов отражает следующие разделы

— тригонометрические функции;

— корни степени n;

— логарифмы;

— показательные и логарифмические уравнения и неравенства;

— тригонометрические уравнения и неравенства;

— иррациональные уравнения;

— преобразование тригонометрических выражений;

— геометрия, стереометрия.

Документы, определяющие содержание экзаменационной работы:

1. Алгебра и начала математического анализа. Сборник рабочих программ. 10 – 11 классы: пособие для учителей общеобразовательных организаций . Базовый и углубленный уровни / [сост. Т. А. Бурмистрова]. -М.: Просвещение, 2016. — 128 с.

Программа реализуется на основе учебника: Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений. Составители: М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2015.

2. Сборник рабочих программ. Геометрия. 10—11 классы. базовый и углубл. уровни: учеб. пособие для учителей общеобразоват. организаций / [сост. Т. А. Бурмистрова]. — М. : Просвещение, 2016. — 143с.

Программа реализуется на основе учебника: Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и профил. уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.В.Кадомцев и др.]. — 23-е изд. — М.: Просвещение, 2014 — 255 с.

Используемые материалы:

3. ЕГЭ-2017. Математика. Базовый уровень: типовые экзаменационные варианты: 30 вариантов, по редакцией И. В. Ященко: изд. «Национальное образование» , 2017. — 192 с.

4. ЕГЭ-2017. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов, по редакцией И. В. Ященко: изд. «Национальное образование» , 2017. — 256 с.

Время выполнения экзаменационной работы 3 урока

Критерии оценивания работы:

Ключи к тестам:

Вариант №1.

Вариант № 2.

Итоговая переводная контрольная работа (тестирование) по математике

ученика(цы) 10 класса _________________________________________________

Бланк ответов №1

Вариант______

Дата проведения

Ответы на задания 1 части:

Бланк ответов №2

Ответы на задания 2 части:

По теме: методические разработки, презентации и конспекты

Учитель математики Денисова Елена Валентиновна

г. Томск, МАОУ СОШ №35

Тест по математике для 10 класса «Промежуточная аттестация по математике

за курс 10 класса в форме ЕГЭ»

Данный материал предназначен для проведения промежуточной аттестации по

математике за курс 10 класса в общеобразовательных классах. Составлен на основе

государственного стандарта среднего (полного) общего образования по математике,

программ общеобразовательных учреждений. Алгебра и начала анализа. 10—11 классы и

Геометрия 10—11 классы – (М.Просвещение, 2009. Составитель Т. А. Бурмистрова),

учебников «Алгебра и начала анализа 10-11», «Мнемозина»— 2010 г. Авторы: А.Г.

Мордкович и «Геометрия 10—11», М. Просвещение 2009 г. Авторы: А.В.Погорелов.

СОДЕРЖАНИЕ И СТРУКТУРА

КОНТРОЛЬНЫХ ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ

Цель использования материалов промежуточной аттестации:

проверка знаний учащихся 10 класса по математике в соответствии с требованиями,

заложенными в образовательном стандарте.

Задачи:

1) провести диагностику усвоения учащимися материала 10 класса;

2) сформировать компетентности, необходимые для успешной сдачи экзамена по

математике в 11 классе.

Предлагаемая работа содержит материалы для подготовки к новой форме проверки

знаний и умений школьников через проведение итоговой аттестации в 10 классе в форме

ЕГЭ.

Контрольно—измерительные материалы содержат 11 заданий. Они состоят из двух

частей: В и С. Задания В1 – В7 направлены на проверку достижения уровня

обязательной подготовки. С помощью этих заданий проверяется знание и понимание

важных элементов содержания (понятий, их свойств и др.), владение основными

алгоритмами. При помощи заданий В

8

, С1 проверяется умение применять знания к

решению математических задач, не сводящихся к прямому применению алгоритма,

приёмов решения задач, а также применить знания в простейших практических ситуациях.

При выполнении заданий части В

8

и задания С

1

учащиеся также должны

продемонстрировать определенную системность знаний и широту представлений, умение

переходить с одного математического языка на другой, узнавать стандартные задачи в

разнообразных формулировках. Задания С

2

, С

3

направлены на дифференцированную

проверку повышенного уровня владения материалом. Это задания высокого уровня

сложности, требующие развёрнутого ответа (с полной записью решения). При

выполнении этих заданий учащиеся должны продемонстрировать умение математически

грамотно записать решение, приводя при этом необходимые обоснования и пояснения.

Задания первой части ученик выполняет на черновике. Затем записывает ответ к

заданию в отведенное место.

Задания второй части выполняются на отдельных листах с полной записью решения.

Для оценивания результатов выполнения работ учащимися наряду с традиционной

отметкой «2», «3», «4» и «5» применяется и ещё один количественный показатель –

общий балл, который формируется путём подсчета общего количества баллов,

полученных учащимися за выполнение каждой части работы. Каждое задание части В

оценивается в 1 балл, С – 2 балла. Таким образом, за работу обучающийся может набрать

максимальное количество баллов – 14. С помощью общего балла, расширяющего

традиционную шкалу оценивания, во—первых, проводится более тонкая дифференциация

математической подготовки, во—вторых, отметка несёт больше информации. Общий балл

нагляден, легко интерпретируется учителем, учеником, родителями. Итак, шкала перевода

набранных баллов в отметку:

0-6 баллов – «2»;

7-9 баллов – «3»;

10-12 баллов – «4»;

13-14 баллов – «5».

Ответы к заданиям работы прилагаются.

ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ РАБОТЫ

Работа состоит из двух частей. На выполнение всей работы отводится 90 минут.

В части В – 8 заданий, в части С – 3 задания.

К заданиям части В полученный ответ надо вписать в отведённом для этого месте. В

случае записи неверного ответа зачеркните его и запишите новый.

Задания части С выполняются на отдельных листах с записью хода решения. Текст

задания можно не переписывать, необходимо лишь указать его номер. Все необходимые

вычисления, преобразования выполняйте в черновике.

Советуем выполнять задания в том порядке, в котором они даны в работе. С целью

экономии времени пропускайте задание, которое не удается выполнить сразу, и

переходите к следующему. Если после выполнения всей работы у вас останется время, то

можно вернуться к пропущенным заданиям.

Вариант 1

1. В доме, в котором живет Ира, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Ира живет в квартире №60. В каком подъезде живет Ира?

2. На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1988 году. Ответ дайте в градусах Цельсия.

3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см. Ответ дайте в квадратных сантиметрах.

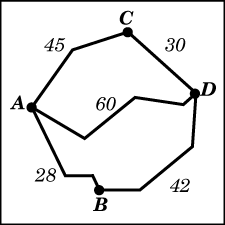
4. Из пункта А в пункт D ведут три дороги. Через пункт В едет грузовик со средней скоростью 35 км/ч, через пункт С едет автобус со средней скоростью 30 км/ч. Третья дорога — без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 40 км/ч. На рисунке показана схема дорог и расстояние (в км) между пунктами по дорогам.

Все три автомобиля одновременно выехали из А. Какой автомобиль добрался до D позже других? В ответе укажите, сколько часов он находился в дороге.

5. Найдите корень уравнения 

6. В треугольнике ABC угол C равен , , . Найдите AC.

7. Найдите значение выражения

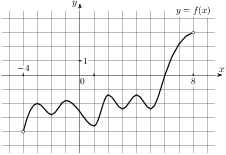
8. На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .

9.Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

10.В прямоугольном параллелепипеде известно, что , , . Найдите длину ребра .

11.Найдите наименьшее значение функции на отрезке .

Задания части С.

С1. Решите уравнение: sin 2x = 2 cos² x. Найдите решение на отрезке [-0,5π;1,5π].

С2. В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 и 6 см. Найти боковое ребро призмы, если ее боковая поверхность равна 120 квадратных сантиметров. . Найдите площадь полной поверхности призмы.

Вариант 2

1. В доме, в котором живет Ира, 9 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Ира живет в квартире №60. В каком подъезде живет Ира?

2. На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура превышала 20 градусов Цельсия в 1988 году.

1. Найдите площадь квадрата, вершины которого имеют координаты (4;3), (10;3), (10;9), (4;9).

1. Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 28 секунд. Петя загружает файл размером 28 Мб за 24 секунды, а Миша загружает файл размером 38 Мб за 32 секунды. Сколько секунд будет загружаться файл размером 665 Мб на компьютер с наибольшей скоростью загрузки?

2. Найдите корень уравнения 

3. В треугольнике  , угол  равен . Найдите внешний угол Ответ дайте в градусах.

1. Найдите , если

2. На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции .

1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

2. Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого , , .

3. Найдите наименьшее значение функции на отрезке

Задания части С.

С1. Решите уравнение :

2 sin² x + 3 sin x — 2 = 0. Найдите решение на отрезке [0;3π].

С2. В правильной четырёхугольной призме площадь основания 144 см², а высота 14 см. Найти диагональ призмы и площадь полной поверхности.

Вариант3

1. В доме, в котором живет Люда, 17 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Люда живет в квартире №80. В каком подъезде живет Люда?

2. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура превышала 10 градусов Цельсия в 1999 году.

1. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;6), (5;6).

1. Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерстяной пряжи синего цвета. Можно купить синюю пряжу по цене 60 рублей за 50 граммов, а можно купить неокрашенную пряжу по цене 50 рублей за 50 граммов и окрасить её. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 граммов пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.

2. Найдите корень уравнения .