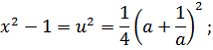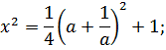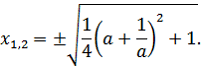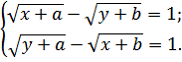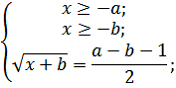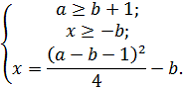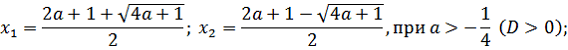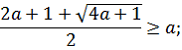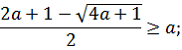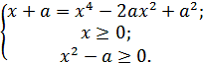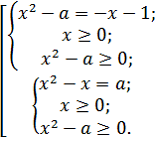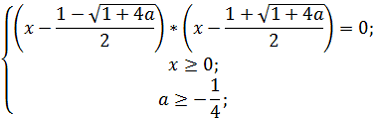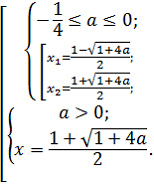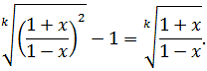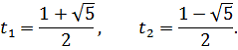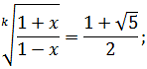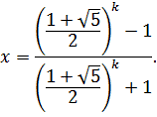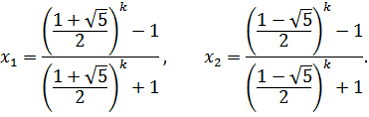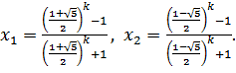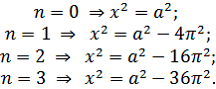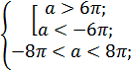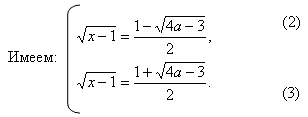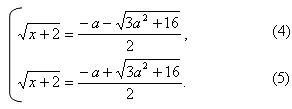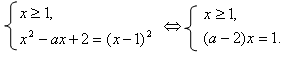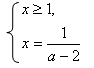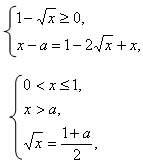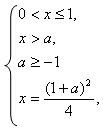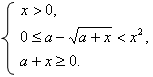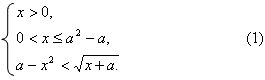Задача 18 ЕГЭ-2021 по математике. Параметры
Посмотрите на условия задач с параметрами ЕГЭ-2021. Вы заметите, что на вид все они похожи. Однако сходство только внешнее, и решаются они по-разному. В этой статье – обзор задач с параметрами ЕГЭ-2021 по математике.
1. Начнем с задачи, которую лучше всего решить аналитическим способом. Слева в уравнении модуль, справа – произведение модуля и корня квадратного. Лучше всего первым действием сделать возведение обеих частей уравнения в квадрат (при неотрицательности подкоренного выражения).
О том, как решать уравнения, где слева модуль и справа модуль, читайте здесь: Уравнения с модулем.
При каких значениях параметра a уравнение
имеет ровно 2 решения?
Уравнение равносильно системе:
Вынесли общий множитель за скобку
Так как и при всех исходное уравнение имеет корни и при всех Значит, исходное уравнение имеет ровно два корня в следующих случаях:
не имеет решений и
2) совпадение корней
Рассмотрим первый случай.
Неравенство — не имеет решений, если
Рассмотрим второй случай.
1) Корни и совпадают, тогда и
Так как исходное уравнение при имеет один корень
2) Корни и совпадают.
Уравнение имеет корни и
3) Корни и совпадают, исходное уравнение имеет ровно два корня.
Мы применили аналитический способ решения: с помощью равносильных переходов от исходного уравнения перешли к такой форме, где сразу видно, какие корни имеет уравнение при определенных значениях параметра.
На Онлайн-курсе подготовки к ЕГЭ на 100 баллов мы подробно рассказывали об этом методе и решали множество задач. Способ хорош тем, что вы просто действуете по образцу – и быстро приходите к ответу.
2. Второе уравнение очень похоже на первое. И первое действие будет таким же: возведением обеих частей в квадрат. А закончим мы – для разнообразия – построением графиков в системе координат (а; х).
Найти a, при которых имеет ровно 2 решения.
Возведем обе части уравнения в квадрат.
Найдем, каким значениям параметра соответствует ровно два значения
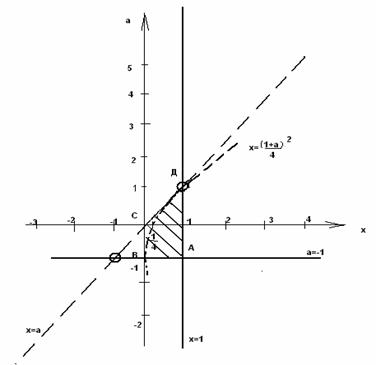
Построим в системе координат графики функций:
Мы находим такие при которых горизонтальная прямая имеет ровно 2 общие точки с совокупностью прямых, являющихся графиком исходного уравнения.
Видим, что в общем случае прямая пересекает каждую из трех прямых, то есть исходное уравнение имеет ровно 3 решения.
Ровно 2 решения будет в случаях, когда прямая проходит через точки пересечения прямых, то есть в случаях совпадения корней.
Данная совокупность имеет ровно два решения в случаях совпадения корней.
О графическом способе решения задач с параметрами читайте здесь: Графический метод решения задач с параметрами.
3. В третьем задании также присутствуют выражения под модулями. Но подход будет другой: мы применим метод интервалов для модулей, о котором можно прочитать здесь: Уравнения с модулем.
С его помощью раскроем модули и получим график функции, заданной описанием: на разных интервалах график этой функции выглядит по-разному, то есть состоит из отдельных кусочков. А дальше – графическое решение.
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Применим метод интервалов для модулей. Уравнение равносильно совокупности систем:
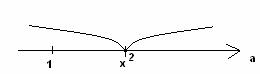
Мы сделали так, потому что при оба модуля раскрываем с противоположным знаком:
Заметим, что если уравнение не выполняется ни при каких
Решим графически полученную совокупность.
Рассмотрим функцию такую, что:
Для функции ось ординат – вертикальная асимптота.
Уравнение имеет ровно два корня при или
Вообще задачи с параметрами, как правило, можно решать многими способами.
4. И наконец, довольно сложное уравнение с тремя модулями. Нам придется раскрывать все эти модули по определению, рассматривая 4 случая. Но ничего страшного здесь нет – просто аккуратность. А потом мы разобьем координатную плоскость (х; а) на области и в каждой из областей построим график уравнения. Кто знаком с методом областей – тот легко с этим справится.
При каких значениях параметра a уравнение имеет ровно три различных решения
Задание 17. Уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 17:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 17 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
Глава 1. Графический подход § 1. Вебинар по задачам 18: модуль и окружности 















Задания по теме «Задачи с параметром»
Открытый банк заданий по теме задачи с параметром. Задания C6 из ЕГЭ по математике (профильный уровень)
Задание №1227
Условие
Найдите все значения a > 0, при каждом из которых система begin(x-4)^2+(|y|-4)^2=9,\ x^2+(y-4)^2=a^2end имеет ровно 2 решения.
Решение
Если y geqslant 0, то первое уравнение задаёт окружность phi _1 с центром в точке C_1 (4; 4) радиуса 3 , а если y то оно задаёт окружность phi _2 с центром в точке C_2 (4; -4) того же радиуса.
При a > 0 второе уравнение задаёт окружность phi с центром в точке C(0; 4) радиуса a . Поэтому задача состоит в том, чтобы найти все значения параметра a , при каждом из которых окружность phi имеет ровно две общие точки с объединением окружностей phi _1 и phi _2.
Координаты точки касания окружностей phi и phi _1 явно видны на чертеже — точки A_1 (1; 4) и B_1 (7; 4) . То есть при a=CA_1=1 и a=CB_1=7 окружности phi и phi _1 касаются. При a > 7 и a окружности phi и phi _1 не пересекаются, при 1 окружности phi и phi _2 имеют 2 общие точки.
Далее, из точки C проведём луч CC_2 и обозначим A_2 и B_2 точки его пересечения с окружностью phi_2 , где A_2 лежит между C и C_2. Заметим, что длина отрезка CC_2= sqrt <4^2+(4-(-4))^<2>>= sqrt <80>= 4sqrt 5.
При a или a > CB_2 окружности phi и phi_2 не пересекаются. При CA_2 окружности phi и phi _2 имеют 2 общие точки. При a =CA_2=4sqrt 5-3 или a=CB_2=4sqrt 5+3, окружности phi и phi _2 касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность phi с одной из окружностей phi _1 и phi _2 имеет 2 общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как 1 то условию задачи удовлетворяют значения ain (1;4sqrt 5-3) cup (7; 4sqrt 5+3).
источники:
http://www.berdov.com/ege/parametr/
http://academyege.ru/theme/zadachi-s-parametrom.html
Анна Малкова
Посмотрите на условия задач с параметрами ЕГЭ-2021. Вы заметите, что на вид все они похожи. Однако сходство только внешнее, и решаются они по-разному. В этой статье – обзор задач с параметрами ЕГЭ-2021 по математике.
1. Начнем с задачи, которую лучше всего решить аналитическим способом. Слева в уравнении модуль, справа – произведение модуля и корня квадратного. Лучше всего первым действием сделать возведение обеих частей уравнения в квадрат (при неотрицательности подкоренного выражения).
О том, как решать уравнения, где слева модуль и справа модуль, читайте здесь: Уравнения с модулем.
При каких значениях параметра a уравнение
имеет ровно 2 решения?
Решение:
Уравнение равносильно системе:
Второе уравнение:
Вынесли общий множитель за скобку
Корни уравнения:
При этом :
Получим:
Так как и
при всех
исходное уравнение имеет корни
и
при всех
Значит, исходное уравнение имеет ровно два корня в следующих случаях:
1) система
не имеет решений и
2) совпадение корней
Рассмотрим первый случай.
Неравенство — не имеет решений, если
Рассмотрим второй случай.
1) Корни и
совпадают, тогда
и
Так как исходное уравнение при
имеет один корень
2) Корни и
совпадают.
Тогда
Уравнение имеет корни и
3) Корни и
совпадают,
исходное уравнение имеет ровно два корня.
Получим:
Мы применили аналитический способ решения: с помощью равносильных переходов от исходного уравнения перешли к такой форме, где сразу видно, какие корни имеет уравнение при определенных значениях параметра.
На Онлайн-курсе подготовки к ЕГЭ на 100 баллов мы подробно рассказывали об этом методе и решали множество задач. Способ хорош тем, что вы просто действуете по образцу – и быстро приходите к ответу.
2. Второе уравнение очень похоже на первое. И первое действие будет таким же: возведением обеих частей в квадрат. А закончим мы – для разнообразия – построением графиков в системе координат (а; х).
Найти a, при которых имеет ровно 2 решения.
Решение:
Возведем обе части уравнения в квадрат.
Найдем, каким значениям параметра соответствует ровно два значения
Построим в системе координат графики функций:
Мы находим такие при которых горизонтальная прямая
имеет ровно 2 общие точки с совокупностью прямых, являющихся графиком исходного уравнения.
Видим, что в общем случае прямая пересекает каждую из трех прямых, то есть исходное уравнение имеет ровно 3 решения.
Ровно 2 решения будет в случаях, когда прямая проходит через точки пересечения прямых, то есть в случаях совпадения корней.
Данная совокупность имеет ровно два решения в случаях совпадения корней.
1)
2)
3)
О графическом способе решения задач с параметрами читайте здесь: Графический метод решения задач с параметрами.
3. В третьем задании также присутствуют выражения под модулями. Но подход будет другой: мы применим метод интервалов для модулей, о котором можно прочитать здесь: Уравнения с модулем.
С его помощью раскроем модули и получим график функции, заданной описанием: на разных интервалах график этой функции выглядит по-разному, то есть состоит из отдельных кусочков. А дальше – графическое решение.
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Решение:
Применим метод интервалов для модулей. Уравнение равносильно совокупности систем:
Мы сделали так, потому что при оба модуля раскрываем с противоположным знаком:
При получим:
При получим:
Заметим, что если уравнение
не выполняется ни при каких
Решим графически полученную совокупность.
Рассмотрим функцию такую, что:
Для функции ось ординат – вертикальная асимптота.
– точка минимума,
– точка максимума,
Уравнение имеет ровно два корня при или
Ответ:
Вообще задачи с параметрами, как правило, можно решать многими способами.
4. И наконец, довольно сложное уравнение с тремя модулями. Нам придется раскрывать все эти модули по определению, рассматривая 4 случая. Но ничего страшного здесь нет – просто аккуратность. Затем мы разобьем координатную плоскость на области и в каждой из областей построим график уравнения. Кто знаком с методом областей – тот легко с этим справится.
При каких значениях параметра уравнение
имеет ровно три различных решения
Решение:
Поскольку получим:
;
Мы хотим найти, при каких значениях параметра эта совокупность уравнений имеет ровно 3 различных решения.
Выразим в каждом уравнении через
:
Изобразим графики этих уравнений в системе координат
Если прямая пересекает совокупность прямых 3 раза, исходное уравнение имеет ровно 3 решения.
Это происходит, если прямая проходит через одну из точек
или
на рисунке. В остальных случаях уравнение имеет ровно 4 решения. Найдем значение параметра
для каждой из этих точек.
1) В точке пересекаются прямые
и
Для точки
2) Точка
3) Точка
4) Точка
Мы нашли все случаи, когда исходное уравнение имеет ровно 3 решения.
Ответ:
5. (Резервный день) Найти все значения параметра при каждом из которых уравнение
имеет хотя бы два различных корня.
Решение:
Замена:
Исходное уравнение имеет хотя бы два различных корня, если уравнение
имеет хотя бы один корень
Если t = 0, то x = 0, тогда
Этот случай рассмотрим отдельно.
1) Случай уравнение
должно иметь хотя бы один положительный корень.
Если уравнение линейное, тогда
– подходит.
Пусть уравнение квадратное.
сумма корней:
произведение корней:
Если то
Тогда т.к.
При этом должно выполняться условие
Получим:
Решим третье неравенство системы:
возведем обе части в квадрат:
при этом
Объединив со случаем a = 2, получим:
Вернемся к случаю, когда – корень уравнения. Тогда
Получим уравнение:
– уравнение имеет, кроме корня
положительный корень
подходит
Ответ:
Вот так в задачах ЕГЭ-2021 по математике можно применить в задачах с параметрами аналитический и графический способы, а также метод областей.
Конечно, это не все. Существует не менее 12 методов решения задач с параметрами. Мы изучаем их все на практике на Онлайн-курсе подготовки к ЕГЭ по математике.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача 18 ЕГЭ-2021 по математике. Параметры» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023
11 апреля 2021
В закладки
Обсудить
Жалоба
Решение иррациональных уравнений и систем уравнений с параметром
Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.
riu.docx
riu.pdf
Автор: Канаева Ирина Витальевна.
Поставничий Юрий Сергеевич
ФГБОУ ВО «Вологодский государственный университет»
студент 1 курса магистратуры факультет прикладной математики, компьютерных технологий и физики
Аннотация
В данной статье рассматривается одна из классификаций методов решения иррациональных уравнений с параметрами. Данная классификация является результатом анализа многих классификаций и объединила в себе самые эффективные методы. Для каждого метода разобраны конкретные примеры с пояснениями и комментариями.
Postavnichiy Yuriy Sergeevich
Vologda State University
1 year master student of the Faculty of Applied Mathematics, Physics and Computer Technology
Abstract
In this article one of classifications of methods of the solution of the irrational equations with parameters is considered. This classification is result of the analysis of many classifications and united in itself the most effective methods. For each method kontkretny examples with explanations and comments are sorted.
Библиографическая ссылка на статью:
Поставничий Ю.С. Методы решения иррациональных уравнений с параметром // Современные научные исследования и инновации. 2015. № 10 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2015/10/58207 (дата обращения: 24.02.2023).
Самым первым иррациональным уравнение, с которым сталкиваются школьники, является уравнение вида:
Решая данное уравнение, ученики знакомятся с иррациональными уравнениями с параметром. Рассматривают самое простейшее решение и исследуют множество случаев, где возникают спорные ситуации, в которых могут появиться посторонние корни или наоборот произойдет потеря корней.
Покажем решение данного уравнения:
Рассматривая разные значения параметра, мы замечаем, что могут возникнуть три случая:
a) если , то уравнение корней не имеет;
b) если , то
;
c) если , то
.
Если классифицировать иррациональные уравнения с параметром, то мы можем получить два основных уравнения общего вида (:
Многие уравнения сводятся именно к решению этих двух или являются частным случаем данных уравнений. При выполнении действий с корнями мы получаем уравнения, более высокого уровня (:
Рассмотрим различные методы решения иррациональных уравнений с параметром на частных примерах, а также подберем систему заданий на отработку того или иного метода.
Замечание: Некоторые уравнения могут быть решены несколькими способами. Способ решения выбирается исходя из удобства применения.
Переход к смешанной системе, путем возведения обеих частей уравнения в необходимую одинаковую степень
При решении уравнений этим методом необходимо помнить, что в результате возведения обеих частей уравнения в одинаковую степень получается уравнение, являющееся следствием исходного, т.е. область определения расширяется, а значит, возможно появление «посторонних корней», которые должны быть устранены проверкой. Именно поэтому мы используем следующую эквивалентность (при ):
Замечание: При возведении обеих частей уравнения в нечетную степень получается уравнение, равносильное исходному.
Пример. Иррациональное уравнение вида
Рассмотрим решение уравнений вида:
Решение. Используя переход к эквивалентной системе и решив полученную систему, найдем решение исходного уравнения:
Ответ: Если то уравнение решений не имеет;если
то решение принимает вид:
Метод замены
Данные метод заключается в замене данной переменной на новую и сведения исходного уравнения к более простому.
Пример. Иррациональное уравнение вида
Для каждого значения параметра a решить уравнение
Решение. Обозначим , где
. Учитывая исходное уравнение, получим систему вида:
Вычитая из первого уравнения второе, получим новое уравнение:
Полученное уравнение равносильно совокупности двух уравнений:
Произведем обратную замену:
Оба уравнения совокупности соответствуют уравнению вида
и решаются методом перехода к смешанной системе. Исходя из этого, решим уравнения, начиная с первого:
Решим квадратное уравнение относительно переменной x, с помощью формул корней квадратного уравнения:
Проверим условие :
и получим, что является корнем уравнения при
.
Условие , выполняется для любого
.
Аналогично решим второе уравнение совокупности и получим
Проверим условие для
:
Получили, что является корнем уравнения
при
Также проверяется условие
для
Решением данного неравенства является пустое множество (), так как отрицательное число всегда меньше выражения с радикалом.
Объединяя полученные решения, запишем ответ.
Метод введения вспомогательного неизвестного (метод подстановки)
Данный метод состоит во введении вспомогательных неизвестных, с помощью которых уравнение сводится к системе рациональных уравнений относительно новых переменных. Например:
Пример 8. Иррациональное уравнение вида
Для каждого значения параметра a решить уравнение
Решение. Прежде чем приступить к решению уравнения нам необходимо найти ОДЗ. Найдем ее:
Найденная область допустимых значений: . Введем вспомогательные неизвестные:
и получим следующую систему:
Заметим, что при система решений не имеет. Так как
то при получаем
Учитывая, что , находим
Значения параметра a, при которых выполнены оба условия и
, найдем, решив систему неравенств
Первое неравенство справедливо при , второе неравенство справедливо при
. Следовательно, оба неравенства справедливы, а значит и оба условия выполняются одновременно при
. При данных значениях параметра получаем уравнение, которое можем решить.
Ответ: Если , то
;если
, то решений нет.
Графический метод
Стандартный способ решения уравнений в отдельных случаях приводит к сложным преобразованиям. Процесс решения может быть упрощен, если применить графический прием. Использование графического метода сводится к построению и анализу графиков функций, с помощью которых составлено уравнение.
Можно выделить две разновидности рассматриваемого метода:
1. изображение на плоскости , где
– неизвестное;
– параметр;2. на плоскости
рассматривается семейство кривых, зависящих от параметра
.
Первый способ используется в задачах, которые содержат лишь неизвестную и параметр, или сводящихся к таким. Второй способ оказывается удобен в задачах с двумя неизвестными и одним параметром.
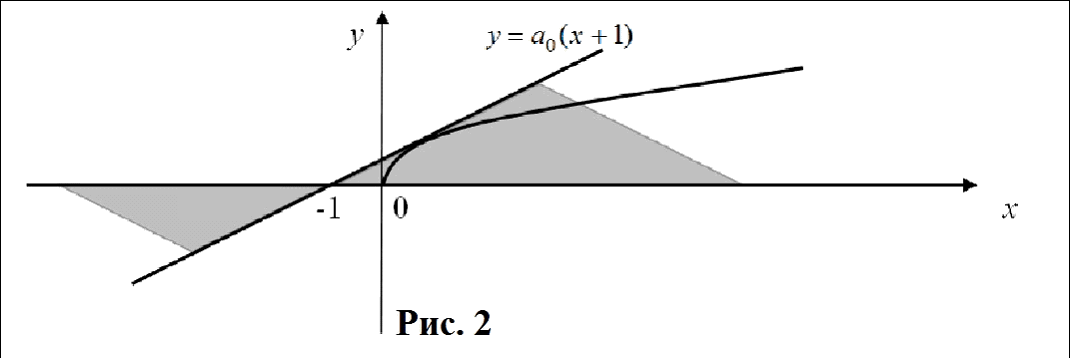
Пример. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы один корень.
Решение. Применяя графический метод решения, найдем все значения параметра, при которых прямая имеет хотя бы одну общую точку с графиком функции
. Заметим, что для прямой
параметр а является угловым коэффициентом (при изменении параметра одна прямая будет переходить в другую с помощью поворота около точки (-1;0), так как для любого
.
По графику (рис. 2) видим, что искомыми являются прямые, лежащие внутри заштрихованной пары вертикальных углов, включая границы. Им соответствуют значения отвечает моменту касания прямой
графика функции
. (Заметим, что
).
Значение находим из условия, что уравнение
имеет ровно один корень. После преобразований получим квадратное уравнение
Так как , то искомое значение
Ответ:
Метод функционального исследования
Иррациональные уравнения с параметром можно решать, основываясь на знаниях о свойствах функций, составляющих данное уравнение. При решении уравнения мы можем ссылаться как на одно свойство, так и на совокупность нескольких свойств. Метод функционального исследования зачастую используют для решения уравнений повышенного уровня. Мы рассмотрим основные свойства, используемые при решении иррациональных уравнений с параметром, и приведем примеры использования данных свойств.
Монотонность
Знание свойств монотонных функций очень часто помогает при решении систем уравнений. Напомним некоторые свойства монотонных функций:
1) Если функции и
возрастающие (убывающие), причем пересечение областей определения данных функций не равно пустому множеству
, то функция
возрастающая (убывающая);
2) Если функции и
возрастающие (убывающие), причем пересечение областей определения данных функций не равно пустому множеству
и
при всех допустимых значениях x, то функция
возрастающая (убывающая).
3) Если функция монотонная, то уравнение
имеет не более одного корня; другими словами, монотонная функция каждое свое значение принимает ровно один раз.
Пример. Решите систему уравнений
Решение. В данной системе вычтем из первого уравнения второе. Получим
Рассмотрим функцию Используя свойство суммы возрастающих функций, делаем вывод что функция
возрастающая. Заметим, что
. Следовательно
. Отсюда
Очевидно что:
Ответ: Если , то
если
, то система решений не имеет.
Метод итерации
Вообще говоря метод итерации можно включить в метод исследования монотонности, но рассмотрим его отдельно, потому что очень часто задачи с итерациями дают на вступительных экзаменах по математике в ведущих ВУЗах России.
Рассмотрим уравнение
n—разОчевидно, что все корни уравнения являются корнями уравнения (1), но эти уравнения, вообще говоря, не эквивалентны. Однако, если функция
строго монотонна на некотором промежутке, то эти уравнения равносильны всюду на этом промежутке.
Рассмотрим практическое применение метода итерации при решении уравнения.
Пример. Найти все значения параметра а, при которых уравнение
имеет два различных корня.
Решение. Приведем данное уравнение к виду
где возрастает на промежутке
. Значит исходное уравнение равносильно уравнению
. Путем рассуждений и используя свойство монотонной функции мы пришли к более простому иррациональному уравнению с параметром, которое можем решить приведением к смешанной системе (см. Пример 3).
Решим уравнение системы, как квадратное относительно переменной .
Проверим условие Для этого подставим вместо
полученное нами значение и решим неравенство относительно параметра:
Данное неравенство будет верным для любого значения параметра
так как область значений функции равна интервалу
при
, а значит
корнем исходного уравнения является при любом
.
Аналогично проверим условие
Получили, что является корнем исходного уравнения при
. Объединяя все результаты рассуждений и решений, делаем вывод, что исходное уравнение имеет два различных корня при
Ответ:
Наибольшее (наименьшее) значение функции и дифференцируемость функции
Для определения наибольшего и наименьшего значений функции на отрезке используют несколько теорем:Теорема ВейерштрассаФункция, непрерывная на отрезке имеет наибольшее и наименьшее значения, которые достигаются либо в критических точках, либо на концах отрезка.Теорема о наибольшем и наименьшем значениях на незамкнутом промежуткеЕсли функция, непрерывная на интервале
, имеет в этом интервале только одну точку экстремума
, и если
– точка максимума, то
– наибольшее значение функции
на интервале
; если
– точка минимума, то
– наименьшее значение функции
на интервале
.
Частные методы решения иррациональных уравнений с параметром
В данном разделе рассмотрим задания, которые решаются с помощью использования нескольких стандартных методов или без их использования, а также задания повышенного уровня сложности.
Пример. Для каждого значения параметра а решить уравнение
Решение. При данное уравнение равносильно совокупности
Отсюда при любом
,
при
.
Ответ: Если , то
;если
, то
.
Замечание. При решении уравнения вида
следует учитывать, что оно равносильно уравнению
Рассмотрим далее решение примера, в котором используется прием решения уравнения относительно параметра.
Пример. Для каждого значения параметра а решить уравнение
Решение. Избавимся от иррациональности в данном уравнении путем перехода к смешанной системе
Раскрывая скобки и группируя члены в уравнении последней системы, получим Выражение в левой части – это квадратный трехчлен относительно а, который можно разложить на множители:
Следовательно,
Первая система полученной совокупности не имеет решений, так как при условии получаем, что
Вторая система равносильна системе
Заметим, что при корни
совпадают и равны
.
Ответ: Если , то решений нет;если
, то
и
;если
и
, то
.
Очень часто параметр стоит либо в под знаком корня, либо отдельно от него; но бывает так, что в качестве параметра рассматривается показателя корня. Рассмотрим такой пример.
Пример. В зависимости от значений параметра решить уравнение
Решение. Подстановкой убеждаемся, что не является корнем исходного уравнения. Поэтому после деления обеих частей уравнения на
получим равносильное уравнение
Заменим , и придем к квадратному уравнению относительно новой переменной
Так как показатель может принимать четные значения, то
в данном случае нужно отбросить, так как
.
Таким образом, при четном показателе имеем
При нечетном показателе уравнение
.gif)
Ответ: Если – четное, то
.gif)
– нечетное, то
Рассмотрим уравнение, в котором сочетаются несколько видов функций.
Пример. При каких а уравнение
имеет ровно 8 корней.
Решение. Решим уравнение, как обыкновенное тригонометрическое:
При каждом количество корней уравнения будет равно двум. Значит, условие нашей задачи будет выполнятся при
. Мы не рассматриваем отрицательные значения
, так как
стоит во второй степени, следовательно
. Выпишем предполагаемые корни:
Для того чтобы наши предполагаемые корни являлись искомыми, необходимо чтобы выполнялись следующие условия:
Ответ:
Количество просмотров публикации: Please wait
Все статьи автора «Поставничий Юрий Сергеевич»
Цель: Познакомить обучающихся с решением иррациональных уравнений и неравенств с параметром. Способствовать развитию навыка решения задач.
Содержание занятий.
Задачи с параметром даются в текстах ЕГЭ.
Фактически задача с одним параметром содержит не одну неизвестную , а две —
и параметр
Множество решений такого уравнения — это множество пар чисел
, подстановка которых в уравнение обращает его в верное равенство. Аналогично, множество решений неравенства с неизвестной
и параметром
— множество пар чисел (
, обращающих его в верное числовое неравенство. На I этапе решения классифицируются типы уравнений и неравенств для каждого значения параметра, а на II этапе – решаются не одно, а несколько уравнений (неравенств) каждого типа. Выделенные два этапа не обязательно идут в строгой последовательности I, II. В процессе решения они могут «переплетаться».
Пример №1 Решить уравнение
Решение. Перепишем уравнение в виде:
(1)
и рассмотрим его как квадратное относительно . Находим дискриминант уравнения D=
. Уравнение (1) имеет решение только в случае, если
.
Заметим, что уравнение (2) имеет решение тогда и только тогда, когда , т. е. при
. Решив уравнения (2) и (3), получим при
Таким образом, приходим к следующему ответу:
при уравнение имеет два корня: х1 и х2 ; при
уравнение имеет один корень: х2; при
решений нет.
Пример №2 Решить уравнение
Решение. Функция определена и возрастает на промежутке
. Наименьшее значение она принимает в точке
;
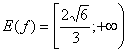
уравнение
имеет единственное решение, при
решений нет.
Итак, пусть . Переписав уравнение в виде
, (1)
возведём обе его части в квадрат:
. (2)
Уравнение (2) является следствием (1). Перепишем его в виде:
(3)
Уравнение (3) является квадратным относительно . Решив его, получаем совокупность двух уравнений:
При уравнение (4) решений не имеет, а уравнение (5) имеет один корень
.
Так как при любом исходное уравнение имеет один корень, и притом только один, то найденный корень и является корнем исходного уравнения.
Ответ: При
, при
решений нет.
Пример №3. Решить уравнение
Решение. Уравнение равносильно системе
При система решений не имеет, при
получим
Заметив, что при
приходим к ответу: при
при
3 решений нет.
Графическое решение
Пример №4
Решить уравнение
Решение. 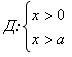
равносильно исходному.
Уравнение равносильно системе
Изобразим на плоскости (х;а) график функции — это парабола с минимумом в точке
, пересекающая ось
в точке
Укажем также области плоскости (х;а), в которых выполняются неравенства системы
— полуплоскость ниже прямой
, не включая эту прямую;
вертикальная полоса между прямыми
и
включающая правую границу;
полуплоскость выше прямой
включая эту прямую.
Таким образом, исходное уравнение имеет решение при указанных условиях, иллюстрирующееся частью параболы, заключённой внутри трапеции АВСД, т. е. при .
При всех остальных действительных значениях решения нет.
Ответ: при
Решений нет при
Пример №5.
Для любого значения решите неравенство
.
Решение. Во-первых, заметим, что левая часть неравенства представляет собой квадратный трёхчлен относительно с корнями
так что левая часть раскладывается на множители
. (1)
Во-вторых, при имеем особый случай:
, решением которого является
.
В- третьих, заметим, что значение разности во второй скобке положительно при . Так что при
неравенство (1) можно переписать в виде
.
При в (1) значение суммы в первой скобке положительно, то есть (1) можно переписать в виде неравенства
.
Наконец, заметим, что входит в последний случай.
Осталось скомпоновать
Ответ: если , то
;
Если то
.
Пример №6 Для каждого значения решите неравенство
Решение. При неравенство не выполняется и оно равносильно системе неравенств
Рассмотрим второе При
нет решений, а для
имеем
Первое из этих неравенств заведомо выполнено (
и
). Получаем систему
Двойное неравенство этой системы непротиворечиво лишь при условии при условии
приводит к условию
.
Итак, остаётся решить последнее неравенство системы (1) при . Основная идея – решаем неравенство относительно
, объявляя на время
параметром.
- Если
, то есть
— уже решение.
- Если же
, то есть
, то
. (1/)
Дискриминант квадратного трёхчлена
,
а его корни и
. Заметим, что очевидно
при х > 0. Значит, решения неравенства (1/) суть
.
Здесь первое неравенство следует из неравенства . Остаётся
для любого
(
При решение последнего неравенства составляют промежутки
С учётом очевидно, остаётся лишь второй промежуток.
Наконец, убедимся, что при
<
.
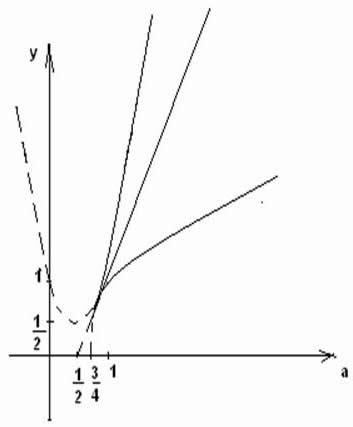
Установим двойное неравенство
При каждое из них сводиться к неравенству
(легко проверить!). Остаётся лишь записать
Ответ: если , то решений нет ;
если , то
.
Задачи для самостоятельной работы
Решим графическим методом.
Левая часть $%y=sqrt{-7-8x-x^2}Rightarrow y^2+(x+4)^2=9 (yge0)$% полуокружность с центром $%(-4;0)$% и радиусом $%3.$%
Правая часть прямая $%y=-ax+2a+3,$% которая проходит через точку $%(2;3),$% параллельна оси $%O_x (a=0)$% или пересекает ось $%Оx$% в точке $%(frac{2a+3}a;0)(ane0).$%
Эта прямая и полуокружность будут иметь точно одну точку пересечения , если
1) $%a=0$%( тогда и только тогда она сопрокасается с полуокружностью, вторая соприкасающая касается с нижней частью окружности.)
2) Точка пересечения с $%Ox$% находится на диаметре полуокружности, но не совпадает с точкой $%(-7;0)Rightarrow -7<frac{2a+3}a le -1 Rightarrow ain[-1;-frac13)$%
Ответ. $%[-1;-frac13)cup {0}$%







.gif)
.gif)

.gif)
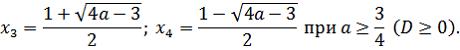
.gif)
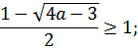

.gif)
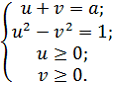
.gif)