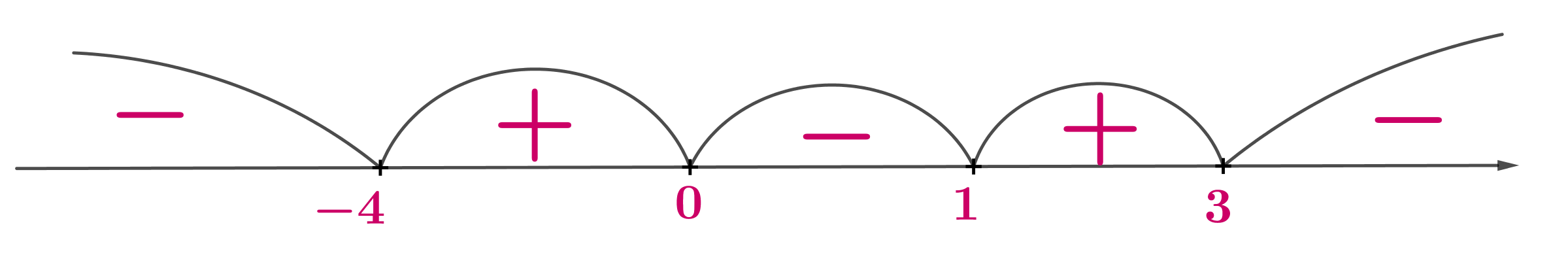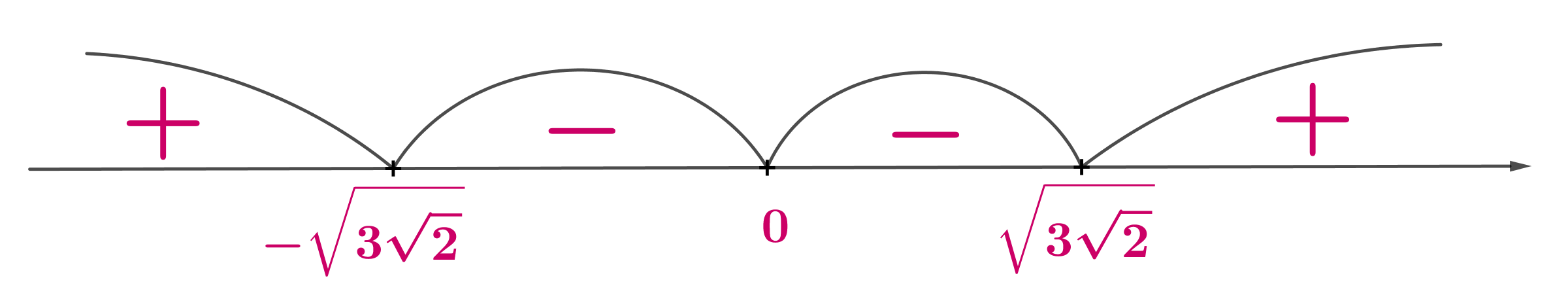1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром
Задание
1
#1220
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+3=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-3). Рассмотрим два случая:
1) (a=0). В этом случае левая часть равна (0), а правая – нет, следовательно, уравнение не имеет корней.
2) (ane 0). Тогда (x=-dfrac{3}{a}).
Ответ:
(a=0 Rightarrow xin varnothing; \
ane 0 Rightarrow
x=-dfrac{3}{a}).
Задание
2
#1221
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+a^2=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-a^2). Рассмотрим два случая:
1) (a=0). В этом случае левая и правая части равны (0), следовательно, уравнение верно при любых значениях переменной (x).
2) (ane 0). Тогда (x=-a).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
ane 0 Rightarrow x=-a).
Задание
3
#1222
Уровень задания: Легче ЕГЭ
Решите неравенство (2ax+5cosdfrac{pi}{3}geqslant 0) при всех значениях параметра (a).
Неравенство можно переписать в виде (axgeqslant -dfrac{5}{4}). Рассмотрим три случая:
1) (a=0). Тогда неравенство принимает вид (0geqslant
-dfrac{5}{4}), что верно при любых значениях переменной (x).
2) (a>0). Тогда при делении на (a) обеих частей неравенства знак неравенства не изменится, следовательно, (xgeqslant
-dfrac{5}{4a}).
3) (a<0). Тогда при делении на (a) обеих частей неравенства знак неравенства изменится, следовательно, (xleqslant -dfrac{5}{4a}).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
a>0 Rightarrow xgeqslant -dfrac{5}{4a}; \
a<0 Rightarrow xleqslant -dfrac{5}{4a}).
Задание
4
#1223
Уровень задания: Легче ЕГЭ
Решите неравенство (a(x^2-6) geqslant (2-3a^2)x) при всех значениях параметра (a).
Преобразуем неравенство к виду: (ax^2+(3a^2-2)x-6a geqslant 0). Рассмотрим два случая:
1) (a=0). В этом случае неравенство становится линейным и принимает вид: (-2x geqslant 0 Rightarrow xleqslant 0).
2) (ane 0). Тогда неравенство является квадратичным. Найдем дискриминант:
(D=9a^4-12a^2+4+24a^2=(3a^2+2)^2).
Т.к. (a^2 geqslant 0 Rightarrow D>0) при любых значениях параметра.
Следовательно, уравнение (ax^2+(3a^2-2)x-6a = 0) всегда имеет два корня (x_1=-3a, x_2=dfrac{2}{a}). Таким образом, неравенство примет вид:
[(ax-2)(x+3a) geqslant 0]
Если (a>0), то (x_1<x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вверх, значит, решением являются (xin (-infty; -3a]cup
big[dfrac{2}{a}; +infty)).
Если (a<0), то (x_1>x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вниз, значит, решением являются (xin big[dfrac{2}{a};
-3a]).
Ответ:
(a=0 Rightarrow xleqslant 0; \
a>0 Rightarrow xin (-infty; -3a]cup big[dfrac{2}{a}; +infty);
\
a<0 Rightarrow xin big[dfrac{2}{a}; -3abig]).
Задание
5
#1851
Уровень задания: Легче ЕГЭ
При каких (a) множество решений неравенства ((a^2-3a+2)x
-a+2geqslant 0) содержит полуинтервал ([2;3)) ?
Преобразуем неравенство: ((a-1)(a-2)x geqslant a-2). Получили линейное неравенство. Рассмотрим случаи:
1) (a=2). Тогда неравенство примет вид (0 geqslant 0), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
2) (a=1). Тогда неравенство примет вид (0 geqslant -1), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
3) ((a-1)(a-2)>0 Leftrightarrow ain (-infty;1)cup (2;+infty)). Тогда:
(xgeqslant dfrac{1}{a-1}). Для того, чтобы множество решений содержало полуинтервал ([2;3)), необходимо, чтобы
(dfrac{1}{a-1} leqslant 2 Leftrightarrow dfrac{3-2a}{a-1}
leqslant 0
Rightarrow ain (-infty; 1)cup [1,5; +infty)).
Учитывая условие (ain (-infty;1)cup (2;+infty)), получаем (ain
(-infty;1)cup (2;+infty)).
4) ((a-1)(a-2)<0 Leftrightarrow ain (1;2)). Тогда:
(xleqslant dfrac{1}{a-1} Rightarrow dfrac{1}{a-1} geqslant 3).
Действуя аналогично случаю 3), получаем (ain (1;
dfrac{4}{3}big]).
Ответ:
(ain (-infty;dfrac{4}{3}big]cup [2;+infty)).
Задание
6
#1361
Уровень задания: Легче ЕГЭ
Определить количество корней уравнения (ax^2+(3a+1)x+2=0) при всех значениях параметра (a).
Рассмотрим два случая:
1) (a=0). Тогда уравнение является линейным: (x+2=0 Rightarrow
x=-2). То есть уравнение имеет один корень.
2) (ane 0). Тогда уравнение является квадратным. Найдем дискриминант: (D=9a^2-2a+1).
Рассмотрим уравнение (9a^2-2a+1=0): (D’=4-36<0), следовательно, уравнение (9a^2-2a+1=0) не имеет корней. Значит, выражение ((9a^2-2a+1)) принимает значения строго одного знака: либо всегда положительно, либо отрицательно. В данном случае оно положительно при любых (a) (в этом можно убедиться, подставив вместо (a) любое число).
Таким образом, (D=9a^2-2a+1>0) при всех (ane 0). Значит, уравнение (ax^2+(3a+1)x+2=0) всегда имеет два корня: (x_{1,2}=dfrac{-3a-1pm
sqrt D}{2a})
Ответ:
(a=0Rightarrow) один корень
(ane 0 Rightarrow) два корня.
Задание
7
#1363
Уровень задания: Легче ЕГЭ
Решить уравнение (sqrt{x+2a}cdot (3-ax-x)=0) при всех значениях параметра (a).
Данное уравнение равносильно системе:
[begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x=-2a \
&3-(a+1)x=0 qquad (*)
end{aligned} end{gathered} right.
end{cases}]
Рассмотрим два случая:
1) (a+1=0 Rightarrow a=-1). В этом случае уравнение ((*)) равносильно (3=0), то есть не имеет решений.
Тогда вся система равносильна (
begin{cases}
xgeqslant 2\
x=2
end{cases} Leftrightarrow x=2)
2) (a+1ne 0 Rightarrow ane -1). В этом случае система равносильна: [begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x_1=-2a \
&x_2=dfrac3{a+1}
end{aligned} end{gathered} right.
end{cases}]
Данная система будет иметь одно решение, если (x_2leqslant -2a), и два решения, если (x_2>-2a):
2.1) (dfrac3{a+1}leqslant -2a Rightarrow a<-1 Rightarrow ) имеем один корень (x=-2a).
2.2) (dfrac3{a+1}>-2a Rightarrow a>-1 Rightarrow ) имеем два корня (x_1=-2a, x_2=dfrac3{a+1}).
Ответ:
(ain(-infty;-1) Rightarrow x=-2a\
a=-1 Rightarrow x=2\
ain(-1;+infty) Rightarrow xin{-2a;frac3{a+1}})

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тема 17.
Задачи с параметром
17
.
25
Метод xOa (параметр как вторая неизвестная)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи с параметром
17.01Задачи из ЕГЭ прошлых лет
17.02Задачи из сборника И.В. Ященко ЕГЭ 2023
17.03Алгебра. Исследование при всех значениях параметра
17.04Алгебра. Связь между множествами решений
17.05Алгебра. Теорема Виета
17.06Алгебра. «Гвозди» для квадратичной функции
17.07Алгебра. Исследование замены
17.08Алгебра. Метод хорошего/плохого корня
17.09Алгебра. Задачи, решающиеся аналитически
17.10Функции. Монотонность: f(x) ∨ const и f(f(x)) = x
17.11Функции. Монотонность: f(t) = f(z)
17.12Функции. Монотонность: f(x) ∨ g(x), f(x)↑, g(x)↓
17.13Функции. Метод главного модуля/слагаемого
17.14Функции. Область значений функций
17.15Функции. Четность/нечетность функций
17.16Функции. Исследование функции на возрастание/убывание
17.17Функции. Сумма взаимно обратных
17.18Функции. Метод оценки
17.19Графика. Базовые задачи
17.20Графика. Нахождение касательной к графику
17.21Графика. Окружность
17.22Графика. Функции с модулем: корыто и другие
17.23Графика. Области
17.24Графика. Отрезок, ромб, квадрат и другие нестандартные графики
17.25Метод xOa (параметр как вторая неизвестная)
17.26Четность как частный случай симметрии
17.27Симметрия
17.28Три неизвестные x,y,z
17.29Задачи с несколькими параметрами
Решаем задачи
Найдите все значения параметра , при каждом из которых уравнение
имеет единственное решение.
Показать ответ и решение
В данное уравнение параметр входит в первой степени, следовательно,
уравнение легко можно переписать в виде (то есть выразить
через
). Сделаем это.
Заметим, что не является решением уравнения, следовательно, разделим
обе части равенства на и получим
Будем рассматривать параметр как переменную. Построим в системе
координат множество
решений уравнения. Если некоторая точка
плоскости с координатами принадлежит этому множеству
то для
исходной задачи это означает, что если параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра при каждом из которых ровно одна точка вида
,
принадлежит множеству решений изображенному на плоскости
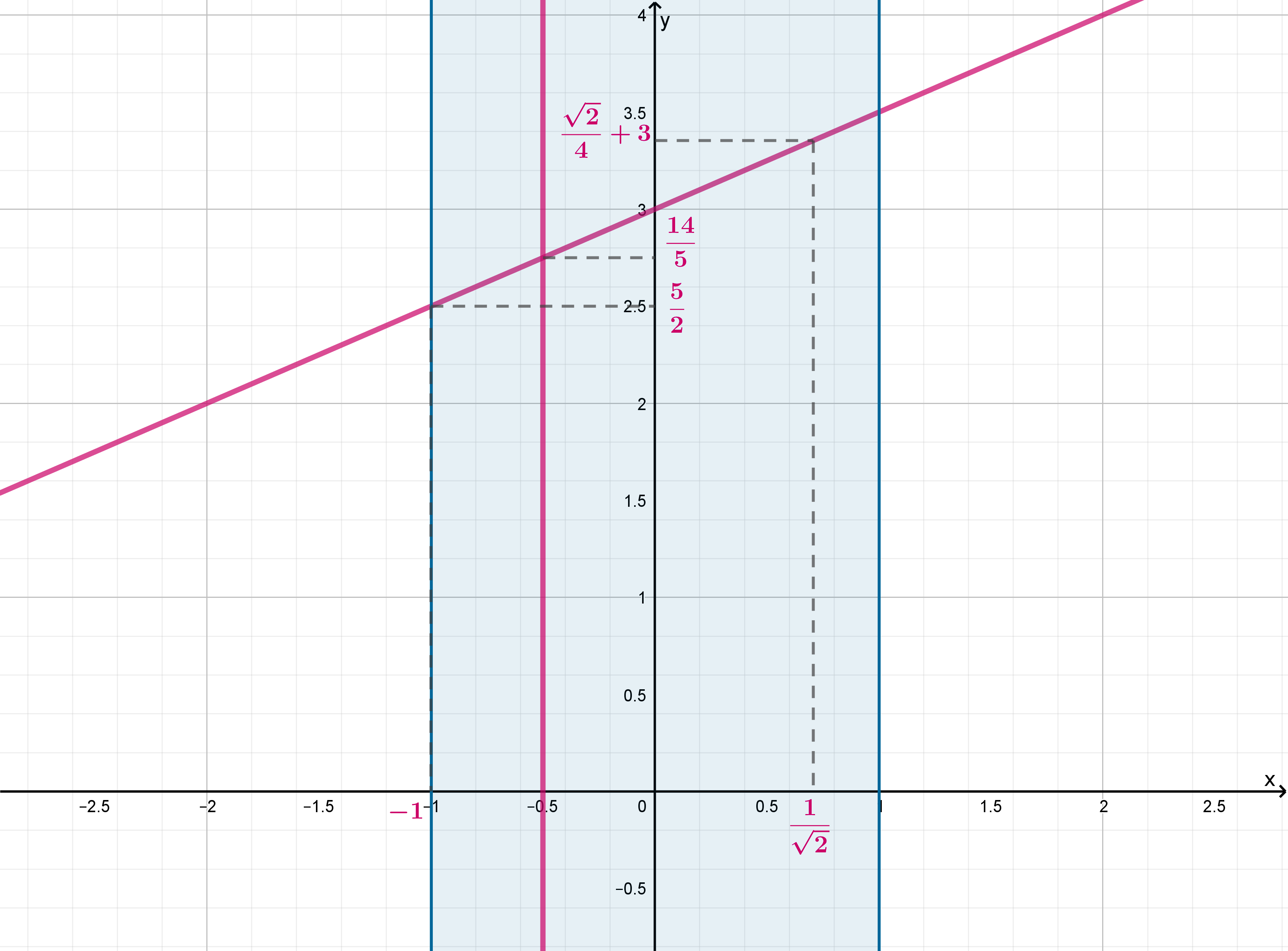
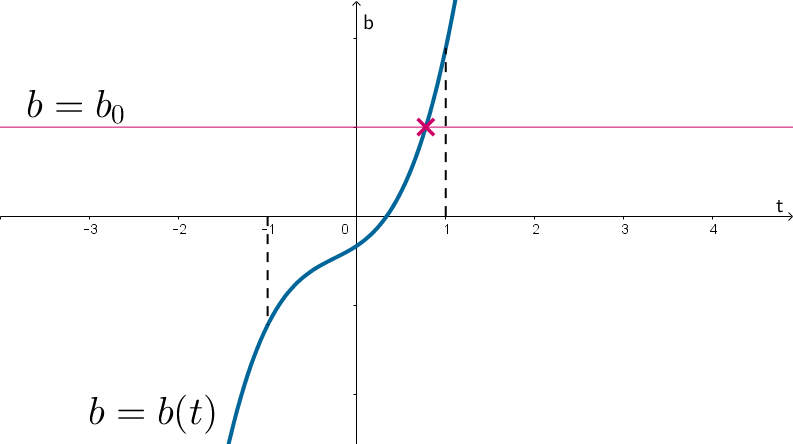
Фактически это равносильно тому, что горизонтальная прямая имеет ровно
одну точку пересечения с множеством .
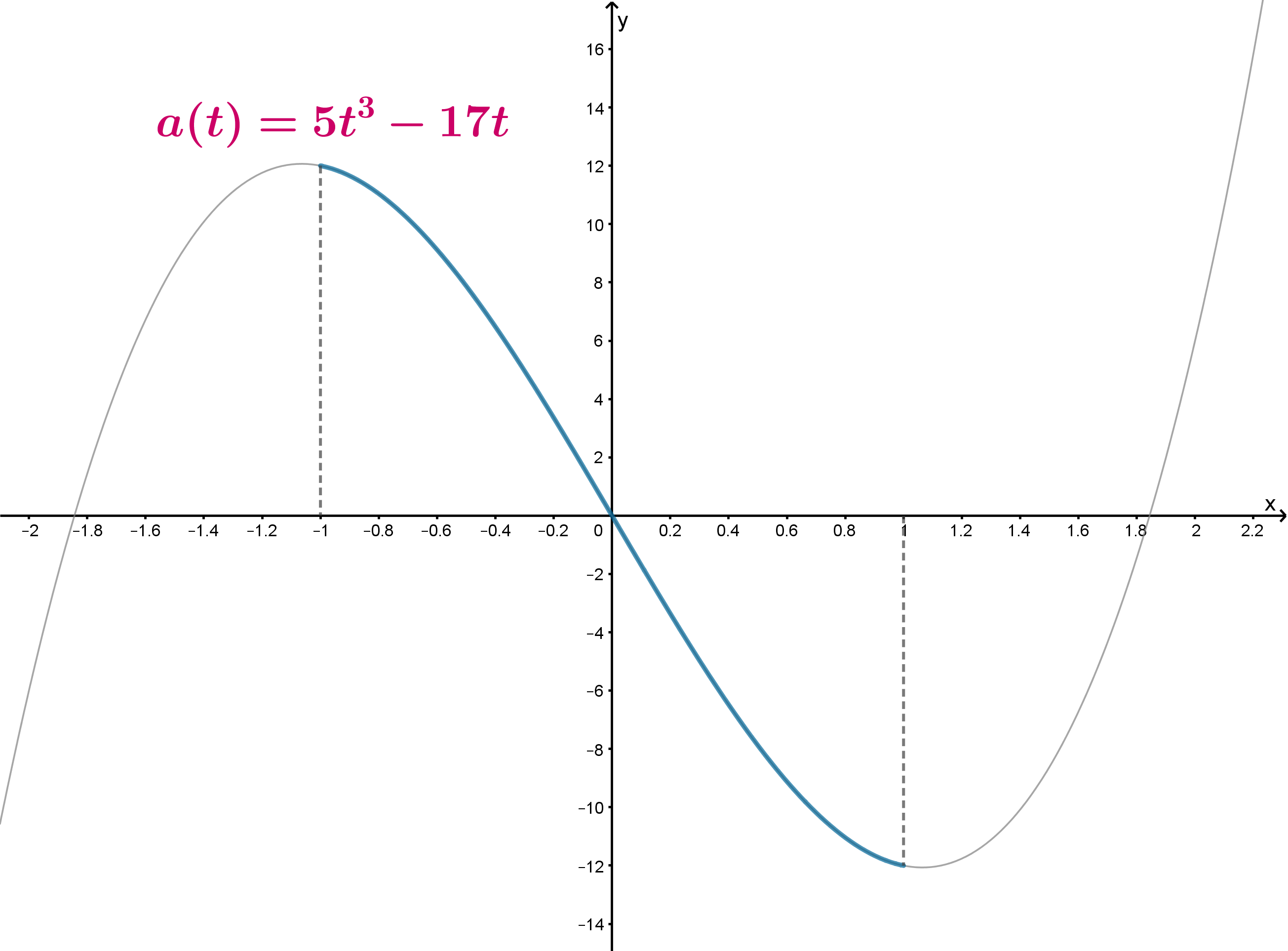
Рассмотрим функцию в системе координат
и
построим схематично ее график. Для этого исследуем ее производную:
Следовательно, производная равна нулю в точках и не существует
в точке . Определим знаки производной на промежутках, на которые эти
точки разбивают область определения производной:
При функция
убывает, при
функция возрастает.
При имеем
, при
имеем
, при
имеем .
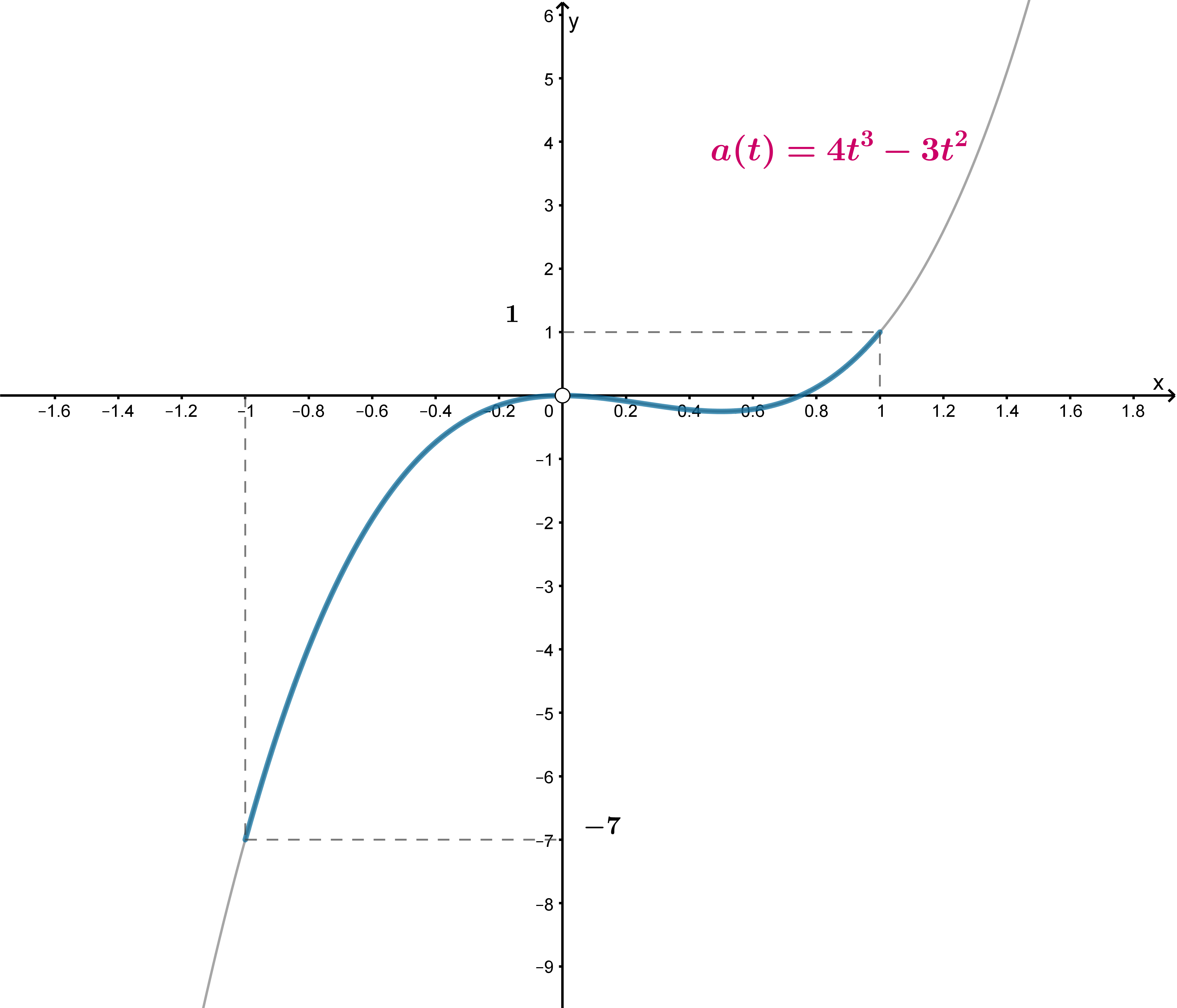
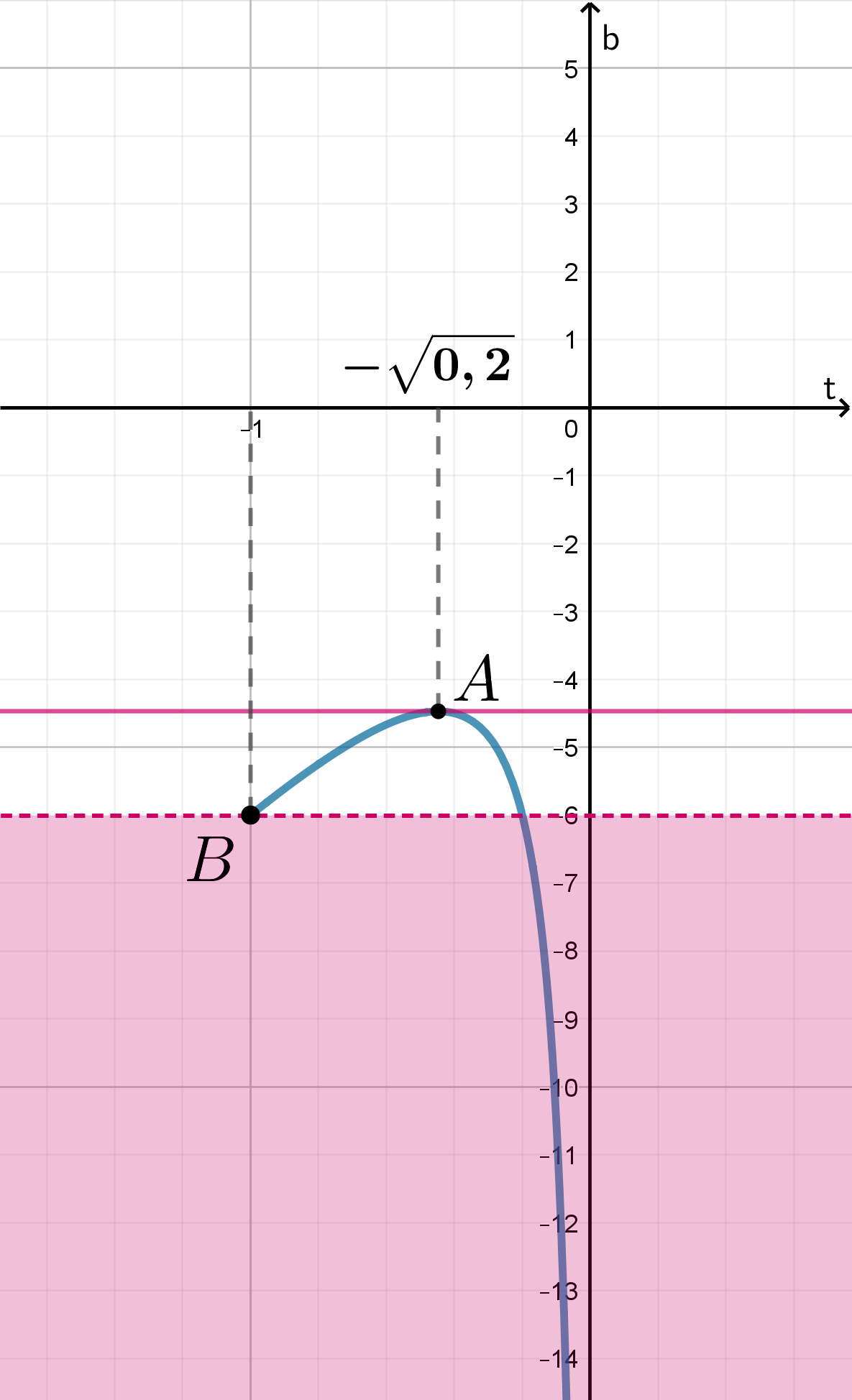
Значит, схематично график ее выглядит следующим образом:
Следовательно, ровно одну точку пересечения с графиком имеет
горизонтальная прямая , если
, то есть при
.
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно три действительных корня.
Показать ответ и решение
Заметим, что не является решением уравнения, следовательно, можно преобразовать уравнение следующим образом:
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений уравнения. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра
при каждом из которых ровно три точки вида ,
принадлежат множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая
имеет три точки пересечения с множеством
.
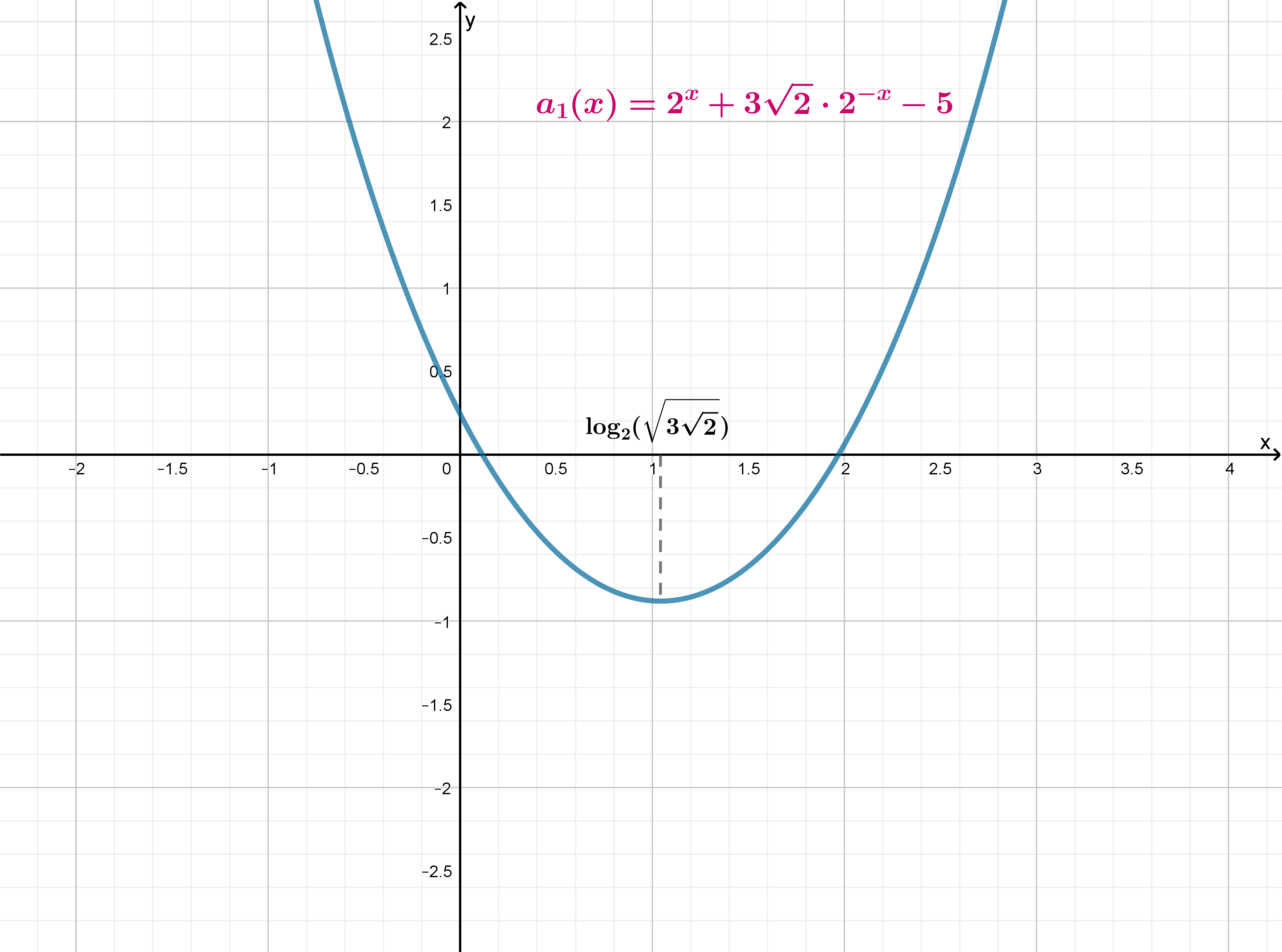
Рассмотрим функцию в системе координат
и построим схематично ее график. Для этого исследуем ее
производную:
Нулем числителя явояется , следовательно, производная равна
Таким образом, производная равна нулю при и не существует при
(точка разрыва графика функции
).
Определим знаки производной:
Следовательно, при функция
убывает, при
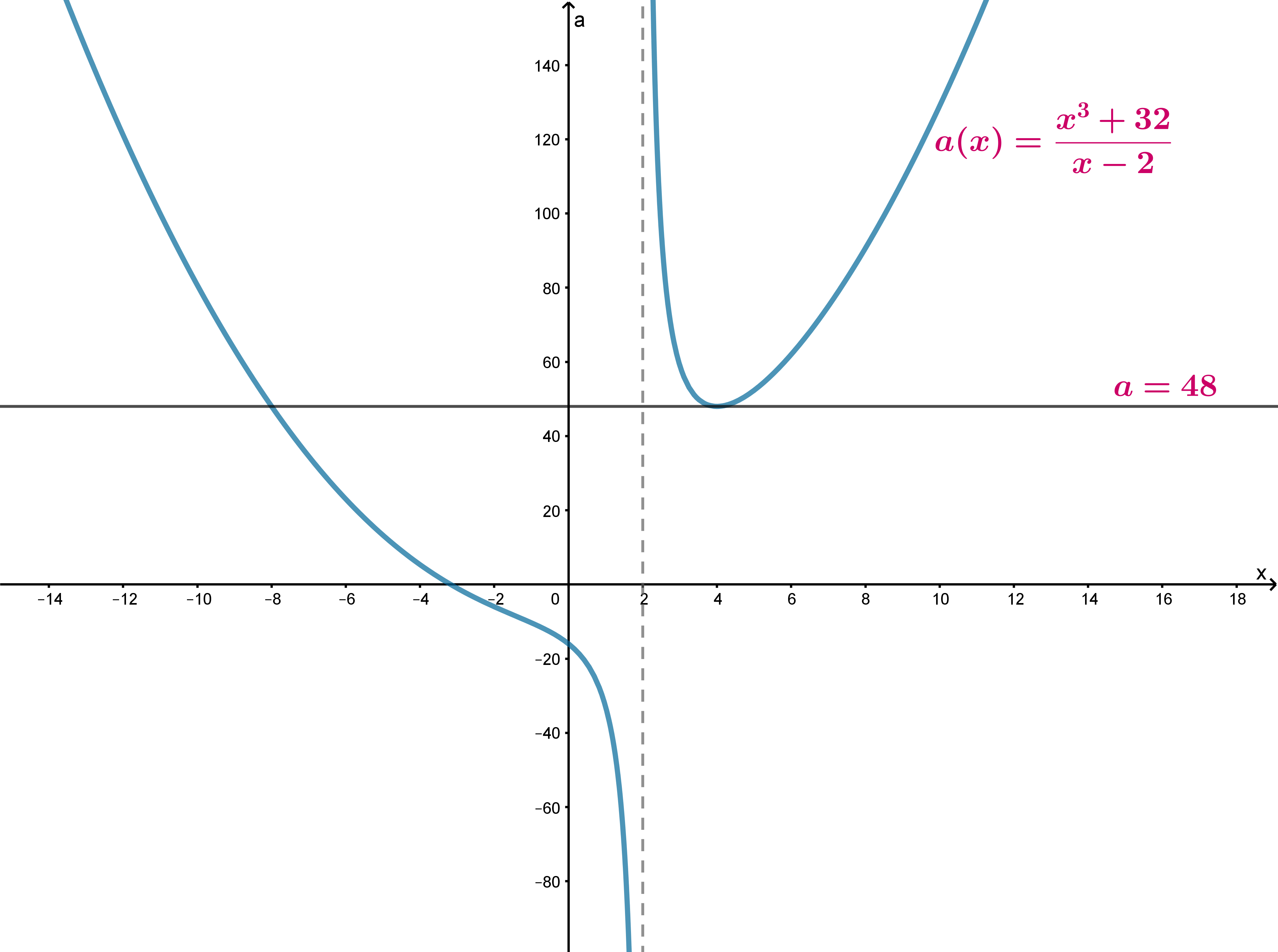
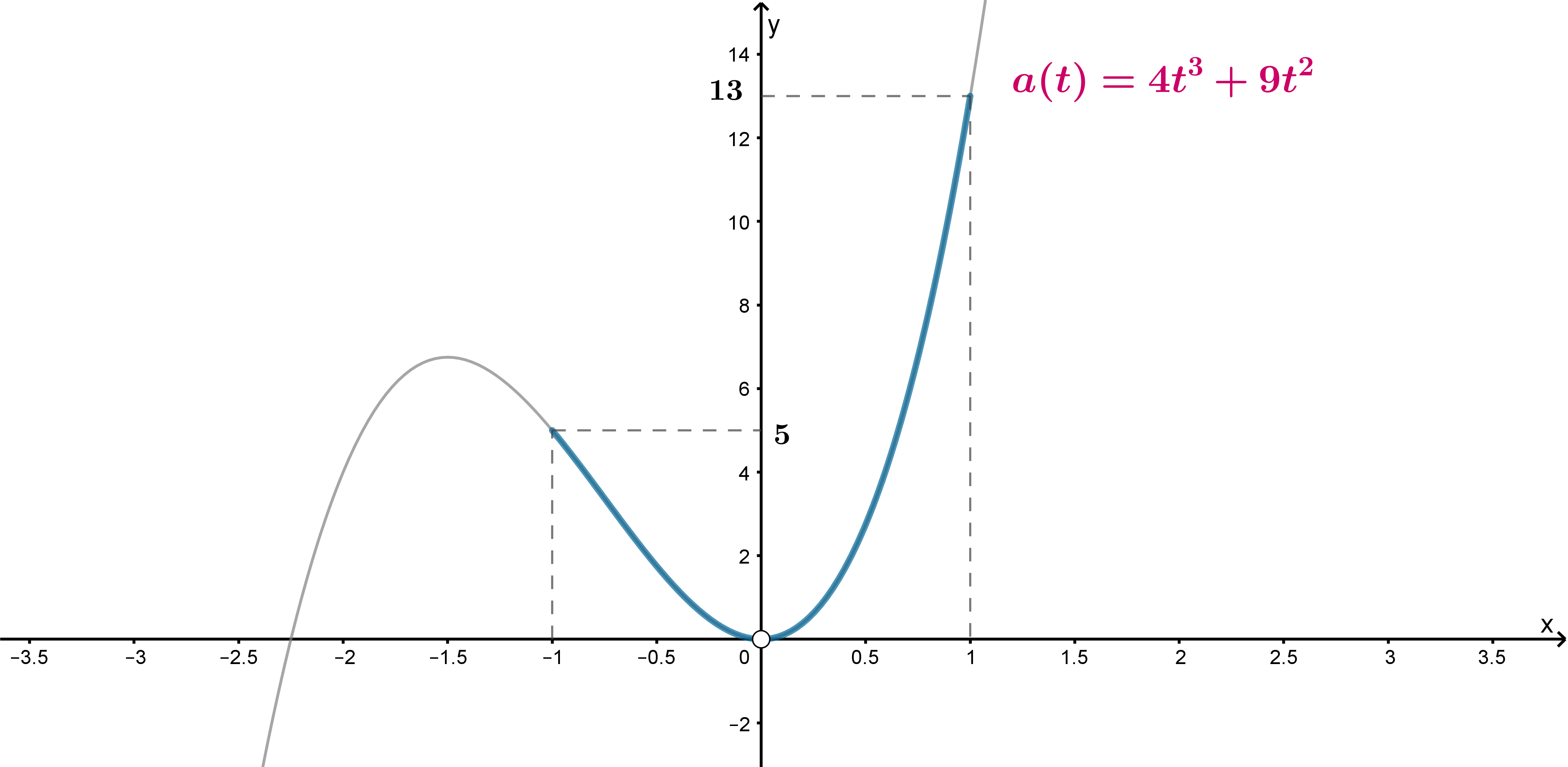
возрастает, значит, схематично ее график
выглядит следующим образом:
При имеем
; при
имеем
; при
имеем
. Тогда при всех
горизонтальная прямая имеет три точки пересечения с графиком функции
.
Так как , то ответ
Ответ:
Найдите все значения параметра при которых уравнение
имеет единственное решение.
Показать ответ и решение
Чтобы разложить числитель на множители, найдем его корни и
то есть решим квадратное относительно
уравнение:
Тогда числитель раскладывается на множители следующим образом:
Получаем, что исходное уравнение эквивалентно системе
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
системы. Если некоторая точка плоскости с координатами принадлежит этому множеству
то для
исходной задачи это означает, что если параметр принимает значение
то
будет одним из решений
системы. Нас просят найти все такие значения параметра
при каждом из которых ровно одна из точек вида
где
принадлежит множеству решений
изображенному на плоскости
Фактически
это равносильно тому, что горизонтальная прямая имеет ровно одну точку пересечения с множеством
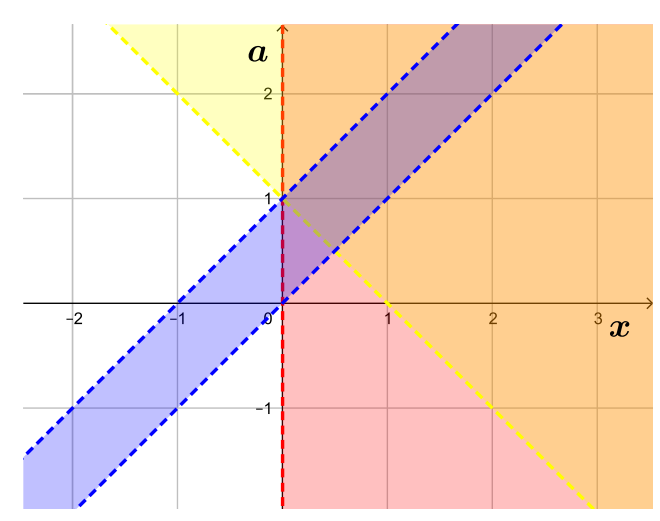
Построим на плоскости множества решений каждого из уравнений совокупности, объединим их, а затем исключим точки,
удовлетворяющие условию
Построим графики.
Множеством решений системы является объединение всех точек наклонных прямых за исключением точек пересечения с
вертикальными прямыми.
Прямые
и
пересекутся в одной точке
в чем легко убедиться подстановкой.
Найдем точки пересечения и
прямой
с прямыми
и
соответственно:
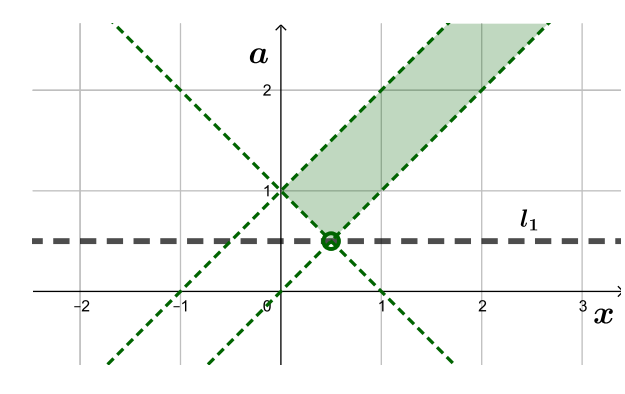
Заметим, что все горизонтальные прямые, кроме тех, которые проходят через одну из точек
или
будут иметь с
ровно две точки пересечения, а значит, нам не подойдут.
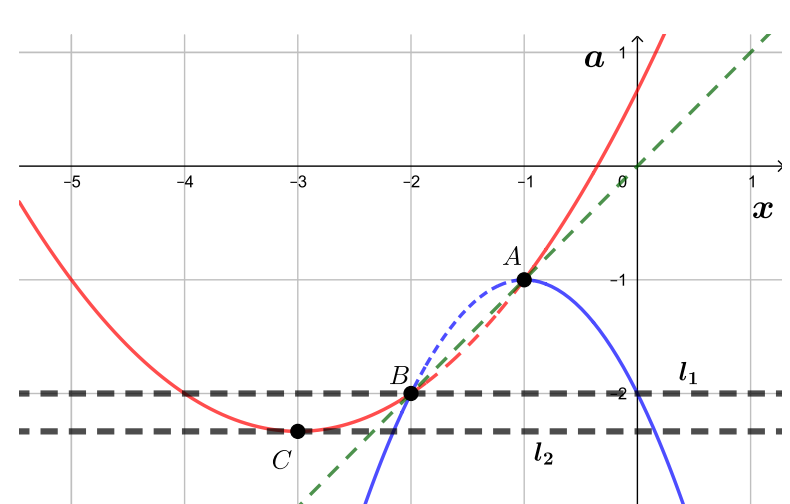
Прямые то есть прямая через точку
и
то есть прямая через точку
будут иметь с
ровно
одну точку пересечения.
Прямая то есть прямая через точку
не будет иметь с
точек пересечения.
Таким образом, подходят только прямые и
и соответствующие им значения параметра
Ответ:
Найдите все значения параметра при которых уравнение
имеет ровно три решения.
Показать ответ и решение
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
Недостаточное обоснование построения |
3 |
|
Верно найдено значение |
2 |
|
Верно сведено к исследованию графически |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите значения параметра , при которых уравнение
имеет
единственное решение.
Показать ответ и решение
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
уравнения. Если некоторая точка плоскости с координатами принадлежит этому множеству
то для
исходной задачи это означает, что если параметр принимает значение
то
будет одним из решений
уравнения. Нас просят найти все такие значения параметра
при каждом из которых ровно одна из точек вида
,
, принадлежит множеству решений
изображенному на плоскости
Фактически это
равносильно тому, что горизонтальная прямая имеет ровно одну точку пересечения с множеством
.
Значит, нам нужно понять, как выглядит график функции . Посчитаем её
производную:
Легко видеть, что производная определена на всей числовой прямой и равна нулю в точках и
.
Применим метод интервалов для определения знаков производной. Обе критические точки встречаются ровно в одном
множителе, следовательно, в них будет меняться знак.
Значит, на промежутках и
функция монотонно возрастает, а на промежутке
—
монотонно убывает. Найдем значения функции в нулях производной
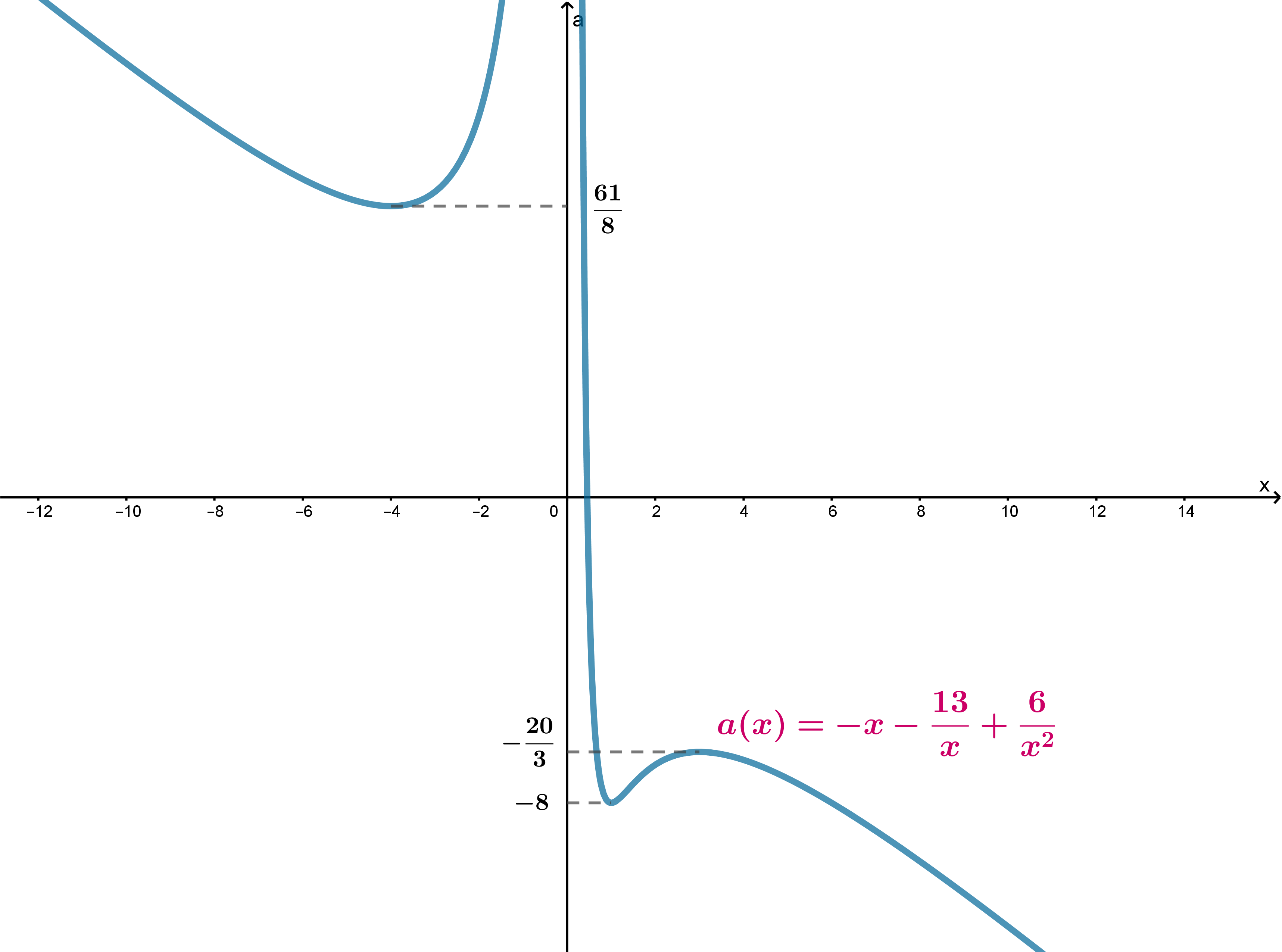
Теперь мы можем нарисовать эскиз графика.
Будем называть часть графика, расположенную левее точки , «левой ветвью», часть правее
точки — «правой ветвью», а между точками
и
— «средней частью». Заметим, что
левая ветвь может принимать сколь угодно большие по модулю отрицательные значения на промежутке
, так как
— это кубический многочлен с положительным коэффициентом при
. По
аналогичным причинам правая ветвь может принимать сколь угодно большие значения на промежутке
.
Рассмотрим все возможные положения горизонтальной прямой:
Значит, только горизонтальные прямые, которые расположены ниже , и прямые, которые расположены выше
, пересекают график
равно в одной точке. Им соответствуют следующие значения параметра:
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
где , имеет хотя бы одно решение.
Показать ответ и решение
Уравнение равносильно (так как )
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений системы. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений системы. Нас просят найти все такие значения
параметра
при
каждом из которых хотя бы одна из точек вида ,
принадлежит множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая имеет хотя бы одну точку пересечения с множеством
.
Найдем точку пересечения прямых:
Точки пересечения прямой и окружности
:
Точки пересечения прямой и окружности
:
Точки пересечения прямой и окружности
:
Точки пересечения прямой и окружности
:
Точки пересечения прямой и окружности
Точки пересечения прямой и окружности
это множество точек прямых
и
, которые лежат в голубой области.
— точка пересечения прямой
и прямой
Таким образом, все розовые положения горизонтальной прямой – это те положения, при которых она НЕ имеет общих точек со
множеством .
Прямая :
;
прямая :
;
прямая :
;
прямая :
Следовательно, ответ или
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет единственное решение.
Показать ответ и решение
Пусть , тогда уравнение имеет вид
Так как не является решением уравнения, то можно разделить обе части равенства на
, получим
Заметим, что , так как
может быть как положительным, так и отрицательным.
Сделаем замену , тогда
, следовательно, уравнение примет вид
Исследуем замену:
Если обозначить — убывающая функция, то
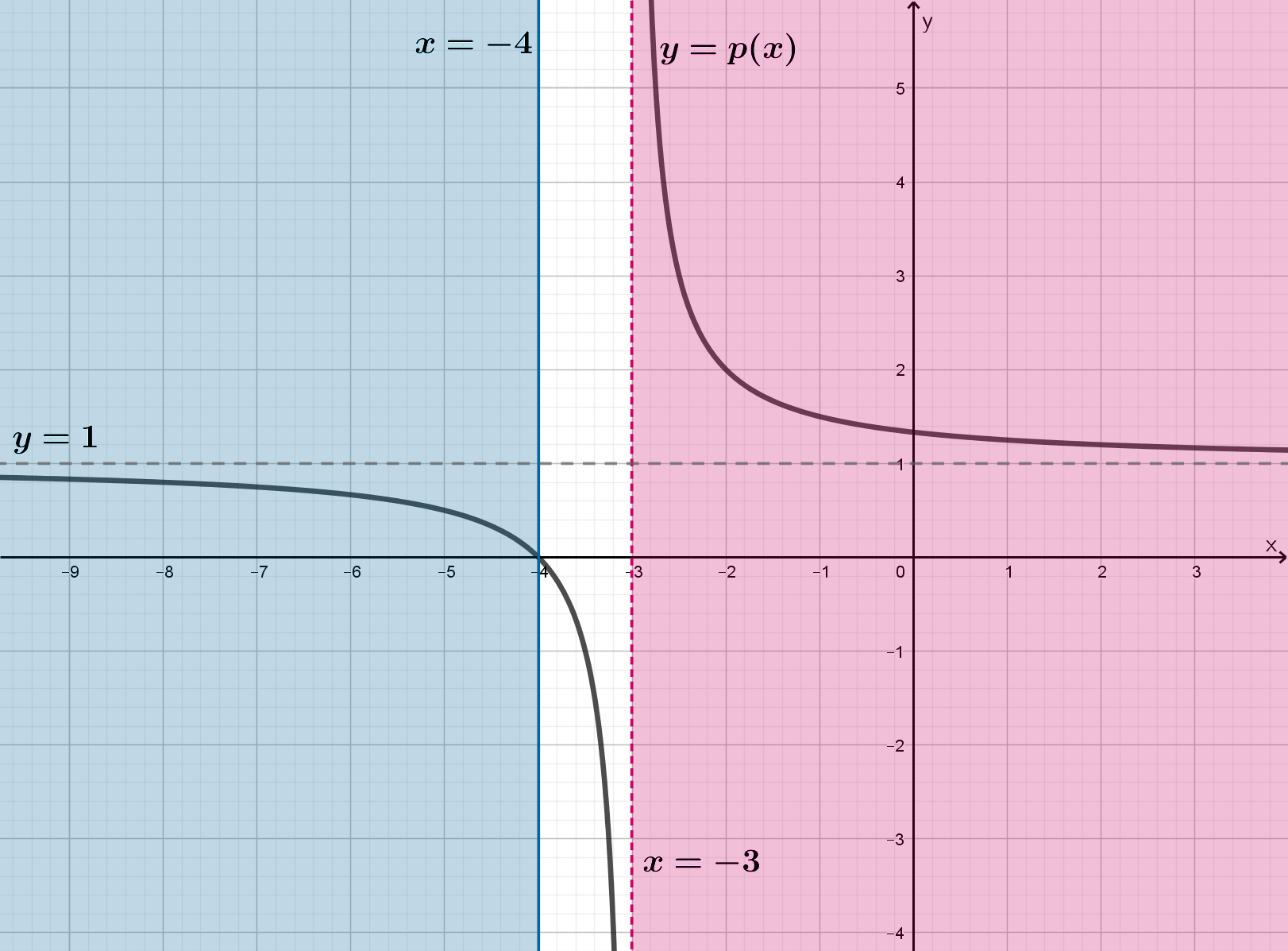
Изобразим график функции :
Заметим, что одному значению (из области значений) соответствует ровно одно значение
При функция
принимает значения от
до
, значит,
принимает значения от
до
.
При функция
принимает значения от
до
, значит,
принимает значения от
до
.
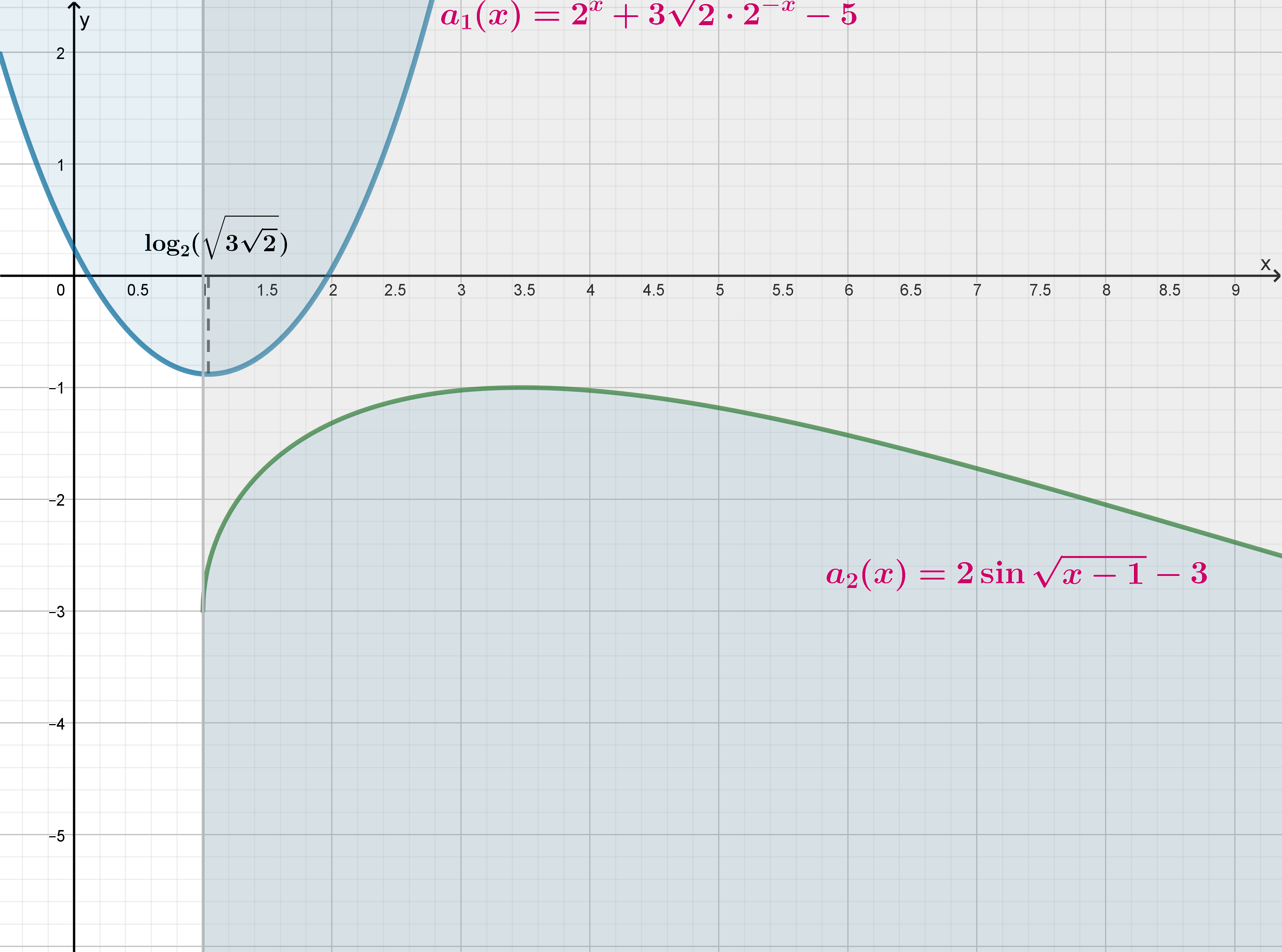
Следовательно, график выглядит следующим образом (
и
— горизонтальные асимптоты):
Значит, область значений , причем заметим, что одному значению
(из области значений) соответствует ровно
одно значение .
Изобразим график функции при
в системе координат
и найдем такие положения
горизонтальной прямой , при которых она с графиком функции
имеет ровно одну точку пересечения:
Следовательно,
Графики функций и
рисовать было необязательно, они изображены лишь для наглядности области значений
функций.
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет ровно один корень на отрезке
Показать ответ и решение
Исходное уравнение равносильно системе
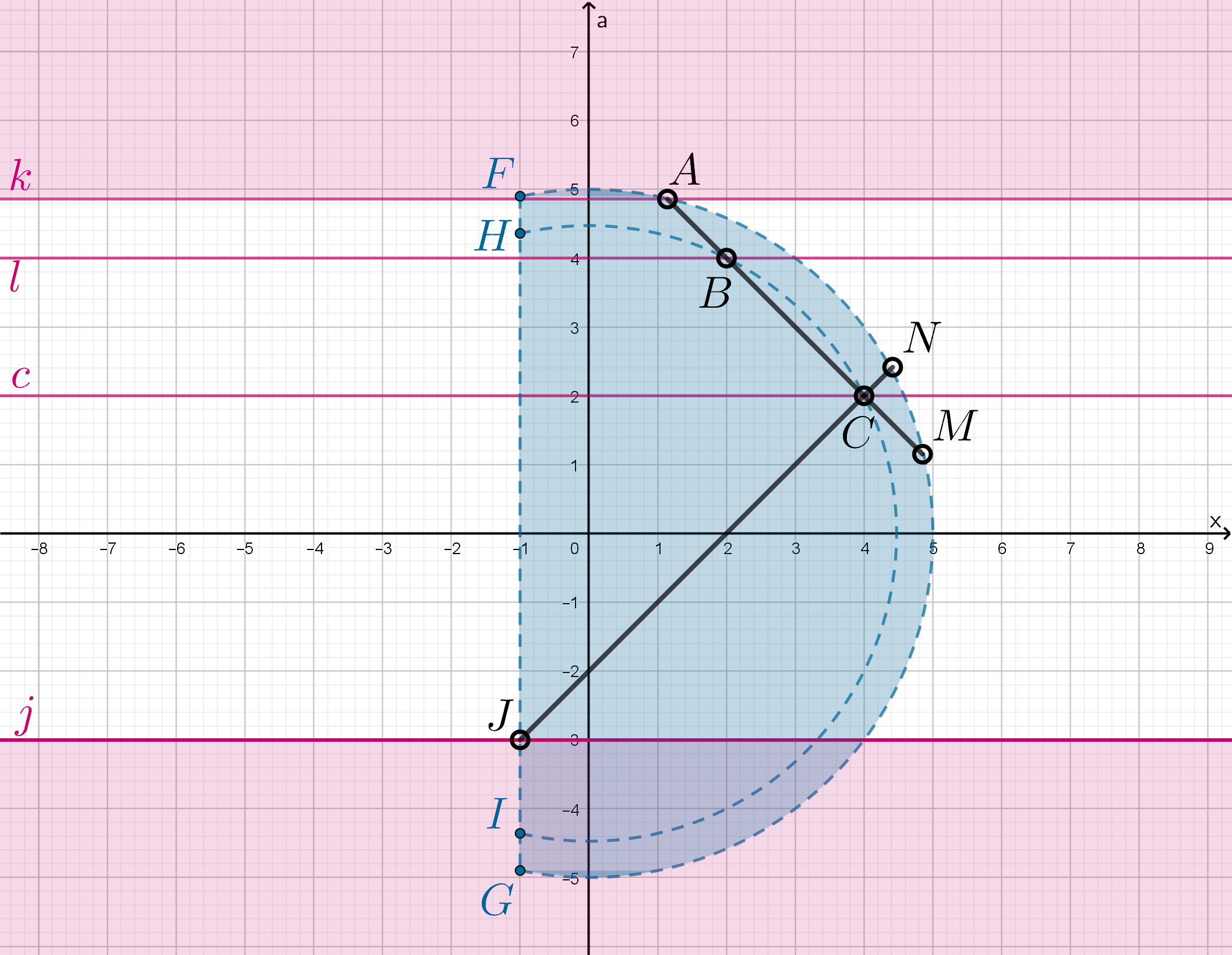
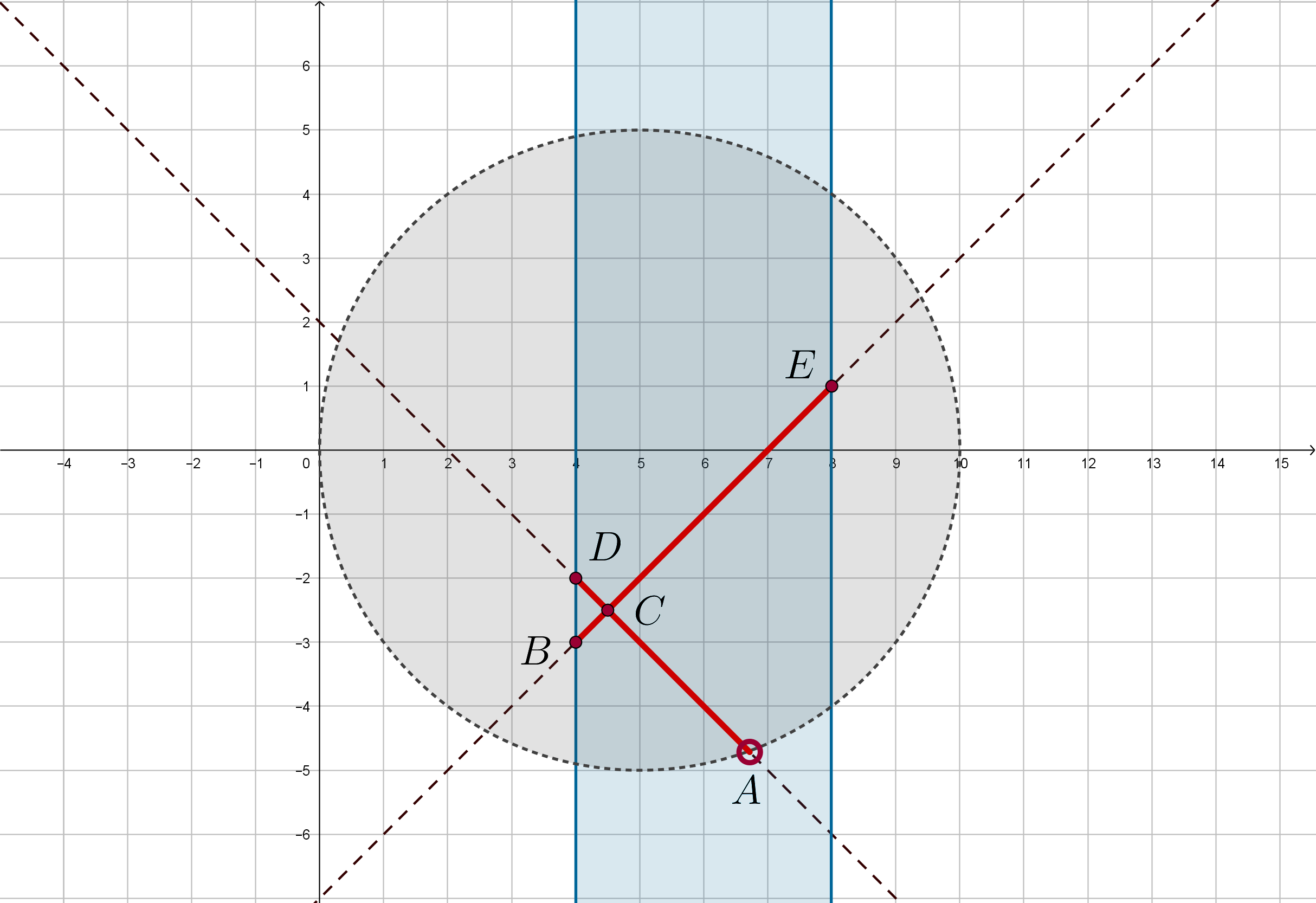
Исследуем данную систему графически в системе координат
Решением системы является множество точек, принадлежащих прямым и лежащих внутри круга с
центром и радиусом 5.
Рассмотрим из этих точек только те, у которых Если для некоторого фиксированного
имеется ровно одна точка
с такой ординатой, то такое нам подходит. Остальные
нам не подходят.
Найдем координаты точек пересечения прямых
и
между собой, с вертикальными
прямыми и
и с окружностью:
Тогда исходное уравнение имеет ровно один корень на отрезке при
Ответ:
Критерии оценки
|
Содержание критерия |
Балл |
|
Обоснованно получен верный ответ |
4 |
|
С |
3 |
|
С |
2 |
|
Верно получена хотя бы одна граничная |
1 |
|
Решение не соответствует ни одному из |
0 |
|
Максимальный балл |
4 |
Найдите все значения параметра , при каждом из которых уравнение
имеет ровно 6 корней на отрезке .
Показать ответ и решение
Пусть , а
. Исследуем, сколько решений относительно переменной
должно иметь исходное уравнение. Так как
, то исходное уравнение должно иметь 6 решений
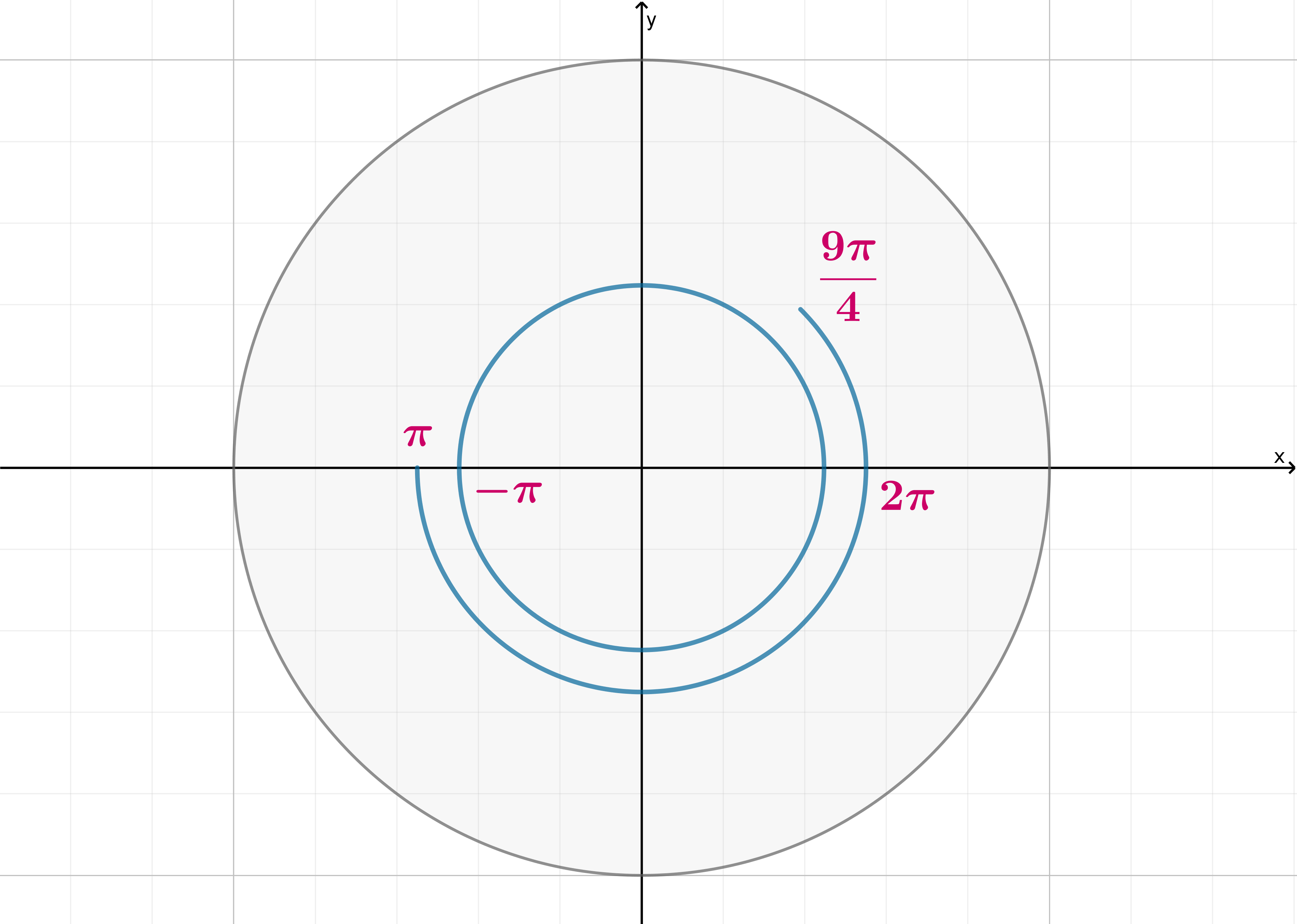
. Отметим этот отрезок на единичной окружности:
- I тип.
дает два решения
;
- II тип.
дает два решения
;
- III тип.
дает три решения
;
- IV тип.
дает четыре решения
Исходное уравнение относительно переменной имеет следующий вид:
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений неравенства. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений неравенства. Нас просят найти все такие значения
параметра
при каждом имеются точки ,
, принадлежащие множеству решений
изображенному на плоскости
, такого вида,
что суммарно получается 6 решений , где
.
Фактически это равносильно тому, что горизонтальная прямая имеет такие точки пересечения с множеством
.
Изобразим множество на координатной плоскости
, учитывая, что
:
Видим, что горизонтальная прямая со множеством
имеет либо одну, либо две точки пересечения. Так как не существует
такого , которое даст 6 решений
, то горизонтальная прямая должна пересекать изображенное множество в двух точках,
причем это точки либо I и IV типа, либо II и IV типа, либо обе III типа. Заметим, что одна из точек — это при любом
положении прямой , а
. Следовательно, вторая точка также должна быть III типа, причем отлична от
Так как , то
.
Ответ:
Найдите все значения параметра , при каждом из которых неравенство
не имеет решений.
Показать ответ и решение
Рассмотрим функции и
. Тогда неравенство примет вид
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений неравенства. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений неравенства. Нас просят найти все такие значения
параметра
при каждом из которых не существует точек вида ,
, принадлежащих множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая
не имеет точек пересечения с множеством
.
Построим графики функций и
. Для этого требуется исследовать данные функции.
-
Функция
является композицией двух функций:
и
, то есть
. Функция
возрастающая, следовательно, характер монотонности функци
определится, если исследовать функцию
:
Производная равна нулю при
и не существует при
, следовательно, эти точки разбивают ее область определения на
промежутки, знаки на которых следующие:Учитывая, что
, на промежутке
функция
возрастает, а при
убывает.
Так как
то при
функция
убывает, а при
эта функция возрастает (композиция двух
функций одинакового характера монотонности — возрастающая, а разного — убывающая).Тогда график функции
выглядит следующим образом:
-
Функция
является композицией двух функций:
и
, то есть
. Функция
возрастающая, следовательно, характер монотонности функциопределится, если исследовать функцию
, у которой
промежутки возрастания/убывания такие же, как у функции.
Следовательно, учитывая, что
при
и
,
функция
возрастает, а при
,
функция убывает.
Так как
то при
и
,
функция
возрастает, а при
,
функция убывает (композиция двух функций одинакового характера
монотонности — возрастающая, а разного — убывающая).Тогда график функции
выглядит следующим образом:
Изобразим оба графика на одной координатной плоскости. Для этого найдем значения функций в некоторых точках:
Тогда решением неравенства будет множество , которое является объединением области 1 и области 2, где
область 1: пересечение областей над графиками функций и
, включая график
и исключая график
;
область 2: пересечение областей под графиками функций и
, включая график
и исключая график
.
Исходное неравенство не имеет решений, если горизонтальная прямая не пересекает закрашенную область
, то есть
находится в полосе между (включая это значение) и
(исключая это значение). Значит, ответ:
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет на отрезке ровно один корень.
Показать ответ и решение
Пусть . Тогда при
,
, уравнение равносильно
Следовательно, полученное уравнение должно иметь единственное решение .
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений уравнения. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра
при каждом из которых имеются точки вида ,
, принадлежащие множеству решений
изображенному на
плоскости Фактически это равносильно тому, что горизонтальная прямая
имеет точки пересечения
,
удовлетворяющие условию , с множеством
.
Исследуем функцию :
. Производная равна нулю в точках
, следовательно, при
производная положительна, значит, функция возрастает, а при
производная отрицательна, значит, функция
убывает.
Определим:
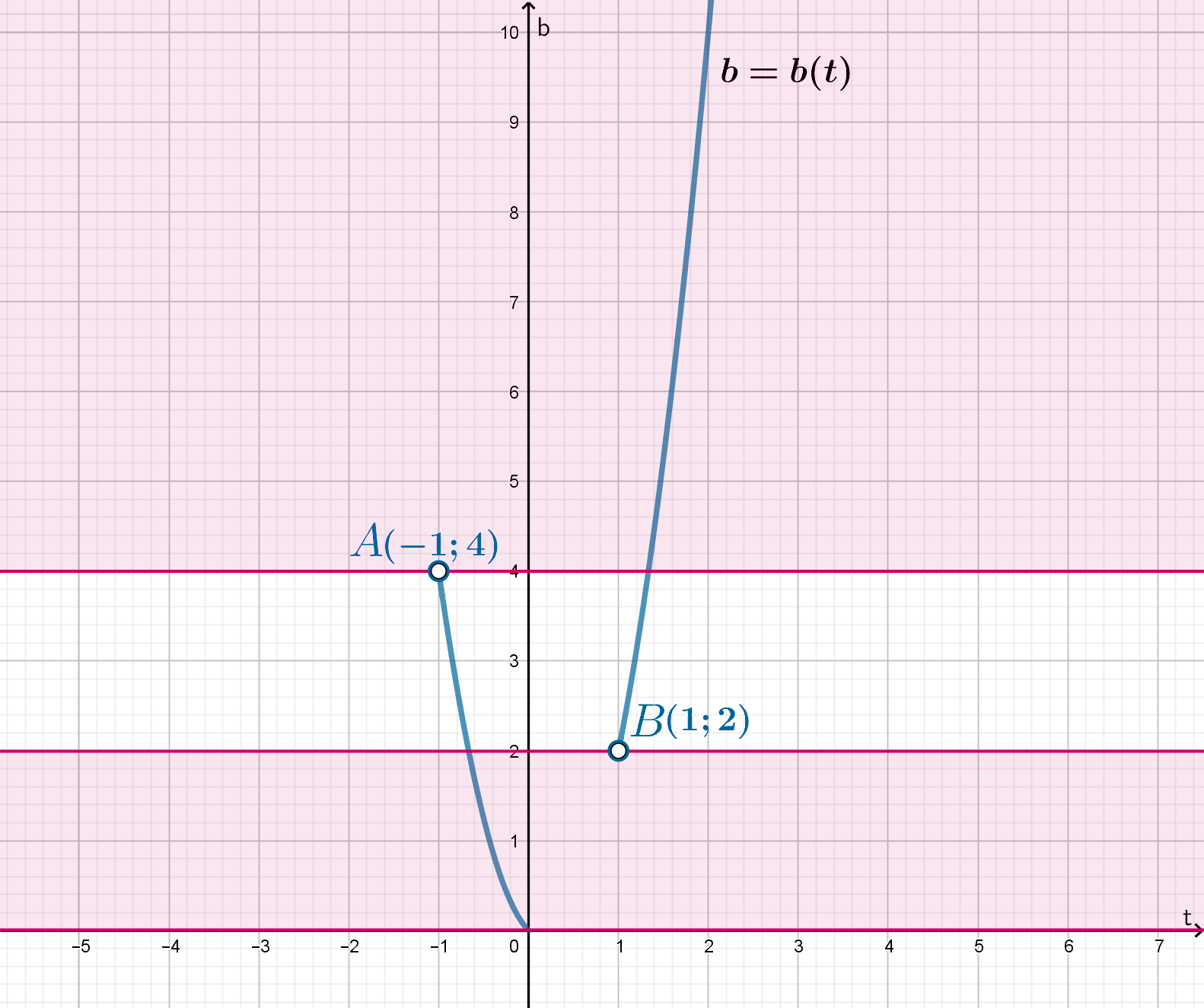
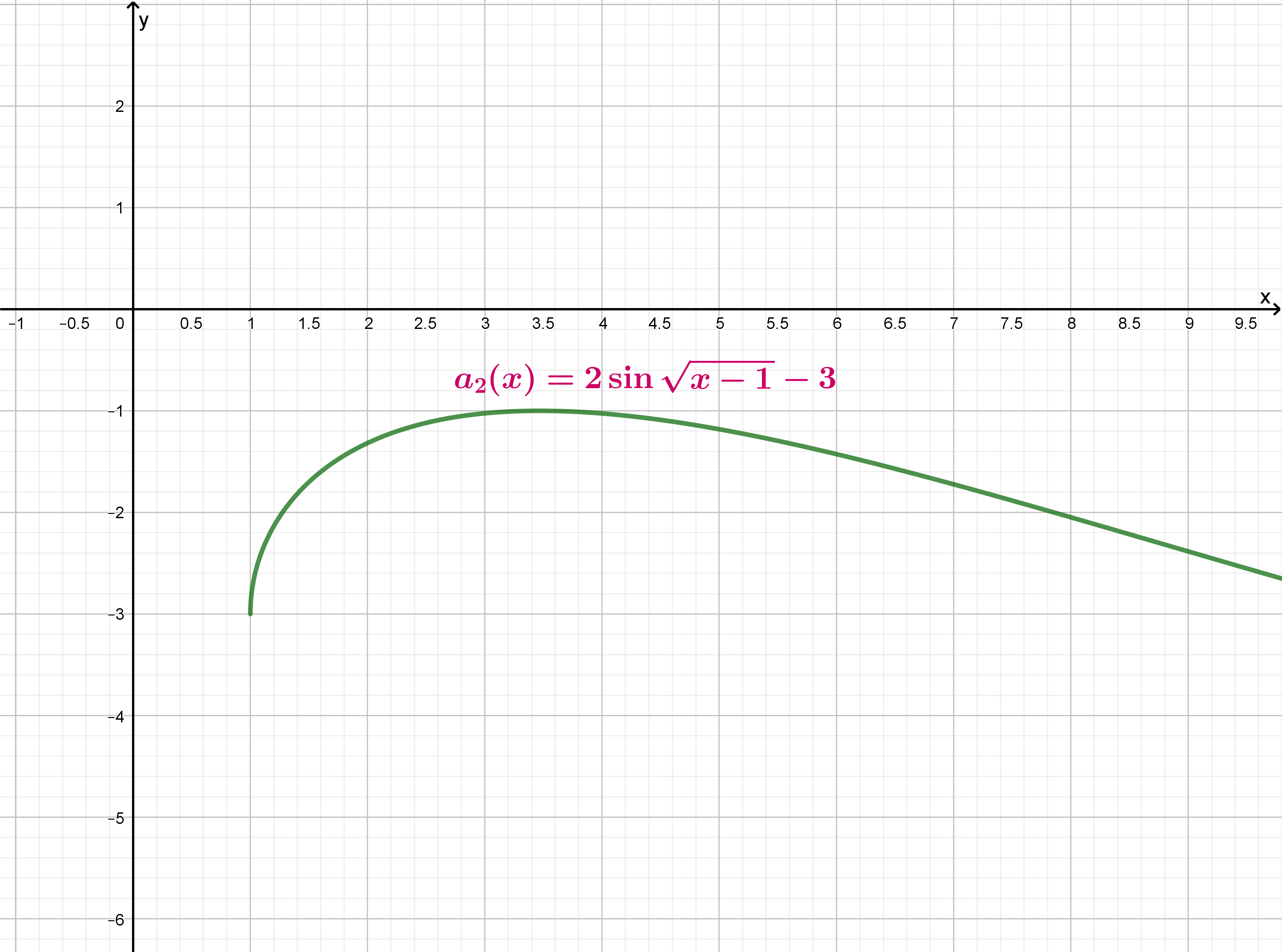
Тогда на промежутке схематично график этой функции выглядит следующим образом:
Следовательно, единственное решение уравнение имеет тогда, когда горизонтальная прямая имеет одну точку пересечения с
изображенным графиком, следовательно, , то есть при
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы один корень.
Показать ответ и решение
Так как , то после замены
уравнение примет вид
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений уравнения. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра
при каждом из которых имеются точки вида ,
, принадлежащие множеству решений
изображенному на
плоскости Фактически это равносильно тому, что горизонтальная прямая
имеет точки пересечения
,
удовлетворяющие условию , с множеством
.
Рассмотрим функцию в системе координат
и построим схематично ее график. Для этого исследуем ее
производную:
Производная положительна при , следовательно, на этом промежутке функция возрастает, и отрицательна при
, следовательно, на этом интервале функция убывает.
Следовательно, на промежутке график функции выглядит следующим образом:
Следовательно, решения у уравнения будут в том случае, если горизонтальная прямая такова, что
, то есть
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет решения.
Показать ответ и решение
Применяя формулы ,
, получаем
Пусть и
, тогда получаем
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений уравнения. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра
при каждом из которых имеются точки вида ,
, принадлежащие множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая
имеет точки пересечения
, удовлетворяющие условию
, с множеством
.
Рассмотрим функцию в системе координат
и построим схематично ее график. Для этого исследуем ее
производную:
Так как дискриминант скобки отрицательный, то
, следовательно,
, значит, функция
возрастает при всех
Тогда горизонтальная прямая имеет точки пересечения с графиком функции
на
в том случае, если
, то есть при
. Тогда
Ответ:
Найдите все значения параметра , при каждом из которых уравнение
имеет решения.
Показать ответ и решение
Пусть , тогда
и уравнение при всех
равносильно
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений уравнения. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений уравнения. Нас просят найти все такие значения
параметра
при каждом из которых имеются точки вида ,
, принадлежащие множеству решений
изображенному на
плоскости Фактически это равносильно тому, что горизонтальная прямая
имеет точки пересечения
,
удовлетворяющие условию , с множеством
.
Рассмотрим функцию в системе координат
и построим схематично ее график. Для этого исследуем ее
производную:
Нули производной , следовательно, на промежутках
и
функция возрастает, на промежутке
функция убывает. Так как
содержится в
, то на исследуемом промежутке функция убывает,
следовательно, схематично график ее выглядит следующим образом:
Следовательно, горизонтальная прямая должна удовлетворять условию
, то есть
Ответ:
Найдите все значения , при каждом из которых система
имеет единственное решение.
(МГУ, 2001)
Показать ответ и решение
Систему можно переписать в виде
Сделаем замену Тогда новая система
должна также иметь единственное решение.
Заметим, что не является решением неравенства
следовательно,
можно разделить обе части двойного неравенства на Получим:
Пусть Тогда неравенство
должно иметь единственное решение
Будем рассматривать параметр как переменную. Построим в системе
координат множество
решений неравенства. Если некоторая точка
плоскости с координатами принадлежит этому множеству
то для
исходной задачи это означает, что если параметр принимает значение
то
будет одним из решений системы. Нас просят найти все такие значения
параметра при каждом из которых ровно одна точка вида
,
принадлежит множеству решений изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая имеет ровно
одну точку пересечения с множеством .
Рассмотрим функции и
в системе координат
Тогда решением неравенства
будут являться те части плоскости
которые находятся не ниже параболы (то есть это точки на границе
параболы или внутри параболы) и не выше параболы (то есть
это точки на границе параболы и внутри параболы). Следовательно, получаем
следующую область:
Заметим, что нам подходят только два положения горизонтальной прямой
при которых эта прямая с множеством
имеет ровно одну общую точку.
Эти прямые — прямая, проходящая через точку (абсцисса которой
положительна) пересечения парабол и
и прямая, проходящая
через вершину параболы
Вершина параболы — точка
Найдем координаты точки
Следовательно, эти прямые задаются уравнениями и
то есть
подходящие нам значения параметра — это
Ответ:
Найдите все значения параметра при каждом из которых уравнение
имеет четыре различных корня.
Показать ответ и решение
Мы имеем уравнение следующего типа:
Следовательно, наше уравнение преобразуется следующим образом:
Будем рассматривать параметр как переменную. Построим в системе
координат множество
решений системы. Если некоторая точка
плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если параметр принимает
значение то
будет одним из решений системы. Нас просят найти все
такие значения параметра
при каждом из которых ровно четыре
точки вида , где
принадлежат множеству решений
изображенному на плоскости Фактически это равносильно тому, что
горизонтальная прямая имеет ровно четыре точки пересечения с
множеством
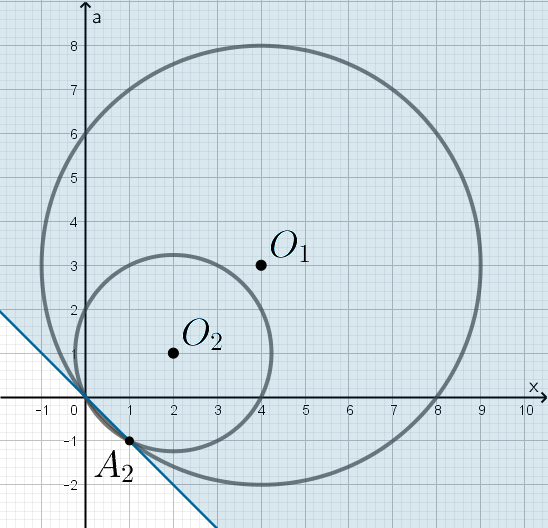
Неравенство системы задает множество точек плоскости
находящихся не ниже прямой Первое и второе уравнения совокупности
задают две окружности.
Первое — окружность с центром в точке радиуса
Второе — окружность с центром в точке радиуса
Заметим, что обе окружности проходят через начало координат, так как в
уравнениях совокупности отсутствуют свободные члены. Следовательно, если
подставить и
уравнения будут верными равенствами.
Тогда — первая точка пересечения окружностей и прямой
Найдем вторую точку пересечения каждой окружности с этой прямой.
Для первой окружности и прямой получаем систему:
Для второй окружности и прямой получаем систему:
Следовательно, вторая точка пересечения первой окружности с прямой
совпадает со второй точкой пересечения второй окружности с прямой. Назовем эту
точку
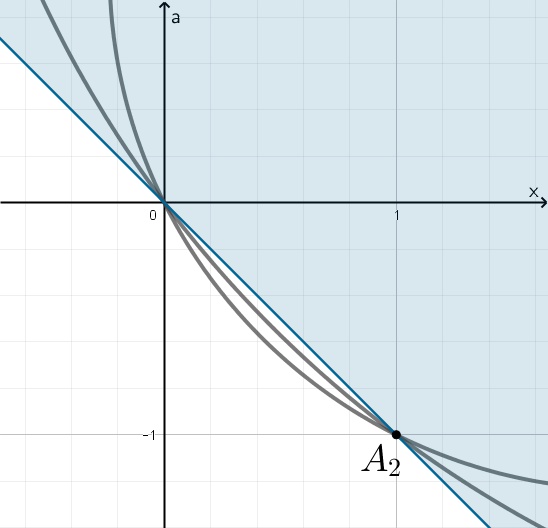
Следовательно, получаем рисунки ниже (на рис. 2 приближено пересечение
прямой с окружностями).
Рис. 1
Рис. 2
Следовательно, части окружностей, находящиеся между их точками
пересечения, не лежат в области Таким образом, множество
решений
системы, а значит и исходного уравнения, на плоскости выглядит
следующим образом:
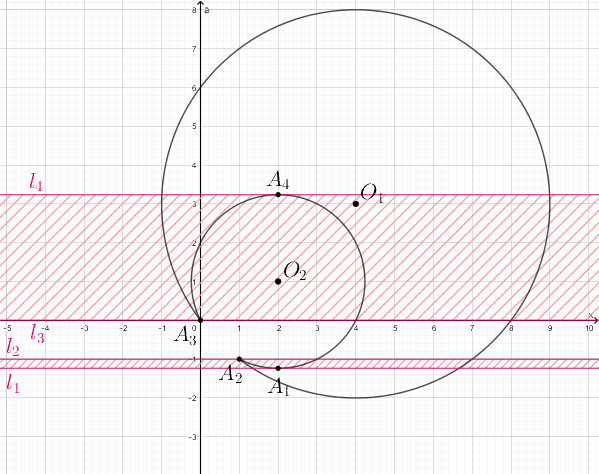
Закрашенные области (между прямыми и
и
, но не включая эти
прямые!) — это те области, в которых может располагаться прямая чтобы
иметь четыре точки пересечения со множеством Каждая
— горизонтальная
прямая, проходящая через
- 1.
- Ордината точки
ищется как разность ординаты центра
окружности и радиуса этой окружности, то есть эта ордината равна
Следовательно, уравнение прямой
- 2.
- Ордината точки
равна -1, следовательно, уравнение
- 3.
- Точка
— начало координат, следовательно, уравнение
- 4.
- Ордината
ищется как сумма ординаты центра
окружности и ее
радиуса, следовательно, эта ордината равнаЗначит, уравнение
Таким образом, подходящие значения параметра:
Ответ:
При каких значениях уравнение
имеет ровно один корень на ?
Показать ответ и решение
1 способ.
Заметим, что не является решением этого уравнения, следовательно, можно разделить обе части равенства на
и
получим
Если исходное уравнение должно иметь ровно один корень на отрезке то новое уравнение должно иметь один корень на
полуинтервале (выше сказали, что
).
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений системы. Если
некоторая точка плоскости с координатами принадлежит этому множеству
то для исходной задачи это означает, что если
параметр принимает значение
то
будет одним из решений системы. Нас просят найти все такие значения
параметра
при
каждом из которых одна точка вида ,
принадлежат множеству решений
изображенному на плоскости
Фактически это равносильно тому, что горизонтальная прямая
имеет одну точку пересечения с множеством
.
Множество представляет собой график функции
. Исследуем эту функцию:
Производная равна нулю в точках , разрывна в точке
, причем при
производная
положительна, следовательно, функция возрастает, а при производная отрицательна, следовательно, функция
убывает.
Таким образом, так как , а при
имеем
, график функции
выглядит следующим
образом:
Розовым цветом показана область, в которой может находиться горизонтальная прямая , чтобы иметь с графиком
на
промежутке ровно одну точку пересечения.
Найдем :
, следовательно,
Найдем :
, следовательно,
Таким образом, или
откуда
или
2 способ.
Для начала заметим, что если , то
.
Теперь сделаем замену ,
, тогда
и исходное уравнение равносильно системе:
При этом, зная решение системы , можно найти корень исходного уравнения, сделав обратную замену:
То, что корень исходного уравнения лежит на промежутке , равносильно тому, что решение системы лежит на промежутке
, так как
Тогда количество корней в исходном уравнении на отрезке будет совпадать с количеством корней в системе
Таким образом, достаточно найти такие значения , при которых система имеет ровно одно решение.
Квадратное уравнение имеет корни (необязательно различные) при . Обозначим их за
и
. По теореме Виета произведение
корней равно , то есть оба корня одного знака.
Для того, чтобы система имела решение, один из корней должен лежать на отрезке , т.е. он не может быть положительным.
Тогда оба корня уравнения должны быть отрицательными.
При этом также по теореме Виета сумма корней равна и должна быть отрицательной, откуда следует, что
.
Рассмотрим два случая: когда (корни совпадают) и когда
(корни различные):
-
:
При
получим
Т.е. система имеет ровно одно решение.
-
:
При положительном дискриминанте уравнение имеет два различных отрицательных корня
и
.
При этом выполнено.
Если
, то оба корня лежат на отрезке
, т.е. система имеет два различных решения, что нам не подходит. Тогда
, т.е.
Если
, то оба корня не принадлежат отрезку
, т.е. система не имеет решений, что нам также не подходит. Тогда
, т.е.
Получили, что в случае
решение будет единственным на отрезке при
Тогда исходная система имеет ровно одно решение на отрезке при
Ответ:
Ответ:
Найдите все значения параметра , при которых неравенство
имеет
хотя бы одно решение.
Показать ответ и решение
Упростим первую систему
Упростим вторую систему
Заметим, что при
Таким образом, мы получили, что вторая система не имеет решений ни при каких .
Далее будем работать только с упрощенной версией первой системы, т.к. только она дает какие-то
решения.
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
системы. Если некоторая точка плоскости с координатами принадлежит этому множеству
, то для
исходной задачи это означает, что если параметр принимает значение
, то
будет одним из решений системы.
Нас просят найти все такие значения параметра
, при каждом из которых хотя бы одна из точек вида
принадлежит множеству решений
, изображенному на плоскости
. Фактически это
равносильно тому, что горизонтальная прямая имеет хотя бы одну точку пересечения с множеством
.
Построим на плоскости множества решений каждого из неравенств системы, а затем пересечем их.
Пересекая описанные области, получим итоговое множество решений (закрашено зеленым).
Любая горизонтальная прямая строго выше прямой будет иметь пересечения с множеством
,
следовательно, при таких система будет иметь решения. При всех остальных положениях горизонтальной прямой ее
пересечение с будет пустым. Следовательно, ответ
Ответ:
Найдите все значения параметра , при которых уравнение
имеет
ровно два решения.
Показать ответ и решение
Будем рассматривать параметр как переменную. Построим в системе координат
множество
решений
совокупности. Если некоторая точка плоскости с координатами принадлежит этому множеству
, то для
исходной задачи это означает, что если параметр принимает значение
, то
будет одним из решений системы.
Нас просят найти все такие значения параметра
, при каждом из которых ровно две из точек вида
принадлежат множеству решений
, изображенному на плоскости
. Фактически это
равносильно тому, что горизонтальная прямая имеет ровно две точки пересечения с множеством
.
Из совокупности мы видим, что «выше» прямой решением будут точки графика параболы
,
а на оставшейся части плоскости (т.е. «ниже» и включая прямую ) решением будут точки графика параболы
.
Найдем точки пересечения парабол.
То есть параболы пересекаются в точках и
. Заметим, что
обе эти точки лежат на прямой «разделения» . Вершина параболы
совпадает с точкой
(легко проверить
подставлением), а вершина параболы это точка
Построим графики. Красным изображена парабола , пунктирная ее часть не удовлетворяет условию
.
Синим изображена парабола , пунктирная ее часть не удовлетворяет условию
. Зеленым изображена линия
«разделения» .
Множеством решений системы является объединение всех точек сплошных частей синего и красного
графиков.
По графику видим, что все горизонтальные прямые, которые «выше», чем (прямая через
) будут иметь ровно две точки пересечения с
. Здесь важно отметить, что горизонтальная прямая,
проходящая через будет касательной к параболе
в ее вершине, следовательно, будет иметь с ней ровно
одну точку пересечения. Прямые и
(прямая через
) будут иметь с
ровно три
точки пересечения. Любая прямая между и
будет иметь четыре точки пересечения с
. Любая
прямая «ниже» снова будет иметь ровно две точки пересечения с
. Таким образом, в ответ войдут
интервалы
Ответ:
Найдите все значения параметра при которых множество решений неравенства
не содержит ни одного решения неравенства
Показать ответ и решение
Ответ:
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите все значения параметра k, при каждом из которых уравнение имеет хотя бы одно решение на интервале
2
Найдите все значения k, при каждом из которых уравнение
имеет хотя бы одно решение на отрезке
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C).
3
Определите, при каких значениях параметра a уравнение
имеет ровно два решения.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
4
Найдите все значения параметра a, при каждом из которых уравнение
имеет корни, но ни один из них не принадлежит интервалу (4; 19).
5
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы один корень на отрезке [5; 23].
Пройти тестирование по этим заданиям
23 апреля 2017
В закладки
Обсудить
Жалоба
Параметры. От простого к сложному. Практикум по решению задач
Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение.
Теоретическое изучение физических процессов, решение экономических задач часто приводит к различным уравнениям или неравенствам, содержащим параметры, и необходимой частью их решения является исследование характера процесса в зависимости от значений параметров. Таким образом, задачи с параметрами представляют собой небольшие исследовательские задачи.
Автор: Агашкова Надежда Анатольевна.
pr-sl-p.pdf
Задачи с параметрами на ЕГЭ по математике
Анна Малкова
Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №17.
И знать здесь действительно нужно много.
Лучше всего начать с темы «Элементарные функции и их графики».
Повторить, что такое функция, что такое четные и нечетные функции, периодические, взаимно обратные.
Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).
Освоить преобразования графиков функций и приемы построения графиков.
И после этого – учимся решать сами задачи №17 Профильного ЕГЭ.
Вот основные типы задач с параметрами:
Что такое параметр? Простые задачи с параметрами
Базовые элементы для решения задач с параметрами
Графический способ решения задач с параметрами
Квадратичные уравнения и неравенства с параметрами
Использование четности функций в задачах с параметрами
Условия касания в задачах с параметрами
Метод оценки в задачах с параметрами
Вот пример решения и оформления задачи с параметром
Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 18
И несколько полезных советов тем, кто решает задачи с параметрами:
1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.
— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.
— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.
2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.
Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».
3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.
4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.
На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 17 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Сразу оговорюсь — для того, чтобы научиться решать задачи с параметром, не выйдет просто прочитать краткую инструкцию с указаниями, что вам делать. Нужно потратить некоторое время, чтобы научиться решать такие задачи. Здесь необходимо развитое аналитическое мышление (задачи бывают совершенно разные и нужно уметь анализировать разные функции), отличное умение решать все типы уравнений и неравенств (если вы не можете решить любое задание С1 или С3, то для вас будет очень сложно решить и С6), знание, как ведут себя различные функции и умение строить их графики. Как видите, все не так уж просто, но и 4 первичных балла дают не просто так. Тем не менее, решить С6 более чем реально, нужно набраться терпения. На самом деле, не так уж и много материала, да и раз вы задумались о С6, скорее всего, большинство необходимых знаний у вас есть, в основном придется потратить время на отработку практических навыков и разбор различных методов решения. Материал разбит на несколько частей, и я рекомендую внимательно их изучить, разбирая представленные примеры.
Решение уравнения или неравенства с параметром обычно предполагает несколько случаев, и ни один из них нельзя потерять.
Для того, чтобы решить задачу с параметром, необходимо для начала преобразовать заданное выражение к более простому виду, если это, конечно, возможно. При этом необходимо понимать, какие преобразования являются равносильными, а какие нет. В противном случае могут появиться посторонние корни, которые будет нужно проверить (это не всегда просто, поэтому рекомендую стараться использовать равносильные преобразования).
Рекомендации к выполнению задания 18 ЕГЭ:
- Надо избавиться от логарифмов, модулей, показательных степеней и т.д.
- Еще раз внимательно прочитать задание. Понять, что от вас требуется.
- Попытаться проанализировать получившееся после преобразований выражение на наличие каких-либо специальных свойств функции (периодичность, возрастание/убывание, четность/нечетность и т.д.)
- Часто решить задачу с параметром можно и удобно при помощи графиков. Иногда удобно выполнять построения на обычной координатной плоскости (Х, У), а иногда удобно построить графики в плоскости (Х, а), где а – параметр. Данный способ решения возможен, если вы видите знакомые функции (параболы, прямые, гиперболы, окружности и т.д.). Разумеется, бывает несколько способов решения поставленной задачи, но графический, как правило, наименее громоздок и прост для понимания. Ведь графики показывают поведение функций, и весь необходимый анализ появится у вас перед глазами.
- Важно помнить, что методы решения уравнения или неравенства зависят от степени многочлена. Для этого необходимо рассматривать те значения параметра, при которых (если это возможно) обращается в нуль коэффициент при старшей степени. Пример: (a*x^2-3*x+1=0), при (a=0) выражение принимает вид (-3*x+1=0), т.е. превращается в линейную функцию, а способы решения квадратного и линейного уравнений различны.
Блок 1. Введение
| 1.1 | Решите уравнения с параметром а: а) ax = − 5; б) (a−1)x = −3; в) (a−2)x = 2−a г) (a−2)x = (a−2)(a+3) |
Смотреть видеоразбор |
| 1.2 | Определите при каких значениях параметра а: а) уравнение |x| = a−3 имеет один корень; б) уравнение |x| = a2−5 не имеет корней. |
Смотреть видеоразбор |
| 1.3 | Функция задана формулой y=x^2+ax+b. Найдите a и b, если: а) график функции проходит через точки (0;3) и (-1;8); б) наименьшее значение, равное −4, функция принимает при x = 1 |
Смотреть видеоразбор |
Блок 2. Координатно-параметрический метод
| 2.1 | Найдите все значения параметра а, при каждом из которых уравнение frac{|3x|-2x-2-a}{x^2-2x-a}=0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.2 | Найдите все значения а, при каждом из которых система уравнений begin{cases} frac{xy^2-3xy-3y+9}{sqrt{x+3}}=0 \ y=ax end{cases} имеет ровно два различных решения | Смотреть видеоразбор |
| 2.3 | Найдите все значения параметра а, при каждом из которых уравнение frac{x^2-4x+a}{5x^2-6ax+a^2} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.4 | Найти все значения а, при каждом из которых уравнение sqrt{3x-2} cdot ln(x-a) = sqrt{3x-2} cdot ln(2x+a) имеет ровно один корень на отрезке [0; 1] | Смотреть видеоразбор |
| 2.5 | Найти все значения а, при каждом из которых уравнение (4^x-3 cdot 2^x + 3a — a^2)cdotsqrt{2-x} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.6 | Найти все действительные значения величины h , при которых уравнение x(x+1)(x+h)(x+1+h) = h^2 имеет 4 действительных корня | Смотреть видеоразбор |
Блок 3. Преобразование графиков
| 3.1 | Найдите все значения a, при каждом из которых наименьшее значение функции f(x) = 2ax+|x^2-8x+7| больше 1 | Смотреть видеоразбор |
| 3.2 | Найти все значения параметра a, при каждом из которых уравнение (|x-2|+|x+a|)^2-7(|x-2|+|x+a|)-4a(4a-7) = 0 имеет ровно два корня | Смотреть видеоразбор |
| 3.3 | Максимальное значение выражения x + 2y при условии log_{frac{x^2+y^2}{2}}ay ge 1 равно 4. Чему равно положительное значение параметра a? | Смотреть видеоразбор |
| 3.4 | Найти все значения параметра a, при каждом из которых уравнение f(x) = |a+2|sqrt[3]{x} имеет 4 решения, где f — чётная периодическая функция с периодом T=frac{16}{3}, определённая на всей числовой прямой, причём f(x)=ax^2, если 0 le x le frac{8}{3} | Смотреть видеоразбор |
Блок 4. Системы с параметром
| 4.1 | Найдите все положительные значения a, при каждом из которых система begin{cases} (|x|-5)^2+(y-4)^2=9 \ (x+2)^2+y^2=a^2 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.2 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} frac{(y^2-xy-4y+2x+4)sqrt{x+4}}{sqrt{5-y}} \ a=x+y end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.3 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} (x-2a+3)^2+(y-4)^2=2,25 \ (x+3)^2+(y-a)^2=a^2+2a+1 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.4 | Найти все значения параметра a, при каждом из которых система begin{cases} ((x-5)^2+(y-3)^2-9)((x-2)^2+(y-1)^2) le 0 \ y=ax+a+3 end{cases} не имеет решений | Смотреть видеоразбор |
Блок 5. Квадратичная функция
| 5.1 | Найти все значения параметра a, при каждом из которых неравенство |frac{x^2+ax+1}{x^2+x+1}| lt 3 выполняется при всех значениях x | Смотреть видеоразбор |
| 5.2 | При каких значениях p вершины парабол y=-x^2+2px+3 и y=x^2-6px+p расположены по разные стороны от оси x? | Смотреть видеоразбор |
| 5.3 | Найти все значения a, при каждом из которых f(x)=x^2-|x-a^2|-5x имеет хотя бы одну точку максимума | Смотреть видеоразбор |
| 5.4 | Найдите все значения параметра a при каждом из которых множество значений функции y=frac{3x+3-2ax}{x^2+2(2a+1)x+4a^2+4a+2} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.5 | Найти все значения параметра a, при каждом из которых множество значений функции y=frac{5a-15x+ax}{x^2-2ax+a^2+25} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.6 | Найдите все значения параметра a, при каждом из которых неравенство |frac{x^2+x-2a}{x+a}-1| le 2 не имеет решений на интервале (1;2) | Смотреть видеоразбор |
| 5.7 | Найдите все значения параметра a, при каждом из которых уравнение frac{a^3-(x+2)a^2+xa+x^2}{a+x} = 0 имеет ровно один корень | Смотреть видеоразбор |
| 5.8 | Найдите все значения a, при каждом из которых множество значений функции y=frac{cos{x}-a}{cos{2x}-4}содержит число −2 | Смотреть видеоразбор |
| 5.9 | Найти все значения параметра a, при каждом из которых уравнение (4cos{x}-3-a)cos{x}-2,5cos{2x}+1,5=0 имеет хотя бы один корень | Смотреть видеоразбор |
| 5.10 | Найти все значения параметра a, при каждом из которых уравнение 4^{|x|}=frac{7a}{a-5}cdot 2^{|x|}-frac{12a+17}{a-5} имеет ровно два различных корня | Смотреть видеоразбор |
| 5.11 | Найдите все значения а, при каждом из которых множество решений неравенства frac{a-(a^2-2a-3)cos{x}+4}{sin^2{x}+a^2+1} lt 1 содержит отрезок [-frac{pi}{3}; frac{pi}{2}] | Смотреть видеоразбор |
Блок 6. Расположение корней квадратного уравнения
| 6.1 | Найти все значения параметра a, при которых разность между корнями уравнения x^2+3ax+a^4=0 максимальна | Смотреть видеоразбор |
| 6.2 | Найти все значения параметра а, при каждом из которых уравнение log_{1-x}(a-x+2) = 2 имеет хотя бы один корень, принадлежащий промежутку (-1;1] | Смотреть видеоразбор |
Блок 7. Аналитический метод
| 7.1 | При каких значениях а корни уравнения |x-a^2|=-a^2+2a+3 имеют одинаковые знаки? | Смотреть видеоразбор |
| 7.2 | Найти все значения параметра а, при которых неравенство x^2+2|x-a| ge a^2 справедливо для всех действительных x | Смотреть видеоразбор |
| 7.3 | Найти все значения параметра а, при каждом из которых уравнение |sin^2{x}+2cos{x}+a|=sin^2{x}+cos{x}-a имеет на промежутке (frac{pi}{2};pi] единственный корень | Смотреть видеоразбор |
| 7.4 | Найти все значения параметра а, при каждом из которых уравнение (x^2-4ax+a(4a-1))^2-3(x^2-4ax+a(4a-1))-|a|(|a|-3)=0 имеет более двух корней | Смотреть видеоразбор |
Блок 8. Функциональные методы
| 8.1 | Найти все значения параметра a, при каждом из которых уравнение x^2+(a+7)^2=|x-7-a|+|x+a+7| имеет единственный корень | Смотреть видеоразбор |
| 8.2 | Найти все значения параметра a, при каждом из которых система begin{cases} ax^2+4ax-8y+6a+28 le 0 \ ax^2-6ay-8x+11a-12 le 0 end{cases} имеет ровно одно решение | Смотреть видеоразбор |
| 8.3 | Найдите все значения параметра alpha из интервала (0; pi), при каждом из которых система begin{cases} x^2+y^2-4(x+y)sin{alpha}+8sin^2{alpha} = 2sin{alpha}-1 \ frac{x}{y}+frac{y}{x} = 2sin{alpha}+4sin^2{alpha} end{cases} имеет единственное решение | Смотреть видеоразбор |
| 8.4 | Найдите все неотрицательные значения параметра a, при каждом из которых множество решений неравенства 1 le frac{2a+x^2-4log_{frac{1}{3}}(4a^2-4a+9)}{5sqrt{18x^4+7x^2}+2a+4+(log_{frac{1}{3}}(4a^2-4a+9))} состоит из одной точки и найти это решение. | Смотреть видеоразбор |
| 8.5 | Найдите все значения a, для каждого из которых уравнение 8x^6+(a-|x|)^3+2x^2-|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.6 | Найти все значения параметра a, при каждом из которых уравнение x^10+(a-2|x|)^5+x^2-2|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.7 | Найти все значения параметра a, при каждом из которых уравнение 64x^6-(a-3x)^3+4x^2+3x=a имеет более одного корня. | Смотреть видеоразбор |
| 8.8 | Найти все значения параметра a, для каждого из которых существует хотя бы одна пара чисел x и y , удовлетворяющих неравенству 5|x-2|+3|x+a| le sqrt{4-y^2}+7 | Смотреть видеоразбор |
| 8.9 | Найти все значения параметра a, при каждом из которых уравнение (log_7(2x+2a)-log_7(2x-2a))^2-8a(log_7(2x+2a)-log_7(2x-2a))+12a^2+8a-4 имеет ровно два корня. | Смотреть видеоразбор |
| 8.10 | Найти все значения параметра a, при каждом из которых уравнение a^2-10a+5sqrt{x^2+25}=4|x-5a|-8|x| имеет хотя бы один корень | Смотреть видеоразбор |
| 8.11 | Найти все значения параметра a, при которых уравнение (a+2)^2 cdot log_3(2x-x^2)+(3x-1)^2 cdot log_{11}(1-frac{x^2}{2})=0 имеет решение | Смотреть видеоразбор |
| 8.12 | При каких значениях параметра a уравнение ax^6=e^x имеет одно положительное решение? | Смотреть видеоразбор |
Блок 9. Разные задачи с параметром
| 9.1 | Найти все значения параметра a, при которых уравнение sqrt{1-(x^2-4x-a^2+2a+3)^6}+sqrt{1+(x^2-4x-a^2+2a+3)^6} = 2 имеет только один положительный корень | Смотреть видеоразбор |
| 9.2 | Найти все положительные значения параметра a, при каждом из которых наименьшее значение f(x)=2x^3-3ax^2+5 на отрезке, заданном неравенством |x-2| le 1, не меньше, чем −3 | Смотреть видеоразбор |
| 9.3 | Найдите все значения параметра b , при каждом из которых для любого a неравенство (x-a-2b)^2+(y-3a-b)^2 lt frac{1}{2} имеет хотя бы одно целочисленное решение (x, y). | Смотреть видеоразбор |
| 9.4 | Найти все a, при каждом из которых уравнение sqrt{a-9cos^4{x}}=sin^2{x} имеет решение | Смотреть видеоразбор |
| 9.5 | Найдите наибольшее целое значение a, при котором уравнение 3x^2-12x+3a+9=4sin{frac{4x-x^2-a-3}{2}} cdot cos{frac{x^2-2x-a-1}{2}} имеет ровно два различных решения | Смотреть видеоразбор |
| 9.6 | Найдите все целые отрицательные значения параметра a, при каждом из которых существует такое действительное число b>a, что неравенство 21b ge 6|a+b|-3|b-2|-|a-b|-9|a^2-b+2|+16 не выполнено | Смотреть видеоразбор |