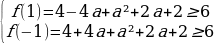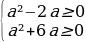Задачи с параметрами на ЕГЭ по математике
Анна Малкова
Задача с параметрами – одна из самых сложных в ЕГЭ по математике Профильного уровня. Это задание №17.
И знать здесь действительно нужно много.
Лучше всего начать с темы «Элементарные функции и их графики».
Повторить, что такое функция, что такое четные и нечетные функции, периодические, взаимно обратные.
Научиться строить графики всех элементарных функций (и отличать по внешнему виду логарифм от корня квадратного, а экспоненту – от параболы).
Освоить преобразования графиков функций и приемы построения графиков.
И после этого – учимся решать сами задачи №17 Профильного ЕГЭ.
Вот основные типы задач с параметрами:
Что такое параметр? Простые задачи с параметрами
Базовые элементы для решения задач с параметрами
Графический способ решения задач с параметрами
Квадратичные уравнения и неравенства с параметрами
Использование четности функций в задачах с параметрами
Условия касания в задачах с параметрами
Метод оценки в задачах с параметрами
Вот пример решения и оформления задачи с параметром
Еще одна задача с параметром – повышенного уровня сложности. Автор задачи – Анна Малкова
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 18
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 18
И несколько полезных советов тем, кто решает задачи с параметрами:
1. Есть два универсальных правила для решения задач с параметрами. Помогают всегда. Хорошо, в 99% случаев помогают. То есть почти всегда.
— Если в задаче с параметром можно сделать замену переменной – сделайте замену переменной.
— Если задачу с параметром можно решить нарисовать – рисуйте. То есть применяйте графический метод.
2. Новость для тех, кто решил заниматься только алгеброй и обойтись без геометрии (мы уже рассказывали о том, почему это невозможно). Многие задачи с параметрами быстрее и проще решаются именно геометрическим способом.
Эксперты ЕГЭ очень не любят слова «Из рисунка видно…» Ваш рисунок – только иллюстрация к решению. Вам нужно объяснить, на что смотреть, и обосновать свои выводы. Примеры оформления – здесь. Эксперты ЕГЭ также не любят слова «очевидно, что…» (когда ничего не очевидно) и «ёжику ясно…».
3. Сколько надо решить задач, чтобы освоить тему «Параметры на ЕГЭ по математике»? – Хотя бы 50, и самых разных. И в результате, посмотрев на задачу с параметром, вы уже поймете, что с ней делать.
4. Задачи с параметрами похожи на конструктор. Разобрав много таких задач, вы заметите, как решение «собирается» из знакомых элементов. Сможете разглядеть уравнение окружности или отрезка. Переформулировать условие, чтобы сделать его проще.
На нашем Онлайн-курсе теме «Параметры» посвящено не менее 12 двухчасовых занятий. Кстати, оценивается задача 17 Профильного ЕГЭ в 4 первичных балла, которые отлично пересчитываются в тестовые!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня
Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.
Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.
«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.
Чему нужно научиться, решая задачи с параметром
В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.
Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.
Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.
Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:
Следующая тема курса – графические методы решения задач с параметром
Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.
На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.
В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.
Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
Купить доступ к этой задаче в составе
экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Разбор задач с параметрами из ЕГЭ по математике, по теме задачи с параметром ЕГЭ, как решать задание 18 в экзамене ЕГЭ, задачи с параметром ЕГЭ, задания с параметром ЕГЭ, задача 18 ЕГЭ, модуль и окружности, решение параметров ЕГЭ, решение задачи 18, система уравнений с параметром, научиться решать задачи с параметрами, сложных задач варианта КИМ ЕГЭ, начертить графики функций, ЕГЭ по математике профильного уровня, методы решения уравнений и неравенств, выпускникам 11 класса в 2018 году, поступающим в технический вуз.
23 апреля 2017
В закладки
Обсудить
Жалоба
Параметры. От простого к сложному. Практикум по решению задач
Решение задач с параметрами является одним из самых трудных разделов школьной математики и требует большого количества времени на их изучение.
Теоретическое изучение физических процессов, решение экономических задач часто приводит к различным уравнениям или неравенствам, содержащим параметры, и необходимой частью их решения является исследование характера процесса в зависимости от значений параметров. Таким образом, задачи с параметрами представляют собой небольшие исследовательские задачи.
Автор: Агашкова Надежда Анатольевна.
pr-sl-p.pdf
Основы работы с параметром
Параметр – это буквенный коэффициент в уравнении.
Параметр – это всегда число, а не переменная, но мы не знаем, чему конкретно равен параметр. Например,
(y = kx + b)
это уравнение прямой, в котором (x) – переменная, (y) – зависимая от неё функция, а (k) и (b) – коэффициенты. Это значит, что (k) и (b) – какие-то числа, параметры. Когда мы видим конкретное уравнение прямой, например,
(y = — 5x + 
мы можем сказать, что в данном случае параметр (k = — 5), а параметр (b = 
УРАВНЕНИЕ С ПАРАМЕТРОМ:
Существуют уравнения, где есть две неизвестных: (x) – корень уравнения и (a) (или любая другая буква) – параметр. Решение таких уравнений сводится не к поиску конкретных корней, а к анализу их количества. Для этого мы предполагаем, чему будут равны корни уравнения при определенных параметрах.
АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЙ С ПАРАМЕТРОМ
-
Записываем все ограничения уравнения для корней – чему не может быт равен (mathbf{x}).
-
Преобразовываем уравнение так, чтобы с одной стороны уравнения остались только иксы с коэффициентами.
-
Предполагаем, что коэффициент перед (mathbf{x}) равен нулю. Выражаем из этого коэффициента параметр после чего выражаем корни уравнения.
-
Предполагаем, что коэффициент не равен нулю и аналогично выражаем корни.
-
Если не удается найти корни в пунктах 3 или 4 из-за алгебраических ограничений или нелогичных выводов, то корней нет. Если корень равен выражению, которое не нарушает законы математики – корень один.
-
Если у уравнения есть корни, проверим их на ограничения для (mathbf{x}) из пункта 1. Находим те параметры, при которых корни равны этим ограничениям. При таких параметрах корней тоже нет.
Рассмотрим примеры.
Пример №1:
Сколько корней имеет уравнение
(ax = 3a + 7)
-
Данное уравнение не имеет ограничений для (x), поэтому перейдем ко второму пункту.
-
Начнем рассуждать. В случае работы с параметром нужно предположить, как мы будем искать корень, если коэффициент при икс равен нулю и если не равен ему. В данном случае коэффициент при иксе и есть параметр. Допустим, (a = 0), тогда уравнение будет иметь вид:
(0 = 7)
Это невозможно, из чего делаем вывод, что при (a = 0) корней нет.
-
Теперь представим, что параметр не равен нулю, а равен любому другому числу (a neq 0), тогда выразим икс:
(x = frac{3a + 7}{a})
При условии, что (a neq 0), а равно обычному числу, (x) будет принимать одно единственное значение.
-
Так мы нашли, при каких параметрах уравнение будет иметь один корень, нужно проверить этот корень на ограничения. Этих ограничений из п.1 нет, значит мы полностью проанализировали уравнение и узнали, сколько корней оно будет иметь во всех возможных случаях изменения параметра:
({корней нет при a = 0 }{один корень frac{3a + 7}{a} при a neq 0 })
Ответ так и запишем.
Ответ: (корней нет при a = 0); (один корень frac{3a + 7}{a} при a neq 0).
При работе с линейными уравнениями нет ограничений для переменных и для параметра. Сейчас мы рассмотрим дробно-рациональное уравнение с параметром, где на каждом этапе нужно помнить об ограничениях в знаменателе.
Пример №2:
Сколько корней имеет уравнение
(frac{4}{x — 3} — frac{k}{2} = 2)
-
Для начала нужно выписать все ограничения для переменной. Знаменатель не может быть равен нулю, значит:
(x — 3 neq 0)
(x neq 3)
(frac{8}{2left( x — 3 right)} — frac{kleft( x — 3 right)}{2left( x — 3 right)} = frac{4left( x — 3 right)}{2(x — 3)})
(frac{8 — kx + k3}{2(x — 3)} = frac{4x — 12}{2(x — 3)})
Ограничение для переменной мы записали, поэтому смело можно убрать знаменатель и приравнять числители. Про ограничение не забывать!
(8 — kx + 3k = 4x — 12)
-
Вправо перенесем все с иксами, а влево перенесем все остальные числа:
(8 + 3k + 12 = 4x + kx)
(20 + 3k = xleft( 4 + k right))
-
Мы снова пришли к ситуации, когда (x) умножается на какое-то число ((4 + k)), значение которого мы не знаем, т. к. в нём есть параметр. Снова анализируем количество корней, если весь коэффициент перед (x) равен нулю, то есть:
(4 + k = 0)
(k = — 4)
тогда
(x = frac{20 + 3k}{0})
Чего не может быть, значит корней нет.
-
Рассмотрим случай, когда (4 + k neq 0):
(k neq — 4)
тогда
(x = frac{20 + 3k}{k})
Получается, что существует один единственный корень.
-
Мы не учли то, что единственным корнем может оказаться число 3, но в начале мы записали ограничение (x neq 3). Поэтому уравнение будет иметь один корень ( x = frac{20 + 3k}{k}) при (k neq — 4), если
(x = frac{20 + 3k}{k} neq 3)
Найдем такой параметр (k), при котором (x = 3). Нужно проверить, есть ли такой параметр, и если есть – исключить его:
(frac{20 + 3k}{k} = 3)
(20 + 3k = 3k)
(20 = 0)
Что невозможно, значит такого параметра не существует, и уравнение имеет ровно один корень без ограничений, кроме (k neq — 4). Запишем ответ.
Ответ: корней нет при (k = — 4); один корень (x = frac{20 + 3k}{k}) при (k neq — 4).
Доклад на
ШМО
«Задачи с
параметрами на ЕГЭ».
Определение. Параметром
называется независимая переменная, значение которой в задаче считается заданным
фиксированным или произвольным действительным числом, или числом, принадлежащим
заранее оговоренному множеству.
Что означает «решить задачу с
параметром»?
Естественно, это зависит от вопроса в задаче. Если,
например, требуется решить уравнение, неравенство, их систему или совокупность,
то это означает предъявить обоснованный ответ либо для любого значения
параметра, либо для значения параметра, принадлежащего заранее оговоренному
множеству.
Если же требуется найти значения параметра, при
которых множество решений уравнения, неравенства и т. д. удовлетворяет
объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных
значений параметра.
Более прозрачное понимание того, что означает решить
задачу с параметром, у читателя сформируется после ознакомления с примерами
решения задач на последующих страницах.
Какие основные типы задач с
параметрами?
Тип 1. Уравнения, неравенства, их
системы и совокупности, которые необходимо решить либо для любого значения
параметра (параметров), либо для значений параметра, принадлежащих заранее
оговоренному множеству.
Этот тип задач является базовым при овладении темой
«Задачи с параметрами», поскольку вложенный труд предопределяет успех и при
решении задач всех других основных типов.
Тип 2. Уравнения, неравенства, их
системы и совокупности, для которых требуется определить количество решений в
зависимости от значения параметра (параметров).
Обращаю внимание на то, что при решении задач данного
типа нет необходимости ни решать заданные уравнения, неравенства, их системы и
совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве
случаев работа является тактической ошибкой, приводящей к неоправданным
затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда
прямое решение в соответствии с типом 1 является единственным разумным путем
получения ответа при решении задачи типа 2.
Тип 3. Уравнения, неравенства, их
системы и совокупности, для которых требуется найти все те значения параметра,
при которых указанные уравнения, неравенства, их системы и совокупности имеют
заданное число решений (в частности, не имеют или имеют бесконечное множество
решений).
Легко увидеть, что задачи типа 3 в каком-то смысле
обратны задачам типа 2.
Тип 4. Уравнения, неравенства, их
системы и совокупности, для которых при искомых значениях параметра множество
решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения
переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества
решений второго уравнения и т. д.
Комментарий. Многообразие задач с
параметром охватывает весь курс школьной математики (и алгебры, и геометрии),
но подавляющая часть из них на выпускных и вступительных экзаменах относится к
одному из четырех перечисленных типов, которые по этой причине названы
основными.
Наиболее массовый класс задач с параметром —
задачи с одной неизвестной и одним параметром. Следующий пункт указывает
основные способы решения задач именно этого класса.
Каковы основные способы
(методы) решения задач с параметром?
Способ I (аналитический). Это способ
так называемого прямого решения, повторяющего стандартные процедуры нахождения
ответа в задачах без параметра. Иногда говорят, что это способ силового, в
хорошем смысле «наглого» решения.
Комментарий. Аналитический способ
решения задач с параметром есть самый трудный способ, требующий высокой
грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости
от задачи (с переменной x и параметром a) рассматриваются графики или в
координатной плоскости (x; y), или в координатной плоскости (x; a).
Комментарий. Исключительная
наглядность и красота графического способа решения задач с параметром настолько
увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать
другие способы решения, забывая общеизвестный факт: для любого класса задач их
авторы могут сформулировать такую, которая блестяще решается данным способом и
с колоссальными трудностями остальными способами. Поэтому на начальной стадии
изучения опасно начинать с графических приемов решения задач с параметром.
Способ III (решение относительно параметра).
При решении этим способом переменные x и a принимаются равноправными и
выбирается та переменная, относительно которой аналитическое решение признается
более простым. После естественных упрощений возвращаемся к исходному смыслу
переменных x и a и заканчиваем решение.
Перейду теперь к демонстрации указанных способов
решения задач с параметром, так как это мой любимый метод решения заданий
данного типа.
Проанализировав
все задания с параметрами, решаемыми графическим методом, я знакомство с
параметрами начинаю с заданий ЕГЭ 2018 года :
При
каком целом значении к уравнение 45х – 3х2 – х3 + 3к =
0 имеет ровно два корня ?
Эти
задания позволяют, во первых, вспомнить как строить графики с использованием
производной, а во-вторых, объяснить смысл прямой у = к.
Подготовку такого ученика учитель проводит в несколько
этапов, выделяя для тренировки отдельных навыков, необходимых для поиска и
реализации длинных решений, отдельные уроки. Эта подборка подходит для стадии
формирования представлений о плавающих рисунках в зависимости от параметра..
Задачи выстроены в порядок возрастания их сложности.
Задание из
ЕГЭ-2020
При каких значениях
параметра a уравнение имеет не
менее двух корней.
Решим эту задачу
графически. Построим график левой части уравнения:
и график правой части: и сформулируем вопрос
задачи так: при каких значениях параметра a графики функций и
имеют две или более
общих точки.
В левой части
исходного уравнения параметр отсутствует, поэтому мы можем построить график
функции .
Будем строить это
график с помощью линейных
преобразований графика функции :
1. Сдвинем график
функции на 3 единицы вниз вдоль оси OY,
получим график функции :
2. Построим график
функции . Для этого часть
графика функции , расположенную ниже оси ОХ,
отобразим симметрично относительно этой оси:
Итак, график
функции имеет вид:
График функции представляет собой семейство прямых с переменным
коэффициентом наклона, равным а, сдвинутых на 1 единицу вниз вдоль оси OY. То
есть точка с координатами (0;1) представляет собой центр вращения этого
семейства прямых:
Рассмотрим положения
прямой , в которых она имеет более
одной точки пересечения с графиком функции :
Прямые АВ и АС имеют
две точки пересечения с графиком функции. Все прямые, расположенные между ними
имеют 3 точки пересечения с графиком функции .
Чтобы найти
коэффициент наклона прямой АВ, найдем абсциссу точки В.
Точка В – это точка
пересечения графика функции с осью ОХ. В этой
точке у=0. Получим уравнение: , отсюда
. Коэффициент а наклона прямой АВ равен тангенсу угла BAD
треугольника ABD и равен
Найдем коэффициент
наклона прямой АС. Точка С – это точка, в которой прямая
касается графика функции (точка С принадлежит части графика
функции , отображенной симметрично относительно
оси ОХ). То есть это точка, в которой графики функции
и имеют одну общую точку.
Теперь нам нужно
найти значение параметра а, при котором уравнение имеет
одно решение.
Умножим обе части
уравнения на х и перенесем все слагаемые влево. Получим квадратное
уравнение Это уравнение имеет
единственный корень, если дискриминант равен нулю.
,
Таким образом, уравнение
имеет два решения, если
или
Уравнение
имеет три решения, если
Задание из ЕГЭ 2021
Найдите все значения a, при каждом из которых
уравнение
имеет ровно два различных корня.
Решение:
Корнями
исходного уравнения являются корни уравнения для которых выполнено
условие
Поскольку уравнение
задаёт
на плоскости Oxa пару прямых l1 и l2,
заданных уравнениями a=2x и a=−2x соответственно. Значит, это уравнение имеет
один корень при a=0 и имеет два корня при a≠0.
Поскольку
уравнение задаёт пару прямых m1 и m2,заданных
уравнениями a=x+3 и a=−x−3 соответственно.
Координаты точки пересечения прямых l1 и m1, являются
решением системы уравнений:
Значит, прямые l1 и m1 пересекаются в точке
(3;6).
Координаты точки пересечения прямых l1 и m2 являются
решением системы уравнений:
Значит, прямые l1 и m2 пересекаются в точке
(−1;−2).
Координаты точки пересечения прямых l2 и m1 являются
решением системы уравнений:
Значит, прямые l2 и m1 пересекаются в точке
(1;−2).
Координаты точки пересечения прямых l2 и m2 являются
решением системы уравнений:
Значит, прямые l2 и m2 пересекаются в точке
(3;−6).
Следовательно, условие выполнено для корней уравнения
при всех a , кроме
a=−6, a =−2, a=2 и a=6 . Таким образом, исходное уравнение имеет ровно два
корня при
Ответ:
Глава 5.
Ответы на задачи для самостоятельного решения
-
a≤
;
≤a≤3; a3.
-
aЄ(
;-1)U(0;
).
-
aЄ{
;-2]U[0;
].
-
aЄ(-∞;0)U(0;2].
-
aЄ(-
;-
)U[-
;
)
-
aЄ(-∞;-
)U(-
;0).
-
a=-1.
-
aЄ(1.5;+∞).
-
aЄ[-2;
].
10) aЄ(-4;-3).
11) (-2;-6), (6;2).
12) aЄ[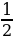
Методическое пособие по решению задач с параметром из ЕГЭ.
Тамбов
2018 год
Оглавление
|
Глава 1.Кратко о параметре |
|
|
Глава 2.Простые примеры задач с параметром |
|
|
Глава 3.Методы решения задач среднего уровня сложности |
|
|
Глава 4.Параметр в ЕГЭ 2018 года |
|
|
Глава 4.1.Функции, зависящие от параметра |
|
|
Глава 4.2.Уравнения с параметром |
|
|
Глава 4.3.Неравенства с параметром |
|
|
Глава 4.4.Системы с параметром |
|
|
Глава 5.Ответы на задачи для самостоятельного решения |
Ответ: a=1/4.
Задачи для самостоятельного решения:
10)Определите все значения параметра a, при каждом из которых система 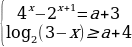
11)При каких значениях параметров a и b система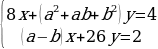
12)Найдите все значения a, при каждом из которых система неравенств 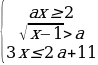
или с точкой В, то условие задачи выполнено.
Решим неравенство 0≤
Ответ: aЄ[1;6].
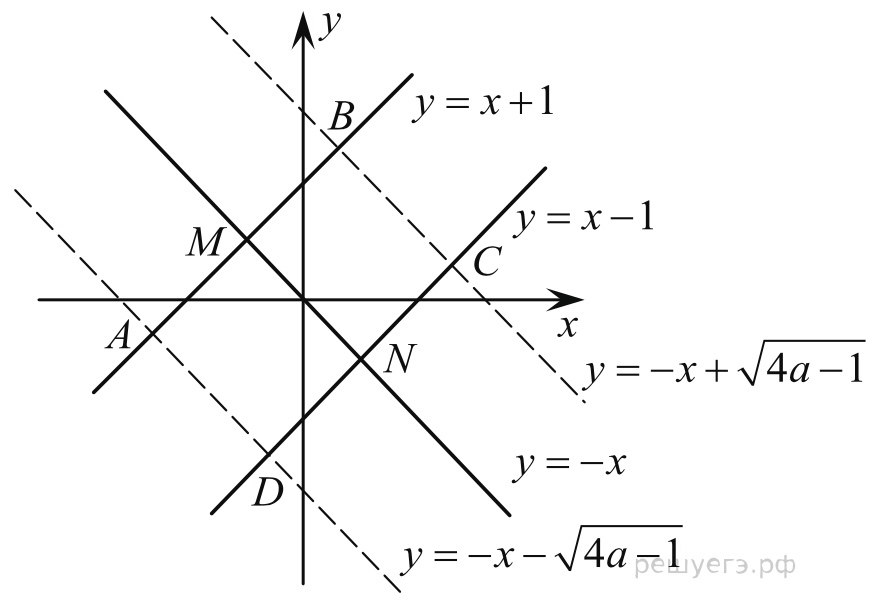
3 задача: Найдите все значения параметра a, при каждом из которых система уравнений 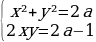
Решение: Заменим первое уравнение разностью, а второе – суммой исходных уравнений: 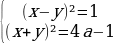
При a система решений не имеет. При a≥1/4 получаем:
y=x-1 или y=x+1
y=- x-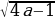
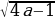
Ясно (см. рисунок), что при a1/4 система имеет четыре решения (координаты точек A, B, C и D), а при a=1/4 — два решения (координаты точек M и N).
Глава 1.
Коротко о параметре
Если в уравнении, помимо переменной x, есть переменная a и требуется решить это уравнение относительно x, считая переменную a постоянной, то данное уравнение будет называться уравнением с одной переменной x и параметром a.
Определение: параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Особенность уравнений с параметрами:
с одной стороны, параметр в уравнении следует считать величиной известной, а с другой — конкретное значение параметра не дано. С одной стороны, параметр является величиной постоянной, а с другой — может принимать различные значения. Получается, что параметр в уравнении — это «неизвестная величина», «переменная постоянная». Этот «каламбур» довольно точно отражает суть тех сложностей, которые встают перед теми, кто решает уравнения с параметром.
Глава 2.
Простые примеры задач с параметром
Чаще всего в задачах содержится один параметр, хотя бывают случаи, когда параметров больше одного. Решить уравнение с параметром – значит указать для каждого значения параметра множество решений уравнения.
Самые простые задачи с параметром и их решения:
-
x/2=a = x=2a при любом a
-
ax=10 = x=10/a = x=10/a при a≠0
-
x=√a = x=√a при a≥0
-
2ax–4=0 = 2ax=4 = x=2/a = x=2/a при a≠0
-
|x|=a–1 = a–1≥0 = x=a–1 или x=1–a при a≥1
Как можно увидеть, простейшие задачи с параметром чем-то напоминают обычные задачи, в которых нужно посчитать значение x. Разница лишь в том, что в данном случае x выражается через переменную a.
Глава 3.
Методы решения задач среднего уровня сложности
ординаты точки А, но не большие 4. Имеем:
a=-(-12+8√2)-4=8-8√2.
Тогда система будет иметь решения при 8-8√2≤a≤4.
Ответ: aЄ[8-8√2;4].
2 задача: Найдите все неотрицательные значения a , при каждом из которых система уравнений 
Решение: Первому уравнению системы удовлетворяют те и только те точки (x;y), которые лежат на отрезке AB прямой, соединяющей точки A(-2;0) и B(0;a), где a≥0, поскольку уравнение задаёт множество точек (x;y), сумма расстояний от каждой из которых до точек А и В равна 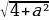
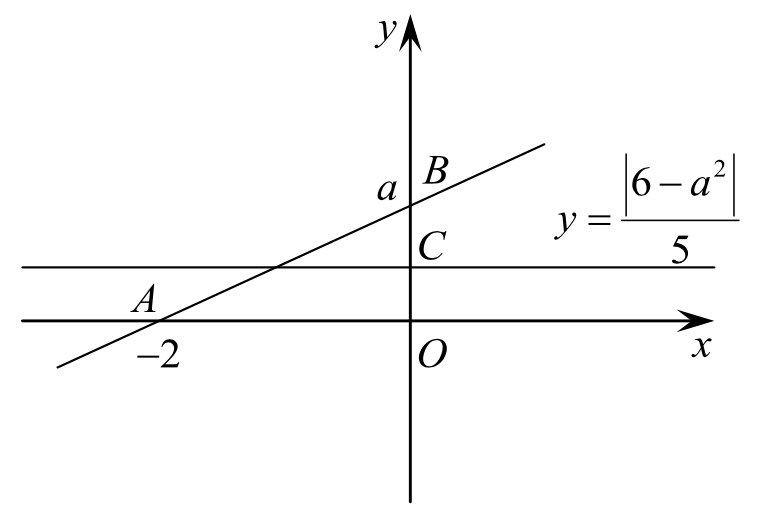
Отсюда следует, что условие задачи выполнено тогда и только тогда, когда точка С лежит между точками О и В, причём если точка С совпадает с точкой А
Решение: Преобразуем систему:
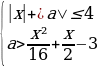
Первое неравенство задает на плоскости xOa квадрат, ограниченный отрезками прямых a=x+4, a=x-4, a=-x-4, a=- x+4, а неравенство 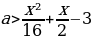
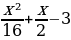
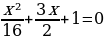
x=-12±8√2
М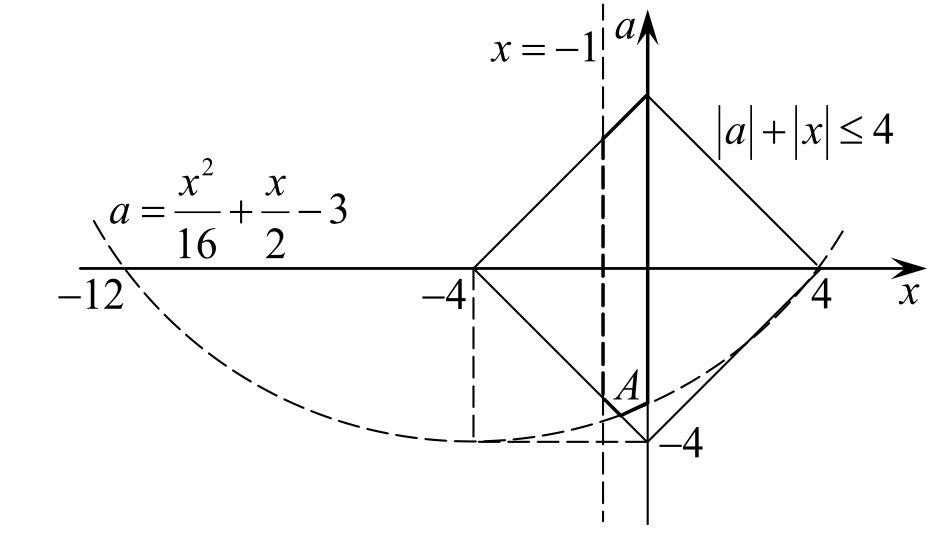
Всего существует 3 основных способа решения задач, содержащих параметр. Рассмотрим каждый из них:
1 способ: аналитический. Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Аналитический способ решения задач с параметром бывает довольно трудным, он требует высокой грамотности и наибольших усилий по овладению им.
Пример задачи с аналитическим способом решения: При каких значениях параметра a уравнение 52x-3*5x+a— -1=0 имеет единственный корень?
Решение: Сделаем замену 5x=t, t0. Тогда наше уравнение примет вид: t2-3*t+a-1=0. У этого уравнения 1 корень будет в двух случаях:
-
Если дискриминант будет равен нулю
-
Если дискриминант будет больше нуля, но один из корней будет отрицательный
Рассмотрим эти два случая:
-
D=9-4a+4=13-4a=0
Отсюда получаем a=13/4 – первый подходящий корень.
2) D=13-4a
Тогда корни будут такие:
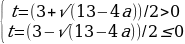
Возьмем первый корень положительным, а второй наоборот. В таком случае условие единственного ответа будет выполнено.
Решая неравенство t=(3+√(13-4a))/20 получаем, что,
a≤1.
Значит в ответ нужно записать, что aЄ(-∞;1)U{13/4}.
2 способ: графический. В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Пример задачи с графическим способом решения: При каких a уравнение |x2+2x–3|–2a=|x–a|+3 имеет ровно три корня?
Решение: Используем графический метод решения. График функции y=|x2+2x–3| отличается от параболы y=x2+2x–3 только тем, что отрицательная ее область зеркально отражается вверх относительно
Задачи для самостоятельного решения:
7)Найдите все целые отрицательные значения параметра a, при каждом из которых существует такое действительное число ba, что неравенство 20b≥6|2a+b|+2|b-2|-|2a—b|-5|4a²-b+2| не выполнено.

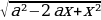
9)Найдите все значения a, при каждом из которых неравенство |x²-4x+a|≤10 выполняется для всех xЄ[a;a+5].
Глава 4.4.
Системы с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра a, при каждом из которых система неравенств 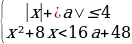
-1/5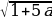
0≤a≤3: (1;2)
3a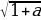
a≥8: пустое множество
Ответ: aЄ(-∞;-1/5]U[8;+∞).
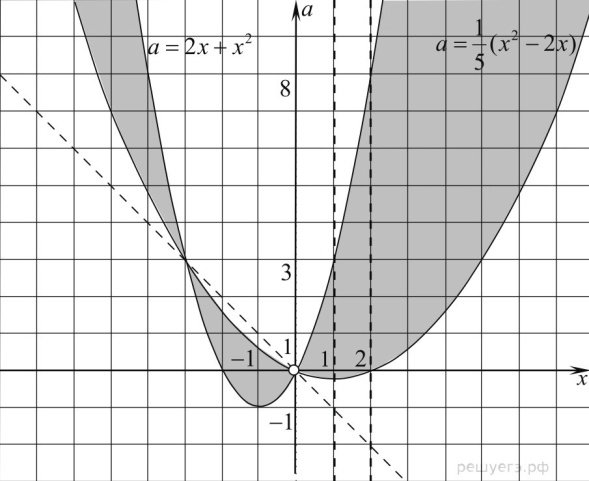
3 задача: Найдите все значения a , при каждом из которых неравенство |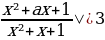
Решение: Поскольку знаменатель левой части больше нуля при любом x, получаем: |x²+ax+1|x²+3x+3.
Решим полученное неравенство:
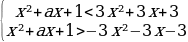
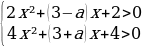
Чтобы любое значение x удовлетворяло этой системе неравенств, дискриминанты левых частей должны быть отрицательными:
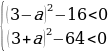
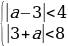
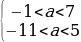
Ответ:aЄ(-1;5).
оси OX (ведь модуль не может принимать отрицательных значений).
График функции y=|x–a|+2a+3 представляет собой всем известную «галочку», вершина которой смещена в точку (a;2a+3). В зависимости от значений параметра возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
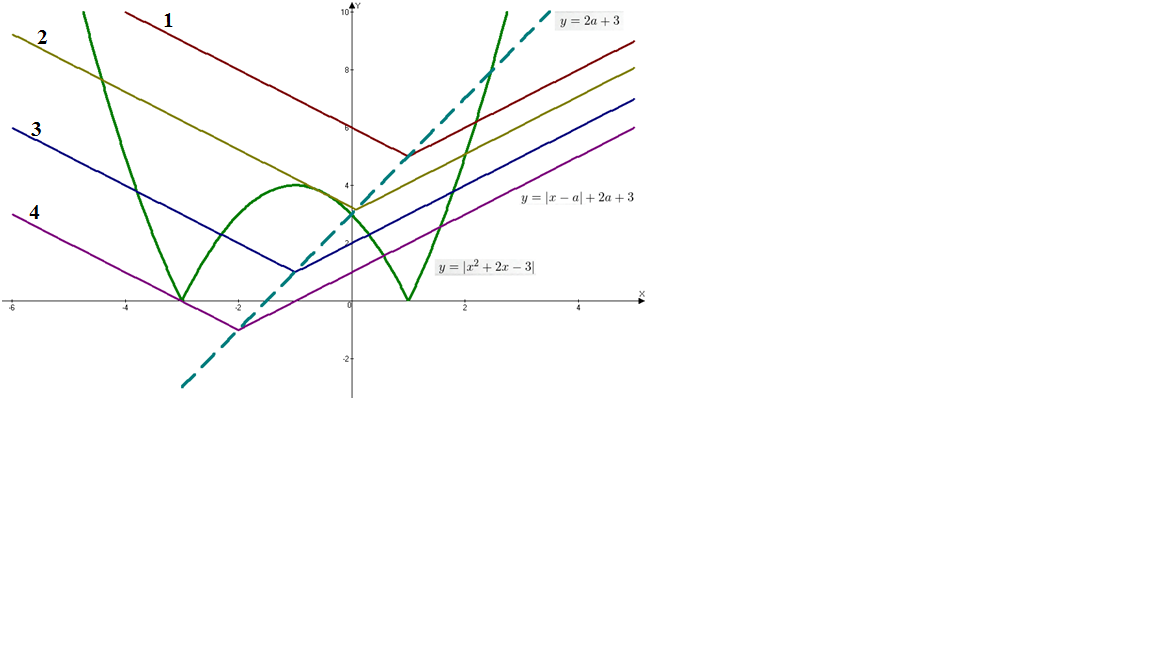
Видно, что три решения уравнение будет в случаях 2 и
4.
Первый случай выполняется при условии выполнении равенства 0=|-3-a|+2a+3. В этом случае модуль раскрывается в минусом, поэтому a=-2.
Во втором случае оба модуля раскрываются с минусом, получается квадратное уравнение x2+x+3a=0.Для выполнения условия, дискриминант этого уравнения должен быть равен 0. Это выполняется при a=1/12.
Значит в ответ нужно записать, что a={-2;1/12}.
3 способ: решение относительно параметра. При таком решении x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Пример задачи с этим способом решения: Для всех действительных значений параметра a решите уравнение x3–-(2–a)x2–ax–a(a–2)=0.
Решение: Для начала давайте раскроем скобки и посмотрим, что у нас получится. После раскрытия скобок уравнение примет вид: x3–a2+ax2–ax+2a–2x2 = 0. Можно заметить, что, являясь кубическим относительно x, это уравнение квадратное относительно переменной a.
достаточно, чтобы одновременно выполнялись 2 условия: f(0)
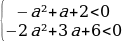
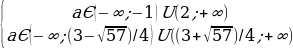
Пересечение этих промежутков и будет ответом.
Ответ: aЄ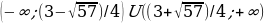
2 задача: Найдите все значения параметра а, при каждом из которых неравенство |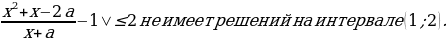
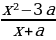
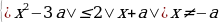
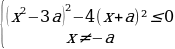
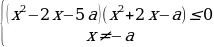
Решим неравенство на интервале (1;2):
a≤-1/5:пустое множество
Неравенства с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения параметра а, при каждом из которых множество решений неравенства 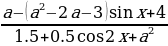
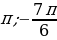
Решение: Заметим, что при любых значениях переменной x и параметра a знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
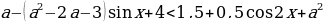
Для того, чтобы множество решений неравенства содержало отрезок [-2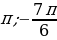
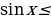
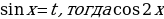
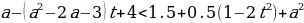
-a²+a+2
Введем функцию: f(t)= t²-(a²-2a-3)t-a²+a+2
Для того, чтобы выполнялось наше условие, необходимо и
Поэтому, считая переменную x параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a: –a2+(x2–x+2)a+x3–-2x2 = 0.
Преобразуем: a2–(x2–x+2)a –x3 + 2x2 = 0.
x2–x+2=x2+(2–x)
–x3+2x2 =x2(2–x)
Легко заметить, что в первом случае можно увидеть сумму квадратов, а во втором их произведение. Поэтому по теореме, обратной теореме Виета получаем, что a1=x2, a2=2–x. Исходное уравнение преобразуется в совокупность из двух: a=x2 и a=2–x.
Из того, что x2=a следует, что:
1)при a решений нет
2)при a=0 решение будет всего одно, x=0
3)при a0 решений два, x=√a и x=–√a
Второе уравнение совокупности будет иметь 1 корень при любом a.
Мы смогли найти все решения исходного уравнения для любого действительного значения параметра: x=2–a
при a; x=0 или x=2 при a=0; x=√a или x=-√a или x=2-a при a0.
Легко заметить, что при a=1 равенства x=2–a и x=√a принимают одинаковое значение x=1. Можно легко найти второй такой корень, приравняв x=2–a и x=–√a. Это будет x=–2 при a=4.
Значит ответ нужно записать в таком виде: x=2-a при a1=0, x2=2 при a=0; x=√a, x=-√a и x=2–x при 0aaa4; x=1, x=–1 при a=1; x=2, x=–2 при a=4.
Глава 4.
Параметр в ЕГЭ 2018 года
Чтобы решить задание 18 по математике профильного уровня нужно знать:
-
Задание 18 в ЕГЭ подразделяется на несколько видов:
-
1) функции, зависящие от параметра;
-
2) уравнения с параметрами;
-
3) неравенства с параметрами;
-
4) системы и неравенства с параметрами.
-
-
Пусть задано уравнение f(x; a) = 0, которое следует решить относительно переменной х, а произвольное действительное число обозначено буквой а, то f(x; a) = 0 – это уравнение с параметром а.
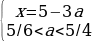
Число x=5-3a лежит на отрезке [0;2], если 1≤a≤5/3. Тогда для второго случая получаем: 1≤a≤5/4.
Корень x=5-3a равен x=3a-1, если a=1.
Значит исходное уравнение имеет ровно один корень на отрезке [0;2] при 7/8.
Ответ: aЄ(7/8;5/4).
Задачи для самостоятельного решения:
4)Найдите все значения а, при каждом из которых уравнение x²+(x-1)*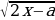
5)Найдите все значения а, при каждом из которых уравнение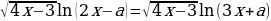
6)Найдите все значения параметра a, при каждом из которых уравнение 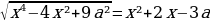
Глава 4.3.
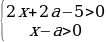
Имеем такую систему:
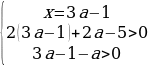
Упрощая эти неравенства, получаем:
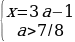
Число 3a-1 лежит на отрезке [0;2], если 1/3≤a≤1. Тогда для первого случая получаем: 7/8
Второй случай:
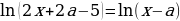
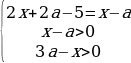
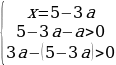
-
Решить неравенство с параметром — это значит исследовать каким будет решение неравенства для всех возможных значений параметра.
-
Решить уравнение с параметром – это значит найти все значения параметров, при которых данное уравнение имеет решение.
Линейные уравнения с параметрами — общий вид ax = b ,где a, b – параметры.
Обратите внимание: для данного вида уравнения контрольным значением параметра является то значение, при котором обращается в нуль коэффициент при неизвестном.
При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.
Особым значением параметра а является значение а=0.
-
1)Если а≠0, то при любой паре параметров а и b оно
-
имеет единственное решение .
-
2)Если а=0, то уравнение принимает вид 0х=b. В этом случает значение b=0 является особым значением параметра b.
-
3)При b≠0 уравнение решений не имеет.
-
4)При b=0 уравнение примет вид:0х=0. Решением данного уравнения является любое действительное число.
Дробно-рациональные уравнения с параметрами, сводящиеся к линейным.
При решении данного типа уравнений следует дробное уравнение заменить целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. Далее следует решать уравнение по известному алгоритму, исключив посторонние корни, т. е. те числа, которые обращают общий знаменатель в ноль (решить уравнения относительно параметра).
Показательные уравнения с параметрами
Многие показательные уравнения с параметрами сводятся к элементарным показательным уравнениям вида аf (x) = bφ(х)
(1), где а 0, b 0.
ОДЗ такого уравнения находится как пересечение
областей допустимых значений функций f(x) и φ(х).
Для решения уравнения (1) нужно рассмотреть
следующие случаи:
-
1)При a=b=1 решением уравнения (1) является область его допустимых значений D.
-
2)При а=1, b≠1 решением уравнения (1) служит решение уравнения φ(х)=0 на области допустимых значений D.
-
3)При а≠1, b=1 решением уравнения (1) служит решение уравнения f(х)=0 на области допустимых значений D.
-
4)При a=b (a0, a≠1, b0, b≠1) уравнение (1) равносильно уравнению f(x)=φ(х) на области D.
-
5)При a≠b (a0, a≠1, b0, b≠1) уравнение (1) тождественно уравнению на области D.
Ответ: a-9/16.
2 задача: Найдите все значения a, при каждом из которых модуль разности корней уравнения x²-6x+12+a²-
-4a=0 принимает наибольшее значение.(Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: По теореме Виета получаем, что 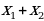
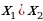
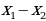
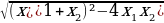
=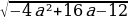
Следовательно, нужно только найти наибольшее значение выражения 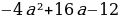
Ответ: a=2. При этом модуль разности корней равен 2.
3 задача: Найдите все значения а, при каждом из которых уравнение 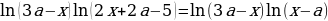
Решение: Имеем уравнение вида ab=ac, откуда на ОДЗ либо a=0, либо b=c. Рассмотрим эти 2 случая:
Первый случай:
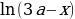
Ответ: a=0, a≥2.
Задачи для самостоятельного решения:
1)Найдите все значения параметра а, при каждом из которых множество значений функции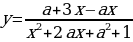
2)Найдите все такие значения параметра a, при каждом из которых наименьшее значение функции y=3|x+a|+|x²-x—
—2| меньше 2.
3)Найдите все такие значения параметра a, при каждом из которых наименьшее значение функции f(x)=|x²+2x-3|+4|x—
-a| не больше 3.
Глава 4.2.
Уравнения с параметром
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых уравнение 64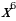
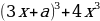
Решение: Преобразуем уравнение 64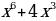
=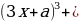
Рассмотрим функцию f(x)=t³+t. Она монотонно возрастает как сумма двух возрастающих функций. Поэтому уравнение f(4x²)=f(3x+a) равносильно уравнению 4x²=3x+a. Оно имеет более одного корня в тех случаях, когда дискриминант уравнения 4x²-3x—a=0 положителен. То есть когда 9+16a0, a-9/16.
Глава 4.1.
Функции, зависящие от параметра
Ниже представлены несколько задач за данную тему и их решения.
1 задача: Найдите все значения a, при каждом из которых наибольшее значение функции f(x)=|x—a|-x² не меньше 1. (Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016)
Решение: Чтобы наибольшее значение данной функции было не меньше 1, необходимо и достаточно, чтобы она в какой-то точке приняла значение 1. Поэтому можно сказать, что |x—a|-x²≥1. В зависимости от переменной a это неравенство равносильно системе неравенств:
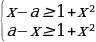
Решая эти неравенства получаем 2 дискриминанта:
D=-3-4a и D=-3+4a. Неравенства будут иметь решения, если эти дискриминанты неотрицательны. Решая -3-4a≥0 и -3+4a≥0 получаем, что a≤-3/4 и a≥3/4.
Ответ: aЄ(-∞;-3/4]U[3/4;+∞).
:
2 задача: Найти все значения параметра a, при каждом из которых среди значений функции y=(x²-2x+a)/(6+x²) есть ровно одно целое число.(Источник: МИОО: Тренировочная работа по математике 2010 год вариант 501. (Часть С))
Решение: Функция определена и непрерывна на всей числовой прямой. Уравнение (x²-2x+a)/(6+x²)=1 при любом a имеет решение x=(a-6)/2. Значит, при любом a одно из значений функции равно 1.
Поскольку функция непрерывна, множество её значений образует промежуток, включающий число 1. Других целых значений функции нет, если для всех x:
0(x²-2x+a)/(6+x²).
Это равносильно системе неравенств:
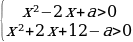
Чтобы неравенства выполнялись для всех x дискриминанты обоих трёхчленов должны быть отрицательны, следовательно: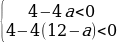
Ответ: aЄ(1;11).
3 задача: Найдите все значения a, при каждом из которых наименьшее значение f(x)=4x²-4ax+a²+2a+2 на множестве |x|≥1 не меньше 6.(Источник: Портал РешуЕГЭ задание 500471)
Решение: Графиком функции f(x)=4x²-4ax+a²+2a+
+2 является парабола, ветви которой направлены вверх, а вершина имеет координаты (a/2;2a+2).
-
Значит, минимум функции f(x) на всей числовой оси достигается при x=a/2.
-
На множестве |x|≥1 эта функция достигает наименьшего значения либо в точке x=a/2, если эта точка принадлежит множеству, либо в одной из граничных точек x=±1.
-
Если наименьшее значение функции не меньше 6, то и всякое значение функции не меньше 6. В частности,
-
-
Упрощая, получаем систему неравенств:
-
-
Решая эту систему, получаем значения a:
-
a€(-∞;-6]U{0}U[2;+∞).
-
Но нам подходят не все данные корни. Сделаем отбор корней.
-
1) Если a≤-6, то a/2≤-3 значит, наименьшее значение функции достигается в точке a/2 и f(a/2)=2a+2=
-
=-10, что не удовлетворяет условию задачи.
-
2) Если a=0, то a/2=0, значит, наименьшее значение функции достигается в одной из граничных точек x=±1, в которых значение функции не меньше 6.
-
3)Если a≥2, то a/2≥1, значит, наименьшее значение функции достигается в точке x=a/2 и f(a/2)=2a+2≥6, что удовлетворяет условию задачи.
Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
М
Тамбов
2018 год
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.
Способ решения параметрических уравнений
- Находим область определения уравнения.
- Выражаем a как функцию от $х$.
- В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
- Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
- Записываем ответ.
Общий вид уравнения с одним параметром таков:
$F(x, a) = 0$
При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.
Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
${f(x)}/{g(x)}; g(x)≠0$
2. Подкоренное выражение должно быть неотрицательным.
$√{g(x)}; g(x)≥0$.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
${f(x)}/{√{g(x)}}; g(x) > 0$
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
$log_{f(x)}g(x) {tableg(x) > 0; f(x) > 0; f(x)≠1;$
Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$
Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D < 0$;
Квадратное уравнение имеет два различных корня, когда $D > 0$;
Квадратное уравнение имеет один корень, если $D=0$
Тригонометрические тождества
1. $tgα={sinα}/{cosα}$
2. $ctgα={cosα}/{sinα}$
3. $sin^{2}α+cos^{2}α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^{2}α}$
$cosα=±√{1-sin^{2}α$
4. $tgα·ctgα=1$
5. $1+tg^{2}α={1}/{cos^{2}α}$
6. $1+ctg^{2}α={1}/{sin^{2}α}$
Формулы двойного угла
1. $sin2α=2sinα·cosα$
2. $cos2α=cos^{2}α-sin^{2}α=2cos^{2}α-1=1-2sin^{2}α$
3. $tg2α={2tgα}/{1-tg^{2}α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos{α-β}+cos{α+β}}/{2}$
$sinα·sinβ={cos{α-β}-cos{α+β}}/{2}$
$sinα·cosβ={sin{α+β}+sin{α-β}}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Решение тригонометрического уравнения с параметром рассмотрим на примере.
Пример:
Найдите все значения параметра с, при каждом из которых уравнение $3cos2x-2sin2x=c$ имеет решение.
Решение:
Преобразуем данное уравнение к виду
$√{3^2+(-2)^2}(cos2xcosφ-sin2xsinφ)=c$
Воспользуемся тригонометрической формулой и свернем второй множитель как косинус суммы
$√{13}cos(2x+φ)=c$, где $φ=arccos{3}/{√{13}}$
Уравнение $√{13}cos(2x+φ)=c$ имеет решения тогда и только тогда, когда $-1≤ {c}/{√{13}} ≤ 1$, домножим полученное неравенство на $√{13}$ и получим
$-√{13} ≤ c ≤ √{13}$
Ответ: $-√{13} ≤ c ≤ √{13}$
Неравенства с параметром
Если имеется неравенство вида $F(a,x) ≤ G(a,x)$ то оно будет иметь одно решение, если $F'(a, x)=G'(a, x)$.
Системы уравнений:
Выделяют четыре основных метода решения систем уравнений:
- Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
- Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
- Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
- Графический метод решения: из каждого уравнения выражается $«у»$, получаются функции, графики которых необходимо построить и посмотреть координаты точек пересечения.
Логарифмические уравнения и системы уравнений
Основное логарифмическое тождество:
$a^{log_{a}b}=b$
Это равенство справедливо при $b> 0, a> 0, a≠1$
Свойства логарифмов:
Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
$log_{а}b^m=mlog_{a}b$;
$log_{a^m}b={1}/{m}log_{a}b$.
$log_{a^n}b^m={m}/{n}log_{a}b$
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
$log_a(bc)=log_{a}b+log_{a}c$
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
$log_a{b}/{c}=log_{a}b-log_{a}c$
4. При умножении двух логарифмов можно поменять местами их основания
$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a, b, c, d >0, a≠1, b≠1$.
5. $c^{log_{a}b}=b^{log_{a}b}$, где $а, b, c > 0, a≠1$
6. Формула перехода к новому основанию
$log_{a}b={log_{c}b}/{log_{c}a}$
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
$log_{a}b={1}/{log_{b}a}$
При решении систем, содержащих логарифмические уравнения, часто удается, избавившись от логарифма, заменить одно или оба уравнения системы рациональными уравнениями. После этого надо выразить одну переменную через другую и после постановки получить уравнение с одной переменной. Кроме того, часто встречаются задачи на замену переменной в пределах одного или обоих уравнений системы и системы, требующие отбора решений.
Логарифмические неравенства:
1. Определить ОДЗ неравенства.
2. По свойствам логарифма преобразовать неравенство к простому виду, желательно получить с двух сторон логарифмы по одинаковому основанию.
3. Перейти к подлогарифмическим выражениям, при этом надо помнить, что:
а) если основание больше единицы, то при переходе к подлогарифмическим выражениям знак неравенства остается прежним;
b) если основание меньше единицы, то при переходе к подлогарифмическим выражениям знак неравенства меняется на противоположный;
с) если в основании находится переменная, надо рассмотреть оба варианта.
4. Решить неравенство.
5. Выбрать решения с учетом ОДЗ из п.1
При решении логарифмических неравенств с переменной в основании легче всего воспользоваться тождественными преобразованиями:
$log_{a}f > b ↔ {table (f-a^b)(a-1) > 0; f > 0; a > 0;$
$log_{a}f+log_{a}g > 0 ↔ {table(fg-1)(a-1)> 0; f > 0,g > 0; a > 0;$
$log_{a}f+b > 0 ↔ {table(fa^b-1)(a-1) > 0; f > 0; a > 0;$
Системы, содержащие показательные уравнения
Свойства степеней
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
Основные методы решения систем, содержащих показательные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – положительность выражения $a^{f(x)}$, которую полезно учитывать, вводя соответствующее ограничение при замене переменной.
Показательные неравенства, сводящиеся к виду $a^{f(x)} ≥ a^{g(x)}$:
1. Преобразовать показательное уравнение к виду $a^{f(x)} ≥ a^{g(x)}$
2. Перейти показателям степеней, при этом если основание степени меньше единицы, то знак неравенства меняется на противоположный, если основание больше единицы – знак неравенства остается прежним.
3. Решить полученное неравенство.
4. Записать результат.
Показательные неравенства, которые можно разложить на множители или сделать замену переменной.
1. Для данного метода во всем неравенстве по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
2. Сделать замену переменной $a^{f(x)}=t, t>0$.
3. Получаем рациональное неравенство, которое можно решить методом интервалов путем разложения на множители выражения.
4. Делаем обратную замену с учетом того, что $t>0$. Получаем простейшее показательное неравенство $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Уравнения с многочленами
Многочлен может обозначаться записью $Р(х)$ — это означает, что многочлен зависит от «х», если записать $Р(х+1)$ — это означает, что в многочлене вместо «х» надо сделать замену на скобку $(х+1)$
Пример:
Найдите значение выражения: $4(p(2x)−2p(x+3))$, если $p(x)=x−6$
Решение:
В данном условии задан многочлен, зависящий от «х», как $p(x)=x−6$.
Чтобы было понятнее, назовем исходный многочлен основной формулой, тогда, чтобы записать $p(2x)$, в основной формуле заменим «х» на «2х».
$p(2x)=2х-6$
Аналогично $p(x+3)=(х+3)-6=х+3-6=х-3$
Соберем все выражение: $4(p(2x)−2p(x+3))=4((2х-6)-2(х-3))$
Далее осталось раскрыть скобки и привести подобные слагаемые
$4((2х-6)-2(х-3))=4(2х-6-2х+6)=4·0=0$
Ответ: $0$
Системы иррациональных уравнений
Основные методы решения систем, содержащих иррациональные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – надо расписать ОДЗ каждого уравнения, а в конце решения выбрать решение системы с учетом ОДЗ.
Чтобы решить иррациональное уравнение, необходимо:
1. Преобразовать заданное иррациональное уравнение к виду
$√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
2. Обе части уравнение возвести в квадрат
$√{f(x)}^2={g(x)}^2$ или $√{f(x)}^2=√{g(x)}^2$
3. Решить полученное рациональное уравнение.
4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)







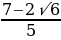 ;
; 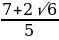 ≤a≤3; a3.
≤a≤3; a3.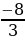 ;-1)U(0;
;-1)U(0;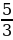 ).
).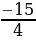 ;-2]U[0;
;-2]U[0;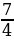 ].
].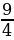 ;-
;-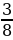 ;
;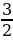 )
)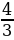 )U(-
)U(-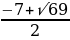 ].
].