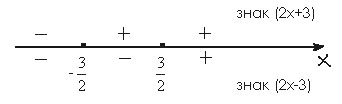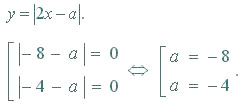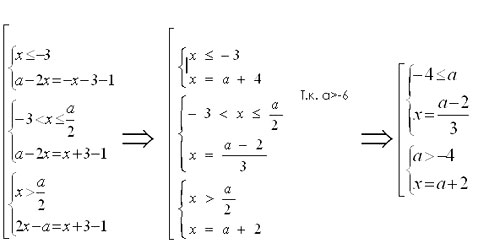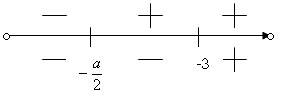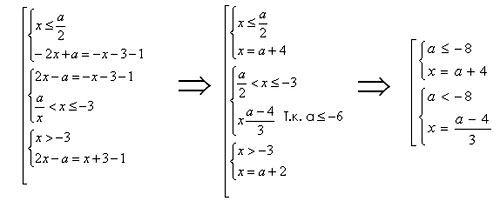Параметрическая плоскость в задачах егэ - Помощь в подготовке к экзаменам и поступлению

Видеокурсы Инны Фельдман
Рубрики
- 01 Задание (2022)
- 02 Задание (2022)
- 03 Задание (2022)
- 04 Задание (2016)
- 05 Задание (2022)
- 06 Задание (2022)
- 07 Задание (2022)
- 08 Задание (2022)
- 11 Задание (2022)
- 12 Задание (2022) (C1)
- 13 Задание (2022) (C2)
- 14 Задание (2022) (C3)
- 15 Задание (2022) (C4)
- 16 Задание (2022)
- 17 Задание (2022) (C6)
- 18 Задание (2022) (С7)
- АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
- База ЕГЭ Задание 19
- База ЕГЭ Задание 20
- БЕЗ РУБРИКИ
- ВИДЕОЛЕКЦИИ
- ВИДЕОТЕКА
- ВИДЕОУРОКИ
- Вопросы для повторения
- Диагностические работы
- Задание 01 (2016)
- Задание 02 (2016)
- Задание 03 (2016)
- ЗАДАЧИ С ПАРАМЕТРОМ
- Задачи с практическим содержанием
- ИНТЕГРАЛ
- Интерактивные модели
- ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- Комбинаторика
- ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- МГУ, ДВИ
- НОВОСТИ
- ОГЭ (ГИА) Задание 11
- ОГЭ (ГИА) Задание 15
- ОГЭ (ГИА) Задание 15
- ОГЭ (ГИА) Задание 24
- ОГЭ (ГИА) Задание 25
- ОНЛАЙН КУРСЫ
- Оплата
- ПЛАНИМЕТРИЯ
- ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- ПОЛЕЗНЫЕ СОВЕТЫ
- ПРЕЗЕНТАЦИИ
- ПРОГРЕССИИ
- ПРОИЗВОДНАЯ
- РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ
- СТЕРЕОМЕТРИЯ
- ТЕКСТОВЫЕ ЗАДАЧИ
- Теория вероятностей
- ТЕОРИЯ ЧИСЕЛ
- Тесты
- Тренировочные варианты
- ТРИГОНОМЕТРИЯ
- УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
- ФУНКЦИИ И ГРАФИКИ

Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.

2013-05-22

Главная » СТАТЬИ » 17 Задание (2022) (C6) » Решение задачи с параметром с помощью параметрической плоскости. Задание С5

22
Май 2013

17 Задание (2022) (C6)ВИДЕОУРОКИЗАДАЧИ С ПАРАМЕТРОМ

Решение задачи с параметром с помощью параметрической плоскости. Задание С5

Предлагаю вам познакомиться с видеорешением Задания С5 для подготовки к ЕГЭ по математике.

Найдите все значения параметра a, при каждом из которых имеет единственный корень уравнение:

$(x+7)^2+(a-6)^2=delim{|}{x-a+13}{|}+delim{|}{x+a+1}{|}$

Попробуйте решить задачу самостоятельно, а потом сверьте свое решение с видеоуроком:

И.В. Фельдман, репетитор по математике.

Отзывов (12)

Ирина

2013-06-01 в 09:37

Интересный способ. а это уравнение можно решить другим способом?

Ответить
- Инна
  
  2013-06-01 в 09:39
  
  Можно.
  
  Ответить
Анна

2013-06-02 в 15:48

Спасибо большое.
Подскажите пожалуйста, а если в уравнении вместо (х+7)^2 стоит просто х^2?

Ответить
- Инна
  
  2013-06-02 в 16:04
  
  Значит центр в точке 0
  
  Ответить
Юрий

2013-09-16 в 20:29

1. В рассмотренном способе предлагаю сразу сделать замену переменных: y=x+7, b=a-6. Тогда все действия существенно упрощаются.
2 На чем основан другой способ решения или с чего начать?

Ответить
Юрий

2013-09-16 в 21:22

С вопросом поспешил, поскольку уже сам додумался.
При предложенной замене переменных найти значения b,при которых совокупность четырех простых квадратных уравнений (полученных после раскрытия модулей в четырех случаях, но без рассмотрения областей в координатной плоскости) имеет единственное решение. Решается совсем просто.

Ответить
Марий

2013-11-11 в 19:02

Именно эта задача допускает решение так называемым методом симметрии: если данное уравнение имеет решение x0, то оно имеет еще решение -x0 — 14.Для единственности необходимо чтобы они равнялись (следовательно x0=-7) и таким образом получить «кандидатов» на роль параметра a. a=6,4 и 8.

Ответить
Елена

2016-01-29 в 07:30

Здравствуйте. Помогите, пожалуйста, решить!
x^2+|x^2-2x|=y^2+|y^2-2y| x+y=a (это система)

при каких значениях параметра имееются 2 решения?

Ответить
- Инна
  
  2016-01-29 в 08:25
  
  Построить график первого уравнения, раскрыв модуль. График должен быть симметричен относительно прямой у=х.
  Двигая прямую у=-х определить, когда она пересекает график в двух точках.
  
  Ответить
  - Елена
    
    2016-01-29 в 11:38
    
    А как правильно раскрыть модуль? Не получается нарисовать график.
    
    Ответить
    - Инна
      
      2016-01-29 в 15:57
      
      Нужно разбить координатную плоскость на области (при х=0, х=2, у=0, у=2 происходит смена знака подмодульных выражений) и в каждой области раскрыть модуль http://prntscr.com/9wf7yu
      
      Ответить
      - Елена
        
        2016-01-29 в 17:50
        
        Спасибо большое!
        
        Ответить

Добавить комментарий

ПАРОЛЬ ДЛЯ БИБЛИОТЕКИ 010101
Подпишитесь на рассылку сайта и ВЫБЕРИТЕ В ПОДАРОК ЛЮБУЮ ВИДЕОЛЕКЦИЮ!
репетитор по информатике
Видеокурсы Анны Малковой.
Рекомендую:
ЕГЭ-ТРЕНЕР, видеоуроки по математике Ольги Себедаш
ЕГЭ-Студия: подготовка к ЕГЭ и олимпиадам
Репетитор по математике. Подготовка к ЕГЭ и ДВИ в МГУ.
Простая физика — сайт Анны Денисовой
EgeMaximum — сайт Елены Репиной
ЕГЭ-ШАНС — сайт Ларисы Гайковой
Последние записи
- Условная вероятность. Формула Байеса
- Новые задачи по теории вероятностей
- Видеолекция «Решение задач на оптимизацию на ЕГЭ по математике»
- Тренировочный вариант №51
- Тренировочный вариант №50
архив записей

архив записей

Источник

Слайд 1

Неравенства с параметрами Метод интервалов на плоскости Гайкович Э.Б. ГБОУ СОШ № 4 Кусто

Слайд 2

1.РЕШИТЬ НЕРАВЕНСТВО ( х-а )(2х+а)(х-2)≥0 При решении методом интервалов: к ак расположить на прямой точки а, -а:2 и 2 ? Какая из этих точек левее, какая правее? Вариантов много и надо все их рассматривать.

Слайд 3

Попробуем поступить по другому…. На координатной плоскости п остроим прямые а = х , а = — 2х и х=2 1.РЕШИТЬ НЕРАВЕНСТВО ( х-а )(2х+а)(х-2)≥0

Слайд 4

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 5

Нас интересуют области, ограниченные красными прямыми . Причем, среди них есть «хорошие» ( как в обычном методе интервалов) и «плохие» . Если координаты какой-то внутренней точки области удовлетворяют данному в условии неравенству, то и координаты всех точек этой области ему удовлетворяют и область «хорошая» .

Слайд 6

х а а =х а=-2х х=2 1 1 -1 -1 Проверяем для точки М (0;1): (0-1)(0+1)(0-1)≥0 ВЕРНО.

Слайд 7

х а а =х а=-2х х=2 1 1 -1 -1 Область – «хорошая»! Выделим ее.

Слайд 8

«Хорошие» и « плохие» области чередуются, если соответствующие скобки в неравенстве встречаются НЕЧЕТНОЕ число раз. Выделим все «хорошие» области.

Слайд 9

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 10

Итак, мы получили области, координаты точек которых удовлетворяют нашему неравенству. Осталось установить зависимость между а и х , т.е ответить на вопрос : « При каких а верно это неравенства и какие х соответствуют этим а.?» Рассмотрим горизонтальную прямую, которая двигается снизу вверх, т.е рассмотрим а от ─∞ до ∞ .

Слайд 11

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 12

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 13

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 14

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 15

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 16

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 17

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 18

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 19

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 20

х а а =х а=-2х х=2 1 1 -1 -1

Слайд 21

Если а≤ -4 , то а ≤ х ≤ 2 и х ≥ -а:2, если -4 ≤ а≤ 0 , то а≤ х ≤ -а:2 и х ≥ 2, если 0 ≤ а≤ 2 , то –а:2 ≤ х ≤ а и х ≥ 2, если а≥2 , то –а:2 ≤ х ≤ 2 и х ≥ а, ОТВЕТ:

Слайд 22

2 .ПРИ КАКИХ а НЕРАВЕНСТВО ( х-а )(2х+а)(х-2)≥0 ВЕРНО ДЛЯ ВСЕХ 3≤ х ≤ 5 ? Выделим область,соответствующую условию: 3≤ х ≤ 5

Слайд 23

х а а =х а=-2х х=2 1 1 -1 -1 -6 3

Слайд 24

х а а =х а=-2х х=2 1 1 -1 -1 -6 3 -6 ≤ а≤ 3 ОТВЕТ:

Источник

Пусть заданы две
функции одного аргумента

(17)

где

(в частности допускается
).
При каждом значении

числа

и

будем понимать как координаты некоторой
точки на плоскости, причем эта точка,
вообще говоря, меняется вместе с
изменением
,
описывая некоторую кривую
.
В этом случае систему уравнений (17)
называют параметрическими уравнениями
линии
,
а аргумент

называют параметром.

Переход от
параметрических уравнений к уравнению

осуществляется исключением параметра

из системы уравнений (17).

Рассмотрим несколько
примеров.

1.

– известные параметрические уравнения
прямой, проходящей через точку

с направляющим вектором
,
.

2.
.
Исключая параметр
,
получаем
,
то есть уравнение параболы,
.

3. Уравнения

– уравнения окружности радиуса
,
т.к.
,
.

4. Уравнения
,

– являются параметрическими уравнениями
эллипса.

5. Циклоида.

Пусть по прямой
без скольжения катится круг радиуса
.
Кривая, описываемая фиксированной
точкой круга, называется циклоидой.
Уравнения циклоиды
.

Рис. 19.

6. Астроида.

Пусть по окружности
радиуса

внутри нее катится без скольжения круг
радиуса
.
Траектория, которую описывает фиксированная
точка, лежащая на границе подвижного
круга, называется астроидой.

—а

Рис. 20.

Уравнения астроиды
,

7. Кардиоида.

Пусть по окружности
радиуса

вне ее катится без скольжения круг того
же радиуса
.
Кривая, которую описывает фиксированная
точка подвижного круга, называется
кардиоидой.

Рис. 21.

Уравнения кардиоиды
,
.

§ 8. Кривые в полярной системе координат.

Рассмотрим полярную
систему координат на плоскости. Пусть
нам задан полюс и полярная ось. Для
произвольной точки

на плоскости обозначим через

расстояние от точки

до точки
,
а через

– угол, на который нужно повернуть
полярную ось до совмещения с лучом.

Рис. 22.

Числа
,
называются полярными координатами
точки
.
Число

называют полярным радиусом (всегда
),
а число

называют полярным углом точки
.
Полярный радиус для любой точки
определяется однозначно, а полярный
угол – с точностью до
,
где

– целое число.

Пусть на плоскости
задана полярная и правая декартова
прямоугольная система координат.

Рис. 23.

Пусть

– произвольная точка плоскости, имеющая
декартовы координаты

и полярные координаты
.
Рассмотрим радиус вектор

точки
.
Сравнивая координаты, получим формулы
перехода от декартовых координат к
полярным:

Формулы перехода
от полярных координат

к декартовым

можно записать в виде:

При

можно вычислить
.

Кривую в полярных
координатах задают в виде уравнения

или явного уравнения в виде
.

Рассмотрим несколько
примеров кривых, заданных в полярных
координатах.

Уравнение
,
где

– постоянное число, задает окружность
радиуса
,
центр которой совпадает с полюсом
.
Уравнение

определяет луч, исходящий из полюса и
составляющий угол

с полярной осью.

– произвольное число.
Выведем полярное
уравнение окружности радиуса

в случае, когда полюс лежит на ней, а
полярная ось проходит через центр
окружности.

Рис. 24.

Возьмем произвольную
точку

на окружности. Треугольник

прямоугольный. Получаем уравнение
окружности в виде
.

Покажем, что
уравнение

и полярных координатах определяет
окружность радиуса
.
Подставим выражения для

и

через

и

в уравнение:
.
Умножая обе части уравнения на
,
получим

или
.
Это уравнение окружности радиуса

с центром в точке
.
Пусть в декартовой
системе координат заданы прямые
,
.
Уравнения этих прямых в полярной системе
координат
,
.
Рассмотрим
уравнение
,
.
Переход к декартовым координатам здесь
довольно громоздкий и приводит к
алгебраическому уравнению высокой
степени. Поэтому посмотрим эту кривую,
исходя из качественных соображений.

Период правой
части уравнения равен
,
поэтому достаточно построить кривую
для значений полярного угла из интервала
.
По свойствам функции
,
см. рис. 22, видно, что полярный радиус
монотонно
возрастает при

и при

монотонно убывает. При
правая
часть уравнения

отрицательна, для этих значений

точек кривой нет. Для остальных значений
кривая получается при повороте на угол

части кривой, расположенной между лучами

и
,
рис. 24.

Рис. 25.

Источник

Цели: показать применение графических
методов решения уравнений с параметрами и
определить удобство и эффективность
использования каждого из них.

обучающая — расширить знания учащихся по
применению графиков для решения уравнений с
параметрами;

развивающая — развить нестандартное
мышление через умение находить рациональные
пути решения, научить переключаться с одного
способа на другой, развить культуру соблюдения
всех этапов аргументации при решении уравнений;

воспитательная — воспитать терпение,
упорство в достижении цели, умение работать в
коллективе.

Задачи:

научить:

1. Пользоваться координатно-параметрическим
методом решения уравнений с параметрами, уметь
отличать его от графического способа.

2. Делать правильный выбор способа решения
уравнения, исходя из условия данной задачи.

3. Организовывать работу в группах.

Ход урока

1. Введение в урок, организационный этап (слайды
1, 2, 3 приложения 1).

2. Повторение теоретического материала.

Учитель. Что значит решить уравнение с
параметром?

Предполагаемый ответ. Решить уравнение с
параметром – это, значит, установить
соответствие, с помощью которого для каждого
значения параметра указывается множество корней
соответствующего уравнения.

Учитель. В зависимости от того, какая роль
параметру отводится в задаче (неравноправная,
или равноправная с переменной), можно
соответственно выделить два основных
графических приёма: первый – построение
графического образа на координатной плоскости (x;
y), второй – на (х; а).

Схематично структура первого метода выглядит
следующим образом. На плоскости (х; y) функция y=f(х;
а) задаёт семейство кривых, зависящих от
параметра а. Понятно, что каждое семейство f
обладает определёнными свойствам, но основным
является осуществление перехода от одной кривой
семейства к другой.

Что касается второго способа, то он основан на
нахождении множества всех точек
координатно-параметрической плоскости, значения
координат х и параметра а каждой из которых
удовлетворяют заданному в условиях задачи
соотношению. Если указанное множество точек
найдено, то можно каждому допустимому значению
параметра а=const поставить в соответствие
координатных точек этого множества, дающие
искомое значение задачи. Этому способу мы
посвятим сегодняшний урок.

Для простоты дальнейшего общения назовём
первый способ графическим, а второй
координатно-параметрическим и продемонстрируем
их использование на примерах.

3. Основная часть.

а) Учащимся предлагается задача, которая
решена каждым из предложенных способов. Решения
представлены на слайдах (4 и 5 приложения 1) и
разбираются подробнейшим образом.

№1. При каких значениях параметра а уравнение
имеет более
двух корней.

Решение. I способ
(координатно-параметрический):

Если подставить х=0 в исходное уравнение, то
получим 6=6, это означает, что х=0 является решением
уравнения при любом а. Пусть теперь х, тогда можно записать а=. Выясним знаки
выражений 2х+3 и 2х-3.

Рис. 1

Рис. 2

а=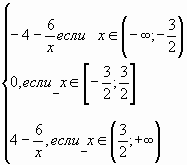

В плоскости построим множество точек (х ;а),
координаты которых удовлетворяют соотношению.

Если а=0, то уравнение имеет бесконечно
множество решений на промежутке , при других значениях а
количество решений уравнения не превышает двух.

Ответ: а=0

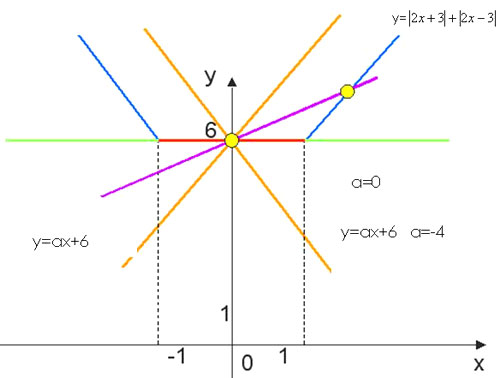
Решение. II способ (графический):

Построим графики функций y= и y=ах+6 и найдём количество точек
их пересечения в зависимости от параметра а.

Рис. 3

Значит, если а=0, тогда х. Если а, то уравнение имеет два решения, но при
а существует
одно решение данного уравнения. То есть
уравнение имеет более двух корней при а=0.

Ответ: а=0.

Учитель: Какой способ вам импонирует в данном
случае?

Предполагаемый ответ. Графический. Он требует
меньше вычислений, хотя определенную трудность
вызывает вычисление параметра на граничных
положениях прямой.

б) Cамостоятельная работа по группам.

Класс разбивается на группы, часть из которых
решает следующую задачу графическим способом, а
часть — координатно-параметрическим. По
истечении времени решения проверяются
посредством мультимедийной доски (слайды № 6, №7
приложения 1).

№2. Найдите все значения параметра а, при
которых уравнение имеет единственное решение.

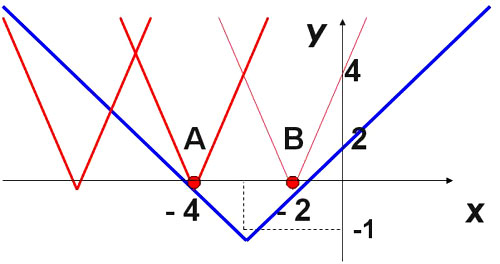
Решение. I способ (графический):

Построим график функций y= и y=

Рис. 4

А(-4; 0), В(-2; 0) координаты этих точек
удовлетворяют уравнению.

Рис. 5

Ответ: а=-8; а=-4.

Решение. II способ
(координатно-параметрический).

Используя определение абсолютной величины,
преобразуем уравнение, в каждой из “частичных
областей”, на которые делят прямые х=-3, х= КП-плоскость,
рассмотрев случаи a<-6 и a>-6, заменив его
равносильной совокупностью.

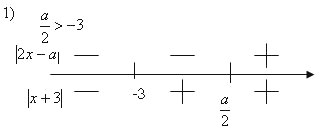
Рис. 6

Рис. 7

Рис. 8

Также как и в первый раз, заменим уравнение
совокупностью.

Рис. 9

Изображённое ниже множество точек (х; а) –
координаты х и параметра а, которые
удовлетворяют уравнению, даёт возможность
ответить на вопрос о единственности решения.

Рис. 10

Ответ: а=-8; а=-4.

в) Решение следующей задачи
координатно-параметрическим способом дает
возможность без усилий давать ответ задачи,
исходя из чертежа. Задача решается на доске и в
тетрадях.

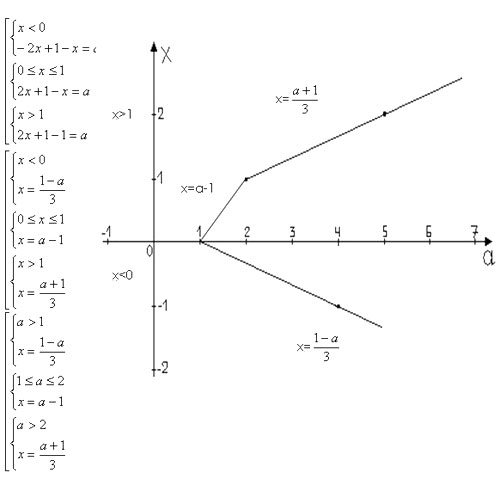
№2. Для каждого значения параметра а решить
уравнение.

Решение. (Координатно-параметрический)

Применяя метод “частичных областей” и
определение абсолютной величины, заменим
уравнение совокупностью трёх систем.

Рис. 11

Используя решение на КП-плоскости, запишем
ответ:

Если а<1, то х

Если 1, то х₁= , х₂=а-1

Если а>2, то х₁=, х₂=

Учитель. Чем отличается постановка последней
задачи от предыдущих?

Предполагаемый ответ: в начальных задачах
основным являлся поиск количества корней, а в
последней — сами корни. И в этом случае
координатно-параметрический способ выдает
готовые решения без дополнительных вычислений.

4. Подведение итогов урока.

Учитель с помощью учеников делает выводы о
новом методе и возможностях его использования.

1. При решении уравнений с параметрами нельзя
говорить о предпочтении одного способа перед
другим.

2. Выбор метода решения зависит от постановки
задачи, т.е. когда нам требуется определить
количество корней уравнения, то удобнее
использовать графический способ, а если нам
необходимо найти корни уравнения в зависимости
от параметра, то эффективнее
координатно-параметрический способ.

5. Домашнее задание.

Решить КП – методом следующие уравнения.

1. ¦Х + 2¦ +¦ Х – 4¦ + ¦Х – 1¦ = a.

2. ¦ X + a – 1¦ = ¦X – a + 1¦.

Комментарий: урок можно отнести к типу
урок-знакомство. Теоретический материал
выдается в описательном порядке, без глубокого
разбора самого метода. Во время урока учащимся
предлагается решение задач известным им
графическим способом, но под другим углом. Этот
метод имеет стройную последовательность
изложения, что не маловажно при записи решений
задач части С, облегчает запись общего ответа к
задаче с параметрами, но не является
единственным. Этот урок можно провести в 10–11
классах в курсе “алгебра и начала анализа”.
Тогда сильные учащиеся могут продолжить
изучение метода при решении различных уравнений
на групповых, дополнительных занятиях или
самостоятельно.

Список литературы:

В.П.Моденов “Задачи с параметрами”.
2. С.В.Кравцев и др. “Методы решения задач по
алгебре”.

Необходимые ресурсы: Microsoft Office PowerPoint 2007 или
2003, Microsoft Office Word 2007 или 2003.

Источник

МОу Шумовская
СОШ

Сборник заданий по
подготовке к решению С5 ЕГЭ по математике: задачи с параметрами

Составитель: Волковская О.П., учитель математики

Пояснительная
записка

В курсе элементарной математики уравнения и
неравенства с параметрами являются одними из самых сложных заданий.

Большая часть задач с параметрами решается при помощи
алгебраических способов, но немаловажной является геометрическая интерпретация,
которая часто и дает ключ к решению. Более того, практически невозможно
представить изложение ряда вопросов (например, исследование квадратного
трехчлена) без графического представления изучаемого объекта.

Графический метод исследования уравнений и неравенств,
содержащих параметр, имеет широкую область применения.

Данное пособие содержит подборку заданий С5 из единого
государственного экзамена для подготовки на уроках математики, так и для
самостоятельного изучения. Приведены примеры решения задач, а также задания для
самостоятельного решения.

Примеры
заданий

1. Задача.

При каких значениях параметра a уравнение

(a — 1)x² + 2x + a — 1 = 0
имеет ровно один корень?
Решение.
При a = 1 уравнение имеет
вид 2x = 0 и, очевидно, имеет единственный корень x = 0.
Если a ≠1, то данное уравнение является квадратным и имеет
единственный корень при тех значениях параметра, при которых дискриминант
квадратного трехчлена равен нулю. Приравнивая дискриминант к нулю, получаем
уравнение относительно параметра a

4a² — 8a = 0,

a = 0 или a = 2.

Ответ: уравнение имеет единственный корень при a ∊ {0;1;2}.

2. Задача. Известно, что

и f₂(x) = 6x—x²-6.

а) Постройте график функции f₁(x)
при a =1.

б) При каком значении a графики
функций f₁(x) и f₂(x)
имеют единственную общую точку?

Решение.
а. Преобразуем f₁(x)

График этой функции при a = 1
изображен на рисунке.
б. отметим, что графики функций y = kx+b и y = ax²+bx+c (a ≠ 0)
пересекаются в единственной точке тогда и только тогда, когда квадратное
уравнение kx+b = ax²+bx+c имеет
единственный корень. Используя представление f₁ из а,
приравняем дискриминант уравнения a = 6x—x²-6
к нулю. Из уравнения 36-24-4a = 0 получаем a = 3.
Проделав то же самое с уравнением 2x—a = 6x—x²-6
найдем a = 2. Нетрудно убедиться, что эти значения параметра
удовлетворяют условиям задачи.

Ответ: a =2
или a=3.

3.Задача.
При каком наименьшем натуральном
значении a уравнение

имеет ровно два решения?

Решение.
Перепишем это уравнение в виде x² +
(2a-2)x — 3a+7 = 0. Это квадратное уравнение, оно
имеет ровно два решения, если его дискриминант строго больше нуля. Вычисляя
дискриминант, получаем, что условием наличия ровно двух корней является
выполнение неравенства a²+a-6 > 0. Решая
неравенство, находим a < -3 или a > 2.
Первое из неравенств, очевидно, решений в натуральных числах не имеет, а наименьшим
натуральным решением второго является число 3.
Ответ: 3.
4. Задача

При каких
значениях a сумма квадратов корней уравнения

больше 12?

Решение.
Дискриминант уравнения x²-2ax+a²—a =
0 равен 4a. Поэтому действительные корни этого уравнения существуют,
если a і 0. Применяя к данному уравнению теорему Виета
получаем x₁+x₂ = 2a и x₁·x₂ = a²—a.
Отсюда x₁²+x₂² =
(x₁+x₂)²-2x₁·x₂ =
2a²+2a. Решениями неравенства 2a²+2a >
12, удовлетворяющими условию a і 0, являются числа a>
2.
Ответ: a > 2.

5. Задача

Найдите все значения параметра , при каждом из которых уравнение $ax+sqrt{-7-8x-x^2}=2a+3$ имеет единственное решение.

Решение [5].

Оставим корень слева, а все
остальное перенесем вправо. Представим наше уравнение в виде системы

$delim{lbrace}{matrix{2}{1}{{y=2a-ax+3} {y=sqrt{-7-8x-x^2}} }}{ }$

Построим график каждой функции и
найдем, при каком значении параметра графики имеют единственную точку
пересечения.

Первая функция: .
Вынесем за
скобку:

График этой функции представляет
из себя семейство прямых, которые имеют различный коэффициент наклона
и общую точку с координатами (2;3):

Вторая функция: $y=sqrt{-7-8x-x^2}$ . Преобразуем
выражение под корнем – выделим полный квадрат:

$sqrt{-7-8x-x^2}=sqrt{-7-(8x+x^2)}=sqrt{-7-(16+8x+x^2-16)}=sqrt{-7+16-{(x+4)}^2}=sqrt{9-{(x+4)}^2}$

График функции $y=sqrt{9-{(x+4)}^2}$ представляет из себя полуокружность с
центром в точке (-4;0) и радиусом 3.

Определим, при каком коэффициенте
наклона прямая имеет с полуокружностью одну точку пересечения:

Мы видим, что прямые,
заключенные между прямыми  и  имеют с полуокружностью одну общую
точку. Прямая   имеет
одну общую точку, а прямая   –
две. Прямая  также
имеет с полуокружностью одну общую точку.

Найдем коэффициенты наклона этих
прямых. Для этого мы рассмотрим соответствующие прямоугольные треугольники:

Коэффициент наклона прямой
равен 1.

Коэффициент наклона прямой равен
3/9=1/3.

Коэффициент наклона прямой равен
нулю.

Итак, прямая и полуокружность
имеют одну общую точку, если и . Умножим
первое неравенство на -1 и получим.

Ответ:

6.
Задача.

Найдите
все значения параметра ,
при каждом из которых неравенство $delim{|}{{x^2-x-2a}/{x-a}-1}{|}<=2$ имеет
единственное решение на отрезке [1;3].

Решение
[5].

1. Упростим
выражение под знаком модуля:

$delim{|}{{x^2-x-2a-x+a}/{x-a}}{|}<=2$
$delim{|}{{x^2-2x-a}/{x-a}}{|}<=2$

2. Неравенство равносильно системе:

Запишем
наше неравенство в виде равносильной системы:

$delim{lbrace}{matrix{2}{1}{{{x^2-2x-a}/{x-a}<=2} {{x^2-2x-a}/{x-a}>=-2} }}{ }» title=»delim{lbrace}{matrix{2}{1}{{{x^2-2x-a}/{x-a}<=2} {{x^2-2x-a}/{x-a}>=-2} }}{ }»/><img src=$

Перенесем
все влево и приведем к общему знаменателю:

$delim{lbrace}{matrix{2}{1}{{{x^2-2x-a-2x+2a}/{x-a}<=0} {{x^2-2x-a+2x-2a}/{x-a}>=0} }}{ }» title=»delim{lbrace}{matrix{2}{1}{{{x^2-2x-a-2x+2a}/{x-a}<=0} {{x^2-2x-a+2x-2a}/{x-a}>=0} }}{ }»/><img src=$
$delim{lbrace}{matrix{2}{1}{{{x^2-4x+a}/{x-a}<=0} {{x^2-3a}/{x-a}>=0} }}{ }» title=»delim{lbrace}{matrix{2}{1}{{{x^2-4x+a}/{x-a}<=0} {{x^2-3a}/{x-a}>=0} }}{ }»/><img src=$

3. Изобразим
на параметрической плоскости решение системы.

Начнем
с первого неравенства. Смена знаков происходит в точках, в которых
числитель и знаменатель дроби равны нулю. Приравняем числитель и знаменатель
дроби к нулю:

Числитель
обращается в ноль в точках параболы . (Нам проще выразить
параметр через переменную , поэтому в нашей
параметрической плоскости вертикальной осью мы назначим ось , а
горизонтальной – ось )

Знаменатель
обращается в ноль в точках прямой . Так как знаменатель
не равен нулю, прямую изображем пунктирной линией.
Точки пересечения графиков и мы
выкалываем:

При
пересечении графиков дробь меняет знак. Определимся со знаками. Возьмем точку с
координатами и подставим
значения и в первое неравенство:

${2^2-4*2+0}/{2-0}<0$ .
Следовательно в области, содержащей эту точку, дробь в левой части первого
неравенства меньше нуля. При переходе через график знак меняется:

Нас
интересуют области, где левая часть неравенства меньше или равна нулю:

Теперь
рассмотрим второе неравенство системы: ${x^2-3a}/{x-a}>=0″ title=»{x^2-3a}/{x-a}>=0″/><img src=$

Числитель
обращается в ноль в точках параболы $a={x^2}/3$ , а знаменатель в точках
прямой :

Определим
знак дроби в левой части неравенства в точке с координатами .

${2^2-3*0}/{2-0}>0″ title=»{2^2-3*0}/{2-0}>0″/><img src=$ .
Нас интересуют области, в которых выполняется неравенство ${x^2-3a}/{x-a}>=0″ title=»{x^2-3a}/{x-a}>=0″/><img src=$ :

Совместим
закрашенные области:

Итак,
множество точек координатной плоскости , удовлетворяющих
системе неравенств представляют из себя такую фигуру:

По
условию задачи, нам нужно узнать, при каком значении параметра неравенство
имеет единственное решение на отрезке [1;3] ,
то есть в этой выделенной области:

Если
мы будем двигать прямую, параллельную оси вдоль оси (ординаты
всех точек этой прямой равны определенному значению параметра), то увидим, что
эта прямая имеет с нужной нам областью одну точку пересечения при :

Ответ:
{3}

7.
Задача

Найдите все значения , при каждом
из которых уравнение $log_{1-x}{(a-x+2)}=2$
имеет хотя бы один корень, принадлежащий промежутку [-1;1).

Решение [5]:

Задачу будем решать с помощью параметрической
плоскости.

Перейдем от уравнения $log_{1-x}{(a-x+2)}=2$ к равносильной системе:

$delim{lbrace}{matrix{4}{1}{{a-x+2>0} {1-x>0} {1-x<>1}{a-x+2=(1-x)^2}}}{ }$

Первые три неравенства системы — ОДЗ исходного
уравнения.

Выразим параметр через
переменную :

$delim{lbrace}{matrix{4}{1}{{a>x-2} {x<1} {x<>0}{a=x^2-x-1}}}{ }$

Изобразим на кординатной плоскости решение
этой системы.

Точки, координаты которых удовлетворяют первому
неравенству системы, расположены выше прямой . Так как
неравенство строгое, прямую изображаем пунктирной линией:

Точки, удовлетворяющие второму неравенству
системы расположены левее прямой . Эту прямую
также изображаем пунктирной линией:

Нас интересует пересечение этих областей:

Прямую также изобразим
пунктиром — точки этой прямой мы должны исключить из решения:

И, наконец парабола . Точки пересечения
параболы с пунктирными линиями выкалываем. Координаты вершины
параболы: , :

По условию задачи корни уравнения должны
принадлежать промежутку [-1;1), то есть интересующая нас область значительно
сужается:

Мы видим, что уравнение имеет хотя бы один корень
при [-5/4;-1)U(-1;1]:

Ответ: [-5/4;-1)U(-1;1]

8. Задача

При каких значениях параметра , при каждом из
которых уравнение ${{4^{-x^2}-a2^{1-x^2}+a}/{2^{1-x^2}-1}}=3$ имеет
хотя бы одно решение.

Решение [6]

Сделаем замену  поэтому  Задачу
можно сформулировать так: найдите значения  при
каждом из которых уравнение  имеет
хотя бы одно решение, удовлетворяющее условию

Перейдем к системе:

Заметим что ни при
одном значении число не
является корнем уравнения.

Рассмотрим функцию Её
график — парабола, ветви которой направлены вверх. Следовательно,
условие задачи выполнено тогда и только тогда, когда выполняется
одно из трех условий:

1) Трёхчлен имеет два
различных корня, и только больший из них лежит на промежутке (0;
1])(см.рис. 1), то есть

2) Трёхчлен имеет два
различных корня, и только меньший из них лежит на промежутке (0;
1])(см.рис. 2), то есть

3) Трёхчлен имеет два
корня,возможно, совпадающих, и оба лежат на промежутке (0; 1])(см.рис.
3), то есть

Эти условия соответствуют
следующим способам расположения графика функции :

Решим систему 1:

Решим систему 2:

Решим систему 3:

Ответ:

9. Задача

Найдите все значения a,
при которых уравнение
имеет на промежутке единственный
корень.

Решение [6].

Рассмотрим два случая.
Первый случай: Исходное
уравнение примет вид

Последнее уравнение
имеет на промежутке  единственный
корень при  откуда Подставив  в
неравенство  получим:  откуда

В этом случае уравнение  при
условии  имеет
на промежутке  единственный
корень  при  и
не имеет на промежутке  корней
при  и
при

Второй случай: Исходное
уравнение примет вид

Последнее уравнение
имеет на промежутке  единственный
корень  Подставив  в
неравенство  получим:  откуда

В этом случае уравнение  при
условии  имеет
на промежутке единственный
корень  при  и
не имеет на промежутке  корней
при

Уравнение на
промежутке

• при не
имеет корней;

• при имеет
единственный корень

• при имеет
два различных корня и

• при имеет
единственный корень

Ответ:

10. Задача

Найдите все значения а,
при каждом из которых уравнение имеет
ровно три различных решения.

Решение.

Запишем уравнение в
виде и
рассмотрим графики функций и .

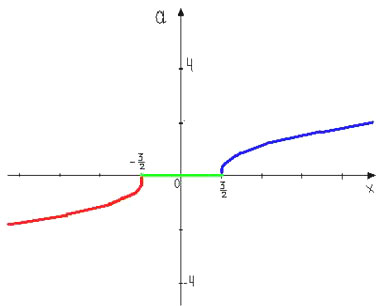
График первой функции
— парабола, график второй функции — угол с вершиной в точке а.

Уравнение будет иметь
три различных решения в следующих случаях.

1. Вершина параболы
совпадает с вершиной угла (рис. 1).

2. Одна из сторон угла
касается параболы (рис. 2).

В первом случае , и уравнение
имеет три корня: 2, 4, 6. Рассмотрим второй случай. Пусть правая сторона
угла касается параболы. Уравнение , а
должно иметь единственное решение.

Приведём уравнение к
стандартному виду:

Из равенства нулю дискриминанта
получаем

откуда .

Если параболы касается
левая сторона угла, получаем уравнение

; .

Оно имеет единственное
решение, только если .

Ответ:
3,5; 4; 4,5.

Задания для самостоятельного решения

1. Найдите все значения параметра а, при каждом из которых график функции
f(x)=x|x-4|-x-a имеет с осью абсцисс ровно три общие точки.

Ответ: (-4 ; 2,25)

2. Найдите все значения a,
при каждом из которых уравнение либо имеет единственное решение, либо не имеет решений.

Ответ: ; .

3. Найдите все значения а, при каждом из которых уравнение
имеет
единственный корень.

Ответ: {1; 5}.

4. Найдите все значения при каждом из которых уравнение

на промежутке имеет больше двух корней.

Ответ:

5. Найдите все значения параметра , при каждом
из которых уравнение $ax-3=sqrt{4x-x^2-3}$ имеет
единственное решение.

Ответ: [1;3)U{(6+2√3)/3}

6. Найдите все значения параметра a, при каждом из которых имеет
единственный корень уравнение: (x+7)²+(a-6)²=|x—a+13|+|x+a+1|

Ответ: {4;8}

7. Найдите все значения a, при каждом из которых
уравнение имеет единственный корень.

Ответ:

8. Найдите все значения a,
при каждом из которых уравнение имеет хотя бы один корень.

Ответ:

9.
Найдите все значения a, при которых уравнение

имеет на промежутке единственный корень.

Ответ:

10.
Найдите все значения a, при которых уравнение

имеет хотя бы
один корень, принадлежащий промежутку (−1; 1].

Ответ:

11.
Найдите все
значения a, при которых
уравнение

имеет хотя бы один корень, принадлежащий промежутку
(-1; 2].

Ответ:

12. Найдите все значения a, при каждом из которых
уравнение

имеет
хотя бы один корень.

Ответ:

13. Найдите все значения а. при каждом из которых уравнение
на
промежутке имеет
более двух корней.

Ответ: .

14. Найдите все значения , при которых уравнение на промежутке имеет ровно два корня.

Ответ: ;

15. При каких уравнение имеет ровно три корня?

Ответ:

Список литературы

1.
Бернштейн,
Е.А., Попов, Н.В. Задачи с параметрами. Учебное пособие для учащихся ОЛ ВЗМШ.
М. 2003. 75 с.

2. ЕГЭ-2013.
Математика: тематический сборник заданий / Под ред. А.Л. Семенова, И.В. Ященко.
— М.: Издательство «Национальное образование», 2012. — (ЕГЭ-2013. ФИПИ-школе)

3. Отличник
ЕГЭ. Математика. Решение сложных задач / ФИПИ авторы- составители: Панферов
В.С., Сергеев И.Н. – М.: Интеллект-Центр, 2012.

4.
Шестаков,
С.А., Юрченко, Е.В. Уравнения с параметрами. М.: Слог, 1993.

5.
Персональный
сайт репетитора по математике И.В. Фельдман http://ege-ok.ru/2013/06/01/zadacha-s-parametrom-zadanie-s5/

6.
Решу
ЕГЭ. Образовательный портал для подготовки к экзаменам. http://reshuege.ru/test?theme=171

Источник

Уравнения с параметром. Задача 18 (С6)

Графический метод в задачах с параметром

Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.

Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.

Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.

Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.

Пример 1

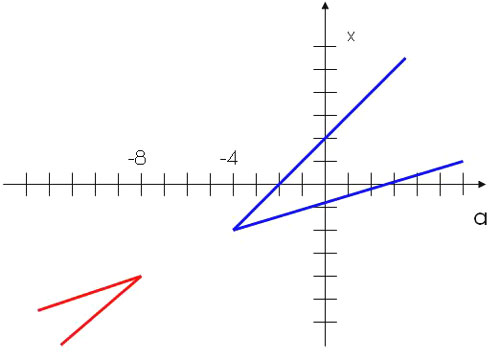
Решить графическим методом уравнение (x^2+3x=5x+3).

Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.

(y=5x+3) – красный график; (y=x^2+3x) – синий график.

Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: ({x}_{1}=-1; {x}_{2}=3).

Ответ: ({x}_{1}=-1; {x}_{2}=3).

Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).

В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac{10+5y}{2}) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):

Все точки, принадлежащие этому графику, будут решениями нашего уравнения. Например, при (x=0) ⇔ (y=-2). Аналогично можно выразить (y=frac{2x-10}{5}). График будет выглядеть так (Рис. 3):

И, разумеется, будет задавать точно такие же пары решений (x) и (y).
Теперь перейдем к уравнениям с параметром. Заметим, что параметр – это обычная переменная, которая ничем не отличается от рассмотренных выше переменных (x) и (y). Поэтому, если мы вместо (y) в уравнении (1) запишем параметр (a), то суть уравнения от этого не поменяется. То есть уравнение (1) можно рассматривать относительно (x) с параметром (y) или наоборот. В дальнейшем параметр будем обозначать за (a).

Разберем уравнение с параметром (6x-5a=15). Будем работать в системе координат ((aOx)). Выразим (x=frac{15+5a}{6}) – это будет общий вид решения. Для того чтобы проиллюстрировать ответ, построим график (x(a)) (Рис. 4).

Пример 2

Найти все значения параметра (a), при которых корни уравнения (6x-5a=15) лежат на отрезке ([-5;5]).

График (x(a)) для этого же примера на рисунке 4.

Иногда для решения удобно построить график зависимости (a(x): a=frac{6x-15}{5}). Давайте так и поступим. Построим график (Рис. 5). И красной областью покажем интервал, который нас интересует по условию задачи. Из рисунка видно, что (a∈[-9;3]) (при (x=5) ⇔(a=3); и при (x=-5) ⇔(a=-9))

На мой взгляд, будет более наглядно, если показывать графический метод на примерах. Поэтому, давайте разберем примеры от простых к сложным, которые могут встретиться на ЕГЭ.

Пример 3

Определить, при каких значениях параметра (a) уравнение (x^2-3x-2a=0) имеет: а) 2 корня; б) 1 корень; в) не имеет корней;

Решение:

1 способ решения:

Приведем уравнение к виду (x^2-3x=2a). И построим графики (y=1/2*(x^2-3x)) (показан красной линией) и (y=a) (синяя линия). Обратите внимание, график (y=a) – это просто семейство прямых параллельных оси (x) в плоскости ((xOy)) (Рис. 6). Точки пересечения красной линии с семейством синих линий – это корни нашего уравнения. Если, например, (a=5), то графики (y=5) и (y=1/2*(x^2-3x)) имеют две общие точки, а значит, и два решения. При (a=-1.125) оба графика имеют только одну общую точку ((1.5;-1.125)) – это единственное решение.

Ответ:
При (a>-1.115) уравнение имеет два корня;
При (a=-1.125) уравнение имеет один корень;
При (a<-1.125) уравнение не имеет корней.

2 способ решения:

Таким же образом можно решить данное уравнение, построив графики в плоскости ((xOa)). Для этого выразим (a=1/2*(x^2-3x).)

Различным значениям параметра (a) можно поставить значения искомого (x), для это проведем горизонтальные линии.

Пример 4

Решить уравнение: (cos^2⁡x-2 cos⁡x+a=0)

Сделаем замену (t=cos⁡x,) тогда ( t^2-2t+a=0,) при (t∈[-1;1].)

Построим в плоскости ((tOa)) график нашей функции (a=2t-t^2:)

Точки пересечения горизонтальных (фиолетовых) прямых с графиком нашей функции соответствуют решениям. Но (t∈[-1;1]), покажем это при помощи зеленой области (Рис.8). Таким образом, нас устраивают решения, которые принадлежат кусочку параболы, попавшей в зеленую область. Как видно из рисунка, (a) может принимать значения (a∈[-3;1]), и каждому значению (a) из этой области соответствует единственное решение. Найдем его, решив уравнение (t^2-2t+a=0;)

$$ {t}_{1}=frac{4-sqrt{4-4a}}{2};$$
$$ {t}_{2}=frac{4+sqrt{4-4a}}{2}.$$

({t}_{2}) не подходит, так как он не удовлетворяет условию (t∈[-1;1]).

Сделаем обратную замену:

$$ cos⁡x=frac{4-/sqrt{4-4a}}{2};$$
$$ x=±arccos⁡(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$

Ответ: При (a∈[-3;1]); $$ x=±arccos⁡(frac{4-sqrt{4-4a}}{2}+2πn,n∈Z$$

Пример 5

Решить уравнение (sin^4⁡x-(a-1) sin^2⁡x-(2a+2)=0.)

Решение:

Сделаем замену: (t=sin^2⁡x ) ⇔ (t^2-(a-1)t-2a-2=0;)

Обратите внимание: (t∈[0;1];)

Выразим (a=frac{t^2+t-2}{t+2}=frac{(t+2)(t-1)}{t+2}=t-1),при (t≠-2).

Таким образом, необходимо решить систему:

$$ begin{cases} a=t-1, \t∈[0;1]. end{cases} $$

Построим решения данной системы на координатной плоскости ((tOa)).

Красной линией показан график (a=t-1), а зеленая область показывает интервал, в котором могут лежать корни. Выделенная часть графика соответствует всем возможным корням при (a∈[-1;0].) Если (a) не принадлежит этому интервалу, то корней нет. Найдем эти решения:
$$ t=a+1,$$ $$sin^2⁡x=a+1,$$ $$ 1-cos⁡2x=a+1,$$ $$ cos⁡2x=-a,$$
$$x=±1/2$$ $$ arccos⁡(-a)+πn,n∈Z.$$

Ответ:При (a∈[-1;0];) $$ x=±1/2 arccos(-a)+πn,n∈Z.$$

Пример 6

Решить уравнение (9^{-|x+1|}-3^{1-|x+1|}-a=0.)

Сделаем замену (t=3^{-|x+1|}), получим (t^2-3t-a=0), где (t∈(0;1].)

Построим график функции (a(t)=t^2-3t), при (t∈(0;1]) в системе координат ((tOa)).

Зеленой областью покажем допустимый интервал, в котором могут находиться корни. Выделенная часть параболы соответствует корням нашего уравнения при (a∈[-2;0)). Таким образом, при (a<-2) и (a≥0) корней нет.

Решим уравнение (t^2-3t-a=0).

При (a∈[-2;0)) $$ {t}_{1}=frac{3-sqrt{9+4a}}{2};$$ $$ {t}_{2}=frac{3+sqrt{9+4a}}{2},$$ так как (t∈(0;1]), то ({t}_{2}) не подходит.

Сделаем обратную замену:

$$ 3^{-|x+1|}=frac{3-sqrt{9+4a}}{2};$$
$$-|x+1|=log_3 (frac{3-sqrt{9+4a}}{2});$$
$$|x+1|=-log_3 (frac{3-sqrt{9+4a}}{2});$$
$$x=-1±log_3 (frac{3-sqrt{9+4a}}{2}).$$

Ответ: (x=-1±log_3 (frac{3-sqrt{9+4a}}{2})) при (a∈[-2;0).)

Пример 7

Решить уравнение (sqrt{a(3^x+1)+9}=2-3^x.)

Сделаем замену (t=3^x, t>0) ⇔ (sqrt{a(t+1)+9}=2-t.)

Данному уравнению равносильна система:

$$ begin{cases} a(t+1)+9=(2-t)^2, \ 2-t ≥ 0, \ t > 0. end{cases} $$
$$ begin{cases} a=frac{(t-5)(t+1)}{t+1}, \ 0 < t ≤ 2. end{cases} $$
$$ begin{cases} a = t-5, \ 0 < t <= 2. end{cases}$$

Построим множество точек, которые удовлетворяют полученной системе:

При (a∈(-5;-3]) ⇔ (t=a+5,) сделаем обратную замену 3(^x=a+5), ⇔ (x=log_3 (a+5).)

При (a∈(-∞;-5]∪(-3;+∞)) корней нет.

Ответ: При (a∈(-5;-3]) ⇔ ( x=log_3 (a+5).)

Пример 8

Решить неравенство (9^x-(a-1) 3^x-a≥0)

Сделаем замену: (t=3^x,) ⇔ (t>0;)

Получаем

$$ begin{cases} t^2-(a-1)t-a≥0, \t>0. end{cases} $$
$$ t(t+1)≥a(t+1); $$

Заметим, что решение (t=-1) не подходит, так как (t>0). Поделим наше неравенство на
(t+1). Так как (t+1>0), то знак неравенства не меняется. Будьте внимательны! В случае, когда нам неизвестен знак выражения, на которое мы делим неравенство, необходимо рассмотреть два случая, когда выражение отрицательно (меняем знак неравенства) и когда положительно (не меняем).

$$ begin{cases} t≥a, \t>0. end{cases} $$

Построим график, получившейся системы неравенств на плоскости ((tOa)).

Оранжевой областью выделено решение первого неравенства системы, синей областью – второго неравенства. Их пересечение – это решение все системы.

Получаем, что при (a≤0) $$ t∈(0;+∞) ⇔ 3^x>0 ⇔ x∈(-∞;+∞)$$

При ( a>0) $$ t∈[a;+∞) ⇔ 3^x≥a ⇔ x≥log_3 a.$$

Ответ: при( a≤0) $$ x∈(-∞;+∞)$$
при (a>0) $$ x≥log_3 a.$$

Пример 9

Найти все значения параметра, при которых функция
$$ f(x)=ln{(p-1)*3^x-4*3^{x/2}+(p+2)} $$
определена при всех (x∈R.)

Решение:

Наша функция будет определена при условии, что выражение под логарифмом будет больше нуля:

$$ (p-1)*3^x-4*3^{x/2}+(p+2) > 0.$$

Сделаем замену: (t=3^{x/2},t > 0).

Получим

$$ begin{cases} (p-1)*t^2-4*t+p+2>0, \ t>0. end{cases} $$

Если (p=1),

$$ begin{cases} -4t+3>0, \ t>0; end{cases} $$
$$ begin{cases} t<0.75, \ t>0; end{cases} $$

Сделаем обратную замену: (0 < 3^{x/2} < 0.75.) Очевидно, что это неравенство не будет выполняться при всех (x), как того требует условие задачи.

Если (p≠-1,)

$$ begin{cases} pt^2-t^2-4t+p+2>0, \t>0; end{cases} $$
$$ begin{cases} p(t^2+1)>t^2+4t-2, \t>0; end{cases} $$
$$ begin{cases} p > frac{t^2+4t-2}{1+t^2}, \t>0. end{cases} $$

Теперь нужно построить график функции (p=frac{t^2+4t-2}{1+t^2}). Для этого исследуем функцию на монотонность и найдем экстремумы.

Найдем производную:

$$ p^{‘}=frac{-4(t-2)(t+1/2)}{1+t^2}^2 ;$$

Как видно из рисунка 13, точка ((-1/2;-3)) – точка минимума; а ((2;2)) – точка максимума.

Найдем асимптоты. Напомню, что вертикальные асимптоты бывают только в точках разрыва, поэтому наличие вертикальной асимптоты можно проверить, взяв предел от функции в точке разрыва. В нашем случае нет точек разрыва, поэтому вертикальных асимптот не будет.

График функции будет иметь горизонтальные асимптоты, если (lim_{t→+∞} p(t)=const) или (lim_{t→-∞} p(t)=const.) Проверим нашу функцию:

$$lim_{t→∞} frac{t^2+4t-2}{1+t^2}=1.$$

Значит, есть горизонтальная асимптота (p=1).

И асимптоты могут быть наклонными: Прямая (p=kt+b) будет наклонной асимптотой к нашему графику ( p=frac{t^2+4t-2}{1+t^2}), если существуют пределы (lim_{t→∞} {frac{p(t)}{t}}=k) и (lim_{t→∞} {(p(t)-kt)}=b.)
В нашей случае наклонной асимптоты не будет.

Подробнее можно посмотреть здесь.

Из полученных данных построим примерный график функции (p=frac{t^2+4t-2}{1+t^2}) :

На рисунке 14 при помощи штриховки показаны точки, которые будут корнями системы

$$ begin{cases} p < frac{t^2+4t-2}{1+t^2}, \ t > 0. end{cases}$$

Если (p>2),то (t>0) или (3^(x/2)>0), а значит и функция (f(x)) определена при любых (x∈R).

Ответ: (p∈(2;+∞).)

Пример 10

Найти при каких значениях параметра (a) система
$$ begin{cases} (2+log_{3} {(frac{1}{9} a+frac{1}{3}-frac{2}{9} y)}=log_{3}{(2a+x-y-6)}, \ sqrt{x}=2+y. end{cases}$$
имеет решение?

Решение:

Преобразуем исходную систему:

$$ begin{cases} a+3-2y=2a+x-y-6, \ frac{1}{9} a+frac{1}{3}-frac{2}{9} y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=3-2y-(2+y)^2+y+6, \ a+3-2y>0, \ x=(2+y)^2. end{cases}$$
$$ begin{cases} a=-y^2-5y+5, \ a>2y-3, \ x=(2+y)^2. end{cases}$$

Построим график полученной системы:

Из рисунка 15 видно, что (a∈(-19;11.25].)

Ответ: (a∈(-19;11.25].)

Пример 11

Найти значения параметра a, при которых система
$$ begin{cases} x+y-1=0, \ 2y=sqrt{ax-1} end{cases} $$
имеет единственное решение.

Решение:

Из второго уравнения следует, что (x=frac{y^2+1}{a}).

Тогда

$$ begin{cases} frac{y^2+1}{a}+y-1=0, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$
$$ begin{cases} a=frac{y^2+1}{1-y}, \ y≥0, \ x=frac{y^2+1}{a}. end{cases} $$

Обратите внимание, что (y=1), (x=0) не может быть решением системы при любых значениях параметра (a).

Исследуем, полученную зависимость (a=frac{y^2+1}{1-y}) на монотонность и найдем экстремумы.

$$ {a}^{‘}=frac{2y(1-y)+(y^2+1)}{1-y}^2 ;$$
$$ {a}^{‘}=frac{-y^2+2y+1}{(1-y)^2} =-frac{(y-1-sqrt{2})(y-1+sqrt{2})}{(1-y)^2} ;$$

Из рисунка 16 видно, что ({y}_{1}=1-sqrt{2}) — точка минимума функции (a=frac{y^2+1}{1-y};) Ей соответствует значение (a=2sqrt{2}-2).

({y}_{2}=1+sqrt{2}) — точка максимума. (a=-2sqrt{2}-2).

Найдем асимптоты (см. пример 9):

$$lim_{y→1} {frac{y^2+1}{1-y}}=∞;$$

Значит (y=1) – вертикальная асимптота.

$$lim_{y→∞} {frac{y^2+1}{1-y}}=∞;$$

Значит горизонтальные асимптоты отсутствуют.

И проверим на наличие наклонных асимптот:

$$ lim_{y→∞} {frac{a(y)}{y}}=lim_{y→∞} {frac{(frac{y^2+1}{1-y})}{y}}=lim_{y→∞} {frac{y^2+1}{y-y^2 }}=$$
$$=lim_{y→∞} {frac{1+frac{1}{y^2}}{-1+frac{1}{y}}}=-1=k;$$
$$lim_{y→∞} {(a(y)-ky)}=lim_{y→∞} {frac{y^2+1}{1-y}+y}=lim_{y→∞} {frac{1+y}{1-y}}=-1;$$

Получим уравнение наклонной асимптоты (a=-y-1).

Красным показа график функции (a=frac{y^2+1}{1-y};) Зеленым – показаны найденные асимптоты; Синяя область удовлетворяет условию (y≥0);

Выделенная бардовым часть графика указывает на возможные корни исходной системы. По условию задачи необходимо найти такие значения параметра (a), чтобы система имела единственное решение. Таким образом, из рисунка следует, что при (a=-2sqrt{2}-2) и (a ≥ 1) система будет иметь единственное решение.

Ответ: (a=-2sqrt{2}-2) и (a≥1)

Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.

Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.

Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.

Использование свойств функции при решении заданий с параметром из ЕГЭ по математике профильного уровня. Симметрия функций и приемы решения.

Квадратные уравнения с параметром. Умение исследовать квадратный многочлен поможет решать задачи с параметром аналитическим методом. Квадратное уравнение решается при помощи дискриминанта или теоремы Виета.

Разбор линейных уравнений с параметром. Для того, чтобы решить такое уравнение, нужно найти все x при всех значениях параметра a

Решение показательных и логарифмических уравнений с параметром

Знакомимся с понятием параметра в уравнениях. Краткие рекомендации к выполнению.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N  — середины рёбер CD и AB, соответственно, а NT  — высота пирамиды NSCD с вершиной N и основанием SCD.

а)  Докажите, что точка T является серединой SM.

б)  Найдите расстояние между NT и SC.

Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 512 (C часть).

Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC₁A₁ является квадратом.

а)  Докажите, что прямые CA₁ и AB₁ перпендикулярны.

б)  Найдите расстояние между прямыми CA₁ и AB₁, если AC  =  4, BC  =  7.

Источник: Задания 14 (C2) ЕГЭ 2017

В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ― Через вершину A проведена плоскость α, перпендикулярная прямой PC и пересекающая ребро PC в точке K.

а)  Докажите, что плоскость α делит высоту PH пирамиды PABCD в отношении 2 : 1, считая от вершины P.

б)  Найдите расстояние между прямыми PH и BK.

Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.

В кубе ABCDA₁B₁C₁D₁ все ребра равны 6.

а)  Докажите, что угол между прямыми AC и BC₁ равен 60°.

б)  Найдите расстояние между прямыми AC и BC₁.

Источник: ЕГЭ по математике 01.06.2018. Основная волна. Вариант 991 (C часть). Он же: вариант 751 (резервная волна 25.06.2018), Задания 14 (С2) ЕГЭ 2018

В кубе ABCDA₁B₁C₁D₁ рёбра равны 1. На продолжении отрезка A₁C₁ за точку C₁ отмечена точка M так, что A₁C₁  =  C₁M, а на продолжении отрезка B₁C за точку C отмечена точка N так, что B₁C  =  CN.

а)  Докажите, что MN  =  MB₁.

б)  Найдите расстояние между прямыми B₁C₁ и MN.

Источник: Резервная волна ЕГЭ по математике 24.06.2019. Вариант 992, Задания 14 (С2) ЕГЭ 2019

Пройти тестирование по этим заданиям

Источник

Видеокурсы Инны Фельдман

Рубрики

Решение задачи с параметром с помощью параметрической плоскости. Задание С5

Отзывов (12)

Добавить комментарий

ПАРОЛЬ ДЛЯ БИБЛИОТЕКИ 010101

Подпишитесь на рассылку сайта и ВЫБЕРИТЕ В ПОДАРОК ЛЮБУЮ ВИДЕОЛЕКЦИЮ!

репетитор по информатике

Видеокурсы Анны Малковой.

Рекомендую:

Последние записи

архив записей

§ 8. Кривые в полярной системе координат.

Графический метод в задачах с параметром

Новое и интересное на сайте: