Задача с параметром и двумя модулями
В этой задаче, если заметить симметрию относительно обеих переменных, то при решении можно обойтись «малой кровью» — решение сводится к определению уравнений прямых первого квадранта, а во все остальные картинку можно отразить симметрично.
Задача. Найти значения параметра , при которых решения неравенства
принадлежат отрезку .
Сразу обратимся к плоскости . Обратим внимание на то, что знак модуля присутствует и в отношении переменной
, и переменная
также под знаком модуля. Поэтому если в решении есть пара
, то и пары
,
,
тоже обязательно будут присутствовать в решении. А это означает, что, если будем рисовать картинку в плоскости
, то можно проработать первый квадрант, а в остальных все будет симметрично. Поэтому раскроем модули
и
с положительными знаками и посмотрим, что будет:
Теперь перепишем так:
И раскроем как разность квадратов:
Линия излома графиков (приравниваем к нулю подмодульное выражение). Выше этой линии модуль раскроется со знаком «минус», а ниже – со знаком «плюс». Тогда имеем выше линии
:
И
Ниже линии излома:
И
Строим в первом квадранте:
Рисунок 1. Построение в первом квадранте.
Строим в оставшихся квадрантах – просто отражаем симметрично построенные в первом квадранте прямые и заштриховываем область, в которой неравенство выполняется зеленым. Чтобы удостовериться, что это действительно так, можно выбрать любую точку в области между прямыми (закрашенной) и подставить ее координаты в неравенство, проверив, выполняется ли оно.
Рисунок 2. Отражение рисунка из первого во все остальные квадранты.
Теперь выделим отрезок коричневыми прямыми и выделим цветом те участки, где решения неравенства принадлежат отрезку:
Рисунок 3. Выделение промежутка и определение значения параметра
После этого можно записывать ответ:
При оформлении подобного задания на ЕГЭ могу посоветовать все же вычислить полученные значения параметра, подставляя и
в уравнения соответствующих прямых, полученные выше.
Ответ:
Автор материала — Анна Малкова
Какими были задачи с параметрами на ЕГЭ-2022? На этой странице — обзор всех типов задач №17, предложенных на ЕГЭ по математике в этом году, с полным решением и оформлением.
Напомним, что «параметры» — одна из дорогостоящих задач ЕГЭ. Она оценивается в 4 первичных балла.
Основной темой задач с параметрами на ЕГЭ этого года были модули.
Если вы не помните, что такое модуль числа, — вам сюда.
Способы решения — разные. В одних задачах удобнее графический способ, в других — аналитический.
Мы начнем с тех задач, которые решаются графическим способом. В первых трех, которые мы здесь разбираем, нам встретится уравнение окружности.
Почитать о нем подробно можно здесь.
1. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Вспомним, как решать уравнения вида
Поэтому исходное уравнение равносильно системе:
Получим:
Изобразим решения системы в координатах
Уравнение задает окружность
с центром
и радиусом 5; уравнение
задает окружность
с центром
и радиусом
; при этом должно выполняться условие
Заметим, что обе окружности проходят через точки и
Найдем, при каких значениях параметра исходное уравнение имеет ровно 4 решения.
При прямая
проходит через точку
общую для двух окружностей; уравнение имеет ровно 3 решения.
Если прямая проходит через точку
(нижнюю точку окружности
), уравнение также имеет 3 решения.
При этом поскольку разность ординат точек Q и A равна
то есть радиусу окружности
При уравнение имеет 4 решения.
Если решений меньше 4.
Если уравнение имеет ровно 3 решения, т.к. точка O(0; 0) общая для обеих окружностей.
Если прямая проходит через B — верхнюю точку окружности
уравнение имеет ровно 3 решения.
В этом случае
При уравнение имеет ровно 4 решения.
Если решений меньше, чем 4.
Объединив случаи, получим ответ.
Ответ:
2. При каких значениях параметра уравнение
имеет ровно 2 решения?
Решение:
Раскроем модуль по определению.
Уравнение (1) задает окружность с центром в точке Р (4; 3) и радиусом 5,
уравнение (2) задает окружность с центром в точке Q(-3; 4) и радиусом 5.
Изобразим график совокупности двух систем в системе координат (x;a).
При получаем часть окружности (1), лежащую ниже прямой a = 7x;
при получаем часть окружности (2), лежащую выше прямой a = 7x.
Исходное уравнение имеет ровно два различных решения, если прямая пересекает график совокупности двух систем ровно два раза.
Прямая проходящая через точку С, пересекает график совокупности двух систем один раз.
Найдем координаты С — самой нижней точки и Е — самой верхней точки правой окружности.
Для этих точек x = 4. Найдем координату a:
или
Координаты точек С (4; и Е (4; 8).
Найдем координаты D — самой нижней точки и F — самой верхней точки левой окружности
Для этих точек x = — 3, найдем координату a.
или
Координаты точек: D (3;
1), F(
3; 9).
Точки А и В, в которых пересекаются две окружности, лежат на прямой
a = 7x (так как при a = 7x выражение под модулем равно нулю).
Подставив a = 7x в уравнение окружности (1) получим:
x = 0 или x = 1.
Получили точки В (0; 0) и А (1; 7).
Прямая пересекает график совокупности двух систем ровно два раза в следующих случаях:
1) если прямая проходит выше точки С, но ниже точки D:
2) если прямая проходит выше точки В, но ниже точки А:
3) если прямая проходит выше точки Е, но ниже точки F:
Если или
то решений нет.
Если или a = 9, уравнение имеет ровно одно решение.
Если или a = 8, ровно три решения.
Если или
ровно четыре решения. Эти случаи нам не подходят.
Ответ: a
3. При каких значениях параметра уравнение
имеет ровно 2 корня?
Решение:
Раскрыв модуль, получим:
Решим систему графически в координатах
Прямая — это биссектриса первого и третьего координатных углов.
Неравенство задает полуплоскость, расположенную ниже прямой
Уравнение задает окружность
1 с центром в точке
и радиусом
Уравнение задает окружность
2 с центром в точке
и радиусом
Заметим, что обе окружности проходят через точки О(0; 0) и М(1; 1). В этом легко убедиться, подставив координаты этих точек в уравнения окружностей.
Исходное уравнение имеет ровно 2 корня, если прямая пересекает совокупность двух окружностей ровно в двух точках, лежащих не выше прямой a = x.
Это происходит в следующих случаях:
1) Прямая проходит выше точки А и ниже точки В на рисунке, где А — нижняя точка окружности
2, В — нижняя точка окружности
1.
2) Прямая проходит выше точки С и ниже точки D на рисунке, где D — верхняя точка окружности
2, С — верхняя точка окружности
1.
3) Прямая проходит выше точки О(0; 0) и ниже точки М(1;1).
Найдем координаты точек А, В, С, D.
Получим, что
Ответ:
Заметим, что в каждом из уравнений присутствовало выражение — как в уравнении окружности. Именно поэтому становилось понятно, что их можно решить графически в координатах x; a.
Теперь — следующий тип задач. Здесь окружностей уже не будет. Зато будет разложение на множители.
4. При каких значениях параметра уравнение
имеет ровно 4 решения?
Решение:
Раскроем модуль. Уравнение равносильно совокупности двух систем:
Упростим по очереди каждую из них.
1) Случай
Найдем дискриминант и корни этого квадратного уравнения.
2) Случай
В этом случае также найдем дискриминант и корни квадратного уравнения.
Получим:
или
.
Решим совокупность двух систем графически в координатах
Если уравнение имеет меньше 4 решений.
Если также меньше 4 решений.
Если прямая проходит через точку A или точку B, уравнение имеет ровно 3 решения.
В точке A пересекаются прямые и
, значит, для этой точки
В точке B пересекаются прямые и
, то для точки B:
.
Уравнение имеет ровно 4 решения, если или
или
.
Ответ:
Следующие две задачи мы решим (для разнообразия) аналитическим способом.
5. При каких значениях параметра уравнение
имеет меньше 4 решений?
Решение:
Уравнение равносильно совокупности:
Рассмотрим каждый случай отдельно
1)
2)
Каждое из уравнений — квадратное и не может иметь больше 2 корней.
Если уравнение (1) имеет 2 неотрицательных корня, а уравнение (2) имеет 2 отрицательных корня, исходное уравнение имеет ровно 4 решения. Найдем, при каких значениях это происходит, а затем исключим эти значения. Получим случай, когда исходное уравнение имеет менее 4 корней.
Исходное уравнение имеет ровно 4 решения, если уравнение имеет два неотрицательных корня, а уравнение
имеет два отрицательных корня.
1 уравнение:
По теореме Виета,
для уравнения

При этом
Оценим и
Сравним т.к.
также
Получим:
2 уравнение:
При этом т.е.
— верно при всех a.
Получим:
Исходное уравнение имеет ровно 4 решения, если выполняется система условий:
При всех остальных значениях a — меньше четырёх решений. Значит, подходят значения
Ответ:
6. Найдите все положительные значения a, при каждом из которых уравнение
имеет ровно 4 корня.
Решение:
Раскроем модуль по определению.
Мы получили совокупность двух систем. Чтобы исходное уравнение имело ровно 4 корня, нужно, чтобы каждая система имела ровно два решения. Решим каждую из систем отдельно.
1) Первая система:
Чтобы квадратное уравнение имело два неотрицательных корня, необходимо и достаточно выполнения условий:
Другой способ: можно рассмотреть квадратичную функцию
и воспользоваться условиями:
Найдем дискриминант соответствующего квадратного уравнения.
при этом
Получим:
Корни уравнения
Отсюда
2) Вторая система:
Чтобы система имела ровно 2 решения, для квадратичной функции
необходимо и достаточно выполнения условий:
— верно для всех
Решение второй системы:
Исходное уравнение имеет ровно 4 различных решения, если
Ответ:
Как всему этому научиться? Если вы решили освоить тему «Параметры» — не нужно начинать со сложных задач. Вначале — подготовительная работа. Элементарные функции и их графики, базовые элементы для решения задач с параметрами. Кроме того, надо отлично знать методы алгебры: разложение выражений на множители, выделение полных квадратов, решение уравнений и неравенств всех типов и многое другое.
Изучить все это можно на Онлайн-курсе подготовки к ЕГЭ по математике. На нем мы решаем и такие задачи, и более сложные. Изучаем не менее 11 методов решения задач с параметрами. Выпускники Онлайн-курса отлично справились с «параметрами» на ЕГЭ-2022.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 121 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите все значения параметра a, при каждом из которых наименьшее значение функции
меньше −2.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 2, Задания 18 (С6) ЕГЭ 2019
Найдите все значения a, при каждом из которых наименьшее значение функции
меньше −2.
Источник: ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 3 (только часть С)., Задания 18 (С6) ЕГЭ 2019
Найдите все значения а, при каждом из которых множество решений неравенства содержит ровно четыре целых значения x.
Источник: А. Ларин: Тренировочный вариант № 144.
Найдите все значения параметра а, при которых неравенство
выполняется для любого действительного числа х.
Источник: А. Ларин. Тренировочный вариант № 328. (часть C).
При каких значениях параметра a неравенство
верно при любом x?
Источник: А. Ларин: Тренировочный вариант № 83.
Найдите все значения параметра a, при каждом из которых наименьшее значение функции
меньше 2.
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4, Задания 18 (С6) ЕГЭ 2019
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы одно решение, удовлетворяющее неравенству
Источник: А. Ларин. Тренировочный вариант № 320. (Часть C)
Найдите все значения а, при которых неравенство
имеет единственное решение.
Источник: А. Ларин. Тренировочный вариант № 335.
Найдите все значения параметра a, при каждом из которых множеством решений неравенства
является ровно один промежуток числовой прямой.
Источник: А. Ларин. Тренировочный вариант № 379.
Источник: А. Ларин: Тренировочный вариант № 107.
Найти все значения параметра a, при каждом из которых неравенство
имеет одно решение.
Источник: Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2, А. Ларин. Тренировочный вариант № 348.
Найдите все значения параметра a, при которых решением неравенства
является отрезок длиной 0,5.
Источник: А. Ларин: Тренировочный вариант № 12.
Найдите все значения параметра a при каждом из которых система
не имеет решений.
Найдите все значения параметра a, при каждом из которых неравенство
имеет ровно два решения.
Источник: А. Ларин. Тренировочный вариант № 372.
Найдите все значения параметра такие, что неравенство
не имеет решений.
Источник: А. Ларин. Тренировочный вариант № 314. (Часть C)
Найдите все значения a, при каждом из которых неравенство
имеет хотя бы одно решение из промежутка [−4; 4].
Источник: Избранные задания по математике из последних сборников ФИПИ
Найдите все значения параметра a, при каждом из которых неравенство
имеет не более двух решений.
Источник: А. Ларин. Тренировочный вариант № 380.
Найдите все значения a, при которых неравенство не имеет решений.
Источник: Пробный экзамен по математике Санкт-Петербург 2014. Вариант 2.
Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства
Источник: А. Ларин: Тренировочный вариант № 50.
Найти все значения параметра a, при каждом из которых неравенство
выполняется для всех x из отрезка
Источник: А. Ларин: Тренировочный вариант № 59.
Всего: 121 1–20 | 21–40 | 41–60 | 61–80 …
Как решать уравнения с параметром и двумя модулями
§ 3. Решение систем с параметром и с модулями
В данном параграфе мы познакомимся со способами решения систем двух линейных уравнений с модулями.
Решите систему уравнений $$ left<beginleft|x-yright|=5,\ 3x+2y=10.endright.$$
Модуль в уравнении `|x-y|=5` можно «раскрыть», пользуясь определением модуля числа:
$$left|x-yright|=left<beginx-y,;mathrm<или>;x-ygeq0,\y-x,;mathrm<или>;x-y =0` записывается в виде `x-y=5`, а при `x-y =0`, система имеет вид:
Итак, `x=5`, `y=0`, условие `x-y>=0` выполняется. Значит, найденные пары чисел является решением исходной системы.
2 случай. Если `x-y =0`, `y>=0`;
4) `x =0`, `y>=0`, система имеет вид:
Оба полученные значения удовлетворяют заданным условиям: `1,5>=0`, `0>=0`.
2 случай. `x>=0`, `y =0`.
3 случай. `x =0` система имеет вид:
Первое уравнение не имеет решения, так как сводится к равенству `0=6`, значит система не имеет решений.
4 случай. `x -5/2`, то `|y+5/2|=y+5/2`; если `y то `|y+5/2|=-y-5/2`.
Выражение `y-1=0`, если `y=1`.
Если `y>1`, то `|y-1|=y-1`, а если `y =1`, то `|y-1|=y-1` и `|y+5/2|=y+5/2`, получаем уравнение:
Тогда `x=1/3(2*2+5)=3`. Число `2>1`, так что пара `(3;2)` является решением системы.
Пусть теперь `-5/2 хождения `y` получаем уравнение
Число `8/13` больше `(-5/2)`, но меньше, чем `1`, поэтому пара чисел `(27/13;8/13)` является решением системы.
Решение уравнений с модулями и параметрами
Презентация к уроку
Загрузить презентацию (434 кБ)
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.
Задачи:
- Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;
- Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.
- Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.
Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.
Структура урока:
- Повторение изученного материала (устный счёт).
- Изучение нового материала.
- Закрепление изученного материала.
- Итог урока.
- Домашнее задание.
1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»
1) «Уравнения, содержащие модуль»
Абсолютной величиной или модулем числа a называется число a, если a > 0, число – a, если a <a, если a > 00, если a = 0– a, если a 0 и | a | > a для всех a € R .
Неравенство | x | 0) равносильно двойному неравенству – a 0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a : | x + 3 | + | y – 2 | = 4;
Расcмотрим четыре случая
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 > 0 | y > 2 | ||
| x + 3 + y – 2 = 4 | y = – x + 3 |
| < | x + 3 > 0 | < | x > – 3 |
| y – 2 < | x + 3 < | x 0 | y > – 2 |
| – x – 3 – y – 2 = 4 | y = x + 9 |
| < | x + 3 < | x 2 – 1) х = а + 1.
Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи: 1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения 2) а = – 1; получаем ОX = О , и очевидно х – любое. Ответ: 3. Решения примеров (из вариантов С) 1. При каком значении параметра р уравнение | х 2 – 5х + 6 | + | х 2 – 5х + 4 | = р имеет четыре корня. Рассмотрим функцию у = | х 2 – 5х + 6 | + | х 2 – 5х + 4 | Так как х 2 – 5х + 6 = (х – 2)(х – 3) и х 2 – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой
Числовая прямая при этом разбивает на 5 промежутков
Для случая 3) х0 = – b | 2a = 2, y0 = 25 : 2 + 25 – 10 = 2,5 Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x 2 + 10x – 10. Построим график функции, заданной равенством Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 2 – | x | = 6 1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10 1. Решить уравнение | x – 5 | – | 2x + 3| = 10 5. Итог урока 1. Определение модуля. 6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012 Уравнения с параметром, содержащие модуль По свойству модуля при всех Учтем, что x ≥ 5, т.е. уравнение будет иметь уравнение будет иметь единственное решение на промежутке x ≥ 5. на промежутке x 1 уравнение имеет два корня При a 1, уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9 Учтем, что x ≥ – 3 Учтем, что x 9, неравенство имеет решение Т.е. при a > 0 a ≥ 0; т.е. 0 ≤ a ≤ 9; Т.е. при 0 ≤ a ≤ 9 уравнение имеет два различных корня. уравнение имеет два равных корня Ответим на поставленный вопрос. 2) y = – a – линейная функция, график прямая, параллельная оси OY. Эскиз графиков. y Найдем нули модуля: 2x + 6 = 0; x = –3; Раскроем модуль на двух промежутках: x ≥ –3 и x 3 /4 |
При 

Ответ: 


При каких значениях a уравнение 

При каких значениях параметра a уравнение 
Так как 


Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:
а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;
б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.
Таким образом, получим совокупность двух систем.


Так как
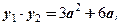






Откуда 
Ответ: 
При каких значениях с уравнение x 2 – ( 3c – 2 ) ∙ | x | + 2c 2 – c = 0 имеет 4 различных корня?
Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.
Таким образом, получим систему неравенств:



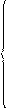
3c – 2 > 0; 
2c 2 – c > 0;
Ответ:
1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000
2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986
3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994
5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999
6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003
источники:
http://urok.1sept.ru/articles/615749
http://megaobuchalka.ru/10/30050.html
Существует ровно три генеральных метода решения задач 17:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 17 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
- Глава 1.
- Графический подход
- § 1.
- Вебинар по задачам 18: модуль и окружности
- § 2.
- Как решать задачу 18: графический подход
- § 3.
- Задача 18: две окружности и модуль
- § 4.
- Задача 18: пересечение графиков окружности и модуля
- § 5.
- Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром.
- Глава 2.
- Аналитический подход
- § 1.
- Задачи 18: Аналитическое решение
- § 2.
- Окружность и модуль: задачи 18 с двумя параметрами
- § 3.
- Аналитическое решение задачи 18 с перебором различных вариантов
- Глава 3.
- Нестандартные приемы
- § 1.
- Задача 18: метод симметричных корней
- § 2.
- Как увидеть симметрию корней в задаче 18?
- § 3.
- Метод мажорант в задаче 18
- § 4.
- Графическое решение сложных задач 18 с модулем
- § 5.
- Задание 18: Симметрия корней в системе уравнений
- § 6.
- Анализ знаков квадратного трёхчлена в сложных задачах 18
- § 7.
- Применение производной для отыскания точек пересечения графиков
- § 8.
- Продвинутый метод симметричных корней
- § 9.
- Новая задача 18 с графическим решением
Министерство образования и науки Республики Бурятия
Муниципальное бюджетное общеобразовательное учреждение
Иройская СОШ
Районная научно исследовательская конференция школьников «Шаг в будущее»
Секция «Алгебра»
Исследование способов решения линейных уравнений
с параметрами, содержащих вложенные модули
Исполнитель Сунгурапова С., учащияся 8 класса
Руководитель Чултумова И.Н., учитель математики
высшей категории
2017 г
Оглавление
Введение 3
- Понятие модуля в математике……………………………………………. 4
- Свойства модуля……………………………………………………………4
- Решение линейных уравнений с модулем. Вложенные модули……… 5
- Понятие параметра в математике…………………………………………5
4.1. Решение линейных уравнений с параметрами……………………………6
- Различные способы решения уравнений с модулем,
содержащих параметр………………………………………………………….. 9
- Уравнения с параметрами на итоговой аттестации, ЕГЭ……………… 12
Заключение …………………………………………………………………….. 13
Список литературы …………………………………………………………….. 15
Приложение……………………………………………………………………… 16
Введение
Исследование многих процессов в жизни осуществляется с использованием параметров. Например, состояние больного терапевт определяет с помощью параметров температуры, давления. Для оценки состояния спортсмена в качестве параметра используется частота сердечных сокращений. Но ни в энциклопедии элементарной математики, ни государственном образовательном стандарте нет понятия «уравнение с параметром», не представлены методы их решения.
В школьных учебниках есть задания с параметрами, однако в них отсутствует компактное и четкое изложение соответствующей теории вопроса; способы, приемы или методы решения не рассматриваются. Задания относятся к заданиям повышенного уровня сложности, часто они приводятся без решения.
При этом часто нужно просто применить свой здравый смысл и потренироваться на простых задачах, тогда решать задачи с параметром станет пусть не всегда легко, но возможно. На решение таких заданий отводится незначительное количество времени. Задания с параметрами включены в материалы итоговой аттестации за курс основной школы, в КИМы и ЕГЭ. Отсюда актуальность этой проблемы обусловлена не столько потребностями Государственной итоговой аттестации, сколько необходимостью создания целостной методики обучения, включающей обеспечение развития у школьников продуктивного уровня усвоения учебного материала по многим темам, в частности, по решению уравнений с параметрами.
Объект исследования: изучение различных способов решения линейных уравнений с параметрами, содержащих вложенные модули.
Предмет исследования: линейные уравнения с параметрами, содержащие вложенные модули.
Цель работы: рассмотреть типовые способы решения уравнений с модулем и показать их использование при решений уравнений с модулем, содержащих параметры.
Задачи исследования: изучить исторический и теоретический материалы по интересующему вопросу; рассмотреть известные определения модуля числа, типовые способы решения задач с модулем и показать использование этих знаний при решении уравнений с модулем, содержащих параметры, выявить практическое применение таких задач.
Практическая значимость работы. Данный способ решения линейных уравнений с параметрами, содержащих вложенные модули будет интересен выпускникам 9 и 11 класса, которым нужно сдать ЕГЭ и ОГЭ.
- Понятие модуля в математике
Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике изучаются понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках. Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.
Существует следующие определения понятия модуля.
Определение 1. Модулем числа а называется само число, если оно не отрицательно и ему противоположное, если число отрицательное.
|a|=a, если а≥0,
|a|=-a, если а<0.
Определение 2. Модулем называется расстояние от начало координат до соответствующей числу а точки на числовой прямой.
2. Свойства модуля.
Свойство 1. Модули противоположных чисел равны, т.е. для всех |a| = |-a|.
Свойство 2. Квадрат модуля числа равен квадрату этого числа, т.е. для всех а
√|а|² = а²
Свойство 3. Арифметический корень из квадрата любого числа есть модуль этого числа, т.е. √а² = |a|
Свойство 4. Модуль любого числа есть число неотрицательное, т.е. для всех а |a|≥0
Свойство 5. Модуль числа не меньше этого числа, т.е. для всех а |a|≥a.
Свойство 6.Модуль числа а равен максимальному из противоположных чисел а и –а .
|a| = -max (a;-a).
Свойство 7. Модуль числа равен расстоянию на числовой оси от начала отсчета до данного числа, т.е. для любого а |a| = 
3. Решение линейных уравнений с модулем. Вложенные модули.
Распространенными примерами с модулями является линейное уравнение типа модуль в модуле. Двойной модуль можно записать в виде формулы ||ax-b|-c|=kx+m.
Если k=0 то такое уравнение с модулем легче решать графическим методом. Классическое раскрытие модулей в таких ситуациях громоздкое и не всегда дает желаемого эффекта. Графический метод позволяет за короткое время выполнить построение модульных функций и найти количество корней уравнения.
Уравнение с модулем – это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Решить уравнение-это значит найти все его корни, или доказать, что корней нет.
Методы решения уравнений с модулем:
1.По определению модуля — «снятие модуля». Решение происходит на основе определения.
2.Аналитический метод — решение уравнений с использованием преобразований выражений, входящих в уравнение и свойств модуля.
3.Метод интервалов: раскрытие модуля на интервалах и полуинтервалах, образованными «нулями» модулей.
4.Графический метод. Суть этого способа заключается в том, чтобы построить графики данных функций, представляющих левую и правую часть уравнения. В случае, если графики пересекутся, то абсциссы точек пересечений данных графиков будут являться корнями данного уравнения.
Методы построения графиков функции с модулем:
По определению. Строятся две прямые у=кх+в, где х>0, у=-кх+в, где х <0
Метод симметрии. Строится график у=кх+в, при х>0.
Часть прямой при х <0 отображается относительно оси абцисс.
Преобразование функций:
а) у=|x|+n график сдвигается вверх по оси ординат на в единиц
б) у=|x|-n график сдвигается вниз по оси ординат
с) у=|x+n| график сдвигается влево по оси абсцисс
d )у=|x-n| график сдвигается вправо по оси абсцисс
Алгоритм построения двойного, тройного модуля достаточно прост и из приведенных ниже примеров понравится многим
Пример 1. Решить уравнение ||x-3|-5|=3.
I способ: Аналитический
- Найдем нуль внутри модуля x-3=0 ; х=3
- Раскроем внутренний модуль при x>3
|x-3-5|=3; |x-8|=3:
а) х-8=3 ; х=11; б) при х<8 : -(х-8)=3 ; -х+8=3; -х=-5; х=5.
3. Раскроем внутренний модуль при х<3
|-(x-3)-5|=3 ; |-x+3-5|=3 |-x-2|=3
а) –х-2=3 ; -х=5 ; х=5; б) -(-х-2)=3 ; х+2=3 ; х=1
Ответ: —5; 1; 5; 11
II способ: Графический
1) Построим график функций : 1) y=|x| ; 2) y=|x-3| ; 3) y=|x-3|-5 ; 4) y=||x-3|-5|
2) Построим график y=3
3) Найдем точки пересечения
Преимущество графического метода над раскрытием модулей для простых уравнений очевидно. Однако графически неудобно искать корни, когда правая сторона имеет вид kx+m, то есть является прямой наклоненной к оси абсцисс под углом.
4. Понятие параметра в математике
Толковый словарь определяет параметр как величину, характеризующую какое — нибудь основное свойство машины, устройства, системы или явления, процесса. (Ожегов С.И. , Шведова Н.Ю. Толковый словарь русского языка. Москва. 1999).
Поскольку в школьных учебниках нет определения параметра, возьмем за основу следующий его простейший вариант.
Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Независимость параметра заключается в его «неподчинении» свойствам, вытекающим из условия задачи. Например, из неотрицательности левой части уравнения |x|=a–1 не следует неотрицательность значений выражения a–1, и если a–1<0, то мы обязаны констатировать, что уравнение не имеет решений.
Параметр (от греческого parametron – отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода. Например, уравнение у = kx c параметром k определяет множество прямых, проходящих через начало координат. Уравнение (х – а)2 + (у – b)2 = 25 с параметрами а,b определяет множество окружностей радиуса 5.
Что означает «решить задачу с параметром»?
Решить уравнение с параметром — это значит, на множестве действительных чисел решить семейство уравнений, получающегося из данного уравнения при всех действительных значениях параметра.
- Решение линейных уравнений с параметрами.
Уравнение F(a, х) = 0 с двумя переменными а и х называется уравнением с параметром а и переменной х, если для каждого значения переменной а необходимо решить соответствующее уравнение с переменной х.
К задачам с параметрами, рассматриваемым в школьном курсе, можно отнести, поиск решений линейных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров.
Нужно усвоить при первом знакомстве с параметром, — это необходимость осторожного, даже деликатного обращения с фиксированным, но неизвестным числом.
Класс линейных уравнений с параметром выделяется с помощью двух характеристик:
1. В уравнении переменная х находится в первой степени;
2. При помощи равносильных преобразований на области допустимых значений параметра уравнение приводится к стандартному виду
f(a)·x + g(a) = 0.
Алгоритм решения линейных уравнений с параметрами
- Найти область допустимых значений параметра.
- Привести уравнение к стандартному виду.
- Найти контрольные значения параметра.
- Для контрольных значений параметра решить частные уравнения .
Для остальных значений параметра найти общие решения по формуле
- Записать ответ.
В зависимости от вида уравнения некоторые пункты алгоритма могут быть опущены.
Пример 1. Решить уравнение 2а(а – 2) · х = а – 2, если а — параметр.
- Область допустимых значений параметра – вся числовая прямая.
- Приведем уравнение к виду 2а(а – 2) · х – а + 2 = 0.
- Контрольными являются те значения параметра, при которых коэффициент при х обращается в нуль. Такими значениями будут а = 0 и а = 2.
- Если а = 0, то уравнение примет вид 0 · х = — 2. Это уравнение не имеет корней.
Если а = 2, то уравнение примет вид 0 · х = 0. Корнем этого уравнения является любое действительное число.
- Если а ≠ 0 и а ≠ 2, то
,
Ответ: если а = 0, то корней нет; если а = 2, то х – любое действительное число;
если а ≠ 0 и а ≠ 2, то 
- Различные способы решения уравнений с модулем, содержащих параметр. Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.
Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Решение уравнения может включать в себя несколько методов решения, соответствующих каждому виду уравнения при определенных значениях параметра. Например, при каком-то значении параметра уравнение линейное, поэтому решаем его аналитически тождественными преобразованиями; при остальных значениях параметра уравнение квадратичное, – решаем его функционально-графическим способом.
Пример 2. |ax-1|=2
Решение уравнения с помощью определения модуля.
1) Если а=0, то уравнение примет вид |-1|=2 – неверное равенство, значит уравнение не имеет корней.
2) Если а≠0, то уравнение имеет два корня.
а)ax-1=2 б)ax-1=-2
ax=3 ax=-1
x=3/a x=-1/a
Пример 3.|x-1|+|x-3|=a
1 способ: Графический.
Построим график функции y=|x-1|+|x-3|
x≤1 1≤x≤3 x≥3
y=1-x+3-x = -2х+4 y=x-1+3-x=2 y=x-1+x-3=2x-4
график
Если а<2, то ломанная и прямая y=a не пересекаются.
Если а=2, то ломанная и прямая y=a совпадают 1≤x≤3.
Если а>2, то ломанная и прямая y=a имеют две точки пересечения. Абциссу одной из них можно найти из уравнения 4-2x=a, откуда x=(4-a)/2. Абциссу другой точки пересечения можно найти из уравнения 2x-4=a, откуда x=(a+4)/2.
2 способ : Метод интервалов.
|x-1|+|x-3| = a
x≤1 1≤x≤3 x≥3
1-x+3-x = a x-1+3-x = a x-1+x-3 = a
4-2x = a 2 = a 2x-4 = a
-2x = a-4 x [1; 3] x = (a+4)/2
x = (a-4)/-2
x = (4-a)/2
Ответ.x = (4-a)/2, x [1; 3], x = (a+4)/2.
Пример 1. Найти все значения р, при которых уравнение |x-3|+|x-4|=p имеет 1 корень, 2 корня, не имеет корней.
Решение:
1)y=|x-3|+|x-4|; y=p
y=|x-3|+|x-4|
Метод промежутков: x-3=0 ; x-4=0
x=3 x=4
(–∞ ;3) : y=-(x-3)-(x-4)=-x+3-x+4=-2x+7
[3;4] : y=|x-3|+|x-4|=1
(4;+ ∞) : y=(x-3)+(x-4)=2x-7
Ответ: p=1, 1 корень ; р>1, 2 корня; р<1, нет
корней
Пример 2. При каком значении параметра a уравнение с модулем
|||x+1|-2|-5|=a имеет 5 решений?
Решение: Имеем уравнение с тремя вложенными модулями. Найдем ответ с графического анализа. Начнем, как всегда, из внутреннего модуля. Он обращается в нуль
|x+1|=0 x=-1 в точке x=-1. Строим график модуль функции в этой точке
Далее график опускаем вниз на двойку и отрицательные значения (y< 0)симметрично переносим вверх. Получим график функции y=||x+1|-2|
Повторно выполним смещение графика модуль функции вниз на 5 и симметрично переносим отрицательные значения функции. В результате получим левую сторону уравнения с модулями
y=|||x+1|-2|-5|.
Параметр а соответствует значению параллельной прямой, которая должна пересечь график модуль функции в 5 точках. Сначала проводим такую прямую, далее ищем точку пересечения ее с осью Oy.
Это прямая y=3, то есть искомый параметр равен a=3.
Методом раскрытия модулей данную задачу можно было решать целый урок, если не больше. Здесь все свелось к нескольким графикам.
Ответ: a=3.
- Уравнения с параметрами на итоговой аттестации, ЕГЭ
Пример 1. Найти все значения а, при каждом из которых уравнение |
|x-1| -2|=2+ |3x-a| имеет единственное решение.
Решение: |x-1| -2|-2 |3x-a|
y=|3x-a| ; y=||x-1|-2|-2
1) Построим график функций: 1)y=|x| ; 2) y=|x-1| ; 3) у=|x-1|-2 ; 4)||x-1|-2| ;
5) y-||x=1|-2|-2
y=|3x-a| — «уголок», вершина которого движется по оси абцисс. Очевидно, что единственное решение будет в точках A,B,C. А(-3;0) ; В(1;0) ; С(5;0)
у=|3x-a| ; 0=|-9-a|=>a=-9 ; 0=|3-a|=>a=3 ; 0=|15-a|=>a=15
. Пример 2. ЕГЭ 2010г. При каком значении параметра уравнение имеет 4 корня а=|||х|-2|-2|?
Решение: применив поэтапно метод симметрию:
Первый раз: у=
Второй раз: у==|||х|-2|-2|
Построим прямую у=а
Ответ: при а=2 уравнение имеет 4корня
Пример 3. ЕГЭ 2009г. Найдите все значения а, при каждом из которых уравнение 
Решение: 
Преобразуем:

— 

Построим графики функций у = а, 

При а =7 прямая пересекает график только в одной точке. Значит, данное уравнение имеет ровно один корень при а =7. Ответ: 7.
Заключение
Я познакомилась с аналитическими и графическими решениями линейных уравнений с модулями и параметром, научилась строить графики линейных функций, содержащих выражение с параметром под знаком модуля. А для этого прочитала и изучила немало дополнительной литературы. Получив эти знания, мне будет совсем нетрудно выбирать рациональный способ решения уравнений.
В результате анализа и сравнения методов построения графиков получила следующие выводы:
— перевод алгебраической задачи на язык графиков позволяет избежать громоздких решений;
— при решении уравнений, содержащих модуль и параметр, графический способ является более наглядным и сравнительно более простым;
— при построении графиков, содержащих 2 или более модулей практичнее метод симметрии;
— хотя графический способ решения уравнений является приближенным, т.к. точность зависит от выбранного единичного отрезка, толщины карандаша, углов под которыми пересекаются линии и т.д., но этот метод позволяет оценивать кол-во корней уравнений для решения уравнений с параметром.
Учитывая, что уравнения с модулем и параметром есть в заданиях ГИА, главным моим результатом является то, что я могу решать линейные уравнения с модулем и параметром графическим способом.
Список использованной литературы
- Горбачев В.И. Элементы теории и общие методы решения уравнений и неравенств с параметрами. -Брянск: Издательство БГПУ, 1998.-264с.
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметром. Киев: РИА «Текст», 1992.-320с.
- Мордкович А.Г. и др. Алгебра.8кл.: Задачник для общеобразоват. учреждений.-3-е изд., испр. — М.: Мнемозина, 2001.
- Советский энциклопедический словарь/ Гл. ред. А.М. Прохоров. – 4- е изд. – М .: Сов. Энциклопедия, 1986.- 1600 с., ил.
- Ястребинецкий Г.А. Уравнения и неравенства, содержащие параметры.- М.: Просвещение, 1972.-128с.
Приложение
Задание 1.
Решить уравнение у2х = у(х + 2) – 2 с параметром у.
- Область допустимых значений параметра – вся числовая прямая.
- Приведем уравнение к виду y(у – 1)х — 2(у – 1) = 0.
- Контрольные значения параметра: у = 0 и у = 1.
- Если у= 1, то уравнение примет вид 0 · х = 0, х – любое число.
Если у = 0, то уравнение примет вид 0 · х = — 2. Это уравнение корней не имеет.
5. Если у ≠ 0 и у ≠ 1, то х = 2(у-1)/ у(у-1)
Ответ: если у =1, то х – любое число;
если у = 0, то корней нет;
если у ≠ 0 и у ≠ 1, 

Задание 2. Решить уравнение 4 
Решение. Перепишем уравнение (1) в виде 4 
у = 

График функции у = 




А) Два графика не будут иметь общих точек, если вершина острого угла окажется между точками А и С, т.е. уравнение (1) не имеет корней при -2 < а < 2.
Б) Два графика будут иметь единственную общую точку, если вершина острого угла совпадает или с точкой А, или с точкой С, т.е. уравнение (1) имеет единственный корень и при а = -2, и при а = 2.
В) Два графика будут иметь две общие точки, если вершина острого угла окажется левее точки А или правее точки С, т.е. уравнение (1) имеет два корня и при а < -2, и при а > 2.
Ответ. а) при а 
Задание 3.
Задание 4. Сколько корней имеет уравнение ||2x-3|-2|=2?
Решение: Правая сторона равна постоянной, поэтому скорее найти решение можно графическим методом. Внутренний модуль обращается в нуль
|2x-3|=0 x=3/2=1,5
в точке x=1,5.
Значит в эту точку смещаем график функции y=|2x|. Для того, чтобы его построить подставьте несколько точек и проведите через них прямые. От полученной функции вычитаем 2 то есть график опускаем на двойку вниз и, чтобы получить модуль переносим отрицательные значения (y< 0)симметрично относительно оси Ox.
Далее остается построить правую сторону (прямую y=2) и подсчитать количество точек пересечения. График модуль функции и прямой приведен ниже
Ответ: три решения.



















 Решить в зависимости от значений параметра а.
Решить в зависимости от значений параметра а. левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a.
левая часть уравнения неотрицательна, следовательно, при a 0 x – 3 = ± a, откуда x = 3 ± a. Учтем, что x 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1
Учтем, что x 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1 единственное решение
единственное решение 
 ;
;  ;
; . уравнение имеет два корня
. уравнение имеет два корня
 x ≥ – 3;
x ≥ – 3;  a ≥ – 9
a ≥ – 9
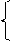 a ≤ 9; уравнение имеет один корень
a ≤ 9; уравнение имеет один корень
 .
.



 y = – a
y = – a