Параметр егэ 2017 основная волна - Помощь в подготовке к экзаменам и поступлению

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи с параметром из ЕГЭ прошлых лет

Задание
1

#6329

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система [begin{cases} (x-2a-2)^2+(y-a)^2=1\
y^2=x^2end{cases}]

имеет ровно четыре решения.

(ЕГЭ 2018, основная волна)

Второе уравнение системы можно переписать в виде (y=pm x). Следовательно, рассмотрим два случая: когда (y=x) и когда (y=-x). Тогда количество решений системы будет равно сумме количества решений в первом и во втором случаях.

1) (y=x). Подставим в первое уравнение и получим: [2x^2-2(3a+2)x+(2a+2)^2+a^2-1=0quad(1)] (заметим, что в случае (y=-x) мы поступим так же и тоже получим квадратное уравнение)
Чтобы исходная система имела 4 различных решения, нужно, чтобы в каждом из двух случаев получилось по 2 решения.
Квадратное уравнение имеет два корня, когда его (D>0). Найдем дискриминант уравнения (1):
(D=-4(a^2+4a+2)).
Дискриминант больше нуля: (a^2+4a+2<0), откуда (ain (-2-sqrt2;
-2+sqrt2)).

2) (y=-x). Получаем квадратное уравнение: [2x^2-2(a+2)x+(2a+2)^2+a^2-1=0quad (2)] Дискриминант больше нуля: (D=-4(9a^2+12a+2)>0), откуда (ain
left(frac{-2-sqrt2}3; frac{-2+sqrt2}3right)).

Необходимо проверить, не совпадают ли решения в первом случае с решениями во втором случае.

Пусть (x_0) – общее решение уравнений (1) и (2), тогда [2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=2x_0^2-2(a+2)x_0+(2a+2)^2+a^2-1] Отсюда получаем, что либо (x_0=0), либо (a=0).
Если (a=0), то уравнения (1) и (2) получаются одинаковыми, следовательно, имеют одинаковые корни. Этот случай нам не подходит.
Если (x_0=0) – их общий корень, то тогда (2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=0), откуда ((2a+2)^2+a^2-1=0), откуда (a=-1) или (a=-0,6). Тогда вся исходная система будет иметь 3 различных решения, что нам не подходит.

Учитывая все это, в ответ пойдут:

[ainleft(dfrac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right)]

Ответ:

(ainleft(frac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right))

Задание
2

#4032

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых система [begin{cases}
(a-1)x^2+2ax+a+4leqslant 0\
ax^2+2(a+1)x+a+1geqslant 0 end{cases}]

имеет единственное решение.

(ЕГЭ 2018, СтатГрад, 19 апреля 2018)

Перепишем систему в виде: [begin{cases}
ax^2+2ax+aleqslant x^2-4\
ax^2+2ax+ageqslant -2x-1
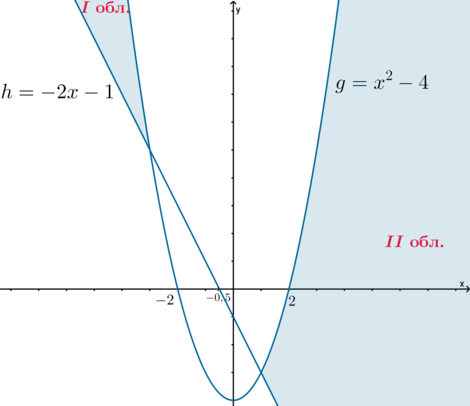
end{cases}] Рассмотрим три функции: (y=ax^2+2ax+a=a(x+1)^2), (g=x^2-4), (h=-2x-1). Из системы следует, что (yleqslant g), но (ygeqslant
h). Следовательно, чтобы система имела решения, график (y) должен находиться в области, которая задается условиями: “выше” графика (h), но “ниже” графика (g):

(будем называть “левую” область областью I, “правую” область – областью II)
Заметим, что при каждом фиксированном (ane 0) графиком (y) является парабола, вершина которой находится в точке ((-1;0)), а ветви обращены либо вверх, либо вниз. Если (a=0), то уравнение выглядит как (y=0) и графиком является прямая, совпадающая с осью абсцисс.
Заметим, что для того, чтобы исходная система имела единственное решение, нужно, чтобы график (y) имел ровно одну общую точку с областью I или с областью II (это значит, что график (y) должен иметь единственную общую точку с границей одной из этих областей).

Рассмотрим по отдельности несколько случаев.

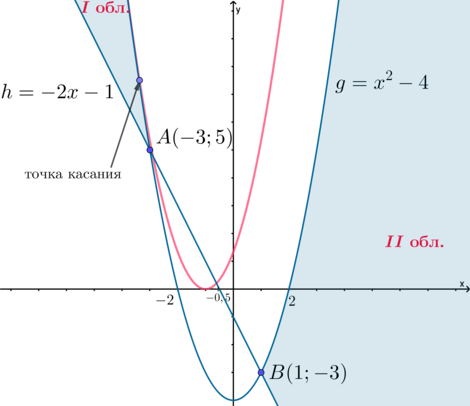
1) (a>0). Тогда ветви параболы (y) обращены вверх. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) касалась границы области I или границы области II, то есть касалась параболы (g), причем абсцисса точки касания должна быть (leqslant
-3) или (geqslant 2) (то есть парабола (y) должна коснуться границы одной из областей, которая находится выше оси абсцисс, раз парабола (y) лежит выше оси абсцисс).

(y’=2a(x+1)), (g’=2x). Условия касания графиков (y) и (g) в точке с абсциссой (x_0leqslant -3) или (x_0geqslant 2): [begin{cases}
2a(x_0+1)=2x_0\
a(x_0+1)^2=x_0^2-4 \
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right. end{cases}
quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right.\[1ex]
a=dfrac{x_0}{x_0+1}\[1ex]
x_0^2+5x_0+4=0 end{cases}] Из данной системы (x_0=-4), (a=frac43).
Получили первое значение параметра (a).

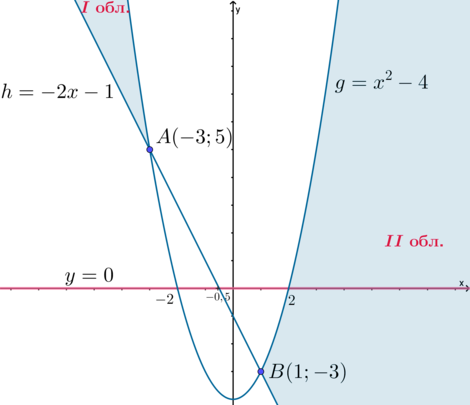
2) (a=0). Тогда (y=0) и видно, что прямая имеет бесконечное множество общих точек с областью II. Следовательно, это значение параметра нам не подходит.

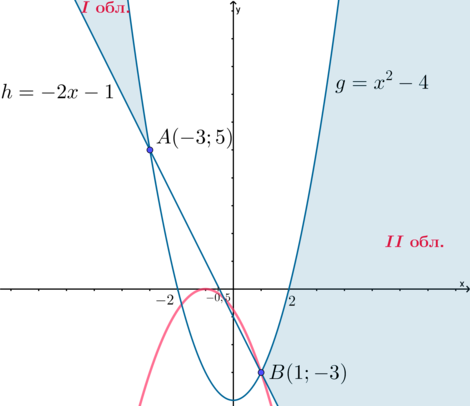
3) (a<0). Тогда ветви параболы (y) обращены вниз. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) имела одну общую точку с границей области II, лежащей ниже оси абсцисс. Следовательно, она должна проходить через точку (B), причем, если парабола (y) будет иметь еще одну общую точку с прямой (h), то эта общая точка должна быть “выше” точки (B) (то есть абсцисса второй точки должна быть (<1)).

Найдем (a), при которых парабола (y) проходит через точку (B): [-3=a(1+1)^2quadRightarrowquad a=-dfrac34] Убеждаемся, что при этом значении параметра вторая точка пересечения параболы (y=-frac34(x+1)^2) с прямой (h=-2x-1) – это точка с координатами (left(-frac13; -frac13right)).
Таким образом, получили еще одно значение параметра.

Так как мы рассмотрели все возможные случаи для (a), то итоговый ответ: [ain left{-dfrac34; dfrac43right}]

Ответ:

(left{-frac34; frac43right})

Задание
3

#4013

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система уравнений [begin{cases}
2x^2+2y^2=5xy\
(x-a)^2+(y-a)^2=5a^4 end{cases}]

имеет ровно два решения.

(ЕГЭ 2018, СтатГрад, 26 января 2018)

1) Рассмотрим первое уравнение системы как квадратное относительно (x): [2x^2-(5y)x+2y^2=0] Дискриминант равен (D=9y^2), следовательно, [x_{1,2}=dfrac{5ypm 3y}4quadRightarrow quad x_1=2y, quad x_2=dfrac12y] Тогда уравнение можно переписать в виде [(x-2y)cdot (2x-y)=0] Следовательно, всю систему можно переписать в виде [begin{cases}
left[begin{gathered}begin{aligned} &y=2x\[1ex]
&y=0,5xend{aligned}end{gathered}right.\[1ex]
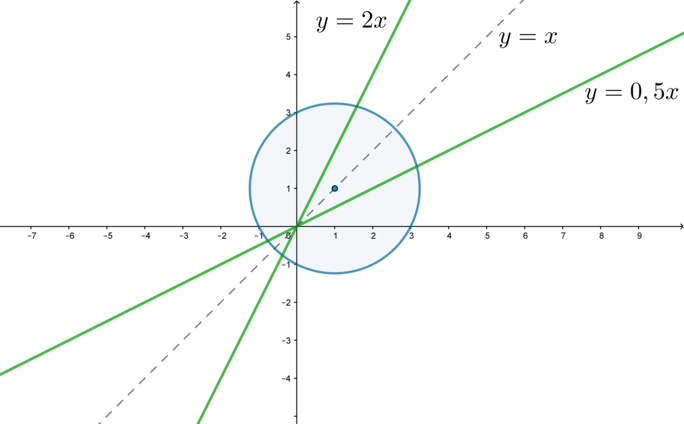
(x-a)^2+(y-a)^2=5a^4end{cases}] Совокупность задает две прямые, второе уравнение системы задает окружность с центром в ((a;a)) и радиусом (R=sqrt5a^2). Чтобы исходное уравнение имело два решения, нужно, чтобы окружность пересекала график совокупности ровно в двух точках. Вот чертеж, когда, например, (a=1):

Заметим, что так как координаты центра окружности равны, то центр окружности “бегает” по прямой (y=x).

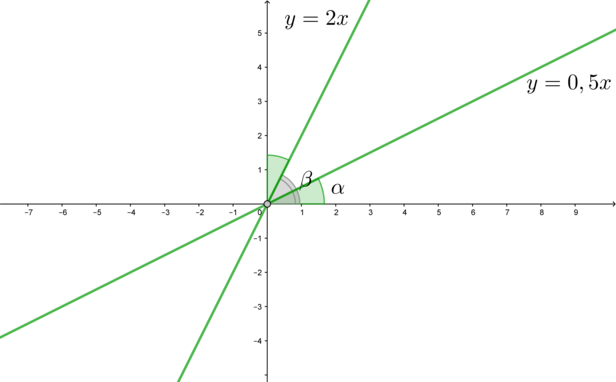
2) Так как у прямой (y=kx) тангенс угла наклона этой прямой к положительному направлению оси (Ox) равен (k), то тангенс угла наклона прямой (y=0,5x) равен (0,5) (назовем его (mathrm{tg},alpha)), прямой (y=2x) – равен (2) (назовем его (mathrm{tg},beta)). Заметим, что (mathrm{tg},alphacdot
mathrm{tg},beta=1), следовательно, (mathrm{tg},alpha=mathrm{ctg},beta=mathrm{tg},(90^circ-beta)). Следовательно, (alpha=90^circ-beta), откуда (alpha+beta=90^circ). Это значит, что угол между (y=2x) и положительным направлением (Oy) равен углу между (y=0,5x) и положительным направлением (Ox):

А так как прямая (y=x) является биссектрисой I координатного угла (то есть углы между ней и положительными направлениями (Ox) и (Oy) равны по (45^circ)), то углы между (y=x) и прямыми (y=2x) и (y=0,5x) равны.
Все это нам нужно было для того, чтобы сказать, что прямые (y=2x) и (y=0,5x) симметричны друг другу относительно (y=x), следовательно, если окружность касается одной из них, то она обязательно касается и второй прямой.
Заметим, что если (a=0), то окружность вырождается в точку ((0;0)) и имеет лишь одну точку пересечения с обеими прямыми. То есть этот случай нам не подходит.
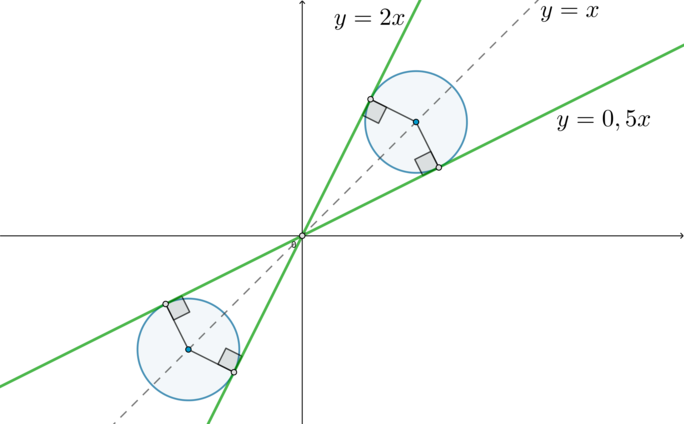
Таким образом, для того, чтобы окружность имела 2 точки пересечения с прямыми, нужно, чтобы она касалась этих прямых:

Видим, что случай, когда окружность располагается в третьей четверти, симметричен (относительно начала координат) случаю, когда она располагается в первой четверти. То есть в первой четверти (a>0), а в третьей (a<0) (но такие же по модулю).
Поэтому рассмотрим только первую четверть.

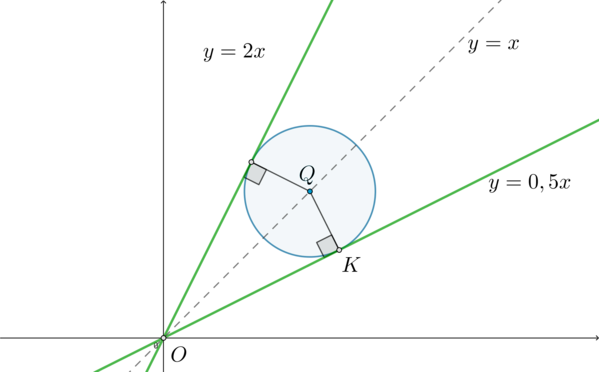
Заметим, что (OQ=sqrt{(a-0)^2+(a-0)^2}=sqrt2a), (QK=R=sqrt5a^2). Тогда [OK=sqrt{2a^2-5a^4}] Тогда [mathrm{tg},angle
QOK=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}] Но, с другой стороны, [mathrm{tg},angle QOK=mathrm{tg},(45^circ-alpha)=dfrac{mathrm{tg},
45^circ-mathrm{tg},alpha}{1+mathrm{tg},45^circcdot
mathrm{tg},alpha}] следовательно, [dfrac{1-0,5}{1+1cdot 0,5}=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}
quadLeftrightarrowquad a=pm dfrac15] Таким образом, мы уже сразу получили и положительное, и отрицательное значение для (a). Следовательно, ответ: [ain {-0,2;0,2}]

Ответ:

({-0,2;0,2})

Задание
4

#3278

Уровень задания: Равен ЕГЭ

Найдите все значения (a), для каждого из которых уравнение [25^x-(a+6)cdot 5^x=(5+3|a|)cdot 5^x-(a+6)(3|a|+5)]

имеет единственное решение.

(ЕГЭ 2017, официальный пробный 21.04.2017)

Сделаем замену (t=5^x, t>0) и перенесем все слагаемые в одну часть: [t^2-bigg((a+6)+(5+3|a|)bigg)cdot t+(a+6)(3|a|+5)=0] Получили квадратное уравнение, корнями которого по теореме Виета являются (t_1=a+6) и (t_2=5+3|a|). Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с (t) тоже имело один (положительный!) корень.
Заметим сразу, что (t_2) при всех (a) будет положительным. Таким образом, получаем два случая:

1) (t_1=t_2): [a+6=5+3|a| quadLeftrightarrowquad 3|a|=a+1 quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} & 3a=a+1\
&3a=-a-1 end{aligned} end{gathered} right. \
a+1geqslant 0 end{cases}quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & a=dfrac12\[2ex]
&a=-dfrac14 end{aligned} end{gathered} right.]

2) Так как (t_2) всегда положителен, то (t_1) должен быть (leqslant
0): [a+6leqslant 0 quadLeftrightarrowquad aleqslant -6.]

Ответ:

((-infty;-6]cupleft{-frac14;frac12right})

Задание
5

#3252

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{x^2-a^2}=sqrt{3x^2-(3a+1)x+a}]

имеет ровно один корень на отрезке ([0;1]).

(ЕГЭ 2017, резервный день)

Уравнение можно переписать в виде: [sqrt{(x-a)(x+a)}=sqrt{(3x-1)(x-a)}] Таким образом, заметим, что (x=a) является корнем уравнения при любых (a), так как уравнение принимает вид (0=0). Для того, чтобы этот корень принадлежат отрезку ([0;1]), нужно, чтобы (0leqslant
aleqslant 1).
Второй корень уравнения находится из (x+a=3x-1), то есть (x=frac{a+1}2). Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть: [left(dfrac{a+1}2-aright)cdot
left(dfrac{a+1}2+aright)geqslant 0quadRightarrowquad
-dfrac13leqslant aleqslant 1] Для того, чтобы этот корень принадлежал отрезку ([0;1]), нужно, чтобы [0leqslant dfrac{a+1}2leqslant 1
quadRightarrowquad -1leqslant aleqslant 1] Таким образом, чтобы корень (x=frac{a+1}2) существовал и принадлежал отрезку ([0;1]), нужно, чтобы (-frac13leqslant aleqslant 1).
Заметим, что тогда при (0leqslant aleqslant 1) оба корня (x=a) и (x=frac{a+1}2) принадлежат отрезку ([0;1]) (то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают: [a=dfrac{a+1}2quadRightarrowquad a=1] Таким образом, нам подходят (ain left[-frac13; 0right)) и (a=1).

Ответ:

(ain left[-frac13;0right)cup{1})

Задание
6

#3238

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых уравнение [xsqrt{x-a}=sqrt{6x^2-(6x+3a)x+3a}]

имеет единственный корень на отрезке ([0;1].)

(ЕГЭ 2017, резервный день)

Уравнение равносильно: [xsqrt{x-a}=sqrt{3a(1-x)}] ОДЗ уравнения: [begin{cases} xgeqslant 0\ x-ageqslant 0\3a(1-x)
geqslant 0end{cases}] На ОДЗ уравнение перепишется в виде: [x^3-a(x^2-3x+3)=0]

1) Пусть (a<0). Тогда ОДЗ уравнения: (xgeqslant 1). Следовательно, для того, чтобы уравнение имело единственный корень на отрезке ([0;1]), этот корень должен быть равен (1). Проверим: [1^3-a(1^2-3cdot 1+3)=0 quadRightarrowquad a=1.] Не подходит под (a<0). Следовательно, эти значения (a) не подходят.

2) Пусть (a=0). Тогда ОДЗ уравнения: (xgeqslant 0). Уравнение перепишется в виде: [x^3=0 quadRightarrowquad x=0] Полученный корень подходит под ОДЗ и входит в отрезок ([0;1]). Следовательно, (a=0) – подходит.

3) Пусть (a>0). Тогда ОДЗ: (xgeqslant a) и (xleqslant 1). Следовательно, если (a>1), то ОДЗ – пустое множество. Таким образом, (0<aleqslant 1) и при этих (a) ОДЗ: (aleqslant xleqslant
1). Следовательно, если корень подойдет по ОДЗ, то он попадет и в отрезок ([0;1]).
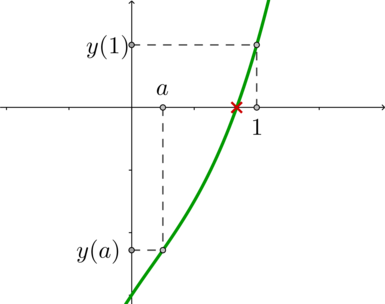
Рассмотрим функцию (y=x^3-a(x^2-3x+3)). Исследуем ее.
Производная равна (y’=3x^2-2ax+3a). Определим, какого знака может быть производная. Для этого найдем дискриминант уравнения (3x^2-2ax+3a=0): (D=4a(a-9)). Следовательно, при (ain (0;1]) дискриминант (D<0). Значит, выражение (3x^2-2ax+3a) положительно при всех (x). Следовательно, при (ain (0;1]) производная (y’>0). Следовательно, (y) возрастает. Таким образом, по свойству возрастающей функции уравнение (y(x)=0) может иметь не более одного корня.

Следовательно, для того, чтобы корень уравнения (точка пересечения графика (y) с осью абсцисс) находился на отрезке ([a;1]), нужно, чтобы [begin{cases} y(1)geqslant 0\
y(a)leqslant 0 end{cases}quadRightarrowquad ain [0;1]] Учитывая, что изначально в рассматриваемом случае (ain (0;1]), то ответ (ain (0;1]).

Итоговый ответ, полученный объединением ответов во всех трех случаях: [ain [0;1]]

Ответ:

([0;1])

Задание
7

#3267

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых уравнение [sqrt{1-4x}cdot ln(9x^2-a^2)=sqrt{1-4x}cdot ln (3x+a)]

имеет ровно один корень.

(ЕГЭ 2017, основная волна)

Данное уравнение можно переписать как [begin{cases}
sqrt{1-4x}cdot ln dfrac{(3x-a)(3x+a)}{3x+a}=0\[2ex]
3x+a>0end{cases} quadLeftrightarrowquad
begin{cases}
sqrt{1-4x}cdot ln (3x-a)=0\
3x+a>0end{cases}] Система имеет два корня:
1) (x_1=frac14), если он удовлетворяет (3x+a>0) и (3x-a>0): [begin{cases}
dfrac34+a>0\[1ex]
dfrac34-a>0end{cases} quadLeftrightarrowquad
-dfrac34<a<dfrac34]
2) (x_2=frac{a+1}3), если он удовлетворяет (3x+a>0) и (1-4xgeqslant 0): [begin{cases}
a+1+a>0\[1ex]
1-dfrac43a-dfrac43geqslant 0end{cases}quadLeftrightarrowquad
-dfrac12<aleqslant -dfrac14]

Рассмотрим случаи, когда данная система имеет ровно один корень. Пусть (x_1ne x_2), то есть (ane -frac14).
1. Пусть (x_1=frac14) – единственное решение системы.
(x_1) будет корнем, если (-frac34<a<frac34), (x_2) не будет корнем, если (ain
left(-infty;-frac12right]cupleft(-frac14;+inftyright)). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain left(-dfrac34;-dfrac12right]cupleft(-dfrac14;dfrac34right)] 2. Пусть (x_2=frac{a+1}3) – единственное решение системы.
(x_1) не будет корнем, если (ain
left(-infty;-frac34right]cupleft[frac34;+inftyright)), (x_2) будет корнем, если (-frac12<aleqslant -frac14). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain varnothing]

Пусть (x_1=x_2). Тогда (a=-frac14). Заметим, что при этом значении что (x_1), что (x_2) являются решением, следовательно, оно нам подходит.
Итоговый ответ: [ain left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)]

Ответ:

(ain
left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)
)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть).

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?

Ответ:

На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат  — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой где n  — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был равен 120 Н · м? Ответ дайте в километрах в час.

Ответ:

На клетчатой бумаге с размером клетки изображен треугольник АВС. Найдите длину его высоты, опущенной на сторону ВС.

Ответ:

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов  — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Ответ:

Найдите корень уравнения

Ответ:

Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах.

Ответ:

Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Ответ:

Найдите значение выражения

Ответ:

Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в

Ответ:

Найдите точку максимума функции

Ответ:

а)  Решите уравнение:

б)  Определите, какие из его корней принадлежат отрезку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM  =  CN : NB = 1 : 2. Точки P и Q  — середины ребер DA и DC соответственно.

а)  Докажите, что P, Q, M и N лежат в одной плоскости.

б)  Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.

Решите неравенство

Точка E  — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а)  Докажите, что CO  =  KO.

б)  Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет площади трапеции ABCD.

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

− каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.

Найти все значения a, при каждом из которых уравнение

имеет ровно один корень на отрезке [0; 1].

На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.

а)  Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?

б)  Может ли ровно одно число на доске оканчиваться на 6?

в)  Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Автор Сообщение

Заголовок сообщения: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 15:10

Зарегистрирован: 01 дек 2016, 21:47
Сообщений: 71

Вот примерно(условие не точно) такой параметр был на сегодняшнем экзамене. Выкладываю для тех, кому интересно это может быть интересно.
`sqrt(3x-5) *ln(a+3x)=sqrt(3x-5)*ln(a-4x)`
При каких `a` уравнение имеет один корень на `[0;1]`

№19
Сумма последотовательности, состоящей из 30 различных натуральных чисел, оканчивающихся на 7 и 3, равна 2502.
a) Может ли количество чисел с последней цифрой 7 равно количеству чисел с последней цифрой 3?
б) Может ли количество чисел с последней цифрой 3 быть равно 2?
Пункт в) к сожалению не помню до конца, поэтому не рискую его писать.

Hecarim

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 15:23

Центр пользователя

Зарегистрирован: 27 окт 2016, 22:00
Сообщений: 43

Параметр был точно такой же

interesant

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 15:40

Центр пользователя

Зарегистрирован: 01 дек 2013, 05:54
Сообщений: 57

Что-то не то. При х из отрезка от 0 до 1 указанный квадратный корень не имеет смысла.

khazh

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 15:42

Центр пользователя

Зарегистрирован: 23 мар 2012, 10:13
Сообщений: 5392

interesant писал(а):

Что-то не то. При х из отрезка от 0 до 1 указанный квадратный корень не имеет смысла.

Да, условие №18 вызывает сомнения в его правильности.

netka

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 16:02

Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань

у нас под корнем было `5x-3`.

может, как в прошлые годы, отдельную тему сделать для заданий с экзамена в разделе ЕГЭ или это нельзя?

khazh

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 16:07

Центр пользователя

Зарегистрирован: 23 мар 2012, 10:13
Сообщений: 5392

netka писал(а):

у нас под корнем было `5x-3`.

Там и в правой части под логарифмом возможно вместо `a-4x` должно быть `4x-a`.

nalex

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 16:08

Центр пользователя

Зарегистрирован: 05 июн 2014, 17:24
Сообщений: 108
Откуда: Москва

Да, поддерживаю!

может, как в прошлые годы, отдельную тему сделать для заданий с экзамена в разделе ЕГЭ или это нельзя?

nalex

Заголовок сообщения: ЕГЭ-2017: основная волна (2 июня)

Добавлено: 02 июн 2017, 16:15

Центр пользователя

Зарегистрирован: 05 июн 2014, 17:24
Сообщений: 108
Откуда: Москва

Обсуждение задач основного периода ЕГЭ-2017

nalex

Заголовок сообщения: Re: Параметр и задание №19 c ЕГЭ 2017. 50 регион.

Добавлено: 02 июн 2017, 16:21

Центр пользователя

Зарегистрирован: 05 июн 2014, 17:24
Сообщений: 108
Откуда: Москва

Создала отдельную тему, чтобы не гулять по форуму

netka писал(а):

у нас под корнем было `5x-3`.

может, как в прошлые годы, отдельную тему сделать для заданий с экзамена в разделе ЕГЭ или это нельзя?

Hecarim

Заголовок сообщения: Re: ЕГЭ-2017: основная волна (2 июня)

Добавлено: 02 июн 2017, 16:31

Центр пользователя

Зарегистрирован: 27 окт 2016, 22:00
Сообщений: 43

15-ый был таким. (Вроде как)
`(log_4 64x)/(log_4 x — 3) + (log_4 x — 3)/(log_4 64x) <= (log_4 x^4 + 16)/((log_4 x)^2)`

Источник

Условия и видеоразбор некоторого варианта части С (задания 13-19) основной волны ЕГЭ-2017 по математике (профильный уровень), который проходил 02.06.2017.

13. а) Решите уравнение $9 cdot 81^{cos x} — 28cdot 9^{cos x} + 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $left[dfrac{5pi}{2}; 4piright]$.

14. На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$ соответственно, причем $AM : BM = CN : NB = 1 : 2$. Точки $P$ и $Q$ — середины сторон $DA$ и $DC$ соответственно.
а) Докажите, что $P$, $Q$, $M$ и $N$ лежат в плоскости.
б) Найти отношение объемов многогранников, на которые плоскость $PQM$ разбивает пирамиду.

15. Решите неравенство $$dfrac{log_4(64x)}{log_4 x — 3} + dfrac{log_4 x — 3}{log_4(64x)} geqslant dfrac{log_4 x^4 + 16}{log_4^2 x — 9}.$$

16. Точка $E$ — середина боковой стороны $CD$ трапеции $ABCD$. На стороне $AB$ взяли точку $K$, так, что прямые $CK$ и $AE$ параллельны. Отрезки $CK$ и $BE$ пересекаются в точке $O$.
а) Докажите, что $CO = KO$.
б) Найти отношение оснований трапеции $BC$ и $AD$, если площадь треугольника $BCK$ составляет 0,09 площади трапеции $ABCD$.

17. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
− каждый январь долг увеличивается на $r%$ по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите $r$.

18. Найти все значения $a$, при каждом из которых уравнение $$sqrt{2x-1} ln(4x-a) = sqrt{2x-1} ln(5x+a)$$ имеет ровно один корень на отрезке $[0;, 1]$.

19. На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6.
б) Может ли ровно одно число на доске оканчивается на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Источник

22 февраля 2018

В закладки

Обсудить

Жалоба

Задачи с параметрами в ЕГЭ разных лет

ЕГЭ 2018. Досрочная волна

ЕГЭ 2017 (2 июня)

ЕГЭ 2017 (досрочная волна)

ЕГЭ 2016 (основная волна)

ЕГЭ 2015 (досрочная волна)

Демоверсии 2015-2018

Источник

Категория: ЕГЭ (диагностич. работы)

Разбор отдельных заданий части С. Основная волна, 2 июня 2017

13.1. а) Решите уравнение $8cdot 16^{cosx}-6cdot 4^{cosx}+1=0.$

б) Найдите корни уравнения из отрезка $[frac{3pi}{2};3pi].$

Решение: + показать

13.2. а) Решите уравнение $log_4(2^{2x}-sqrt3cosx-sin2x)=x.$

б) Найдите корни уравнения из отрезка $[-frac{pi}{2};frac{3pi}{2}].$

Решение: + показать

14.1. Дана пирамида , в основании которой – трапеция , причём $angle BAD+angle ADC=90^{circ}.$
Плоскости и и перпендикулярны плоскости основания пирамиды.

Прямые и пересекаются в точке .
а) Доказать, что
б) Найти $V_{PKBC},$ если а высота пирамиды равна

Решение:+ показать

14.2. На ребрах и треугольной пирамиды отмечены точки и

соответственно, причем . Точки и – середины рёбер и соответственно.

а) Докажите, что точки и лежат в одной плоскости.

б) Найдите, в каком отношении эта плоскость делит объем пирамиды.

Решение: + показать

14.3. Основанием прямой треугольной призмы является прямоугольный треугольник с прямым углом . Диагонали боковых граней и равны и соответственно,

а) Докажите, что треугольник прямоугольный.

б) Найдите объем пирамиды

Решение: + показать

15.1. Решить неравенство

$frac{log_2(4x^2)+35}{log_2^2x-36}geq -1.$

Решение: + показать

15.2. Решить неравенство

$frac{log_4(64x)}{log_4x-3}+frac{log_4x-3}{log_4(64x)}geq frac{log_4x^4+16}{log_4^2x-9}.$

Решение: + показать

16.1. Точка – середина боковой стороны трапеции На стороне отмечена точка так, что Прямые пересекаются в точке

а) Докажите, что

б) Найдите отношение оснований трапеции и если площадь треугольника составляет $frac{9}{64}$ площади трапеции

Решение: + показать

16.2. Две окружности с центрами и пересекаются в точках и , причём точки и лежат по разные стороны от прямой . Продолжения диаметра первой окружности и хорды этой окружности пересекают вторую окружности в точках и соответственно.

а) Докажите, что треугольники и подобны.

б) Найдите , если радиус второй окружности втрое больше радиуса первой и .

Решение: + показать

16.3. Основания трапеции равны и , а её диагонали равны и .

а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.

Решение: + показать

17.1. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

− каждый январь долг увеличивается на % по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.

Если ежегодно выплачивать по рублей, то кредит будет полностью погашен за года, а если ежегодно выплачивать по рублей, то кредит будет полностью погашен за года. Найдите .

Решение:+ показать

17.2. В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
– в январе каждого года долг увеличивается на % по сравнению с предыдущим годом

– с февраля по июнь нужно выплатить часть долга одним платежом. Определите, на какую сумму взяли в кредит в банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на рублей больше суммы взятого кредита.

Решение:+ показать

17.3. В июле планируется взять кредит в банке на сумму млн. рублей на неко- торый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на % по сравнению с концом преды- дущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила млн. рублей?

Решение:+ показать

18.1. Найти все значения параметра , при каждом из которых уравнение

$sqrt{5x-3}cdot ln(x^2-6x+10-a^2)=0$

имеет ровно один корень на отрезке

Решение:+ показать

19.1. На доске написано различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру , или на цифру . Сумма написанных чисел равна .

а) Может ли на доске быть поровну чисел, оканчивающихся на и на .

б) Может ли ровно одно число на доске оканчивается на ?

в) Какое наименьшее количество чисел, оканчивающихся на , может быть записано на доске?

Решение: + показать

Источник


1012	Две окружности с центрами O1 и O2 пересекаются в точках A и B, причем точки O1 и O2 лежат по разные стороны от прямой AB. Продолжение диаметра CA первой окружности и хорды CB этой же окружности пересекают вторую окружность в точках D и E соответственно. а) Докажите, что треугольники CBD и O1AO2 подобны. б) Найдите AD, если угол DAE равен углу BAC, а радиус второй окружности в четыре раза больше радиуса первой и AB = 2 Решение	Две окружности с центрами O1 и O2 пересекаются в точках A и B, причем точки O1 и O2 лежат по разные стороны от прямой AB ! Задача 16 на две окружности из реального ЕГЭ 02.06.2017 вариант 3

472	При каких значениях параметра a уравнение tg(pix-1)*ln(x+a)=0 имеет единственное решение на отрезке [0;1] Решение	реальный ЕГЭ 2017 (вариант 18_?)

471	При каких значениях параметра a уравнение tg(pix)*ln(x+a)=ln(x+a) имеет единственное решение на отрезке [0;1] Решение	реальный ЕГЭ 2017 (вариант 18_?) Два способа

470	При каких значениях параметра a уравнение x^2+(x-1)*sqrt(3x-a)=x имеет единственное решение на отрезке [0;1]. Решение График	реальный ЕГЭ 2017 (вариант 18.6.3)

469	При каких значениях параметра a уравнение ln(3a-x)ln(2x+2a-5)=ln(3a-x)ln(x-a) имеет единственное решение на отрезке [0;2]. Решение График	реальный ЕГЭ 2017 (вариант 18.6.2)

468	Найдите все значения параметра a, при каждом из которых уравнение sqrt(5x-3)*ln(x^2-6x+10-a^2)=0 имеет ровно один корень на отрезке [0;3]. Решение График	реальный ЕГЭ 2017 (вариант 18.4)

467	Найдите все значения параметра a, при каждом из которых уравнение ln(4x-1)*sqrt(x^2-6x+6a-a^2)=0 имеет ровно один корень на отрезке [0;3] Решение График	реальный ЕГЭ 2017 (вариант 18.3) Два способа

466	Найдите все значения параметра a, при каждом из которых уравнение sqrt(3x-2)ln(x-a)=sqrt(3x-2)ln(2x+a) имеет ровно один корень на отрезке [0;1] Решение График	реальный ЕГЭ 2017 (вариант 18.2.3)

465	Найдите все значения параметра a, при каждом из которых уравнение sqrt(5x-3)ln(3x-a)=sqrt(5x-3)ln(4x+a) имеет ровно один корень на отрезке [0;1] Решение График	реальный ЕГЭ 2017 (вариант 18.2.2) #Два способа

464	Найдите все значения параметра a, при каждом из которых уравнение sqrt(2x-1)ln(4x-a)=sqrt(2x-1)ln(5x+a) имеет ровно один корень на отрезке [0;1]. Решение График	ЕГЭ 2017 реал (вариант 18.2)