Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
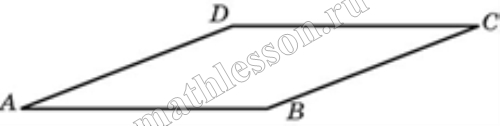
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Свойства параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма в точке пересечения делятся пополам.
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Пусть и
— биссектрисы углов параллелограмма, прилежащих к стороне
. Сумма углов
и
равна
. Углы
и
— половинки углов
и
. Значит, сумма углов
и
равна
градусов. Из треугольника
находим, что угол
— прямой.
Ответ: .
Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна . Найдите его большую сторону.
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.
Углы и
, а также
и
— накрест лежащие. Накрест лежащие углы равны. Значит, угол
равен углу
, а угол
— углу
.
Получаем, что треугольники и
— равнобедренные, то есть
, а
.
Тогда .
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Запишем формулы площади параллелограмма:
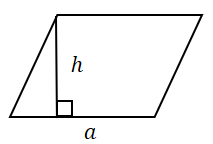
, где
— основание параллелограмма,
— его высота.
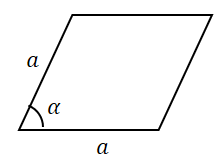
, где
и
— стороны параллелограмма,
— угол между ними.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Параллелограмм иu0026nbsp;его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
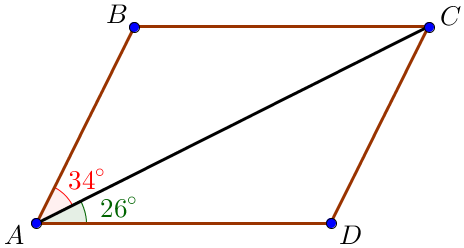
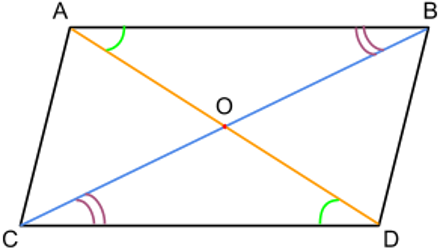
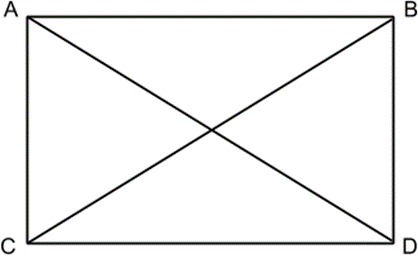
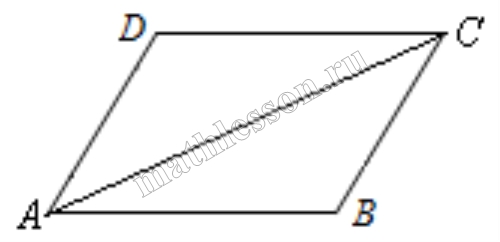
Пусть диагональ (displaystyle AC) образует со стороной (displaystyle AD) угол (displaystyle color{green}{26^circ } small,) а со стороной (displaystyle AB) – угол (displaystyle color{red}{34^circ} small.)
Тогда
(displaystyle color{green}{angle CAD} = color{green}{26^circ } small,) (displaystyle color{red}{angle BAC} = color{red}{34^circ }small.)
Найдем углы параллелограмма.
(displaystyle color{blue}{angle BAD} = color{red}{angle BAC }+ color{green}{angle CAD} = color{red}{34^circ }+ color{green}{26^circ} = color{blue}{60^circ } small.)
По свойству параллелограмма сумма углов, прилежащих к одной стороне, равна (displaystyle 180^circ small.) Значит,
(displaystyle angle ADC + color{blue}{angle BAD }= 180^circ small.)
Тогда
(displaystyle angle ADC = 180^{circ} — color{blue}{angle BAD }= 180^circ — color{blue}{60^circ} = 120^circ small.)
Так как (displaystyle 120>60) , то наибольший угол параллелограмма составляет (displaystyle 120^circ small.)
Ответ: (displaystyle 120^circ small.)
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
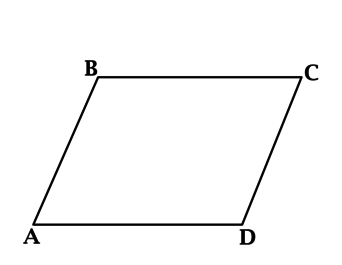
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
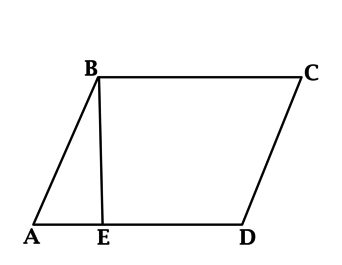
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
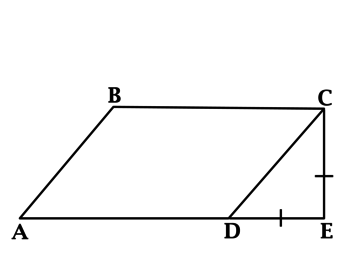
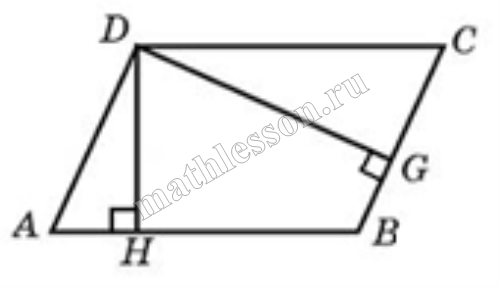
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Среди произвольных четырехугольников можно выделить два особенных: параллелограмм и трапеция. Параллелограммы можно разделить на:
- произвольный параллелограмм,
- прямоугольник;
- ромб;
- квадрат.
Часто для решения задания достаточно знать определение фигуры и уметь им пользоваться.
Параллелограмм.
Параллелограмм ― это четырёхугольник, у которого противоположные стороны равны и параллельны (АВ || CD, AC || BD).
То есть, если у четырехугольника есть хотя бы одна пара равных и параллельных противоположных сторон, то этот четырехугольник – параллелограмм, а значит, все его противоположные стороны равны и параллельны.
Свойства параллелограмма
Из определения параллелограмма вытекает ряд его свойств. Для любого параллелограмма (то есть произвольного и особенного, вроде ромба или прямоугольника) выполняются условия:
1. Противоположные стороны равны (АВ = СD, AC = BD).
2. Противоположные углы равны (∠А = ∠D, ∠B = ∠C).
3. Сумма углов, прилежащих к одной стороне, равна 180°: ∠BAC + ∠ACD = 180°, ∠ABD + ∠BCD = 180° (это вытекает из параллельности противоположных сторон, так как указанные углы являются односторонними).
4. Из параллельности сторон вытекает равенство частей углов (например, ∠DAB = ∠ADC; ∠BCD = ∠ABC как накрестлежащие).
5. Две диагональ делят параллелограмм на две пары равных треугольников ∆ABC = ∆BCD, ∆ABD = ∆ACD (по стороне и двум углам).
6. Диагонали параллелограмма точкой пересечения делятся пополам (АО = OD, CO = OB).
Интересные, но редко применимые свойства параллелограмма:
7. Биссектрисы противоположных углов параллелограмма всегда параллельны.
8. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом.
Признаки параллелограмма
Для того, чтобы в задании с развернутым ответом доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон: AB||CD и BC||AD.
2. Четырехугольник имеет пару параллельных и равных сторон: AB||CD, AB = CD (или BC||AD, BC = AD).
3. В четырехугольнике противоположные стороны попарно равны: AB = CD, BC = AD.
4. В четырехугольнике противоположные углы попарно равны: ∠DAB = ∠BCD, ∠ABC = ∠CDA.
5. В четырехугольнике диагонали точкой пересечения делятся пополам: AO = OC, BO = OD.
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°: ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°.
Формулы площади параллелограмма
Существую три формулы площади параллелограмма, которые применимы как для произвольного параллелограмма, так и для ромба, прямоугольника, квадрата.
|
1 |
2 |
3 |
|
|
|
|
|
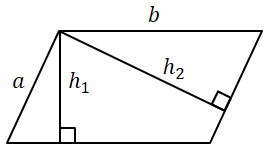
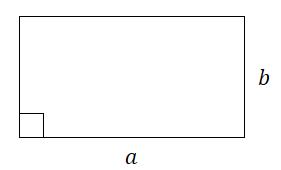
$S = bh_1 = ah_2$ |
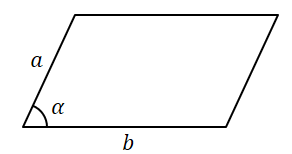
$S = ab;sin alpha$ |
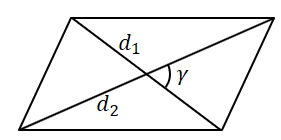
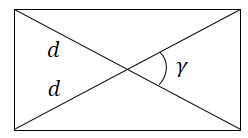
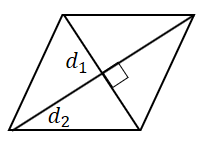
$S = frac{1}{2}d_1d_2sin gamma$ |
|
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. |
Площадь параллелограмма равна произведению его сторон на синус угла между ними. |
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними. |
Прямоугольник
Прямоугольник ― это параллелограмм, у которого все углы прямые. Для того, чтобы параллелограмм был прямоугольником, достаточно, чтобы хотя бы один его угол был равен 90°, тогда и все остальные будут равны 90°.
Кроме свойств параллелограмма, у прямоугольника есть и несколько своих:
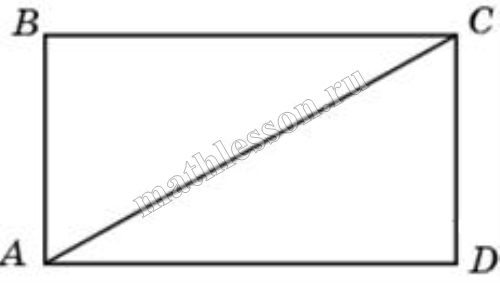
1. Диагонали прямоугольника равны (AD = BC).
Стороны прямоугольника являются его высотами.
В связи с этими свойствами, формулы площади параллелограмма для прямоугольника можно немного изменить. 1 и 2 формула обращаются в одну, во второй формуле произведение диагоналей можно заменить на квадрат одной диагонали.
|
1 |
2 |
|
|
|
|
$S = ab$ |
$S = frac{1}{2}d^2singamma$ |
|
Площадь прямоугольника равна произведению его смежных сторон. |
Площадь прямоугольника равна половине произведения квадрата его диагонали на синус угла между диагоналями. |
Ромб
Ромб ― это параллелограмм, у которого все стороны равны. На самом деле, достаточно, чтобы были равны хотя бы две его соседние стороны, тогда все стороны будут равны.
Кроме свойств параллелограмма, у ромба есть несколько своих:
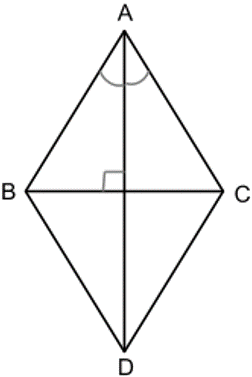
1. Диагонали ромба являются биссектрисами его углов.
2. Диагонали ромба пересекаются под прямым углом (AD ⊥ BC).
То есть, параллелограмм является ромбом, если выполняется хотя бы одно из условий:
- Две его смежные стороны равны;
- Его диагонали пересекаются под прямым углом;
- Одна из диагоналей делит содержащие её углы пополам;
- Все высоты равны.
На основании свойств можно немного изменить формулы площади параллелограмма для ромба:
|
1 |
2 |
3 |
|
|
|
|
|
$S = ab$ |
$S = a^2 sin alpha$ |
$S = frac{1}{2}d_1d_2$ |
|
Площадь ромба равна произведению его стороны на высоту (при чем для любой стороны это выражение будет одинаковым, так как стороны равны). |
Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами. |
Площадь ромба равна половине произведения его диагоналей. |
Квадрат
Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны (AB = BC = CD = DA и ∠A = ∠B = ∠C = ∠D = 90°). То есть квадрат сочетает в себе свойства и ромба, и прямоугольника, поэтому ему присущи не только свойства параллелограмма, но и ромба с прямоугольником. Надо запомнить, что любой квадрат является ромбом и прямоугольником, но не любой ромб или прямоугольник является квадратом.
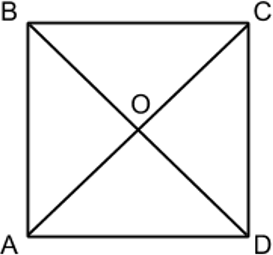
Центры вписанной и описанной окружностей квадрата совпадают и одновременно являются точкой пересечения диагоналей (т. О).
Формулы площади квадрата:
|
1 |
2 |
|
|
|
|
$S = ab$ |
$S = frac{1}{2}d^2sin gamma$ |
|
Площадь квадрата равна его стороне, возведенной в квадрат. |
Площадь квадрата равна одной второй квадрата его диагонали. |
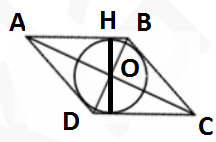
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 6. Найдите его большую сторону.
Решение:
Давайте найдем здесь пары накрест лежащих углов – это углы 2 и 5; 3 и 6. Напомню, что накрест лежащие углы равны.
Методом пристального взгляда замечаем, что ∆ABE и ∆ECD – равнобедренные треугольники, тогда AB=AE=DC=DE.
BC – большая сторона. AD – большая сторона.
BC = AD = AE+ED = AB+CD = AB+AB = 2AB = 12
Ответ: 12
ЕГЭ Профиль
Планиметрия: задачи, связанные с углами
Параллелограммы
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1001
|
В параллелограмме ABCD AB = 3, AD = 21, $$sin a = frac{6}{7} $$ . Найдите большую высоту параллелограмма. |
|
Ответ: 18
Задание 1003
|
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. |
|
Ответ: 6
Задание 1004
|
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2. |
|
Ответ: 18
Задание 1011
Диагонали ромба равны $$2sqrt{5}$$ и $$4sqrt{5}$$ . Найдите радиус вписанной в ромб окружности.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
|
Площадь ромба вычисляется как половина произведения диагоналей. То есть $$S = 0.5 *2sqrt{5}*4sqrt{5}=20$$ С другой стороны, площадь равна произведению основания на высоту, а высота равна двум радиусам вписанной окружности. То есть S = AB * 2 OH = AB * 2r Найдем AB по теореме Пифагора из треугольника ABO (его катеты равны половинам диагоналей): $$AB = sqrt{sqrt{5}^{2}+2sqrt{5}^{2}}=sqrt{5+20}=5$$ Приравняем площади: 20 = 5 * 2r, r = 2 |
|
Задание 1019
|
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника. |
|
Ответ: 14
Задание 1020
|
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. |
|
Ответ: 48
Задание 1021
|
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника. |
|
Ответ: 13
Задание 1022
| Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах. |  |
Ответ: 30
Задание 1023
|
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма. |
|
Ответ: 6
Задание 1024
|
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма |
 |
Ответ: 8
Задание 1025
|
Найдите площадь ромба, если его высота равна 2, а острый угол 30°. |
|
Ответ: 8
Задание 1027
|
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. |
|
Ответ: 3
Задание 1028
|
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ. |
|
Ответ: 2
Задание 1029
|
Диагональ параллелограмма образует с двумя его сторонами углы 24 и 36. Найдите больший угол параллелограмма. Ответ дайте в градусах. |
|
Ответ: 120
Задание 1030
|
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма. |
|
Ответ: 10