Относительность движения егэ теория

Правило (закон) сложения скоростей

Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.

Рассмотрим вывод закона сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта (displaystyle O). Эту систему отсчёта обозначим K и будем называть неподвижной.

Вторая система отсчёта, обозначаемая K’, связана с телом отсчёта (displaystyle O’), которое движется относительно тела (displaystyle O) со скоростью (displaystyle vec{u}). Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы (displaystyle K’) перемещаются параллельно самим себе (нет вращения системы координат), так что вектор (vec{u}) можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта K обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью (vec{u}), то система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта (displaystyle K’.)

Заметим, что скорость любой точки вагона равна (displaystyle vec{u}). Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью (displaystyle vec{u}). Муха переносится вагоном, и потому скорость (displaystyle vec{u}) движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Тогда появляются ещё две скорости, которые нужно рассмотреть. Скорость мухи относительно вагона (то есть в движущейся системе (displaystyle K’)) обозначается (displaystyle vec{v’}) и называется относительной скоростью.

Скорость мухи относительно земли (то есть в неподвижной системе (displaystyle K)) обозначается (displaystyle vec{v}) и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.

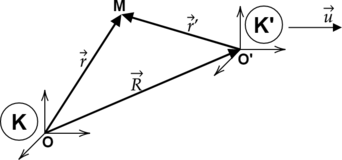
На вышеприведенном рисунке муха обозначена точкой M. Далее,

(displaystyle vec{r}) — радиус-вектор точки M в неподвижной системе (displaystyle K);

(displaystyle vec{r’}) — радиус-вектор точки M в движущейся системе (displaystyle K’);

(displaystyle vec{R}) — радиус-вектор тела отсчёта (displaystyle O’) в неподвижной системе (displaystyle K).

Как видно из рисунка [displaystyle vec{r}=displaystyle vec{R}+displaystyle vec{r’}] Дифференцируя это равенство, получим [frac {dvec{r}}{dt}=frac {dvec{R}}{dt}+frac {dvec{r’}}{dt}, (1)] Производная (displaystyle frac {dvec{r}}{dt}) есть скорость точки (displaystyle M) в системе (displaystyle K), то есть абсолютная скорость: [frac {dvec{r}}{dt}=vec{v}] Аналогично производная (displaystyle frac {dvec{r’}}{dt}) есть скорость точки (displaystyle M) в системе (displaystyle K’), то есть относительная скорость: [frac {dvec{r’}}{dt}=vec{v’}] А (displaystyle frac {dvec{R}}{dt}) — это скорость точки (displaystyle O’) в неподвижной системе, то есть, переносная скорость (displaystyle vec{u}) движущейся системы относительно неподвижной: [displaystyle frac {dvec{R}}{dt}=vec{u}] Таким образом, из равенства (1) получаем [fbox{${vec{v}=vec{u}+vec{v’}}$}]

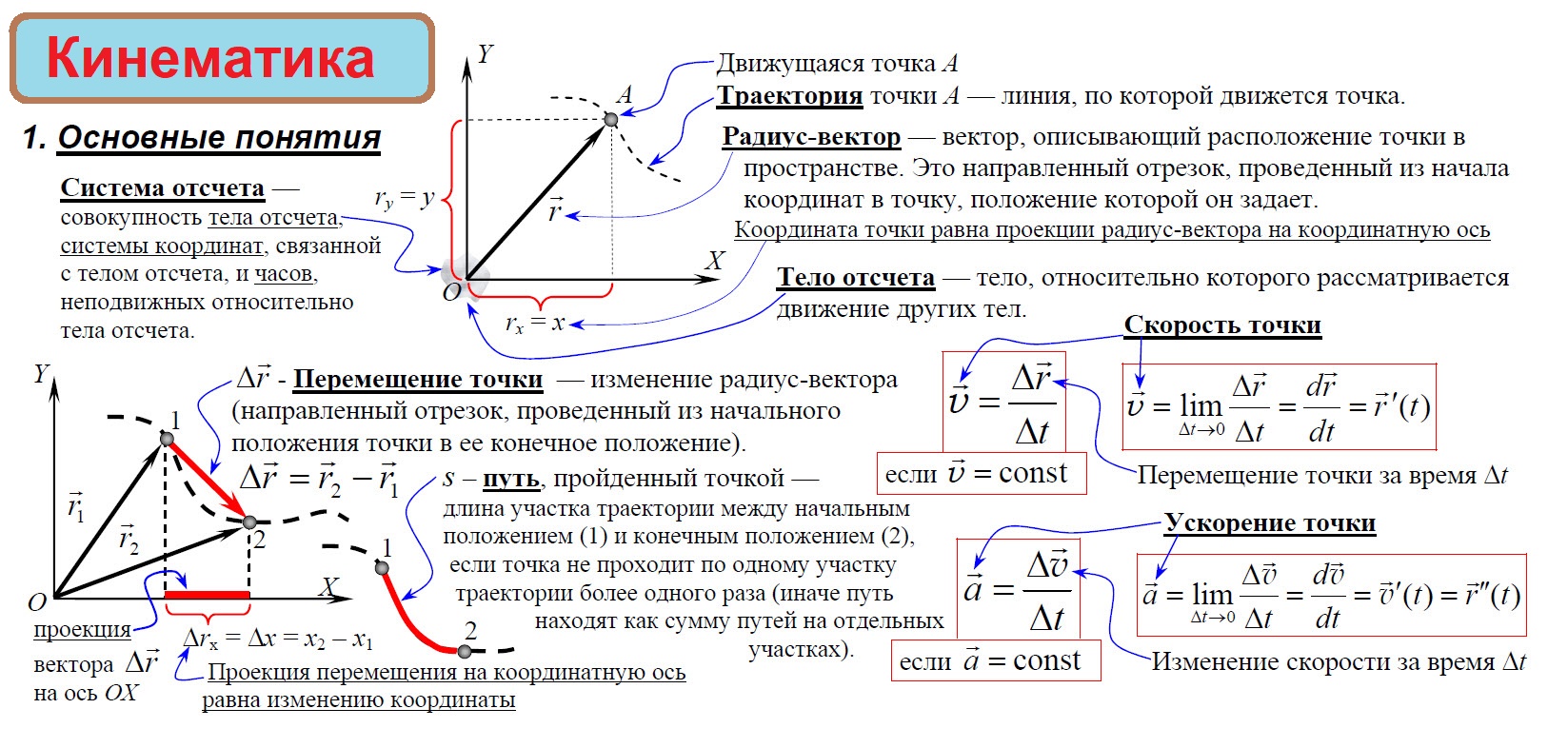
КИНЕМАТИКА.
Теория и формулы (кратко и сжато)

Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.

Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.

Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.

Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.

Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).

Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.

Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.

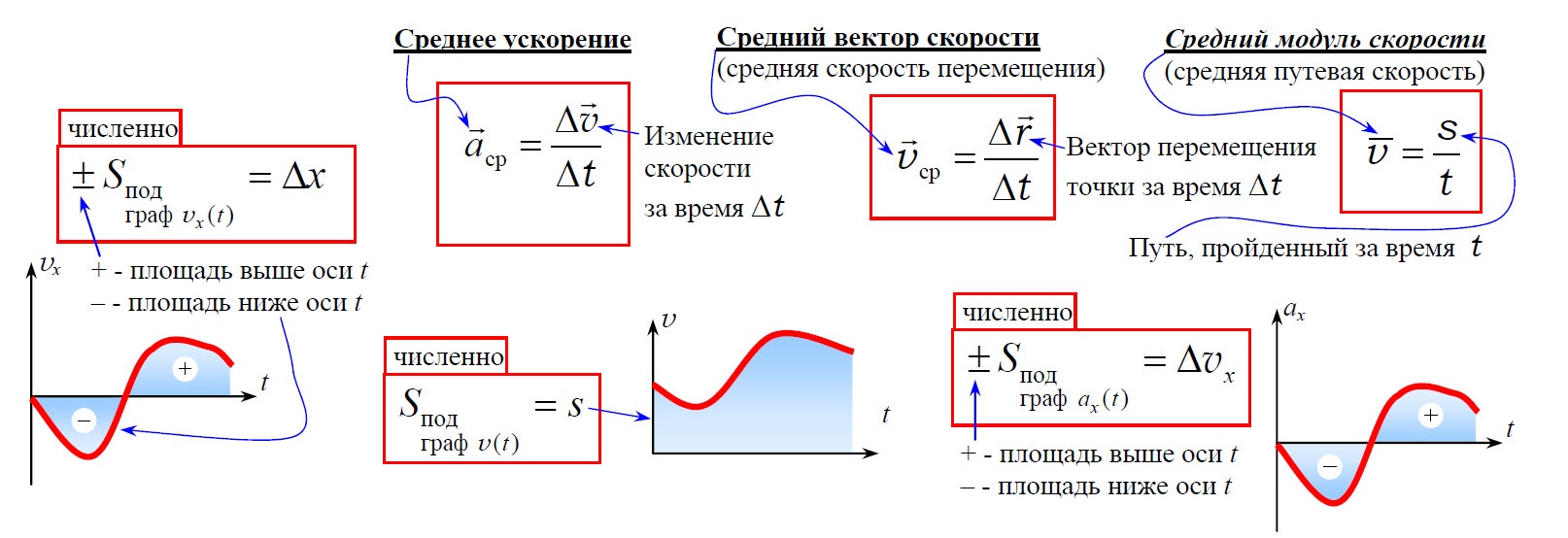
Типы движений

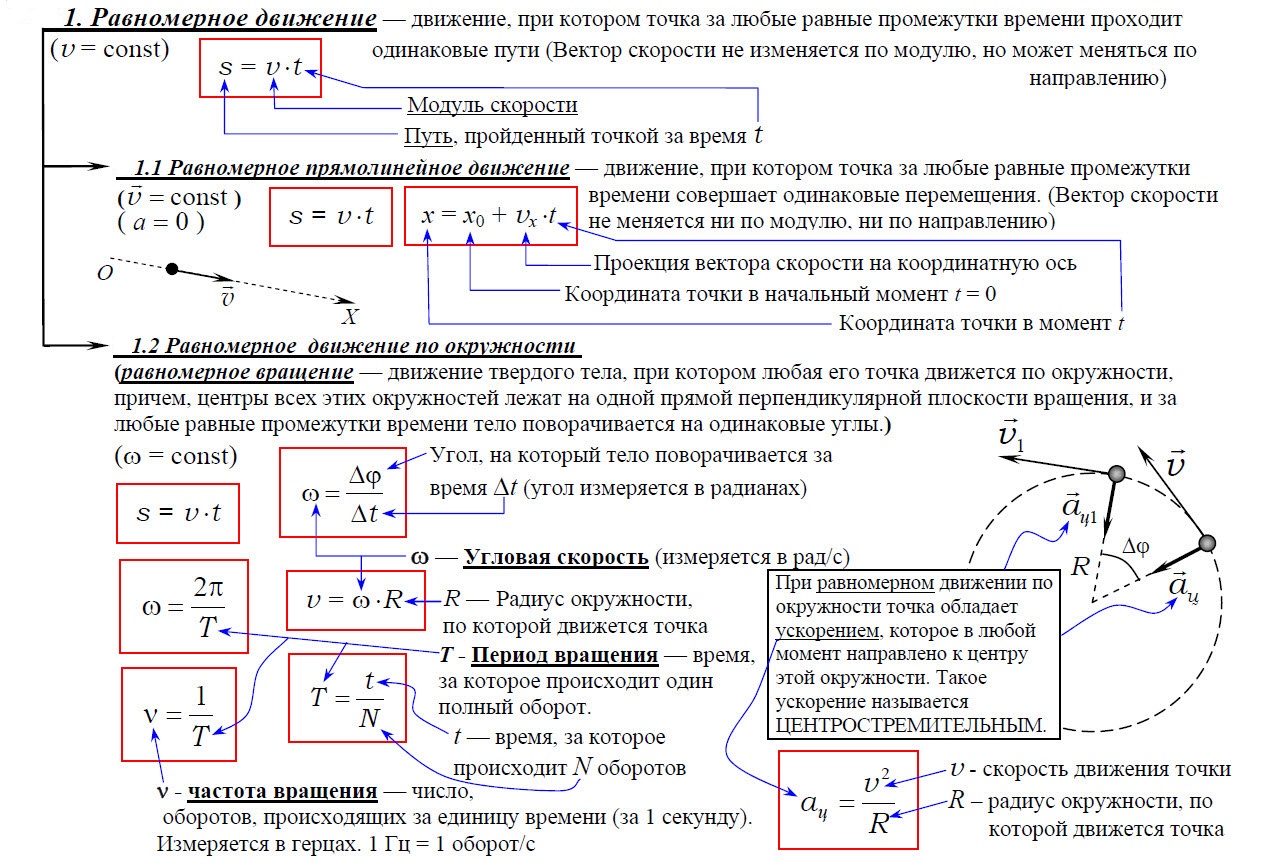
1. Равномерное движение

1.1. Равномерное прямолинейное движение

Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.

Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.

Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.

Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.

Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.

1.2 Равномерное движение по окружности (равномерное вращение)

Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

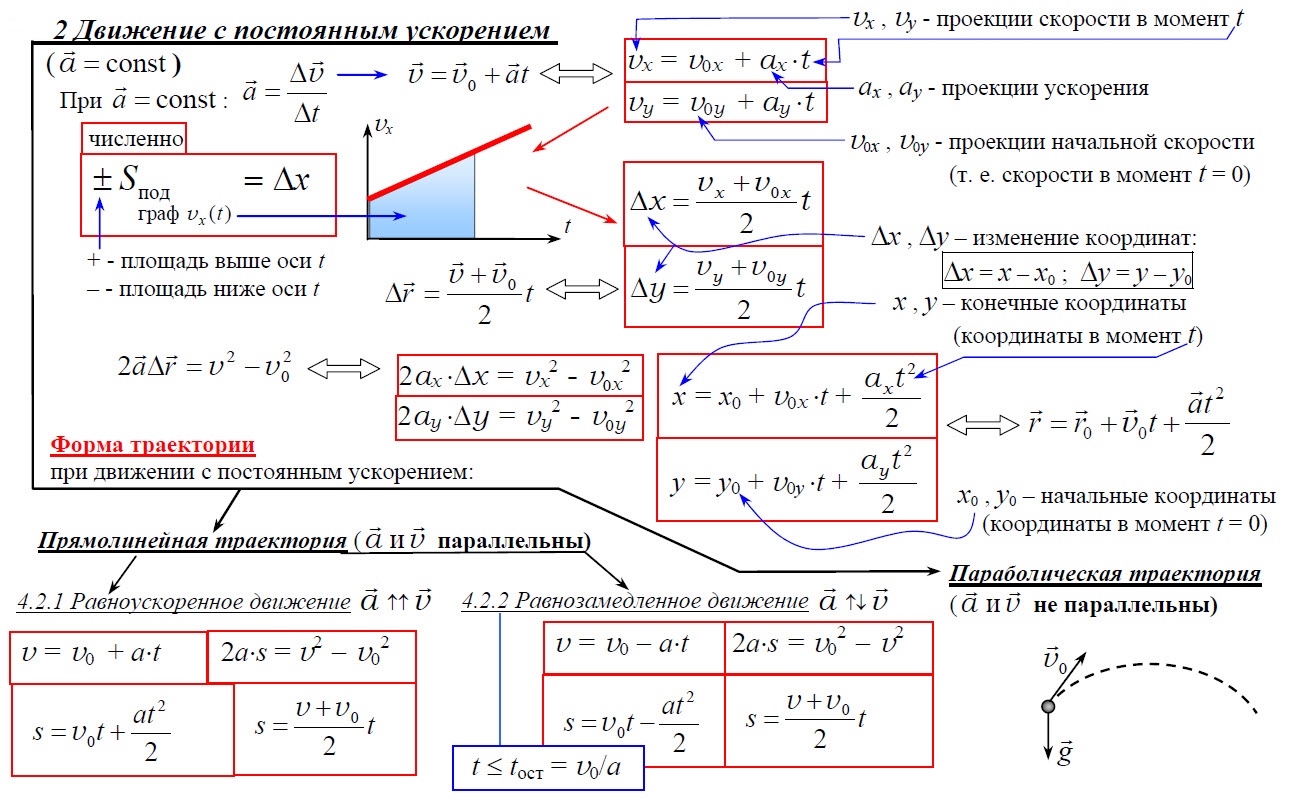
2. Движение с постоянным ускорением

Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.

Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.

Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.

Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt  показывает, что скорость линейно зависит от времени.

Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.

3. Гармоническое движение

Виды движений

Прямолинейное движение

Криволинейное движение

Частные случаи равноускоренного движения под действием силы тяжести

Частные случаи решения задач

Дополнительные материалы по кинематике

Кинематика. Таблица кратко.

Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

С данной темы приступаем к повторению первого раздела физики,
который называется «Кинематика». И в начале вспомним основные понятия,
относящиеся к данному разделу, а также поговорим об относительности движения.

Кинематика, как часть механики, была известна еще со времен
Аристотеля. Однако впервые раздел кинематики был четко выделен в курсе
«Физической и экспериментальной механики» генерала Жана-Виктора Понселе,
который читал его в Парижском университете с 1837 по 1848 годы.

Кинематика — это раздел механики, в котором изучают
движение тел, без рассмотрения причин, вызвавших это движение.

Основной задачей кинематики является нахождение
положения тела в произвольный момент времени, если известны его положение,
скорость и ускорение в начальный момент времени.

Наиболее простым видом движения в природе является механическое
движение. Под механическим движением понимают изменение положения
тел (или частей одного тела) друг относительно друга в пространстве с течением
времени.

Простым примером механического движения может служить лодка,
плывущая по реке. Она меняет свое положение относительно берега, деревьев и
человека, находящихся на берегу. И таких примеров можно привести достаточно
много.

Чтобы изучать движение тела, нужно прежде всего уметь
определять это положение. Здесь важно помнить, что положение тела
можно задать только относительно какого-либо другого тела, которое, обычно,
называют телом отсчета. И так, тело отсчета — это тело
(или группа тел), принимаемое в данном случае за неподвижное, относительно
которого рассматривается движение других тел.

Тело отсчета можно выбрать совершенно произвольно. В рассмотренном
примере, им может служить рыбак, стоящий на берегу реки, или деревья, кусты,
береговая линия.

Для описания движения мало выбрать тело отсчета, необходимо
еще указать и систему координат, связав ее с телом отсчета, и способ измерения
времени. Так вот, совокупность тела отсчета, системы координат и способа
измерения времени создают систему отсчета, относительно которой и
рассматривают движение тела.

Положение тела в пространстве можно определить с помощью
радиус-вектора или при помощи координат. Радиус-вектор — это вектор,
который соединяет исследуемую точку и начало координат. Радиус-вектор
обозначается латинской буквой  и,
как и любой другой вектор, имеет длину и направление.

Под координатой точки понимают проекцию конца
радиус-вектора на выбранную координатную ось.

Таким образом, для того, чтобы в рассмотренном примере
определить координату точки М, необходимо опустить с конца
радиус-вектора два перпендикуляра — на ось Ox и
ось Oy. Тогда найденные значения x и y и будут являться
координатами точки M.

Еще одно затруднение, с которым можно столкнуться,
при изучении движения тела, это то, что каждое тело имеет определенные размеры,
следовательно, разные его части, разные точки тела находятся в разных местах
простран­ства. Так как же определить положение всего тела? В общем слу­чае
это сделать трудно. Но оказывается, во многих случаях нет необхо­димости
указывать положение каждой точки движущего­ся тела.

Зачем, например, описывать движение каждой точки самолета,
если эти движения ничем не различаются между собой?

Движение тела, при котором все его точки движутся
одина­ково, называют поступа­тельным.

Не нужно описывать движение каждой точки тела и
тогда, когда размеры тела малы по сравнению с расстоянием, которое оно
проходит, или по сравнению с расстояниями от него до дру­гих тел.

На­пример, сидя в автомобиле, его нельзя считать
точкой, по отношению к водителю или пассажиру, но, например, автомобиль мал по
сравнению с протяженностью расстояния, которое ему предстоит преодолеть, и
поэтому автомобиль считают точкой при описании его движения.

Так же поступают в астрономии при изучении движений
небесных тел. Планеты, звезды и Солнце, конечно, не малые тела.

Но, например, в сравнении с масштабами нашей
галактики «Млечный путь» и Землю и Солнце мы можем принимать за точку, которая
движется вокруг другой точки — центра галактики.

А можно ли галактику принять за точку?
Конечно же да, но только в случаях рассмотрения ее движения относительно других
галактик или всей Вселенной.

Поэтому говоря в дальнейшем о движении тела, в
действительности будем иметь в виду движение какой-нибудь точки этого тела. Не
надо забывать при этом, что эта точка ма­териальна, то есть она отличается от
обычных тел лишь тем, что она не имеет размеров.

Таким
образом, материальная точка — это тело, размерами которого в данных
условиях движения можно пренебречь.

Линия,
которую описывает движущееся тело в определенной системе координат, называется траекторией.
Например, в идеализированной модели движения Луны вокруг Земли, в системе
отсчета, связанной с Землей, траекторией движения Луны будет являться
окружность.

А
в системе отсчета, связанной с Солнцем это кривая, чем-то напоминающая лепестки
цветка (такую кривую еще называют циклоидой).

Если можно найти длину траектории, которую описало тело за
некоторый промежуток времени, то можно определить путь, пройденный
телом. Обозначается путь малой латинской буквой s.
Следует также помнить, что путь — величина скалярная и всегда
положительная.

В тех случаях, когда траектория движения не известна,
определить положение тела, то есть его координаты, в конце пути нельзя,
даже если известны начальное положение тела и длина пройденного им пути.

Допустим, известно, что некоторое тело начинает двигаться из
точки О и за один час проходит 20 км.

Для ответа на вопрос, где будет находиться тело спустя один
час после его выхода из точки О, не хватает информации о его движении. Ведь
тело могло, например, двигаться прямолинейно в северном направлении и оказаться
в точке А, находящейся на расстоянии 20 км. А могло также, дойдя до
точки B, находящейся на расстоянии 10 км от точки О, повернуть на восток и вернуться в
точку О. При этом пройденный путь также окажется равным 20 км. При
заданном значении пути, тело могло оказаться в любой точке пространства,
ограниченного окружностью, радиуса 20 км.

Чтобы избежать такой неопределенности, для нахождения
положения тела в пространстве в заданный момент времени, была введена
физическая величина, называемая перемещением.

Перемещением тела называют направленный отрезок
прямой, соединяющий начальное положение тела с его конечным положением.

Как видно из рисунка, перемещение тела равно
геометрической разности радиус-векторов тела в начальный и конечный моменты
времени.

Для того, чтобы определить проекцию перемещения на
выбранную координатную ось, необходимо найти координаты тела в начальный и
конечный моменты времени, и найти их разность.

Необходимо отметить, что модуль перемещения не может быть
больше пути.

Знак равенства относится только к случаю прямолинейного
движения, если направление движения не изменяется.

Скорость — это мера механического состояния тела,
которая характеризует быстроту изменения положения тела относительно данной
системы отсчета и является векторной физической величиной.

Известно, что тело в редких случаях движется с неизменной
скоростью, поэтому для характеристики такого движения было введено понятие
средней скорости. И так, средняя скорость — это векторная физическая
величина, численно равная отношению перемещения к промежутку времени, за
который оно произошло, и направленная вдоль перемещения.

Так же в физике различают понятие мгновенной скорости,
то есть скорости тела в данный момент времени или в данной точке траектории.
Она равна пределу, к которому стремится средняя скорость за бесконечно малый
промежуток времени.

 – это производная от радиус-вектора по времени.

Следует помнить, что мгновенная скорость всегда направлена
по касательной к траектории движения тела, а в
случае прямолинейного движения совпадает с ней.

Следующей важной характеристикой движения является ускорение.
Ускорение — это векторная физическая величина, характеризующая быстроту
изменения скорости. Оно показывает, на какую величину изменяется скорость тела
за единицу времени.

Среднее ускорение — векторная физическая величина,
численно равная отношению изменения скорости ко времени, за который оно
произошло.

где  —
это производная от скорости по времени.

Для того, чтобы найти направление вектора среднего ускорения,
необходимо найти направление вектора изменения скорости. Для этого параллельным
переносом совмещают начало вектора начальной скорости с началом вектора
конечной скорости и строят их разность.

Вектор среднего ускорения направлен параллельно вектору
скорости в сторону вогнутости траектории.

Важно запомнить, что, зная траекторию
движения тела, можно определить направление вектора его скорости,
но не ускорения. Ведь направление ускорения определяется направлением
равнодействующей сил, действующих на тело.

На рисунке изображен автомобиль. Что можно сказать о данном
автомобиле: движется он или покоится? Однозначного ответа нет. Ведь не известно,
относительно чего рассматривать его движение.

А вот так?

Здесь можно сказать, что автомобиль движется относительно
дороги.

А что можно сказать о водителе данного автомобиля: он
движется или покоится?

В данном примере оба ответа будут правильными, ведь
относительно дороги водитель действительно движется вместе с автомобилем, а
относительно автомобиля он покоится.

А что можно сказать о траектории его движения? И опять здесь
нет однозначного ответа.

Так как в разных системах отсчета будут
различны вид траектории, значение скорости и других величин! В этом и
заключается относительность движения.

Вот еще один пример. Два велосипедиста на велосипеде-тандеме
движутся по проселочной дороге. Движутся ли они относительно друг друга?

Правильный ответ — «нет», так как положение их тел
относительно друг друга не меняется с течением времени.

А вот еще один классический пример. Мальчик переходит с кормы
на нос лодки, которая сама движется по течению реки. Когда мальчик доходит до
носа лодки, отсчет времени прекращают. Каково перемещение мальчика относительно
берега реки?

Для ответа на этот вопрос необходимо определить перемещение
мальчика, относительно лодки.

И перемещение лодки относительно берега, за этот промежуток
времени.

Тогда очевидно, что перемещение мальчика относительно
берега будет равно геометрической сумме перемещений мальчика относительно
лодки, и лодки, относительно берега.

Таким образом, если тело одновременно участвует в
нескольких движениях, то результирующее перемещение точки равно векторной
сумме перемещений, совершаемых ею в каждом из движений. В этом состоит
установленный экспериментально принцип независимости движений.

Основные выводы:

В рамках данной темы были повторены основные понятия кинематики,
поговорили о механическом движении тел и способах его описания. А также
разобрались с понятием относительности механического движения.

Физика ЕГЭ теория + примеры. Раздел 1. МЕХАНИКА. Кинематика. Тема: Механическое движение.

Механическое движение. Теория

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.

■ Виды движений

Движение может быть двух видов: прямолинейным и криволинейным.

Прямолинейное движение

Равномерное — движение, при котором тело за равные промежутки времени проходит одинаковое расстояние. При равномерном движении скорость тела остаётся постоянной.

Пример. В таблице представлена зависимость координат тела от времени.

Неравномерное — движение, при котором тело за равные промежутки времени проходит неодинаковое расстояние. Например, тело за первые 10 мин прошло 30 м, а за следующие 10 мин — 40 м.

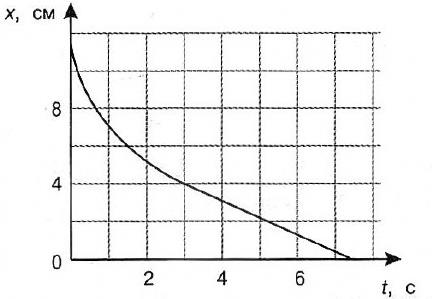
Один из видов неравномерного движения: равнопеременное — движение, при котором за равные промежутки времени скорость тела изменяется на одну и ту же величину. Например, шарик уронили в воду с некоторой высоты. Первые 3 с шарик двигался равноускоренно, а после 3 с движение продолжалось с постоянной скоростью. На рисунке показан график изменения координаты шарика с течением времени.

График изменения координаты шарика с течением времени, где х — координата тела, t — время движения.

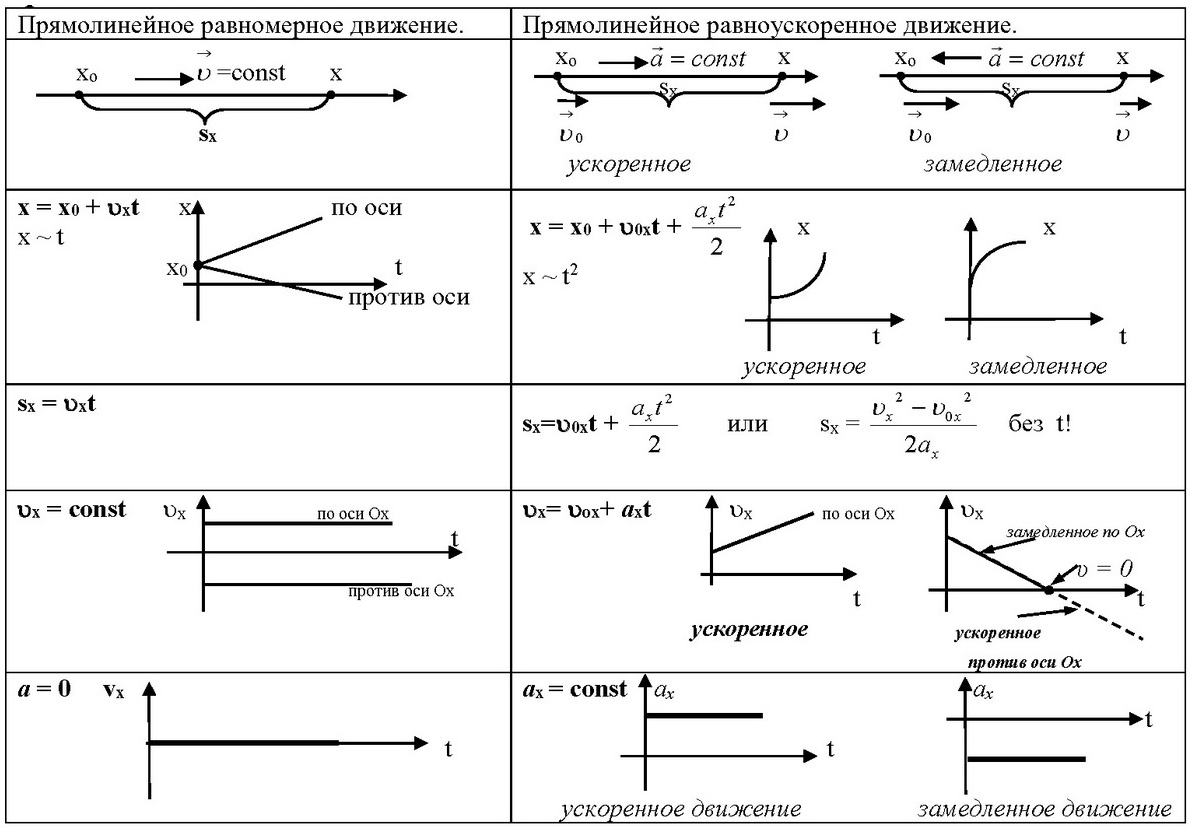
Таблица. Прямолинейное движение

Криволинейное движение

Вращательное — движение в одном направлении по плоской (или пространственной) замкнутой траектории. Примером может служить движение Земли вокруг Солнца.

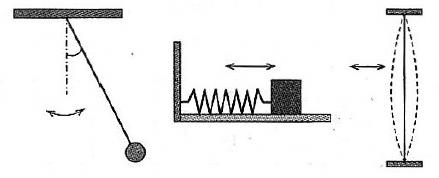
Колебательное — движение вдоль одного и того же отрезка с изменением направления.

Таблица. Криволинейное движение

■ Относительность механического движения

Относительность механического движения — это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

■ Система отсчёта

Тело отсчёта — произвольно выбранное тело, относительно которого определяется положение движущейся материальной точки (или тела).

Система отсчёта — совокупность системы координат и часов, связанных с телом отсчёта. В прямоугольной системе координат положение точки в пространстве задаётся её проекциями на три взаимно перпендикулярные оси. Совокупность координат x(t), y(t), z(t) в момент времени t определяет закон движения материальной точки в координатной форме.

Механическое движение.
Практические задания

№ 1. Четыре объекта двигались по шоссе (ось Ох). В таблице представлена зависимость их координат от времени.

У какого из тел скорость могла быть постоянна и отлична от нуля?

№ 2. Мячик катится по горке. Изменение его координаты с течением времени в инерциальной системе отсчёта показано на графике. Охарактеризуйте движение мячика на каждом участке.

№ 3. Эскалатор метро поднимается со скоростью 1 м/с. Может ли человек, находящийся на нём, быть в покое в системе отсчёта, связанной с землёй?

1. Может, если движется в противоположную сторону со скоростью 1 м/с.
2. Может, если движется в ту же сторону со скоростью 1 м/с.
3. Может, если стоит на эскалаторе.
4. Не может ни при каких условиях.

Вы смотрели: Физика ЕГЭ теория + примеры. Раздел 1. МЕХАНИКА. Кинематика. Тема: Механическое движение.

Просмотров:
4 395

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:

s′ = s₁ + s₂

s′ — перемещение МТ относительно НСО, s₁— перемещение МТ относительно ПСО, s₂ — перемещение ПСО относительно НСО.

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ + s₂

• Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = s₁ – s₂

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:

s′ = √(s₁² + s₂²)

• Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s₁=0, перемещение s′ = s₂
• Если тело движется относительно двух НСО, то его перемещение относительно НСО₁ равно перемещению движения относительно НСО₂. В этом случае одну из систем можно принять за ПСО с нулевой скоростью. Тогда ее перемещение относительно НСО будет равно 0. При s₂=0, перемещение s′ = s₁

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

s′=|s₁ – s₂|=|10 – 2|=8 (м).

Относительность скорости в ПСО и НСО

Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:

v′ = v + u

v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Полезные факты

• Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v + u

• Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = v – u

• Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:

v′ = √(v² + u²)

• Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
• Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2. В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u

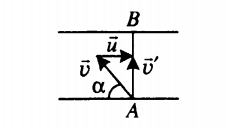
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v_отн = v₁– v₂

v_отн — относительная скорость, или скорость первого тела относительно второго, v₁ и v₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

• v₁₂ — скорость первого тела относительно второго. Ее проекция равна:

v_12x = v_1x – v_2x

• v₂₁ — скорость второго тела относительно первого. Ее проекция равна v_21x = v_2x – v_1x

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Полезные факты

• Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:

v_отн = |v₁ – v₂|

• Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:

v_отн = |v₁ + v₂|

• Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:

v_отн = √(v₁² + v₂²)

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .

Сложение двух сонаправленных векторов
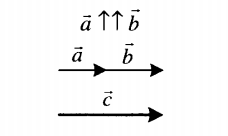	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
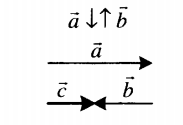	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
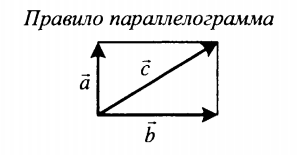
Сложение двух векторов, расположенных друг к другу под углом
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
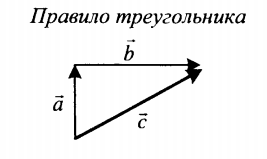	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .
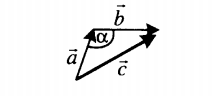	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .
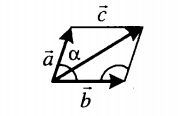	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .

Правила вычитания векторов

Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Вычитание двух сонаправленных векторов
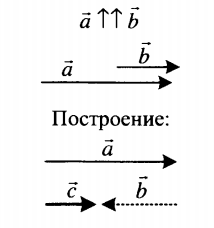	Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|.
Вычитание двух противоположно направленных векторов
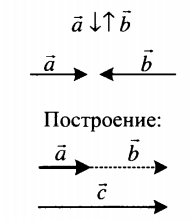	Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b.
Вычитание двух векторов, расположенных друг к другу под углом
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
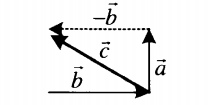	Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: .
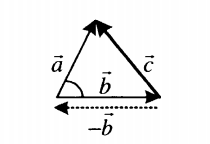	Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: .

Алиса Никитина | Просмотров: 7.1k