МАОУ «Свердловская СОШ №2»
План- конспект открытого урока
по математике в 11 Б классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Сушкова Э.А.,
учитель математики
МАОУ «Свердловская СОШ №2»
Апрель 2021 г
https://yandex.ru/efir?stream_id=vIL5MDlVhUGQ&from_block=player_context_menu_yavideo
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
- Систематизировать теоретические знание по теме.
- Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
- перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
- умножение (деление) обеих частей уравнения на отличную от нуля число;
- возведение уравнения в нечетную степень;
- извлечение корня нечетной степени с обеих частей уравнения:
- логарифмирование показательного уравнения;
- применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
- возведение уравнения в четную степень;
- потенцирование логарифмического уравнения;
- освобождение уравнения от знаменателя;
- приведение подобных членов;
- применение формул (тригонометрических, логарифмических и других).
- Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
;
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
- Повторить теорию по темам:
- Уравнения-следствия.
- Равносильность уравнений системам.
- Равносильность уравнений на множествах.
VII Подведение итогов урока.
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Классная работа.
Тема урока
К= В
К
Устная работа
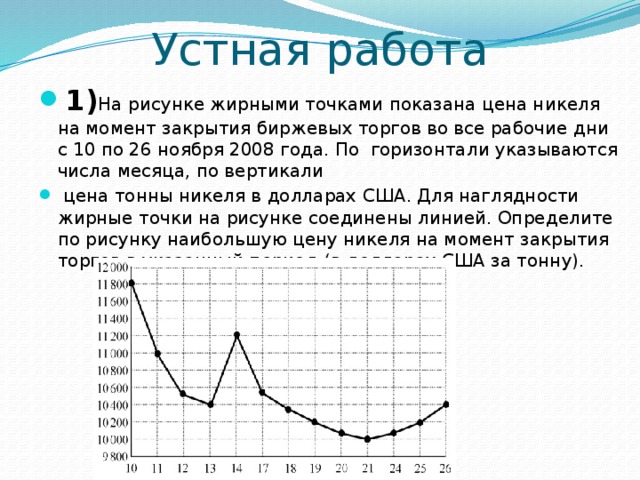
- 1) На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали
- цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену никеля на момент закрытия торгов в указанный период (в долларах США за тонну).
Устная работа
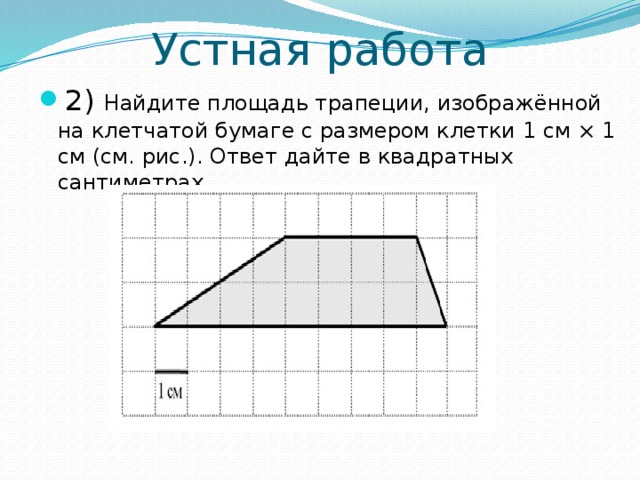
- 2) Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Устная работа
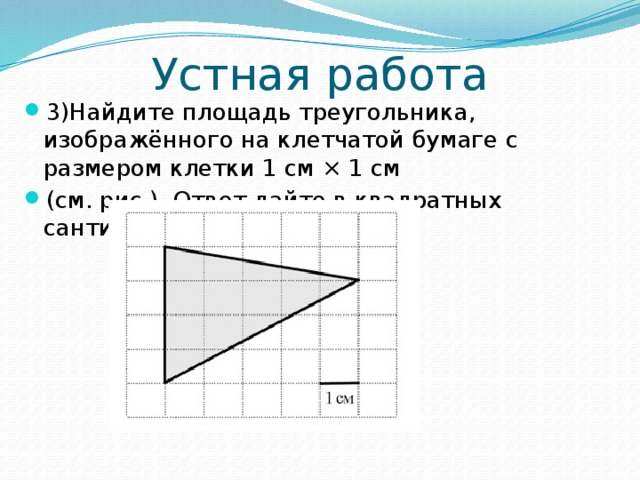
- 3)Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см
- (см. рис.). Ответ дайте в квадратных сантиметрах.
Устная работа
- 4) Найдите корень уравнения
Устная работа
- 5) В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Устная работа
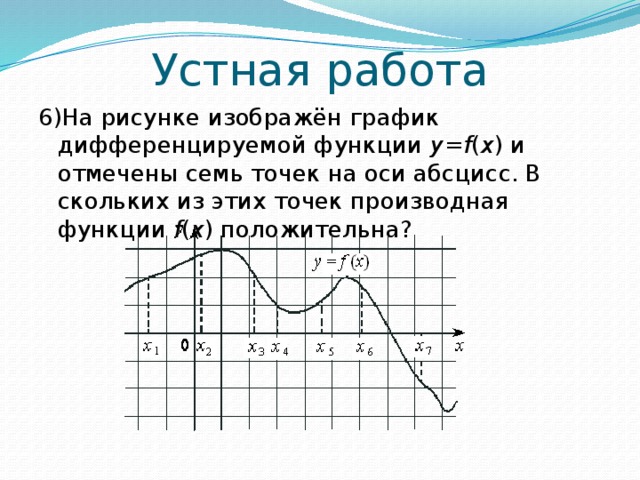
6)На рисунке изображён график дифференцируемой функции y = f ( x ) и отмечены семь точек на оси абсцисс. В скольких из этих точек производная функции f ( x ) положительна?
Устная работа
7) Установите соответствие между величинами и их возможными значениями:к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А)рост ребёнка 1) 32 км
Б)толщина листа бумаги 2) 30 м
В)длина автобусного маршрута 3) 0,2 мм
Г)высота жилого дома 4) 110 см
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
А
Б
В
Г
Устная работа

№ 1
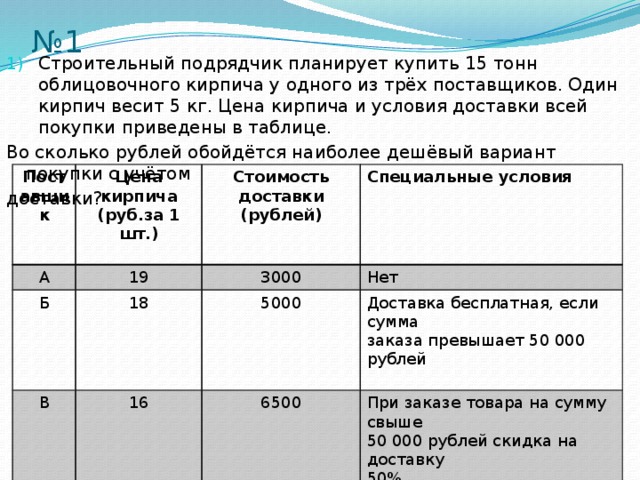
- Строительный подрядчик планирует купить 15 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом
доставки?
Поставщик
А
Цена кирпича
(руб.за 1 шт.)
19
Б
Стоимость
В
Специальные условия
доставки
3000
18
Нет
16
(рублей)
5000
Доставка бесплатная, если сумма
6500
заказа превышает 50 000 рублей
При заказе товара на сумму свыше
50 000 рублей скидка на доставку
50%
№ 2. Найдите sinα , если cosα = — 0,6
и π
№ 3. Найдите корень уравнения
4) Найдите наибольшее значение функции
y =
на отрезке [0; 3].
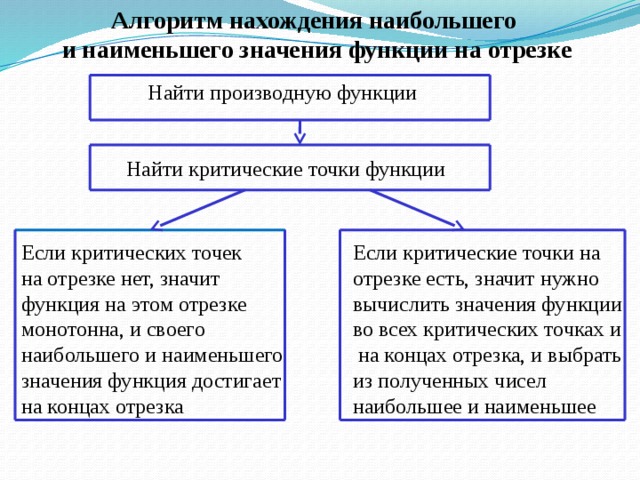
Алгоритм нахождения наибольшего
и наименьшего значения функции на отрезке
Найти производную функции
Найти критические точки функции
Если критических точек
Если критические точки на
на отрезке нет, значит функция на этом отрезке монотонна, и своего наибольшего и наименьшего
отрезке есть, значит нужно
вычислить значения функции
значения функция достигает на концах отрезка
во всех критических точках и
на концах отрезка, и выбрать
из полученных чисел
наибольшее и наименьшее
.
В7**
Найдите корень уравнения
В1***
В столовой пансионата на каждого отдыхающего полагается 400 мл сока вдень. Какое наименьшее число 3-х литровых банок сока необходимо приобрести столовой пансионата на 7 дней, если в пансионате отдыхают 98 человек?
В1*
Оптовая цена учебника составляет 160 рублей. Розничная цена на 35% выше оптовой. Какое наибольшее число учебников можно купить по розничной цене на 8000 рублей?
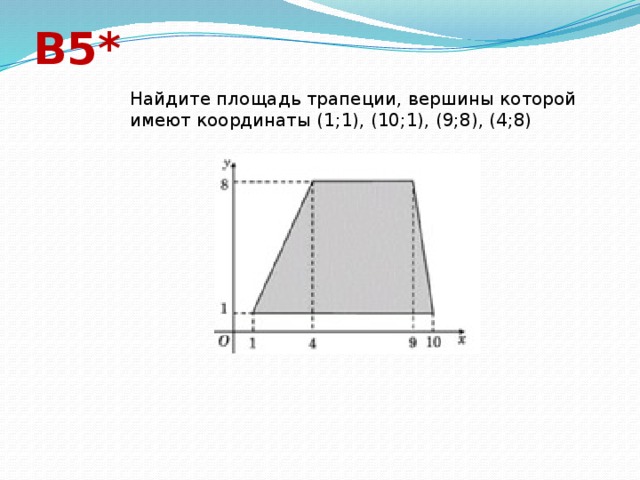
В5*
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;8), (4;8)
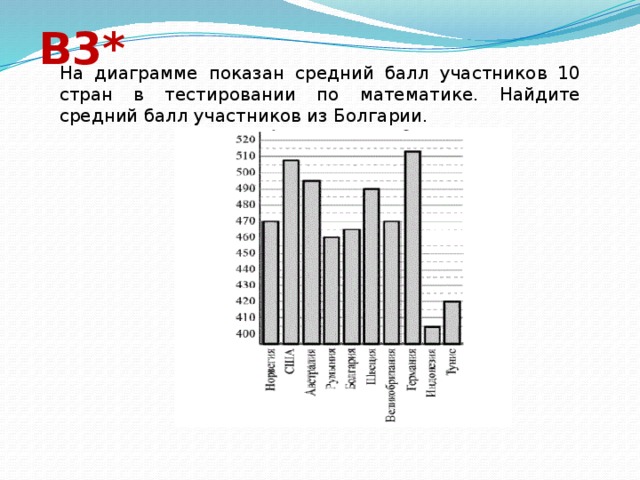
В3*
На диаграмме показан средний балл участников 10 стран в тестировании по математике. Найдите средний балл участников из Болгарии.
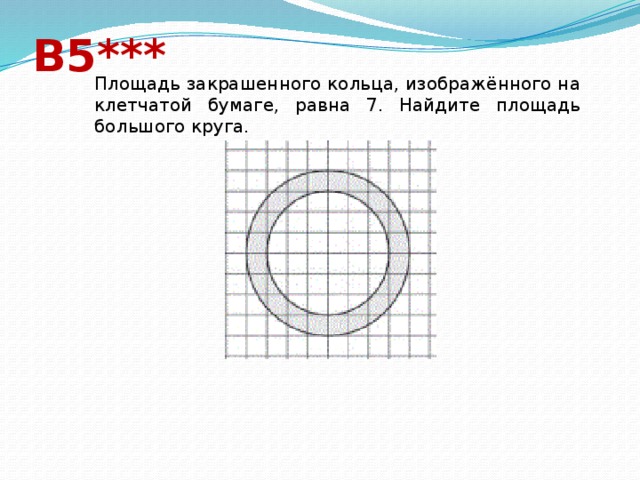
В5***
Площадь закрашенного кольца, изображённого на клетчатой бумаге, равна 7. Найдите площадь большого круга.
Интрнет –ресурсы для подготовки к ЕГЭ
- www.fipi.ru
- http://mathege.ru —
- http://egetrener.ru/
- http://ege-trener.ru/
- uztest.ru
- www.ege.edu.ru
- On-line видеолекции «Консультации по ЕГЭ» по всем предметам.
- Ролики категории ЕГЭ. Лекции по математике
- http://www.alexlarin.narod.ru/ege.html
- http://www.diary.ru/~eek/
- http://4ege.ru/ — ЕГЭ портал, всё последнее к ЕГЭ. Вся информация о егэ . ЕГЭ 2017.
Домашнее задание
Пройти тестирование на сайте alexlarin.net
Желаю успехов на экзаменах!
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
пос. Мизур Алагирского района РСО-Алания
Открытый урок по теме
«Решение заданий ЕГЭ»
Учитель математики Агузарова Л.Д.
п. Мизур
2021г
Тема: Решение заданий ЕГЭ
(задачи с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения, логарифмические неравенства )
Цели занятия:
Образовательные:
-
Повторить материал по данной теме;
Развивающие:
-
Развитие познавательного интереса учащихся к уроку математики;
-
Развитие логического мышления;
-
Развитие скорости и аккуратности;
-
Развитие навыков коллективной работы в сочетании с индивидуальной.
Воспитательные:
-
Воспитание трудолюбия ;
-
Воспитание уважения к окружающим;
Тип урока: урок актуализации знаний и умений (урок повторения).
Ход урока
I. Организационный этап.
Приветствие. Открыли тетради, записали на полях число, классная работа.
I I. Проверка домашней работы
Как у вас обстоят дела с домашней работой? Для того чтобы урок прошел успешно, я должна знать какие затруднения у вас были в домашней работе. Поднимите руки у кого они были.
I I I. Постановка цели и задач урока.
У вас на столах лежат листы, посмотрите на заголовок и попробуйте сформулировать тему нашего урока. «Решение заданий ЕГЭ». Посмотрите на содержание и попробуйте сформулировать цели урока. Сегодня у нас необычный урок, на котором мы будем повторять почти все виды уравнений. Перед вами стоит задача – показать свои знания и умения по решению задач с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения. А так же задание 15 из второй части профильного уровня.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать самостоятельно.
IV. Актуализация знаний
-
Что такое процент? Какие три типа задач на % существуют? (% от числа, целого по части процента, сколько % составляет одна величина от другой)
-
Что такое корень уравнения? Что значить решить уравнение?
V. Повторение
Прототип задания 1 Задания с практическим содержанием
-
Шариковая ручка стоит 30 рублей. Какое наибольшее количество таких ручек можно будет купить на 300 рублей после повышения цены на 25%?
-
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
-
Для приготовления маринада для огурцов на 1 литр воды требуется 10 г лимонной кислоты. Лимонная кислота продается в пакетиках по 15 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 8 литров маринада?
-
В летнем лагере 152 ребенка и 21 воспитатель. Автобус рассчитан не более чем на 30 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Прототип задания 5
Рациональные уравнения
-
=
Показательные уравнения
-
(
)х+4=49
-
2х-3=
-
(0,2)5+4х=125
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде степени с одним и тем же основанием
-
Переходим к линейному уравнению и решаем уравнение.
-
Записываем ответ.
Логарифмические уравнения
-
log3(x+6)=log3(10-x)-1
-
log2(8-x)=2 log2(4+x)
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде логарифма с одним и тем же основанием.
-
Потенцируем и решаем уравнение.
-
Проверяем корни.
-
Записываем ответ.
Иррациональные уравнения
-
√2х-3=х-3
VI. Применение знаний и умений в новой ситуации
Решить рациональное уравнение
(2х-11)2=(2х-1)2
(х-11)4=(х+3)4
Решить логарифмическое неравенство
х2log243(4-x)≤ log3(x2-8x+16)
VII.. Контроль усвоения, обсуждение допущенных ошибок
Самостоятельная работа в парах
Решите уравнения
Вариант 1
Решите уравнение
-
25-х=64
-
42х-17=
-
√4х+16=10
-
log8(x+4)=log8(5x-16)
-
=
Вариант 2
Решите уравнение
-
21-х=32
-
35х-12=
-
√14-5х=3
-
log2(x+3)=log2(3x-15)
-
=
VIII .Домашнее задание варианты 11-14 задания 7
IX. Рефлексия
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
Цель: повторение и закрепление, практическое
применение усвоенных теоретических знаний.
Задачи:
Образовательные:
- Сформировать у учащихся умение использовать
приобретенные знания в практической
деятельности и повседневной жизни; - Отрабатывать навыки решения задач
практического значения, - Отработать навыки решения уравнений различного
типа.
Развивающие:
- Развивать и совершенствовать умения применять
накопленные знания в измененной ситуации, делать
выводы и обобщения.
Воспитательные:
- Подготовка к ЕГЭ, воспитывать настойчивость в
достижении поставленной цели.
Оборудование: мультимедийная установка,
презентация.
Ход занятия
1. Организационный этап.
Задача: подготовить учащихся к работе на
занятии.
2. Вводный этап.
Учитель: Прежде чем вы узнаете тему
сегодняшнего урока, я хотела бы
продемонстрировать вам видео сюжет.http://www.youtube.com/watch?v=NgGGcuB2lrM
(Ученики смотрят фильм о значении витаминов в
жизни людей). Как вы думаете, почему наш урок
начался с этого видеофрагмента?
Ученики отвечают.
Учитель: Действительно, мы заговорили о
витаминах потому, что их названия точно такие же,
как названия заданий на экзамене по математике в
форме ЕГЭ.
Ваша задача на уроке сегодня отработать и
закрепить навыки решения некоторых заданий из
экзаменационного материала. Для этого в
предложенной презентации каждый отвечающий
должен выбрать задание определённого номера
различной сложности и решить его.
3. Основная часть.
Учитель: показывает презентацию “Витаминный
коктейль”.
Ученики:Выбирают задания, щёлкнув мышью в
определённую ячейку таблицы и перейдя по
гиперссылке на соответствующий слайд. Затем
решают эти задания. Чтобы вернуться к номерам
заданий, необходимо навести мышью на название
задания, щёлкнуть на него и вернуться к таблице
заданий.
4. Подведение итогов.
5. Постановка домашнего задания.
Подобрать на сайте www.mathege.ru открытого банка
заданий ЕГЭ по математике заданий В1-В9 и
выполнить не менее 10.
Презентация на тему «Урок-соревнование. Подготовка к ЕГЭ» 11 класс
-
Скачать презентацию (0.43 Мб)
-
522 загрузки -
4.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Презентационная работа по математике, созданная преподавателем в рамках подготовки учащихся к ЕГЭ. Работа включает в себя ряд практических заданий, развивающих мышление и логику. Итогом занятия станет тестирование.
Краткое содержание
- Зарядка для ума
- Практические задания
- Тестирование
-
Формат
pptx (powerpoint)
-
Количество слайдов
18
-
Аудитория
-
Слова
-
Конспект
Отсутствует
-
Предназначение
-
Для проведения урока учителем
-
Содержание
-
-
-
Слайд 3
- ГОЛОС
- ГОЛОС
- ГОЛОС
- ГОЛОС
-
Слайд 4
ГОЛОС В1.
В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?
6
-
Слайд 5
Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
7
-
Слайд 6
Для приготовления вишневого варенья на 1 кг вишни нужно 1,5 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 27 кг вишни?
41
-
Слайд 7
ГОЛОС В2
30 больных перенесли инфаркт (нарушение питания участка сердечной мышцы и его омертвение). Известно, среди них 80% курящих. Сколько человек могли бы быть здоровыми?
24
-
Слайд 8
Средний вес новорожденного ребенка 3 кг 300 грамм. Если у ребенка курящий отец, то его вес будет меньше среднего на 125 г, если курящая мать меньше на 300г. Определите, сколько % теряет в весе новорожденный, если: а)курит папа; б) курит мама? Ответ округлите до единиц.
а) 4
б) 9
-
Слайд 9
Определите, сколько % своего дохода тратит на сигареты человек, выкуривающий одну пачку в сутки, если одна пачка сигарет стоит 50 рублей, ежемесячная зарплата 15000 рублей.
10
-
Слайд 10
ГОЛОС В3
Проект 1
Проект 2
-
Слайд 11
ГОЛОС В6
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая
0,25
-
Слайд 12
В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
0,995
-
Слайд 13
В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Найти вероятность того, что в этом билете не будет вопроса о грибах.
0,92
-
Слайд 14
Катя дважды бросает игральный кубик. В сумме у нее выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.
0,4
-
Слайд 15
Тестирование
В1 В6 В3 В2
-
Слайд 16
Ответы к тестам
В1тВ6 В3 В2
-
Слайд 17
- На уроке я работал активно / пассивно
- Своей работой на уроке я доволен / не доволен
- Урок для меня показался коротким / длинным
- За урок я не устал / устал
- Мое настроение стало лучше / стало хуже
- Материал урока мне был полезен/ бесполезен
- интересен/ скучен
-
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации












Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Решение задач с физическим и практическим содержанием ЕГЭ по математике.
Учитель: Васильева Вадия Фаритовна
Тип урока: формирование новых знаний и их применение.
Межпредметные связи: математика, физика.
Методы работы: кейс-технология.
Тип кейса: обучающий
Цели урока:
1. Подготовка к ЕГЭ. Разработка и составление рекомендаций по решению задач физического и практического содержания №10 профильного уровня ЕГЭ по математике.
2.Развитие исследовательских навыков, умения анализировать, систематизировать, интерпретировать полученные результаты.
3.Повышение интереса учащихся к математике. Расширение кругозора через решение задач связанными с жизненными ситуациями.
Задачи урока:
Образовательные: Систематизировать знания и умения учащихся по решению задач физического и практического содержания.
Развивающие: Развивать умение работать с информацией в нестандартной ситуации; развивать логическое мышление, память, наблюдательность, умение представлять решение; развивать самостоятельную, творческую, исследовательскую деятельность; развивать способность к самооценке.
Воспитательные: Воспитывать уважительное отношение к товарищам, умение работать в команде; умение критически относиться к мнению одноклассников.
Метапредметные УУД:
1.Регулятивные:
1)определять цели, включая постановку новых целей, преобразование практической задачи в познавательную;
2)принимать решения в проблемной ситуации на основе переговоров;
2. Познавательные:
1) учиться основам реализации проектно-исследовательской деятельности;
2) осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
3.Коммуникативные:
1) учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
2)формулировать собственное мнение и позицию, аргументировать и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности;
3)работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации; интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми.
Содержание кейса.
1. Текст «Трудности ЕГЭ»
2. План работы группы.
3. Правила работы с кейсом.
4. Характеристика задания.
5. Задания группам.
6. Лист достижений группы.
7. Домашнее задание.
ХОД УРОКА.
1этап. Постановка проблемы, определение темы и цели урока. (10 мин)
Слово учителя:
-Здравствуйте ребята! Сегодня я хочу начать урок словами Д.Пойа «Если хочешь научиться плавать — смело входи в воду, а если хочешь научиться решать задачи — бери и решай».
-В последнее время вся деятельность на уроке направлена на то, чтобы качественно подготовиться к ЕГЭ. Сегодня мы будем это делать с помощью кейсов, работая в группах. Что это такое вы уже знаете, но я ещё раз напомню. Кейс — это набор документов, направленных на решение задач определённого типа. Работая вместе, вы чётко соблюдаете правила работы в группе (эти правила вы найдёте в кейсе). Чтобы определить тему урока и цель, предлагаю ознакомиться с первым документом кейса.
Один из учеников зачитывает текст из кейса вслух.
Первый документ. Текст «Трудности ЕГЭ»
Усилия практически всех выпускников 11 класса направлены на поступление в любой достаточно престижный ВУЗ. С этой целью они и выбирают сдавать профильный уровень ЕГЭ по математике. В настоящий момент выявилась одна из жестких проблем: как показал обзор источников информации по подготовке к ЕГЭ, зачастую, вместо стандартно сформулированных математических задач, на экзаменах появляются задания, отражающие «какие-то связи» с реальной жизнью. Ситуация усугубляется тем, что встреча с любыми величинами, напоминающими таковые в учебниках физики, приводит некоторых учеников в состояние стойкого оцепенения (ну не получается у них подружиться с физикой). Решая задания с кратким ответом, некоторые ребята сразу узнают своего «противника» — задание №10 с физическим и практическим содержанием. Им сложно оценить величие и различие слов «доход», «прибыль», «выручка», «рейтинг», мелькающих в этих задачах. Более того, там встречаются и худшие монстры: брошенные камни, то вертикально вниз, то вертикально вверх, перегревающиеся приборы, законы излучения звезд и другие не менее «интересные» задачи. Просмотрев учебник математики, мы понимаем, что там нет таких задач. К счастью, у нас много друзей. И почему бы не сосредоточить их интеллектуальные ресурсы во времени и пространстве на выработку каких -то подходов и тактик решения этой проблемы: как одолеть задание №10? Может, кто-то уже его победил? Может у кого-то есть верный способ, как обойти проблему? И как понять, нужно ли вообще волноваться по данному поводу?
Слово учителя:
-Итак, определяем тему урока: (Решение задачи №10 с физическим и прикладным содержанием)
-Какую цель вы сегодня поставите перед собой на уроке? (овладение приёмами решения задачи №10 профильного ЕГЭ по математике, разработка рекомендаций к решению задач этого типа)
-Как вы кратко охарактеризуете эту задачу? (Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства средствами математики).
-Каждой группе нужно разработать и представить на уроке сколько получится, но, желательно, не менее пяти рекомендаций по решению задания № 10 профильного ЕГЭ по математике. Доказать преимущества своих рекомендаций. У каждой группы будет ровно одна задача. На эту работу отводится 10 мин. Если группа справится раньше, представитель сразу выходит на презентацию и защиту решения.
2 этап. Работа над проблемой. (10 мин)
Далее учащиеся сначала самостоятельно изучают содержимое кейса, затем задают уточняющие вопросы, учитель даёт необходимые комментарии.
Второй документ. «План работы группы»
1. Определить руководителя группы, перед которым будет стоять задача координировать работу группы и оценивать работу её участников.
2. Определить секретаря, который будет фиксировать предложенные решения и представителя, который будет защищать эти решения.
3. Внимательно изучить материалы кейса
4. Проанализировать материал и обсудить изученную информацию
5. Обменяться мнениями и составить план работы над задачей
6. Зафиксировать основные и второстепенные проблемы.
7. Работать сообща над проблемой (дискуссия)
8. Выработать решение задачи с оформлением.
9. Представить решение и общие рекомендации по решению задач этого типа.
10. Доказать его оптимальность (чем выгодно это решение).
Третий документ. Правила работы с кейсом в группе.
|
Этапы |
Цель этапа |
|
Знакомство с конкретным случаем |
Понимание проблемной ситуации и ситуации принятия решения |
|
Поиск: оценка информации, полученной из материалов задания, и самостоятельно привлеченной информации |
Научиться добывать информацию, необходимую для поиска решения и оценивать ее |
|
Обсуждение: обсуждение возможностей альтернативных решений |
Развитие альтернативного мышления |
|
Резолюция: нахождение решения в группах |
Сопоставление и оценка вариантов решения. |
|
Диспут: отдельные группы защищают свое решение |
Аргументированная защита решений |
|
Сопоставление итогов: сравнение решений, принятых в группах |
Оценить взаимосвязь интересов, в которых находятся отдельные решения |
Четвёртый документ. Характеристика задания.
Задачи с физическим содержанием
Задачи больше по физике, чем по математике, но необходимые формулы и величины даны в условии. Большинство задач сводится к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства.
Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ (имеются задачи, в которых нужно выбрать одно из двух решений, имеются и другие нюансы).
Есть задачи которые сводятся к решению показательных, логарифмических, тригонометрических уравнений и неравенств. Ответ в любом случае, должен получиться в виде целого числа или конечной десятичной дроби.
На экзамене с этим заданием успешно справляются около 40%.выпускников. Наибольшая трудность в заданиях такого типа – чтение, понимание условия, применение математических знаний. Около 15% участников экзамена просто не взялись за эту технически простую задачу.
На что необходимо обратить внимание:
1.Если в вопросе прозвучало «определить наибольшее значение», «определить наименьшее значение», то задача в большинстве случаев решается через составление неравенства.
2. Правильно определяйте знак при составлении неравенства. Например: b не менее 21 записывается как b≥21.
3. Если в вопросе задачи прозвучало «сколько», то составляется уравнение.
4. Не забывайте про единицы измерения, если это необходимо (переводим метры в сантиметры, наоборот и пр.) Все величины подставлять в одних единицах измерения.
5. Не упускайте из виду, в каких единицах измерения требуется записать ответ (например, решив задачу, вы получили 0,5 часа, в условии сказано записать ответ в минутах, получается 30 минут; если запишите 0,5 – это ошибка и потерянный бал, хотя задача решена, верно).
Пятый документ Задачи для групп.
1 группа
№10 . Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в К) от времени работы: T(t)=T0 +b t+a t2, где t — время (в мин.), T0 =1380 К, a=− 15 К / мин2, b=165 К / мин. Известно, что при температуре нагревательного элемента свыше 1800 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.
2 группа
№10. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1,6+13 t−5 t2, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 6 метров?
3 группа
№10. Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a=9000 км /ч. Скорость v (в км/ч) вычисляется по формуле v=√2la, где l — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 120 км/ч.
4 группа
№10. Груз массой 0,38 кг колеблется на пружине. Его скорость v (в м/с) меняется по закону v=v0sin
в секундах, T=8 с — период колебаний, v0=2 м /с. Кинетическая
энергия E (в Дж) груза вычисляется по формуле E=(mv2)/2, где m — масса груза (в кг), v — скорость груза (в м/с). Найдите кинетическую энергию груза через 7 секунд после начала колебаний. Ответ дайте в джоулях.
5 группа
№10. Независимое агентство намерено ввести рейтинг R новостных изданий на основе показателей информативности In, оперативности Op и объективности Tr публикаций. Каждый отдельный показатель — целое число от 0 до 3. Составители рейтинга считают, что информативность публикаций ценится втрое, а объективность — вчетверо дороже, чем оперативность, то есть R=(3In+Op+4Tr)/A. Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило рейтинг 30.
3 этап. Защита своих идей. (10 мин)
На этом этапе дети в произвольной форме проводят презентацию решений и формулирование рекомендаций. Скорее всего все группы не успеют выступить, поэтому, защита может быть перенесена на следующий урок с последующим фронтальным закреплением.
ПРОЕКТ ПРЕДЛОЖЕНИЙ, как общий вывод, записывается в тетрадь.
4 этап. Подведение итогов (рефлексия) (5 мин)
Подведение итогов проходит в форме пресс-конференции, в ходе которой учащиеся отвечают на вопросы:
• Что общего в представленных заданиях?
• Что отличает группу заданий №10 от других заданий?
• Есть ли такие задачи в наших учебниках?
• Что хотят проверить составители подобных заданий?
• Хватит ли времени решить все задачи открытого банка задач?
• Стоит ли это делать?
• Являются ли задачи с практическим содержанием №10 отражением реальных жизненных ситуаций?
• Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?
• Можете ли вы сами найти информацию для подготовки к ЕГЭ в сети Интернет, полезные ссылки на on-line тестирование? Все ли они помогут при подготовке к экзаменам?
• Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие?
5 этап. Домашнее задание. (в кейсе)
Задания практического содержания №10из открытого банка задач ФИПИ на карточках с полным оформленным решением в тетради.
Приложение
Лист достижений группы № ______
Руководитель группы _______________________________
Секретарь_________________________________________
Участники группы
_________________________________________
_________________________________________
_________________________________________
Количество набранных баллов группы
I этап работы в группе ( поиск, обсуждение, нахождение решений) (от 0 до 5 баллов)
II этап работы в группе (составление рекомендаций по решению) (от 0 до 5 баллов)
III этап (защита решений и представление рекомендаций)
Оценивание работы отметкой каждого участника группы.

























































![4) Найдите наибольшее значение функции y = на отрезке [0; 3].](https://fsd.multiurok.ru/html/2018/01/14/s_5a5b75fea9f71/img12.jpg)





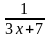 =
=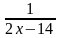
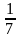 )х+4=49
)х+4=49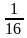
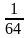
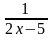 =
=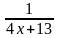
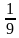
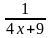 =
=