МАОУ «Свердловская СОШ №2»
План- конспект открытого урока
по математике в 11 Б классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Сушкова Э.А.,
учитель математики
МАОУ «Свердловская СОШ №2»
Апрель 2021 г
https://yandex.ru/efir?stream_id=vIL5MDlVhUGQ&from_block=player_context_menu_yavideo
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
- Систематизировать теоретические знание по теме.
- Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
- перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
- умножение (деление) обеих частей уравнения на отличную от нуля число;
- возведение уравнения в нечетную степень;
- извлечение корня нечетной степени с обеих частей уравнения:
- логарифмирование показательного уравнения;
- применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
- возведение уравнения в четную степень;
- потенцирование логарифмического уравнения;
- освобождение уравнения от знаменателя;
- приведение подобных членов;
- применение формул (тригонометрических, логарифмических и других).
- Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
;
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточек с сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
- Повторить теорию по темам:
- Уравнения-следствия.
- Равносильность уравнений системам.
- Равносильность уравнений на множествах.
VII Подведение итогов урока.
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Классная работа.
Тема урока
К= В
К
Устная работа
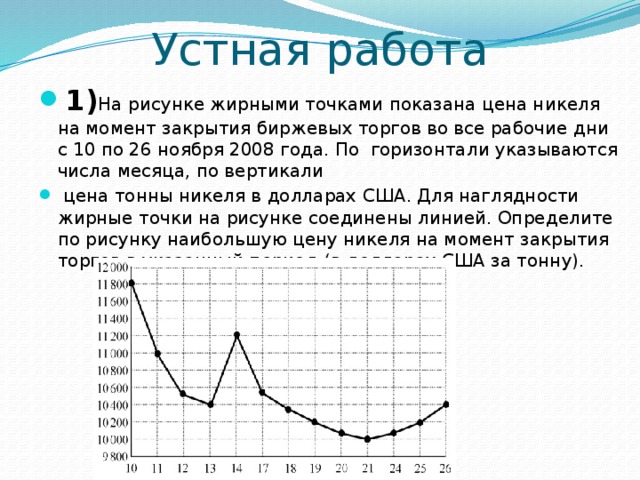
- 1) На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали
- цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену никеля на момент закрытия торгов в указанный период (в долларах США за тонну).
Устная работа
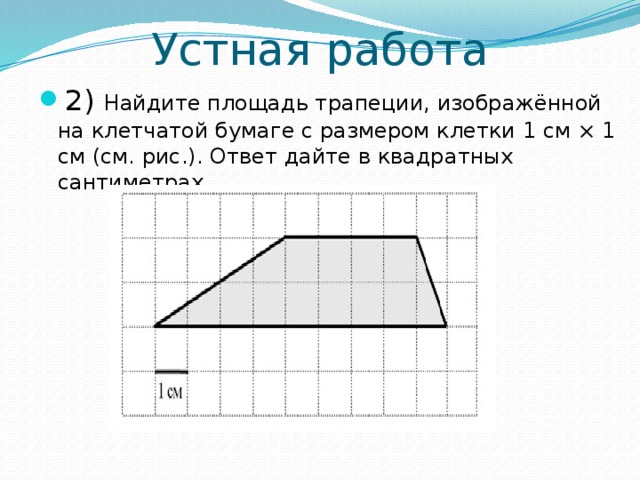
- 2) Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Устная работа
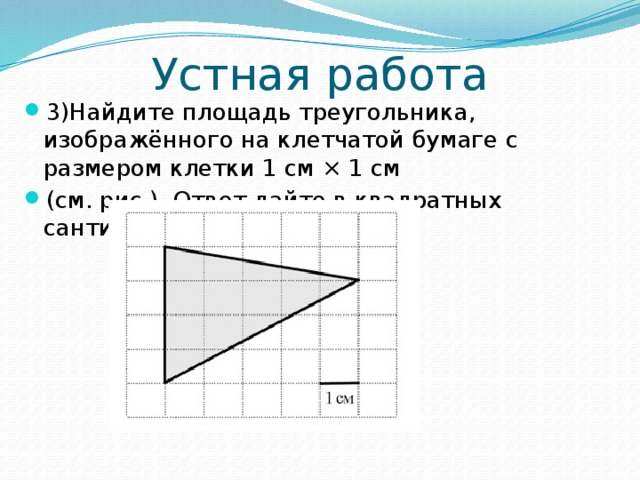
- 3)Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см
- (см. рис.). Ответ дайте в квадратных сантиметрах.
Устная работа
- 4) Найдите корень уравнения
Устная работа
- 5) В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Устная работа
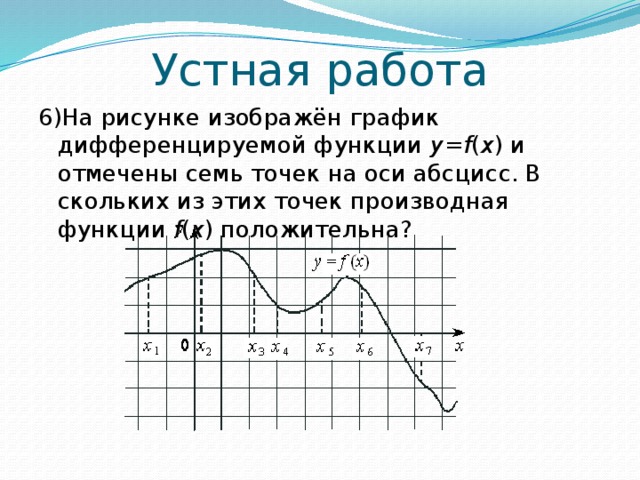
6)На рисунке изображён график дифференцируемой функции y = f ( x ) и отмечены семь точек на оси абсцисс. В скольких из этих точек производная функции f ( x ) положительна?
Устная работа
7) Установите соответствие между величинами и их возможными значениями:к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А)рост ребёнка 1) 32 км
Б)толщина листа бумаги 2) 30 м
В)длина автобусного маршрута 3) 0,2 мм
Г)высота жилого дома 4) 110 см
В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.
А
Б
В
Г
Устная работа

№ 1
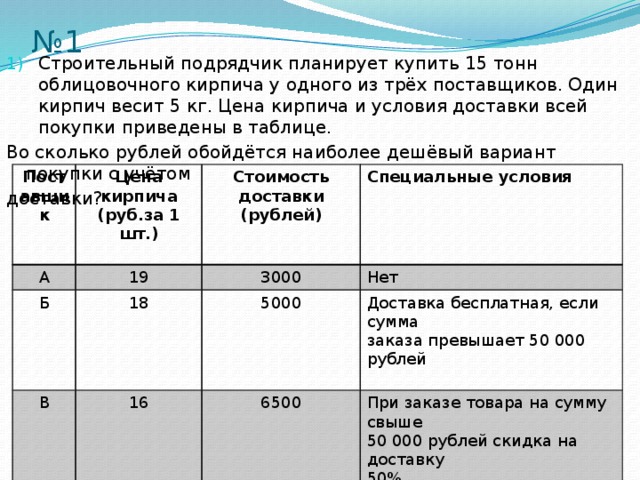
- Строительный подрядчик планирует купить 15 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича и условия доставки всей покупки приведены в таблице.
Во сколько рублей обойдётся наиболее дешёвый вариант покупки с учётом
доставки?
Поставщик
А
Цена кирпича
(руб.за 1 шт.)
19
Б
Стоимость
В
Специальные условия
доставки
3000
18
Нет
16
(рублей)
5000
Доставка бесплатная, если сумма
6500
заказа превышает 50 000 рублей
При заказе товара на сумму свыше
50 000 рублей скидка на доставку
50%
№ 2. Найдите sinα , если cosα = — 0,6
и π
№ 3. Найдите корень уравнения
4) Найдите наибольшее значение функции
y =
на отрезке [0; 3].
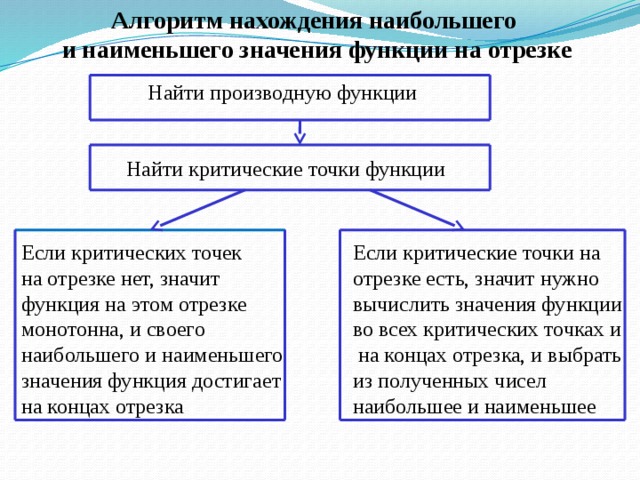
Алгоритм нахождения наибольшего
и наименьшего значения функции на отрезке
Найти производную функции
Найти критические точки функции
Если критических точек
Если критические точки на
на отрезке нет, значит функция на этом отрезке монотонна, и своего наибольшего и наименьшего
отрезке есть, значит нужно
вычислить значения функции
значения функция достигает на концах отрезка
во всех критических точках и
на концах отрезка, и выбрать
из полученных чисел
наибольшее и наименьшее
.
В7**
Найдите корень уравнения
В1***
В столовой пансионата на каждого отдыхающего полагается 400 мл сока вдень. Какое наименьшее число 3-х литровых банок сока необходимо приобрести столовой пансионата на 7 дней, если в пансионате отдыхают 98 человек?
В1*
Оптовая цена учебника составляет 160 рублей. Розничная цена на 35% выше оптовой. Какое наибольшее число учебников можно купить по розничной цене на 8000 рублей?
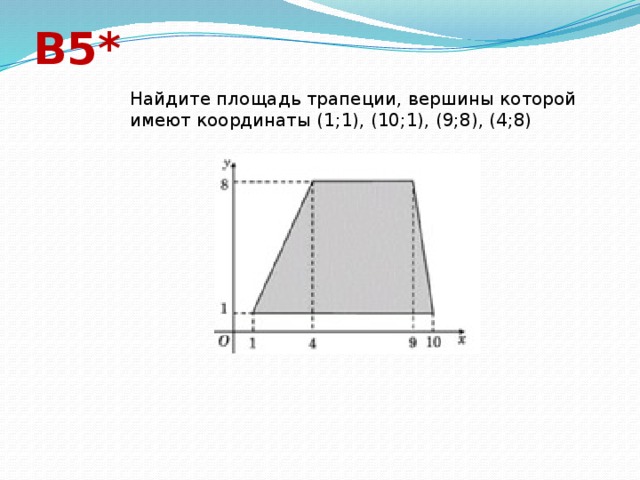
В5*
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;8), (4;8)
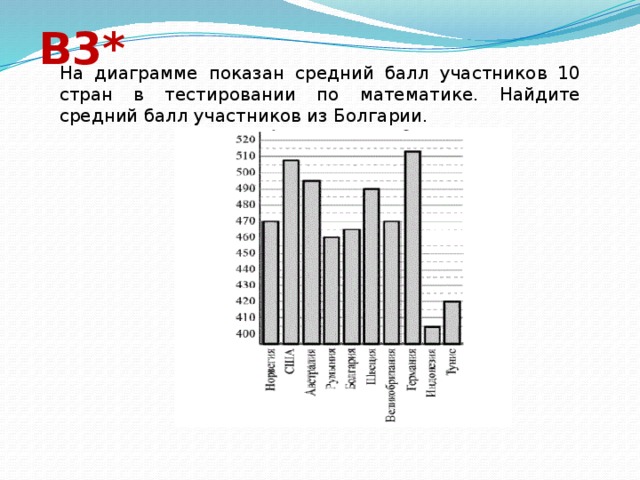
В3*
На диаграмме показан средний балл участников 10 стран в тестировании по математике. Найдите средний балл участников из Болгарии.
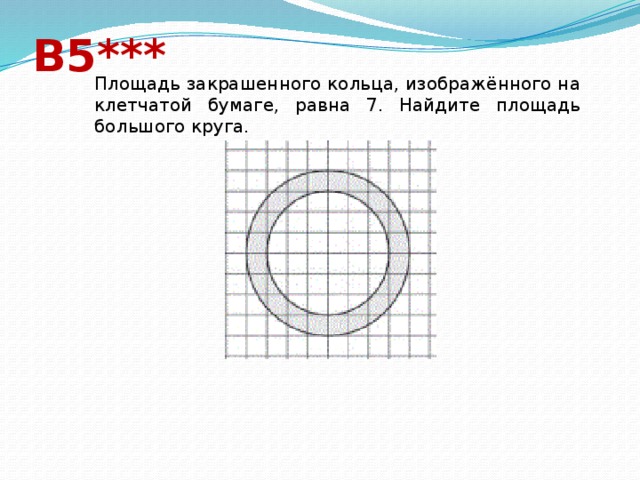
В5***
Площадь закрашенного кольца, изображённого на клетчатой бумаге, равна 7. Найдите площадь большого круга.
Интрнет –ресурсы для подготовки к ЕГЭ
- www.fipi.ru
- http://mathege.ru —
- http://egetrener.ru/
- http://ege-trener.ru/
- uztest.ru
- www.ege.edu.ru
- On-line видеолекции «Консультации по ЕГЭ» по всем предметам.
- Ролики категории ЕГЭ. Лекции по математике
- http://www.alexlarin.narod.ru/ege.html
- http://www.diary.ru/~eek/
- http://4ege.ru/ — ЕГЭ портал, всё последнее к ЕГЭ. Вся информация о егэ . ЕГЭ 2017.
Домашнее задание
Пройти тестирование на сайте alexlarin.net
Желаю успехов на экзаменах!
Цель: повторение и закрепление, практическое
применение усвоенных теоретических знаний.
Задачи:
Образовательные:
- Сформировать у учащихся умение использовать
приобретенные знания в практической
деятельности и повседневной жизни; - Отрабатывать навыки решения задач
практического значения, - Отработать навыки решения уравнений различного
типа.
Развивающие:
- Развивать и совершенствовать умения применять
накопленные знания в измененной ситуации, делать
выводы и обобщения.
Воспитательные:
- Подготовка к ЕГЭ, воспитывать настойчивость в
достижении поставленной цели.
Оборудование: мультимедийная установка,
презентация.
Ход занятия
1. Организационный этап.
Задача: подготовить учащихся к работе на
занятии.
2. Вводный этап.
Учитель: Прежде чем вы узнаете тему
сегодняшнего урока, я хотела бы
продемонстрировать вам видео сюжет.http://www.youtube.com/watch?v=NgGGcuB2lrM
(Ученики смотрят фильм о значении витаминов в
жизни людей). Как вы думаете, почему наш урок
начался с этого видеофрагмента?
Ученики отвечают.
Учитель: Действительно, мы заговорили о
витаминах потому, что их названия точно такие же,
как названия заданий на экзамене по математике в
форме ЕГЭ.
Ваша задача на уроке сегодня отработать и
закрепить навыки решения некоторых заданий из
экзаменационного материала. Для этого в
предложенной презентации каждый отвечающий
должен выбрать задание определённого номера
различной сложности и решить его.
3. Основная часть.
Учитель: показывает презентацию “Витаминный
коктейль”.
Ученики:Выбирают задания, щёлкнув мышью в
определённую ячейку таблицы и перейдя по
гиперссылке на соответствующий слайд. Затем
решают эти задания. Чтобы вернуться к номерам
заданий, необходимо навести мышью на название
задания, щёлкнуть на него и вернуться к таблице
заданий.
4. Подведение итогов.
5. Постановка домашнего задания.
Подобрать на сайте www.mathege.ru открытого банка
заданий ЕГЭ по математике заданий В1-В9 и
выполнить не менее 10.
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
пос. Мизур Алагирского района РСО-Алания
Открытый урок по теме
«Решение заданий ЕГЭ»
Учитель математики Агузарова Л.Д.
п. Мизур
2021г
Тема: Решение заданий ЕГЭ
(задачи с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения, логарифмические неравенства )
Цели занятия:
Образовательные:
-
Повторить материал по данной теме;
Развивающие:
-
Развитие познавательного интереса учащихся к уроку математики;
-
Развитие логического мышления;
-
Развитие скорости и аккуратности;
-
Развитие навыков коллективной работы в сочетании с индивидуальной.
Воспитательные:
-
Воспитание трудолюбия ;
-
Воспитание уважения к окружающим;
Тип урока: урок актуализации знаний и умений (урок повторения).
Ход урока
I. Организационный этап.
Приветствие. Открыли тетради, записали на полях число, классная работа.
I I. Проверка домашней работы
Как у вас обстоят дела с домашней работой? Для того чтобы урок прошел успешно, я должна знать какие затруднения у вас были в домашней работе. Поднимите руки у кого они были.
I I I. Постановка цели и задач урока.
У вас на столах лежат листы, посмотрите на заголовок и попробуйте сформулировать тему нашего урока. «Решение заданий ЕГЭ». Посмотрите на содержание и попробуйте сформулировать цели урока. Сегодня у нас необычный урок, на котором мы будем повторять почти все виды уравнений. Перед вами стоит задача – показать свои знания и умения по решению задач с практическим содержанием, рациональные, показательные, логарифмические, иррациональные уравнения. А так же задание 15 из второй части профильного уровня.
Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сегодня работать самостоятельно.
IV. Актуализация знаний
-
Что такое процент? Какие три типа задач на % существуют? (% от числа, целого по части процента, сколько % составляет одна величина от другой)
-
Что такое корень уравнения? Что значить решить уравнение?
V. Повторение
Прототип задания 1 Задания с практическим содержанием
-
Шариковая ручка стоит 30 рублей. Какое наибольшее количество таких ручек можно будет купить на 300 рублей после повышения цены на 25%?
-
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
-
Для приготовления маринада для огурцов на 1 литр воды требуется 10 г лимонной кислоты. Лимонная кислота продается в пакетиках по 15 г. Какое наименьшее число пачек нужно купить хозяйке для приготовления 8 литров маринада?
-
В летнем лагере 152 ребенка и 21 воспитатель. Автобус рассчитан не более чем на 30 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
Прототип задания 5
Рациональные уравнения
-
=
Показательные уравнения
-
(
)х+4=49
-
2х-3=
-
(0,2)5+4х=125
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде степени с одним и тем же основанием
-
Переходим к линейному уравнению и решаем уравнение.
-
Записываем ответ.
Логарифмические уравнения
-
log3(x+6)=log3(10-x)-1
-
log2(8-x)=2 log2(4+x)
Алгоритм решения задания:
-
Определяем вид уравнения.
-
Представляем правую часть в виде логарифма с одним и тем же основанием.
-
Потенцируем и решаем уравнение.
-
Проверяем корни.
-
Записываем ответ.
Иррациональные уравнения
-
√2х-3=х-3
VI. Применение знаний и умений в новой ситуации
Решить рациональное уравнение
(2х-11)2=(2х-1)2
(х-11)4=(х+3)4
Решить логарифмическое неравенство
х2log243(4-x)≤ log3(x2-8x+16)
VII.. Контроль усвоения, обсуждение допущенных ошибок
Самостоятельная работа в парах
Решите уравнения
Вариант 1
Решите уравнение
-
25-х=64
-
42х-17=
-
√4х+16=10
-
log8(x+4)=log8(5x-16)
-
=
Вариант 2
Решите уравнение
-
21-х=32
-
35х-12=
-
√14-5х=3
-
log2(x+3)=log2(3x-15)
-
=
VIII .Домашнее задание варианты 11-14 задания 7
IX. Рефлексия
Продолжи предложение
Сегодня на уроке я научился…
Сегодня на уроке мне понравилось…
Сегодня на уроке я повторил…
Сегодня на уроке я закрепил…
19.12.2022
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
1. Систематизировать теоретические знание по теме.
2. Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперь приступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знак
Оценить
124
Содержимое разработки
МБОУ СОШ №1 с. Кизляр
План- конспект открытого урока
по математике в 11 классе
«Подготовка к ЕГЭ. Решение сложных комбинированных уравнений»
Урок разработала и провела:
Магометова Х. Н.,
учитель математики
МБОУ СОШ №1 с. Кизляр
Апрель 2021 г
Тип урока: семинарское занятие.
Цели урока:
Познавательные: повторить и обобщить изученный за курс средней школы материал по математике, закрепить навыки решения сложных уравнений различными методами.
Развивающие: развивать ключевые коммуникативные компетенции, речь, внимание, память, логическое мышление, умение обобщать, делать выводы, развивать навыки самоконтроля и творческие способности учащихся.
Воспитательные: совершенствовать навыки этичного межличностного общения, сознательное отношение к математике; активизировать познавательную деятельность в коллективе, формировать навыки сотрудничества в решении поисковых задач, воспитывать у учащихся морально-ценностные чувства.
Задачи урока:
-
Систематизировать теоретические знание по теме.
-
Развивать умение работать с заданиями ЕГЭ.
Совершенствовать навыки решения сложных уравнений различными методами.
Ход урока:
I Организационный момент:
а) готовность класса к уроку;
б Слово учителя: Ребята, сегодня у нас необычный урок. Мы проверим наши знания, уровень нашей подготовки к сдаче ЕГЭ. И я хочу начать сегодняшний урок с притчи.
— Учитель, я уже целый год живу у тебя, но до сих пор выполняю только работы по хозяйству. Когда ты будешь меня учить? Разве я для этого пришёл к тебе в ученики, скажи?
— Имей терпение, — ответил учитель, — ещё не пришло время. Иди в нижнюю долину и посади дерево, вырасти его, а я подумаю.
Долгий и тяжёлый путь проделал ученик, пока спустился в долину. По дороге он выкопал маленький саженец и посадил его. С той поры, дважды в день он проходил опасный путь, между хижиной и долиной, чтобы полить деревце. Изо дня в день, он присматривал за деревом. Так прошёл год. Усилия его не пропали даром. Дерево выросло высоким и крепким. Однажды на рассвете, он вышел из хижины и увидел своего учителя, сидящего у ручья под деревом.
— Учитель! – обрадовался юноша. – Как я счастлив вновь увидеть тебя! Я должен извиниться перед тобой, что не смог стать твоим учеником, обманув твоё доверие! Ты подумал, что я слаб, когда я остался жить в долине. Но я должен был заботиться о своём деревеИ теперь, ты вряд ли возьмёшь меня обратно…
Выслушав пылкую речь юноши, старик сказал ему: — Именно в этот год, ты вместе с деревом взращивал такие качества своего характера, которые тебе помогут постигать знания.
Твоё дерево говорит о твоей готовности. Посмотри!
Ответственность ты имел, но только по необходимости, Был нетерпелив и эмоционален, как переплетенные побеги саженца. Чтобы обрести знания, нужна, прежде всего, дисциплина.
Ибо корни дерева – твоя ответственность,
ствол дерева – твоё терпение,
ветви дерева – спокойствие,
а листья – знания!
И вам я желаю такого же упорства и терпения, чтобы хорошо подготовиться к ЕГЭ и успешно его сдать.
А теперьприступим к выполнению заданий.
Проверка дз.
Дать определение уравнения и его корня, равносильности двух уравнений.
Ответ:
Арифметическое выражение, содержащее неизвестную переменную и знаки равенства называют уравнением. Значение переменной, превращающее уравнение в верное равенство, называют корнем уравнения. Два уравнения называют равносильными, если любой корень первого уравнения является корнем второго уравнения и любой корень второго уравнения является корнем первого уравнения.
Дать определение равносильности преобразования уравнения и перечислить основные равносильные преобразования.
Ответ:
Замену одного уравнения другим, равносильным ему уравнением называют равносильным преобразованием уравнения.
Равносильными преобразованиями уравнения являются:
-
перенос члена уравнения с противоположным знаком из одной части уравнения в другую;
-
умножение (деление) обеих частей уравнения на отличную от нуля число;
-
возведение уравнения в нечетную степень;
-
извлечение корня нечетной степени с обеих частей уравнения:
-
логарифмирование показательного уравнения;
-
применение тождеств, т. е равенств, справедливых для любого числа.
Рассказать, какие равносильные преобразования нужно выполнить, чтобы решить следующие уравнения

Дайте определение уравнения – следствия и перечислите преобразования, приводящие к уравнению следствия.
Ответ:
Пусть даны два уравнения. Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют уравнением- следствием первого.
Замену уравнения другим уравнением, которое является его следствием, называют переходом к уравнению- следствию.
При переходе к уравнению- следствия возможно появление лишних корней, посторонних для исходного уравнения, поэтому проверка полученных корней является обязательной частью решения уравнения.
Преобразованиями, приводящими к уравнению- следствия является:
-
возведение уравнения в четную степень;
-
потенцирование логарифмического уравнения;
-
освобождение уравнения от знаменателя;
-
приведение подобных членов;
-
применение формул (тригонометрических, логарифмических и других).
-
Расскажите, каким способом приводится следующие уравнения к уравнению – следствия.



Карточки имеются у каждого ученика на парте.
Сложные уравнения можно решить, приводя их к системам. Правила перехода от уравнений к равносильным системам:
1.
2.
3.
4.
5.
6.
7.
М-область существования
8.
9.
10.
11.
Работа в группах.
Запишите системы, равносильные уравнениям. (Работы выполняют на листочках)..
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Очень часто можно встретить уравнение, которое имеет дополнительное условие, например:
Как можно упростить решение такого типа уравнения?
Разбор решения на доске.
Ответ:
Учитывая, что левая часть уравнения неотрицательное число получаем 




Самыми сложными считаются уравнения с параметром. Дайте определение уравнения с параметром. Давайте рассмотрим несколько таких уравнений с использованием свойств функций:
а)

Ответ:
Для каждого значения a рассмотрим функцию
Она определена на множестве R, четная, поэтому, если 

Уравнение (1) имеет три корня тогда и только тогда, когда оно имеет 

При 

При 


Видеоурок.
Максимум за выполнение данного задания(18 задание) можно получить 4 балла.
В задачах с параметром допускают весьма разнообразные способы решений. Наиболее распространенными из них являются;
Чисто алгебраический способ решения;
-способ решения,основанный на построении и исследовании геометрической модели данной задачи;
-функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Критерии оценивания:
|
Обоснованно получен верный ответ |
4 балла |
|
|
С помощью верного рассуждения получены оба верных значения параметра, но -или в ответ включены и одно-два неверных значения; -или решение недостаточно обосновано. |
3 балла |
|
|
С помощью верного рассуждения получено хотя бы одно верное значение параметра |
2 балла |
|
|
Задача сведена к исследованию: -или взаимного расположения трех окружносей; -или двух квадратных уравнений с параметром. |
1 балл |
|
|
Решение не соответствует ни одному из критериев, перечисленных выше |
О баллов |
Выполнения тренировочных упражнений на закрепление навыков и умений решать уравнения.
-
-
;
-
VI Домашнее задание:
Разбор заданий типа С с индивидуальных карточекс сайта www.ege.edu.ru Банк заданий на доске.
Карточка №1
С1.(В13)
Карточка №2
C1.(B1)
Карточка №3
C1.(B12)
Карточка №4
C1.(B19)
Карточка №5
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка №6
С5. Найти все значения a, такие, что уравнение имеет единственное решение:
Карточка № 7
Найти наибольший корень уравнения:

Карточка № 8
Найти значение р, при которых уравнение

Карточка №9
Решить уравнение
-
Повторить теорию по темам:
-
Уравнения-следствия.
-
Равносильность уравнений системам.
-
Равносильность уравнений на множествах.
VII Подведение итогов урока.
-
Оцените вашу работу на уроке.
Сколько баллов вы набрали?
К какому выводу пришли?
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Лист самооценки работы учащегося
———————————————————————————(Ф.И. учащегося)
———————————————————————————(тема урока)
|
Мой вклад… |
Баллы |
|||
|
1(плохо) |
2(слабо) |
3(хорошо) |
4(отлично) |
|
|
В поисках материала по теме |
||||
|
В теоретическом изучении материала |
||||
|
В решении примеров |
||||
|
В групповой работе |
||||
|
В защите работ, анализе решений |
Перевод баллов:
0-9 баллов-2
10-13 баллов-3
14-16 баллов-4
15-20 баллов-5
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/518910-plankonspekt-otkrytogo-uroka-po-matematike-v

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!
Работа учителя математики
высшей квалификационной категории
МАОУ «Гимназия №23»
г.Троицка Челябинской области
Русиной Анны Николаевны.
Открытый урок математики в
11классе(80минут).
Тема урока: Решение текстовых экзаменационных задач.
Тип урока: Повторительно-обобщающий урок.
Цели урока:
Обучающие: закрепить умения и навыки применения ранее полученных
знаний при решении текстовых задач в выполнении заданий ЕГЭ разного уровня
сложности, стимулировать учащихся к овладению рациональными приемами и методами
решения текстовых задач.
Развивающие: развивать мышление , вычислительные навыки,
продолжать формировать грамотную математическую речь.
Воспитательные: воспитывать внимание, познавательную активность,
формировать положительную мотивацию к учению.
Ход урока.
1.Организационный момент.(3мин)
Приветствие учеников,
сообщение темы, целей урока.
2. Актуализация темы.(4мин)
Ребята, какие типы текстовых
задач вы знаете?
Какие основные величины
характеризуют тот или иной тип задачи?
Итак:
1тип: Задачи на движение.
а) движение навстречу друг
другу, движение в одном направлении, движение в противоположных направлениях;
б) движение по воде: по
течению реки, против течения, по озеру.
2 тип :Задачи на
проценты.
а) товар и его стоимость,
повышение и понижение стоимости;
б) суммы вкладов в банки и
банковские процентные ставки ( увеличение или уменьшение процентных ставок);
3 тип: Задачи « на
работу», где основными величинами
являются – время, объем совершенной работы, производительность труда.
3. Решение текстовых
задач. (40мин)
I. Рассмотрим
решение задач 1 типа.
Задача №1.
Из Челябинска в Троицк
выехали два автомобиля. Первый проехал весь путь с постоянной скоростью. Второй
автомобиль проехал половину пути со скоростью, на 14км/ч меньше скорости
первого автомобиля, а оставшийся путь со скоростью, на 22км/ч большей скорости
первого автомобиля. В конечный путь оба автомобиля прибыли одновременно.
Определите скорость первого автомобиля.(Ответ дайте в км/ч).
Устные рассуждения и
решение.
Возьмем в качестве
неизвестной величины именно то, что необходимо найти в условии задачи.
Обозначим, например за 2 – длину всего пути (т.к.речь в задаче идет о половинах,
то целесообразно, чтобы половины были целыми числами).
Пусть х км/ч – скорость
первого автомобиля, тогда ( х-14) км/ч — скорость
второго автомобиля. Первый
автомобиль затратит на весь путь часов.
Второй первую половину пути
проедет за часов, а вторую —
часов.
Так как на весь путь
автомобили затратили одинаковое время, то получим уравнение:
=
+
.
Решение дробного
рационального уравнения сведется к решению равносильного линейного уравнения,
которое имеет единственный корень
х = 77.
Ответ: 77км/ч скорость
первого автомобиля.
А теперь решите задачу на
движение самостоятельно.
Задача №2.
Города А,В и С соединены
прямолинейным шоссе, причем город В расположен между городами А и С. Из города
А в сторону города С выехал легковой автомобиль , и одновременно с ним из
города В в сторону города С выехал грузовик. Через сколько часов после выезда
легковой автомобиль догонит грузовик, если скорость легкового автомобиля на
20км/ч больше скорости грузовика, а расстояние между городами А и В равно 60км.
(Ответ: через 3 часа).
Ребята объясняют решение
задачи.
II. Рассмотрим решение задач второго типа.
Задача №3.
Клиент взял в банке кредит
в размере 200000рублей с годовой процентной ставкой 26 %.Он должен погашать
кредит, внося в банк ежемесячно одинаковую сумму денег, чтобы через 5 лет
выплатить всю сумму, взятую в банке, вместе с процентами. Сколько рублей он
должен вносить в банк ежемесячно?
Устные рассуждения и
решение.
Необходимо узнать какую сумму
денег должен вернуть клиент банку.
1) 100 % + 26 % = 126
%(должен вернуть клиент в процентах).
2) 126 %=1,26 ( перевели
проценты в число)
200000 × 1,26 = 252000 рублей должен вернуть клиент через 5
лет.
3) Так как 5 лет = 60 мес.,
то 252000 : 60 = 4200 рублей будет возвращать клиент банку ежемесячно.
Ответ: 4200рублей.
А теперь решите следующую
задачу самостоятельно.
Задача №4.
Куртка стоила 2100 рублей.
После уценки она стала стоить 1365 рублей. На сколько процентов была снижена
цена куртки ?
(Ответ: на 35 %)
Ребята объясняют решение
задачи.
III. Рассмотрим
решение задач третьего типа.
Задача №5.
Два маляра работая вместе,
могут за 1 час покрасить стену площадью 40м2.
Первый маляр, работая
отдельно, может покрасить 50м2 стены на 4 часа быстрее, чем второй
покрасит 90м2 такой же стены. За сколько часов первый маляр сможет
покрасить 100м2 стены ?
Устные рассуждения и
решение.
Такие задачи удобно решать
с помощью таблиц.
Пусть первый маляр покрасит
х (м2) стены за 1 час, а второй маляр – у (м2).
По смыслу задачи х > 0, у > 0. Составим таблицу:
|
Норма ( |
Время (ч) |
Площадь (м2) |
|
|
1 маляр |
х |
1 |
х |
|
2 маляр |
у |
1 |
у |
Два маляра, работая вместе,
за 1 час покрасят 40м2 стены, т.е. х + у = 40
|
Норма ( |
Время (ч) |
Площадь (м2) |
|
|
1 маляр |
х |
|
50 |
|
2 маляр |
у |
|
90 |
По условию задачи, первый
маляр, работая отдельно, может покрасить 50м2 стены на 4 часа
быстрее, чем второй покрасит 90м2 такой же стены, т.е.
—
= 4.
Составим систему уравнений:
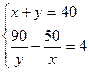
Решим систему способом
подстановки: у = 40 – х, получим : —
= 4.
Решение этого дробного
рационального уравнения сводится к решению квадратного уравнения: х2
— 50х – 500 = 0, корни которого х = 25, х = — 20.
Так как х > 0, то х = 25(м2) покрасит первый маляр за 1 час.
Тогда 100м2 первый
маляр покрасит за 100 : 25 = 4часа.
Ответ: за 4часа первый маляр покрасит100м2 стены.
Решите задачу самостоятельно.
Задача №6.
Два штукатура, выполняя
вместе работу, смогут закончить ее за 6 дней. Сколько времени понадобится для
выполнения всего задания первому из них, если второму для этого требуется на 5
дней меньше.
( Ответ:15 дней.)
Ребята объясняют решение
задачи.
Мы разобрали три типа
текстовых задач, а теперь выполните самостоятельную работу. Удачи.
IV Самостоятельная работа (26мин)
Вариант 1.
1. Два велосипедиста
одновременно отправились в 153-километровый пробег. Первый ехал со скоростью,
на 8км/ч большей, чем скорость второго, и прибыл к финишу на 8 часов раньше
второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
2. Тюбик с краской стоит 200
рублей. Какое наибольшее число тюбиков можно купить на 800 рублей во время
распродажи, если скидка составляет 35%.
3. На изготовление 20 деталей
первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 60
таких же деталей. Известно, что первый рабочий за час делает на 4 детали
больше, чем второй. Сколько деталей в час делает второй рабочий?
Вариант2.
1. Расстояние между
пристанями А и В равно 48км. Отчалив от пристани А в 10 часов утра, теплоход
проплыл по течению реки с постоянной скоростью до пристани В.После трехчасовой
стоянки у пристани В теплоход отправился в обратный рейс и прибыл в А в тот же
день в 22.00. Найдите скорость теплохода в неподвижной воде, если скорость
течения реки 4км/ч.
2. После повышения цены на
15% пылесос стал стоить 3082рубля. Сколько рублей стоил пылесос до повышения
цены?
3. На изготовление 48 деталей
первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96
таких же деталей. Известно, что первый рабочий за час делает на 4 детали
больше, чем второй. Сколько деталей в час делает второй рабочий?
V. Домашнее задание(3мин)
Учитель поясняет задание,
обращает внимание на то, что к выполнению домашнего задания нужно подойти
творчески, применяя навыки, полученные на уроке.( Задачи отправляю в
электронные дневники, прикрепляя файл)
Задача №1.
Цена холодильника в
магазине ежегодно уменьшается на одно и то же число процентов от предыдущей
цены. Определите на сколько процентов каждый год уменьшалась цена холодильника,
если выставленный на продажу за 8000 рублей, он через 2 года был продан за
6480рублей?
Задача №2.
Теплоход, скорость которого
в неподвижной воде равна 20км/ч, проходит по течению реки до пункта назначения
и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное
теплоходом за весь рейс, если скорость течения равна 4км/ч, стоянка длится 3
часа, а в исходный пункт теплоход возвращается через 13 часов после отплытия из
него.
Задача №3.
Каждый из двух рабочих
одинаковой квалификации может выполнить заказ за 15часов. Через 5 часов после
того, как один из них приступил к выполнению заказа, к нему присоединился
второй рабочий, и работу над заказом они довели до конца уже вместе. За сколько
часов был выполнен заказ?
VI. Подведение итогов урока.(4мин)
(Учитель комментирует работу
класса, выставляет оценки за урок).
Сегодня на уроке мы разобрали
3 типа текстовых задач. На экзамене вы должны применить свои умения и навыки и
применять их в каждой конкретной ситуации, выбирать для решения любой способ. А
урок мне хочется закончить словами:
Что есть больше всего на
свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого.
Фалес.
Желаю вам достичь желаемого.
Спасибо за урок, за
сотрудничество. Успехов!
Приложение1(классная работа, раздаточный материал)
Задача №1.
Из Челябинска в Троицк
выехали два автомобиля. Первый проехал весь путь с постоянной скоростью. Второй
автомобиль проехал половину пути со скоростью, на 14км/ч меньше скорости
первого автомобиля, а оставшийся путь со скоростью, на 22км/ч большей скорости
первого автомобиля. В конечный путь оба автомобиля прибыли одновременно.
Определите скорость первого автомобиля.(Ответ дайте в км/ч).
Задача №2.
Города А,В и С соединены
прямолинейным шоссе, причем город В расположен между городами А и С. Из города
А в сторону города С выехал легковой автомобиль , и одновременно с ним из
города В в сторону города С выехал грузовик. Через сколько часов после выезда
легковой автомобиль догонит грузовик, если скорость легкового автомобиля на
20км/ч больше скорости грузовика, а расстояние между городами А и В равно 60км.
Задача №3.
Клиент взял в банке кредит
в размере 200000рублей с годовой процентной ставкой 26 %.Он должен погашать
кредит, внося в банк ежемесячно одинаковую сумму денег, чтобы через 5 лет
выплатить всю сумму, взятую в банке, вместе с процентами. Сколько рублей он
должен вносить в банк ежемесячно?
Задача №4.
Куртка стоила 2100 рублей.
После уценки она стала стоить 1365 рублей. На сколько процентов была снижена
цена куртки ?
Задача №5.
Два маляра работая вместе,
могут за 1 час покрасить стену площадью 40м2.
Первый маляр, работая
отдельно, может покрасить 50м2 стены на 4 часа быстрее, чем второй
покрасит 90м2 такой же стены. За сколько часов первый маляр сможет
покрасить 100м2 стены ?
Задача №6.
Два штукатура, выполняя
вместе работу, смогут закончить ее за 6 дней. Сколько времени понадобится для
выполнения всего задания первому из них, если второму для этого требуется на 5
дней меньше.
|
Номер задачи |
ответ |
|
№1 |
77км/ч |
|
№2 |
через 3 часа |
|
№3 |
4200рублей |
|
№4 |
на 35 % |
|
№5 |
за 4часа |
|
№6 |
15 дней |
Приложение2.(самостоятельная работа, раздаточный материал)
Вариант 1.
1. Два велосипедиста
одновременно отправились в 153-километровый пробег. Первый ехал со скоростью,
на 8км/ч большей, чем скорость второго, и прибыл к финишу на 8 часов раньше
второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
2. Тюбик с краской стоит 200
рублей. Какое наибольшее число тюбиков можно купить на 800 рублей во время
распродажи, если скидка составляет 35%.
3. На изготовление 20 деталей
первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 60
таких же деталей. Известно, что первый рабочий за час делает на 4 детали
больше, чем второй. Сколько деталей в час делает второй рабочий?
Вариант2.
1. Расстояние между
пристанями А и В равно 48км. Отчалив от пристани А в 10 часов утра, теплоход
проплыл по течению реки с постоянной скоростью до пристани В.После трехчасовой
стоянки у пристани В теплоход отправился в обратный рейс и прибыл в А в тот же
день в 22.00. Найдите скорость теплохода в неподвижной воде, если скорость
течения реки 4км/ч.
2. После повышения цены на
15% пылесос стал стоить 3082рубля. Сколько рублей стоил пылесос до повышения
цены?
3. На изготовление 48 деталей
первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96
таких же деталей. Известно, что первый рабочий за час делает на 4 детали
больше, чем второй. Сколько деталей в час делает второй рабочий?
Вариант1.
|
Номер задачи |
ответ |
|
№1 |
17км/ч |
|
№2 |
6 штук |
|
№3 |
6 деталей. |
Вариант2.
|
Номер задачи |
ответ |
|
№1 |
12км/ч |
|
№2 |
2680 рублей. |
|
№3 |
8 деталей. |
Приложение3.(домашняя работа)
Задача №1.
Цена холодильника в
магазине ежегодно уменьшается на одно и то же число процентов от предыдущей
цены. Определите на сколько процентов каждый год уменьшалась цена холодильника,
если выставленный на продажу за 8000 рублей, он через 2 года был продан за
6480рублей?
Задача №2.
Теплоход, скорость которого
в неподвижной воде равна 20км/ч, проходит по течению реки до пункта назначения
и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное
теплоходом за весь рейс, если скорость течения равна 4км/ч, стоянка длится 3
часа, а в исходный пункт теплоход возвращается через 13 часов после отплытия из
него.
Задача №3.
Каждый из двух рабочих
одинаковой квалификации может выполнить заказ за 15часов. Через 5 часов после
того, как один из них приступил к выполнению заказа, к нему присоединился
второй рабочий, и работу над заказом они довели до конца уже вместе. За сколько
часов был выполнен заказ?
|
Номер задачи |
ответ |
|
№1 |
10% |
|
№2 |
192км |
|
№3 |
10часов. |

























































![4) Найдите наибольшее значение функции y = на отрезке [0; 3].](https://fsd.multiurok.ru/html/2018/01/14/s_5a5b75fea9f71/img12.jpg)





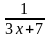 =
=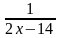
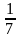 )х+4=49
)х+4=49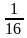
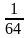
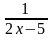 =
=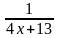
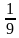
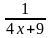 =
=








































 ;
;






