Открытый урок по геометрии 11 класс подготовка к егэ

Обобщающий урок по геометрии в 11 классе

по теме: «Площади. Подготовка к ЕГЭ»

Триединая цель урока:

Образовательная:

систематизировать и обобщить знания учащихся по теме «Площади»

Развивающая:

— способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения.

— способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях

Воспитательная:

содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.

Задачи урока:

  1. Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»
  2. Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда
  3. Научить учащихся находить главное
  4. Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства      товарищества, культуры общения, чувства ответственности.

План урока:

Содержание этапов урока

Виды  и формы
работы

1. Организационный момент.

1. Приветствие учащихся.

2. Постановка целей урока и  знакомство учащихся с планом урока.

2. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Составление первой части кластера

3.  Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач

Решение задач из сборника ЕГЭ (работа устно)

4.  Обобщение и коррекция  опорных знаний по теме «Площади многогранников и тел вращения»

Составление второй части кластера (групповая работа)

5.  Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач

Решение задач из сборника ЕГЭ (работа в тетрадях)

6.  Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач практического содержания

Решение практической задачи (работа с карточкой)

7.  Подведение итогов урока.

1. Домашнее задание

2. Рефлексия  урока учащимися и учителем

3. Выставление оценок

Ход урока:

  1. Организационный момент

— приветствие учащихся;

— психологический настрой для вовлечения в работу по теме;

— объяснение учащимся правил работы на уроке;

— мотивация учебной  деятельности через осознание учащимися значимости изучаемого   материала;

— сообщение темы, цели и задачи урока, этапов урока.

  1. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).

На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.

Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

  1. Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.

После небольшого обсуждения в парах, ответы вслух. Обсуждение.

Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

  1. Площадь какой фигуры находили?
  2. Какую формулу применяли?
  3. Можно ли решить данную задачу другим способом?

                     Предлагаемые задачи для устной работы:(приложение 3)

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

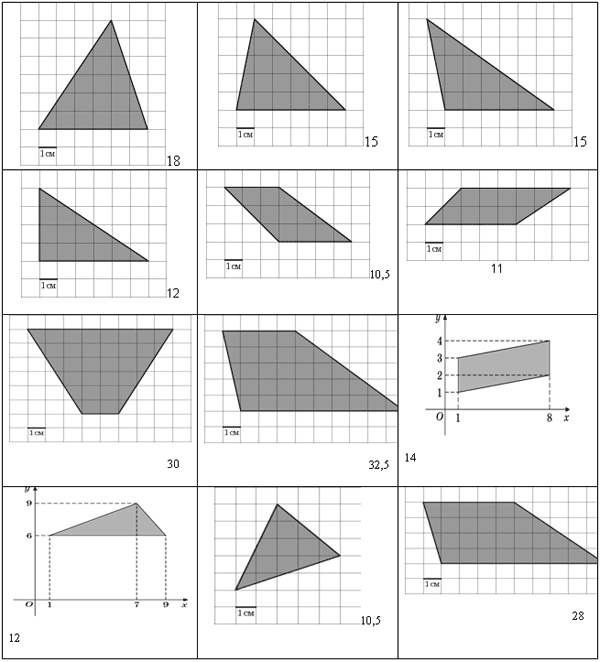
На клетчатой бумаге с клетками размером 1см×1см изображена фигура.  Найдите его площадь.

pic.3018

pic.1415

pic.415

pic.812

pic.11210,5

pic.11611

pic.118

                                                    30

pic.120

                                                      32,5

p3-1/p3-1.5

14

p4-1/p4-1.1227

12

pic.9410,5

pic.170

                                                       28
  1. Обобщение и коррекция  опорных знаний по теме «Площади многогранников и тел вращения»

Учащимся предлагается составить вторую часть кластера по теме «Площади».

Необходимо записать справа виды многогранников и тел вращения и их площадей.

Предлагается групповое обсуждение, при котором учитель записывает все варианты, которые предлагают учащиеся, учащиеся заполняют свой кластер. Одновременно идет корректировка знаний по теме.

Приложение 1 — (Примерный кластер по теме «Площади» и основные формулы площадей. В зависимости от времени урока, учащимся можно предложить заготовку с рисунками (приложение 2) или чистый лист, на котором они будут составлять кластер. При этом все чертежи разрешается строить без линейки и карандаша).

  1. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач

Учащимся предлагается решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работа у доски с записями решений. Учащиеся делают записи в тетради.

Обсуждение.

Вопросы, задаваемые при обсуждении задач:

  1. Площадь какой фигуры находили?
  2. Какие формулы применяли?

Задачи из сборника для решения у доски

(количество задач может быть от 3 до 10 в зависимости от времени урока и уровня данного класса)

  1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
  2. Площадь поверхности куба равна 18. Найдите его диагональ.
  3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
  4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
  5. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
  6. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
  7. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
  8. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  √3, а высота равна 2.
  9. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
  1. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач практического содержания.

Учащимся предлагается решить практическую задачу

Задача:   Определить площадь поверхности тетрапакета для молока (или сока)

  1. Закрепить практические навыки вычисления площади поверхности многогранников, формирование умений у учащихся вести исследовательскую работу;
  2. Определить количество картона, необходимое для изготовления тетрапакетов  различной формы.
  3. Выяснить экономическую выгоду.

Ход работы:

  1. Определить основные формулы для работы
  2. Измерить размеры тетрапакетов
  3. Сделать необходимые вычисления и заполнить таблицу

Таблица 1. Определение площади поверхности тетрапакета, имеющего форму  прямоугольного параллелепипеда (вместимость  0,2 литра)

Кол-во

пакетов

Длина

(а)

Ширина

(b)

Высота

(h)

S основания

(2аb)

S боковой

 Поверхности

(2аh +2аh)

S полной поверхности

(2(ав +аh +bh)

    1

4,6

3,8

12

34,96

201,6

236,56

  3000

709680

Таблица 2. Определение площади поверхности тетрапакета, имеющего форму  правильного тетраэдра  (вместимость  0,2  литра)

Кол-во

пакетов

Сторона

грани  

(а, b, с)

Полупериметр

Грани   Р/2

     (3a/2)

S1

одной грани

(по ф-ле Геррона)

S

полной поверхности

(S1 ×4)

    1

10, 13,13

  18

60

240

  3000

720000

                     Определим экономически выгодную упаковку. Найдем, сколько завод будет  экономить картона в день, если будет выпускать 3000 пакетов молока.

Экономия на одном пакете составляет:  3,44 (см²)

Экономия на выпуске 3000 пакетов по 0,2 литра : 3000 × 3,44 = 10320(см²)

Экономия на выпуске 3000 пакетов по 1 литру: 3000 × 9,06 = 27180 (см²)

Для сравнения: площадь одного листа картона  5246 см²

Вывод:  экономически более выгоден пакет, имеющий форму прямоугольного параллелепипеда.

  1. Подведение итогов урока
  1. Домашнее задание.

— Задачи из банка открытых задач ЕГЭ

  №5061, 5067,5201, 21337

— оформить кластер, ответить на вопросы, отмеченные в кластере

  1. Выставление оценок
  2. Рефлексия

-что дает нам прием «Кластер»?

-имеет ли практическое значение данная тема?

-понравился ли вам урок?

4.         Итог

Сегодня на уроке мы с вами обобщили тему «Площади» и систематизировали основные формулы с помощью приема «Кластер», увидели практическое применение  данной темы для решения задач, применили  знания при решении задач ЕГЭ.

Работа по закреплению данной темы будет продолжаться, так как в нашем кластере остались не заполненные места и вопросы.

Использованы материалы по подготовке к единому государственному экзамену- банк открытых заданий по математике, размещенный на официальном сайте www.ege.edu.ru

Приложение 4  — самоанализ данного урока с описанием приема «Кластер».

Источник

Урок математики в 11 классе.

Тема: «Повторение. Подготовка к ЕГЭ».

Цель урока:

  1. Повторение материала, подготовка учащихся к экзаменам.

  2. развитие логического мышления, навыков самостоятельной и групповой деятельности.

  3. Воспитание коллективизма.

План урока:

  1. Оргмомент.

  2. Устная работа. Задания типа В2

  3. Повторение темы « Площади». Составление кластера.

  4. Повторение темы «Логарифмы», использование ЭОРов.

  5. Подведение итогов урока

(Тип урока:  урок повторения и закрепления пройденного материала.

Методы обучения: словесный,  наглядный, практический (частично-поисковый,  метод самостоятельной работы).

Средства обучения:  наглядный материал  (карточки, плакаты, учебное пособие «Банк открытых заданий ЕГЭ»).

Формы работы:  групповая, индивидуальная.

Триединая цель урока:

  • Образовательная:

    • систематизировать и обобщить знания учащихся по теме «Площади».

  • Развивающая:

    • способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения;

    • способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

  • Воспитательная:

    • содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.

Задачи урока:

  • Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»

  • Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда

  • Научить учащихся находить главное

  • Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства      товарищества, культуры общения, чувства ответственности. )

Ход урока.

  1. Оргмомент.

  1. Устные упражнения: Разрешите открыть урок с высказывания Декарта: «Я мыслю, следовательно, существую». Сейчас вам дается возможность проявить свою мысль при выполнении ряда заданий для подготовки к ЕГЭ.

ЕГЭ это вершина ,к которой мы медленно поднимаемся, переходя из класса в класс, изучая одну тему за другой. Задания ЕГЭ это ступени, по которым легче покорить эту вершину. Сегодня на уроке мы преодолеем вместе с вами некоторые из этих ступеней.

Итак , первая ступенька на которую мы с вами сегодня поднимемся -задания В2. Их можно решить устно. Мы сейчас рассмотрим несколько разных заданий этого типа.

Задание B2

На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.

Определите по графику, сколько дней из данного периода осадков выпало между 2 и 8 мм.

Ответ: 3

Задание B2

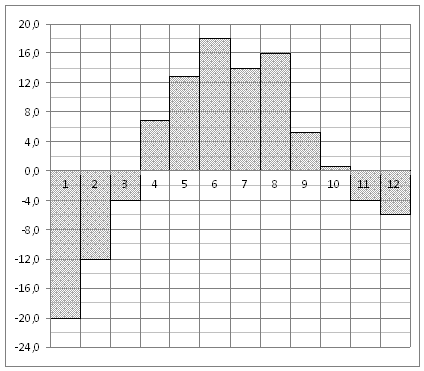
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году.

Ответ: 38

Задание B2

Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее  ° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы.

Ответ: 7

Задание B2

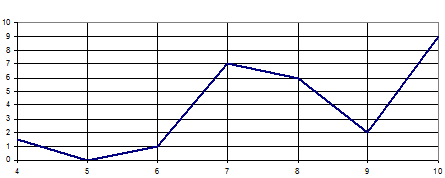
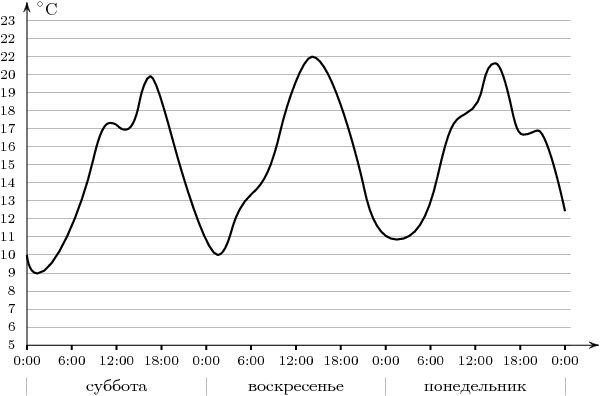
На графике показано изменение температуры воздуха в некотором населённом пункте на протяжении трех суток, начиная с 0 часов субботы. На оси абсцисс отмечается время суток в часах, на оси ординат — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха в ночь с субботы на воскресенье. Ответ дайте в градусах Цельсия.

Ответ: 10

Задание B2

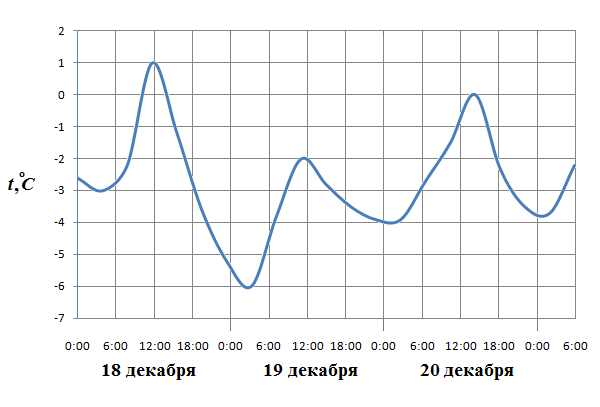
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 19 декабря.

Ответ: 4

Задание B2 (18881)

(показов: 1885, ответов: 1026)

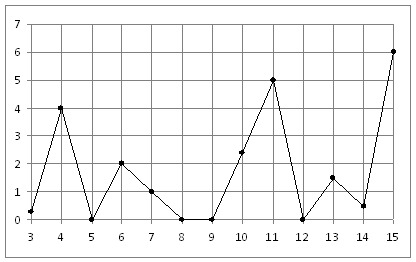
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа выпало наибольшее количество осадков.

Ответ: 15

Задание B2

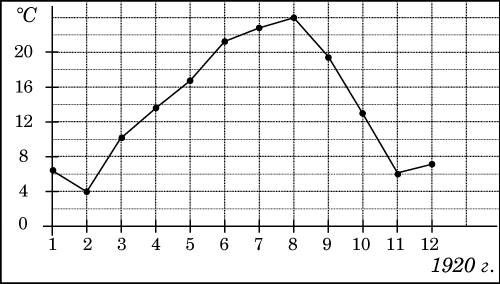
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года.

Ответ: 6

Задание B2

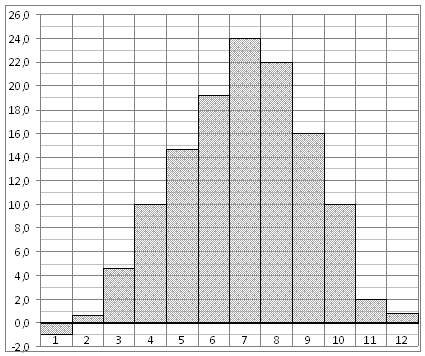
На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1988 году.

Ответ: 24

Задание B2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

Ответ: 3

  1. Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

Формулы для кластера

  1. (ромб)

  2. (трапеция)

  3. (параллелепипед) S = ha

S= аbsinγ

S= (d1×d2×sinγ)

2

  1. (прямоугольник) S = a*b

  2. (квадрат)

  3. (прямоугольный треугольник)

  4. (треугольник)

Формула Геррона

S= 1/2ab sinγ

S=1/2 r×P

S= abc

4R

  1. (круг)

(круговой сектор) S=πR²α

360

  1. (правильные многоугольники) n=3, S=a²√3

4

n =4, S=a²

n=6, S=3√3a²

2

  1. (пирамида)

(правильная пирамида) Sбок=1/2Pоснd (апофему)

(усеченная пирамида) Sбок=1/2(P1 +P2)d (апофему)

  1. (куб) S = 6a²

  1. (прямоугольный параллелепипед) S = 2(ab+bc+ac)

  2. (цилиндра) S бок= 2πRh

Sпол=2πR(R + h)

  1. (призма)S= Sбок + 2Sосн

(прямой призмы) Sбок= Ph

  1. (конус) Sбок=πrl

Sпол=πr(l + r)

(усеченный конус) Sбок=π (r + r1) l

  1. (сфера)

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.
После небольшого обсуждения в парах, ответы вслух. Обсуждение.
Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

  • Площадь какой фигуры находили?

  • Какую формулу применяли?

  • Можно ли решить данную задачу другим способом?

Предлагаемые задачи для устной работы:

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура.  Найдите его площадь.

  1. Теперь давайте перейдем к заданиям типа В5, В7. Логарифмы. Перед вами лежат формулы, выражающие свойства логарифмов. При работе можете ими пользоваться.

ЭОРы: а) работа вместе с учителем

Б) самостоятельная работа ученика.

Одновременно класс работает с ним, корректирует знания.

  1. Откройте «Репетитор по математике. Варианты ЕГЭ, 2012 год». Выполняете каждый свой вариант. Начинаем выполнять тест. Результаты тестирования отправьте на печать.

  2. Подведение итогов урока

  3. 1. Домашнее задание.

  4. – Задачи из банка открытых задач ЕГЭ: №5061, 5067,5201, 21337.
    – Оформить кластер, ответить на вопросы, отмеченные в кластере

  5. 2. Выставление оценок

  6. 3. Рефлексия

  7. – Что дает нам прием «Кластер»?
    – Имеет ли практическое значение данная тема?
    – Понравился ли вам урок?

  9. Сегодня мы проводим урок – отчет самостоятельного решения

задачи. Вы решали одну задачу разными способами. Мы ждем от вас красивого решения, а добиться этого можно лишь в результате кропотливой работы над задачей.

Красивое решение приходит тогда, когда придумано несколько вариантов решения задачи. Метода, который гарантировал бы решение любой задачи – нет. Но все же существуют весьма общие приемы, которые при умелом применении заметно облегчают решение многих трудных задач. Разработка этих приемов называется — эвристика. Слово происходит от знаменитого «Эврика».

«Эврика» — нашел! – воскликнул, согласно легенде, древнегреческий ученый Архимед, выскочив из ванны, он понял как решить, возникшую перед ним задачу.

Стихотворение (читает ученица)

Преданье старинное знает весь свет,

Как, нежась горячею ванной,

Открыл свой великий закон Архимед,

Связав его с выходкой странной.

Сияющий выскочил вон Архимед,

Из ванны горячей, где мылся,

И прямо из бани, как был, неодет,

Куда-то бежать он пустился.

Картина, достойная кисти богов,

По улице, солнцем согретой,

Пунктир оставляя из мокрых следов,

Бежит Архимед неодетый.

Толпа сиракузцев несется во след,

В восторге от бешеной гонки,

И громко ликует, когда Архимед,

Выкрикнул «Эврика» звонко.

«Нашел!» Он нашел тот желанный ответ,

Который искал так упорно.

«Нашел!» В упоенье кричал Архимед,

«Нашел!» — повторяли задорно.

Подобно Архимеду, вы искали решение задачи, каждая группа предлагает свой способ. Когда вы получили задание сделать проект решения задачи, то вы думали, что это невозможно, но сейчас посмотрим, что из этого получилось

  1. Заключение.

Сейчас, прослушав несколько способов решения одной задачи, мы повторили несколько тем. Вы должны выбрать тот способ решения, который вам больше понравился, и если на экзамене вам встретилась задача, которую не можете решить, то вспомните, что можно попытаться решить другим способом.

В этом году вы выпускаетесь из школы и вас ждут большие жизненные испытания. Так вы должны знать, что безвыходных ситуаций не бывает.

В любой ситуации можно найти решение.

Закончим наш урок словами Эйнштейна: «Каждый важный успех приносит новые вопросы».

Источник

Технологическая карта урока геометрии в 11 классе «Подготовка к ЕГЭ. Площади»

I Организационный этап
 

Деятельность учителя

Деятельность учеников

  

Организация внимания школьников; Проверка готовности к уроку.

«Добрый день, друзья! Я рада вас видеть, и очень

хочу начать работу с вами! (хорошего вам настроения!)»

Девиз урока: «С малой удачи начинается большой успех»

Улыбнитесь друг другу, не волнуйтесь, я уверена, что присутствующие на уроке желают вам только добра и успехов. И так, в добрый путь!

Доброжелательный настрой

Полная готовность класса к уроку;

Быстрое включение уч-ся в деловой ритм;

  

Мотивация к учебной деятельности

Формулирование темы урока

обоснова-

ние выбора темы

Формулирование целевых установок урока и плана работы,

постановка

целей

урока

Тема нашего урока «Решение задач ЕГЭ. Площади»

По теме площади в типовых вариантах ЕГЭ существует два типа заданий, каких?

1.Вычисление площадей фигур в планиметрии – задание типа В5

2. Вычисление площадей поверхности геометрических тел — задание В10

Как вы считаете, что нам нужно знать по теме урока для успешного усвоения материала? Построим дерево темы «Площади на ЕГЭ»

Поставьте цели урока.

С вашего разрешения конкретизирую цели урока:

1. вычисление площадей треугольников, многоугольников, кругов и секторов

2.повторение формул вычисления площадей призм, пирамид , цилиндров, конусов, шаров 3.

решение задач на вычисление площадей поверхности названных геометрических тел

Ученики отвечают.

Предлагают, как нарисовать дерево темы

Повторить формулы площадей

Решить типовые задания по теме урока

Получить новые знания по теме

площади

             
            
   

II.Обобщение и коррекция  опорных знаний по теме «Площади плоских фигур»

тестирование

Учащимся предлагается выполнить задания по вычислению площадей плоских геометрических фигур на плоскости. Работа по вариантам. ( Ребята, вы должны выполнить на задания, записать ответы в лист контроля.) При этом вы можете карандашом делать записи и построения в листе заданий. Вы должны как можно быстрее и точнее найти ответы на диагностическую работу « Площади многоугольников» Время будет ограничено.

Выполнение тестов. (Работа с раздаточным материалом)

Взаимопроверка, оценивание знаний по теме «Площади»

Работа с листками контроля знаний

Дополнительные задачи для успешно выполнивших задание уч-ся

  

III. Обобщение и коррекция  опорных знаний по теме «Площади многогранников и тел вращения»

кластер

Учащимся предлагается составить кластер — справочник по теме «Площади поверхностей геометрических тел». 
Необходимо записать справа от видов многогранников и тел вращения — формулы вычисления их площадей

составление кластер — справочник

корректировка знаний формул с помощью ИКТ

  

IV. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач

Использование заданий на узнавание уч-ся изученных познавательных объектов

Учащимся предлагается решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике».

Задания на выделения всех признаков понятий и их связи друг с другом (проверяется полнота знаний)

Работа с записями решений ответов. обсуждение с учителем результатов деятельности. Самооценка и оценка учителя знаний учащихся по теме..

 

V Рефлексия

мобилизация уч-ся на рефлексию . Барометр настроения

« МОИ МАЛЕНЬКИЕ ДОСТИЖЕНИЯ»

Выбор « МОИ МАЛЕНЬКИЕ ДОСТИЖЕНИЯ»

2

3-4

5

  

. VII. Итог

Сегодня на уроке мы с вами обобщили тему «Площади» и систематизировали основные формулы с помощью приема «Кластер», увидели практическое применение  данной темы для решения задач, применили  знания при решении задач ЕГЭ. 
Работа по закреплению данной темы будет продолжаться,

Подведение итогов урока по алгоритму «ДЕЛО» (достиг ли цели учения, какие затруднения возникли, как преодолеть свои учебные проблемы)

  

д/з

Три уровня д/з на ваш выбор

Решение опорных задач по теме «Площади»(карточки)

2.Проект « Детская игрушка – сложная поверхность»

Проект « Площадь школьного прибора»

Проект « Подборка задач практического содержания

по теме «Площади многогранников и тел вращения»

Записывают д/з в дневник

Получают информацию

о сдаче зачёта  по теме занятия        

  
Источник

6 октября 2014

В закладки

Обсудить

Жалоба

Методическая разработка урока геометрии

Данная разработка может быть использована на уроках повторения планиметрии в 11 классе при подготовке к ЕГЭ.

Она содержит конспект урока, дидактический материал-набор задач, презентацию к уроку.

Автор: Геннадиевна Почечуева Инна, МАОУ «ЛИЦЕЙ№29″г. Тамбова.

geometri.rar

Источник

Обобщающий урок по геометрии в 11 классе

по теме: «Площади. Подготовка к ЕГЭ»

Триединая цель урока:

Образовательная:

систематизировать и обобщить знания учащихся по теме «Площади»

Развивающая:

— способствовать формированию умений применять приемы: сравнения, обобщения,

выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи,

составлять модель решения.

— способствовать развитию умений и навыков применять математические знания к решению

практических задач, ориентироваться в простейших геометрических конструкциях

Воспитательная:

содействовать воспитанию интереса к математике, активности, мобильности, умения

общаться.

Задачи урока:

1. Выявить уровень подготовки учащихся по геометрии по данной теме,

систематизировать полученные знания с помощью приема «Кластер»

2. Помочь в развитии и самореализации творческих способностей личности; обучить

приемам организации интеллектуального труда

3. Научить учащихся находить главное

4. Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства

товарищества, культуры общения, чувства ответственности.

План урока:

1. Организационный момент.

1. Приветствие учащихся.

2. Постановка целей урока и

знакомство учащихся с планом

урока.

2. Обобщение и коррекция опорных знаний по теме

«Площади плоских фигур»

Составление первой части

кластера

3. Деятельность учащихся по самостоятельному

применению знаний и умений при решении простейших

геометрических задач

Решение задач из сборника

ЕГЭ (работа устно)

4. Обобщение и коррекция опорных знаний по теме

«Площади многогранников и тел вращения»

Составление второй части

кластера (групповая работа)

5. Деятельность учащихся по самостоятельному

применению знаний и умений при решении геометрических

задач

Решение задач из сборника

ЕГЭ (работа в тетрадях)

6. Деятельность учащихся по самостоятельному

применению знаний и умений при решении геометрических

задач практического содержания

Решение практической задачи

(работа с карточкой)

7. Подведение итогов урока.

1. Домашнее задание

2. Рефлексия урока учащимися

и учителем

3. Выставление оценок

Ход урока:

I. Организационный момент

— приветствие учащихся;

— психологический настрой для вовлечения в работу по теме;

— объяснение учащимся правил работы на уроке;

— мотивация учебной деятельности через осознание учащимися значимости изучаемого

материала;

— сообщение темы, цели и задачи урока, этапов урока.

II. Обобщение и коррекция опорных знаний по теме «Площади плоских фигур»

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого

находится лист (формат А4).

На листе делается посередине надпись «Площади». Затем учащимся предлагается слева

записать виды плоских фигур и их площадей.

Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое

обсуждение полученного кластера. Корректировка кластера.

III. Деятельность учащихся по самостоятельному применению знаний и умений при

решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий

ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно

необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей,

можно пользоваться составленным кластером.

После небольшого обсуждения в парах, ответы вслух. Обсуждение.

Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

1. Площадь какой фигуры находили?

2. Какую формулу применяли?

3. Можно ли решить данную задачу другим способом?

Предлагаемые задачи для устной работы:(приложение 3)

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

На клетчатой бумаге с клетками размером 1см×1см изображена фигура. Найдите его

площадь.

IV. Обобщение и коррекция опорных знаний по теме «Площади многогранников и тел

вращения»

Учащимся предлагается составить вторую часть кластера по теме «Площади».

Необходимо записать справа виды многогранников и тел вращения и их площадей.

Предлагается групповое обсуждение, при котором учитель записывает все варианты, которые

предлагают учащиеся, учащиеся заполняют свой кластер. Одновременно идет корректировка

знаний по теме.

Приложение 1 — (Примерный кластер по теме «Площади» и основные формулы площадей. В

зависимости от времени урока, учащимся можно предложить заготовку с рисунками

(приложение 2) или чистый лист, на котором они будут составлять кластер. При этом все

чертежи разрешается строить без линейки и карандаша).

V. Деятельность учащихся по самостоятельному применению знаний и умений при

решении геометрических задач

Учащимся предлагается решить несколько задач из сборника «Банк открытых заданий ЕГЭ по

математике». Работа у доски с записями решений. Учащиеся делают записи в тетради.

Обсуждение.

Вопросы, задаваемые при обсуждении задач:

1. Площадь какой фигуры находили?

2. Какие формулы применяли?

Задачи из сборника для решения у доски

(количество задач может быть от 3 до 10 в зависимости от времени урока и уровня данного

класса)

1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и

4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро,

выходящее из той же вершины.

2. Площадь поверхности куба равна 18. Найдите его диагональ.

3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона

основания которой равна 5, а высота 10.

4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с

диагоналями, равными 6 и 8, и боковым ребром, равным 10.

5. Правильная четырехугольная призма описана около цилиндра, радиус основания и

высота которого равны 1. Найдите площадь боковой поверхности призмы.

6. Через среднюю линию основания треугольной призмы, площадь боковой поверхности

которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите

площадь боковой поверхности отсеченной треугольной призмы.

7. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра

равны 13. Найдите площадь поверхности этой пирамиды.

8. Найдите площадь боковой поверхности правильной треугольной призмы, описанной

около цилиндра, радиус основания которого равен √3, а высота равна 2.

9. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра

равны 13. Найдите площадь боковой поверхности этой пирамиды.

VI. Деятельность учащихся по самостоятельному применению знаний и умений при

решении геометрических задач практического содержания.

Учащимся предлагается решить практическую задачу

Задача: Определить площадь поверхности тетрапакета для молока (или сока)

1. Закрепить практические навыки вычисления площади поверхности многогранников,

формирование умений у учащихся вести исследовательскую работу;

2. Определить количество картона, необходимое для изготовления тетрапакетов

различной формы.

3. Выяснить экономическую выгоду.

Ход работы:

1. Определить основные формулы для работы

2. Измерить размеры тетрапакетов

3. Сделать необходимые вычисления и заполнить таблицу

Таблица 1. Определение площади поверхности тетрапакета, имеющего форму

прямоугольного параллелепипеда (вместимость 0,2 литра)

S боковой

Поверхности

(2аh +2аh)

S полной

поверхности

(2(ав +аh +bh)

Таблица 2. Определение площади поверхности тетрапакета, имеющего форму правильного

тетраэдра (вместимость 0,2 литра)

Полуперим

етр

Грани Р/2

(3a/2)

S1

одной грани

(по ф—ле

Геррона)

S

полной поверхности

(S1 ×4)

Определим экономически выгодную упаковку. Найдем, сколько завод будет экономить

картона в день, если будет выпускать 3000 пакетов молока.

Экономия на одном пакете составляет: 3,44 (см²)

Экономия на выпуске 3000 пакетов по 0,2 литра : 3000 × 3,44 = 10320(см²)

Экономия на выпуске 3000 пакетов по 1 литру: 3000 × 9,06 = 27180 (см²)

Для сравнения: площадь одного листа картона 5246 см²

Вывод: экономически более выгоден пакет, имеющий форму прямоугольного

параллелепипеда.

VII. Подведение итогов урока

1. Домашнее задание.

— Задачи из банка открытых задач ЕГЭ

№5061, 5067,5201, 21337

— оформить кластер, ответить на вопросы, отмеченные в кластере

2. Выставление оценок

3. Рефлексия

—что дает нам прием «Кластер»?

—имеет ли практическое значение данная тема?

—понравился ли вам урок?

4. Итог

Сегодня на уроке мы с вами обобщили тему «Площади» и систематизировали основные

формулы с помощью приема «Кластер», увидели практическое применение данной темы для

решения задач, применили знания при решении задач ЕГЭ.

Работа по закреплению данной темы будет продолжаться, так как в нашем кластере остались

не заполненные места и вопросы.

Использованы материалы по подготовке к единому государственному экзамену— банк

открытых заданий по математике, размещенный на официальном сайте www.ege.edu.ru

Приложение 4 — самоанализ данного урока с описанием приема «Кластер».

Источник

Тема урока: «Решение задач на нахождение объемов многогранников:куба, прямоугольного параллелепипеда и прямой призмыпри подготовке к ЕГЭ».

Тип урока.Обобщение и систематизация знаний.

Технология. Традиционное обучение.
Цель урока.Обобщить и систематизировать знания по теме «Объемы куба, прямоугольного параллелепипеда и призмы».
Задачи урока.

Образовательные.Повторить и систематизировать формулы для вычисления объемов многогранников. Продолжить формирование навыков решения задач по теме.
Развивающие.Учить детей приемам мыслительной деятельности. Развивать кругозор. Развивать самостоятельность учащихся, логическое мышление, математическую речь. Способствовать формированию интеллектуальных умений и владению анализом и синтезом, доказательством, обобщением.
Воспитательная.Воспитывать стремление учащихся к получению новых знаний, культуру учебного труда. Формировать объективную самооценку знаний.
Оборудование. Проектор, документ копир, компьютер,презентация, карточки с заданиями, листы оценивания, кластер.

Ход урока.
I. Организационный момент.

Здравствуйте!
Проверьте свою готовность к уроку, садитесь.
Известный швейцарский математик Джордж Полиа сказал: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». Слайд 1
Исходя из этого, давайте сформулируем тему сегодняшнего урока, а также цели задачи. Данная тема широко представлена в первой части КИМ-ов ЕГЭ по математике как, на базовом, так и на профильном уровнях. Поэтому сегодня мы сделаем акцент на решении задач из открытого банка ЕГЭ.

Слайд 2-3.

На уроке мы будем пользоваться карточками самооценки, карточками с заданиями и листами-кластерами. Не забывайте выставлять себе туда оценки. Запишите дату и тему урока в рабочую тетрадь.
II. Актуализация опорных знаний. Слайды (1-6)
Для того чтобы успешно решать задачи, необходимо повторить основной теоретический материал. Сегодня это свойства объёмов, теоремы и формулы для вычисления объемов. В тетради соответственно делайте записи

Устный опрос.

1.Какие единицы объёма знаете, (старинные единицы объёма). Чтобы найти объем, сначала выбирают единицу измерения. В Древнем Риме, например, одной из единиц объема служила амфора (около 25,5 л). Нефть во всем мире принято сейчас измерять в англо-американских единицах – бареллях, т.е в бочках ёмкостью 159 л. В России распространенная в быту мера объема – ведро.

Каждое из рассматриваемых нами тел имеет объём, который можно измерить с помощью выбранной нами единицы измерения объёмов. За единицу измерения объёмов примем куб ребро, которого равно единице измерения отрезков. Куб с ребром 1 см называют 1 кубическим см и обозначают см3. Аналогично определяются кубический метр, кубический миллиметр. Кубический дециметр имеет отдельное название 1 литр. Соотношение между данными единицами проходят в 5 классе:

1 см3=1000 мм3

1дм3=1000 см3

1 м3= 1000 дм3.

В практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел. 
Среди них английские меры:

Бушель – 36,4 дм3

Галлон – 4,5 дм3

Баррель (сухой) – 115,628 дм3

Баррель (нефтяной) – 158,988 дм3

Английский баррель для сыпучих веществ 163,65 дм3.

Меры когда-то, применявшиеся в России:

Ведро – 12 дм3

Бочка – 490 дм3

Штоф – 1,23 дм3 = 10 чарок

Чарка – 0,123 дм3=0,1 штофа = 2 шкалика

Шкалик – 0,06 дм3 = 0,5 чарки.

2. Назовите свойства объема

Равные тела имеют равные объемы

Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.

Если одно тело содержит другое, то объем первого тела не меньше объема второго.

Следствие: объем куба с ребром 1/n равен 1/n3

3.По какой общей формуле можно вычислить объем куба.

4.Сформулируйте теорему об объёме прямоугольного параллелепипеда.

Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений.

V = авс

5.Приведите следствия из данной теоремы (2 следствия).

Следствие 1. Объем прямоугольного параллелепипеда равен произведению основания на высоту.V = Sh

Следствие 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.

6.Дайте определение прямой призмы, правильной прямой призмы

ПРИЗМА — многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы.

Прямая призма — призма, у которой все боковые ребра перпендикулярны основанию, в противном случае призма называется наклонной.

7.А как вычислить объём прямой правильной призмы, в основании которой лежит треугольник, квадрат, шестиугольник (а если ромб, трапеция).Для этого вам поможет кластер.

Оценивание правильный ответ оценивается 1 баллом.

2. Устная работаСлайды (7-11)

А теперь перейдем к решению задач по готовым чертежам с целью закрепления формул для вычисления объемов геометрических тел.

Найти объём прямоугольного параллелепипеда.№1-3

4 50

4. Объем куба равен 64. Найдите площадь его поверхности.

5. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые).

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

III. Математический диктант. Слайд ( 12-13)

Решение простейших задач из ЕГЭ на вычисление объёма по вариантам. В тетрадях вы запиваете формулу, выполняете вычисления и записываете ответ. Время на решение даётся 5 мин.

Вариант I.

Найти объём куба с ребром длиной 3 м.

Найти объём прямоугольного параллелепипеда, если известны три его измерения a=3,b= 4, c=8.

Найти объём прямой призмы, , в основании которой лежит прямоугольный треугольник с катетами √13 см и √5, а её высота равна 5 см.

Вариант II.

Найти объём куба с ребром длиной 4 см.

Найти объём прямоугольного параллелепипеда, если известны три его измерения a=2,b= 5, c=6.

Найти объём прямой призмы, в основании которой лежит прямоугольный треугольник с катетами √11 дм и 4 дм, а её высота равна  3√11 дм.

Взаимопроверка в парах.

Оценивание Ученики сами проверяют по готовым ответам на слайде. За правильно выполненную задачу ставится 1 балл.

Давайте закрепим знание формул при решении задач из сборника «Банк открытых заданий ЕГЭ по математике.


IV. Деятельность учащихся по применению знаний и умений при решений задач из сборника «Банк открытых заданий ЕГЭ по математике».

Работа в группах.
Решаем задачи в группах. (3 группы). Для каждой группы даю по 2 задачи. В тетрадях каждый участник группы записывает дано, выполняет чертёж, решение и записывает ответ. Один из представителей команды с тетрадью выходит к доске и приводит решение задачи, используя копир.

Слайд (14)

1 группа

Вспомнить формулу нахождения массы тела через плотность и объем.

1.Слиток золота имеет форму прямоугольного параллелепипеда с измерениями 10 см, 8 см и 5см. Плотность золота равна 19, 32 г/см³. Найдите его массу.

Легенде об Архимеде. Слайд (15)

 В III веке до нашей эры царь древнегреческого города Сиракузы попросил проверить ученого Архимеда, из чистого ли золота сделал мастер ему корону. Проблема здесь вот в чем. Когда царь заказывал корону, он дал мастеру определенную массу золота. Когда мастер вернул золото в виде короны, то оно весило столько, сколько и масса данного золота. Но ведь мастер мог схитрить.

Если взять из общей массы золота немного золота и положить туда равную взятой массе золота массу серебра (которое дешевле), то никто и не заметит. Ведь на глаз не отличишь, а масса такая, какая и должна быть.

Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: m = ρV. Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. Просто при равной массе отличались бы объемы кусков. Но как определить объем короны? По-сути именно эта задача стояла перед Архимедом.

И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Если объемы окажутся равными, то значит ювелирный мастер честно выполнил свою работу. Архимед выскочил из ванной и побежал проверять свое открытие.

Архимед погрузил в воду корону и измерил, как увеличился объем воды. (Хотя на самом деле Архимед мог измерять потерю веса при погружении тела в воду. Потеря веса равна весу вытесненной воды. А вес воды зависит от вытесненного объема. В свою очередь вытесненный объем воды равен объему погруженного в воду тела.) Также он погрузил в воду кусок золота, у которого масса была такая же как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Архимед был рад своему открытию, а вот ювелир не очень.

Задача на нахождение объёма сложной детали базового уровня

2.В сосуд, имеющий форму правильной треугольной призмы, налили 2300   воды и погрузили в воду деталь.

При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали.

Ответ выразите в см3.

2 группа Слайд (16)

Задача на вычисление объёма сложенной фигуры из частей (профильный уровень).

1.Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые .

2.Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему

из этой же вершины.

3 группа Слайд (16)

1.Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны √3.

2.Одна из граней прямоугольного параллелепипеда — квадрат.

Диагональ параллелепипеда равна и образует с плоскостью этой грани угол 45.Найдите объем параллелепипеда

Оценивание Ученики, которые выполняли задачи на доске(Кто отвечал у доски), самостоятельно в тетради

( работали с места) оценивают себя. За правильно выполненную задачу ставится 1 балл.

Ребята переходим к решению самостоятельной работы по вариантам, решение выполняйте в тетрадях, записывая с условие задачи (дано, найти), формулу, решение, ответ, делайте необходимые чертежи. Записи делайте аккуратно. Тетрадь вы сдаёте для дальнейшей проверки.V. Самостоятельная работа учащихся. Слайд (18)

А теперь вам предлагается самостоятельно решить 4 задачи. На работу даётся 12 мин.
ВариантI.

1.Вариант 29, №16 стр. 183 (из сборника базового уровня). В прямоугольном параллелепипедеABCDA1B1C1D1 известныAB=3,AD=5 и диагональ боковой грани A1D1=√34. Найдите объём прямоугольного параллелепипеда ABCDA1B1C1D1.

2 . Вариант 31, №16 стр.195 (из сборника базового уровня). Сторона основания прямой призмы MNPM1N1P1 равна 6, а высота призмы 5√3. Найти объём призмы MNPM1N1P1.

3. Вариант 33, № 8 стр. 209 (из сборника профильного уровня). Объём куба равен 64. Найти площадь его поверхности.

4. Вариант 39, №16 стр. 243 (из сборника базового уровня). В прямоугольном параллелепипедеABCDA1B1C1D1рёбра AB,AD и диагональ AD1 соответственно равны 7, 5 и 13. Найдите объём прямоугольного параллелепипедаABCDA1B1C1D1.

ВариантII.

1.Вариант 30, №16 стр. 189 (из сборника базового уровня). В прямоугольном параллелепипедеABCDA1B1C1D1 известныAB=6,AD=7 и диагональ боковой грани A1D1=√58. Найдите объём прямоугольного параллелепипеда ABCDA1B1C1D1.

2 . Вариант 32, №16 стр. 201 (из сборника базового уровня). Сторона основания прямой призмы MNPM1N1P1 равна 10, а высота призмы 4√3. Найти объём призмы MNPM1N1P1.

3. Вариант 34, № 8 стр. 214 (из сборника профильного уровня). Объём куба равен 27. Найти площадь его поверхности.

Вариант 40, №16 стр. 249 (из сборника базового уровня). В прямоугольном параллелепипедеABCDA1B1C1D1рёбра AB,AD и диагональ AD1 соответственно равны 6, 15 и 17. Найдите объём прямоугольного параллелепипедаABCDA1B1C1D1.

Проверка выполнение самостоятельной работы. Сдаётся тетрадь на проверку.
Оценки за самостоятельную работу я скажу на следующем уроке.
VI. Итог урока.
Итак, наш урок подошел к концу.
VII. Домашнее задание.Слайд 19.
Повторить формулы объемов п.74-76, № 658. 
Подготовка к ЕГЭ.

Базовый уровень, вариант 33, 34 №16 стр.205-213 (из сборника базового уровня).

Профильный уровень, вариант 35, 36 № 8 стр.219-224 (из сборника профильного уровня).

VIII. Рефлексия Слайд 20.

Я слышу – я забываю,

я вижу – я запоминаю,

я делаю – я усваиваю.

Китайская мудрость

Спасибо за урок.

Приложение1.

Приложение2. Карта оценивания.

Ф.И.___________________________________________________________________________

Дата ___.___.___г.

Тема урока: _____________________________________________________________________

________________________________________________________________________________

№

Этапы урока

Количество баллов

Знание теории.

Решению задач по готовым чертежам

Математический диктант.

Работа в группах.

Самостоятельная работа

Приложение3.

11 класс Геометрия Прямоугольный параллелепипед Задания В9,В11 ОБЗ

№

Домашняя контрольная работа

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответы

№

Контрольное домашнее задание

27

8

48

4

10

9

24

6

1,5

66

Ход урока

№ cлайда

Деятельность учителя

Деятельность учащихся

Организационный этап.

Задача этапа: подготовка учащихся к работе на уроке

Приветствие учащихся.

Раздача карты урока.

Слайд1

Тема урока: «Прямоугольный параллелепипед
в задачах В9 и В11 ЕГЭ»

На уроке вам будут предложены задачи из открытого банка задач по математике ЕГЭ 2011-2012 гг.

Учащиеся записывают дату урока и тему. Подписывают фамилию и имя на карте урока.

Проверка домашнего задания.

Собрать контрольное домашнее задание на проверку. При возникновении вопросов и трудностей у учащихся назначить индивидуальную консультацию.

Подготовительный этап.

Задача этапа: обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности, актуализация опорных знаний

Форма организации познавательной деятельности — фронтальная.

Методы обучения: репродуктивный и частично-поисковый

Решение задач по готовым чертежам.

Слайд2

Работа со справочной таблицей.

Вопросы для учащихся.

Является ли прямоугольный параллелепипед призмой?

Какой многоугольник является гранью прямоугольного параллелепипеда?

Как расположено боковое ребро прямоугольного параллелепипеда к основаниям?

Под каким углом пересекаются грани прямоугольного параллелепипеда?

Сформулировать теорему о длине диагонали прямоугольного параллелепипеда.

Сформулировать теорему Пифагора.

Записать формулы полной поверхности и объёма прямоугольного параллелепипеда через его измерения.

Учащиеся просматривают справочные таблицы и отвечают на вопросы.

Записать формулы по вопросам 4, 5, 6. Слайд 3

Слайд 4,5,6.

№3.

Решение задач с использованием готовых чертежей:

№1.

Ответ:50.

№2.

Ответ:5.

№3.

Ответ:45°.

Слайды 7-13

Применение знаний и способов действий.Задача этапа: обеспечение усвоения новых способов действий на уровне применения в изменённой ситуации

Форма организации познавательной деятельности: фронтальная, индивидуальная.

Методы обучения: поисковые

№4.

№5.

№6.

№7.

№8.

Рис .эадачи №7.

№9.

№10.

Рис. задачи №9.

№ 4. Объем куба равен 64.

Найдите площадь его поверхности.

Ответ:96.

№5. ОБЗ ЕГЭ №245376. Найдите квадрат расстояния между вершинами B₂ и D₃ многогранника , изображенного на рисунке. Все двугранные углы многогранника прямые.

Ответ:11.

№ 6.Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Ответ:60°.

№7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ:188.

№8. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ:456.

№9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ:130.

№10. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые).

Ответ:84.

Слайд 7-13

Контроль и самопроверка знаний.

Задача этапа: выявление качества и уровня овладения знаниями и способами действий, обеспечение их коррекции.

Выборочная проверка карты урока. Оценить работу учащихся, которые выполнили 10 задач.

Проверка решения с помощью интерактивной доски.

Во время демонстрации своего решения одним учеником, остальные заполняют карту урока.

Слайд 14.

Информация о домашнем задании.

Задача этапа: обеспечение понимания цели, содержания и способов выполнения домашнего задания. Решить №1-10.

Дать рекомендации по оформлению работы.

Приложение3.Домашняя работа

Подведение итогов урока.

Задача этапа: дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы.

Класс: 11
Предмет: геометрия
УМК Л.С. Атанасян «Геометрия 10-11»
Тема: « Решение задач на нахождение объемов многогранников (прямые призмы) при подготовке к ЕГЭ».
Цель урока: Развитие деятельностных способностей у обучающихся в ходе решения задач при изучении темы «Нахождение объемов многогранников (прямые призмы)»
Планируемый результат: 
Личностные: развивать умение делать выбор методов решения, осуществлять самоконтроль; формировать уважительное отношение обучающихся друг к другу, в том числе людям разного социального статуса. 
Метапредметная: уметь применять имеющиеся знания в нестандартных ситуациях.
Предметные: актуализировать знания обучающихся по теме «Нахождение объемов многогранников (прямые призмы) при подготовке к ЕГЭ».
Риски эффективности урока: — невладение некоторыми учащимися необходимым материалом;
— затянутость самостоятельной работы;
— отсутствие у некоторых учащихся выполненного домашнего задания.
Способы избегания рисков: — организация в начале урока повторения ранее пройденного материала;
— тьюторская деятельность учителя во время работы; 
— организация раздаточного материала.
Необходимое оборудование: интерактивная доска, набор задач на вычисление объёмов многогранников.

Тест

Объясните, что выбирают за единицу измерения объёма.

За единицу измерения объёма принимают ________________________ _________________________________________________________________________

Объясните, какой куб называют кубическим сантиметром.

__________________________________________________________________________________________________________________________________________________________________

 Сформулируйте свойства объёма.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________

Фигура составлена из равных кубов. Объём каждого куба равен V. Найдите объём фигуры.

Решение: ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Запишите формулу объёма прямоугольного параллелепипеда.

________________________________________________________________________________________________________

Как изменится объём куба, если каждую его сторону: а) увеличить в два раза; б) уменьшить в два раза.

Ответ: а) объём куба _____________________________________________________________

Б) объём куба___________________________________________________________________

Тест

Объясните, что выбирают за единицу измерения объёма.

За единицу измерения объёма принимают ________________________ _________________________________________________________________________

Объясните, какой куб называют кубическим сантиметром.

__________________________________________________________________________________________________________________________________________________________________

Сформулируйте свойства объёма.

1)____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2)____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Фигура составлена из равных кубов. Объём каждого куба равен V. Найдите объём фигуры.

Решение: ___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Запишите формулу объёма прямоугольного параллелепипеда.

________________________________________________________________________________________________________

Как изменится объём куба, если каждую его сторону: а) увеличить в два раза; б) уменьшить в два раза.

Ответ: а) объём куба _____________________________________________________________

Б) объём куба___________________________________________________________________

Урок математики в 11 классе.

21.02.2017

учитель Миронова С.С.

Тема урока. Решение задач по теме «Объем прямой призмы и цилиндра».

Тип урока. Урок общеметодологической направленности.

Технология. Системно-деятельностный метод обучения.

Цель урока. Обобщить и систематизировать знания по теме «Объем прямой призмы и цилиндра».

Задачи урока.

Образовательные.

Повторить и систематизировать формулы для вычисления объемов куба, прямоугольного параллелепипеда, прямой призмы и цилиндра.

Продолжить формирование навыков решения задач по теме.

Развивающие.

Учить детей приемам мыслительной деятельности. Развивать самостоятельность учащихся, логическое мышление, математическую речь. Способствовать формированию интеллектуальных умений и владению мыслительными операциями, анализом и синтезом, обобщением. Создавать условия для включения каждого ученика в активную учебно-познавательную деятельность. Развивать умение работать с КИМами.

Воспитательная.

Воспитывать стремление учащихся к получению новых знаний. Воспитывать культуру учебного труда. Воспитывать навыки коммуникативной деятельности. Формировать объективную самооценку знаний.

Компетенции, формируемые на уроке.

Общекультурные, учебно-познавательные, информационные, коммуникативные.

УУД, формируемые на уроке.

Л – личностные( определение цели и задач урока, выбор действия по достижению цели, осознание практической важности изучаемой темы)

П – познавательные (использование научных методов познания, умение делать выводы)

Р – регулятивные (умение выявить проблему, умение определять и сохранять цель, контролирование и оценивание своей работы и полученного результата)

К – коммуникативные (восприятие мнения других людей, умение выражать свою точку зрения)

Оборудование.

Презентация, карточки самооценки, карточки с заданиями и критериями оценки.

Ход урока.

Этапы урока

Цель и содержание этапа

Деятельность учителя

Деятельность учащихся

УУД

Оценка результатов деятельности учеников

1. Мотивация к учебной деятельности.

Цель: выработать на личностно значимом уровне внутренней готовности к выполнению нормативных требований учебной деятельности.

— Здравствуйте! Садитесь!

— Проверьте свою готовность к уроку.

— Какую тему мы изучали на прошлом уроке? На последних пяти уроках?

— Известный швейцарский математик Джордж Полиа сказал: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».

— Исходя из этого, сформулируйте тему сегодняшнего урока, а также цель и задачи.

— Данная тема широко представлена в первой части КИМов ЕГЭ по математике и на базовом, и на профильном уровнях. И сегодня мы должны уделить этому внимание.

— Сегодня на уроке мы снова будем пользоваться карточками самооценки. Не забывайте выставлять себе туда оценки.

1. Создает условия для пробуждения внутренней потребности включения в деятельность («хочу»).

2. Актуализирует требования (мотивацию) учебной деятельности («мне надо»).

3. определяет степень сложности учебной деятельности («смогу»).

4. Организует работу по определению темы учебного занятия.

5. Совместно формулируют цели учебного занятия.

Ученики встали, настроились на работу, проверили наличие учебных предметов, поделились эмоциями.

Формулируют тему, цель и задачи урока.

Самоопределение к деятельности (Л);

Планирование учебного сотрудничества с учителем и сверстниками (К).

— Выражение своих мыслей с достаточной полнотой и точностью (К)

— Аргументирование своего мнения и позиции в коммуникации (К)

Психологическая настроенность, готовность к уроку, быстрое включение в работу.

2. Актуализация и пробное учебное действие.

Цель: активизировать мыслительную деятельность учащихся и организовать осознание ими внутренних потребностей к построению способа действий.

— Перед уроком мы проверили домашнее задание.

— А теперь посмотрим как вы усвоили тему предыдущего урока. Решим задачи по теме «Объем цилиндра».

1. Высота бака цилиндрической формы равна 20 см, а площадь его основания 150 см2. Чему равен объем этого бака (в литрах)?

В 1 литре 1000 см3.

2. Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объем второй кружки больше объема первой?

3. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ .

4. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ .

— Оцените решение задач по теме.

— Кто поставил себе «5», «4», «3»?

1. Активизирует мыслительную деятельность обучающихся по выбору способов действий.

2. Проводит проверку домашнего задания и предлагает задания, которые приближают учащихся к восприятию новых знаний.

1. Актуализируют изученный ранее материал.

2. Анализируют действия по заданной теме.

3. Обосновывают выбор способа действий.

4. Выполняют самостоятельно задания на повторение.

— Мыслительные операции (обобщение, анализ, синтез, сравнение) (П)

— Осознанные и произвольные речевые высказывания (К)

— Волевая саморегуляция в затруднении (Р)

— Выражение своих мыслей с достаточной полнотой и точностью (К)

— Аргументирование своего мнения и позиции в коммуникации (К)

Устная оценка учителя.

Самооценка учащихся.

3.Систематизация знаний.

Цель: обеспечить систематизацию знаний и способов действий в памяти учащихся.

— Для того чтобы успешно решать задачи, необходимо повторить основной теоретический материал. Сегодня это формулы для вычисления объемов изученных тел и вычисления площадей многоугольников.

— Я предлагаю вам составить кластер. У вас на партах лежат листы формата А4 с графическими изображениями. Их нужно заполнить необходимыми формулами.

-Возникли ли у вас затруднения? В чем причина этих затруднений? Остались ли у вас незаполненные поля?

— Оцените заполнение кластера.

— Кто поставил себе «5», «4», «3»?

— А теперь перейдем к решению задач по готовым чертежам с целью закрепления формул для вычисления объемов геометрических тел. Эти задачи являются типичными задачами КИМов по изучаемой нами теме.

1. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

2. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

4. Найдите объем правильной шестиугольной призмы, все ребра которой равны .

— Оцените свою работу.

— Кто поставил себе «5», «4», «3»?

Учитель выступает в роли организатора.

Следит за хронометрией урока.

Систематизируют теоретический материал, заполняя кластер.

Решают фронтально несколько типовых заданий на применение полученных знаний.

Проговаривают вслух выполненные шаги решения.

Проверяют и оценивают свои результаты.

Мыслительные операции (П)

Использование знаково-символических средств (П)

Самостоятельное создание способов решения проблем поискового характера (Р)

Адекватное использование речевых средств для решения коммуникативных задач (К)

Выражение своих мыслей с достаточной полнотой и точностью (К)

Аргументирование своего мнения и позиции в коммуникации (к)

Самооценка.

Устная оценка учителя.

4. Включение системы знаний в учебную деятельность.

Цель: формировать учебную деятельность на основе системы знаний об окружающей действительности.

— Мы знаем, что основная трудность, с которой приходится сталкиваться при подготовке к экзамену, — нетипичность формулировок заданий в вариантах ЕГЭ. Поэтому сегодня мы сделаем акцент на решении задач из открытого банка ЕГЭ.

— Наибольшее затруднение вызывают задачи на комбинацию тел, уровень жидкости в сосуде и объем детали сложной формы..

— Я предлагаю поработать в паре.

— Вы решаете задачи.

— Затем заслушаем ваши решения.

Задание для работы в паре.

1.В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. найдите объем детали. Ответ выразите в см3.

2. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.

3. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

4. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

— Заслушиваем краткие решения каждой задачи.

— Оцените свою работу.

Учитель выступает в роли организатора.

Следит за хронометрией урока.

Учащиеся работают в парах с заданиями.

Проговаривают вслух выполненные шаги.

Объясняют свое решение классу.

Формирование способности к новому способу действия

Овладение знаниями и умениями аналитического характера, развитие устной речи учащихся (К).

Развитие познавательного интереса, расширение кругозора учащихся (П). Умение самостоятельно получать новые знания, обобщать и делать выводы; умение анализировать языковой материал (П).

Самооценка. Устная оценка учителя.

5*. Закрепление системы знаний с формулированием проблемы.

Цель: закрепить систему знаний через способы действий.

Самостоятельная работа.

— Перед вами лежат задания, в варианте десять задач. Вам необходимо решить любые три из них. Какие задачи выполнить – выбирайте сами.

— Оцените свою работу.

Учитель выступает в роли организатора.

Следит за хронометрией урока.

Самостоятельно выполняют задания с опорой на систему знаний.

Умение самостоятельно и с помощью учителя получать новые знания, обобщать и делать выводы; умение анализировать языковой материал (П).

Достаточный объем словарного запаса (К).

Самооценка.

6. Рефлексия учебной деятельности.

Цель: самооценка учащимися своей деятельности, метода преодоления трудностей, оценка нового способа действий.

Итак, наш урок подошел к концу.

Поставьте себе общую отметку за урок в оценочном листе.

Кто поставил «5»? «4»? «3»?

Выполнили мы задачи, поставленные перед уроком? Обоснуйте.

Что было самым сложным на уроке? Что понравилось?

Над чем еще нужно поработать каждому их вас?

Организует рефлексию по вопросам и самооценку собственной учебной деятельности.

Соотносят цель и результат учебной деятельности.

Фиксируют степень соответствия.

Личностный результат УУД:

— способность к самооценке.

Оценка деятельности; саморегуляция (Р).

Умение выражать свои мысли (К).

Самооценка. Устная оценка учителя.

7. Домашнее задание.

Повторить формулы для вычисления объемов.

1) Решить остальные задачи на карточке для самостоятельной работы.

2) Подобрать и решить 5 разных задач по теме из вариантов для подготовки к ЕГЭ.

Одно из заданий 1 или 2 на выбор.

Инструктаж.

Определяет домашнее задание.

Слушают, записывают, уточняют способы работы и ее объем.

Планирование, прогнозирование (Р), оценивание трудности выполнения (Л).

Цель урока: Развитие деятельностных способностей у обучающихся в ходе поисковой работы при изучении темы «Нахождение объемов многогранников (прямые призмы, пирамиды) и тел вращения»

Планируемый результат:

Личностные: развивать умение делать выбор методов решения, осуществлять самоконтроль; формировать уважительное отношение обучающихся друг к другу, в том числе людям разного социального статуса.

Метапредметная: уметь применять имеющиеся знания в нестандартных ситуациях.

Предметные: актуализировать знания обучающихся по теме «Нахождение объемов многогранников (прямые призмы, пирамиды) и тел вращения при подготовке к ЕГЭ».

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/419980-tema-uroka-reshenie-zadach-na-nahozhdenie-obe

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Открытый урок в 11 классе по математике подготовка е егэ с презентацией
  • Открытый урок в 11 классе по математике по теме подготовка к егэ
  • Открытый вариант по физике 2022 егэ
  • Открытый вариант по математике 2 егэ
  • Открытый вариант егэ физика 2022

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии