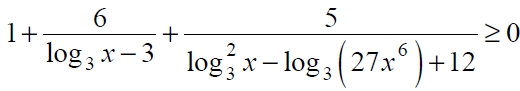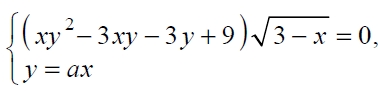ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
ФИПИ опубликовал открытые варианты контрольных измерительных материалов единого государственного экзамена 2022 года.
→ Математика профильная: matematika-prof_var_1_2022.pdf | Разбор
→ Математика базовая: matematika-baz_var_1_2022.pdf | Разбор
→ Русский язык: russkij-jazyk_var_1_2022.pdf | Разбор | Сочинение
Ответы
→ Физика: fizika_var_1_2022.pdf | Разбор
→ Обществознание: obschestvoznanie_var_1_2022.pdf | Разбор
→ Литература: literatura_var_1_2022.pdf
→ Информатика: informatika_var_1_2022.pdf | Доп. файлы: inf_1_ege2022.zip
→ География: geografija_var_1_2022.pdf
→ Биология: biologija_var_1_2022.pdf | Разбор
→ История: istorija_var_1_2022.pdf
Ответы
→ Химия: himija_var_1_2022.pdf
Ответы
→ Английский: angl_1_ege2022.zip
Письменная часть: anglijskij-jazyk-pch_var_1_2022.pdf
Устная часть: anglijskij-jazyk-uch_var_1_2022.pdf
Аудирование: anglijskij-pch-audirovanie.mp3
УЧ (задание 3): anglijskij-uch_zadanie-3.mp3
Ответы
→ Немецкий: nem_1_ege2022.zip
Письменная часть: nemeckij-jazyk-pch_var_1_2022.pdf
Устная часть: nemeckij-jazyk-uch_var_1_2022.pdf
Аудирование: nemeckij-pch-audirovanie.mp3
УЧ (задание 3): nemeckij-uch_zadanie-3.mp3
→ Французский: fran_1_ege2022.zip
Письменная часть: francuzskij-jazyk-pch_var_1_2022.pdf
Устная часть: francuzskij-jazyk-uch_var_1_2022.pdf
Аудирование: francuzskij-pch-audirovanie.mp3
УЧ (задание 3): francuzskij-uch_zadanie-3.mp3
→ Испанский: isp_1_ege2022.zip
Письменная часть: ispanskij-jazyk-pch_var_1_2022.pdf
Устная часть: ispanskij-jazyk-uch_var_1_2022.pdf
Аудирование: ispanskij-pch-audirovanie.mp3
УЧ (задание 3): ispanskij-uch_zadanie-3.mp3
→ Китайский: kit_1_ege2022.zip
Письменная часть: kitajskij-jazyk-pch_var_1_2022.pdf
Устная часть: kitajskij-jazyk-uch_var_1_2022.pdf
Аудирование: kitajskij-pch-audirovanie.mp3
- 01.05.2022
Открытые варианты ЕГЭ за 2022 год, которые являются аналогом вариантов досрочного ЕГЭ 2022 по математике профильного уровня. Ранее ФИПИ публиковал просто варианты после проведения досрочной волны. Но с 2021 года появилась практика называть их «открытыми вариантами», хотя все эксперты сходятся в том, что на самом деле это и есть один из вариантов досрочного ЕГЭ текущего года по математике.
- Реальные варианты ЕГЭ 2022
Открытый вариант, как и демоверсия 2022 года, содержат ответы и разбор второй, сложности части варианта. Мы собрали для вас подробные видеоразборы от репетиторов. Поэтому вы можете не только проверить ответ, но и разобрать каждое задание.
- Другие предметы из открытых вариантов 2022
Некоторые задания из открытого варианта профиля
Задание 8
Имеется два сосуда. Первый содержит 40 кг, а второй — 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится
раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько
процентов кислоты содержится в первом сосуде?
Задание 10
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая
батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того,
что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет
забракована системой контроля.
Задание 11
Найдите наименьшее значение функции y = x x − 9x + 25 на отрезке [1; 50].
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Видеоразбор открытого варианта
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
ФИПИ опубликовал открытые варианты КИМ ЕГЭ 2022 года.
Открытые варианты созданы для ознакомления со сложностью и структурой заданий единого государственного экзамена.
→ русский язык
→ математика профильная
→ математика базовая
→ обществознание
→ физика
→ биология
→ химия
→ история
→ литература
→ информатика → доп. файлы
→ география
→ английский язык
→ китайский язык
→ немецкий язык
→ французский язык
→ испанский язык
Смотрите также:
Коды предметов ЕГЭ 2022
Расписание ЕГЭ 2022
Скачать бланки ЕГЭ 2022
Открытые варианты ЕГЭ 2021 от ФИПИ
Тренировочные варианты ЕГЭ 2022 по русскому языку
Решение заданий Открытого варианта досрочного периода ЕГЭ 2022 по математике (профильный уровень). Официальный досрочный вариант. Досрочник КИМ ФИПИ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.
Задание 1.
Найдите корень уравнения log4(x – 4) = 3.
Задание 2.
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 7 спортсменов из Германии и 9 спортсменов из США. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что двенадцатым будет выступать спортсмен из Германии.
Задание 3.
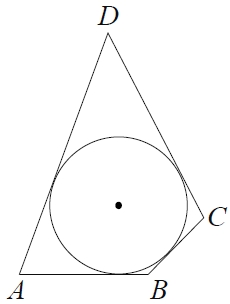
В четырёхугольник ABCD вписана окружность, AB = 10, CD = 17. Найдите периметр четырёхугольника ABCD.
Задание 4.
Найдите значение выражения frac{14^{6,4}cdot 7^{-5,4}}{2^{4,4}}.
Задание 5.
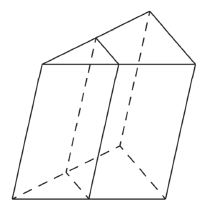
Через среднюю линию основания правильной треугольной призмы, объём которой равен 84, проведена плоскость, параллельная боковому ребру. Найдите объём отсечённой треугольной призмы.
Задание 6.
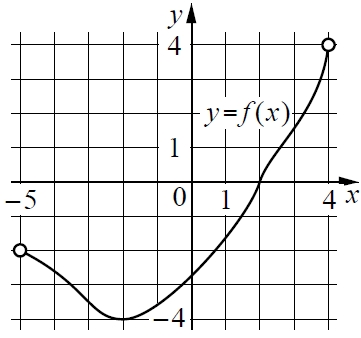
На рисунке изображён график функции y = f (x), определённой на интервале (−5;4). Найдите корень уравнения f ‘(x) = 0.
Задание 7.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 299 МГц. Скорость погружения батискафа v (в м/с) вычисляется по формуле v=ccdot frac{f-f_{0}}{f+f_{0}}, где c =1500 м/с – скорость звука в воде, f0 – частота испускаемых импульсов (в МГц), f – частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 5 м/с. Ответ дайте в МГц.
Задание 8.
Имеется два сосуда. Первый содержит 40 кг, а второй – 25 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 36 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
Задание 9.
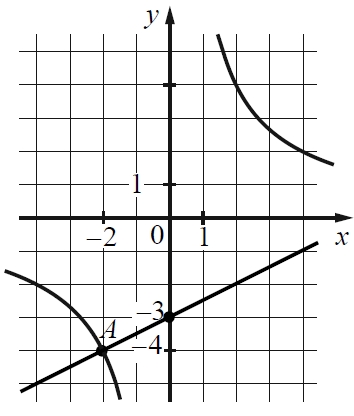
На рисунке изображены графики функций видов f (x) = frac{k}{x} и g (x) = ax + b, пересекающиеся в точках A и B. Найдите абсциссу точки B.
Задание 10.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Задание 11.
Найдите наименьшее значение функции y = x√x − 9x + 25 на отрезке [1; 50].
Задание 12.
а) Решите уравнение 16sin x – 6·4sin x + 8 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-5pi;-frac{7pi}{2}].
Ответ задания: а)frac{pi}{2}+2pi n,frac{pi}{6}+2pi n,frac{5pi}{6}+2pi n,nepsilon Z; \ б)-frac{7pi}{2};-frac{23pi}{6}.
Задание 13.
Различные точки A, B и C лежат на окружности основания конуса с вершиной S так, что отрезок AB является её диаметром. Угол между образующей конуса и плоскостью основания равен 60°.
а) Докажите, что cos∠ASC + cos∠BSC = 1,5.
б) Найдите объём тетраэдра SABC, если SC = 1, cos∠ASC = frac{2}{3}.
Задание 14.
Решите неравенство
Задание 15.
15 декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 16 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг будет возрастать на r % по сравнению с концом предыдущего месяца (r – целое число);
– со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
– 15-го числа каждого месяца с 1-го по 15-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
– 15-го числа 15-го месяца долг должен быть равен 500 тысяч рублей;
– к 15-му числу 16-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что сумма всех платежей после полного погашения кредита будет составлять 1228 тысяч рублей.
Задание 16.
В треугольнике ABC точки M и N лежат на сторонах AB и BC соответственно так, что AM : MB = CN : NB = 2:3. Окружность, вписанная в треугольник ABC, касается отрезка MN в точке L.
а) Докажите, что AB + BC = 4AC.
б) Найдите радиус окружности, вписанной в треугольник ABC, если ML = frac{9}{5}, LN = 3.
Задание 17.
Найдите всe значения параметра a, при каждом их которых система уравнений
имеет ровно три различных решения.
Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S быть равной 16frac{5}{6}?
б) Может ли S быть равной 569frac{29}{126}?
в) Найдите наибольшее целое значение S, если каждое из исходных чисел было трёхзначным.
Ответ задания: а) да; б) нет; в) 2004.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Чтобы получить школьный аттестат, государственный экзамен по математике сдать нужно обязательно. Его результаты влияют на шанс поступления в некоторые вузы на направления подготовки бакалавров и специалистов в областях математики, физики, информатики и некоторых других специальностей. Если в перечне обязательных испытаний вуза стоит «Математика», значит придётся готовиться к профильному уровню. Если она не числится, будет достаточно сдать базу. Уровни отличаются структурой билетов и сложностью. «Базовых» вопросов всего 21 и им достаточно краткого ответа. Профильная версия состоит из двух типов заданий: с кратким и развернутым ответами. В неё входят задачи по чтению графиков, более сложные алгебраические, арифметические и тригонометрические примеры.
Способ подготовки к итоговой проверке каждый определяет сам: можно нарабатывать математические навыки с учителем, репетитором или самостоятельно. Фундаментом могут стать любые учебники, рекомендованные Министерством образования. Успешность подготовки повысится при решении типовых заданий ЕГЭ 2023 от составителя экзаменационных билетов — ФИПИ. В их открытой базе есть все математические задания, которые сдавались в рамках итоговой экзаменации прошлых лет. Задания текущего года попадают в базу данных после того, как прошли досрочные экзамены, в конце учебного года. Шанс увидеть на экзамене билет с уже знакомыми вопросами крайне невелик, но рассмотреть материалы актуального года стоит, чтобы составить общее впечатление о структуре билетов.