Нестандартные способы решения заданий егэ

Нестандартные
способы решения задач ЕГЭ типа С

Попова
Татьяна Спартаковна, учитель математики

 Практика
показывает, что задачи с параметрами представляют для выпускников наибольшую
сложность как в логическом, так и в техническом плане и поэтому умение их решать
во многом предопределяет успешную сдачу экзамена.

На
экзаменах часто встречаются задачи,  отличающиеся большим разнообразием идей и
необходимостью применения очень разные методы решений. Первое решение задачи
редко бывает лучшим, и естественно нужно стремиться к тому, чтобы найти более
простое и красивое решение. Умение выбрать подходящий метод вырабатывается в
процессе решения одной и той же задачи различными методами. Получив несколько
решений данной задачи, нетрудно выделить лучшее и оценить методы решения. 

В
данной работе приведены наиболее рациональные и красивые способы решения
некоторых задач части С, предлагаемых на ЕГЭ. Например, при решении следующей и
подобных ей задач, часто применяется исследование корней квадратного трехчлена
на числовой оси в зависимости от параметра а.  Теперь рассмотрим другое
решение.

1. Найдите все значения а, для которых при
каждом х из промежутка [-3; -1) значение выражения х⁴-7х²-3
не равно значению выражения ах².

            Решение:

Рассмотрим функции у=
х⁴-7х²-3 и у= ах². Введем
замену х²=t. Задача получает следующую формулировку: 

Найдите все
значения а, для которых при каждом t из
промежутка (1; 9] значение выражения t ²-7 t -3
не равно значению выражения аt.

График функции f(t)=
t ²-7 t
-3 представляет собой параболу на
интервале (1;9],  графиком функции у= аt является
прямая, проходящая через начало координат (см. рис1) Значит, нужно найти такие а,
что прямая и парабола на интервале (1; 9] не имеют общих точек. Для этого
найдем значения функции  f(t) на концах интервала: f(1)=-9 и f(9)=15. Так
как а есть тангенс угла наклона прямой у= аt, получаем, что а и а.

1.  Три числа, принадлежащие интервалам (0;2), (2;3), (3;5) являются
   членами арифметической прогрессии. Какие значения может принимать величина
   , если число а принадлежит промежутку
   (0;2), d— разность прогрессии?

Решение: по условию задачи ; ;

На
координатной плоскости с горизонтальной осью d и
вертикальной осью а построим прямые а=0; а=2; а+d=2; а+d=3; а+2d=3; а+2d=5. Замкнутая
область в виде шестиугольника, ограниченная прямыми, есть множество чисел,
удовлетворяющих условию (см. рис2). — уравнение окружности
с центром в начале координат, радиус которой должен принимать значение из
данной области. Наименьшего значения радиус достигает в точке (1;1) и равен , наибольшее значение равно 2,5 в точке
(2,5;0). Ответ: (;2,5).

1. Найти все
   значения а, при которых уравнения  и
    имеют одинаковое число корней.

Решение:

1) Построим графики функций  и у=ах на одной координатной плоскости.
Видно, что при а=0 уравнение имеет 2 корня. Рассмотрим производную функции  при : . Теперь найдем точку касания х₀ и
угловой коэффициент касательной: зная, что угловой коэффициент касательной есть
производная в точке касания х₀ и в то же время тангенс угла наклона
касательной выпишем уравнение . х₀=0. Находим,
что а=4. Значит приуравнение имеет 3 корня. При уравнение имеет 1 корень. Рассматривая
функцию  на промежутках ( находим,
что а=-4. Значит, при    функция имеет 2 корня, при     1 корень.                               
                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

2)
Рассмотрим  и у=ах. Рассуждая аналогично, находим,
что при  и при а=-4 прямая у=ах служит касательной
к графику функции . Делаем вывод, что при а=0 нет
решений, при  и  имеется
1 корень, при  и а=-4  2 корня, при  и  имеется
3 корня. Теперь сопоставляя эти промежутки, выясняем, что при  (-4;0) и (;4) уравнения имеют одинаковое количество
корней.  

Математика, которая мне нравится!

Обучение – ремесло, использующее бесчисленное множество маленьких трюков.

Д. Пойа

МБОУ «Ивановская средняя общеобразовательная школа»

Нестандартные способы решения заданий при подготовке к ГИА.

Мы разработали этот шаблон так, чтобы у каждого члена группы проекта был набор слайдов с собственной темой. Чтобы добавить новый слайд в набор, сделайте следующее.

Укажите, куда вы хотите добавить слайд. Для этого в области эскизов выберите существующий слайд, нажмите кнопку «Создать слайд», а затем выберите макет.

У нового слайда будет такая же тема, как и у ранее выбранного.

Будьте осторожны! Не раздражайте выступающих неожиданной сменой темы. Это может случиться, если выбрать вариант темы на вкладке макетов. В этом случае изменится оформление всех слайдов в презентации.

Подготовила: учитель математики первой квалификационной категории МБОУ «Ивановская СОШ» Минаева И. И.

Решение текстовых задач нестандартным способом

Задача на движение

Пароход вниз по течению реки проплыл путь за 2 часа, а вверх против течения

реки за 3 часа. Сколько времени понадобится плоту, чтобы проплыть тот же путь?

• Решение с помощью дробей:
• Примем за 1 весь путь.
• 1:2=1/2 (расстояния)  — часть пути, которую проплывает катер за 1 час по течению;
• 1:3=1/3 (расстояния)  — часть пути, которую проплывает катер за 1 час против течения;
• Так их разница составляет удвоенную скорость течения, то

(1/2 — 1/3):2=1/12 (расстояния)  — часть пути, которую проплывает плот за 1 час.

• 1:1/12=12 (часов)  — время движения плота.

Ответ: 12 ч

• Решение с помощью уравнения:

• Пусть х км/ч – скорость парохода, а

у км/ч скорость течения реки.

• Составим уравнение:

2( х + у ) = 3( х – у )

х = 5у

2( 5у + у ) = 12у

12у(км) – весь путь.

Т.к. у км/ч- скорость течения, то

время равно 12у : у = 12 ( ч )

Ответ: 12 ч

Задача на части

Мама в три раза старше дочери, папа на четыре года старше мамы,

всем вместе 81 год. Сколько лет папе?

Решение:

• Если бы возраст папы был на  4  года меньше,то всем вместе было бы   
•   81 — 4 = 77 лет.
• Если возраст дочери принять за  1  часть, то возраст мамы составит 3 части, папы  3  части, т.е.  77  лет составят 7  частей .

Поэтому

77:7=11(лет)  возраст дочери;

      11· 3=33(года)  маме,

33+4=37 (лет)  папе

Ответ: 37 лет

Задача на пропорции

Бригада студентов из 16 человек за 20 дней собрала 180 тонн картофеля. Сколько картофеля уберет бригада из 12 человек за 28 дней, если будет работать с такой же производительностью?

Решение — рассуждение:

• 1 человек за 20 дней соберет в 16 раз меньше, т.е. 180/16 т;
• 12 человек за 20 дней соберут в 12 раз больше, т.е. (180/16) · 12 т;
• 12 человек за 1 день соберут в 20 раз меньше, т.е. (180·12/16):20 т;
• 12 человек за 28 дней соберут в 28 раз больше, т.е. (180 · 12/16 · 20) · 28 т.
• Результат вычисления: 189 тонн.
• Ответ: 189 тонн.

Решение с помощью пропорции.

16 чел. – за 20 дней – 180 тонн

12 чел. – за 28 дней – X тонн

12 человек за 28 дней собрали 189 тонн картофеля.

Ответ: 189 тонн.

6

Нестандартные способы решения квадратных уравнений.

Свойства коэффициентов

квадратного уравнения

Пусть дано квадратное уравнение ах 2 + bх + с = 0 , где а ≠0 .

Свойство 1

Если а + b + с = 0 (т. е. сумма коэффициентов уравнения равна нулю), то х 1 = 1, х 2 = с/а

Свойство 2

Если а – b + с = 0, или а + с = b, то х 1 = – 1, х 2 = – с/а

6

Закрепление

х 2 + 4х – 5 = 0              

a = 1, b = 4, c = – 5      

a + b + c = 0                  

x 1 = 1, x 2 = – 5                 

           3х 2 +2х – 1 = 0  

       a = 3, b = 2, c = –1

          a + c = b     

  x 1 = – 1, x 2 = 1/3

6

Свойства коэффициентов

квадратного уравнения

Свойство 3

В уравнении вида ах 2 + (а 2 + 1)х + а = 0 х 1 = -а, х 2 = -1/а

Например

а) 6х 2 + 37х + 6 =0           

a = c = 6, b = 37  =  6 2 +1

x 1 = – 6, x 2 = – 1/6      

6

Свойства коэффициентов квадратного уравнения

Свойство 4

В уравнении вида ах 2 — (а 2 + 1)х + а = 0 х 1 = а, х 2 = 1/а

Например

15х 2 — 226х + 15 =0           

a = c = 15, b = -226 = -(15 2 +1)

x 1 = 15, x 2 = 1/15      

Свойства коэффициентов

квадратного уравнения

Свойство 5

В уравнении вида ах 2 + (а 2 — 1)х — а = 0 х 1 = — а, х 2 = 1/а

Например

17х 2 + 288х — 17 =0           

a = 17, c = -а = -17, b = 288  =  17 2 -1

x 1 = – 17, x 2 = 1/17     

Свойства коэффициентов квадратного уравнения

Свойство 6

В уравнении вида ах 2 — (а 2 — 1)х — а = 0 х 1 = а, х 2 = -1/а

Например

г) 10х 2 — 99х — 10 =0           

a = c = 10, b = 99 =  10 2 -1

x 1 = 10, x 2 = – 1/10      

Вычисление площади многоугольника нестандартным способом

6

Формула Пика, или как считать площади многоугольников. (полезно при решении задач в ОГЭ и ЕГЭ)

Формула Пика (теорема Пика)  — классический результат комбинаторной геометрии и геометрии чисел.

Площадь многоугольника с целочисленными вершинами равна

В + Г/2 − 1,

где В есть количество целочисленных точек внутри многоугольника,

а Г   — количество целочисленных точек на границе многоугольника .

В=7 , Г=8 , В + Г/2 − 1= 10

6

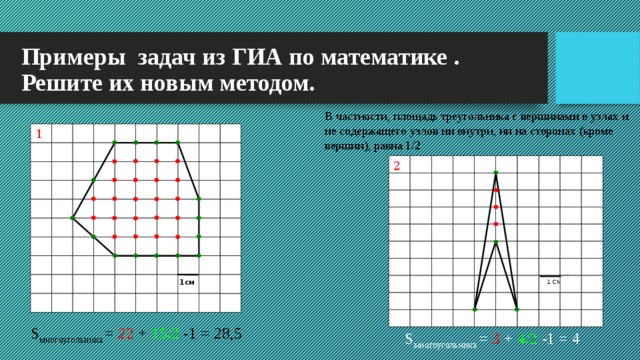
Примеры задач из ГИА по математике . Решите их новым методом.

В частности, площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2

1

2

1см

1 СМ

1 см

S многоугольника = 22 + 15/2 -1 = 28,5

S многоугольника = 3 + 4/2 -1 = 4

16

Нестандартное решение

стереометрических задач

16

Прямоугольный треугольник и его элементы

Пифагоровы числа

Теорема Пифагора:

с²=а²+ b²

а

b

3

5

4

c

12

8

5

13

15

7

24

17

20

21

12

25

35

29

9

37

40

41

А

с

b

В

С

а

Задачи из ГИА

В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SA = 13, BD = 10. Найдите длину отрезка SO.

Решение.

с=13, a=5, b=?

с²=а²+b²

13²=5²+ b²

b²=13²-5², b²=169-25=144, b=12

С

b

a

Ответ: b=12

19

Более сложные задачи ГИА

а

b

3

4

5

c

12

5

8

13

15

7

24

20

17

21

12

25

35

9

29

40

37

41

Решение.

SO=15, SA=25

15

3

25

20

5

4

5

АО=20, значит АС=40

Ответ: 40

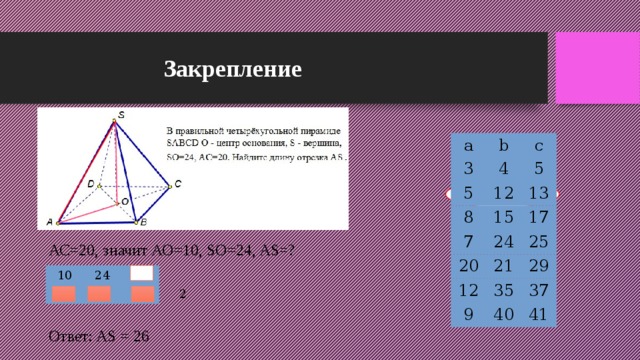
Закрепление

а

b

3

c

4

5

12

8

5

13

15

7

24

17

20

25

21

12

35

9

29

37

40

41

АС=20, значит АО=10, SO=24, AS=?

10

5

24

26

12

13

2

Ответ: AS = 26

Задачи из второй части профильного уровня ЕГЭ

Поэтапно – вычислительный метод

Задача №3. В правильной четырехугольной призме АВСDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 3 : 2. Найдите угол между плоскостями АВС и ВЕD 1 .

1 способ

D 1

О – точка пересечения прямой ED 1 c плоскостью (АВС).

A 1

АPЕ – линейный угол между плоскостями АВС и ВЕD 1

C 1

2

B 1

E

F

5

3

А

O

D

2

P

C

2

В

Координатный метод

E(2;0;3), B(2;2;0), D 1 (0;0;5),

2x+3y+2z-10=0;

(2;3;2)

В правильной четырехугольной призме АВСDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА 1 отмечена точка Е так, что АЕ : ЕА 1 = 3 : 2. Найдите угол между плоскостями АВС и ВЕD 1 .

2 способ

Решение.

z

D 1

C 1

α : a 1 x + b 1 y + c 1 z + d 1 =0

Вектор нормали плоскости α :

(a 1 ; b 1 ; c 1 )

β : a 2 x + b 2 y + c 2 z + d 2 =0

Вектор нормали плоскости β :

A 1

B 1

(a 2 ; b 2 ; c 2 )

(0; 0;5),

D(0;0;0), D 1 (0;0;5), DD 1 (0; 0;5), т. е.

2

F

E

5

a=c

2a+3c+d=0

5c+d=0

2a+2b+d=0

d=-5c

b=1,5c

D

3

C

y

2

А

2

В

x

24

Спасибо за внимание!

Коллеги, желаю Вам успехов и достижений !

Литература и интернет ресурсы :

1) Интернет ресурсы: Википедия: формула Пика;

2) Открытый банк заданий по математике ОГЭ и ЕГЭ на сайте: mathege.ru и mathgia.ru;

• Мне нравится 

Уравнения являются неотъемлемой частью любого задания на экзаменах по математике. Поэтому уравнениям необходимо уделять особое внимание при подготовке к ЕГЭ и ГИА.

Существует ряд нестандартных методов решения уравнений. К числу таких методов относятся, прежде всего, методы, основанные на применении численных неравенств, свойств монотонности или ограниченности функций. В школе изучению таких методов уделяется, к сожалению, мало внимания.

Применение нестандартных методов решения задач по математике требует нетрадиционного мышления, необычных в своей логике рассуждений. Незнание таких методов и приемов существенно уменьшает область успешно решаемых задач по математике и соответственно снижает шансы на получение высокого оценочного балла. Использование нестандартных методов к тому же способствует развитию нового, нешаблонного мышления, которое можно успешно применять и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и т.д.).

Приведенные ниже примеры будут полезны для подготовки к сдаче ЕГЭ и ГИА, а так же для подготовки к поступлению в ВУЗы, особенно в такие, где традиционно предъявляются высокие требования к математическим знаниям.

Пример 1.

Решить уравнение х² – √(56 – х) = 56.

Решение.

В уравнении областью допустимых значений переменной х является решение системы неравенств

{56 – х ≥ 0,
{х² – 56 ≥ 0,

то есть х ≤ -2√14 или 2√14 ≤ х ≤ 56.

Обозначим √(56 – х) = у. Тогда из исходного уравнения получаем систему уравнений

{х² – у = 56,
{у² = 56 – х, где у ≥ 0.

Если из первого уравнения системы вычесть второе уравнение, то получим х² – у – у² = х.

Его можно переписать в виде (х – у)(х + у) – (х + у) = 0 и (х + у)(х – у – 1) = 0.

Из последнего уравнения следует, что для решения системы уравнений необходимо рассмотреть два случая.

1) Пусть х + у = 0. Тогда х = -у. Так как у ≥ 0, то х ≤ 0.

Поскольку у = -х, то из первого уравнения системы получаем уравнение

х² + х = 56 = 0,

которое имеет единственный отрицательный корень х = -8. Поскольку х ≤ -2√14 , то х = -8 является корнем исходного уравнения.

2) Пусть х – у – 1 = 0. Тогда у = х – 1. Так как у ≥ 0, то х ≥ 1.

Отсюда и из области допустимых значений переменной х исходного уравнения следует, что 2√14 ≤ х ≤ 56.

Если у = х – 1, то из первого уравнения системы получаем квадратное уравнение

х² – х – 55 = 0, положительным корнем которого является х = (1 + √221)/2.

Поскольку 2√14 < (1 + √221)/2 < 56 , то найденное значение х также является решение исходного уравнения.

Ответ: -8; (1 + √221)/2.

Пример 2.

Решить уравнение 1/[х] + 1/{х} = 1/х, где [х], {х} – целая и дробная части действительного числа х соответственно.

Решение.

Обозначим [х] = а и {х} = b.

Так как х = [х] + {х}, то уравнение принимает вид

1/а + 1/b = 1/(a + b), где a ≠ 0 и b≠ 0.

Покажем, что полученное уравнение корней не имеет.

С этой целью приведем это уравнение к общему знаменателю и получим уравнение

b(a + b) + a(a + b) = ab, которое равносильно а² + ab + b² = 0.

Так как а² + ab + b² = (a + b/2)² + 3/4b² и b ≠ 0,

то b2 > 0 и а² + ab + b² > 0.

Полученное неравенство и означает, что рассматриваемое уравнение корней не имеет.

Ответ: нет решений.

Пример 3.

Решить уравнение (3 + √(5 – х))^½ = √х.

Решение.

Нетрудно видеть, что областью допустимых значений переменной х из исходного уравнения являются 0 ≤ х ≤ 5.

Поскольку на области допустимых значений х левая часть уравнения представляет собой убывающую функцию, а правая его часть – возрастающую функцию, то уравнение может иметь не более одного корня. Подбором легко определить, что единственным корнем уравнения является х = 4.

Ответ: 4.

Пример 4.

Решить уравнение sin 3x – 2sin 18x · sin x = 3√2 – cos 3x + 2cos x.

Решение.

Представим уравнение в равносильном виде

sin 3x + cos 3x = 3√2 + 2(sin 18x · sin x + cos x).

Воспользуемся дважды неравенством Коши – Буняковского

(a₁b₁ + a₂b₂)² ≤ (a₁² + a₂²)(b₁² + b₂²).

Тогда (sin 3x + cos 3x)² ≤ (1² + 1²)(sin² 3x + cos² 3x) = 2,

(sin 18x · sin x + cos x)² ≤ (sin² 18x + 1²)(sin² x + cos² x) ≤ 2.

Следовательно, sin 3x + cos 3x ≤ √2 и sin 18x · sin x + cos x ≥ -√2.

Если принять во внимание уравнение

sin 3x + cos 3x = 3√2 + 2(sin 18x · sin x + cos x),

то нетрудно заметить, что равенство в нем может достигаться лишь в том случае, когда обе его части равны √2.

Таким образом, получаем систему уравнений

{sin 3x + cos 3x = √2,
{sin 18x · sin x + cos x = -√2.

Так как -1 ≤ sin 18x ≤ 1 и -√2 ≤ sin x + cos x ≤ √2,

то равенство sin 18x · sin x + cos x = -√2 имеет место лишь в том случае, когда

sin 18x = 1 и sin x + cos x = -√2 или

sin 18x = -1 и sin x – cos x = √2.

Следовательно, из системы уравнений получаем совокупность двух систем уравнений:

{sin 3x + cos 3x = √2,
{sin 18x = 1,
{sin x + cos x = -√2.

Или

{sin 3x + cos 3x = √2,
{sin 18x = -1,
{sin x – cos x = √2.

Она равносильна более простой совокупности систем уравнений:

{sin (3x + п/4) = 1,
{sin 18x = 1,
{sin (x + п/4) = -1

или

{sin (3x + п/4) = 1,
{sin 18x = -1,
{sin (x – п/4) = 1.

Решая уравнения каждой системы данной совокупности, получаем:

{x = п/12 · (8n + 1),
{x = п/36 · (4m + 1),
{x = п/4 · (8k – 3)

или

{x = п/12 · (8n + 1),
{x = п/36 · (4m – 1),
{x = п/4 · (8k + 3),

где n, m, k – целые числа.

Для того, чтобы завершить решение уравнения

sin 3x – 2sin 18x · sin x = 3√2 – cos 3x + 2cos x,

необходимо построить пересечение множеств решений каждого из уравнений систем совокупности.

Рассмотрим первую систему уравнений совокупности.

Пусть п/12 · (8n + 1) = п/36 · (4m + 1).

Тогда 3 · (8n + 1) = 4m + 1 и 12n + 1 = 2m.

Так как для произвольных целых n и m левая часть равенства 12n + 1 = 2m является нечетной, а правая его часть – четной, то данная система уравнений является несовместной.

Рассмотрим вторую систему уравнений совокупности.

Пусть п/12 · (8n + 1) = п/36 · (4m – 1). Отсюда 3 · (8n + 1) = 4m – 1 и 6n + 1 = m.
Тогда х = п/36 · (4m – 1) = п/36 · (4 · (6n + 1) – 1) = п/12 · (8n + 1).

Далее построим пересечение с множеством решений третьего уравнения, т.е.

пусть п/12 · (8n + 1) = п/4 · (8k + 3).

Отсюда получаем 8n + 1 = 3 · (8k + 3) и n = 3k + 1.

Тогда результатом пересечения множеств решений всех трех уравнений второй системы уравнений совокупности является

х = п/12 · (8n + 1) = п/12 · (8 · (3k + 1) + 1) = п/4 · (8k + 3), где k – целое число.

Ответ: п/4 · (8k + 3), где k – целое число.

 Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Необходимая теория

Натуральные числа — это числа 1,2,3, … – то есть те, что мы используем для счёта предметов. Ноль не является натуральным числом. Множество натуральных чисел обозначается N.

Целые числа — это 0,±1,±2,±3 … Множество целых чисел обозначается Z.

Рациональные — числа, которые можно записать в виде дроби , где р – целое, а q – натуральное. Например, – рациональные числа. Рациональные числа – это периодические десятичные дроби. Множество рациональных чисел обозначается Q

Иррациональные числа – те, которые нельзя записать в виде или в виде периодической десятичной дроби. Числа π и е, – иррациональные.

Множества рациональных и иррациональных чисел вместе образуют множество действительных чисел R.

Дальше мы будем говорить о натуральных числах.

Число a делится на число b не равное нулю, если найдется такое число c такое, что a = bc. Например, 15 делится на 3, а 49 делится на 7. Обозначается это так: a ⋮ b
Если a делится на b, то число b называется делителем числа a.
— Если числа a и b делятся на c, то a + b тоже делится на c.
— Если числа a и b делятся на c, а m и n – целые, то ma + nb тоже делится на c

Признаки делимости:

a ⋮ 2 ⇔ последняя цифра числа a четная.
a ⋮ 3 ⇔ сумма цифр числа a делится на 3;
a ⋮ 5 ⇔ число a заканчивается на 0 или на 5;
a ⋮ 4 ⇔ число, составленное из двух последних цифр числа a, делится на 4.
a ⋮ 8 ⇔ число, составленное из трех последних цифр числа a, делится на 8.
a ⋮ 9 ⇔ сумма цифр числа a делится на 9.
a ⋮10 ⇔ последняя цифра числа a равна 0;
a ⋮11 ⇔ суммы цифр на четных и нечетных позициях числа a равны или их разность кратна 11.

Формула деления с остатком. Если a = bс + r, то число а делится на b с остатком r. Немного непривычно, что формула деления с остатком не содержит знака деления.

Например, при делении 9 на 4 мы получаем частное 2 и остаток 1, то есть 9 = 4∙2 + 1.
При делении 53 на 5 мы получим 10 и в остатке 3, то есть 53 = 5∙10 + 3.
Остаток от деления любого нечётного числа на 2 равен единице. Поэтому любое нечётное число может быть записано в виде 2n + 1, а четное – в виде 2n.

Простые числа – те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19…

Любое натуральное число можно разложить на простые множители.

Например, 72 = 2∙2∙2∙3∙3, а 98 = 2∙7∙7.

Основная теорема арифметики: любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.

Например, 72 = 2³∙3²; 98 = 2∙7².

Количество делителей натурального числа равно .

Наименьшее общее кратное двух чисел (НОК) — это наименьшее число, которое делится на оба данных числа.
Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое делятся два данных числа.

Многие нестандартные задачи решаются с помощью метода «Оценка плюс пример».

«Оценка плюс пример» — это специальное математическое рассуждение, которое применяется в некоторых задачах при нахождении наибольших или наименьших значений.

Предположим, что мы ищем наименьшее значение некоторой величины A. Действуем в два этапа.
1. Оценка. Показываем, что выполнено неравенство A ≥ α.
2. Пример. Предъявляем пример, когда достигается равенство A = α.

Примеры решения нестандартных задач:

1. Два брата продали стадо овец, выручив за каждую овцу столько рублей, сколько было в стаде овец. Решив разделить выручку поровну, они поступили следующим образом: каждый брат, начиная со старшего, брал из общей суммы по 10 рублей. После того, как в очередной раз старший брат взял 10 рублей, остаток от выручки оказался меньше 10 рублей. Желая его компенсировать, старший брат отдал младшему свой нож. Во сколько рублей был оценен этот нож? (Все суммы денег – целое количество рублей).

Посмотреть решение (задача 2)

2.

На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.

а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?

б) Может ли ровно одно число на доске оканчиваться на 6?

в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Посмотреть решение

Нестандартные задачи на ЕГЭ — это задачи на числа и их свойства. В вариантах ЕГЭ это задача № 19.