На рисунке изображены графики двух линейных функций найдите абсциссу точки пересечения графиков егэ - Помощь в подготовке к экзаменам и поступлению

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Линейные функции

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 10 № 508895

На рисунке изображён график функции Найдите

Аналоги к заданию № 508895: 508896 508897 508898 508899 508900 508901 508902 Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 10 № 508903

На рисунке изображён график функции Найдите значение x, при котором

Аналоги к заданию № 508903: 508904 508905 508906 508907 508908 508909 508910 Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 10 № 509197

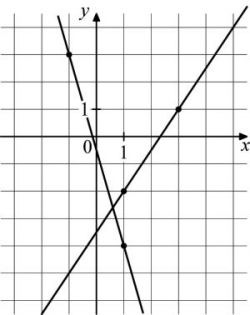
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Аналоги к заданию № 509197: 509213 509241 509198 509199 509200 509201 509202 509203 509204 509205 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 10 № 509229

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Аналоги к заданию № 509229: 509237 509230 509231 509232 509233 509234 509235 509236 509238 509239 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 10 № 621771

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Решение:

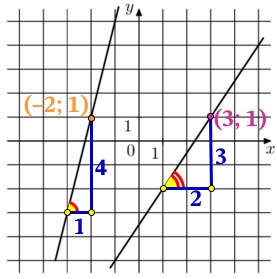
На рисунке изображены прямые, линейных функции их вид имеет вид:

y = kx + b

Найдём k и b функции справа.
k – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:

k=tg{color{Red}alpha}=frac{color{Blue} 3}{color{Blue} 2}=1,5

Подставим в общий вид функции значение k и координаты точки (3; 1) найдём b:

y = kx + b
1 = 1,5·3 + b
1 = 4,5 + b
1 – 4,5 = b
–3,5 = b

Функции справа имеет вид:

y = 1,5x – 3,5

Найдём k и b функции слева.

k=tg{color{Red}alpha}=frac{color{Blue} 4}{color{Blue} 1}=4

Подставим в общий вид функции значение k и координаты точки (–2; 1) найдём b:

y = kx + b
1 = 4·(–2) + b
1 = –8 + b
1 + 8 = b
9 = b

Функции слева имеет вид:

y = 4x + 9

В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения:

1,5x – 3,5 = 4x + 9
1,5x – 4x = 9 + 3,5
–2,5x = 12,5
x=frac{12,5}{–2,5}=-5

Ответ: –5.

Источник

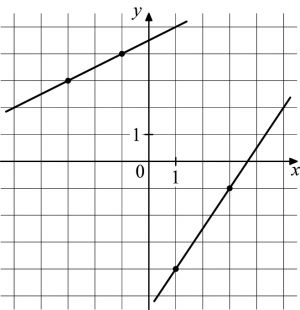
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

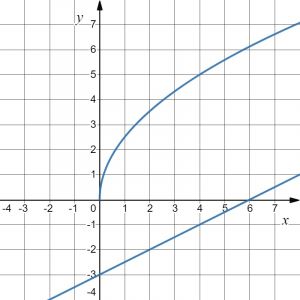
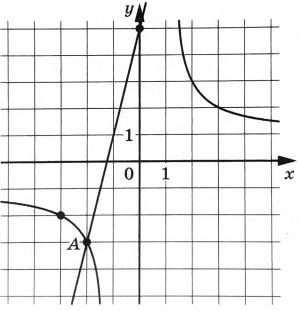
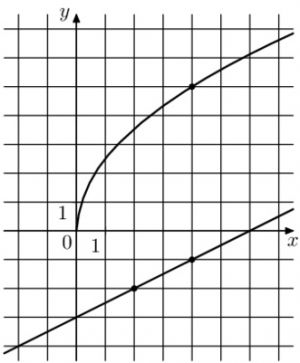
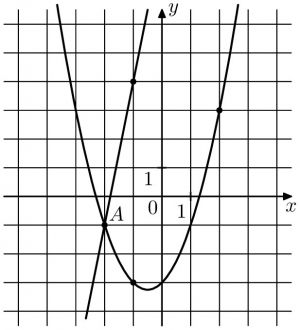
На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точке A. Найдите ординату точки A.

На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.

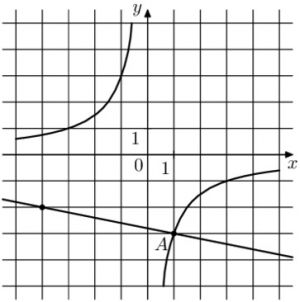
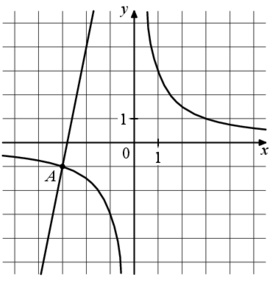
На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках (A(-2;-3)) и (B(x_0;y_0)). Найдите (x_0).

На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках A и B. Найдите ординату точки B.

На рисунке изображены графики функций (f(x)=asqrt{x}) и (g(x)=kx+b), которые пересекаются в точке A. Найдите абсциссу точки A.

На рисунке изображены графики функций (f(x)=dfrac{k}{x}) и (g(x)=ax+b), которые пересекаются в точках A и B. Найдите абсциссу точки B.

На рисунке изображены графики функций (f(x)=3x+3) и (g(x)=ax^2+bx+c), которые пересекаются в точках (A(-1;0)) и (B(x_0;y_0)). Найдите (y_0).

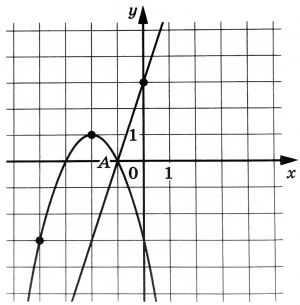
На рисунке изображены графики функций (fleft(xright)=5x+9) и (gleft(xright)=ax^2+bx+c), которые пересекаются в точках А и В. Найдите абсциссу точки В.

На рисунке изображены графики двух линейных функций. Найдите абциссу точки пересечения графиков.

Источник

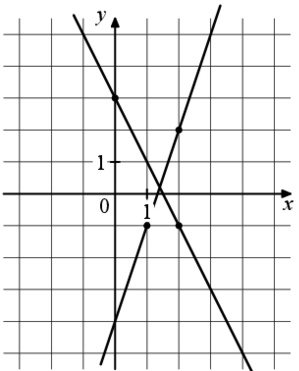
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков

Статград Тренировочная работа №1 28.09.2021 Вариант МА2110109 Задание 9 № задачи в базе 2989

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков

Ответ: -12

ФИПИ 2023 🔥 …

Примечание: На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков ! Статград Тренировочная работа №1 28.09.2021 Вариант МА2110109 Задание 9

Рейтинг сложности задачи:

Графическое решение

Источник

На рисунке изображены графики двух линейных

Здравствуйте, несколько задачек на простейшую функцию. Изображен график прямой, указаны точки. Требуется найти значение функции в определённой точке, или точку при данном значении. Также еще даны две прямые, необходимо найти координату точки пересечения.

508895. На рисунке изображен график функции f (x)=kx+b. Найдите f (-5).Даны две точки (-1;-3) и (3;4). Можем составить систему и вычислить коэффициенты:

Подставляем полученный коэффициент в одно из уравнений и вычисляем b:Имеем функцию:Вычисляем:

Ответ: -10

*Найдите значение х, при котором f (х)= -13,5

509197. На рисунке изображены графики двух линейных функции. Найдите абсциссу точки пересечения графиков.

Необходимо найти уравнения прямых. Далее решить систему. Ее решение будет являться координатой точки пересечения данных прямых.

Общее уравнение прямой имеет вид f (x)=kx+b. Имеем координаты точек: для первой прямой (-3;-3) и (-2;1). Для второй прямой (1;-2) и (3;1).

Первая прямая:*Вычли из первого второе почленно. Следовательно b равно:Получили уравнение f (x)=4x+9.

Вторая прямая:*Вычли из первого второе почленно.

Следовательно:Получили уравнение f (x)=1,5x-3,5

Решаем систему:Таким образом, координата точки пересечения прямых (–5; –11). Абсцисса равна –5, ордината –11.

509229. На рисунке изображены графики двух линейных функции. Найдите абсциссу точки пересечения графиков.

Аналогично предыдущей задаче. Имеем координаты точек: для первой прямой (–2;4) и (–1; –1). Для второй прямой (–1;2) и (2; –1).

Вычислим коэффициенты для первой прямой (подставляем координаты):*Вычли из первого второе почленно.

Следовательно:Получили уравнение f (x)= –5x–6

Второе уравнение:*Вычли из первого второе почленно. Вычисляем b:Получили уравнение f (x)= –x+1

Решаем систему:Таким образом, координата точки пересечения прямых (–1,75;2,75). Абсцисса равна –1,75, ордината 2,75.

Учитесь с удовольствием!

С уважением, Александр.

Категория: Графики функций | ЕГЭ-№10

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Источник

Задание #1851

#1851

Сложность «Легко»

№ 509199

Официальное задание из открытого банка ЕГЭ

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Ответ / Решение

Параметры задания

comment Комментарии

Чтобы оставлять комментарии, необходимо войти.

Войти

Источник

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков

Статград Тренировочная работа №1 28.09.2021 Вариант МА2110109 Задание 9 № задачи в базе 2989

На рисунке изображены графики двух линейных

Задание #1851

Новое и интересное на сайте: