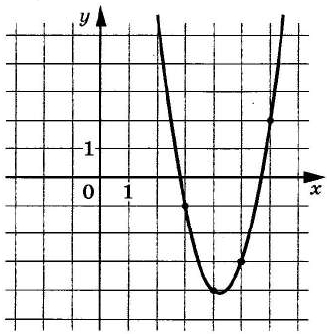
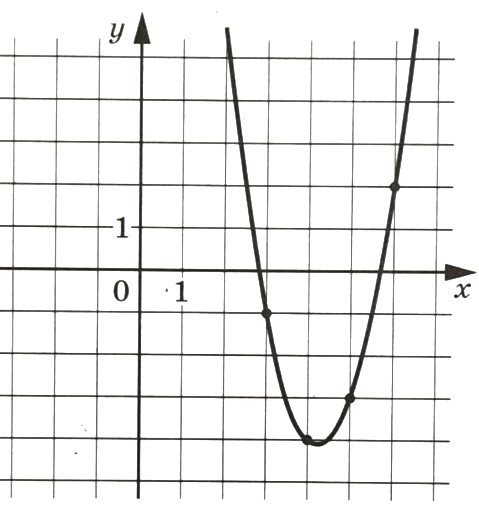
На рисунке изображён график функции f(x) = ax2 + bx + c. Найдите с.
Источник: Ященко ЕГЭ 2023 (36 вар)
Решение:
Возьмём 3 точки принадлежащие графику функции и составим систему из трёх уравнений:
begin{cases} 2=acdot 6^{2}+bcdot 6+c \ -1=acdot 3^{2}+bcdot 3+c \ -3=acdot 5^{2}+bcdot 5+cend{cases}\begin{cases} 2=acdot 36+bcdot 6+c \ -1=acdot 9+bcdot 3+c : \ -3=acdot 25+bcdot 5+cend{cases}\вычтем :1е :уравнение :из: 2го :и: 3го :уравнения:\begin{cases}-1-2=acdot 9-acdot 36+bcdot 3-bcdot 6+c-c : \ -3-2=acdot 25-acdot 36+bcdot 5-bcdot 6+c-cend{cases}\begin{cases}-3=-acdot 27-bcdot 3 : \ -5=-acdot 11-b:{color{Blue} |cdot 3} end{cases}\begin{cases}-3=-acdot 27-bcdot 3 : \ -15=-acdot 33-bcdot 3end{cases}\вычтем: 2е: уравнение: из :1го: уравнения:\-3-(-15)=-acdot 27-(-acdot 33)-bcdot 3-(-bcdot 3)\-3+15=-acdot 27+acdot 33-bcdot 3+bcdot 3 \12=acdot 6\a=frac{12}{6}=2
Найдём b, подставив значение а = 2 в любое из уравнений после вычитания из них 1-го уравнения:
–3 = –a·27 – b·3
–3 = –2·27 – b·3
–3 = –54 – b·3
–3 + 54 = –3·b
51 = –3·b
b=frac{51}{-3}=-17
Подставим значения а и b в любое из уравнений, найдём с:
-1=acdot 9+bcdot 3+c \-1=2cdot 9+(-17)cdot 3+c \-1=18-51+c \-1=-33+с\-1+33=с\с=32
Ответ: 32.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 44
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
На чтение 2 мин. Просмотров 4.2k.
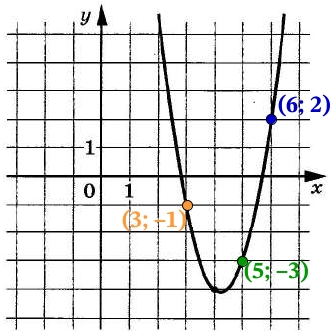
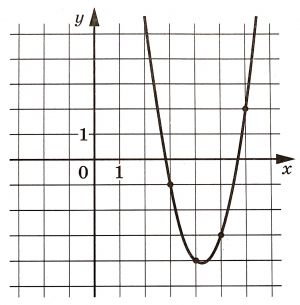
На рисунке изображён график функции f (x)=ax^2+bx+c. Найдите c.
Решение:
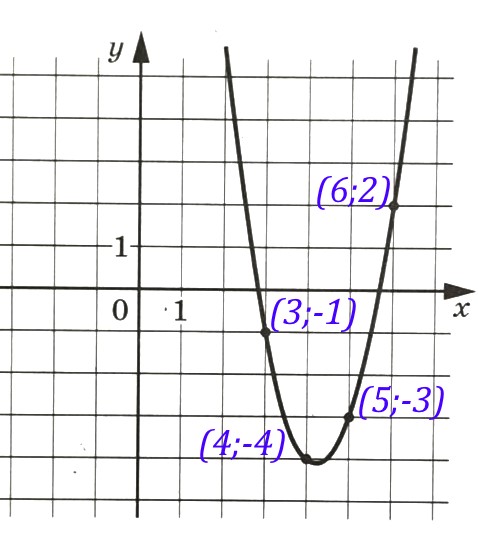
Нам даны точные координаты четырех точек — они отмечены на рисунке точками. Это точки с координатами (3; -1), (4; -4), (5; -3), (6; 2).
В уравнении f (x)=ax^2+bx+c три неизвестных, значит, нам достаточно взять три точки и подставить их координаты в уравнение функции, а затем решить полученную систему из трех уравнений с тремя неизвестными.
Итак, получим:
begin{cases} 9a+3b+c=-1 (1), \ 16a+4b+c=-4 (2), \ 25a+5b+c=-3 (3). end{cases}
От второго уравнения системы отнимем первое уравнение:
16a-9a+4b-3b+c-c=-4- (-1)
7a+b=-3
Теперь отнимем от (3) -го (2) -е уравнение, получим:
25a-16a+5b-4b+c-c=-3- (-4)
9a+b=1
И нашу систему можно записать в виде:
begin{cases} 9a+3b+c=-1, \ 7a+b=-3, \ 9a+b=1. end{cases}
Теперь из (3) вычтем (2):
9a-7a+b-b=1- (-3)
2a=4
a=2
Найдем b из равенства: 9a+b=1; b=1-9a=1-18=-17
Полученные значения и
подставим в (1):
9a+3b+c=-1
9 cdot 2+3 cdot (-17)+c=-1
18-51+c=-1
c=-1+51-18
c=50-18
c=32
Уравнение функции тогда f (x)=2x^2-17x+32
Проверим правильность найденной функции, подставив в полученное уравнение координаты четвертой точки (6; 2), которые мы не использовали для составления системы уравнений:
2=2 (6)^2-17 cdot 6+32
2=72-102+32
2=-30+32
2=2
Все верно. Таким образом, значение с=32.
Ответ: 32.
( 2 оценки, среднее 5 из 5 )
1
2
3
4
5
6
7
8
9
На рисунке изображён график функции
Найдите значение f(8).
10
На рисунке изображён график функции
Найдите значение f(0,5).
11
Источник: ЕГЭ по математике 28.03.2022. Досрочная волна. Москва. Вариант 1
12
13
На рисунке изображён график функции newline $fleft(xright)=2x^{2} +bx+c$. Найдите $fleft(-3right)$.
14
На рисунке изображён график функции newline $fleft(xright)=-2x^{2} +bx+c$. Найдите $fleft(3right)$.
15
На рисунке изображён график функции $fleft(xright)=-2x^{2} +bx+c$. Найдите $fleft(-2right)$.
16
На рисунке изображён график функции $fleft(xright)=x^{2} +bx+c$. Найдите $fleft(-1right)$.
17
На рисунке изображён график функции newline $fleft(xright)=2x^{2} +bx+c$. Найдите $fleft(-6right)$.
18
На рисунке изображён график функции $fleft(xright)=-x^{2} +bx+c$. Найдите $fleft(-8right)$.
19
20
На рисунке изображён график функции $fleft(xright)=ax^{2} -8x+c$. Найдите $fleft(-2right)$.
21
На рисунке изображён график функции $fleft(xright)=ax^{2} -3x+c$. Найдите $fleft(5right)$.
22
На рисунке изображён график функции newline $fleft(xright)=ax^{2} -7x+c$. Найдите $fleft(7right)$.
23
На рисунке изображён график функции $fleft(xright)=ax^{2} +10x+c$. Найдите $fleft(-1right)$.
24
На рисунке изображён график функции $fleft(xright)=ax^{2} -17x+c$. Найдите $fleft(1right)$.
25
На рисунке изображён график функции $fleft(xright)=ax^{2} -13x+c$. Найдите $fleft(-0,5right)$.
26
27
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+2$. Найдите $fleft(-3right)$.
28
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx-3$. Найдите $fleft(8right)$.
29
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+4$. Найдите $fleft(6right)$.
30
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+4$. Найдите $fleft(-8right)$.
31
На рисунке изображён график функции newline $fleft(xright)=ax^{2} +bx+11$. Найдите $fleft(0,5right)$.
32
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx-31$. Найдите $fleft(2right)$.
33
Источник: А. Ларин: Тренировочный вариант № 100.
34
На рисунке изображён график функции newline $fleft(xright)=ax^{2} +bx+c$. Найдите $fleft(-7right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
35
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$. Найдите $fleft(10right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
36
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$. Найдите $fleft(2right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
37
На рисунке изображён график функции mbox{$fleft(xright)=ax^{2} +bx+c$}. Найдите $fleft(-2right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
38
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$. Найдите $fleft(-1right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
39
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$. Найдите $fleft(1right)$.
Источник: А. Ларин: Тренировочный вариант № 100.
40
41
На рисунке изображён график функции linebreak $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(2right)$.
42
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(-1right)$.
43
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(-8right)$.
44
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(-1right)$.
45
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(1right)$.
46
На рисунке изображён график функции $fleft(xright)=ax^{2} +bx+c$, где числа $a$, $b$ и $c$~— целые. Найдите $fleft(-6right)$.
Источник: А. Ларин: Тренировочный вариант № 110.
Задание:
На рисунке изображен график функции вида f(x)=ax2+bx+c. Найдите c.
Ответ: 32
Решение:
Подробное решение
Решение из Youtube-канала uchus.online
- 1
- 2
- 3
- 4
- 5
Оценка: 5.0 из 1
Комментарии
Всего комментариев: 0
|
|||
|
|||
|
💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.
|
3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10] |
Смотреть видеоразбор похожего >> |
|
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74] |
Смотреть видеоразбор похожего >> |
|
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19] |
Смотреть видеоразбор похожего >> |
|
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49] |
Смотреть видеоразбор похожего >> |
|
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29] |
Смотреть видеоразбор похожего >> |
|
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17] |
Смотреть видеоразбор похожего >> |
|
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5] |
Смотреть видеоразбор похожего >> |
|
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6] |
Смотреть видеоразбор похожего >> |
|
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6] |
Смотреть видеоразбор похожего >> |
|
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1] |
Смотреть видеоразбор похожего >> |
|
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3] |
Смотреть видеоразбор похожего >> |
|
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64] |
Смотреть видеоразбор похожего >> |
|
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2] |
Смотреть видеоразбор похожего >> |
|
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82] |
Смотреть видеоразбор похожего >> |
|
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22] |
Смотреть видеоразбор похожего >> |
|
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4] |
Смотреть видеоразбор похожего >> |
|
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8] |
Смотреть видеоразбор похожего >> |
|
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7] |
Смотреть видеоразбор похожего >> |
|
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29] |
Смотреть видеоразбор похожего >> |
|
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38] |
Смотреть видеоразбор похожего >> |
|
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2] |
Смотреть видеоразбор похожего >> |
|
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20] |
Смотреть видеоразбор похожего >> |
|
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08] |
Смотреть видеоразбор похожего >> |
|
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4] |
Смотреть видеоразбор похожего >> |
|
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3] |
Смотреть видеоразбор похожего >> |
|
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8] |
Смотреть видеоразбор похожего >> |
|
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9] |
Смотреть видеоразбор похожего >> |
|
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13] |
Смотреть видеоразбор похожего >> |
|
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24] |
Смотреть видеоразбор похожего >> |
|
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1] |
Смотреть видеоразбор похожего >> |
|
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5] |
Смотреть видеоразбор похожего >> |
ЕГЭ Профиль №10. Парабола
Скачать файл в формате pdf.
ЕГЭ Профиль №10. Парабола
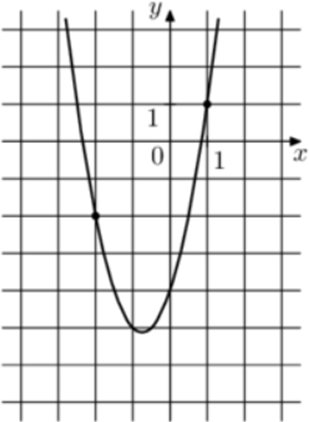
| Задача 1. На рисунке изображён график функции (fleft( x right) = 2{x^2} + b,x + c.) Найдите (fleft( { — 5} right).)
Ответ
ОТВЕТ: 31. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 2 + b + c,,,,}\{ — 2 = 8 — 2b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 6 + 3b,,,,,,, Leftrightarrow ,,,,,,,b = 3.) Тогда: (1 = 2 + 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 5} right) = 2 cdot {left( { — 5} right)^2} + 3 cdot left( { — 5} right) — 4 = 31.) Ответ: 31. |
|
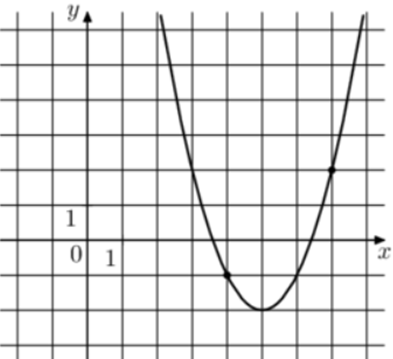
| Задача 2. На рисунке изображён график функции (fleft( x right) = {x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {4; — 1} right)) и (left( {6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 16 + 4b + c,,,,}\{ — 1 = 36 + 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 20 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 10.) Тогда: ( — 1 = 16 — 40 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
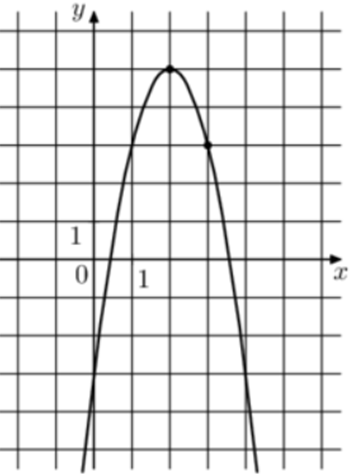
| Задача 3. На рисунке изображён график функции (fleft( x right) = — 2{x^2} + b,x + c.) Найдите (fleft( 6 right).)
Ответ
ОТВЕТ: — 27. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = — 2 + b + c,,,,,,,,}\{3 = — 18 + 3b + c,,,}end{array}} right.)Вычтем из первого уравнения второе: (0 = 16 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = 8.)Тогда: (3 = — 2 + 8 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 6 right) = — 2 cdot {6^2} + 8 cdot 6 — 3 = — 27.) Ответ: – 27. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 6 right) = — 2 cdot {left( {6 — 2} right)^2} + 5 = — 27.) Ответ: – 27. |
|
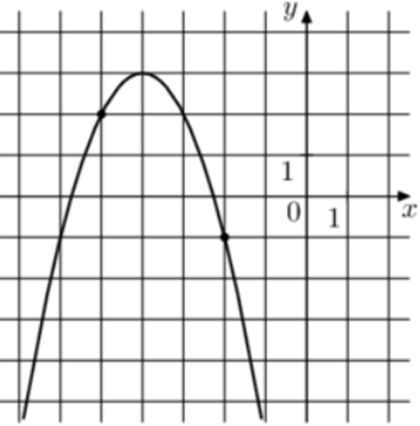
| Задача 4. На рисунке изображён график функции (fleft( x right) = — {x^2} + b,x + c.) Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 3;2} right)) и (left( { — 5;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = — 9 — 3b + c,,,,,,,,}\{2 = — 25 — 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = 16 + 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 8.) Тогда: (2 = — 9 + 24 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} + 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
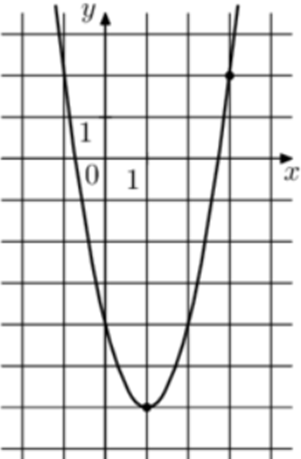
| Задача 5. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 4,x + c.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: 26. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1; — 6} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 6 = a — 4 + c,,,,,,,,}\{2 = 9a — 12 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 8 = — 8a + 8,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 6 = 2 — 4 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 4x — 4) и (fleft( { — 3} right) = 2 cdot {left( { — 3} right)^2} — 4 cdot left( { — 3} right) — 4 = 26.) Ответ: 26. 2 Способ Заметим, что графиком является парабола (fleft( x right) = 2{x^2}), вершина которой находится в точке (left( {1; — 6} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = 2{left( {x — 1} right)^2} — 6) и (fleft( { — 3} right) = 2 cdot {left( { — 3 — 1} right)^2} — 6 = 26.) Ответ: 26. |
|
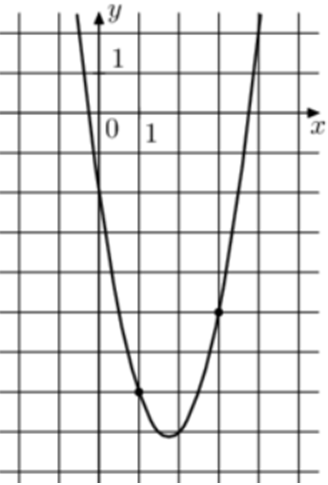
| Задача 6. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 7,x + c.) Найдите (fleft( 7 right).)
Ответ
ОТВЕТ: 47. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 7} right)) и (left( {3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 7 = a — 7 + c,,,,,,,,}\{ — 5 = 9a — 21 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 8a + 14,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 7 = 2 — 7 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 7x — 2) и (fleft( 7 right) = 2 cdot {7^2} — 7 cdot 7 — 2 = 47.) Ответ: 47. |
|
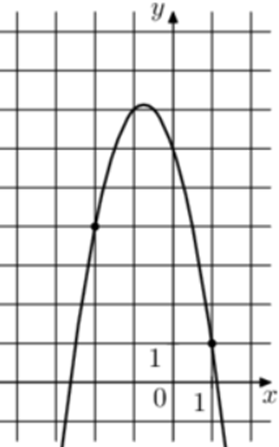
| Задача 7. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 3,x + c.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: — 14. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a — 3 + c,,,,,,,,}\{4 = 4a + 6 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (1 = — 2 — 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 6.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 3x + 6) и (fleft( { — 4} right) = — 2 cdot {left( { — 4} right)^2} — 3 cdot left( { — 4} right) + 6 = — 14.) Ответ: – 14. |
|
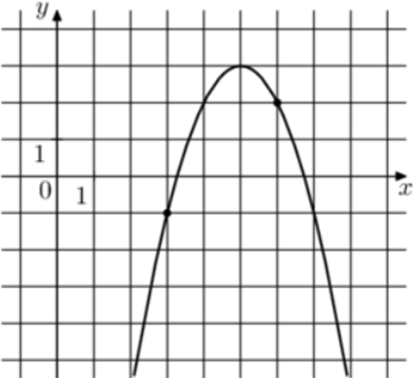
| Задача 8. На рисунке изображён график функции (fleft( x right) = a,{x^2} + 10,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 33. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {3; — 1} right)) и (left( {4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 9a + 30 + c}\{2 = 16a + 40 + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — 10,,,,,,, Leftrightarrow ,,,,,,,a = — 1.) Тогда: ( — 1 = — 9 + 30 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 22.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} + 10x — 22) и (fleft( { — 1} right) = — {left( { — 1} right)^2} + 10 cdot left( { — 1} right) — 22 = — 33.) Ответ: – 33. 2 способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( {5;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x — 5} right)^2} + 3) и (fleft( { — 1} right) = — {left( { — 1 — 5} right)^2} + 3 = — 33.) Ответ: – 33. |
|
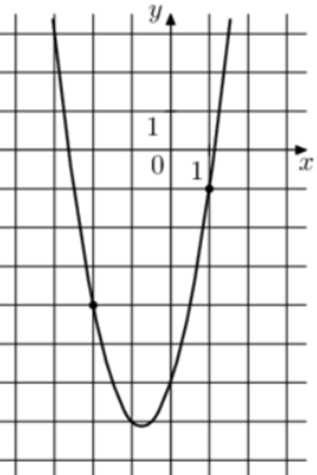
| Задача 9. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 6.) Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: 48. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 1} right)) и (left( { — 2; — 4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6,,,,,,,,,,,,,,,,,,,,,}\{ — 4 = 4a — 2b — 6left| {:left( { — 2} right)} right.,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{ — 1 = a + b — 6}\{2 = — 2a + b + 3}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 1 = 2 + b — 6,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 6) и (fleft( { — 6} right) = 2 cdot {left( { — 6} right)^2} + 3 cdot left( { — 6} right) — 6 = 48.) Ответ: 48. |
|
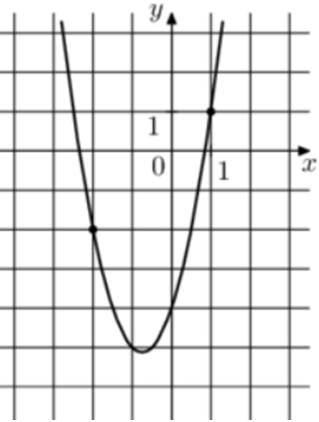
| Задача 10. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 4.) Найдите (fleft( { — 4} right).)
Ответ
ОТВЕТ: 16. |
 |
|
Решение
Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,,,,,,,,,,,,,,,,,,,}\{-2 = 4a — 2b — 4left| {:left( { — 2} right)} right.,,,}end{array},,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{*{20}{c}}{1 = a + b — 4,,,,,,,}\{1 = — 2a + b + 2}end{array}} right.} right.) Вычтем из первого уравнения второе: (0 = 3a — 6,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = 2 + b — 4,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 4} right) = 2 cdot {left( { — 4} right)^2} + 3 cdot left( { — 4} right) — 4 = 16.) Ответ: 16. |
|
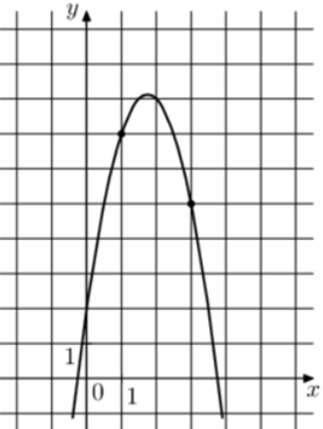
| Задача 11. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + 2.) Найдите (fleft( { — 3} right).)
Ответ
ОТВЕТ: — 37. |
 |
|
Решение
Парабола проходит через точки (left( {1;7} right)) и (left( {3;5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{7 = a + b + 2,,,,,,,,}\{5 = 9a + 3b + 2,,,,}end{array},,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b,,,,,,,,,,,,}\{3 = 9a + 3bleft| {:3} right.}end{array}} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b}\{1 = 3a + b}end{array}} right.,,,,,,,,,) Вычтем из первого уравнения второе: (4 = — 2a,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (5 = — 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 7x + 2) и (fleft( { — 3} right) = — 2 cdot {left( { — 3} right)^2} + 7 cdot left( { — 3} right) + 2 = — 37.) Ответ: – 37. |
|
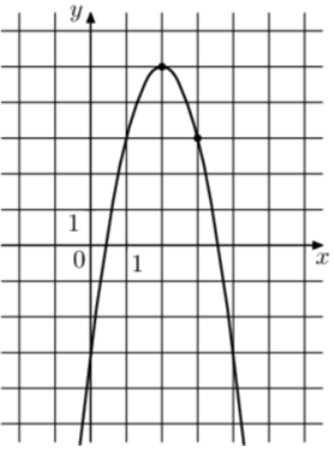
| Задача 12. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 3.) Найдите (fleft( 8 right).)
Ответ
ОТВЕТ: — 67. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = a + b — 3,,,,,,,,,,,,,,,,,,}\{3 = 9a + 3b — 3left| {:3} right.,,,,,}end{array},,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{3 = a + b — 3}\{1 = 3a + b — 1}end{array}} right.} right.) Вычтем из первого уравнения второе: (2 = — 2a — 2,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (3 = — 2 + b — 3,,,,,,,, Leftrightarrow ,,,,,,,,b = 8.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 8 right) = — 2 cdot {8^2} + 8 cdot 8 — 3 = — 67.) Ответ: – 67. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 8 right) = — 2 cdot {left( {8 — 2} right)^2} + 5 = — 67.) Ответ: – 67. |
|
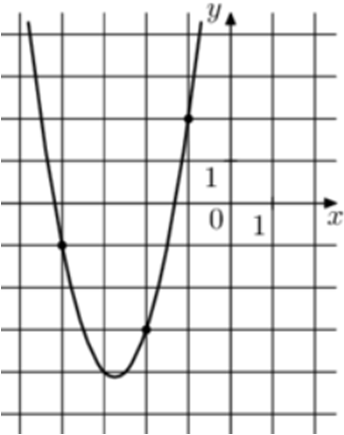
| Задача 13. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 7} right).)
Ответ
ОТВЕТ: 32. |
 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2; — 3} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,}\{ — 3 = 4a — 2b + c}\{ — 1 = 16a — 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (5 = — 3a + b.) Вычтем из первого уравнения третье: (3 = — 15a + 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,1 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{5 = — 3a + b}\{1 = — 5a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (5 = — 3 cdot 2 + b,,,,,, Leftrightarrow ,,,,,,b = 11) и (2 = 2 — 11 + c,,,,, Leftrightarrow ,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( { — 7} right) = 2 cdot {left( { — 7} right)^2} + 11 cdot left( { — 7} right) + 11 = 32.) Ответ: 32. |
|
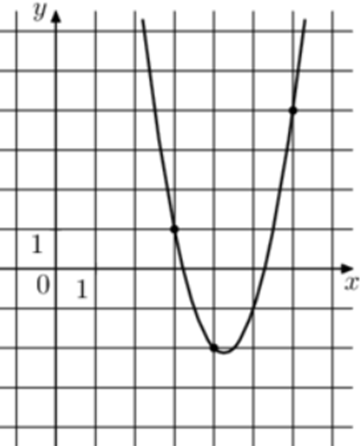
| Задача 14. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( {10} right).)
Ответ
ОТВЕТ: 64. |
 |
|
Решение
Парабола проходит через точки (left( {3;1} right)), (left( {4; — 2} right)) и (left( {6;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 9a + 3b + c,,,,,,,,,}\{ — 2 = 16a + 4b + c}\{4 = 36a + 6b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 7a — b) Вычтем из первого уравнения третье: ( — 3 = — 27a — 3bleft| {:left( { — 3} right),,,,,,,,, Leftrightarrow ,,,,,,,,,1 = 9a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{1 = 9a + b}end{array}} right.) Прибавим к первому уравнению второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (3 = — 7 cdot 2 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 17) и (1 = 9 cdot 2 + 3 cdot left( { — 17} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = 34.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 17x + 34) и (fleft( {10} right) = 2 cdot {10^2} — 17 cdot 10 + 34 = 64.) Ответ: 64. |
|
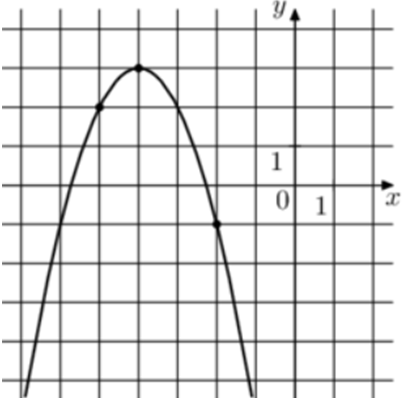
| Задача 15. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: — 33. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 5;2} right)) и (left( { — 6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 25a — 5b + c,,,,,,,}\{ — 1 = 36a — 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 21a + 3bleft| {:3,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 7a + b} right..) Вычтем из первого уравнения третье: (0 = — 32a + 4bleft| {:4,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = — 8a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 7a + b}\{0 = — 8a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 1 = — 7 cdot left( { — 1} right) + b,,,,,, Leftrightarrow ,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( 2 right) = -{2^2} — 8 cdot 2 — 13 = — 33.) Ответ: – 33. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}) вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( 2 right) = — {left( {2 + 4} right)^2} + 3 = — 33.) Ответ: – 33. |
|
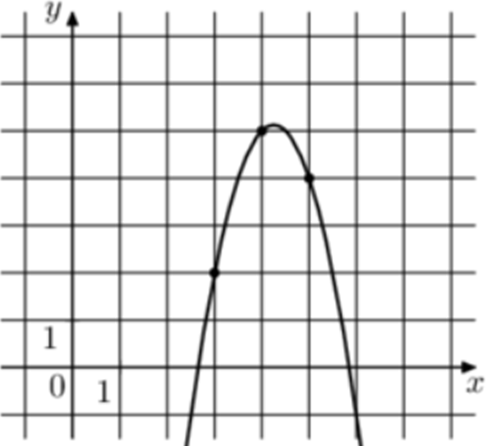
| Задача 16. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: — 50. |
 |
|
Решение
Парабола проходит через точки (left( {3;2} right)), (left( {4;5} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{5 = 16a + 4b + c,,,,,,}\{4 = 25a + 5b + c,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — b.) Вычтем из первого уравнения третье: ( — 2 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 7a — b}\{ — 1 = — 8a — b}end{array}} right.) Прибавим к первому уравнению второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 7 cdot left( { — 2} right) — b,,,,,,, Leftrightarrow ,,,,,,,b = 17) и (2 = 9 cdot left( { — 2} right) + 3 cdot 17 + c,,,,,, Leftrightarrow ,,,,,,c = — 31.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 17x — 31) и (fleft( { — 1} right) = — 2 cdot {left( { — 1} right)^2} + 17 cdot left( { — 1} right) — 31 = — 50.) Ответ: – 50. |
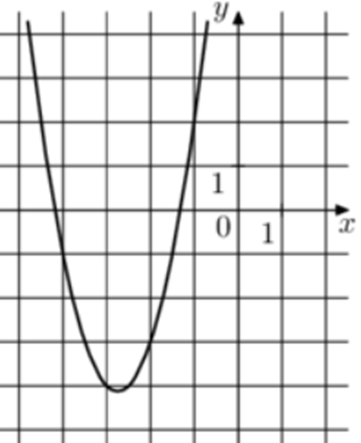
| Задача 17. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( 2 right).)
Ответ
ОТВЕТ: 41. |
 |
|
Решение
Парабола проходит через точки (left( { — 2; — 3} right)), (left( { — 3; — 4} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = 4a — 2b + c,,,,,,,,,}\{ — 4 = 9a — 3b + c,,,,,,,,}\{ — 1 = 16a — 4b + c,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Прибавим к первому уравнению второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (1 = — 5 cdot 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 11) и ( — 3 = 4 cdot 2 — 2 cdot 11 + c,,,,,,, Leftrightarrow ,,,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( 2 right) = 2 cdot {2^2} + 11 cdot 2 + 11 = 41.) Ответ: 41. |
|
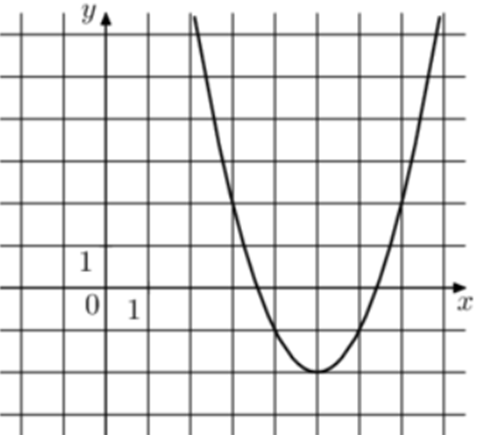
| Задача 18. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 1} right).)
Ответ
ОТВЕТ: 34. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( {3;2} right)), (left( {4; — 1} right)) и (left( {5; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{ — 1 = 16a + 4b + c,,,,,,,}\{ — 2 = 25a + 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (3 = -7a — b.) Вычтем из первого уравнения третье: (4 = — 16a — 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,,,2 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{3 = — 7a — b}\{2 = — 8a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (3 = — 7 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 10) и (2 = 9 cdot 1 + 3 cdot left( { — 10} right) + c,,,,,, Leftrightarrow ,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34. |
|
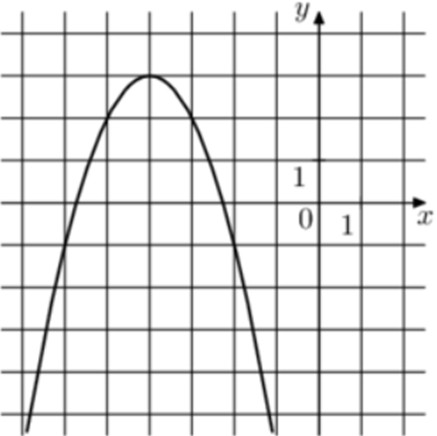
| Задача 19. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 8} right).)
Ответ
ОТВЕТ: — 13. |
 |
|
Решение
1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 3;2} right)) и (left( { — 4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 9a — 3b + c,,,,,,,}\{3 = 16a — 4b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 4 = — 12a + 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 2 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 2 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 3 = — 5 cdot left( { — 1} right) + b,,,,,,, Leftrightarrow ,,,,,,,b = — Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} — 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13. |
|
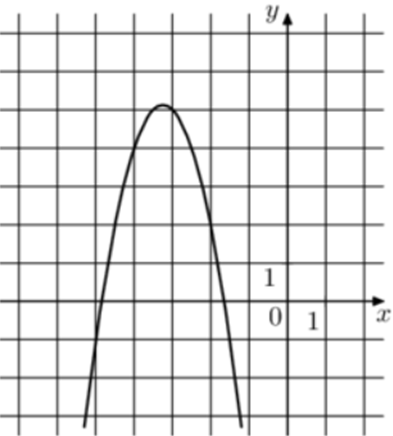
| Задача 20. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 6} right).)
Ответ
ОТВЕТ: — 10. |
 |
|
Решение
Парабола проходит через точки (left( { — 2;2} right)), (left( { — 3;5} right)) и (left( { — 4;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = 4a — 2b + c,,,,,,,,,}\{5 = 9a — 3b + c,,,,,,,,}\{4 = 16a — 4b + c,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 3 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 5 cdot left( { — 2} right) + b,,,,,,, Leftrightarrow ,,,,,,b = — 13) и (2 = 4 cdot left( { — 2} right) — 2 cdot left( { — 13} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = — 16.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 13x — 16) и (fleft( { — 6} right) = — 2 cdot {left( { — 6} right)^2} — 13 cdot left( { — 6} right) — 16 = — 10.) Ответ: – 10. |
|
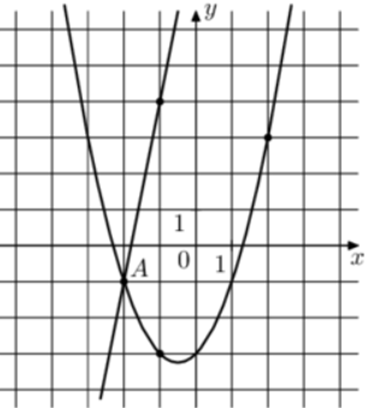
| Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 1; — 3} right)) и (left( {1; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{ — 3 = a — b + c,,,,,,,,,,,,,,,}\{ — 1 = a + b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 3a — b.) Вычтем из первого уравнения третье: (0 = 3a — 3bleft| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{2 = 3a — b}\{0 = a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 2a,,,,, Leftrightarrow ,,,,a = 1.) Тогда: (0 = 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 1) и ( — 1 = 4 cdot 1 — 2 cdot 1 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} + x — 3.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x + 9) и параболы (gleft( x right) = {x^2} + x — 3) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} + x — 3}\{y = 5x + 9,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,{x^2} + x — 3 = 5x + 9,,,,,, Leftrightarrow ,,,,,,{x^2} — 4x — 12 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 2,,,,{x_2} = 4.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна 4. Ответ: 4. |
|
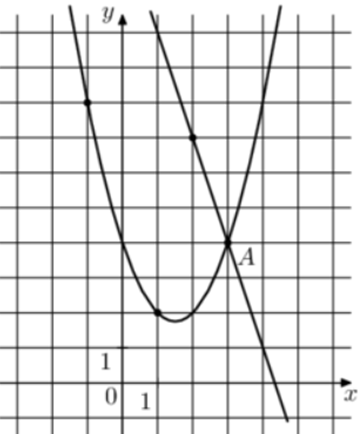
| Задача 22. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 3. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,{x^2} — 3x + 4 = — 3x + 13,,,,,,, Leftrightarrow ,,,,,,,{x^2} = 9,,,,,,, Leftrightarrow ,,,,,{x_1} = 3,,,,{x_2} = — 3.) Значение (x = 3) является абсциссой точки А. Следовательно, абсцисса точки В равна – 3. Ответ: – 3. |
|
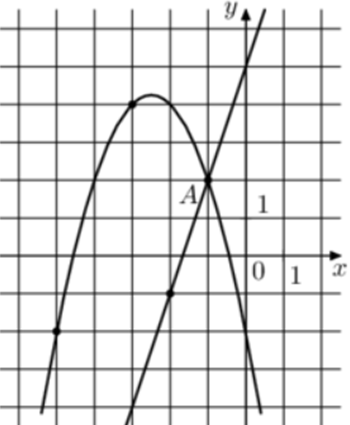
| Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 7. |
 |
|
Решение
Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2;4} right)) и (left( { — 4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = 4a — 2b + c,,,,,,,,,,,,,,,}\{2 = 16a — 4b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 3a + b.) Вычтем из первого уравнения третье: (0 = — 15a + 3bleft| {:3,,,,,,,, Leftrightarrow ,,,,,,,0 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 2 = — 3a + b}\{0 = — 5a + b,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 2 = — 3 cdot left( { — 1} right) + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и (2 = — 1 + 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} — 5x — 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 3x + 5) и параболы (gleft( x right) = — {x^2} — 5x — 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} — 5x — 2}\{y = 3x + 5,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,, — {x^2} — 5x — 2 = 3x + 5,,,,,, Leftrightarrow ,,,,,{x^2} + 8x + 7 = 0,,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = — 7.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 7. Ответ: – 7. |
|
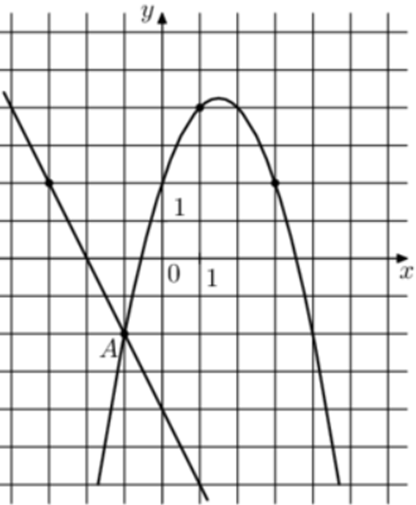
| Задача 24. На рисунке изображены графики функций (fleft( x right) = — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 6. |
 |
|
Решение
Парабола проходит через точки (left( { — 1; — 2} right)), (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = — 2b,,,,,,, Leftrightarrow ,,,,,,b = 3.) Вычтем из первого уравнения третье: ( — 4 = — 8a — 4bleft| {:left( { — 2} right),,,,,,,,, Leftrightarrow ,,,,,,,,2 = 4a + 2b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{b = 3,,,,,,,,,,,,,,,,}\{2 = 4a + 2b,,,}end{array},,,,, Leftrightarrow ,,,,,,2 = 4a + 2 cdot 3,,,,,,,, Leftrightarrow ,,,,,,,,,a = — 1} right..) Тогда: ( — 2 = — 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,,c = 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} + 3x + 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 2x — 4) и параболы (gleft( x right) = — {x^2} + 3x + 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} + 3x + 2}\{y = — 2x — 4,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — ,{x^2} + 3x + 2 = — 2x — 4,,,,,, Leftrightarrow ,,,,,{x^2} — 5x — 6 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 6. Ответ: 6. |
|
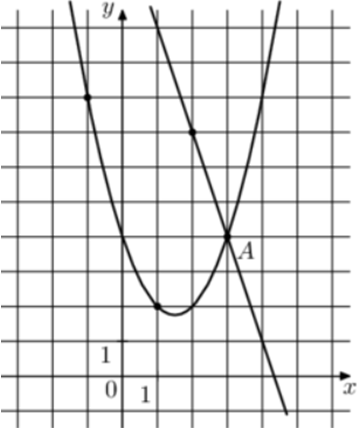
| Задача 25. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 22. |
 |
|
Решение
Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,}end{array}} right.,,, Leftrightarrow ,,,{x^2} — 3x + 4 = 13 — 3x,,, Leftrightarrow ,,,{x^2} = 9,,,, Leftrightarrow ,,,{x_1} = 3,,,,{x_2} = — 3,,, Leftrightarrow ,,,{y_1} = 4,,,{y_2} = 22.) Следовательно, (Aleft( {3;4} right)) и (Bleft( { — 3;22} right)). Таким образом, ордината точки В равна 22. Ответ: 22. |
|
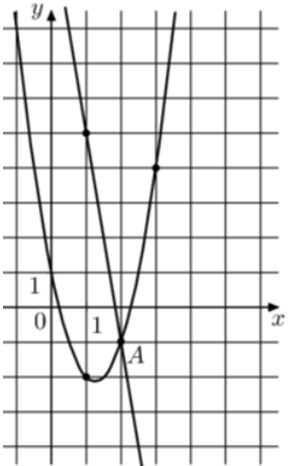
| Задача 26. На рисунке изображены графики функций (fleft( x right) = — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 26. |
 |
|
Решение
Парабола проходит через точки (left( {1; — 2} right)), (left( {2; — 1} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 2 = a + b + c}\{ — 1 = 4a + 2b + c}\{4 = 9a + 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: ( — 6 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 3 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{ — 3 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: ( — 1 = — 3 cdot 2 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и ( — 2 = 2 — 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = 2{x^2} — 5x + 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 6x + 11) и параболы (gleft( x right) = 2{x^2} — 5x + 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 2{x^2} — 5x + 1}\{y = — 6x + 11,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,2{x^2} — 5x + 1 = — 6x + 11,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + x — 10 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = — frac{5}{2},,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = — 1,,,,,{y_2} = 26.) Следовательно, (Aleft( {2; — 1} right)) и (Bleft( { — frac{5}{2};26} right)). Таким образом, ордината точки В равна 26. Ответ: 26. |
|
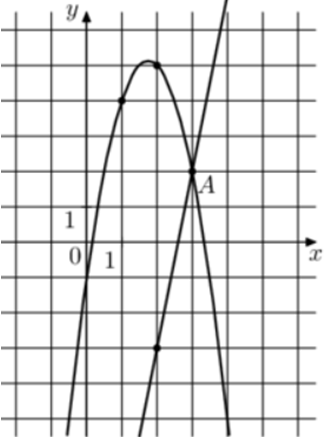
| Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 23. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,, Leftrightarrow ,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x — 13) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = 5x — 13,,,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = 5x — 13,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 2x — 12 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 3,,,,,,{x_2} = — 2,,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 2,,,,,{y_2} = — 23.) Следовательно, (Aleft( {3;2} right)) и (Bleft( { — 2; — 23} right)). Таким образом, ордината точки В равна – 23. Ответ: – 23. |
|
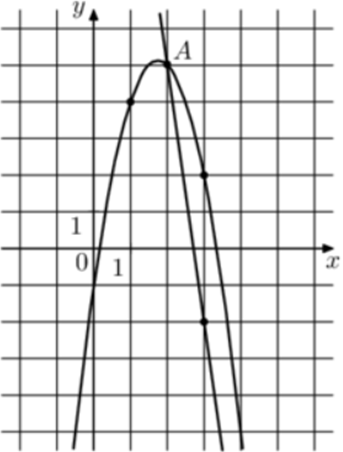
| Задача 28. На рисунке изображены графики функций (fleft( x right) = — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
|
Решение
Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft| {:2,,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 7x + 19) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = — 7x + 19,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = — 7x + 19,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 14x + 20 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = 5,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 5,,,,,{y_2} = — 16.) Следовательно, (Aleft( {2;5} right)) и (Bleft( {5; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16. |
|
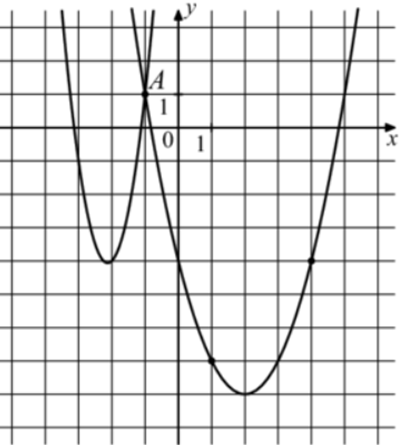
| Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} + 17x + 14) пересекает ось ординат в точке (left( {0;14} right)). Значит, график (y = fleft( x right)) изображён слева, а график (gleft( x right) = a{x^2} + bx + c) справа. Заметим, что графиком функции (y = gleft( x right)) является парабола (gleft( x right) = {x^2}), вершина которой находится в точке (left( {2; — 8} right)). Следовательно, ее уравнение будет иметь вид: (gleft( x right) = {left( {x — 2} right)^2} — 8 = {x^2} — 4x — 4.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} + 17x + 14}\{y = {x^2} — 4x — 4,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,4{x^2} + 17x + 14 = {x^2} — 4x — 4,,,,,,, Leftrightarrow ,,,,,,,3{x^2} + 21x + 18 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} + 7x + 6 = 0,,,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = — 1,,,,{x_2} = — 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
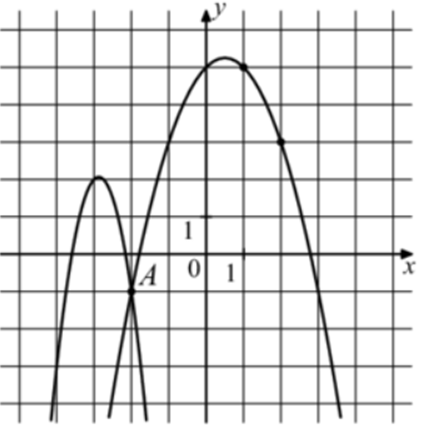
| Задача 30. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} — 23x — 31) пересекает ось ординат в точке (left( {0; — 31} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( { — 2; — 1} right)), (left( {1;5} right)) и (left( {2;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 4a — 2b + c}\{5 = a + b + c,,,,,,}\{3 = 4a + 2b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = 3a — 3b.) Вычтем из первого уравнения третье: ( — 4 = — 4b,,,,,, Leftrightarrow ,,,,,b = 1.) Тогда: ( — 6 = 3a — 3,,,,,, Leftrightarrow ,,,,,,a = — 1) и ( — 1 = — 4 — 2 + c,,,,,, Leftrightarrow ,,,,,,,c = 5.) Следовательно: (gleft( x right) = — {x^2} + x + 5.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} — 23x — 31}\{y = — {x^2} + x + 5,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — 4{x^2} — 23x — 31 = — {x^2} + x + 5,,,,, Leftrightarrow ,,,,,3{x^2} + 24x + 36 = 0left| {:3,,,, Leftrightarrow ,} right.) ( Leftrightarrow ,,,,,,{x^2} + 8x + 12 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = — 2,,,,,,{x_2} = — 6.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6. |
|
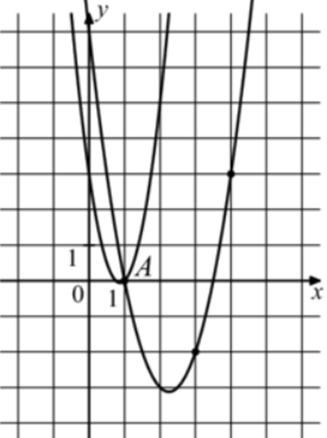
| Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 33. |
 |
|
Решение
График функции (fleft( x right) = 4{x^2} — 7x + 3) пересекает ось ординат в точке (left( {0;3} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( {1;0} right)), (left( {3; — 2} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{0 = a + b + c,,,,,,,,}\{ — 2 = 9a + 3b + c}\{3 = 16a + 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 8a — 2bleft| {: 2,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b.} right.) Вычтем из первого уравнения третье: ( — 3 = — 15a — 3bleft| {:3} right.,,,,,, Leftrightarrow ,,,,, — 1 = — 5a — b.) Таким образом, получим систему уравнений: (left{ {begin{array}{*{20}{c}}{1 = — 4a — b}\{ — 1 = — 5a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = — 4 cdot 2 — b,,,,,, Leftrightarrow ,,,,,,b = — 9) и (0 = 2 — 9 + c,,,,,,, Leftrightarrow ,,,,,,,c = 7.) Следовательно: (gleft( x right) = 2{x^2} — 9x + 7.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} — 7x + 3}\{y = 2{x^2} — 9x + 7}end{array},,,,,,, Leftrightarrow ,,,,,,4{x^2} — 7x + 3 = 2{x^2} — 9x + 7,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + 2x — 4 = 0left| {:2,,,,, Leftrightarrow } right.} right.) ( Leftrightarrow ,,,,,,,{x^2} + x — 2 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 2,,,,,,,,,,,,,,{y_1} = 0,,,,{y_2} = 33.) Следовательно, (Aleft( {1;0} right)) и (Bleft( { — 2;33} right)). Таким образом, ордината точки В равна 33. Ответ: 33. |
|
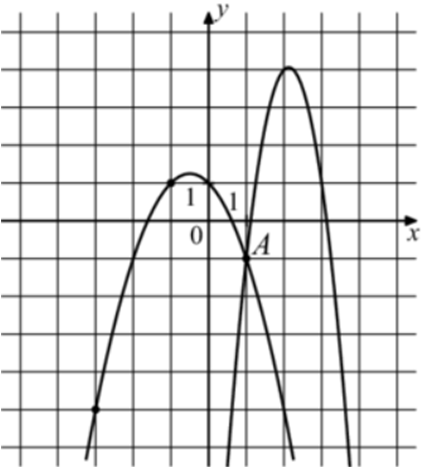
| Задача 32. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 29. |
 |
|
Решение
График функции (fleft( x right) = — 4{x^2} + 17x — 14) пересекает ось ординат в точке (left( {0; — 14} right)). Значит график функции (y = fleft( x right)) изображен справа, а график (gleft( x right) = a{x^2} + bx + c) слева, который проходит через точки (left( {1; — 1} right)), (left( { — 1;1} right)) и (left( { — 3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = a + b + c,,,,,,}\{1 = a — b + c,,,,,,,,}\{ — 5 = 9a — 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 1.) Вычтем из первого уравнения третье: (4 = — 8a + 4b,,,,, Leftrightarrow ,,,,,4 = — 8a — 4,,,,,, Leftrightarrow ,,,,,,a = — 1.) Тогда: ( — 1 = — 1 — 1 + c,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно: (gleft( x right) = — {x^2} — x + 1.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 4{x^2} + 17x — 14}\{y = — {x^2} — x + 1,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,, — 4{x^2} + 17x — 14 = — {x^2} — x + 1,,,,,, Leftrightarrow ,,,,,3{x^2} — 18x + 15 = 0left| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} — 6x + 5 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 5,,,,,,,,,{y_1} = — 1,,,,{y_2} = — 29.) Следовательно, (Aleft( {1; — 1} right)) и (Bleft( {5; — 29} right)). Таким образом, ордината точки В равна – 29. Ответ: – 29. |

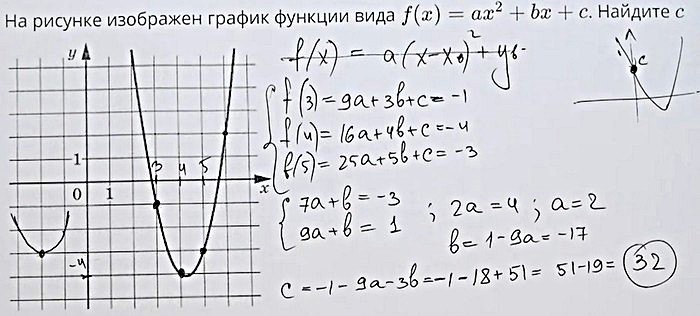






















.png)

.png)












