СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Многоугольники: вычисление длин и углов
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д4 № 27449
Найдите косинус угла
В ответе укажите значение косинуса, умноженное на
Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все
Методы геометрии: Теорема косинусов
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
2
Задания Д4 № 27450
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.
Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Задания Д4 № 27451
Найдите синус угла
В ответе укажите значение синуса, умноженное на
Аналоги к заданию № 27451: 27452 27453 510060 Все
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Задания Д4 № 27456
На клетчатой бумаге с размером клетки 1
1 изображён угол. Найдите тангенс этого угла.
Аналоги к заданию № 27456: 26074 26077 26080 27454 27455 513703 Все
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
5
Задания Д4 № 27459
Найдите тангенс угла AOB. Сторона одной клетки равна 1.
Аналоги к заданию № 27459: 27457 27458 Все
Методы геометрии: Теорема косинусов
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Задача 53690 на клетчатой бумаге с размером клетки…
Условие
на клетчатой бумаге с размером клетки 1х1 изображён угол, найдите косинус этого угла

математика
3898
Решение
★
Все решения
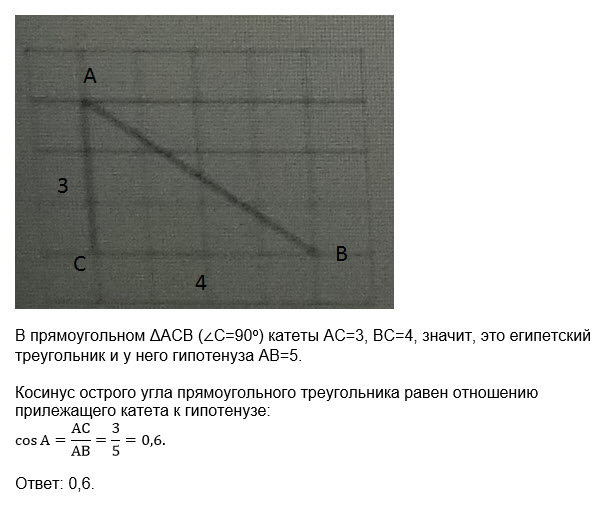
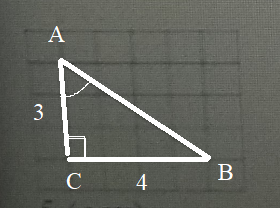
Достраиваем угол до прямоугольного треугольника АВС
∠ C=90 °
Катет АС=3 клеточкам
катет BC= 4 клеточкам
1 клеточка =1 см
АС=3 см
ВС=4 см
По теореме ПИфагора
AB^2=AC^2+BC^2=3^2+4^2=9+16=25
AB=5 cм
Косинус острого угла прямоугольного треугольника равен
отношению прилежащего катета к гипотенузе:
[m]cos angle A= frac{AC}{AB}=frac{3}{5}=0,6[/m]
О т в е т .0,6
Написать комментарий
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Помним, что каждая клетка представляет собой квадрат.
(blacktriangleright) В равных прямоугольниках равны диагонали.
(blacktriangleright) Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
(blacktriangleright) В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.
И наоборот: катет, равный половине гипотенузы, лежит против угла (30^circ) (рис. 1).
(blacktriangleright) Медиана, проведенная к основанию в равнобедренном треугольнике, является высотой и биссектрисой (рис. 2).
Задание
15
#3714
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с размером клетки (1times1) изображен равнобедренный прямоугольный треугольник. Найдите радиус описанной около него окружности.
Центр окружности, описанной около прямоугольного треугольника, лежит в середине его гипотенузы, то есть радиус этой окружности равен половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна (5). Следовательно, радиус равен (2,5).
Ответ: 2,5
Задание
16
#3715
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с размером клетки (1times1) изображен равнобедренный прямоугольный треугольник. Найдите длину его биссектрисы, выходящей из вершины прямого угла.
Так как треугольник равнобедренный, то биссектриса, проведенная к гипотенузе-основанию, является также медианой. По свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна (5). Следовательно, медиана (она же биссектриса) равна (2,5).
Ответ: 2,5
Задание
17
#3716
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с размером клетки (1times1) изображен равнобедренный прямоугольный треугольник. Найдите длину его высоты, выходящей из вершины прямого угла.
Так как треугольник равнобедренный, то высота, проведенная к гипотенузе-основанию, является также медианой. По свойству медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. У данного прямоугольного треугольника гипотенуза равна (5). Следовательно, медиана (она же высота) равна (2,5).
Ответ: 2,5
Задание
18
#3717
Уровень задания: Равен ЕГЭ
На клетчатой бумаге с размером клетки (1times1) отмечены точки (A,
B, C). Найдите расстояние от точки (A) до прямой (BC).
Проведем прямую (BC) и перпендикуляр (AH):
Из рисунка видно, что (AH=4).
Ответ: 4
Задание
19
#3718
Уровень задания: Равен ЕГЭ
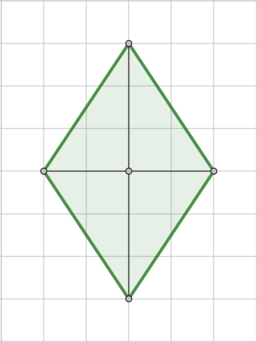
На клетчатой бумаге с размером клетки (1times1) изображен ромб. Найдите его площадь.
Проведем диагонали данного ромба:
Площадь ромба равна полупроизведению диагоналей, следовательно, [S=dfrac12cdot 4cdot 6=12]
Ответ: 12
Задание
20
#3719
Уровень задания: Равен ЕГЭ
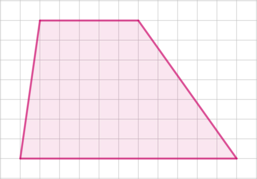
На клетчатой бумаге с размером клетки (1times1) изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме оснований. Большее основание равно (11), меньшее равно (5), следовательно, средняя линия равна ((11+5):2=8).
Ответ: 8
Задание
21
#3720
Уровень задания: Равен ЕГЭ
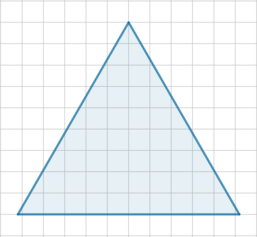
На клетчатой бумаге с размером клетки (1times1) изображен равносторонний треугольник. Найдите радиус описанной около него окружности.
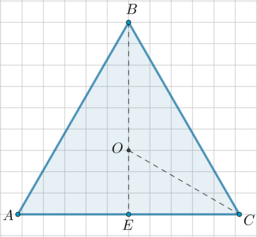
Отметим точки (A, B, C, E):
(BEperp AC), причем (BE=9). Центр описанной окружности лежит на пересечении серединных перпендикуляров, в равностороннем треугольнике серединные перпендикуляры – это и высоты, и медианы, и биссектрисы.
То есть центр описанной окружности лежит на высоте (BE), которая также является и медианой. Пусть (O) – центр этой окружности (а значит, и точка пересечения медиан треугольника). Так как медианы треугольника точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB:OE=2:1), откуда [OB=dfrac23BE=6] Заметим, что по определению радиус описанной около треугольника окружности – это отрезок, соединяющий центр окружности с вершиной треугольника, то есть (OB). Таким образом, радиус равен (6).
Ответ: 6

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ