Задание 1
Некоторое число уменьшили на 20%. На сколько процентов надо увеличить результат, чтобы получить первоначальное число?
Ответ: 25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
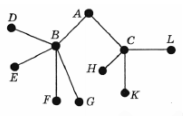
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по обществознанию в 2007 году (по 1000‐бальной шкале). По данным диаграммы найдите число стран, в которых средний балл участников не меньше, чем 515.
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
Центральный угол на 360 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Ответ: 36
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.
Ответ: 0,125
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Решите уравнение: $$log_{frac{1}{8}}x+5log_{4}x+log_{sqrt{2}}x=16frac{2}{3}$$
Ответ: 16
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен $$frac{sqrt{2}}{10}$$
Ответ: 14
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
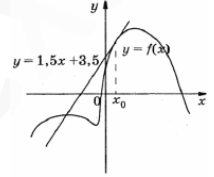
На рисунке изображен график функции f(x) и касательная к этому графику, проведенная в точке x0. Уравнение касательной дано на рисунке. Найдите значение производной функции y=2f(x)-1 в точке x0
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
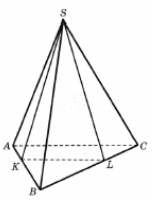
В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками K и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ выразите в градусах.
Ответ: 90
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
Найдите значение выражения $$sqrt{|40sqrt{2}-57|}-sqrt{|40sqrt{2}+57|}$$
Ответ: -10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10
Автомобиль разгоняется с места с постоянным ускорением a=2,0 м/с2 и через некоторое время достигает скорости v=7 м/с. Какое расстояние к этому моменту прошел автомобиль? Ответ выразите в метрах. Скорость v, пройденный путь l, время разгона t и ускорение a связаны соотношениями $$v=at$$, $$l=frac{at^2}{2}$$.
Ответ: 122,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11
Из города в деревню одновременно отправились бегун Б и пешеход П1 , а в тот же момент из деревни в город вышел пешеход П2. Скорости пешеходов были равны. Встретившись, Б и П2 некоторое время стояли на месте, а затем направились в деревню. При этом Б побежал с прежней скоростью, равной 12 км/ч, а П2 уменьшил свою скорость в полтора раза. В результате в деревню сначала прибежал Б, а затем через промежуток времени, в два раза больший длительности встречи Б и П2, одновременно пришли оба пешехода. Найти скорость пешехода П1 .
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
Найдите наименьшее значение функции $$y=frac{x^3+x^2+9}{x}$$ на отрезке [1;10]
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
а) Решите уравнение $$log_{3+2x-x^2}(frac{sin x+sqrt{3}cos x}{sin 3x})=frac{1}{log_{2}(3+2x-x^2)}$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[frac{pi}{2};frac{5pi}{4}]$$
Ответ: а) $$frac{pi }{6}$$; б) нет решений
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р – середина А1D1, точка Q делит отрезок АВ1 в отношении 2:1, считая от вершины А, R – точка пересечения отрезков ВС1 и В1С.
а) Найдите площадь сечения куба плоскостью PQR
б) Найдите отношение, в котором плоскость сечения делит диагональ АС1 куба
Ответ: а) $$frac{sqrt{5}}{2}$$; б) 2:1
Задание 15
Решите неравенство: $$frac{14^{x}}{7(log_{7}(x-3)^{2})^{4}cdot log_{6}(x+2))}leq frac{(4cdot 2^{x})^{x}}{4(log_{7}(x-3)^{2})^{4}cdot log_{6}(x+2))}$$
Ответ: $$(-1;log_{2}{1,75}],[1;2),(2;3),(3;4),(4;+infty)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
Окружность радиуса $$sqrt{3}$$ касается прямой a в точке А, а прямой b в точке В так, что хорда АВ стягивает дугу окружности в 600. Прямые a и b пересекаются в точке F. Точка С расположена на луче FA, а точка D – на луче BF так, что AC=BD=2.
а) Докажите, что треугольник BAD – прямоугольный
б) Найдите длину медианы треугольника CBD, проведенную из вершины D.
Ответ: $$frac{3}{2}$$
Задание 17
В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес изделия составляют 400 тыс.руб. и 12 кг для первого типа, 500 тыс.руб. и 16 кг для второго типа, 600 тыс.руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
Ответ: 10,5 млн. руб., 12,6 млн. руб.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
Найдите все значения параметра a, при каждом из которых уравнение $$sqrt{3a+sqrt{3a+2x-x^2}}=2x-x^2$$ имеет решения.
Ответ: $$[-frac{1}{12};0]$$
Задание 19
Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел в А равно q и никакие два числа в множестве А не являются взаимно простыми. Найдите все числа множества А, если:
а) q=210 , произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа.
б) q=390, произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа.
в) q=330, произведение всех чисел из А не является четвертой степенью никакого целого числа, а сумма всех чисел из А равна 755.
Ответ: а) 6, 10, 14, 30, 42, 70, 105, 210; б) 15, 30, 39, 65, 78, 130, 195, 390; в) 6, 15, 30, 33, 66, 110, 165, 330
А. Ларин. Тренировочный вариант № 300.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р — середина А1D1, точка Q делит отрезок АВ1 в отношении 2 : 1, считая от вершины А, R — точка пересечения отрезков ВС1 и В1С.
а) Найдите площадь сечения куба плоскостью PQR.
б) Найдите отношение, в котором плоскость сечения делит диагональ АС1 куба.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Окружность радиуса касается прямой a в точке А, а прямой b в точке В так, что хорда АВ стягивает дугу окружности в 60°. Прямые a и b пересекаются в точке F. Точка С расположена на луче FA, а точка D — на луче BF так, что AC = BD = 2.
а) Докажите, что треугольник BAD — прямоугольный.
б) Найдите длину медианы треугольника CBD, проведенную из вершины D.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес изделия составляют 400 тыс. руб. и 12 кг для первого типа, 500 тыс. руб. и 16 кг для второго типа, 600 тыс. руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определите минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых уравнение
имеет решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел в А равно q и никакие два числа в множестве А не являются взаимно простыми. Найдите все числа множества А, если:
а) q = 210, произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа.
б) q = 390, произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа.
в) q = 330, произведение всех чисел из А не является четвертой степенью никакого целого числа, а сумма всех чисел из А равна 755.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Регистрация Форум Текущее время: 13 мар 2023, 09:33 Сообщения без ответов | Активные темы Страница 1 из 5 [ Сообщений: 47 ] На страницу 1, 2, 3, 4, 5 След. Начать новую тему»> Ответить Тренировочный вариант №300
Тренировочный вариант №300
Страница 1 из 5 [ Сообщений: 47 ] На страницу 1, 2, 3, 4, 5 След. Текущее время: 13 мар 2023, 09:33 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
| 2076 | Найдите наименьшее значение функции y=(x^3+x^2+9)/x-x^2 на отрезке [1; 10] |
Тренировочный вариант 300 от Ларина Задание 12 | |
| 2075 | Найдите значение выражения sqrt(abs(40sqrt(2)-57))-sqrt(40sqrt(2)+57) |
ларин егэ по математике 2020 профильный уровень Вариант 300 Задание 9 | |
| 2074 | а) Решите уравнение log_{3+2x-x^2}((sin(x)+sqrt(3)cos(x))/sin(3x))=1/log_{2}(3+2x-x^2) б) Укажите корни этого уравнения, принадлежащие отрезку [pi/2; (5pi)/4]. |
Решите уравнение log 3+2x-x2 (sinx + sqrt3 cosx / sin 3x =1 / log 2 (3+2x -x2) ! Тренировочный вариант 300 от Ларина Задание 13 ЕГЭ | |
| 1754 | В правильной треугольной пирамиде SABC ребра BA и BC разделены точками К и L так, что BK=BL=4 и KA=LC=2. Найдите угол между плоскостью основания ABC и плоскостью сечения SKL. Ответ дайте в градусах |
В правильной треугольной пирамиде SABC ребра BA и BC разделены точками К и L ! ларин егэ по математике 2020 профильный уровень Вариант 300 Задание 8 # ларин егэ по математике 2020 профильный уровень Вариант 280 Задание 8 | |
| 1611 | Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка P – середина ребра A1D1, точка Q делит отрезок AB1 в отношении 2:1, считая от вершины А, R – точка пересечения отрезков BC1 и B1C. a) Найдите отношение, в котором плоскость сечения делит диагональ AC1 куба. б) Найдите периметр сечения куба плоскостью PQR |
Тренировочный вариант 273 от Ларина Задание 14 | |
О категории
Вариант от 15 февраля 2020 года.
Практика (19)
Некоторое число уменьшили на 20%. На сколько процентов надо увеличить результат, чтобы получить первоначальное число? [Ларин1]
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по обществознанию в 2007 году (по 1000-бальной шкале). По данным диаграммы найдите число стран, в которых средний балл участников не меньше, чем 515.
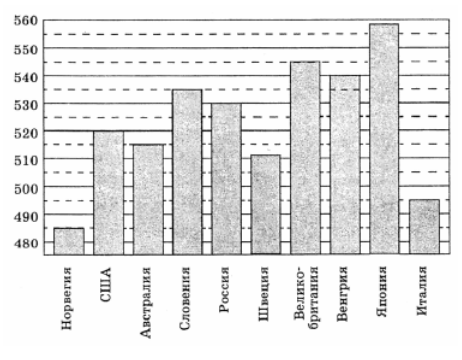
Центральный угол на 36 ° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. [Ларин 3]
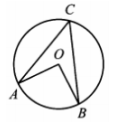
Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.
Решите уравнение
log(1/8)x+5log4x+log(sqrt(2))x = 16 целых 2/3
Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен sqrt(2)/10 [Ларин 6]
На рисунке изображен график функции у = f(x) и касательная к этому графику, проведенная в точке x_0 . Уравнение касательной дано на рисунке. Найдите значение производной функции у = 2f(x)-1 в точке x_0
В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками K и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ выразите в градусах. [ларин 8]
Найдите значение выражения
sqrt(|40sqrt(2)-57|) — sqrt(40sqrt(2)+57)
Автомобиль разгоняется с места с постоянным ускорением а = 0,2 м/с^2 и через некоторое время достигает скорости v = 7 м/с. Какое расстояние к этому моменту прошел автомобиль? Ответ выразите в метрах. Скорость v, пройденный путь l, время разгона t и ускорение a связаны соотношениями v = at; l = at^2/2
Из города в деревню одновременно отправились бегун Б и пешеход П1 , а в тот же момент из деревни в город вышел пешеход П2 . Скорости пешеходов были равны. Встретившись, Б и П2 некоторое время стояли на месте, а затем направились в деревню. При этом Б побежал с прежней скоростью, равной 12 км/ч, а П2 уменьшил свою скорость в полтора раза. В результате в деревню сначала прибежал Б, а затем через промежуток времени, в два раза больший длительности встречи Б и П2 , одновременно пришли оба пешехода. Найти скорость пешехода П1
Найдите наименьшее значение функции [m]у = frac{x^3+x^2+9}{x}-x^2[/m] на отрезке [1;10]
а) Решите уравнение
log(3+2x-x^2)((sinx+sqrt(3)cosx)/(sin3x)) = 1/log2(3+2x-x^2)
б) Укажите корни этого уравнения, принадлежащие отрезку [Pi/2; 5Pi/4]
Дан куб ABCDA_1B_1C_1D_1 с ребром длины 1. Точка P — середина A_1D_1, точка Q делит отрезок АВ_1 в отношении 2:1, считая от вершины А, R — точка пересечения отрезков ВС_1 и В_1С.
а) Найдите площадь сечения куба плоскостью PQR
б) Найдите отношение, в котором плоскость сечения делит диагональ АС_1 куба.
Решите неравенство:
[m]frac{14^x}{7(log_7(x-3)^2)^4*log_6(x+2)} ≤ frac{(4*2^x)^x}{4(log_7(x-3)^2)^4*log_6(x+2)}[/m]
Окружность радиуса sqrt(3) касается прямой а в точке А, а прямой b в точке В так, что хорда АВ стягивает дугу окружности в 60 ° . Прямые а и b пересекаются в точке F. Точка С расположена на луче FA, а точка D — на луче BF так, что AC=BD=2.
а) Докажите, что треугольник BAD — прямоугольный
б) Найдите длину медианы треугольника CBD, проведенную из вершины D.
В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес изделия составляют 400 тыс.руб. и 12 кг для первого типа, 500 тыс.руб. и 16 кг для второго типа, 600 тыс.руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
Найдите все значения параметра а, при каждом из которых уравнение
[m]sqrt{3a+sqrt{3a+2x-x^2}} = 2x-x^2[/m]
имеет решения.
Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел в А равно q и никакие два числа в множестве А не являются взаимно простыми. Найдите все числа множества А, если:
а) q = 210, произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа.
б) q = 390, произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа.
в) q = 330, произведение всех чисел из А не является четвертой степенью никакого целого числа, а сумма всех чисел из А равна 755.
Тренировочный вариант №300 Алекса Ларина ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 17.11.2021 (17 ноября 2021 года)
Тренировочный вариант №300: вариант | ответы
Усложненная версия варианта: вариант | ответы
Вариант Алекса Ларина №300 ОГЭ 2022 по математике:
Два друга Дима и Юра задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из двенадцати отдельных клиньев, натянутых на каркас из двенадцати спиц (см. выше рис. 1).
Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Дима и Юра сумели измерить расстояние между концами соседних спиц (см. выше рис. 2). Оно оказалось равно 30 см. Высота купола зонта (см. выше рис. 3) оказалась равна 29 см, а расстояние между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – 116 см.
1)Длина зонта в сложенном виде равна 28 см и складывается из длины ручки (см. выше рис. 4) и трети длины спицы (зонт в три сложения). Найдите длину спицы (в см), если длина ручки зонта равна 6,2 см.
Ответ: 65,4
2)Поскольку зонт сшит из треугольников, рассуждал Дима, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности (в см 2) зонта методом Димы, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 63,7 см. Ответ округлите до десятков.
Ответ: 11470
4)Юра нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле S 2 Rh , где – радиус сферы, а – высота сегмента. Рассчитайте площадь поверхности купола зонта (в см2) методом Васи. Число R h округлите до 3,14. Ответ округлите до целого числа.
Ответ: 13204
5)Рулон ткани имеет длину 16 м и ширину 150 см. На фабрике из этого рулона были вырезаны треугольные клинья для 18 зонтов, таких же, как зонт, который был у Димы и Юры. Каждый треугольник с учётом пропуска на швы имеет площадь 1 000 см2. Оставшаяся ткань пошла на обрезки. Сколько процентов ткани рулона пошло на обрезки?
Ответ: 10
10)Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда A должна сыграть два матча — с командой и с командой . Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда B C A .
Ответ: 0,25
14)Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
Ответ: 77200
17)Найдите площадь трапеции, изображённой на рисунке.
Ответ: 3864
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними. 1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. 2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны. 3) Смежные углы равны.
Ответ: 1
21)От пристани A к пристани , расстояние между которыми равно 238 км, отправился с постоянной скоростью первый теплоход, а через 7 часов после этого следом за ним со скоростью, на 17 км/ч большей, отправился второй. Найдите скорость (в км/ч) первого теплохода, если в пункт B оба теплохода прибыли одновременно.
Ответ: 17
23)Каждое основание AD и трапеции BC ABCD продолжено в обе стороны. Биссектрисы внешних углов A и B этой трапеции пересекаются в точке P , биссектрисы внешних углов C и пересекаются в точке R . Найдите периметр трапеции D ABCD , если длина отрезка PR равна 24.
Ответ: 48
24)Окружности с центрами в точках и I J пересекаются в точках A и , причём точки и B I J лежат по одну сторону от прямой AB . Докажите, что AB IJ .
25)В прямоугольном треугольнике ABC с прямым углом проведена биссектриса угла B , A . Известно, что она пересекае рединный перпендикуляр, проведённый к стороне точке т се BC в K . Найдите град меру угла усную BCK , если известно, что угол ACB равен 40.
Ответ: 25
Усложненная версия варианта Ларина:
На плане (см. рис. выше) изображена местность, прилегающая к пруду. Для удобства план нанесён на сетку. Сторона одной квадратной клетки сетки соответствует 300 м. Населённые пункты обозначены на плане жирными точками. Рядом с прудом находится еловая роща, обозначенная на плане цифрой 1. В еловой роще расположена деревня Марьино. От этой деревни проложена дорога до посёлка Линёво. Далее дорога идёт к деревне Сосново, расположенной по другую сторону пруда от деревни Марьино. Деревня Сосново соединена дорогой с деревней Клёново, обозначенной на плане цифрой 3. Деревня Клёново также соединена дорогой с деревней Рябино (отмечена на плане цифрой 4). Большая часть изображённой на плане местности – поля, используемые для выращивания пшеницы.
1)Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
Ответ: 2736
2)Автомобиль расходует 8 л топлива на путь 100 км. Сколько литров топлива израсходует автомобиль при поездке из деревни Марьино в деревню Сосново?
Ответ: 0,432
3)Найдите площадь (в км2) еловой рощи.
Ответ: 2,88
4)Найдите расстояние (в метрах) по дороге от деревни Марьино до деревни Сосново.
Ответ: 5400
5)Для улучшения сообщения между населёнными пунктами планируется построить ещё одну дорогу от деревни Марьино до деревни Клёново, либо от деревни Марьино до деревни Рябино. Дорога должна соединить населённые пункты по прямой. Цена прокладки дороги по еловой роще – 17 млн рублей за 1 км, прокладка дороги по полю – 8 млн рублей за 1 км. Из указанных вариантов строительства дорог выберете тот, стоимость которого будет ниже. В ответе укажите стоимость (в млн рублей) выбранного варианта дороги.
Ответ: 29,4
14)Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько тысяч долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?
Ответ: 35
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними. 1) Смежные углы всегда равны. 2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой. 3) Любые два равносторонних треугольника подобны.
Ответ: 23
21)Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность. Во второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала?
Ответ: 8
23)Четырехугольник KLMN вписанный и описанный одновременно; A и — точки касания вписанной окружности со сторонами B KL и LM . Найдите радиус вписанной окружности, если известно, что AK BM 121.
Ответ: 11
24)В круге провели несколько (конечное число) различных хорд так, что каждая из них проходит через середину какой‐либо другой из проведённых хорд. Докажите, что все эти хорды являются диаметрами круга.
25)Ровно четыре вершины правильного двенадцатиугольника расположены в серединах сторон квадрата (см. рис). Найдите площадь двенадцатиугольника, если известно, что площадь квадрата равна 40.
Ответ: 30
Другие тренировочные варианты ОГЭ 2022 по математике:
Математика 9 класс работа статград ОГЭ 2022 варианты МА2190201-МА2190204
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Канал видеоролика: Виктор Осипов
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #егэпоматематике #ответы_егэ #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Разбор Варианта ОГЭ Ларина №290 (№1-25) обычная версия ОГЭ-2022.
Виктор Осипов

Разбор Варианта ОГЭ Ларина №292 (№1-25) обычная версия ОГЭ-2022.
Виктор Осипов

Разбор Варианта ОГЭ Ларина №293 (№1-25) обычная версия ОГЭ-2022.
Виктор Осипов

Разбор Варианта ОГЭ Ларина №294 (№1-25) обычная версия ОГЭ-2022.
Виктор Осипов
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
23.11.2021








 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 




