Задание 1
Найдите корень уравнения $$4^{5x+2}=0,8cdot 5^{5x+2}$$
Ответ: -0,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 2
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 3
В тупоугольном треугольнике АВС известно, что АС=ВС=10, высота АН равна $$sqrt{51}$$. Найдите косинус угла АСВ.
Ответ: -0,7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 4
Найдите значение выражения $$frac{5sin 61^{circ}}{sin 299^{circ}}$$
Ответ: -5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 5
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Ответ: 72
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 6
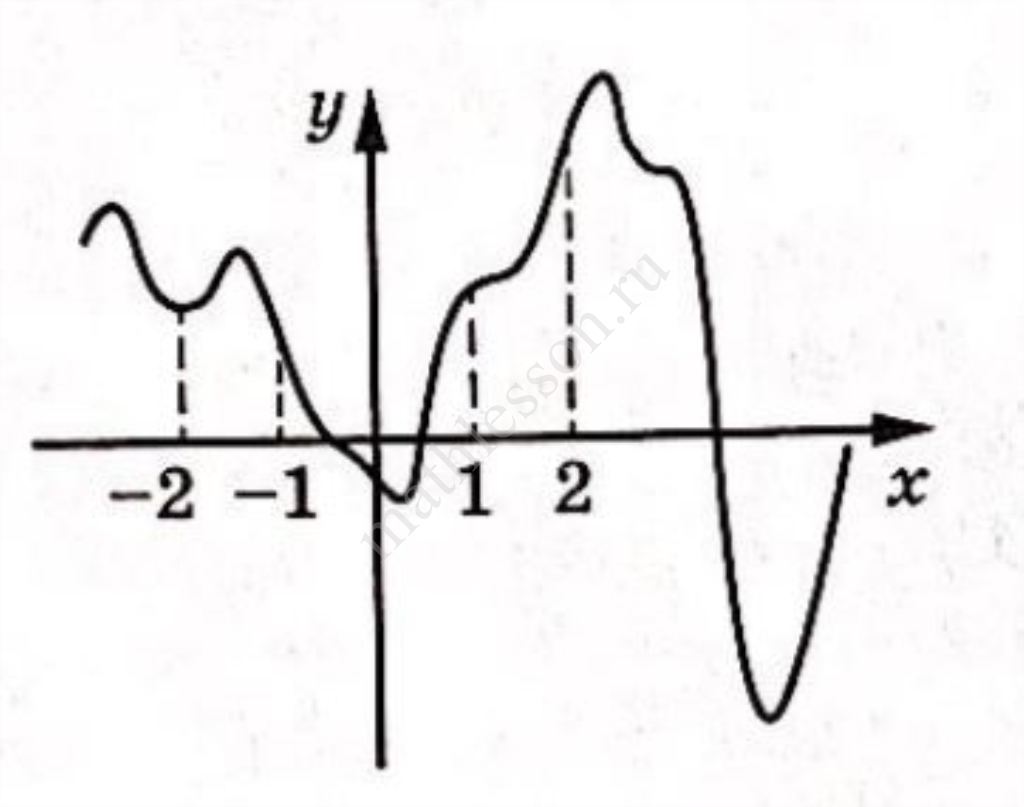
На рисунке изображён график y=f(x). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: -1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 7
При температуре 0°C рельс имеет длину l0=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t_{0})=l_{0}(1+alpha cdot t^{circ})$$, где $$alpha=1,2cdot 10^{-5}$$(°C) — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.
Ответ: 50
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 8
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Ответ: 17,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 9
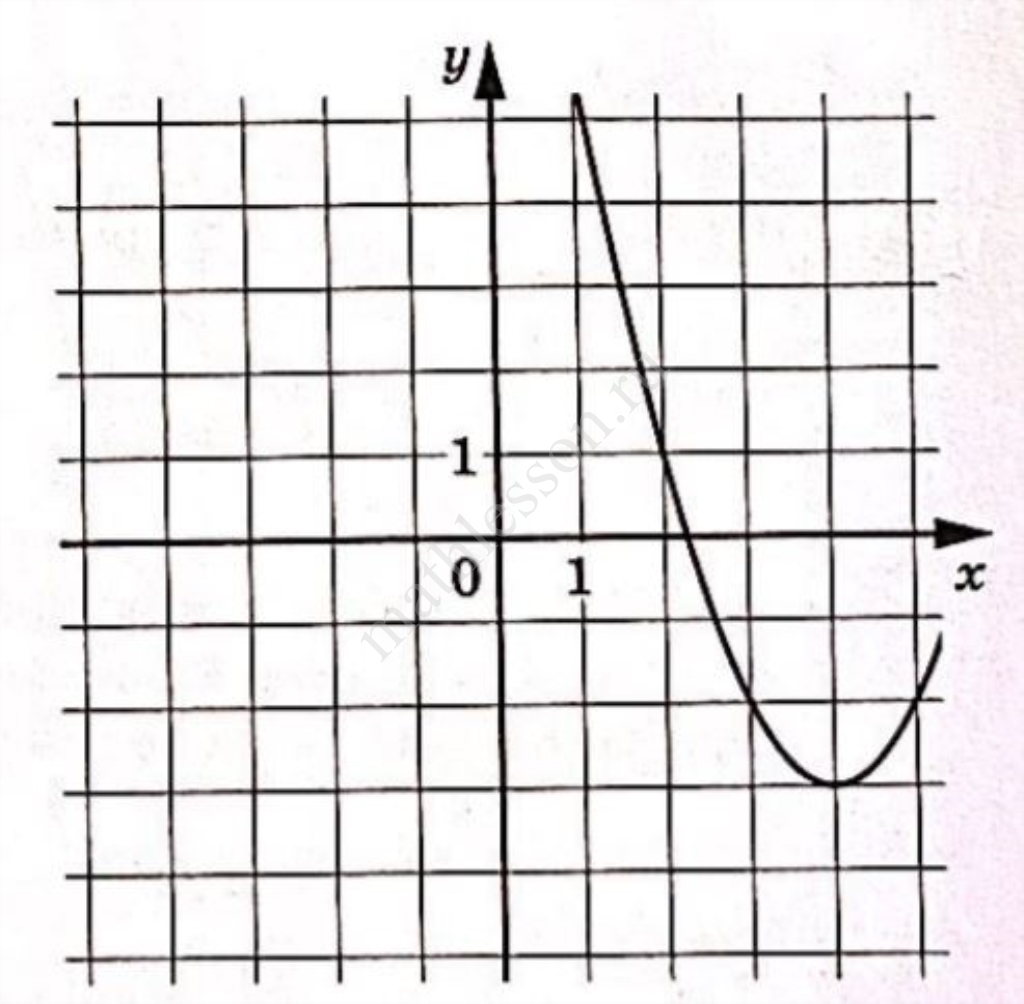
На рисунке изображён график функции $$f(x)=ax^{2}+bx+c$$, где числа a,b и с — целые. Найдите $$f(-5)$$.
Ответ: 72
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 10
Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 30% этих стёкол, вторая — 70%. Первая фабрика выпускает 5 % бракованных стёкол, а вторая — 4 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,043
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 11
Найдите наименьшее значение функции $$y=frac{4}{3}xsqrt{x}-3x+9$$ на отрезке $$[0,25;30]$$.
Ответ: 6,75
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 12
а) Решите уравнение $$2sin^{3}(pi+x)=frac{1}{2}cos (x-frac{3pi}{2})$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{7pi}{2};-frac{5pi}{2}]$$
Ответ: а) $$pi k;pm frac{pi}{6}+pi n, k,n in Z$$ б) $$-frac{19pi}{6};-3pi;-frac{17pi}{6}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 13
В правильной треугольной пирамиде SABC сторона основания АВ равна 16, высота SH равна 10. Точка К — середина бокового ребра SA. Плоскость, параллельная плоскости АВС, проходит через точку К и пересекает рёбра SB и SC в точках Q и Р соответственно.
а) Докажите, что площадь четырёхугольника BCPQ составляет $$frac{3}{4}$$ треугольника SBC.
б) Найдите объём пирамиды KBCPQ.
Ответ: $$80sqrt{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
Решите неравенство: $$(4^{x}-5cdot 2^{x})-20(4^{x}-5cdot 2^{x})leq 96$$
Ответ: $$(-infty;0];[2;3]$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 15
В июле 2025 года планируется взять кредит в банке на 8 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028 и 2029 годов долг возрастает на 20 % по сравнению с концом предыдущего года;
— в январе 2030, 2031, 2032 и 2033 годов долг возрастает на 18 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2033 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1125 тысяч рублей?
Ответ: 600 тыс. руб.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 16
Точки А, В, С, D и Е лежат на окружности в указанном порядке, причём АЕ=ED=CD, а прямые АС и BE перпендикулярны. Отрезки АС и BD пересекаются в точке Т.
а) Докажите, что прямая ЕС пересекает отрезок TD в его середине.
б) Найдите площадь треугольника АВТ, если BD=6, $$AE=sqrt{6}$$
Ответ: $$frac{8sqrt{}5}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 17
Найдите все значения а, при каждом из которых уравнение $$|x^{2}-a^{2}|=|x+a|cdot sqrt{x^{2}-4ax+5a}$$ имеет ровно один корень.
Ответ: $$-5;(0;1)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 18
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.
а) Может ли сумма этих чисел быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?
Ответ: а)да б)нет в)97
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Перейти к содержимому
И.В. Ященко ЕГЭ-2022. Сборник тренировочных вариантов. Книга предназначена для подготовки учащихся к ЕГЭ по математике базового уровня. В сборнике представлены: 30 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ 2022 года; ответы ко всем заданиям и критерии оценивания.
Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться:
Главная » Математика » ЕГЭ 2022 Математика. Типовые тестовые задания. Профильный уровень. 14 вариантов — Ященко В.И.
Авторы пособия — ведущие специалисты, принимающие непосредственное участие в разработке методических материалов для подготовки к выполнению контрольных измерительных материалов ЕГЭ. Пособие содержит 14 типовых вариантов экзаменационных заданий, составленных с учётом всех особенностей и требований Единого государственного экзамена по математике профильного уровня в 2022 году. Назначение пособия — предоставить читателям информацию о структуре и содержании контрольных измерительных материалов 2022 г. по математике профильного уровня, степени трудности заданий. В сборнике даны ответы на все варианты тестов и приводятся решения всех заданий одного из вариантов. Кроме того, приведены образцы бланков, используемых на ЕГЭ для записи ответов и решений. Пособие может быть использовано учителями для подготовки учащихся к экзамену по математике в форме ЕГЭ, а также старшеклассниками и выпускниками — для самоподготовки и самоконтроля.
- Рубрика: Математика / ЕГЭ / ЕГЭ по математике
- Автор: Ященко И.В.
- Год: 2022
- Для учеников: 11 класс
- Язык учебника: Русский
- Формат: PDF
- Страниц: 73
| 3577 | В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD Решение |
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525 |  |
| 3334 | В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, точка G — середина ребра SC. а) Постройте прямую пересечения плоскостей ABG и GDF. б) Найдите угол между плоскостями ABG и GBF Решение |
а) Постройте прямую пересечения плоскостей ABG и GDF ! 36 вариантов ФИПИ Ященко 2022 Вариант 36 Задание 13 | |
| 3309 | Найдите наибольшее значение функции y=ln((x+9)^5)-5x на отрезке [-8,5; 0]Решение  График |
Найдите наибольшее значение функции y= ln(x+9)5 -5x на отрезке [-8,5; 0] ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 11 | |
| 3308 | а) Решите уравнение ((0.25)^sin(x))^cos(x)=2^(-sqrt(2)sin(x)) б) Найдите все корни этого уравнения, принадлежащие промежутку [2pi; (7pi)/2].Решение График |
а) Решите уравнение ((0,25) sinx) cosx = 2 -sqrt2 sinx ! 36 вариантов ФИПИ Ященко 2022 Вариант 34 Задание 12 | |
| 3307 | На рисунке изображён график функций f(x)=(kx+a)/(x+b). Найдите k
|
На рисунке изображён график функций f(x)= kx+a / (x+b). Найдите k ! 36 вариантов ФИПИ Ященко 2022 Вариант 33 Задание 9 | |
| 3306 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точках A(x0; y0) и B(4; 5). Найдите y0
|
На рисунке изображены графики функций, которые пересекаются в точках A(x0; y0) и B(4; 5) ! 36 вариантов ФИПИ Ященко 2022 Вариант 32 Задание 9 | |
| 3305 | Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68 % кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 75 % кислоты. Сколько процентов кислоты содержится в первом сосуде?Решение |
Имеется два сосуда. Первый содержит 55 кг, а второй — 20 кг растворов кислоты различной концентрации ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 8 | |
| 3304 | На рисунке изображены графики функций f(x)=asqrtx. и g(x)=kx+b., которые пересекаются в точке A. Найдите абсциссу точки A
|
На рисунке изображены графики функций. Найдите абсциссу точки A ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 9 | |
| 3303 | За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки. Найдите вероятность того, что рядом с любым мальчиком будут сидеть две девочкиРешение |
За круглый стол на 6 стульев в случайном порядке рассаживаются 3 мальчика и 3 девочки ! 36 вариантов ФИПИ Ященко 2022 Вариант 31 Задание 10 | |
| 3302 | В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зелёных, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зелёных, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цветаРешение |
Найдите вероятность того, что случайно выбранные чашка и блюдце будут одинакового цвета ! 36 вариантов ФИПИ Ященко 2022 Вариант 30 Задание 10 | |
Показать ещё…
Показана страница 1 из 27
ID товара
2903623
Год издания
2022
ISBN
978-5-4454-1538-1
Количество страниц
80
Размер
28x21x0.5
Тип обложки
Мягкий переплет
Тираж
7000
Вес, г
150
Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
В сборнике представлены:
— 10 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2022 года;
— инструкция по выполнению экзаменационной работы;
— ответы ко всем заданиям;
— решения и критерии оценивания заданий 13-19.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации в форме ЕГЭ, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Серия подготовлена разработчиками контрольных измерительных материалов (КИМ) единого государственного экзамена.
В сборнике представлены:
— 10 типовых экзаменационных вариантов, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня 2022 года;
— инструкция по выполнению экзаменационной работы;
— ответы ко всем заданиям;
— решения и критерии оценивания заданий 13-19.
Выполнение заданий типовых экзаменационных вариантов предоставляет обучающимся возможность самостоятельно подготовиться к государственной итоговой аттестации в форме ЕГЭ, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов освоения школьниками образовательных программ среднего общего образования и интенсивной подготовки обучающихся к ЕГЭ.
Национальное образование
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.
Правила начисления бонусов
Книга «ЕГЭ-2022. Математика. Профильный уровень. Типовые экзаменационные варианты. 10 вариантов» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Иван Ященко
«ЕГЭ-2022. Математика. Профильный уровень. Типовые экзаменационные варианты. 10 вариантов» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.