Математика егэ сечения многогранников - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

Главная » ЕГЭ » ЕГЭ. Математика. Профильный уровень. Сечения многогранников — Резникова Н.М. и др.

Задачи, связанные с сечениями многогранников, занимают важное место в контрольно-измерительных материалах ЕГЭ по математике. При этом, в учебных программах школьного курса по геометрии отводится крайне мало часов на изучение этой темы, в связи с чем учебники содержат недостаточное количество задач. Предлагаемое пособие призвано разрешить это противоречие. В начале пособия приведены краткие теоретические сведения. В первых двух разделах содержатся подготовительные задачи: в заданиях первого раздела необходимо в многограннике построить точку пересечения прямой и плоскости, провести отрезок, по которому плоскость сечения пересекает грань многогранника, и т.д. Во втором разделе представлены задания на построение сечений многогранника (призмы, пирамиды). В третьем — задачи, соответствующие заданию 14 профильного уровня ЕГЭ по математике. Предлагаемое пособие будет полезно учащимся, самостоятельно осваивающим тему «Построение сечений многогранников», а также учителям математики,

Рубрика: ЕГЭ / ЕГЭ по математике
Автор: Резникова Н.М. и др.
Год: 2016
Для учеников: 11 класс
Язык учебника: Русский
Формат: PDF
Страниц: 64

Источник

14. Задачи по стереометрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на построение сечений

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Важные факты и теоремы, необходимые для построения сечений

(blacktriangleright) Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются.
Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.

(blacktriangleright) Теорема о параллельности трех прямых: если (aparallel b, bparallel c), то и (aparallel c).

(blacktriangleright) Определение: прямая и плоскость параллельны, если они не имеют общих точек.

Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.

(blacktriangleright) Определение: две плоскости параллельны, если они не имеют общих точек.

Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.

(blacktriangleright) Если две плоскости пересекаются, то их линия пересечения — прямая.

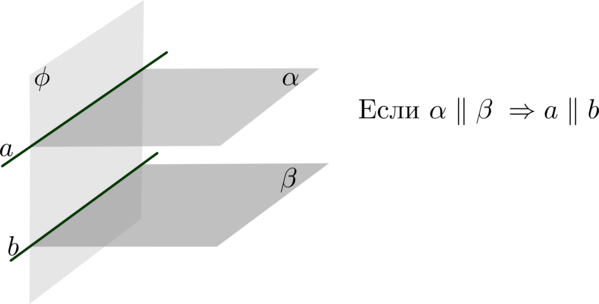
(blacktriangleright) Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)

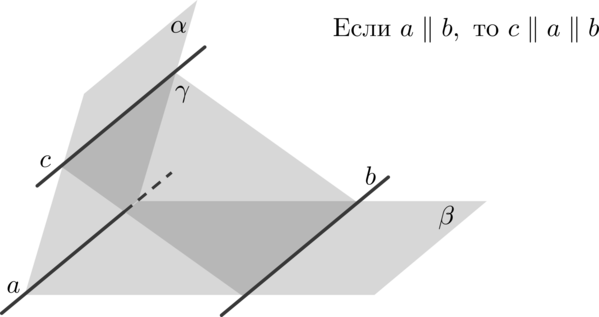
(blacktriangleright) Если плоскости (alpha) и (beta) пересекаются по прямой (a), а плоскости (beta) и (gamma) пересекаются по прямой (b), причем (aparallel b), то плоскости (alpha) и (gamma) пересекутся по прямой (cparallel aparallel b).

Задание
1

#999

Уровень задания: Легче ЕГЭ

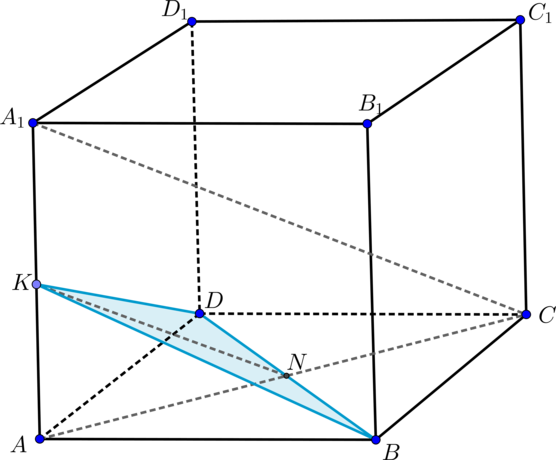
Дан куб (ABCDA_1B_1C_1D_1). Через точку (K), середину ребра (AA_1), и точку (B) проведите плоскость (alpha) параллельно диагонали (A_1C).

Т.к. (A_1Cparallel alpha Rightarrow A_1C) параллельна некоторой прямой, содержащейся в (alpha). Рассмотрим плоскость (AA_1C_1C), в которой находится (A_1C). Т.к. точка (Kin AA_1C_1C), то проведем в этой плоскости (KN parallel A_1C) (по теореме Фалеса (N) – середина (AC)).

Т.к. (ABCDA_1B_1C_1D_1) – куб, то (N) – точка пересечения диагоналей квадрата (ABCD), следовательно, (Nin BD). Таким образом, получили сечение (KBD) куба плоскостью (alpha).

Ответ:

Рисунок.

Задание
2

#3981

Уровень задания: Легче ЕГЭ

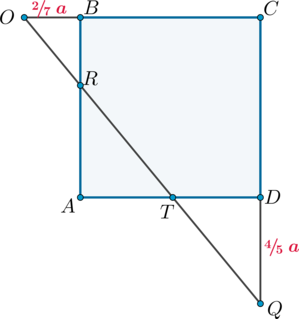
Дан куб (ABCDA_1B_1C_1D_1). На ребрах (AA_1) и (BC) отмечены точки (M) и (N) соответственно, причем (AM:MA_1=2:1), а (N) – середина (BC). Найдите сечение куба плоскостью (DMN).

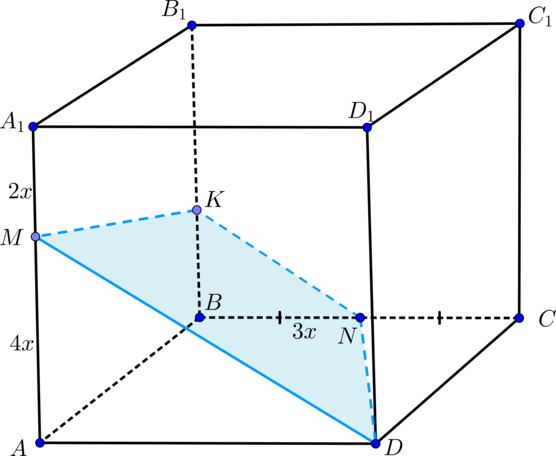
Т.к. грани (ADD_1A_1) и (BCC_1B_1) куба параллельны, то плоскость (DMN) пересечет их по параллельным прямым. Таким образом, проведем (NKparallel DM). Таким образом, (DNKM) – искомое сечение.

Необходимо найти точное расположение точки (K).

Обозначим ребро куба за (6x). Т.к. (bigtriangleup ADM sim
bigtriangleup BNK Rightarrow dfrac{BK}{AM}=dfrac{BN}{AD}
Rightarrow BK=2x). Таким образом, (BK:KB_1=1:2).

Ответ:

Рисунок.

Задание
3

#3804

Уровень задания: Равен ЕГЭ

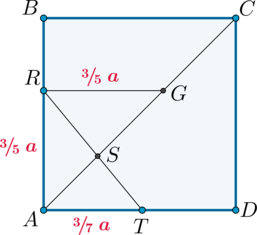
(SABCD) – четырехугольная пирамида, в основании которой лежит квадрат (ABCD), а две боковые грани (SAB) и (SAD) представляют собой прямоугольные треугольники с прямым углом (angle A).

1) Проведите плоскость (alpha) через точку пересечения диагоналей основания параллельно грани (SBC).

2) Найдите площадь сечения пирамиды плоскостью (alpha), если (SA=AB=a).

1) Пусть (ACcap BD=O). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Заметим, что т.к. (angle SAB=angle SAD=90^circ Rightarrow
SAperp
(ABC)).

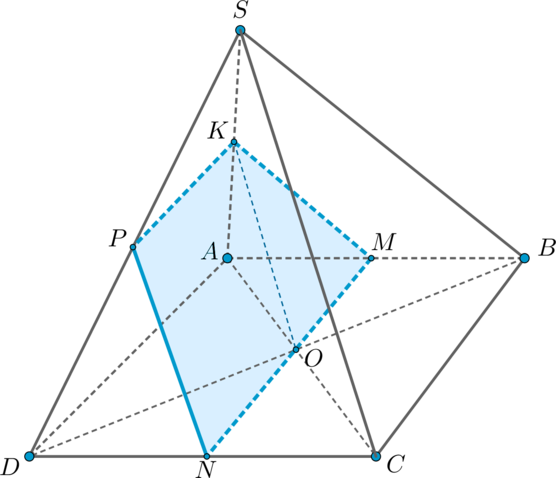
Проведем в плоскости (SAC) прямую (OKparallel SC). Т.к. (O) – середина (AC), то по теореме Фалеса (K) – середина (SA). Через точку (K) в плоскости (SAB) проведем (KMparallel SB) (следовательно, (M) – середина (AB)). Таким образом, плоскость, проходящая через прямые (OK) и (KM), и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки (O) и (M), получим прямую (MN).

Т.к. (alphaparallel (SBC)),то (alpha) пересечет плоскость (SCD) по прямой (NPparallel SC) (если (NPcap SC ne varnothing), то (alphacap (SBC)ne varnothing), что невозможно ввиду их параллельности).

Таким образом, (KMNP) – искомое сечение, причем (KPparallel
ADparallel MN Rightarrow) это трапеция.

2) Т.к. все точки (K,M,N,P) – середины отрезков (SA, AB, CD, SD) соответственно, то:

а) (MN=AD=a)

б) (KP=dfrac{1}{2}AD=dfrac{a}{2})

в) (KM=dfrac{1}{2}SB=dfrac{asqrt2}{2})

Заметим, что по теореме о трех перпендикулярах (SBperp BC
Rightarrow KMperp MN). Таким образом, (KMNP) – прямоугольная трапеция.

(S_{KMNP}=dfrac{KP+MN}{2}cdot KM=dfrac{3sqrt2}{8}a^2)

Ответ:

1) Рисунок.

2) (dfrac{3sqrt2}{8}a^2)

Задание
4

#1003

Уровень задания: Равен ЕГЭ

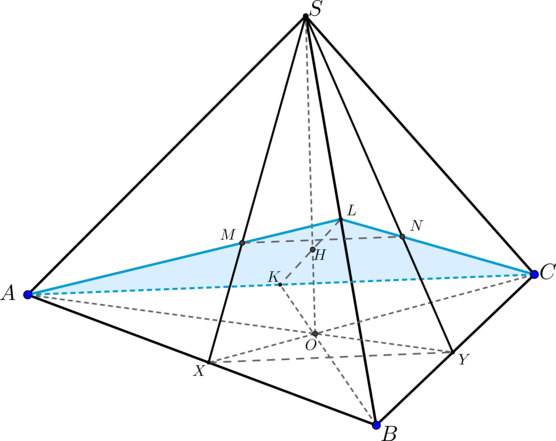
Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).

1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.

Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).

Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).

2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).

Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).

Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).

Тогда по теореме косинусов для (triangle KLB):

(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})

Значит, (S_{ALC}=dfrac{567}{4}).

Ответ:

(dfrac{567}{4}).

Задание
5

#3792

Уровень задания: Сложнее ЕГЭ

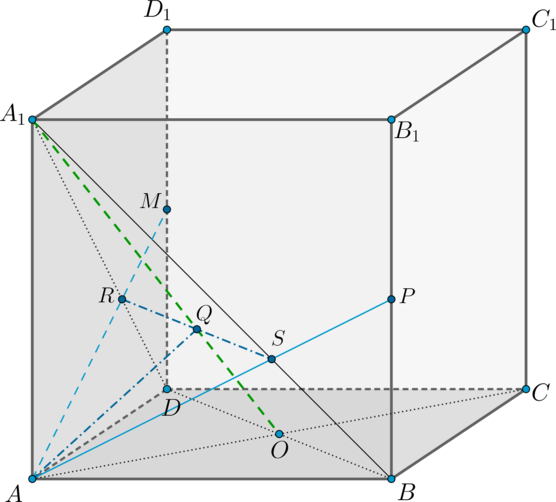
Дан куб (ABCDA_1B_1C_1D_1). Диагонали основания (AC) и (BD) пересекаются в точке (O). Найдите сечение куба плоскостью (alpha), проходящей через точку (A) перпендикулярно прямой (A_1O).

1) Если (A_1Operp alpha), то (A_1O) перпендикулярно двум пересекающимся прямым, лежащим в плоскости (alpha). Построим эти две прямые.

Рассмотрим плоскость (AA_1C_1C) ((A_1O) лежит в этой плоскости). Проведем в ней (AQperp A_1O). Теперь необходимо через их точку пересечения (точку (Q)) провести еще одну прямую перпендикулярно (A_1O).

Рассмотрим для этого плоскость (A_1BD) ((A_1O) лежит в этой плоскости). Проведем через точку (Q) прямую (RSperp A_1O). Т.к. по теореме о трех перпендикулярах (A_1Operp BD) как наклонная ((A_1Aperp (ABC), AOperp BD) – проекция), то (RSparallel BD).

2) Проведем прямые (AR) и (AS). Они могут пересечь либо сами ребра (DD_1) и (BB_1), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек (R) и (S).

Обозначим ребро куба за (a). Тогда (AO=dfrac{asqrt2}{2}=dfrac
a{sqrt2}). Рассмотрим прямоугольный (triangle AA_1O). Так как (AQperp A_1O), то по свойству прямоугольного треугольника (triangle AA_1Qsim triangle AA_1O). Следовательно, [dfrac{A_1Q}{AA_1}=dfrac{AA_1}{A_1O}] Так как по теореме Пифагора (A_1O=sqrt{a^2+frac{a^2}2}=dfrac{sqrt6 a}2), то [A_1Q=dfrac{AA_1^2}{A_1O}=dfrac{sqrt6}3a]

Так как (RSparallel BD), то (triangle A_1DOsim triangle A_1RQ), следовательно, [dfrac{A_1R}{A_1D}=dfrac{A_1Q}{A_1O}=dfrac{sqrt6}3:dfrac{sqrt6}2=
dfrac23] Аналогично (A_1S:A_1B=2:3).

Заметим, что (triangle AA_1Rsim triangle MDR) с коэффициентом подобия (2) ((A_1R:RD=2:1)), следовательно, (MD=frac12AA_1).
Аналогично (PB=frac12AA_1).

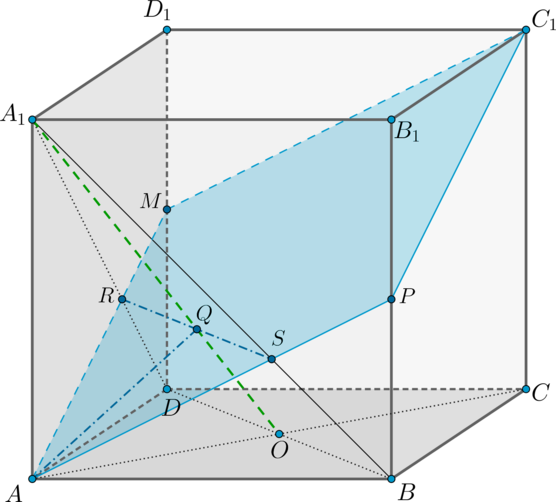
Таким образом, получили линии пересечения плоскостей (AA_1D_1) и (AA_1B_1) с плоскостью (alpha) – прямые (AM) и (AP).

3) Так как плоскости (AA_1B_1) и (DD_1C_1) параллельны, то плоскость (alpha) пересечет их по параллельным прямым. Следовательно, в плоскости (DD_1C_1) через точку (M) нужно провести прямую, параллельную (AP).
Так как (M) и (P) – середины (DD_1) и (BB_1), то (MC_1parallel
AP).

Таким образом, сечение куба плоскостью (alpha) – это четырехугольник (AMC_1P) (который, вообще говоря, является ромбом, так как (AM=AP=MC_1) и (MC_1parallel AP)).

Ответ:

Рисунок.

Задание
6

#2451

Уровень задания: Сложнее ЕГЭ

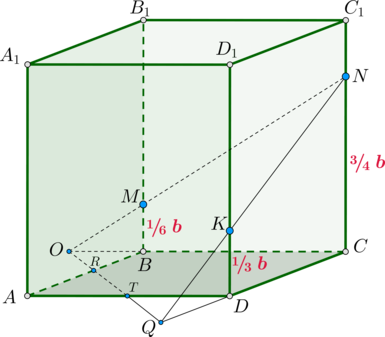
Дан прямоугольный параллелепипед (ABCDA_1B_1C_1D_1), в основании которого лежит квадрат (ABCD). На ребрах (BB_1), (CC_1), (DD_1) отмечены точки (M, N, K) соответственно так, что (BM:MB_1=1:5), (CN:NC_1=3:1), (DK:KD_1=1:2).
Найдите отношение отрезков, на которые делит плоскость (MNK) диагональ (AC).

Обозначим ребро основания за (a), а боковое ребро за (b). Тогда из условия задачи следует, что (BM=frac16b), (CN=frac34b), (DK=frac13b).

Найдем положение точек (R) и (T), в которых плоскость пересекает ребра (AB) и (AD) соответственно.

1) Продлим отрезки (NK) и (CD) до пересечения в точке (Q). Тогда (triangle QDKsim triangle QNC). Следовательно,

[dfrac{QD}{QC}=dfrac{KD}{NC} quad Rightarrow quad
dfrac{QD}{QD+a}=dfrac{frac13b}{frac34b}=dfrac49 quad
Rightarrow quad QD=dfrac45a.]

Аналогично из (triangle OMBsim triangle ONC) получаем, что [OB=dfrac27a.]

Соединив точки (Q) и (O), получим точки пересечения плоскости с ребрами (AB) и (AD).

2) Рассмотрим основание.

(triangle OBRsim triangle OCQ), следовательно,

[dfrac{OB}{OC}=dfrac{BR}{CQ} quad Rightarrow quad
dfrac{frac27a}{frac97a}=dfrac{BR}{frac95a} quad Rightarrow
quad BR=dfrac25a.]

(triangle OBRsim triangle TAR), следовательно,

[dfrac{OB}{AT}=dfrac{BR}{AR}quad Rightarrow quad
dfrac{frac27a}{AT}=dfrac{frac25a}{frac35a} quad Rightarrow
quad AT=dfrac37a.]

3) Для того, чтобы найти, в каком отношении (RT) поделит (AC), проведем прямую (RGparallel AD), (Gin AC).

Тогда (triangle ARG) – прямоугольный и (angle RAG=45^circ), то есть он равнобедренный и (RG=frac35a). Тогда по теореме Фалеса (AG:AC=AR:AB=3:5), следовательно, т.к. (AC=asqrt2), то (AG=frac{3sqrt2}5a).

(triangle ASTsim triangle RSG), следовательно,

[dfrac{AT}{RG}=dfrac{AS}{SG} quad Rightarrow quad
dfrac{frac37a}{frac35a}=dfrac{AS}{frac{3sqrt2}5a-AS} quad
Rightarrow quad AS=dfrac{sqrt2}4a.]

Тогда (SC=asqrt2-frac{sqrt2}4a=frac{3sqrt2}4a) и (AS:SC=1:3).

Ответ:

(1:3)

Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.

Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.

Полезная информация

Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.

Необходимо запомнить

Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».

Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.

В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.

Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Сечения многогранников, теория ЕГЭ по математике

05.10.2015

Данный блок теории по математике посвящён теме «Сечения многогранников» и ориентирован на подготовку и успешную сдачу ЕГЭ по математике.

В настоящем пособии собрано более трехсот задач, в каждой из которых требуется построить сечение многогранника и найти его площадь.

Предлагаемые задачи носят тренировочный характер, решение которых не только вырабатывает навыки нахождения площадей многоугольников, но, что более важно, учит проводить дополнительные построения, развивает пространственные представления учащихся.

Особенностью пособия является наличие для каждой задачи группы из нескольких аналогичных ей задач. Это позволяет лучше понять решение задачи, научиться видеть аналогию между различными задачами, применять метод решения одной задачи для решения аналогичных задач.

Т.к. задания ЕГЭ по математике меняются почти каждый год, решено не привязывать теорию к заданиям, а выдавать тематическими разделами.

Автор: В.А. Смирнов и др.

СКАЧАТЬ PDF https://down.ctege.info/ege/obshee/matem/geometriya/matem-ege-geometriya02-sechenie-mnogogrannikov.pdf

Другие темы из этого блока:

Расстояния и углы в пространстве
Сечения многогранников
Вписанные и описанные фигуры в пространстве
Объемы и площади поверхностей в пространстве
Объемы многогранников
Тела и поверхности вращения
Фигуры в пространстве
Графики

Источник

В задачах на построение сечений мы применяем все те определения, теоремы, свойства и признаки, которые изучаем и доказываем на уроках в школе.

Например, если две плоскости имеют общую точку, то они пересекаются по прямой. Это значит, что плоскость сечения и, например, плоскость грани пирамиды будут пересекаться по прямой, и на чертеже будет показана часть этой прямой – отрезок.

Как вы думаете — может ли восьмиугольник быть сечением куба?

И может ли правильный пятиугольник быть сечением куба?

Чтобы соединить какие-либо две точки на чертеже, нам нужна плоскость, в которой эти точки лежат. Иногда это грань объемного тела. Иногда – вспомогательная плоскость.

А вообще сечение — это плоская фигура, которая образуется при пересечении объемного тела плоскостью и граница которой лежит на поверхности этого объемного тела.

Конечно, восьмиугольник сечением куба быть не может. Ведь у куба 6 граней, и поэтому сечение куба не может иметь больше 6 сторон.

При построении сечений мы часто используем следующие теоремы:

1. Линии пересечения параллельных плоскостей третьей плоскостью параллельны.

Именно поэтому правильный пятиугольник не может быть сечением куба. Ведь 4 из 5 сторон этого пятиугольника лежат в параллельных гранях куба и поэтому параллельны. А у правильного пятиугольника параллельных сторон нет.

2. Теорема о прямой и параллельной ей плоскости:

Пусть прямая m параллельна плоскости α. Если плоскость β проходит через прямую m и пересекает плоскость α по прямой c, то c параллельна m.

Эта теорема помогает, например, при построении сечений пирамиды.

Разберем несколько задач на построение сечений.

1. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка М лежит на ребре AD, N — на ребре DC, К — на ребре АВ.

Проведем МК в плоскости грани ABD и MN в плоскости грани ADC.

Продлим отрезки MN и АС;

Проведем РК в плоскости нижней грани; четырехугольник MNLK — искомое сечение.

2. Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K. Точка N лежит на ребре

Покажем, что плоскость сечения пересекает плоскость основания пирамиды по прямой NT, параллельной МК.

Прямая МК параллельна АВ, лежащей в плоскости основания АВС. Значит,

Плоскость сечения проходит прямую МК, параллельную плоскости АВС. По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и плоскости АВС параллельна прямой МК. Трапеция MKNT — искомое сечение.

3. Постройте сечение куба проходящее через вершину D_1 и середины ребер и BC.

Пусть М — середина АВ, N — середина ВС, Продолжим прямую MN до пересечения с продолжениями ребер DC и AD;

Треугольники АМР и KCN — прямоугольные равнобедренные, причем $AP = CK = frac{AB}{2}.$

Проведем D_1K — в плоскости задней грани и D_1P — в плоскости левой грани куба;

$D_1Kcap {CC}_1=F,{D}_1Pcap AA_1=T,$

Пятиугольник $MNFD_{1}T$ — искомое сечение. В нем есть параллельные стороны: так как линии пересечения параллельных плоскостей третьей плоскостью параллельны.

4. Постройте сечение куба проходящее через вершину В и середины ребер AA_1 и CC_1.

Пусть М — середина ребра $AA{}_{1}$ , N — середина ребра $CC_{1}.$

Поскольку линии пересечения параллельных плоскостей третьей плоскостью параллельны, плоскость сечения пересекает заднюю грань по прямой, параллельной ВМ, а левую грань — по прямой, параллельной BN. Тогда искомое сечение — ромб $BND{}_{1}M.$

5. Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, точку М, делящую ребро АS в отношении , и точку N — середину апофемы грани SBC.

Пусть SH — апофема грани SBC; N—середина SH.

Проведем MN в плоскости ASH;

Четырехугольник KMEF — искомое сечение.

Постройте сечение правильного тетраэдра АВСS, проходящее через точку К — середину ребра АВ, и точки М и Т — центры граней АSС и SBC.

Пусть SЕ и SH — апофемы граней ASC и SBC; точки М и Т делят отрезки SЕ и SH в отношении 2:1, считая от точки S.

Из подобия треугольников SMT и SEH получим, что Значит

По теореме о прямой и параллельной ей плоскости, линия пересечения плоскости сечения и нижней грани параллельна прямой МТ. Это значит, что плоскость сечения пересекает грань АВС по прямой АВ. Достроим сечение.

где — середина ;

— искомое сечение.

7. Постройте сечение куба , проходящее через точку М, лежащую на ребре DD_1 и точки Т и К, принадлежащие граням АВС и $DCC_{1}$ .

Точки М и К лежат в плоскости задней грани $DCC{}_{1}D{}_{1}$ . Соединив М и К, получим, что

$MKcap CC{}_{1}=E,(MK)cap (DC)=P.$

Соединив точки Р и Т в нижней грани, получим FN — линию пересечения плоскости сечения с нижней гранью;

. Трапеция FMEN — искомое сечение.

8. И самый сложный случай. Построим сечение куба плоскостью МNK, где , причем расстояния от точек М и N до плоскости АВС различны.

Пусть точки $M{}_{1}$ и $N{}_{1}$ — проекции точек M и N на плоскость нижней грани

Плоскость $(MNN{}_{1})$ проходит через параллельные прямые $MM{}_{1}$ и $NN{}_{1}$ .

Проведем в этой плоскости MN и $M{}_{1}N{}_{1};$

$(MN )cap ( M{}_{1}N{}_{1})=P$ .

Точки Р и К лежат в нижней грани куба, следовательно, плоскость сечения пересекает нижнюю грань по прямой РК. Дальнейшее построение — очевидно.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Стереометрия. Задачи на построение сечений» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Задачи на построение сечений

Полезная информация

Сечения многогранников, теория ЕГЭ по математике

Новое и интересное на сайте: