Мат проф егэ статград

Решение и ответы заданий варианта 2210209 СтатГрад 13 декабря ЕГЭ 2023 по математике (профильный уровень). ГДЗ профиль для 11 класса. +Задания №1, №4, №6 из варианта 2210211.

Все материалы получены из открытых источников и публикуются после окончания тренировочного экзамена в ознакомительных целях.

Задания №13,16,17,18 долго оформлять, решу их позже, если будет время и желание. Решены те задания, у которых кнопка «Смотреть решение» зелёная.

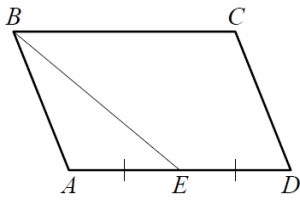
Задание 1.
Площадь параллелограмма ABCD равна 96. Точка Е – середина стороны AD. Найдите площадь треугольника ABE.

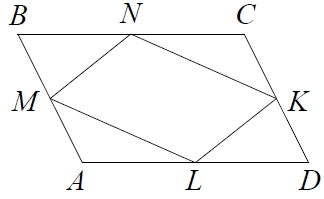
Задание 1 из варианта 2210211.
Площадь параллелограмма ABCD равна 26. Найдите площадь параллелограмма MNKL , вершинами которого являются середины сторон данного параллелограмма.

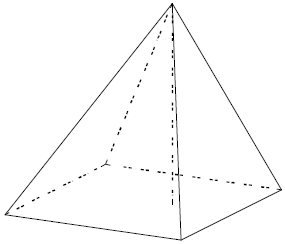
Задание 2.
Основанием пирамиды является прямоугольник со сторонами 2 и 7. Её объём равен 14. Найдите высоту этой пирамиды.

Задание 3.
На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет выступать прыгун из Польши.

Задание 4.
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.

Задание 4 из варианта 2210211.
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 4. Какова вероятность того, что для этого потребовалось два броска?

Задание 5.
Решите уравнение sqrt{-35-12x}=-x. Если уравнение имеет больше одного корня, в ответе запишите больший из корней.

Задание 6.
Найдите значение 13cos(frac{pi}{2} − α), если cosα = −frac{12}{13} и α∈ (frac{pi}{2}; π).

Задание 6 из варианта 2210211.
Найдите значение frac{4cos(–pi–beta)+3sin(frac{3pi}{2}+beta)}{cos(beta+3pi)}.

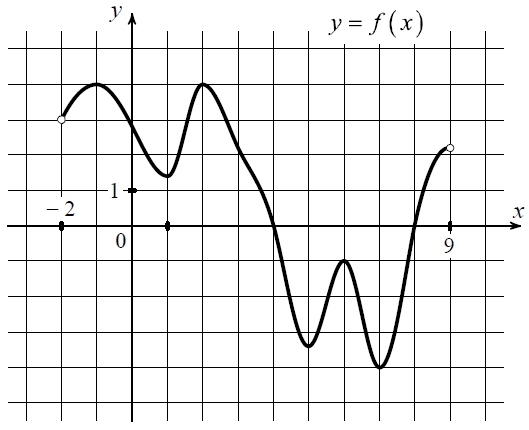
Задание 7.
На рисунке изображён график функции y = f(x), определённой на интервале (−2; 9). Определите количество точек, в которых производная функции f(x) равна 0.

Задание 8.
Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P=m(frac{v^{2}}{L}-g), где m – масса воды в килограммах, v – скорость движения ведёрка в м/с, L – длина верёвки в метрах, g – ускорение свободного падения (считайте g = 10 м/с²). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 90 см? Ответ дайте в м/с.

Задание 9.
Первый садовый насос перекачивает 6 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 3 минуты. Сколько минут эти два насоса должны работать одновременно, чтобы перекачать 5 литров воды?

Задание 10.
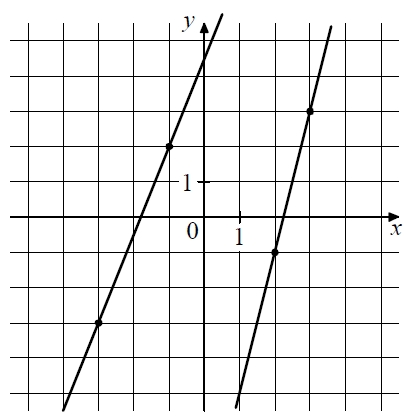
На рисунке изображены графики линейных функций, которые пересекаются в точке A. Найдите абсциссу точки A.

Задание 11.
Найдите наименьшее значение функции y = 10x − 10ln(x + 4) + 23 на отрезке [−3,5; 0].

Задание 12.
а) Решите уравнение 15^sinx = 3^sinx·5^–cosx.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{3pi}{2};3pi].

Задание 13.
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 5 и BC = √23 . Длины боковых рёбер пирамиды SA = 2√15, SB = √85, SD = √83.
а) Докажите, что SA – высота пирамиды SABCD.
б) Найдите угол между прямыми SC и BD.

Задание 14.
Решите неравенство

(3x³ – 18x² + 27x)·(x – 3)^–1 – (6x³ – 11x² – 44x – 30)·(2x + 3)^–1 ≤ 11.

Задание 15.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо оплатить часть долга одним платежом;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма платежей после полного погашения равнялась 4,6 млн рублей?

Задание 16.
Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠BB₁C₁ = ∠BAH.
б) Найдите расстояние от центра окружности, описанной около треугольника ABC, до стороны BC, если B₁C₁ = 9 и ∠BAC = 60°.

Задание 17.
Найдите все значения a, при каждом из которых уравнение

2sqrt{x^{4}+(a-3)^{4}}=|x+a-3|+|x-a+3|

имеет единственное решение.

Задание 18.
Сначала Маша написала на доске 15 натуральных чисел (необязательно различных), каждое из которых не превосходит 30. Затем вместо некоторых из чисел (возможно, одного) она написала на доске числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, она с доски стёрла.
а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось?
б) Среднее арифметическое первоначально написанных чисел равнялось 25. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 32?
в) Среднее арифметическое первоначально написанных чисел равнялось 25. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

Источник варианта: СтатГрад/statgrad.org.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.4 / 5. Количество оценок: 7

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!