(извлечения)
Задание №17 – это текстовая задача с экономическим
содержанием.
|
Содержание критерия |
Баллы |
|
Обоснованно получен верный |
3 |
|
Верно — неверный ответ из-за — верный ответ, но решение |
2 |
|
Верно |
1 |
|
Решение |
0 |
|
Максимальный |
3 |
Несколько подробнее: 1 балл можно выставлять в тех
случаях, когда сюжетное условие задачи верно сведено к решению математической
(арифметической, алгебраической, функциональной, геометрической) задачи. Именно
к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему
функцию и т.п. Грубо говоря, предъявленный текст должен включать направление,
«продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в
себя условие выставления 1 балла, но существенно ближе к верному решению
задачи.
Здесь предполагается завершенное, практически полное
решение соответствующей математической задачи. Типичные допустимые погрешности
здесь – вычислительные ошибки (при наличии всех шагов решения) или недостаточно
полные обоснования.
Отметим, что термин «математическая
модель», быть может, излишне высокопарен для сравнительно простых задач
экономического содержания, предлагаемых на ЕГЭ. Однако, по нашему мнению, он
наиболее лаконичен, общеупотребим и достаточно ясен для того, чтобы пытаться
отыскать ему адекватную замену. Следует подчеркнуть, что один и тот же сюжет
может быть успешно сведен к различным математическим моделям и доведён до
верного ответа. По этой причине в критериях проверки нигде нет жесткого
упоминания о какой-либо конкретной (арифметической, алгебраической,
геометрической, функциональной) модели.
Вообще, способов верного решения заданий этого типа
никак не меньше, чем для привычных текстовых задач. Возможен и стиль,
приближенный к высшей математике, и наивный подход, напоминающий арифметический
способ решения текстовых задач, и метод использующий специфические для
математической экономики понятия (целевая функция, симплекс-метод и т.п.).
Задача 17 (демонстрационный вариант 2018 г).
Задача 1.
15-го
января планируется взять кредит в банке на шесть месяцев в размере
1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого
месяца долг увеличивается на r процентов по
сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число
каждого месяца необходимо выплатить часть долга;
— 15-го
числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0 |
Задача 2.
В
июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его
возврата таковы:
—
каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
—
с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если
ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за
4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет
полностью погашен за 2 года. Найдите r.
Критерии 15 задания профиля и рекомендации по проверке в нашей новой статье. 28 марта посетил практический семинар на базе одной из школ города, где был выдан обширный материал по профильной задаче 15 на вклады и кредиты. Делюсь с вами критериями оценки для экспертов.
Задание №15 – это текстовая задача с экономическим содержанием.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 3 |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано | 2 |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Несколько подробнее: 1 балл можно выставлять в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической, алгебраической, функциональной, геометрической) задачи. Именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию и т.п. Грубо говоря, предъявленный текст должен включать направление, «продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в себя условие выставления 1 балла, но существенно ближе к верному решению задачи.
Здесь предполагается завершенное, практически полное решение соответствующей математической задачи. Типичные допустимые погрешности здесь – вычислительные ошибки (при наличии всех шагов решения) или недостаточно полные обоснования.
Отметим, что термин «математическая модель», быть может, излишне высокопарен для сравнительно простых задач экономического содержания, предлагаемых на ЕГЭ. Однако, по нашему мнению, он наиболее лаконичен, общеупотребим и достаточно ясен для того, чтобы пытаться отыскать ему адекватную замену. Следует подчеркнуть, что один и тот же сюжет может быть успешно сведен к различным математическим моделям и доведён до верного ответа. По этой причине в критериях проверки нигде нет жесткого упоминания о какой-либо конкретной (арифметической, алгебраической, геометрической, функциональной) модели.
Вообще, способов верного решения заданий этого типа никак не меньше, чем для привычных текстовых задач. Возможен и стиль, приближенный к высшей математике, и наивный подход, напоминающий арифметический способ решения текстовых задач, и метод использующий специфические для математической экономики понятия (целевая функция, симплекс-метод и т.п.).
Задача 15 (демонстрационный вариант 2019 г).
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы: — 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задача 1.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы: — 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
Задача 2.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: — каждый январь долг увеличивается на r % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга. Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Примеры оценивания решений задания 15
Пример 1.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.
Пример 2.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.
Пример 3.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.
Пример 4.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите .
Ответ: 10.
Пример 5.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите .
Ответ: 10.
Пример 6.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.
27 февраля 2022
В закладки
Обсудить
Жалоба
Оценивание заданий второй части профильного ЕГЭ по математике
В пособии подробно разбираются задания второй части профильного ЕГЭ по математике, критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку.
В пособии использованы работы участников ЕГЭ 2016–2021 гг.
Задание № 12 — тригонометрическое, логарифмическое или показательное уравнение.
Задание 13 — стереометрическая задача, она разделена на пункты, а и б. В пункте, а нужно доказать геометрический факт, в пункте б найти (вычислить) геометрическую величину.
Задание № 14 — это неравенство: дробно-рациональное, логарифмическое или показательное.
Задание № 15 — это текстовая задача с экономическим содержанием.
Задание № 16 — это планиметрическая задача. В пункте, а теперь нужно доказать геометрический факт, в пункте б — найти (вычислить) геометрическую величину.
Задание № 17 — это уравнение, неравенство или их системы с параметром.
Задание 18 проверяет достижение следующих целей изучения математики на профильном уровне: «развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и её приложений в будущей профессиональной деятельности».
math2.pdf
Шкала перевода баллов ЕГЭ по математике 2023 и критерии оценивания заданий
Математика ЕГЭ (Профильный уровень)
Минимальный порог для поступления в ВУЗы и получения аттестата — 27.
Математика ЕГЭ (Базовый уровень)
Минимальный порог для поступления в ВУЗы и получения аттестата — 7.
Критерии оценивания по заданиям математика (профильный уровень)
Каждое из заданий 1-11 считается выполненным верно, если
экзаменуемый дал верный ответ в виде целого числа или конечной
десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.
Обоснованно получены верные ответы в обоих пунктах – 2 балла.
Обоснованно получен верный ответ в пункте а или б, ИЛИ
получены неверные ответы из-за вычислительной ошибки, но
при этом имеется верная последовательность всех шагов
решения обоих пунктов: пункта а и пункта б – 1 балл.
Решение не соответствует ни одному из критериев,
перечисленных выше – 0 баллов.
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) — 3 балла
Получен обоснованный ответ в пункте б) ИЛИ
имеется верное доказательство утверждения пункта а ) и при обоснованном
решении пункта б) получен неверный ответ из-за арифметической ошибки — 2 балла
Имеется верное доказательство утверждения пункта а)
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен — 1 балл
Решение не соответствует ни одному из критериев,
приведённых выше – 0 баллов.
Обоснованно получен верный ответ – 2 балла.
Обоснованно получен ответ, отличающийся от верного исключением точек,
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения — 1 балл
Решение не соответствует ни одному из критериев,
приведённых выше – 0 баллов.
Обоснованно получен верный ответ – 2 балла.
Верно построена математическая модель – 1 балл.
Решение не соответствует ни одному из критериев,
приведённых выше – 0 баллов.
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) – 3 балла
Получен обоснованный ответ в пункте б)
ИЛИ
имеется верное доказательство утверждения пункта а ) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки – 2 балла.
Имеется верное доказательство утверждения пункта а)
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен – 1 балл.
Решение не соответствует ни одному из критериев,
приведённых выше – 0 баллов.
Обоснованно получен верный ответ – 4 балла.
С помощью верного рассуждения получены искомые значения, возможно неверные, из-за одной допущенной вычислительной ошибки (описки) – 3 балла.
С помощью верного рассуждения получено одно значение параметра (возможно неверное из-за одной вычислительной ошибки), а второе значение потеряно в результате ошибки (например «потеряны» модули) – 2 балла.
Задача сведена к исследованию взаимного расположения графиков неравенства и уравнения (приведен правильный рисунок) – 1 балл.
Решение не соответствует ни одному из критериев,
приведённых выше – 0 баллов.
Верно получены все перечисленные (см. критерий на 1 балл) результаты. – 4 балла.
Верно получены три из перечисленных результатов – 3 балла
Верно получены два из перечисленных результатов – 2 балла
Верно получен один из перечисленных результатов: – 1 балл.
— пример в п. а ;
— обоснованное решение п. б ;
— искомая оценка в п. в;
— пример в п. в, обеспечивающий точность предыдущей оценки.
Решение не соответствует ни одному из критериев,
приведённых выше 0 баллов.
Перевод баллов ЕГЭ по другим предметам
РЕШЕНИЕ
ЭКОНОМИЧЕСКИХ ЗАДАЧ
ПРИ
ПОДГОТОВКЕ К ЕГЭ
Содержание
1.
Введение
2.
Критерии
оценивания задач с экономическим содержанием
3.
Основные
формулы для решения задач
4.
Решение задач на «вклады и кредиты»
Текстовая
задача с экономическим содержанием –
относительно новый вид заданий, появившихся в КИМ ЕГЭ профильного уровня.
Решение
таких задач связано со знанием некоторых специфических математических моделей
из области экономики, умением переводить сформулированные в виде текста условия
в уравнения и неравенства и пониманием того, как решения полученных уравнений и
неравенств соотносятся с тем, что написано в условии задачи, – то есть какой
смысл имеют полученные результаты.
С чего начать подготовку к решению экономической задачи?
Решение любой текстовой задачи складывается из нескольких основных
моментов:
• чтение условия
задачи; читайте его до тех пор, покуда сможете, не подглядывая в
текст, объяснять суть описанного в задаче процесса (без конкретных числовых
данных, конечно, – зазубривать ничего не нужно);
•
выбор переменных; для каждого типа задач существуют
рекомендации, какие величины лучше всего обозначать как переменные (и это не
всегда те величины, о которых идет речь в вопросе задачи); переменных при
решении текстовой задачи нужно вводить столько, сколько их нужно для того,
чтобы просто и логично составить уравнения и неравенства (не бойтесь, если
переменных оказалось слишком много – например, больше, чем число уравнений:
если вы все делаете правильно, то «лишние» переменные взаимно уничтожатся
или сократятся; еще один вариант – в процессе решения надо будет найти не
сами переменные по отдельности, а какую-либо их комбинацию);
• составление
уравнений и неравенств, формализация того, что необходимо найти в
процессе решения задачи; при составлении уравнений обращайте внимание на
единицы измерения – они должны быть одинаковыми для всех одноименных величин;
• решение полученного уравнения, неравенства или системы;
• исследование
полученного результата и нахождение ответа на вопрос задачи.
Критерии оценивания задания №17 ЕГЭ
(Задача с экономическим
содержанием)
|
Содержание критерия |
Баллы |
|
Обоснованно получен верный ответ. |
3 |
|
Верно построена математическая недостаточно обосновано. |
2 |
|
Верно построена математическая модель, и решение исследованию этой модели, при этом решение |
1 |
|
Решение не соответствует ни одному из критериев, выше. |
0 |
|
Максимальный балл |
3 |
Основные
формулы для решения задач
Простые
задачи на применение формул.
В понедельник цена на товар поднялась на
несколько процентов.
Во вторник она понизилась на это же число
процентов. В результате цена товара стала на 4% ниже первоначальной. На сколько
процентов поднималась цена на товар?
Решение.
Пусть А – цена товара, а на х% она
поднялась в понедельник и стала
А(1 + 0,01х) рублей. Во вторник она
понизилась и стала
А(1 + 0,01х)(1 – 0,01х) = А(1 – 0,0001х2),
что составляет 96% от первоначальной цены
А(1
– 0,0001х2) = 0,96А
0,0001х2
=0,04
х2
=400
х
=20
Ответ: цена на товар поднималась на 20%
Цена на чайник уменьшается ежемесячно на
одно и то же число процентов от предыдущей цены. Определить на сколько
процентов уменьшалась ежемесячно цена, если выставленный на продажу за 4500
рублей чайник, через 2 месяца был продан за 3645 рублей?
Решение.
Пусть цена уменьшалась на х%, тогда
4500(1 – 0,01х)2 = 3645
(1 – 0,01х)2 = 0,81
1 – 0,01х = 0,9
х = 10
Ответ: на 10% уменьшалась ежемесячно цена.
Задачи
на «вклады и кредиты»
31 декабря 2014
года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема
выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем
Дмитрий переводит в банк X рублей. Какой должна быть сумма X,
чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение.
Пусть сумма кредита равна S,
а годовые составляют а%. Тогда 31 декабря каждого года оставшаяся сумма
долга умножается на коэффициент b = 1 + 0,01а. После первой
выплаты сумма долга составит S1 = Sb − X. После второй
выплаты сумма долга составит
S2 =S1b – X = (Sb-X)b
– X = Sb2 – Xb – X = Sb2 – (1+b)X
По условию двумя выплатами Дмитрий
должен погасить кредит полностью, поэтому Sb2 –(1+b)X = 0 откуда
При S = 4 290 000 и а
= 14,5, получаем: b = 1,145 и
Ответ: 2 622
050.
31 декабря 2014
года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема
выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет
проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12,5%), затем
Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке,
если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Заметим сначала, что увеличить
число на 12,5% это тоже самое, что умножить это число на . Пусть Ярослав взял в банке S рублей,
а его ежегодный платеж равен X (в данном случае X= 2132325).
Тогда из условия следует уравнение:
Раскрывая скобки,
получаем следующее:
Отсюда
Ответ: 6409000
рублей.
31 декабря 2014 года Алексей взял в
банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплаты кредита
следующая — 31 декабря каждого следующего года банк начисляет проценты на
оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей
переводит в банк X рублей. Какой должна быть сумма X, чтобы
Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Пусть сумма кредита равна S, а
годовые составляют p%. Тогда
31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b=1+0,01p. После
первой выплаты сумма долга составит S1=Sb—X. После
второй выплаты сумма долга составит
S2 = S1b-X = (Sb-X)b
– X = Sb2— (1+b)X
После третьей выплаты сумма
оставшегося долга равна
После четвертой выплаты сумма
оставшегося долга равна
По условию четырьмя выплатами
Алексей должен погасить кредит полностью, поэтому
и
При S = 6902000 и p = 12,5 получаем:
b = 1,125 =
9/8
Ответ: 2 296 350 рублей.
15-го августа
планируется взять кредит в банке на 17 месяцев. Условия его возврата таковы:
— 1-го числа
каждого месяца долг возрастёт на р% по сравнению с концом предыдущего
месяца;
— со 2-го по 14-е
число каждого месяца необходимо выплатить часть долга;
— 15-го числа
каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е
число предыдущего месяца.
Известно, что
общая сумма выплат после полного погашения кредита на 18% больше суммы, взятой
в кредит. Найдите р.
Решение:
Пусть S – сумма в
кредит на 17 месяцев, х= S/17 – ежемесячные выплаты.
Долг: S; S –x; S – 2x; …; S –
16x
Проценты: 0,01рS; 0,01p(S-x); 0,01p(S-2x);
…; 0,01p(S-16x)
Общая сумма выплат: S + 0,01p(S +S
–x + S – 2x + …+S – 16x) = S + 0,01p(17S — (x + 2x + 3x+…+16x)) = S + 0,01p(17S
– 136x) =
= S+0,01p(17S – 136*S/17) = S + 0,01p(17S
-8S) = S +0,09pS.
Так как по условию общая сумма
выплат на 18% больше, чем сумма взятая в кредит, то получим уравнение:
S + 0,09pS = 1,18S
1 + 0,09p = 1,18 p =
2
Ответ: 2%
По вкладу «А» банк
в конце каждого года планирует увеличивать на 17% сумму, имеющуюся на вкладе в
начале года, а по вкладу «Б» — увеличивать эту сумму на 9% в первый год и на
целое число n процентов
за второй год. Найдите наименьшее значение n, при
котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при
одинаковых суммах первоначальных взносов.
Решение:
Пусть S –
первоначальная сумма, тогда
На вкладе «А» через два года S (1 +
0,17)2 = 1,172S = 1,3689S
На вкладе «Б» через два года (1 +
0,09)(1 + 0,01n)S = 1,09(1
+ 0,01n)S
По условию решим неравенство
1,09(1 + 0,01n)S > 1,3689S
1 + 0,01n>1,2558…
n>25,58…
Значит, n =26
Ответ: 26%
Рекомендации по подготовке к выполнению задания №1 7 (финансово-экономические задачи) ЕГЭ профильного уровня
Критерии проверки задания №17
Содержание критерия
Обоснованно получен верный ответ
Баллы
Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат:
— неверный ответ из-за вычислительной ошибки;
— верный ответ, но решение недостаточно обосновано
3
Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено
2
Решение не соответствует ни одному из критериев, перечисленных выше
1
0
Задание 17 на ЕГЭ по математике профильного уровня
Основные ошибки, допускаемые участниками экзамена :
– неверное составление модели;
– вычислительные (арифметические);
– прекращение решения на промежуточном шаге, то есть без
доведения ответа до числового значения;
– решение методом перебора без обоснования единственности;
– использование в решении без вывода формул для задач о
кредитовании, отсутствующих в учебниках (решение имеет вид
«формула – ответ»), что можно трактовать как отсутствие
построения модели задачи.
Что можно ожидать в качестве задания 17 на экзамене?
Различные типы задания №17 в вариантах ЕГЭ по математике (профильный уровень)
Задачи
на кредиты и оптимизацию производства товаров или услуг
Задание №17. Задачи на кредиты (схема 1 – платеж равными взносами)
Схема 1. Пусть планируется взять кредит в банке на некоторую сумму S . Условия его возврата таковы:
– в начале года долг увеличивается на r % по сравнению с концом прошлого года;
– до конца каждого года необходимо выплатить одним платежом часть долга.
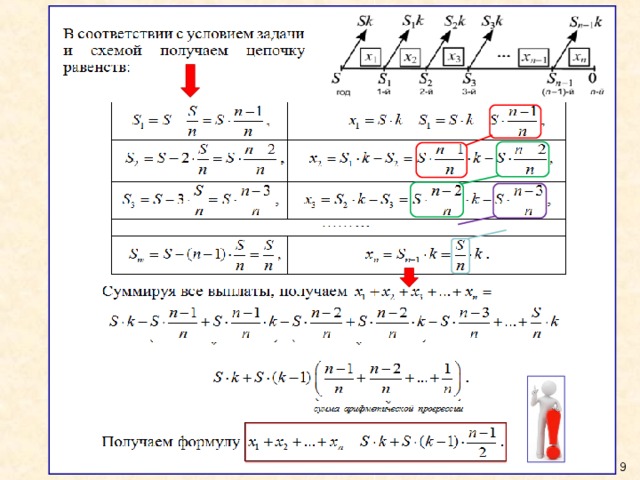
Найти общую сумму платежей, внесенных клиентом, после погашения кредита, если все ежегодные платежи равны между собой .
Решение.
Задание №17. Задачи на кредиты (схема 2 – уменьшение долга каждый год на одну и туже величину)
Схема 2. Пусть планируется взять кредит в банке на некоторую сумму S . Условия его возврата таковы:
– в начале года долг увеличивается на r % по сравнению с концом прошлого года;
– до конца каждого года необходимо выплатить одним платежом часть долга;
– после внесения платежа каждый год долг должен быть на одну и ту же величину меньше долга на конец предыдущего года .
Найти общую сумму внесенных платежей после погашения кредита.
Решение.
Задание №17 на кредиты (кредит выплачивается равными платежами)
17
Пример 1. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 30% по сравнению с концом прошлого года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за 3 года) и сумма платежей превысит взятую в банке сумму на 156060 рублей?
Решение.
3 года – 3 строчки для вывода
Задание №17 на кредиты (уменьшение долга каждый год на одну и туже величину)
17
Пример 2 . В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Решение.
Задание №17 на кредиты (ЕГЭ 2018)
17
Решение задания №17 (ЕГЭ 2018)
Задание №17 на кредиты (долг в соответствии с данной таблицей)
ЕГЭ 2016
17
Решение задания
ЕГЭ 2015
Задание №17 (задача на оптимизацию)
Целевые функции
В задачах оптимизации обычно заданы определённые условия производства какой-либо продукции или услуги и требуется найти значения некоторых величин с целью максимизации прибыли или минимизации расходов.
Математическая модель ( т.е. формализация условия задачи посредством неравенств и уравнений, задающих связи между данными величинами ) любой из таких задач обычно приводит к одному-двум линейным уравнениям (неравенствам) относительно двух данных неизвестных и к одному линейному или простейшему нелинейному уравнению, которое связывает данные неизвестные и величину, максимум или минимум которой надо определить.
После введения в качестве новой неизвестной (параметра) этой величины (её обычно называют целевой функцией ) задача сводится к определению наибольшего (наименьшего) значения параметра, при котором полученное уравнение имеет хотя бы один корень на множестве неотрицательных чисел, удовлетворяющий данным ограничениям.
Задание №17 (задача на оптимизацию)
17
Пример 3 . Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Владимир платит рабочему 500 рублей, а на заводе, расположенном во втором городе – 300 рублей.
Владимир готов выделять 1200000 рублей на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Способы решения (задача на оптимизацию)
Решение. 1- й способ ( введение параметра).
Способы решения (задача на оптимизацию)
Решение. 2- й способ ( с использованием производной).
Способы решения (задача на оптимизацию)
Продолжение решения
Пример задания 17 из вариантов ЕГЭ 2015 года
Задание №17 (задача на оптимизацию)
17
Пример 4. Пенсионный фонд владеет ценными бумагами, которые стоят t 2 тыс. рублей в конце года t ( t =1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счет в банке, при этом в конце каждого года сумма на счете будет увеличиваться в 1 + r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счете была наибольшей. Расчеты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года.
При каких положительных значениях r это возможно?
Задание №17 (задача на оптимизацию)
Способы решения (задача на оптимизацию)
Решение. 1- й способ (предложенный в критериях).
Способы решения (задача на оптимизацию)
Решение. 2 — й способ (с использованием производной).
Продолжение решения
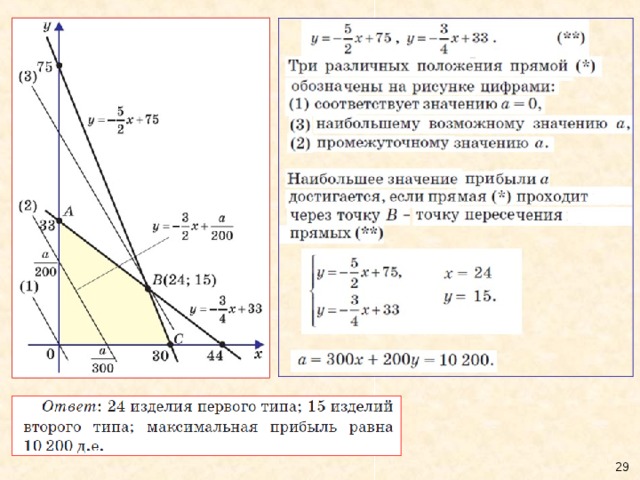
Графический способ нахождения экстремума линейной целевой функции
Если точка экстремума имеет дробное значение
Замечание. Если бы в аналогичной задаче координаты точки B оказались дробными числами, нужно было бы найти ближайшие к B точки четырёхугольника OABC или его внутренней области (это справедливо и для любого другого многоугольника) с целыми координатами (их называют опорными ) и выбрать ту из них, для которой прямая ( * ) (или аналогичная ей) пересекает ось абсцисс (или ось ординат) в точке, наиболее удалённой от начала координат.
Дале необходимо исследовать, будет ли решение, полученное с помощью этой прямой, оптимальным.
Нелинейная целевая функция
Тренировочная работа
21.12. 201 7
Подготовительные задания 17
31
31
31
31
31
Ответы к подготовительным заданиям 17
31
Зачетные задания 17
31
Ответы к зачетным заданиям 17
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
4 балла
Обоснованно получен верный ответ
3 балла
С помощью верного рассуждения получены оба верных значения параметра, но
- или в ответ включены также и одно-два неверных значения;
- или решение недостаточно обосновано
2 балла
С помощью верного рассуждения получено хотя бы одно верное значение параметра
1 балл
Задача сведена к исследованию:
- или взаимного расположения трёх окружностей;
- или двух квадратных уравнений с параметром
0 баллов
Решение не соответствует ни одному из критериев, перечисленных выше
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.