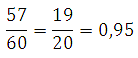Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
2
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
3
В среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
4
Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал
5
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Пройти тестирование по этим заданиям
Приложение 1
Классическое определение вероятности
1. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того,
что ему попадется выученный вопрос.
2. В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По
вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите ве—
роятность того, что к ней приедет зеленое такси.
3. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один
пирожок. Найдите вероятность того, что он окажется с вишней.
4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в
сумме выпадет 8 очков. Результат округлите до сотых.
5. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
того, что орел выпадет ровно один раз.
6. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные
— из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите ве—
роятность того, что спортсменка, выступающая первой, окажется из Китая.
7. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероят—
ность того, что один случайно выбранный для контроля насос не подтекает.
8. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок
со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется каче—
ственной. Результат округлите до сотых.
9. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов
из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают
спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который вы—
ступает последним, окажется из Швеции.
10. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три
дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями.
Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора
М. окажется запланированным на последний день конференции?
11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые
пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминто—
нистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероят—
ность того, что в первом туре Руслан Орлов будет играть с каким—либо бадминтонистом из
России?
12. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четы—
ре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами
групп:1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Ка—
кова вероятность того, что команда России окажется во второй группе?
13. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая
цифра будет чётной?
14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на
три?
15. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые
должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняет—
ся жребию. Какова вероятность того, что А. пойдёт в магазин?
16. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из ко—
манд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Най—
дите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
17. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятству—
ют событию «А = сумма очков равна 5»?
18. На рок—фестивале выступают группы — по одной от каждой из заявленных стран. Порядок
выступления определяется жребием. Какова вероятность того, что группа из Дании будет
выступать после группы из Швеции и после группы из Норвегии? Результат округлите до
сотых.
Задание 677
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Ответ: 0,95
Скрыть
Андрей выучил: $$60-3=57$$ вопросов. В таком случае вероятность того, что ему попадется выученный: $$P=frac{57}{60}=0,95$$
Задание 678
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Ответ: 0,4
Скрыть
Для этого необходимо количество зеленых машин поделить на общее количество машин: $$P=frac{8}{20}=0,4$$
Задание 679
На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Ответ: 0,25
Скрыть
Для этого необходимо количество пирожков с вишней поделить на общее количество пирожков всех: $$P=frac{4}{16}=0,25$$
Задание 680
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Ответ: 0,14
Скрыть
Если бросается две кости одновременно, то общее количество исходов вычисляется как: $$N=6^{2}=36$$ (количество сторон предмета возводится в степень количества бросков). Исходы, при которых может получится 8 очков следующие (первое число — первый кубик, второе число — второй кубик): 2+6 ; 3+5 ; 4+4 ; 5+3 ; 6+2 — то есть $$n=5$$
$$P=frac{5}{36}approx 0,14$$
Задание 681
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Ответ: 0,5
Скрыть
Всего количество исходов $$N=2^{2}=4$$(количество сторон монеты в степени равной количеству бросков), исходов, когда орел ровно один раз всего 2 (ОР и РО). Тогда вероятность составляет $$P=frac{n}{N}=0,5$$
Задание 682
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Ответ: 0,25
Скрыть
Количество спортсменок из Китая составляет: $$n=20-8-7=5$$
Вероятность равна отношению количество спортсменок из Китая к общему количеству спортсменок: $$P=frac{n}{N}=frac{5}{20}=0,25$$
Задание 683
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Ответ: 0,006
Скрыть
Общее количество насосов в таком случае составляет : $$N=2982+18=3000$$
В таком случае вероятность равна отношению количества подтекающих, к общему количеству насосов:$$P=frac{18}{3000}=0,006$$
Задание 684
Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
Ответ: 0,92
Скрыть
Количество сумок без дефектов: $$n=100-8=92$$
Вероятность, что будет без дефекта вычисляется как отношение количества без дефектов, к общему количеству:$$P=frac{92}{100}=0,92$$
Задание 685
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Ответ: 0,36
Скрыть
Всего спортсменов: $$N=4+7+9+5=25$$.
В таком случае вероятность того, что последний будет из Швеции вычисляется как отношение количества спортсменов из Швеции к общему количеству: $$P=frac{9}{25}=0,36$$
Задание 686
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Ответ: 0,16
Скрыть
На четвертый день запланировано: $$n=frac{75-17*3}{2}=12$$. Вероятность того, что выступление будет в последний день вычисляется как отношение количества докладов, запланированных в последний день, к общему количеству докладов: $$P=frac{12}{75}=0,16$$
Задание 687
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?
Ответ: 0,225
Скрыть
На оставшиеся 4 дня приходится: 80-8=72 выступления. Следовательно, каждый из оставшихся дней будет проходить : $$frac{72}{4}=18$$ выступлений ( в том числе и в третий ). Тогда, вероятность выступления исполнителя из России в третий день ( как и в любой и 4 оставшихся ) составляет: $$frac{18}{80}=0,225$$
Задание 688
На конференцию приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Ответ: 0,3
Скрыть
Общее количество исполнителей: 3+3+4=10. Исполнителей из России 3, следовательно, вероятность выступления восьмым ( как и любым другим по счету ) исполнителя из России составит: $$frac{3}{10}=0,3$$
Задание 689
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.
Ответ: 0,36
Скрыть
Кроме Руслана Орлова из России 10-1=9 бадминтонистом, а всего 26-1=25 бадминтонистом. Тогда, вероятность играть с кем-либо из России у него составит: $$frac{9}{25}=0,36$$
Задание 690
В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по теме «Ботаника». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Ботаника».
Ответ: 0,2
Скрыть
Для этого необходимо найти отношения количества вопросов по теме «Ботаника» к общему количеству вопросов: $$frac{11}{55}=0,2$$
Задание 691
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства».
Ответ: 0,6
Скрыть
Найдем вероятность того, что вопрос будет по теме «Неравенства»: $$frac{10}{25}=0,4$$. Тогда вероятность противоположного события, что вопрос будет не по теме «Неравенства» составляет : $$1-0,4=0,6$$
|
математика в10 Классическое определение вероятности
|
|
.
.
.
.
спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 
выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна 
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,622 -
гуманитарные
33,648 -
юридические
17,917 -
школьный раздел
611,562 -
разное
16,897
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
«Простые» задачи.
(решаются сразу по формуле)
«Простые» задачи с элементами дополнительных вычислений.
Задачи, содержащие логику и вычисления.
Задачи, использующие методы подбора и вычисления.
Задачи, включающие в себя: логику, метод подбора, вычисления.
В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение.
На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист П. полетит первым рейсом вертолёта, равна:
Ответ: 0,2.
На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Решение.
Андрей выучил 60 – 3 = 57 вопросов. Поэтому вероятность того, что на экзамене ему попадется выученный вопрос равна
Ответ: 0,95.
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.
Решение.
На циферблате между десятью часами и одним часом три часовых деления. Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
Ответ: 0,25.
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Решение.
Обозначим выпадение орла буквой О, а выпадение решки буквой Р. Возможных восемь исходов:
OOO, OОР, ОРО, ОРР,
РОО, РОР, РРО, РРР
Из них благоприятными являются OОР, ОРО и РОО. Поэтому искомая вероятность равна то есть 0,37. (Этот подход затруднителен в случае большого числа бросаний монетки.)
Ответ: 0,375.
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Решение.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия):
…Д…Ш…Н…, …Д…Н…Ш…, …Ш…Н…Д…, …Ш…Д…Н…, …Н…Д…Ш…, …Н…Ш…Д…
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
Ответ: 0,33.
Дата: 2014-09-16
1476
Категория: Вероятность
Метка: ЕГЭ-№3
1001. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный билет.
Число всевозможных исходов 60 (общее число билетов), число благоприятных исходов 57 (число выученных билетов). Вероятность того, что Андрею попадёт выученный билет, равна 57 к 60 или
Ответ: 0,95
Используя этот сайт, Вы соглашаетесь с тем, что мы сохраняем и используем файлы cookies, а также используем похожие технологии для улучшения работы сайта.
Ok