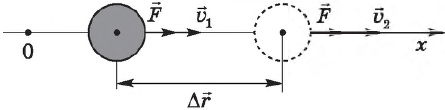
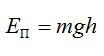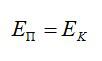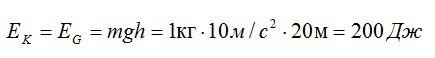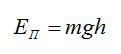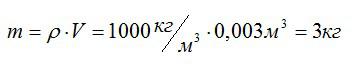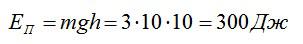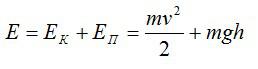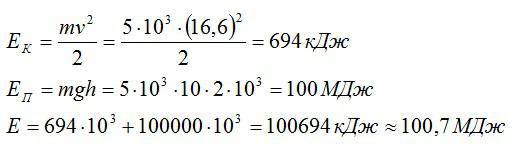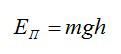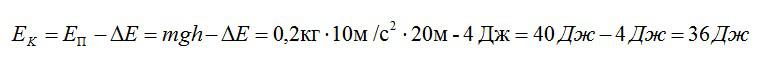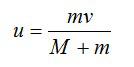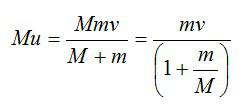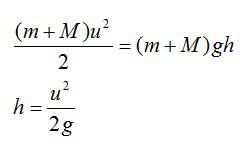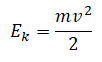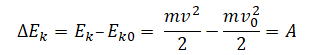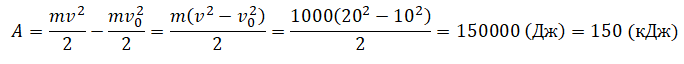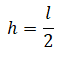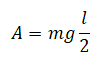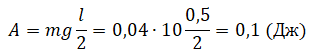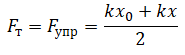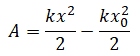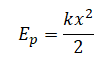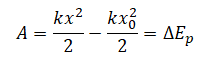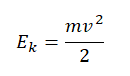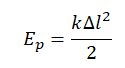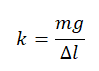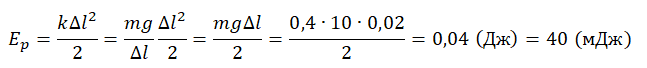Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
$p↖{→}=mυ↖{→}$
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$
где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$
Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
$∆p↖{→}=F↖{→}∆t$
Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+…$
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
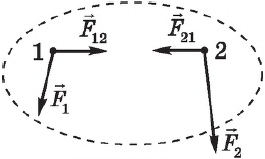
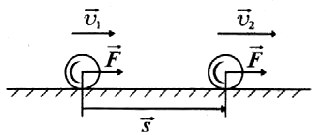
Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$
Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.
Следовательно,
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:
${∆p_{сист}}↖{→}=F↖{→}∆t$
где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:
$m_{p}υ_p=m_{газ}·υ_{газ}$
Отсюда следует, что скорость ракеты
$υ_p=({m_{газ}}/{m_p})·υ_{газ}$
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
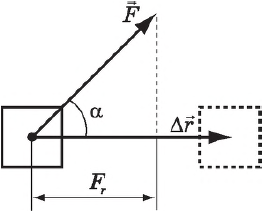
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
$A=F|∆r↖{→}|cosα$
где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.
Работа — величина скалярная. Если $α < 90°$, то $А > 0$, а если $90° < α < 180°$, то $A < 0$; если же $α = 90°$, то $А = 0$. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. Также при движении спутника по круговой орбите сила тяготения не совершает работу.
При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.
Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.
Работа силы тяжести
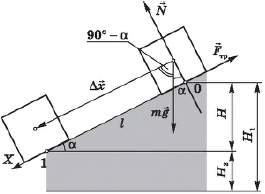
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.
Выразим $∆x$ через $H$ и $α$:
$∆x={H}/{sinα}$
Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° — α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:
$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
- работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
- при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.
Работа силы трения
Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:
$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$
Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то
$A_{тр}=μmgHctgα$
Работа силы упругости
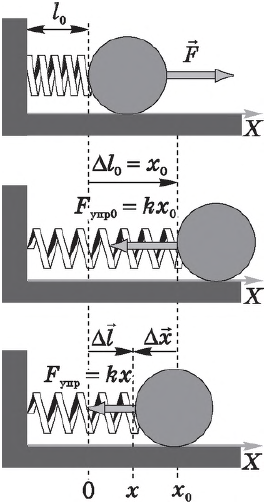
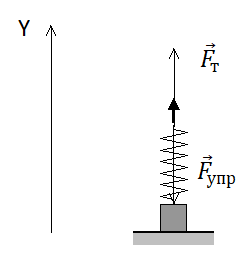
Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:
$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$
Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:
$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$
Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.
Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.
Мощность силы
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).
Мощность определяется формулой:
$N={A}/{∆t}$
где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.
Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:
$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.
Кинетическая энергия. Закон изменения кинетической энергии
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.
Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.
Энергия, которой обладает тело вследствие движения, называется кинетической энергией.
Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.
Найдем кинетическую энергию тела массой $m$, движущегося со скоростью $υ$. Поскольку кинетическая энергия — это энергия, обусловленная движением, нулевым состоянием для нее является то состояние, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем его кинетическую энергию.
Для этого подсчитаем работу на участке перемещения $∆r↖{→}$ при совпадении направлений векторов силы $F↖{→}$ и перемещения $∆r↖{→}$. В этом случае работа равна
$A=F·∆x,$
где $∆x=∆r$
Для движения точки с ускорением $α=const$ выражение для перемещения имеет вид:
$∆x=υ_1t+{at^2}/{2},$
где $υ_1$ — начальная скорость.
Подставив в уравнение $A=F·∆x$ выражение для $∆x$ из $∆x=υ_1t+{at^2}/{2}$ и воспользовавшись вторым законом Ньютона $F=ma$, получим:
$A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$
Выразив ускорение через начальную $υ_1$ и конечную $υ_2$ скорости $a={υ_2-υ_1}/{t}$ и подставив в $A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$ имеем:
$A={m(υ_2-υ_1)}/{2}·(2υ_1+υ_2-υ_1)$
или
$A={mυ_2^2}/{2}-{mυ_1^2}/{2}$
Приравняв теперь начальную скорость к нулю: $υ_1=0$, получим выражение для кинетической энергии:
$E_K={mυ}/{2}={p^2}/{2m}$
Таким образом, движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую необходимо совершить, чтобы увеличить скорость тела от нуля до значения $υ$.
Из $E_K={mυ}/{2}={p^2}/{2m}$ следует, что работа силы по перемещению тела из одного положения в другое равна изменению кинетической энергии:
$A=E_{K_2}-E_{K_1}=∆E_K$
Равенство $A=E_{K_2}-E_{K_1}=∆E_K$ выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за это время силой, действующей на тело.
Потенциальная энергия
Потенциальной энергией называется энергия, определяемая взаимным расположением взаимодействующих тел или частей одного и того же тела.
Поскольку энергия определяется как способность тела совершать работу, то потенциальную энергию, естественно, определяют как работу силы, зависящую только от взаимного расположения тел. Таковой является работа силы тяжести $A=mgh_1-mgh_2=mgH$ и работа силы упругости:
$A={kx_0^2}/{2}-{kx^2}/{2}$
Потенциальной энергией тела, взаимодействующего с Землей, называют величину, равную произведению массы $m$ этого тела на ускорение свободного падения $g$ и на высоту $h$ тела над поверхностью Земли:
$E_p=mgh$
Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости (жесткости) $k$ тела на квадрат деформации $∆l$:
$E_p={1}/{2}k∆l^2$
Работа консервативных сил (тяжести и упругости) с учетом $E_p=mgh$ и $E_p={1}/{2}k∆l^2$ выражается следующим образом:
$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.
Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.
Закон изменения и сохранения механической энергии
Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:
$E=E_k+E_p$
Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).
Согласно теореме о кинетической энергии,
$E_k-E_{k_1}=A_p+A_{пр},$
где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.
В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:
$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$
где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.
Итак, закон изменения механической энергии гласит:
Изменение механической энергии системы равно работе всех непотенциальных сил.
Механическая система, в которой действуют только потенциальные силы, называется консервативной.
В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:
В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):
$E_k+E_p=E_{k_1}+E_{p_1}$
Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).
Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.
Закон сохранения механической энергии является следствием однородности времени.
Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.
Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.
В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.
Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.
В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.
Вот как в современной физике формулируется понятие энергии:
Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
Правило рычага гласит:
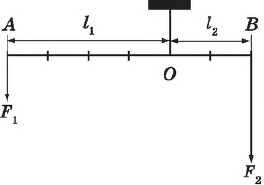
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Неподвижный блок
Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:
$F_1=F_2$
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок
Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:
$F_1={F_2}/{2}$
где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
Полиспаст (система блоков)
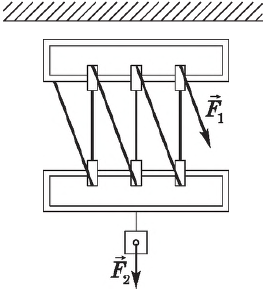
Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:
$F_1={F_2}/{2n}$
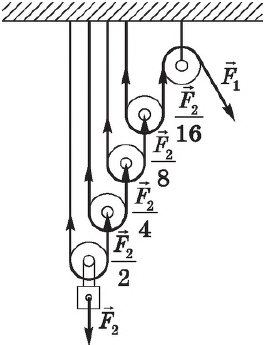
Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:
$F_1={F_2}/{2^n}$
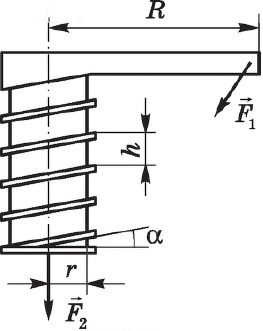
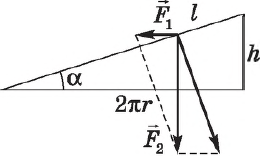
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
Условие равновесия сил, действующих на винт, имеет вид:
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
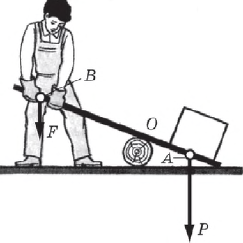
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Столкновение тел. Упругий и неупругий удары
Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.
Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$
Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).
Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.
Для абсолютно упругого удара справедливы уравнения
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ’_1}↖{→}+m_2{υ’_2}↖{→};$
${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ’_1)^2}/{2}+{m_2(υ’_2)^2}/{2}$
где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ’_1, υ’_2$ —скорости шаров после удара.
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 44 1–20 | 21–40 | 41–44
Добавить в вариант
Небольшое тело массой 0,2 кг бросили вертикально вверх. На рисунке показан график зависимости потенциальной энергии
тела от времени t в течение полета. На какую максимальную высоту поднялось тело? Ответ выразите в метрах.
Массивный груз, подвешенный к потолку на невесомой пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины и потенциальная энергия груза в поле тяжести, когда груз движется вверх от положения равновесия?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Потенциальная
энергия пружины |
Потенциальная
энергия груза в поле тяжести |
Источник: ЕГЭ по физике 2017. Досрочная волна. Вариант 101
Растянутая на 2 см стальная пружина обладает потенциальной энергией упругой деформации 4 Дж. На сколько увеличится потенциальная энергия упругой деформации при растяжении этой пружины еще на 2 см? (Ответ дайте в джоулях.)
В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника, его потенциальная энергия и период обращения?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость | Период
обращения |
Потенциальная
энергия |
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 5.
В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника, его потенциальная энергия и центростремительное ускорение?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость | Потенциальная энергия | Ускорение |
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 6.
Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом потенциальная энергия спутника в поле тяжести Земли и
его период обращения вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Потенциальная энергия | Период обращения спутника вокруг Земли |
Источник: Демонстрационная версия ЕГЭ−2019 по физике
Механическая энергия системы изменилась от величины –5 Дж до величины 3 Дж. Это означает, что на данную механическую систему действовали внешние силы. Какова работа этих сил? (Ответ дайте в джоулях.)
Однородный столб массой m и высотой H стоит вертикально. После того, как основание столба подпиливают у самой земли, он начинает падать. При этом нижний конец столба не отрывается от земли. Через некоторое время столб составляет с вертикалью угол α. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) потенциальная энергия столба относительно поверхности земли в момент начала падения
Б) потенциальная энергия столба относительно поверхности земли в момент, когда столб составляет с вертикалью угол α
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Однородный столб массой m и высотой H стоит вертикально. После того, как основание столба подпиливают у самой земли, он начинает падать. При этом нижний конец столба не отрывается от земли. Через некоторое время столб составляет с горизонтом угол α. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) потенциальная энергия столба относительно поверхности земли в момент начала падения
Б) потенциальная энергия столба относительно поверхности земли в момент, когда столб составляет с горизонтом угол α
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Тело массой 2 кг, брошенное с уровня земли вертикально вверх со скоростью 10 м/с, упало обратно на землю. Какой потенциальной энергией обладало тело относительно поверхности земли в верхней точке траектории? Сопротивлением воздуха пренебречь. (Ответ дайте в джоулях.)
Какова энергия упругой деформации сжатой на 10 см пружины, если её жёсткость равна 5000 Н/м? Ответ дайте в джоулях.
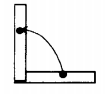
Человек взялся за конец лежащего на земле однородного стержня длиной 2 м и массой 100 кг и поднял этот конец на высоту 1 м. Какую работу он совершил? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Комета движется по эллиптической орбите вокруг Солнца. Изменяются ли перечисленные в первом столбце физические величины во время ее удаления от Солнца и если изменяются, то как? Считаем, что на комету действует только сила тяготения Солнца. Установите соответствие между физическими величинами, перечисленными в первом столбце, и возможными видами их изменений, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Скорость
Б) Ускорение
В) Кинетическая энергия
Г) Потенциальная энергия
Д) Полная механическая энергия
ИХ ИЗМЕНЕНИЯ
1) Не изменяется
2) Только увеличивается по величине
3) Только уменьшается по величине
4) Увеличивается по величине и изменяется по направлению
5) Уменьшается по величине и изменяется по направлению
6) Увеличивается по величине, не изменяется по направлению
7) уменьшается по величине, не изменяется по направлению
| A | Б | В | Г | Д |
Маленькой шайбе, покоящейся у основания гладкой наклонной плоскости, сообщают начальную скорость V0, направленную вдоль наклонной плоскости вверх (см. рис.). Наклонная плоскость достаточно длинная. Установите соответствие между зависимостями физических величин от времени и графиками.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) модуль ускорения a
Б) потенциальная энергия U (относительно начального положения шайбы)
ГРАФИК
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Упругая лёгкая пружина жёсткостью 80 Н/м одним концом прикреплена к лапке штатива. К свободному концу пружины подвешен груз массой 200 г. Определите потенциальную энергию растянутой пружины. Ответ запишите в миллиджоулях.
Потенциальная энергия упругой пружины при её растяжении на 2 см равна 2 Дж. Найдите модуль изменения потенциальной энергии этой пружины при уменьшении её растяжения на 0,5 см. Ответ дайте в джоулях.
Источник: Демонстрационная версия ЕГЭ—2023 по физике
Искусственный спутник движется по эллиптической орбите вокруг Земли. Изменяются ли перечисленные в первом столбце физические величины во время его приближения к Земле и если изменяются, то как? Установите соответствие между физическими величинами, перечисленными в первом столбце, и возможными видами их изменений, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Скорость
Б) Ускорение
В) Кинетическая энергия
Г) Потенциальная энергия
Д) Полная механическая энергия
ИХ ИЗМЕНЕНИЯ
1) Не изменяется
2) Только увеличивается по величине
3) Только уменьшается по величине
4) Увеличивается по величине и изменяется по направлению
5) Уменьшается по величине и изменяется по направлению
6) Увеличивается по величине, не изменяется по направлению
7) уменьшается по величине, не изменяется по направлению
| A | Б | В | Г | Д |
Комета движется по эллиптической орбите вокруг Солнца. Как изменяются перечисленные в первом столбце физические величины во время её приближения к Солнцу, если считать, что на нее действует только тяготение Солнца? Установите соответствие между физическими величинами, перечисленными в первом столбце, и изменениями, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Скорость
Б) Ускорение
В) Кинетическая энергия
Г) Потенциальная энергия
Д) Полная механическая энергия
ИХ ИЗМЕНЕНИЯ
1) Не изменяется
2) Только увеличивается по величине
3) Только уменьшается по величине
4) Увеличивается по величине и изменяется по направлению
5) Уменьшается по величине и изменяется по направлению
6) Увеличивается по величине, не изменяется по направлению
7) уменьшается по величине, не изменяется по направлению
| A | Б | В | Г | Д |
В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличивается. Как изменяются в результате этого перехода потенциальная энергия спутника и центростремительное ускорение?
Для каждой величины определите соответствующий характер изменения:
1. увеличилась
2. уменьшилась
3. не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Потенциальная энергия | Центростремительное ускорение |
Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1
Всего: 44 1–20 | 21–40 | 41–44
А почему-бы и нет? У нас уже были задачи на свободное падение, законы Ньютона, силу трения и проч. и проч. Сегодня решаем задачи на кинетическую и потенциальную энергию.
А вообще, помните, что мы занимаемся далеко не только решением задач. Наш телеграм – это полезная информация для студентов всех специальностей, новости, лайфхаки, акции и скидки.
Задачи на кинетическую и потенциальную энергию
Приведем примеры задач на нахождение кинетической и потенциальной энергии с решением. Прежде чем приступать к практике, почитайте теорию по теме, повторите общую памятку по решению задач по физике и на всякий случай держите под рукой полезные формулы.
Задача №1 на кинетическую энергию
Условие
Максимальная высота, на которую поднимается тело массой 1 кг, подброшенное вертикально вверх, составляет 20 м. Найдите, чему была равна кинетическая энергия сразу же после броска.
Решение
Потенциальная энергия тела над поверхностью Земли составляет:
Здесь m – масса тела, g – ускорение свободного падения, h – высота. Согласно закону сохранения энергии, потенциальная энергия тела в наивысшей точке должна равняться кинетической энергии тела в начальный момент, то есть:
Принимая ускорение свободного падения равным 10 м/с2, находим кинетическую энергию тела сразу же после броска:
Ответ: 200 Дж.
Задача №2 на потенциальную энергию
Условие
Чему равна потенциальная энергия трех кубических дециметров воды на высоте 10 м?
Решение
По определению, потенциальная энергия равна в поле силы тяжести равна:
Масса трех кубических дециметров воды (трех литров) легко находится из формулы для плотности воды:
Осталось вычислить потенциальную энергию:
Ответ: 300 Дж.
При решении задач не забывайте переводить все размерности величин в систему СИ.
Задача №3 на полную механическую энергию
Условие
Какова полная механическая энергия дирижабля массой 5 тонн, если он летит на высоте 2 км со скоростью 60 км/ч?
Решение
Полная механическая энергия состоит из кинетической и потенциальной энергий:
Вычислим:
Ответ: 100,7 МДж.
Задача №4 на кинетическую и потенциальную энергию
Условие
Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счет сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
Решение
Перед началом падения потенциальная энергия шарика составляет:
По закону сохранения энергии, эта энергия должна перейти в кинетическую энергию Ек за вычетом потери за счет сопротивления воздуха дельта Е. Таким образом, можем найти кинетическую энергию:
Ответ: 36 Дж.
Задача №5 кинетическую и потенциальную энергию
Условие
Шарик висит на нити. В нем застревает пуля, летящая горизонтально, в результате чего нить отклоняется на некоторый угол. Как изменятся при увеличении массы шарика следующие величины: импульс, полученный шариком в результате попадания в него пули; скорость, которая будет у шарика тотчас после удара; угол отклонения нити?
Решение
Согласно закону сохранения импульса, скорость шарика с застрявшей в нем пулей равна
Здесь M и m – массы шарика и пули соответственно, v – скорость пули перед ударом. Таким образом, при увеличении массы шарика его скорость после удара уменьшится.
Найдем импульс, переданный шарику при попадании пули:
Следовательно, с увеличением массы шарика переданный ему импульс увеличивается.
Согласно закону сохранения энергии, кинетическая энергия пули перейдет в потенциальную энергию шарика с пулей:
Таким образом, при увеличении массы шарика угол отклонения нити уменьшится, поскольку уменьшится скорость u.
Ответ: см решение выше.
Вопросы на потенциальную и кинетическую энергию
Вопрос 1. Что такое энергия? Что такое механическая энергия?
Ответ. Для энергии существует множество определений. В наиболее общем смысле:
Энергия – мера способности тела совершать работу.
Механическая энергия – это энергия, связанная с движением тела или его положением в пространстве. Механическая энергия в механике описывается суммой кинетической и потенциальной энергии.
Вопрос 2. Сформулируйте закон сохранения энергии
Ответ. Закон сохранения энергии является фундаментальным физическим принципом. Для каждого вида энергии он имеет свою формулировку. Для механической энергии:
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается неизменной.
Вопрос 3. Какие силы называются консервативными?
Ответ. Консервативные, или потенциальные силы – это силы, работа которых не зависит от формы траектории. В качестве примера такой силы можно привести силу тяжести.
Вопрос 4. Какую энергию называют кинетической?
Ответ. Кинетическая энергия является энергией движения. Ею обладают только движущиеся тела, она зависит от массы тела и его скорости.
Вопрос 5. Какую энергию называют потенциальной?
Ответ. Потенциальная энергия является энергией взаимодействия в поле консервативных сил. Она зависит от положения тела и выбора системы отсчета. Например, потенциальная энергия тела в поле силы тяжести зависит от массы тела, ускорения свободного падения и высоты над нулевым уровнем.
Не знаете, как решать задачи на кинетическую или потенциальную энергию? Проблемы с выполнением любых других студенческих работ? Обращайтесь в профессиональный сервис для учащихся за помощью и консультациями.
«Кинетическая и потенциальная энергия»
Код ОГЭ 1.17. Кинетическая и потенциальная энергия. Формула для вычисления кинетической энергии. Формула для вычисления потенциальной энергии тела, поднятого над Землей.
Энергия – физическая величина, характеризующая состояние тела или системы тел. Причиной изменения состояния системы тел (изменения энергии) является работа внешних по отношению к рассматриваемой системе сил. В механике энергия тела или системы тел определяется взаимным положением тел (потенциальная энергия) и их скоростями (кинетическая энергия).
Единица измерения энергии в СИ – джоуль.
Кинетическая энергия – часть механической энергии, энергия движущегося тела. Скалярная величина, численно равная половине произведения массы тела на квадрат скорости:
Теорема о кинетической энергии: Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела: A = Wk2 – Wk1 = ΔWk.
Причём если А > 0, то Wk увеличивается, и если А < 0, то Wk уменьшается.
Эта теорема справедлива для любого движения и для сил любой природы.
Кинетическая энергия – величина относительная, зависящая от выбора СО, так как скорость тела зависит от выбора СО. Если тело разгоняется из состояния покоя, то Wk1 = 0, А = Wk2. Следовательно, физический смысл кинетической энергии: кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости.
Внимание! Кинетическая энергия механической системы тел равна сумме кинетических энергий всех частей системы.
Потенциальная энергия – часть механической энергии тела (системы тел), энергия взаимодействия тел или частей тела. Потенциальная энергия определяется взаимным расположением тел или частей тела, то есть расстояниями между ними.
Потенциальная энергия относительна, зависит от выбора системы отсчёта, в частности от выбора тела отсчёта, которому соответствует нулевой уровень потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести численно равна произведению массы тела на ускорение свободного падения и на высоту относительно выбранного нулевого уровня: Wп = mgh.
Связь работы силы тяжести и изменения потенциальной энергии:
A = mg (h1 – h2) = – (mgh2 – mgh2) = – (Wп2 – Wп1) = – ΔWп
Внимание! Работа сила тяжести равна изменению потенциальной энергии тела в поле силы тяжести, взятому с противоположным знаком.
Конспект урока «Кинетическая и потенциальная энергия».
Следующая тема: «Механическая энергия».
Потенциальная и кинетическая энергия. Закон сохранения механической энергии
1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ( E ). Единица работы — ( [E,] ) = 1 Дж.
При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ( E=A ).
2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.
Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.
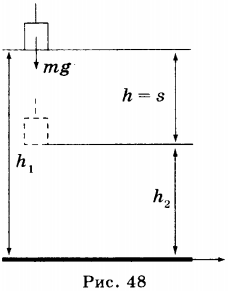
Если тело массой ( m ) падает с высоты ( h_1 ) до высоты ( h_2 ), то работа силы тяжести ( F_т ) на участке ( h=h_1-h_2 ) равна: ( A = F_тh = mgh = mg(h_1 — h_2) ) или ( A = mgh_1 — mgh_2 ) (рис. 48).
В полученной формуле ( mgh_1 ) характеризует начальное положение (состояние) тела, ( mgh_2 ) характеризует конечное положение (состояние) тела. Величина ( mgh_1=E_{п1} ) — потенциальная энергия тела в начальном состоянии; величина ( mgh_2=E_{п2} ) — потенциальная энергия тела в конечном состоянии.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.
Если тело находится на некоторой высоте ( h ) относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ( E_п=mgh ). Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.
В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.
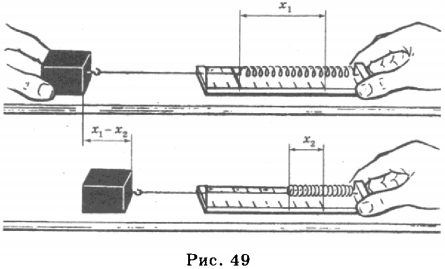
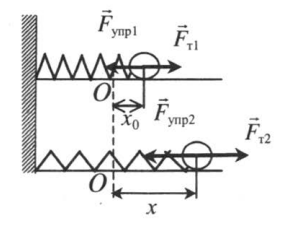
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ( x_1 ), то в пружине возникнет сила упругости ( F_{упр1} ), направленная вправо (рис. 49).
Если теперь предоставить пружину самой себе, то её правый конец переместится, удлинение пружины будет равно ( x_2 ), а сила упругости ( F_{упр2} ).
Работа силы упругости равна
[ A=F_{ср}(x_1-x_2)=k/2(x_1+x_2)(x_1-x_2)=kx_1^2/2-kx_2^2/2 ]
( kx_1^2/2=E_{п1} ) — потенциальная энергия пружины в начальном состоянии, ( kx_2^2/2=E_{п2} ) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.
Можно записать ( A=E_{п1}-E_{п2} ), или ( A=-(E_{п2}-E_{п1}) ), или ( A=-E_{п} ).
Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.
Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ( x ), то потенциальная энергия пружины в данном состоянии равна ( E_п=kx^2/2 ).
4. Движущиеся тела так же могут совершить работу. Например, движущийся поршень сжимает находящийся в цилиндре газ, движущийся снаряд пробивает мишень и т.п. Следовательно, движущиеся тела обладают энергией. Энергия, которой обладает движущееся тело, называется кинетической энергией. Кинетическая энергия ( E_к ) зависит от массы тела и его скорости ( E_к=mv^2/2 ). Это следует из преобразования формулы работы.
Работа ( A=FS ). Сила ( F=ma ). Подставив это выражение в формулу работы, получим ( A=maS ). Так как ( 2aS=v^2_2-v^2_1 ), то ( A=m(v^2_2-v^2_1)/2 ) или ( A=mv^2_2/2-mv^2_1/2 ), где ( mv^2_1/2=E_{к1} ) — кинетическая энергия тела в первом состоянии, ( mv^2_2/2=E_{к2} ) — кинетическая энергия тела во втором состоянии. Таким образом, работа силы равна изменению кинетической энергии тела: ( A=E_{к2}-E_{к1} ), или ( A=E_к ). Это утверждение — теорема о кинетической энергии.
Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.
5. Полная механическая энергия ( E ) тела — физическая величина, равная сумме его потенциальной ( E_п ) и кинетической ( E_п ) энергии: ( E=E_п+E_к ).
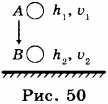
Пусть тело падает вертикально вниз и в точке А находится на высоте ( h_1 ) относительно поверхности Земли и имеет скорость ( v_1 ) (рис. 50). В точке В высота тела ( h_2 ) и скорость ( v_2 ) Соответственно в точке А тело обладает потенциальной энергией ( E_{п1} ) и кинетической энергией ( E_{к1} ), а в точке В — потенциальной энергией ( E_{п2} ) и кинетической энергией ( E_{к2} ).
При перемещении тела из точки А в точку В сила тяжести совершает работу, равную А. Как было показано, ( A=-(E_{п2}-E_{п1}) ), а также ( A=E_{к2}-E_{к1} ). Приравняв правые части этих равенств, получаем: ( -(E_{п2}-E_{п1})=E_{к2}-E_{к1} ), откуда ( E_{к1}+E_{п1}=E_{п2}+E_{к2} ) или ( E_1=E_2 ).
Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.
В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ( m_1 ) в три раза больше массы другого тела ( m_2 ). Относительно поверхности Земли потенциальная энергия
1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела
2. Сравните потенциальную энергию мяча на полюсе ( E_п ) Земли и на широте Москвы ( E_м ), если он находится на одинаковой высоте относительно поверхности Земли.
1) ( E_п=E_м )
2) ( E_п>E_м )
3) ( E_п<E_м )
4) ( E_пgeq E_м )
3. Тело брошено вертикально вверх. Его потенциальная энергия
1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории
4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?
1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз
5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?
1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж
6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия
1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза
7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела
1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза
8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела
1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения
9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.
1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг
10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.
1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с
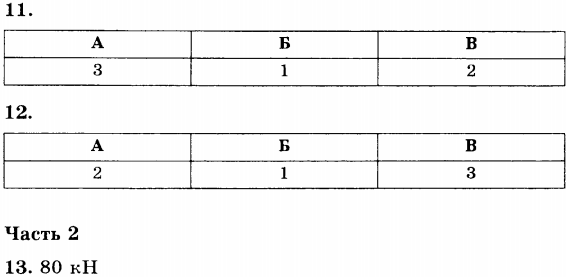
11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ( E=mv^2/2 )
2) ( E=kx^2/2 )
3) ( E=mgh )
12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия
ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется
Часть 2
13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.
Ответы
Потенциальная и кинетическая энергия. Закон сохранения механической энергии
2.9 (58.36%) 134 votes
Совершение работы телом не проходит бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.
Если тело или система тел могут совершить работу, говорят, что они обладает механической энергией.
Определение
Механическая энергия — скалярная физическая величина, являющаяся единой мерой всех форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Механическая энергия обозначается буквой E. Единица изменения энергии — Джоуль (Дж).
Виды механической энергии
В механике состояние системы определяется положением тел и их скоростями. Поэтому в ней выделяют два вида энергии: потенциальную и кинетическую.
Определение кинетической энергии
Кинетическая энергия — это энергия, которой обладает движущееся тело. Она обозначается как Ek. Кинетическая энергия тела зависит от его массы и скорости. Численно она равна половине произведения массы тела на квадрат его скорости:
Определение потенциальной энергии
Потенциальная энергия — это энергия взаимодействующих тел. Она обозначается как Ep.
Потенциальная энергия в поле тяготения Земли численно равна произведению массы тела на его высоту (расстояние от поверхности планеты) и на ускорение свободного падения:
Ep=mgh
Потенциальная энергия упруго деформированного тела определяется формулой:
Ep=kx22
k — жесткость пружины, x — ее удлинение.
Пример №1. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м. Определить его потенциальную и кинетическую энергию в верхней точке.
Потенциальная энергия мяча в поле тяготения Земли равна:
Ep = mgh = 0,4∙10∙3 = 12 (Дж)
В верхней точке полета скорость мяча равна нулю. Следовательно, кинетическая энергия мяча в этой точке тоже будет равна нулю:
Ek = 0 (Дж).
Теорема о кинетической энергии
Теорема о кинетической энергии
Изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело:
Эта теорема справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести.
Пример №2. Скорость движущегося автомобиля массой 1 т изменилась с 10 м/с до 20 м/с. Чему равна работа равнодействующей силы?
Сначала переведем единицы измерения в СИ: 1 т = 1000 кг. Работа равна изменения кинетической энергии, следовательно:
Работа и потенциальная энергия тела, поднятого над Землей
Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.
Работа силы тяжести
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
A = – ∆Ep = –(mgh – mgh0) = mg(h0 – h)
Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.
Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30о. Определить работу, совершенную силой тяжести.
Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:
A = mg(h0 – h) = 0,1∙10(2∙sin30o – 0) =2∙0,5 = 1 (Дж)
Потенциальная энергия протяженного тела
Работа силы тяжести
Потенциальная энергия протяженного тела выражается через его центр масс. К примеру, чтобы поднять лом длиной l и массой m, нужно совершить работу равную:
A = mgh
где h — высота центра массы лома над поверхностью Земли. Так как лом однородный по всей длине, его центр масс будет находиться посередине между его концами, или:
Отсюда работа, которую необходимо совершить, чтобы поднять этот лом, будет равна:
Пример №4. Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?
Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:
Работа и изменение потенциальной энергии упруго деформированного тела
Вспомним, что работа определяется формулой:
A = Fs cosα
Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:
Модуль силы тяги равен по модулю силе упругости, поэтому:
Перемещение определяется формулой:
s = x – x0
Следовательно, работа силы тяги по сжатию или растяжению пружины равна:
Но известно, что потенциальная энергия упруго деформированного тела равна:
Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:
Задание EF18117
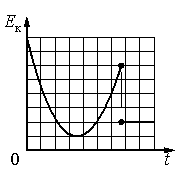
Ответ:
а) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.
б) Тело брошено под углом к горизонту с поверхности Земли и упало на Землю.
в) Тело брошено под углом к горизонту с поверхности Земли и упало на балкон.
г) Тело брошено вертикально вверх с балкона и упало на Землю.
Алгоритм решения
1.Описать изменение кинетической энергии в течение всего времени движения тела.
2.Установить характер движения тела в течение этого времени.
3.Проанализировать все ситуации и выбрать ту, которая не противоречит установленному характеру движения тела.
Решение
Согласно графику, кинетическая энергия тела сначала уменьшалась, а затем увеличилась. Затем она резко уменьшилась до некоторого значения и осталась постоянной.
Кинетическая энергия тела определяется формулой:
Кинетическая энергия зависит прямо пропорциональной от квадрата скорости. Следовательно, когда уменьшается кинетическая энергия, скорость тоже уменьшается. Когда она возрастает — скорость тоже возрастает. Когда она постоянная — скорость тоже постоянна и не равна нулю.
Если тело брошено под углом к горизонту, скорость сначала будет уменьшаться, так как ускорение свободного падения направлено вниз. Если тело бросить вертикально вверх, скорость тоже сначала будет уменьшаться. Но в этом случае при достижении верхней точки траектории на момент скорость тела будет равна нулю. Следовательно, график зависимости кинетической энергии от времени в этот момент тоже должен быть равен нулю. Но это не так. Поэтому последний вариант ответа не подходит.
Если бы тело упало на неподвижный объект, его скорость относительно Земли стала бы равной нулю. Но так как его кинетическая энергия не равна нулю и является постоянной, тело начало двигаться с постоянной скоростью. Это возможно только в случае, если тело упало на объект, движущийся с постоянной скоростью. Поэтому из всех вариантов ответа подходит только первый, когда тело падает в проезжающий мимо грузовик.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18192
Ответ:
а) 40 мДж
б) 20 мДж
в) 80 мДж
г) 200 мДж
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, указать силы, действующие на пружину, выбрать систему отсчета.
3.Записать формулу для вычисления потенциальной энергии в пружине.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса бруска: m = 4 кг.
• Удлинение пружины: ∆l = 2 см.
Переведем сантиметры в метры:
2 см = 0,02 м
Выполним рисунок. Для описания ситуации нам понадобится только одна ось: Oy.
Потенциальная энергия деформированной пружины определяется формулой:
Так как брусок поднимают за прикрепленную к нему пружину медленно, можно считать, что это движение равномерное (и прямолинейное). Поэтому, согласно второму закону Ньютона:
Fт = Fупр
Чтобы оторвать брусок от поверхности стола, модуль силы тяги должен быть равен модулю силы тяжести. Поэтому:
Fт = Fтяж =Fупр
Или:
mg = k∆l
Теперь можем выразить жесткость пружины:
Подставим жесткость пружины в формулу потенциальной энергии и сделаем вычисления:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18553

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 10.4k
Тема 3.
Статика. Гидростатика. Механические колебания и волны. Импульс. Законы сохранения в механике
3
.
11
Закон сохранения энергии и изменения энергии
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
статика. гидростатика. механические колебания и волны. импульс. законы сохранения в механике
3.01Давление
3.02Гидростатика. Сила Архимеда
3.03Момент силы, механическое равновесие тела
3.04Механические колебания
3.05Волны
3.06Импульс
3.07Закон сохранения импульса и изменения импульса
3.08Работа силы
3.09Кинетическая энергия
3.10Потенциальная энергия силы тяжести и пружины
3.11Закон сохранения энергии и изменения энергии
3.12Мощность. КПД. Энергия
Решаем задачи
Шарик массой 100 г падает с высоты 10 м с нулевой начальной скоростью. К моменту падения на землю
потеря полной механической энергии за счёт сопротивления воздуха составила 10%. Какова
кинетическая энергия шарика (в Дж) в этот момент?
Показать ответ и решение
Найдем центр тяжести слоя воды. Так как вода однородна, то её центр тяжести находится ровно
посередине, то есть на высоте м от дна. Найдем также массу воды в бассейне:
где
– глубина бассейна.
Тогда по закону сохранения энергии
Показать ответ и решение
Так как тело падает из состояния покоя, то начальная скорость при падении равна 0. При движении
вниз выполняется закон сохранения энергии.
После соударение шарика об землю будет выполнено равенство (часть энергии переходит в
тепло):
Подставим (1) в (2)
Выразим :
Мячик падает на землю с высоты м с нулевой начальной скоростью. Найдите скорость мячика в
момент удара о поверхность земли, если за счёт силы сопротивления воздуха он потерял
первоначальной энергии. Ответ дайте в м/с.
Шарик массой 400 г падает с высоты 12,25 м. Начальная скорость шарика равна нулю. Потеря энергии
за счёт сопротивления воздуха составила 4 Дж. Какая скорость была у шарика в момент падения на
землю? Ответ дайте в м/с.
Показать ответ и решение
По закону сохранения энергии с учетом потерь:
Отсюда:
Шарик массой 100 г падает с высоты h с начальной скоростью, равной нулю. Скорость шарика в момент
перед падением на землю равна 8 м/с. Чему равна его потенциальная энергия в момент начала
падения, если потеря энергии за счет сопротивления воздуха составила 1 Дж. Ответ дайте в
Дж.
Показать ответ и решение
По закону сохранения энергии с учетом потерь:
А
значит:
Шарик массой 100 г падает с высоты 100 м с начальной скоростью, равной нулю. Чему равна его
кинетическая энергия в момент перед падением на землю, если потеря энергии за счёт сопротивления
воздуха составила 20 Дж? Ответ дайте в Дж.
Демоверсия 2019
Показать ответ и решение
Из закона о сохранении энергии:
где
– масса шарика,
– начальная высота,
– потери за счет сопротивления воздуха.
Автомобиль с выключенным двигателем проехал 28,8 м вниз по дороге, проложенной под углом к
горизонту. При этом его начальная скорость была равна 6 м/с. Какова конечная скорость автомобиля?
Трением пренебречь. Ответ дайте в м/с.
Камень бросили вертикально вверх с начальной скоростью м/с. Найдите массу камня (в кг),
если на максимально достигнутой высоте потенциальная энергия камня составила 40 Дж?
Сопротивлением воздуха пренебречь. Ответ дайте в кг.
Мячик массой 0,5 кг, брошенный вертикально вверх, обладал кинетической энергией Дж.
На какую максимальную высоту поднялся мячик? Сопротивлением воздуха пренебречь.
Автомобиль с выключенным двигателем сняли со стояночного тормоза, и он покатился под уклон,
составляющий угол к горизонту. Проехав 10 м, он попадает на горизонтальный участок
дороги. Чему равна скорость автомобиля в начале горизонтального участка дороги? Трением
пренебречь.
Досрочная волна 2020
Показать ответ и решение
Из закона сохранения энергии
где
– масса автомобиля,
– путь автомобиля.
Откуда скорость:
Максимальная высота, на которую шайба массой 40 г может подняться по гладкой наклонной плоскости
относительно начального положения, равна 0,2 м. Определите кинетическую энергию шайбы в
начальном положении. Сопротивлением воздуха пренебречь.
Демоверсия 2020
Показать ответ и решение
Из закона сохранения энергии:
У основания гладкой наклонной плоскости шайба массой 10 г обладает кинетической энергией 0,04 Дж.
Определите максимальную высоту, на которую шайба может подняться по плоскости относительно
основания. Сопротивлением воздуха пренебречь. Ответ дайте в метрах
Демоверсия 2018
Показать ответ и решение
Из закона сохранения энергии:
где
– масса тела,
– скорость тела в начальный момент времени,
– максимальная высота
подъема.
Показать ответ и решение
Запишем закон сохранения энергии
Отсюда сжатие
Показать ответ и решение
Потенциальная энергия пружины перейдет в потенциальную энергию «высоты»
Показать ответ и решение
Потенциальная энергия пружины:
Вся потенциальная энергия перейдет в кинетическую
Выразим скорость