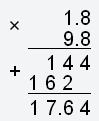Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 63 1–20 | 21–40 | 41–60 | 61–63
Добавить в вариант
Тип 8 № 513940
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 20 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513941
Груз массой 0,4 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 23 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513942
Груз массой 0,32 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 27 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513943
Груз массой 0,7 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 22 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513944
Груз массой 0,4 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 26 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513945
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 30 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513946
Груз массой 0,3 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 33 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513947
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 37 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513948
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 32 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513949
Груз массой 0,4 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 36 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513950
Груз массой 0,2 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 40 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513951
Груз массой 0,4 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 43 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513952
Груз массой 0,25 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 47 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513953
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 42 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513954
Груз массой 0,5 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 46 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513955
Груз массой 0,58 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 50 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513956
Груз массой 0,58 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 50 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513957
Груз массой 0,5 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 53 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513958
Груз массой 0,38 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Тип 8 № 513959
Груз массой 0,8 кг колеблется на пружине. Его скорость υ меняется по закону где t — время с момента начала колебаний, T = 2 с — период колебаний,
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
где m — масса груза в килограммах, υ — скорость груза в м/с. Найдите кинетическую энергию груза через 52 секунды после начала колебаний. Ответ дайте в джоулях.
Аналоги к заданию № 28013: 513931 513932 513933 513934 513935 513936 513937 513938 513939 513940 … Все
Классификатор алгебры: Тригонометрические уравнения и неравенства
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения, Разные задачи с прикладным содержанием
Решение
·
Прототип задания
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Всего: 63 1–20 | 21–40 | 41–60 | 61–63
Задание № 21674
Кинетическую энергию (в Дж) тела можно рассчитать по формуле [math]E_k=frac{mv^2}2[/math], где m — масса тела (в кг), v — скорость тела (в м/с). Какова масса тела в (кг.), если при скорости 120 м/с оно приобретает энергию 36 000 Дж?
Решать другие задания по теме: Задачи с прикладным содержанием
Показать ответ
Комментарий:
[math]E=frac{mU^2}2[/math]
[math]m=frac{2E}{U^2}[/math][math]=frac{2ast36000}{14400}=frac{360}{72}=5[/math]
Ответ: 5
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 4 проверяются навыки работы с формулами. Школьник должен уметь выражать искомую величину из формулы и находить ее значение по исходным данным. Здесь вы можете узнать, как решать задание 4 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.
Закон Гука можно записать в виде F = kx, где F — сила (в ньютонах)
Закон Гука можно записать в виде F = kx, где F — сила (в ньютонах), с которой сжимают пружину, x — абсолютное удлинение (сжатие) пружины (в метрах), а k — коэффициент упругости. Пользуясь этой формулой, найдите x (в метрах), если даны F и k.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула
Перевести температуру из шкалы Фаренгейта в шкалу Цельсия позволяет формула tC = 5/9 ⋅ (tF – 32), где tC — температура в градусах по шкале Цельсия, tF — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия соответствует температура по шкале Фаренгейта?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Найдите h из равенства E = mgh
Найдите h из равенства E = mgh, если даны g, m и E.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Найдите m из равенства E = mv^2 / 2
Найдите m из равенства E = mv 2 / 2, если даны v и E.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Найдите x из равенства f = kx
Найдите x из равенства f = kx, если даны f и k.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует температуре по шкале Фаренгейта? Ответ округлите до десятых.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Площадь четырёхугольника можно вычислить по формуле S = d1 ⋅ d2 ⋅ sinα / 2
Площадь четырёхугольника можно вычислить по формуле S = d1 ⋅ d2 ⋅ sinα / 2, где d1 и d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если даны d1, sinα и S.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если даны мощность и сила тока.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Площадь любого выпуклого четырехугольника можно вычислять по формуле
Площадь любого выпуклого четырехугольника можно вычислять по формуле S = 1/2 ⋅ d1 ⋅ d2 ⋅ sinα, где d1, d2 — длины его диагоналей, а α угол между ними. Вычислите sinα, если даны S, d1, d2.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Площадь треугольника можно вычислить по формуле S = (a + b + c)r / 2
Площадь треугольника можно вычислить по формуле S = (a + b + c)r / 2, где a, b, c — длины сторон треугольника, r — радиус вписанной окружности. Вычислите длину стороны c, если даны S, a, b, r.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Длину биссектрисы треугольника, проведённой к стороне a, можно вычислить
Длину биссектрисы треугольника, проведённой к стороне a, можно вычислить по формуле l = 2 ⋅ b ⋅ c ⋅ cos(α/2) / (b + c). Вычислите cos(α/2), если даны b, c, l.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Количество теплоты (в джоулях), полученное однородным телом при нагревании
Количество теплоты (в джоулях), полученное однородным телом при нагревании, вычисляется по формуле Q = cm(t2 — t1), где c — удельная теплоёмкость (в Дж/(кг⋅К)), m — масса тела (в кг), t1 — начальная температура тела (в кельвинах), а t2 — конечная температура тела (в кельвинах). Пользуясь этой формулой, найдите Q, если даны t2, c, m и t1.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Радиус окружности, описанной около треугольника, можно вычислить по формуле
Радиус окружности, описанной около треугольника, можно вычислить по формуле R = a/(2sinα), где a — сторона, а α — противолежащий ей угол треугольника. Пользуясь этой формулой, найдите R, если даны a и sinα.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Работа постоянного тока (в джоулях) вычисляется по формуле A = U^2 ⋅ t / R
Работа постоянного тока (в джоулях) вычисляется по формуле A = U 2 ⋅ t / R, где U — напряжение (в вольтах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если даны t , U и R.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Мощность постоянного тока (в ваттах) вычисляется по формуле P = U^2/R
Мощность постоянного тока (в ваттах) вычисляется по формуле P = U 2 / R, где U — напряжение (в вольтах), R — сопротивление (в омах). Пользуясь этой формулой, найдите P (в ваттах), если даны R и U.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Теорему косинусов можно записать в виде cosγ = (a² + b² — c²) / (2ab)
Теорему косинусов можно записать в виде cosγ = (a² + b² — c²) / (2ab) где a, b и c — стороны треугольника, а γ — угол между сторонами a и b. Пользуясь этой формулой, найдите величину cosγ если даны a, b и c.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Кинетическая энергия тела (в джоулях) вычисляется по формуле E = m ⋅ v^2 / 2
Кинетическая энергия тела (в джоулях) вычисляется по формуле E = m ⋅ v 2 / 2, где m — масса тела (в килограммах), а v — его скорость (в м/с). Пользуясь этой формулой, найдите E (в джоулях), если даны v и m.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Площадь прямоугольника вычисляется по формуле S = d^2 ⋅ sinα / 2
Площадь прямоугольника вычисляется по формуле S = d 2 ⋅ sinα / 2, где d — диагональ, α — угол между диагоналями. Пользуясь этой формулой, найдите S , если даны d и sinα.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
В строительной фирме «Родник» стоимость (в рублях) колодца из железобетонных колец
В строительной фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С = a + bn, где n ― число колец, установленных при копании колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из d колец. Ответ укажите в рублях.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Площадь трапеции S в кв.м. можно вычислить по формуле S = (a + b)/2 ⋅ h
Площадь трапеции S в кв.м. можно вычислить по формуле S = (a + b)/2 ⋅ h, где a, b — основания трапеции, h — высота (в метрах). Пользуясь этой формулой, найдите S, если даны a, b и h.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 4.
Задание №4 ЕГЭ по математике базового уровня
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
- Подставить все значения в данную формулу.
- Произвести вычисления.
По условию задания дана высота h=0,9 м и ускорение свободного падения g=9,8 м/с2. Подставим эти значения в формулу вычисления скорости v, получим: Делаем умножение 1,8 на 9,8, имеем:
м/с.
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью
Ф, если заряд на его обкладке равен 0,019 Кл.
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Подставим в формулу энергии конденсатора значения q=0,019 Кл и C = Ф, получим:
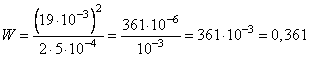
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью
Ф, если заряд на его обкладке равен 0,07 Кл.
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Подставим в формулу энергии конденсатора значения q=0,07 Кл и C = Ф, получим:
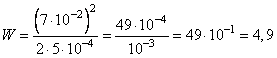
Задание 4 ЕГЭ математика (профильный уровень)
В четвертом задании предстоит вычислить вероятность события. Вычисления довольно простые, достаточно знать определение вероятности и простейшие способы ее вычисления. Также надо уметь работать с обыкновенными дробями, переводить обыкновенные дроби в десятичные, округлять десятичные дроби, составлять и решать линейные уравнения.
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты
Вероятность всегда выражается дробью, в знаменателе которой стоит общее число исходов, а в числителе – число исходов, удовлетворяющих условию. Чаще всего задача сводится именно к вычислению числа исходов (примеры 1-2). Иногда к сложению или умножению вероятностей отдельных событий (примеры 3-6), и очень редко к нескольким действиям (примеры 7-8).
Знать определения и правила надо. Но при решении задач на вероятность важнее иметь хороший практический навык. Это позволит на экзамене не углубляться в простом задании в сложные математические законы и сэкономить время и собственные нервы. На самом деле трудных задач в четвертом задании нет вообще.
Пример №1.
Для призов участникам технического конкурса в магазине приобрели 30 раскрасок, из которых 10 с танками, 11 с самолетами, а остальные с космическими кораблями. Призы определяются жеребьевкой. Дима хочет получить раскраску с космическими кораблями. Какова вероятность, что его желание исполнится?
Решение: Сначала определим число раскрасок с космическими кораблями: 30-10-11=9
Теперь можем вычислить вероятность: 9/30=0,3
Пример №2
В упаковке лежат блокноты с цветными обложками: 12 с красной, 7 с синей, 9 с черной, 8 с желтой и 14 с белой. Из упаковки вынимают 1 блокнот. Найдите вероятность того, что обложка этого блокнота желтая.
Решение: Всего блокнотов: 12+7+9+8+14=50
Вероятность того, что попадется блокнот с желтой обложкой: 8/50=0,16
Пример №3
В киоске продаются уцененные авторучки. Вероятность неисправности авторучки составляет 0,09. Найдите вероятность того, что приобретенная наугад авторучка исправна.
Решение: Сумма вероятностей купить исправную или неисправную авторучку равна единице. Чтобы определить вероятность покупки хорошей ручки надо из единицы вычесть вероятность покупки неисправной ручки: 1-0,09=0,91
Пример №4
Два кубика бросают одновременно. Найти вероятность выбросить 9 очков.
Решение: Подберем пары чисел от 1 до 6, которые в сумме дают 9
3+6
4+5
5+4
6+3
Понятно, что на первом кубике может выпасть 4 из 6 возможных чисел. Вероятность составляет: 4/6=2/3
При бросании второго кубика должно выпасть 1 число из 6, вероятность этого события 1/6.
Тогда вероятность того, что сумма очков составит 9, равна произведению вероятностей: 2/3*1/6=2/18=1/9=0,11
Эту задачу можно решить с помощью таблицы, где в верхней строке указано число на перовом кубике, в левом столбце – число на втором, а в ячейках – их сумма. (Такую таблицу можно за минуту набросать на черновике)
Из таблицы видно, что из 36 возможных исходов, 9 очков выпадает в 4-х случаях. Т.е. вероятность составляет 4/36=1/9=0,11
Пример №5
Дима хорошо подготовился к олимпиаде по физике. С вероятностью 0,98 он станет призером и с вероятностью 0,84 – победителем олимпиады. С какой вероятностью Дима станет призером, но не станет победителем олимпиады по физике?
Решение: Победитель одновременно является и призером олимпиады. Поэтому вероятность стать призером (0,98) можно представить в виде суммы вероятности стать победителем (0,84) и вероятности стать просто призером (Х).
Х+0,84=0,98
Х=0,98-0,84
Х=0,14
Пример №6
В дежурном отряде 7 мальчиков и 14 девочек. Дежурство распределяется по жребию. На центральные ворота лагеря нужны двое дежурных. Найти вероятность, что дежурить на воротах будут двое мальчиков.
Решение: Первым дежурным окажется мальчик с вероятностью: 7/21=1/3
Второй дежурный выбирается из 20 оставшихся детей, из которых мальчиков осталось только 6: 6/20=3/10
Вероятность, что на воротах будут дежурить два мальчика: 1/3*3/10=0,1
Пример №7
В сквере имеется сеть дорожек, ведущих к смотровым площадкам. Водопад можно наблюдать с площадок F и G. Турист отправляется из точки А. На каждой развилке он выбирает произвольное направление (кроме направления назад). С какой вероятностью турист сможет увидеть водопад?
Решение: Так как водопад виден с двух площадок, то для решения задачи нужно сложить вероятность того, что турист попадет на площадку F, и вероятность того, что он попадет на площадку G
Для площадки F: 1/2*1/3=1/6
Для площадки G: 1/2*1/2=1/4
Для двух площадок: 1/6+1/4=4/24+6/24=10/24=0,42
Пример №8
К зачету надо выучить 10 вопросов. Саша выучил 2, а остальные только прочитал. Если Саше попадется выученный билет, то он сдаст зачет с вероятностью 0,9. Если Саше попадется вопрос, который он только прочитал, то вероятность сдать зачет 0,3. Вопросы на зачете распределяются случайным образом. Найти вероятность того, что Саша сдаст зачет.
Решение: Из 10 билетов выучены 2, не выучены 8. Вероятность получить выученный вопрос 2/10, вероятность получить не выученный вопрос 8/10.
Вероятность сдать зачет по выученному билету: 2/10*0,9=0,18
Вероятность сдать по невыученному билету: 8/10*0,3=0,24
Итоговая вероятность: 0,18+0,24=0,42
Несколько советов по решению 2 задания
Сложнее всего определить, когда вероятности двух событий надо перемножать, а когда складывать. Попадаются задачи, когда надо сделать и то, и другое. Если вы нашли вероятности отдельных событий, но не можете определиться, что с ними делать дальше – доверьтесь интуиции.
Если вы понимаете что вероятность двух событий больше, чем вероятность каждого в отдельности – складывайте. (Например, вероятность выбросить решку на одной из двух монет очевидно больше, чем выбросить решку на одной монете.)
Если вероятность двух событий меньше, чем каждого в отдельности – перемножайте. (Например, вероятность выбросить решку на обеих монетах меньше, чем вероятность выбросить решку на одной из них.)
Понятно, что интуиция – подход ненаучный. Но на ЕГЭ в задании с кратким ответом лучше дать какой-нибудь ответ, чем не дать никакого.
Однако не забывайте, что профильный ЕГЭ по математике является не только выпускным, но и вступительным испытанием. Большинство школьных задач на вероятность можно решить путем логических рассуждений. Это создает иллюзию легкости теории вероятности и математической статистики. Но на самом деле это одна из самых передовых и востребованных областей математики, и в ВУЗе вы ощутите её сложность в полной мере.
Тема 16.
Электродинамика (изменение физических величин в процессах)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
электродинамика (изменение физических величин в процессах)
16.01Электрическое поле. Электростатика
16.02Электрический ток. Электрические цепи
16.03Магнитное поле
16.04Электромагнитная индукция
16.05Колебательный контур
16.06Оптика
Решаем задачи
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца,
действующая на электрон, и период его обращения, если увеличить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения.
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут
повторяться.
Показать ответ и решение
При движении электрона в магнитном поле на него действует сила Лоренца, при этом электрон движется по окружности. Запишем
второй закон Ньютона:
Кинетическая энергия находится по формуле , если ее увеличить, то скорость электрона вырастет, значит сила
Лоренца , тоже увеличится. А — 1.
Период обращения найдем по формуле:
Так как масса электрона, его заряд и внешнее магнитное поле не менялись, то и период обращения не изменится. Б —
3
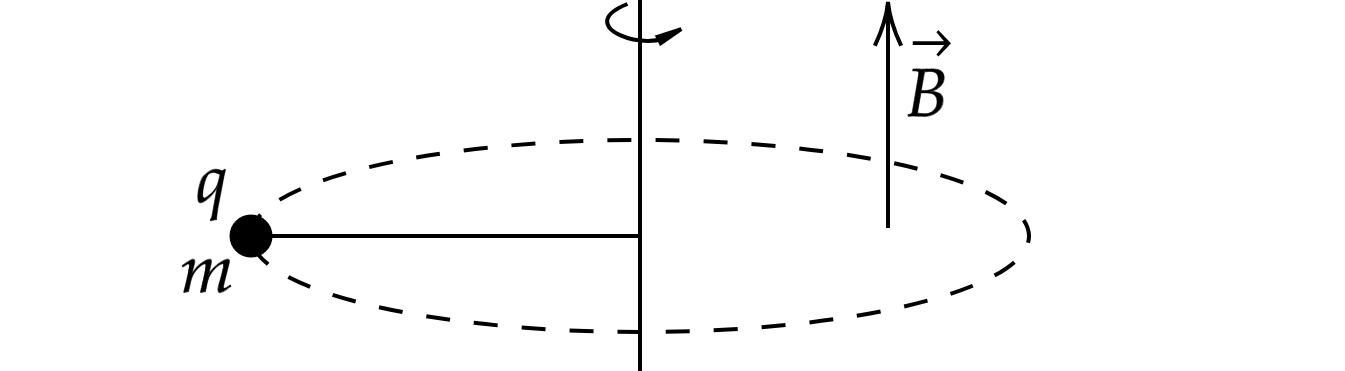
Маленький шарик массой и зарядом
, закрепленный тонкой непроводящей нитью, вращается на гладкой поверхности по
окружности с постоянной по модулю скоростью в однородном магнитном поле
. Как изменятся сила Лоренца и сила
натяжения нити, если увеличить массу шарика.
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
Показать ответ и решение
Сила Лоренца – 3
Сила Лоренца находится по формуле:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Она не зависит от массы, а значит она неизменна.
Сила натяжения нити – 1
Второй закон Ньютона:
где – сила натяжения нити. Согласно правилу левой руки, сила Лоренца будет направлена вдоль радиус-вектора, выходящего
из центра окружности. Тогда Второй закон Ньютона можно переписать в виде
Так как сила Лоренца не зависит от массы, то сила натяжения нити будет увеличиваться.
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период
его обращения, если увеличить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
Показать ответ и решение
Сила Лоренца, действующая на электрон – 1
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Кинетическая энергия находится по формуле:
– масса. Так как кинетическая энергия увеличивается, а масса остается неизменной, то увеличивается скорость частицы, а
значит и увеличивается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона:
Распишем центростремительное ускорение, как
Выразим радиус вращения
Период же находится по формуле:
Подставив в формулу периода радиус, получим
Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется),
следовательно, период не изменяется.
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период
его обращения, если уменьшить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
Показать ответ и решение
Сила Лоренца, действующая на электрон – 2
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Кинетическая энергия находится по формуле:
– масса. Так как кинетическая энергия уменьшается, а масса остается неизменной, то уменьшается скорость частицы, а
значит и уменьшается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона:
Распишем центростремительное ускорение, как
Выразим радиус вращения
Период же находится по формуле:
Подставив в формулу периода радиус, получим
Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется),
следовательно, период не изменяется.
Частица массой , несущая заряд
, движется в однородном магнитном поле с индукцией
по окружности радиусом
со скоростью
. Как изменится радиус траектории и период обращения частицы при уменьшении скорости ее
движения?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Показать ответ и решение
1) Радиус траектории – 2
На частицу будет действовать сила Лоренца, которая будет создавать центростремительное ускорение
Отсюда радиус траектории равен
Значит при уменьшении скорости радиус траектории тоже уменьшается.
2) Период обращения – 3
Период обращения равен
Из первого пункта подставим радиус и получим
Получили, что период не зависит от скорости, а значит и не будет изменяться.
Протон в однородном магнитном поле между полюсами магнита под действием силы Лоренца движется по окружности радиусом .
В этом же поле по окружности с таким же радиусом стала двигаться –частица. Как изменились период обращения в магнитном
поле и модуль импульса – частицы по сравнению с протоном? Для каждой величины определите соответствующий характер
изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Досрочная волна 2019
Показать ответ и решение
Из второго закона Ньютона:
Поскольку массы и заряды протона и –частицы связаны соотношениями
заключаем, что при таком же радиусе окружности, скорость – частицы должна быть в 2 раза меньше скорости
протона.
А) Период же равен:
Так как , а
он увеличится.
Так как период увеличивается в 2 раза, радиус тоже увеличивается в 2 раза
Б) Импульс:
Масса увеличится в 4 раза, а скорость уменьшится в 2 раза, значит, импульс увеличится в 2 раза.
Альфа-частица движется по окружности в однородном магнитном поле. Как изменятся ускорение альфа-частицы и частота её
обращения, если уменьшить её кинетическую энергию? Для каждой величины определите соответствующий характер
изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться
Демоверсия 2020
Показать ответ и решение
Кинетическая энергия равна
раз кинетическая энергия уменьшается, то и уменьшается и скорость.
А) Ускорение из второго закона Ньютона:
где – заряд,
– магнитная индукция,
– масса частицы.
Следовательно, ускорение уменьшается.
Б) Распишем ускорение, как и получим
Циклическая частота не изменяется, следовательно не изменяется и частота обращения
Частица массой , несущая заряд
, движется в однородном магнитном поле с индукцией В по окружности радиусом
со
скоростью . Как изменятся радиус орбиты и сила Лоренца, действующая на частицу, если её скорость уменьшится? Для каждой
величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Демоверсия 2019
Показать ответ и решение
А) Запишем второй закон Ньютона:
Следовательно радиус уменьшится.
Б) Сила Лоренца равна:
Следовательно, сила Лоренца уменьшится
Частица массой , несущая заряд
, движется в однородном магнитном поле с индукцией
по окружности радиусом
со
скоростью . Как изменится радиус траектории и кинетическая энергия частицы при уменьшении скорости ее движения? Для
каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Основная волна 2020
Показать ответ и решение
А) По второму закону Ньютона:
Скорость уменьшается, следовательно, радиус тоже уменьшится.
Б) Кинетическая энергия:
Скорость уменьшается, следовательно, кинетическая энергия уменьшается
Обновлено: 02.01.2023
Задание
Кинетическая энергия тела (в джоулях) вычисляется по формуле E = mv2/2, где m – масса тела (в килограммах), а v – его скорость (в м/с). Пользуясь этой формулой, найдите Е (в джоулях), если v = 4 м/с и m = 10 кг.
Решение
Подставляем все известные параметры в формулу и находим кинетическую энергию тела:
E = mv2/2 = 10*42/2 = 10*16/2 = 10*8 = 80
80 джоулей – кинетическая энергия тела.
Ответ: 80
Закон сохранения импульса, кинетическая и потенциальные энергии, работа и мощность силы, закон сохранения механической энергии
В. З. Шапиро
Третье задание ЕГЭ по физике проверяет знания по разделу «Законы сохранения в механике». Оно относится к заданиям базового уровня. В нём отсутствует возможность выбора ответа. Для его решения необходимо знать и уметь применять законы сохранения импульса и энергии.
Применение формулы закона сохранения энергии
Необходимая теория: Энергия
1. Шарик массой 100 г падает с некоторой высоты. Начальная скорость шарика равна нулю. Его кинетическая энергия при падении на землю равна 6 Дж, а потеря энергии за счёт сопротивления воздуха составила 1 Дж. С какой высоты упал шарик?
Ответ: ______________________ м.
Так как в момент падения шарик имел кинетическую энергию 6 Дж, а потеря механической энергии из-за сопротивления воздуха составила 1 Дж, то первоначальное значение потенциальной энергии равно: Eп1 = 6 + 1 = 7 (Дж).
По формуле для расчета потенциальной энергии тела, поднятого на высоту h от поверхности Земли, рассчитаем эту неизвестную высоту.
Ответ: 7 м.
При использовании закона сохранения энергии необходимо записать, какой энергией обладало тело в начальный момент времени или в первоначальной точке. После этого рассматриваем последующую ситуацию. Это не тот случай, когда можно взять готовую формулу, подставить в неё значение и получить ответ.
2. Автомобиль с выключенным двигателем сняли со стояночного тормоза, и он покатился под уклон, составляющий угол 30° к горизонту. Проехав 10 м, он попадает на горизонтальный участок дороги. Чему равна скорость автомобиля в начале горизонтального участка дороги? Трением пренебречь.
Ответ: ___________________________ м/с.
В этой задаче необходим чертеж.
Из соотношений в прямоугольном треугольнике получим:
(м).
– согласно закону сохранения энергии.
(м/с).
Ответ: 10 м/с.
Секрет решения. В большинстве задач по физике рисунки и чертежи помогают лучше понять условие. Это прежде всего относится к задачам, в которых используются какие-либо геометрические построения.
Применение формулы для расчета кинетической энергии тела
3. Скорость груза массой 0,3 кг равна 2 м/с. Какова кинетическая энергия груза?
Ответ: ___________________________ Дж.
Кинетическая энергия тела рассчитывается по формуле
(Дж).
Ответ: 0,6 Дж.
Секрет решения. В таких задачах необходимо обратить внимание на систему СИ. Простая, на первый взгляд, задача может иметь «подводные камни», связанные с неправильным использованием системы единиц.
Применение формулы для расчета потенциальной энергии упруго деформированного тела
Необходимая теория: Энергия
4. При упругой деформации 2 см стальная пружина имеет потенциальную энергию 2 Дж. Какой станет потенциальная энергия этой пружины при увеличении деформации на 1 см?
Потенциальную энергию упруго деформированной пружины можно рассчитать по формуле:
Разделив Eп2 на Eп1, получим
Ответ: 4,5 Дж.
Секрет решения. Внимательно читайте условие задачи. Условие – это ключ к решению. В этой задаче важно понять, что во втором случае деформация пружины составляет 3 см. Кроме этого, при нахождении отношений деформаций мы не использовали систему СИ, так как при делении результат от этого не изменится.
Сравнение кинетических энергий тела с использованием графика
5. Скорости движения двух одинаковых автомобилей изменяются с течением времени в соответствии с графиками на рисунке. Определите отношение кинетических энергий автомобилей в момент времени t1 .
Ответ: ________________________.
Так как на графике не указаны конкретные значения скоростей автомобилей, то их можно выразить в некоторых условных единицах.
Ответ: 16.
При решении задач нужно уметь «читать» графики. Ведь графические зависимости аналогичны текстовому описанию, но просто по-другому выглядят.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 3 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
17. Электродинамика (изменение физических величин в процессах)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Кольцо из проволоки находится в однородном магнитном поле. Модуль индукции магнитного поля уменьшают с постоянной скоростью. Затем кольцо заменяют на другое с площадью в два раза больше, оставляя расположение относительно линий магнитной индукции тем же, при этом скорость изменения модуля индукции магнитного поля уменьшают в 4 раза. Как в результате этого изменятся следующие физические величины: ЭДС индукции, возникающая в кольце и cкорость изменения потока через кольцо .
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
[begin{array}{|c|c|}
hline
text{ ЭДС индукции,}&text{ Скорость изменения магнитного }\
text{ возникающая в кольце}&text{ потока через кольцо}\
hline
&\
hline
end{array}]
ЭДС индукции, возникающая в кольце – 2
ЭДС индукции: [xi_i=-frac{Delta text{Ф}}{Delta t}] где (Delta text{ Ф}) – изменение потока вектора магнитной индукции, (t) – время. [xi_i=-Scos alpha dfrac{Delta B}{t},] где (Delta B) – изменение модуля вектора магнитной индукции, (S) – площадь рамки, (alpha) – угол между нормалью к поверхности и вектором (vec{B}). Значит ЭДС индукции уменьшается в 2 раза, так как площадь увеличивается в 2 раза, а скорость изменения модуля магнитной индукции уменьшается в 4 раза.
Скорость изменения магнитного потока через кольцо – 2
Изменение магнитного потока: [text{ Ф}=Delta BScosalpha] Так как площадь увеличивается в 2 раза, а скорость изменения модуля магнитной индукции уменьшается в 4 раза, то и магнитный поток скорость изменения магнитного потока уменьшается.
Ответ: 22
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период его обращения, если уменьшить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
[begin{array}{|c|c|}
hline
text{ Сила Лоренца, }&text{ Период обращения }\
text{ действующая на электрон}&\
hline
&\
hline
end{array}]
Сила Лоренца, действующая на электрон – 2
Сила Лоренца: [F_L=Bvqsinalpha] где (B) – модуль вектора магнитной индукции, (v) – скорость заряда, (q) – заряд, (alpha) – угол между вектором магнитного поля и скоростью движения частицы. Кинетическая энергия находится по формуле: [E=dfrac{mv^2}{2},] (m) – масса. Так как кинетическая энергия уменьшается, а масса остается неизменной, то уменьшается скорость частицы, а значит и уменьшается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона: [F_L=ma_{text{цс}}] Распишем центростремительное ускорение, как (dfrac{v^2}{R}) [Bvq=frac{mv^2}{R}] Выразим радиус вращения [R=frac{mv}{Bq}] Период же находится по формуле: [T=dfrac{2 pi R }{v}] Подставив в формулу периода радиус, получим [T=dfrac{2 pi m}{Bq}] Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется), следовательно, период не изменяется.
Ответ: 23
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период его обращения, если увеличить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
[begin{array}{|c|c|}
hline
text{ Сила Лоренца, }&text{ Период обращения }\
text{ действующая на электрон}&\
hline
&\
hline
end{array}]
Сила Лоренца, действующая на электрон – 1
Сила Лоренца: [F_L=Bvqsinalpha] где (B) – модуль вектора магнитной индукции, (v) – скорость заряда, (q) – заряд, (alpha) – угол между вектором магнитного поля и скоростью движения частицы. Кинетическая энергия находится по формуле: [E=dfrac{mv^2}{2},] (m) – масса. Так как кинетическая энергия увеличивается, а масса остается неизменной, то увеличивается скорость частицы, а значит и увеличивается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона: [F_L=ma_{text{цс}}] Распишем центростремительное ускорение, как (dfrac{v^2}{R}) [Bvq=frac{mv^2}{R}] Выразим радиус вращения [R=frac{mv}{Bq}] Период же находится по формуле: [T=dfrac{2 pi R }{v}] Подставив в формулу периода радиус, получим [T=dfrac{2 pi m}{Bq}] Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется), следовательно, период не изменяется.
Ответ: 13
Проволочная обмотка генератора переменного тока равномерно вращается в постоянном магнитном поле. Угловую скорость вращения увеличивают. Как изменятся частота генерируемого переменного тока и амплитуда ЭДС индукции, действующей в обмотке?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
[begin{array}{|c|c|}
hline
text{ Частота переменного тока }&text{ ЭДС индукции в обмотке}\
hline
&\
hline
end{array}]
Частота переменного тока – 1
Так как угловая скорость рамки увеличивается, то и полный оборот вокруг оси она будет совершать быстрее, а это означает, что период обращения уменьшится, период и частота связаны формулой: [nu=dfrac{1}{T}] Так как период уменьшается, то частота увеличивается.
ЭДС индукции в обмотке – 1
[xi_i=-frac{Delta text{Ф}}{Delta t}] где (Delta text{ Ф}) – изменение потока вектора магнитной индукции, (t) – время. [xi_i=-Scos alpha dfrac{Delta B}{t},] где (Delta B) – изменение модуля вектора магнитной индукции, (S) – площадь рамки, (alpha) – угол между нормалью к поверхности и вектором (vec{B}). Так как увеличивается скорость движения рамки, то и увеличивается скорость изменения потока, а значит и увеличивается ЭДС индукции в обмотке.
Ответ: 11
Маленький шарик массой (m) и зарядом (q), закрепленный тонкой непроводящей нитью, вращается на гладкой поверхности по окружности с постоянной по модулю скоростью (v) в однородном магнитном поле (vec{B}). Как изменятся сила Лоренца и сила натяжения нити, если увеличить массу шарика.
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
[begin{array}{|c|c|}
hline
text{ Сила Лоренца }&text{ Сила натяжения нити}\
hline
&\
hline
end{array}]
Сила Лоренца – 3
Сила Лоренца находится по формуле: [F_L=Bvqsinalpha] где (B) – модуль вектора магнитной индукции, (v) – скорость заряда, (q) – заряд, (alpha) – угол между вектором магнитного поля и скоростью движения частицы. Она не зависит от массы, а значит она неизменна.
Сила натяжения нити – 1
Второй закон Ньютона: [vec{F_L}+vec{T}=ma] где (T) – сила натяжения нити. Согласно правилу левой руки, сила Лоренца будет направлена вдоль радиус-вектора, выходящего из центра окружности. Тогда Второй закон Ньютона можно переписать в виде [T=ma pm F_L] Так как сила Лоренца не зависит от массы, то сила натяжения нити будет увеличиваться.
Ответ: 31

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ