1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
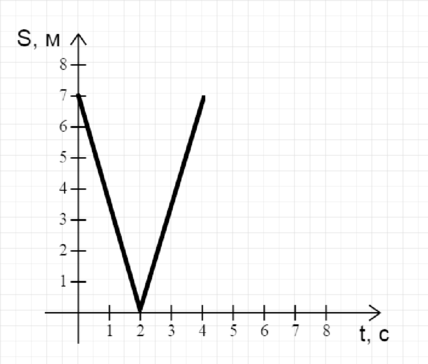
Из двух концов комнаты навстречу друг другу с постоянной скоростью движутся МО и Рыжий Боб. На графике показана зависимость расстояния между ними от времени. Скорость МО равна 3,14 м/с. С какой скоростью движется Рыжий Боб? (Ответ дайте в м/с) 
По графику определяем, что расстояние между МО и Рыжим Бобом в начальный момент времени (S=7) м, а время, спустя которое они встретятся, (t=2) c. Перейдем в подвижную систему отсчета относительно МО. Тогда по закону сложения скоростей Рыжий Боб будет двигаться к нему со скоростью: [upsilon=upsilon_1+upsilon_2,] где (upsilon_1) и (upsilon_2) — скорости МО и Рыжего Боба соответственно (относительно неподвижной системы отсчета).
По закону равномерного прямолинейного движения: [S=upsilon t] Подставим сюда предыдущую формулу, и получим: [S=(upsilon_1+upsilon_2)t] Осталось выразить отсюда скорость Рыжего Боба: [upsilon_2=dfrac{S}{t}-upsilon_1=dfrac{7 text{ м}}{2~c}-3{,}14 text{ м/c} = 0{,}36 text{ м/c} .]
Ответ: 0,36
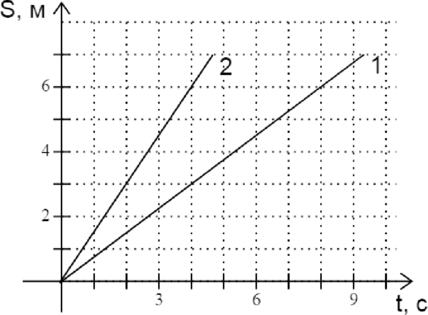
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Определите, во сколько раз скорость второго тела (upsilon_2) больше скорости первого тела (upsilon_1). 
Т.к. пройденные пути тел линейно увеличиваются, тела движутся равномерно и прямолинейно.
По графику определяем, что первое тело за время (t_1=4) с проходит путь (S_1=3) м, а второе тело за время (t_2=2~c) проходит путь (S_2=3) м. По закону равномерного прямолинейного движения: [S_1=upsilon_1t_1
quad
S_2=upsilon_2t_2] Отсюда выразим (upsilon_1) и (upsilon_2): [upsilon_1=dfrac{S_1}{t_1}; quad
upsilon_2=dfrac{S_2}{t_2}.] Найдем (dfrac{upsilon_2}{upsilon_1}): [dfrac{upsilon_2}{upsilon_1}=dfrac{dfrac{S_2}{t_2}}{dfrac{S_1}{t_1}}=dfrac{dfrac{3 text{ м}}{2~c}}{dfrac{3 text{ м}}{4~c}}=2]
Ответ: 2
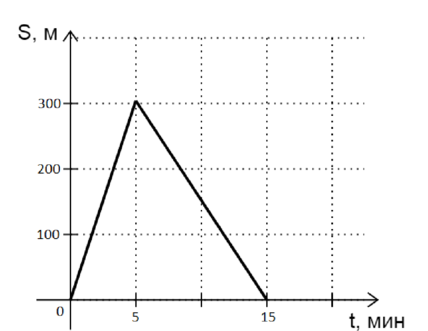
Дима каждый день ходит в школу. На рисунке представлен график движения Димы из дома в школу и обратно. Дом находится в точке (S=0), а школа — в точке (S=300) м. Чему равен модуль скорости Димы на пути из школы домой? (Ответ дайте в м/с)
Рассмотрим график: весь путь Дима двигался прямолинейно и равномерно (но в точке (S=300) м изменил свою скорость). Сначала он двигался из дома в школу со скоростью (upsilon_1) в течение времени (t_1=5) мин, после чего возвращался из школы домой cо скоростью (upsilon_2) в течение времени (t_2): [t_2=15text{ мин}-5text{ мин}=10text{ мин}=10cdot60text{ c}=600~text{ с}.] Чтобы найти (upsilon_2), нам необходимо рассмотреть участок движения Димы по пути из школы домой ((S_2)).
По закону равномерного прямолинейного движения: [S_2=upsilon_2t_2,] где (S_2=0text{ м}-300text{ м}=-300text{ м}).
Отсюда выражаем (upsilon_2): [upsilon_2=dfrac{S_2}{t_2}=dfrac{-300~text{м}}{600~text{c}}=-0,5~text{м/с}] Значит, (|upsilon_2|=|-0,5|text{ м/с}=0,5text{ м/с })
Ответ: 0,5
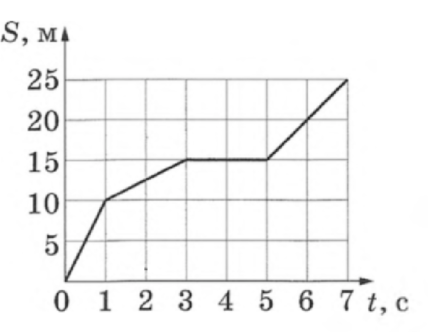
На рисунке представлен график зависимости пути (S), пройденного материальной точкой, от времени (t). Определите скорость (upsilon) точки на интервале времени от 5 с до 7 с. (Ответ дайте в м/с) 
Т.к. пройденный путь материальной точки на интервале времени от 5 c до 7 c линейно увеличивается, материальная точка на этом интервале движется равномерно и прямолинейно. По закону равномерного прямолинейного движения:
[Delta S=upsilonDelta t,] где (Delta S=25 text{ м}-15text{ м}=10text{ м}), а (Delta t=7text{ c}-5text{ c}=2text{ c}). Выразим (upsilon): [upsilon=dfrac{Delta S}{Delta t}=dfrac{10text{ м}}{2text{ c}}=5text{ м/c}]
Ответ: 5
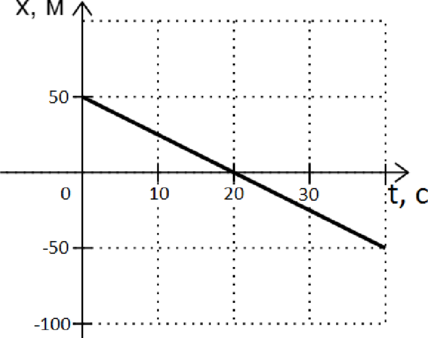
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении по оси Ox. Чему равна (upsilon_x) проекция скорости тела на ось Ох? (Ответ дайте в м/с)
Т.к. пройденный путь тела линейно уменьшается, тело движется равномерно и прямолинейно, и скорость тела постоянна: (upsilon_x=const). По закону прямолинейного равномерного движения тела: [Delta S=upsilon_xDelta t,] где (Delta S=-50text{ м}-50text{ м}=-100) — перемещение тела, а (Delta t=40 c) — время перемещения.
Отсюда выразим (upsilon_x): [upsilon_x=dfrac{Delta S}{Delta t}=dfrac{-100text{ м}}{40text{ c}}=-2,5~dfrac{text{м}}{text{c}}]
Ответ: -2,5
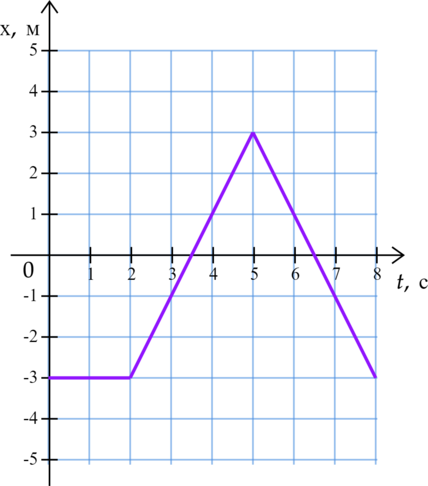
На рисунке приведен график зависимости координаты тела от времени при прямолинейном движении по оси (x). Какова проекция (upsilon_x) скорости тела в промежутке от 5 (c) до 8 (c)? (Ответ дайте в м/с) 
Найдем изменение координаты тела в промежутке от 5 (c) до 8 (c). Для этого из конечной координаты вычтем начальную: [Delta x=x_text{к}-x_text{н}]
Подставим исходные данные: [Delta x=(-3)text{ м}-3text{ м}=-6text{ м}]
Найдем изменение времени в промежутке от 5 (c) до 8 (c): [Delta t=t_text{к}-t_text{н}]
Подставим исходные данные: [Delta t=8text{ с}-5text{ с}=3text{ c}]
Найдем проекцию скорости тела:
[upsilon_x=frac{Delta x}{Delta t}]
Подставим исходные данные: [upsilon_x=frac{-6text{ м}}{3text{ c}}=-2text{ м/c}]
Ответ: -2
Движение двух велосипедистов задано уравнениями (x_1=3t) (м) и (x_2=12-t) (м). Велосипедисты двигаются вдоль одной прямой. Найдите координату (x) места встречи велосипедистов. (Ответ дайте в метрах)
1 способ:
Велосипедисты встретятся, если совпадут их координаты, отсюда: [x_1=x_2]
Подставим уравнения: [3t=12-t] [4t=12]
Отсюда время, в которое встретятся велосипедисты: [t=3text{ c}]
Найдем координату (x) места встречи велосипедистов, для этого подставим время (t) в оба уравнения: [x_1=3cdot3=9text{ м}] [x_2=12-3=9text{ м}]
2 способ:
Изобразим движение велосипедистов: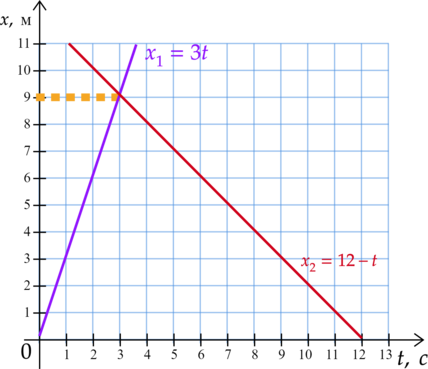 
Найдем пересечение графиков и опустим перпендикуляр к оси (oY). Отсюда очевидно, что ответ 9 м.
Ответ: 9
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
- ЕГЭ по физике
Подборка заданий по кинематике для подготовки к ЕГЭ по физике в 11 классе.
→ Скачать задания
→ Скачать ответы
Данный тренинг соответствует разделу кодификатора 1. 1 — кинематика.
Этот раздел содержит 8 различных типов задач на разные темы. (1. 1. 1 — 1. 1. 
В тренинге задачи подобраны в соответствие с кодификатором.
Пример заданий:
Камень падает с высокого обрыва, двигаясь по вертикали. Сопротивление воздуха пренебрежимо мало. Модуль средней скорости камня с течением времени
1) увеличивается
2) уменьшается
3) не изменяется
4) сначала увеличивается, а затем начинает уменьшаться
Ответ: _____.
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Модуль скорости движения мотоцикла относительно автомобиля равен
1) 20 км/ч
2) 20 км/ч
3) 120 км/ч
4) 50 км/ч
Ответ: _____.
Связанные страницы:
Уважаемый посетитель!
Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты
Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое
Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород
Тип обращения Вопрос Предложение Благодарность Жалоба
Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое
* Все поля обязательны для заполнения
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности
Полная теория по Кинематике, теория и практика ЕГЭ по физике
- 30.09.2013
Полный материал по физике на тему: Кинематика.
Материал содержит в себе необходимую теорию по теме, а также множество различных практических заданий и тестов, ориентированных на ЕГЭ.
Вместе с этим материалом вы сможете максимально качественно изучить раздел физики «Кинематика» для ЕГЭ.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
КИНЕМАТИКА.
Теория и формулы (кратко и сжато)
Кинематика – раздел физики, изучающий способы математического описания движения без выяснения его причин.
Механическое движение – изменение положения тела относительно других тел с течением времени. Способы описания: словесный, табличный, графический, формулами.
Материальная точка – тело, собственными размерами которого в данных условиях можно пренебречь.
Траектория – линия, которую описывает материальная точка при своём движении в пространстве. По виду траектории все движения делятся на прямолинейные и криволинейные.
Система отсчёта – часы и система координат, связанные с условно выбираемым телом отсчёта (наблюдателем).
Относительность движения – различие скорости, направления и траектории движения в различных системах отсчёта.
Перемещение – вектор, проведённый из начального положения материальной точки в её конечное положение.
Типы движений
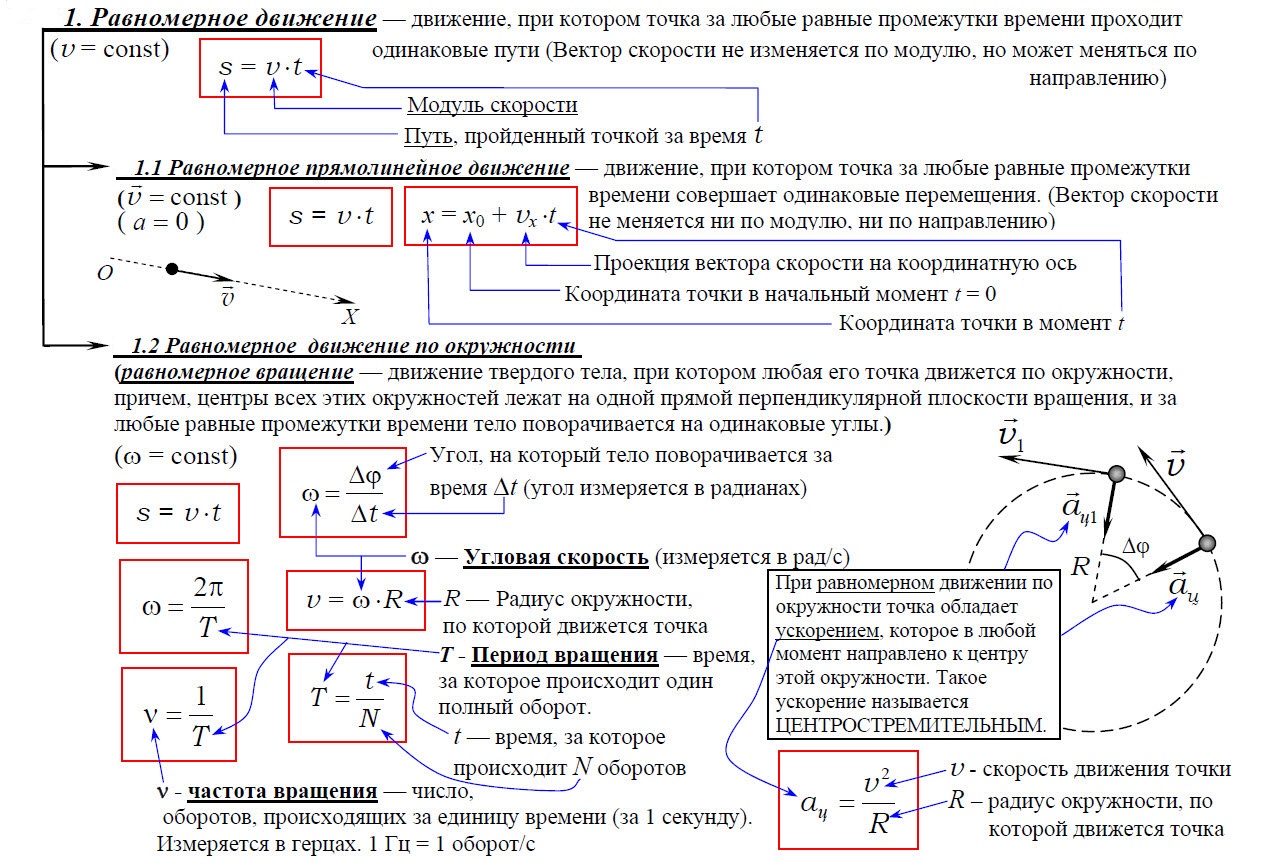
1. Равномерное движение
1.1. Равномерное прямолинейное движение
Равномерное движение – движение тела, при котором за равные интервалы времени оно преодолевает равные части пути.
Скорость равномерного движения равна отношению пройденного пути к интервалу времени, за который этот путь пройден.
Скорость равномерного прямолинейного движения равна отношению перемещения к интервалу времени его совершения.
Уравнение равно-прямолинейного движения x = xo + υoxt показывает, что координата линейно зависит от времени.
Мгновенная скорость равна отношению перемещения к бесконечно малому интервалу времени, за который оно произошло.
1.2 Равномерное движение по окружности (равномерное вращение)
Равномерное движение по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.
Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.
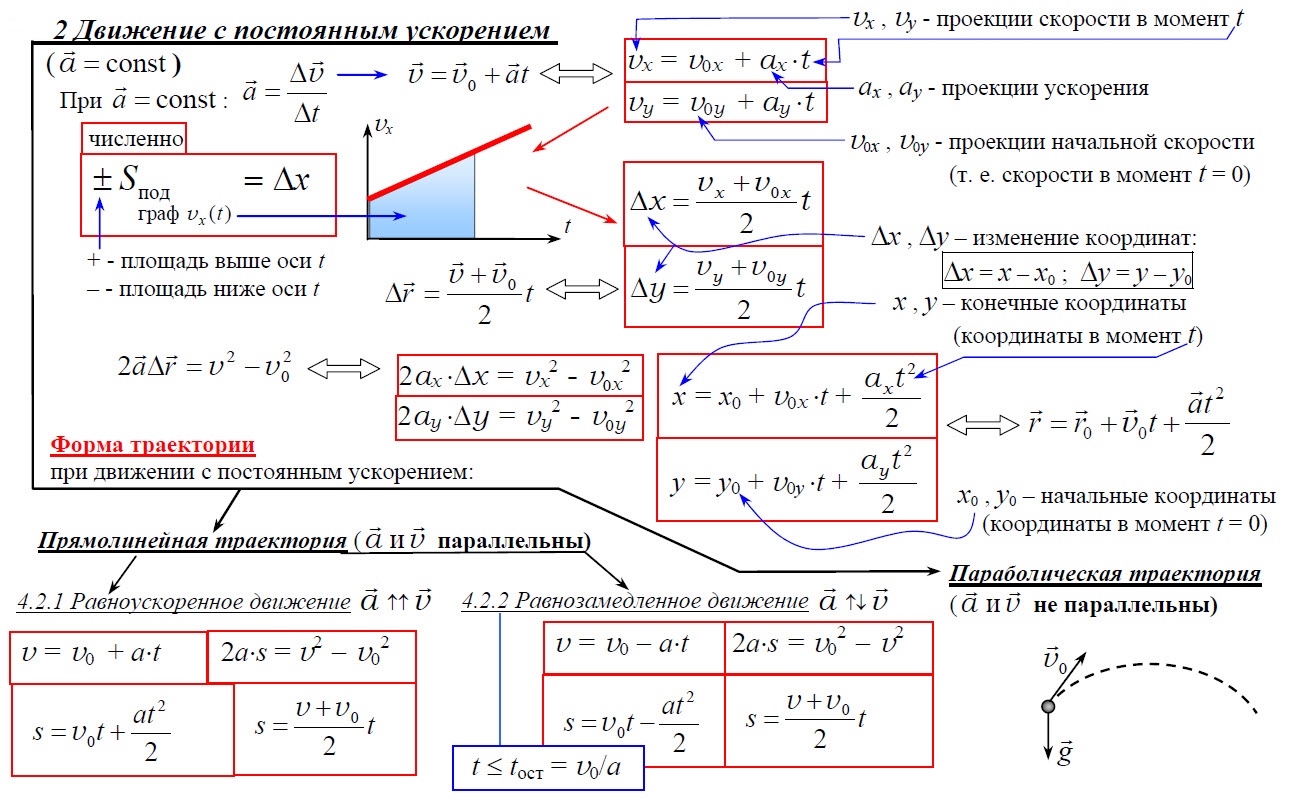
2. Движение с постоянным ускорением
Равноускоренное движение – движение, при котором мгновенная скорость за любые равные интервалы времени меняется одинаково.
Мгновенное ускорение равно отношению изменения мгновенной скорости тела к бесконечно малому интервалу времени, за который это изменение произошло.
Ускорение равноускоренного движения равно отношению изменения мгновенной скорости тела к интервалу времени, за который это изменение произошло.
Уравнение равноускоренного движения y = yo + υoyt + ½ayt² показывает, что координата квадратично зависит от времени. Уравнение υy = υoy + ayt показывает, что скорость линейно зависит от времени.
Центростремительное ускорение – ускорение, всегда направленное к центру окружности при равномерном движении по ней материальной точки. Модуль центростремительного ускорения равен отношению квадрата модуля скорости равномерного движения по окружности к её радиусу.
3. Гармоническое движение
Виды движений
Прямолинейное движение
Криволинейное движение
Частные случаи равноускоренного движения под действием силы тяжести
Частные случаи решения задач
Дополнительные материалы по кинематике
Кинематика. Таблица кратко.
Это конспект по физике «Кинематика. Теория и формулы для ЕГЭ» + шпаргалка.
Еще конспекты для 10-11 классов:
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться к ЕГЭ по физике 2022 года.
Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по физике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Подготовка к ЕГЭ по физике
Кинематика, часть 1
- По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах
- На рисунке представлен график зависимости модуля скорости тела от времени. Какой путь пройден телом за вторую секунду? (Ответ дайте в метрах.)
- На рисунке представлен график зависимости пути от времени. Определите по графику скорость движения велосипедиста в интервале от момента времени 1 с до момента времени 3 с после начала движения. (Ответ дайте в метрах в секунду.)
- Тело движется по оси Ox. На графике показана зависимость проекции скорости тела на ось Ox от времени. Каков путь, пройденный телом к моменту времени t = 4 с? (Ответ дайте в метрах.)
5. Тело движется по оси Ох. По графику зависимости проекции скорости тела vx от времени t установите, какой путь прошло тело за время от t1 = 0 до t2 4 с. (Ответ дайте в метрах.) 
6. На рисунке изображены графики зависимости модуля скорости движения четырёх автомобилей от времени. Один из автомобилей за первые 15 с движения проехал наибольший путь. Найдите этот путь. Ответ выразите в метрах.
7. На рисунке представлен график зависимости модуля скорости 
автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 30 до 50 с после начала движения. (Ответ дайте в метрах.)
8. Небольшое тело начинает равноускоренное двигаться вдоль оси OX без начальной скорости. На рисунке приведён график зависимости координаты x этого тела от времени t. Чему равна проекция скорости vx этого тела в момент времени t = 3 c? Ответ выразите в м/с.
9. Небольшое тело начинает равноускоренное двигаться вдоль оси OX без начальной скорости. На рисунке приведён график зависимости координаты x этого тела от времени t. Чему равна проекция скорости vx этого тела в момент времени t = 3 c? Ответ выразите в м/с.
10. Точечное тело движется вдоль оси Оx. В начальный момент времени тело находилось в точке с координатой x = −5 м. На рисунке изображена зависимость проекции скорости Vx этого тела от времени t. Чему равна координата этого тела в момент времени t = 4 с? (Ответ дайте в метрах.) 
11. Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций Vx, Vy и Vz скорости 
этого тела на оси OX, OY и OZ от времени t. Чему равен модуль скорости этого тела в момент времени t = 3 с? (Ответ дайте в метрах в секунду.)
12. На рисунке приведён график зависимости проекции скорости тела Vx от времени. Чему равна проекция ускорения этого тела ax в интервале времени от 8 до 10 с? Ответ выразите в м/с2.
13.Точечное тело движется вдоль горизонтальной оси Ох. На рисунке представлен график зависимости проекции скорости vx этого тела от времени t. Определите путь, пройденный телом за интервал времени от 0 с до 4 с. Ответ, выразите в м.
14 Автомобиль движется вдоль прямой дороги. На рисунке представлен график зависимости проекции a его ускорения от времени t. Известно, что при t = 0 автомобиль покоился. Какой путь прошёл автомобиль за промежуток времени от 10 с до 15 с? Ответ выразите в метрах. 
15. Два точечных тела 1 и 2 движутся вдоль оси OX. Зависимости координат x этих тел от времени t изображены на рисунке. В какой момент времени проекции скоростей этих тел будут приблизительно одинаковыми? Ответ укажите с точностью до целого.
16.Два точечных тела 1 и 2 движутся вдоль оси OX. Зависимости координат x этих тел от времени t изображены на рисунке. В какой момент времени проекции скоростей этих тел будут приблизительно одинаковыми? Ответ укажите с точностью до целого.
17. Покоившееся точечное тело начинает движение вдоль оси Ox. На рисунке показан график зависимости проекции ax ускорения этого тела от времени t. Определите, какой путь в метрах прошло тело за третью секунду движения.
18.На рисунке показан график зависимости от времени для проекции 
скорости тела. Какова проекция 
ускорения этого тела в интервале времени от 5 до 6 c? Ответ дайте в м/с2. 
19.Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость проекции скорости Vx этого тела от времени t. Чему равен модуль изменения координаты этого тела за третью секунду движения?
20.Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость проекции скорости Vx этого тела от времени t. Чему равен модуль изменения координаты этого тела за четвёртую секунду движения?
21.Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость координаты x этого тела от времени t. Определите проекцию скорости этого тела на ось OX в интервале времени от 4 до 6 секунд.
22.Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
23. Тело движется вдоль оси Оx. По графику зависимости проекции скорости тела vx от времени t установите модуль перемещения тела за время от t1 = 6 с до t2 = 10 с.
24. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в м/с.
25.Точечное тело движется вдоль оси OX. На рисунке изображён график зависимости проекции скорости V этого тела на ось OX от времени t. В момент времени t = 0 с тело имеет координату x = 10 м. Найдите координату этого тела в момент времени t = 3 с. Ответ дайте в метрах.
26. Материальная точка начинает двигаться по плоскости в момент времени t = 0. Её координаты x и y зависят от времени t по законам 
и 
(время измеряется в секундах, координаты — в метрах). Чему равен модуль перемещения точки за первую секунду движения?
27. На рисунке приведён график зависимости проекции vx скорости тела от времени t. Определите путь, пройденный телом в интервале времени от 0 до 5 с. Ответ приведите в метрах.
28. Тело движется по прямой с постоянным ускорением, не изменяя направления движения. За три секунды модуль скорости тела увеличился от 3 до 11 м/с. Какой путь прошло тело за это время? Ответ дайте в метрах.
29. На рисунке изображены графики зависимостей скоростей V двух точечных тел от времени t. Известно, что в начальный момент времени координата второго тела равна нулю, и в момент времени t = 10 с тела встретились. Определите начальную координату первого тела. Ответ дайте в метрах.
30. Материальная точка движется прямолинейно с постоянным ускорением вдоль оси Ох. График зависимости её координаты от времени 
изображён на рисунке. Определите проекцию ах ускорения этого тела. Ответ дайте в м/с2.
31. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно. Пункт A находится в точке 
а пункт Б — в точке 
Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.) 
32. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
33. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
34. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
35. Движение двух велосипедистов задано уравнениями 
и 
Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
36. Пешеход идет по прямолинейному участку дороги со скоростью 4 км/ч. Навстречу ему движется автобус со скоростью 40 км/ч. С какой скоростью (в км/ч) должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
37. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
38. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
39.Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
40 На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наименьший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.
41. На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наибольший модуль проекции скорости велосипедиста на ось Оx? Ответ выразите в м/с.
42. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
43. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Чему равен максимальный модуль ускорения? Ответ выразите в м/с2.
44. Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид: S= 4t + t2
Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
45. При прямолинейном движении зависимость координаты тела x от времени t имеет вид:
X = 5 + 2t + 4t2
Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
46. Зависимость координаты x тела от времени t имеет вид:
X = 20 – 6t + 2t2
Через сколько секунд после начала отсчета времени t = 0 с проекции вектора скорости тела на ось Ox станет равной нулю?
47. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 16 с? Ответ выразите в м/с2.
48. Автомобиль движется прямолинейно. На графике представлена зависимость скорости автомобиля от времени. Чему равен минимальный модуль ускорения? Ответ выразите в м/с2.
49. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста — 0,5 м/с2. Сколько секунд длился спуск?
50. Небольшое тело движется вдоль оси Ox. Его координата x изменяется с течением времени t по закону
X = 2 + t — t2
где t выражено в секундах, а x — в метрах. Чему равна проекция ускорения этого тела на ось Ox в момент времени t = 1 c? (Ответ дайте в метрах в секунду в квадрате.)
51. Точечное тело начинает движение из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой горизонтальной поверхности. Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)
|
Момент времени t, c |
Координата тела x, м |
|
0 |
2 |
|
3 |
6,5 |
|
4 |
10 |
52. Мальчик съезжает на санках равноускоренно со снежной горки. Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с2, начальная скорость равна нулю. Какова длина горки? (Ответ дайте в метрах.)
53. Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с? (Ответ дайте в метрах.)
54. При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
55. Небольшое тело движется вдоль горизонтальной оси Ox. В момент времени t = 0 c координата этого тела равна x0 = 2 м. На рисунке приведена зависимость проекции скорости vx этого тела на ось Ox от времени t. Чему равна координата тела в момент времени t = 4c?
56. Тело движется равноускоренно, не изменяя направления движения. За две секунды модуль скорости тела увеличился от 4 м/с до 5 м/с. Какой путь прошло тело за это время?
