1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Движение по окружности
Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. [omega=dfracvarphi t=dfrac{2pi}{t}]
Период обращения — это время одного полного оборота.
Частота обращения — величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. [nu=dfrac1T]
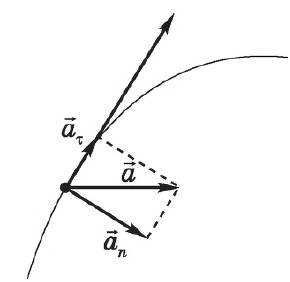
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. [a_text{цс}=dfrac{v^2}{r}]
Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. [overrightarrow a_text{полн}=overrightarrow a_text{тан}+overrightarrow a_text{цс}]
Шарик движется по окружности радиусом (R_1 = 2) м со скоростью ( upsilon_1 = 3) м/с. Во сколько раз изменится его центростремительное ускорение, если радиус его окружности уменьшить в (n = 3) раза, а скорость увеличить в (k = 5) раз?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon_1^2}{R_1} qquad (1)] [a_{text{ц2}} = frac{upsilon_2^2}{R_2} qquad (2)]
По условию задачи: [upsilon_2=kupsilon_1 qquad (3)] [R_2 = frac{R_1}{n} qquad (4)]
Подставляя (3), (4) и (1) в (2) получаем: [a_{text{ц2}} = dfrac{(kupsilon_1)^2}{dfrac{R_1}{n}} = nk^2frac{upsilon_1^2}{R_1} = nk^2a_{text{ц1}}] [frac{a_{text{ц2}}}{a_{text{ц1}}} = nk^2 = 3cdot5^2 = 75]
Ответ: 75
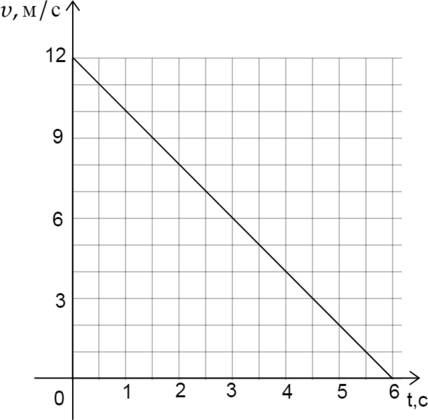
Тело движется по окружности радиусом (R=4) м. В какой момент времени центростремительное ускорение (a_text{цс} = 1 text{ м/с$^2$})?
При движении по окужности центростремительное ускорение можно найти по следующей формуле: [a_text{цс} = frac{upsilon^2}{R}] где (v) – скорость тела
Отсюда: [upsilon = sqrt{a_text{цс} cdot R} = sqrt{1 cdot 4} = 2text{ м/с }] По графику видно, что (upsilon = 2) м/с в момент времени (t=5) с.
Ответ: 5
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Центростремительное ускорение (нормальное): (displaystyle a_{text{цс}}=frac{upsilon^2}R=frac{(20 text{ м/с})^2}{100 text{ м}}=4) м/с(^2)
Ответ: 4
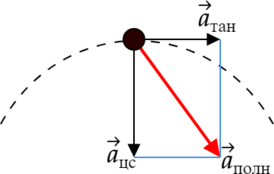
Велосипедист едет по круговому треку и замедляется. На рисунке указано направление скорости велосипедиста. Под каким номером верно указано направление центростремительного ускорения? Тангенциального ускорения? Куда направлено полное ускорение? (В ответе укажите последовательность цифр, например: 153)
Нормальная составляющая ускорения (центростремительное ускорение) характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело.
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости:
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным
Полное ускорение – это сумма нормального и тангенциального: [vec{a}_{text{полн}}=vec{a}_{text{норм}}+vec{a}_{text{танг}}]
Центростремительное ускорение направлено к центру (4). Так как велосепидист замедляется, то тангенциальное направлено против скорости (2). Полное ускорение является суммой 2 и 4, следовательно полное ускорение под номером 3.
Ответ: 423
Тело равномерно движется по окружности. Угловая скорость тела равна (w=6,5) рад/с. За какое время (t) тело совершит 5,5 оборотов? Принять (pi=3,14). Ответ округлить до десятых.
Cпособ 1:
Найдем длину дуги окружности: [l=2pi r,] где (r) — радиус окружности.
Т.к. тело прошло эту длину 5,5 раз, оно прошло путь: [S=5,5l=11pi rquad(1)] Выразим формульно линейную скорость (v) и угловую скорость тела:
[begin{cases}
v=2pi rnu\
w=2pinu
end{cases}
Rightarrow
v=wrquad(2)]
Т.к. тело движется равномерно, (v=const). По закону равномерного движения: [S=vt] Подставим ((1)) и ((2)): [11pi r=wrt] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Cпособ 2 :
Выразим формульно (w): [w=dfrac{Deltavarphi}{t},quad(1)] где (Deltavarphi) — угол поворота тела. [Deltavarphi=dfrac{S}{r},] где (S=5,5l=5,5cdot2pi r=11pi r) — путь, пройденный телом. [Deltavarphi=dfrac{11pi r}{r}=11piquad(2)] Подставим (2) в (1): [w=dfrac{11pi}{t}] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Ответ: 5,3
Две материальные точки движутся по окружностям радиусами (R_1) и (R_2), причем (R_2 = 3R_1). Скорости тел равны. Чему равно отношение их центростремительных ускорений?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon^2}{R_1}] [a_{text{ц2}} = frac{upsilon^2}{R_2}]
Тогда искомое отношение равно: [frac{a_{text{ц1}}}{a_{text{ц2}}} = frac{dfrac{upsilon^2}{R_1}}{dfrac{upsilon^2}{R_2}} = frac{R_2}{R_1} = frac{3R_1}{R_1} = 3]
Ответ: 3
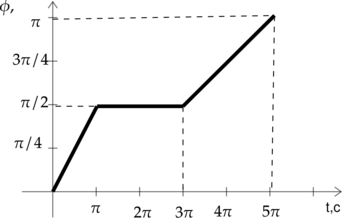
Точечное тело равномерно движется по окужности радиусом (R=2) м. На рисунке изображён график зависимости угла поворота (varphi) от времени (t). Найдите значение линейной скорости тела в интервале времени (3pi<t<5pi).
Линейная скорость тела, движущегося по окружности: [upsilon = omega cdot R qquad (1)] где (omega) – угловая скорость.
Угловая скорость: [omega = frac{Deltavarphi}{Delta t} qquad (2)] Подставив (2) в (1), получим: [upsilon = frac{Deltavarphi}{Delta t} cdot R] [upsilon = frac{dfrac{pi}{2}}{2pi} cdot 2 =0,5 text{ м/с}]
Ответ: 0,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Кинематика. Равномерное прямолинейное движение, равноускоренное прямолинейное движение, движение по окружности.
В. З. Шапиро
Первое задание ЕГЭ по физике проверяет ваши знания по разделу «Кинематика». Оно относится к базовому уровню, и в нем нет возможности выбора ответа. Для его решения необходимо проанализировать условие задачи, внимательно рассмотреть график зависимости кинематической величины от времени (при наличии такого графика), правильно подобрать формулу, провести расчет и записать ответ в предлагаемых единицах измерения.
Определение кинематических величин по графику
1. На рисунке приведён график зависимости проекции скорости тела от времени t.
Определите проекцию ускорения тела в промежутке времени от 15 до 20 с.
Ответ: _________________________ м/с2.Решение:
На графике представлена зависимость проекции скорости от времени. На участке от 15 до 20 с скорость тела изменяется от 10 м/с до -10 м/с. Это говорит о равноускоренном движении, причем проекция ускорения тела должна быть отрицательной. Для решения задачи необходимо воспользоваться формулой для определения проекции ускорения:
Проведем расчет:
(м/с2).Полученный результат подтверждает, что движение равноускоренное, причем проекция ускорения отрицательная.
Ответ: -4 м/с2.
Секрет решения: Долгое время в учебниках физики движение с переменной скоростью делилось на равноускоренное и равнозамедленное
Но в последнее время в основном применяют термин «равноускоренное движение», подразумевая постоянство ускорения. Только знак проекции ускорения определяет возрастание или убывание скорости движения тела.
Необходимая теория: Равноускоренное движение
2. На рисунке приведён график зависимости координаты тела x от времени t при его прямолинейном движении по оси x.
Определите проекцию скорости тела в промежутке времени от 25 до 30 с.
Ответ: ___________________________ м/с.
Согласно представленному графику, зависимость координаты тела от времени является линейной. Это указывает на равномерный характер движения тела. Чтобы решить задачу, необходимо воспользоваться формулой для определения скорости при равномерном движении:
Проведем расчет:
(м/с)
Ответ: -2 м/с.
Проекция скорости получилась отрицательной, и это означает, что в указанный временной интервал тело двигалось в направлении, противоположном выбранной оси Ох.
Необходимая теория: Вычисление перемещения по графику проекции скорости
3. Автомобиль движется по прямой улице вдоль оси Ox. На графике представлена зависимость проекции его скорости от времени.
Определите путь, пройденный автомобилем за 30 с от момента начала наблюдения.
Ответ: _________________________ м.
Так как по условию задачи нам дается график зависимости проекции скорости от времени, то пройденный путь будет определяться площадью геометрической фигуры под графиком. Для вычисления площади получившегося пятиугольника его можно разбить на несколько фигур, например, на две трапеции (см. рис.).
Используя известные формулы для нахождения площади трапеции, можно рассчитать путь за первые 10 с и последующие 20 с (от 10 с до 30 с).
(м);
(м);
(м).
Ответ: 450 м.
Полученный пятиугольник можно разбить не только на две трапеции. Здесь можно выделить трапецию, прямоугольник и треугольник. Тогда необходимо рассчитывать площади трех фигур и так же их суммировать.
4. На рисунке приведен график зависимости проекции скорости тела, движущегося вдоль оси Ох, от времени.
Определите проекцию перемещения тела за 10 с от начала наблюдения.
Ответ: ________________________ м.
Так же, как в задаче №3, модуль перемещения будет определяться площадью геометрической фигуры под графиком. Но проекция перемещения за время от 0 до 6 с будет положительной, а от 6 до 10 с отрицательной. Общая проекция перемещения будет определяться их суммой.
(м);
(м);
(м).
Ответ: 20 м.
При расчете можно получить положительное число, но надо помнить, что в интервале от 6 до 10 с тело движется в направлении, противоположном оси Ох. Это означает, что проекция перемещения будет отрицательной. Пройденный путь за указанное время от 0 до 10 с определяется суммой модулей проекций перемещений и будет равным 60 м.
Относительность движения
5. Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показана зависимость расстояния между автомобилями от времени. Скорость второго автомобиля 25 м/с. С какой скоростью движется первый автомобиль?
Ответ: ________________________ м/с.
Формула для нахождения относительной скорости в векторной форме имеет вид:
Если два тела движутся навстречу друг другу, то в проекциях на ось оХ это уравнение выглядит следующим образом:
С учетом данных графика можно рассчитать относительную скорость этих автомобилей при движении навстречу друг другу. Это происходит на интервале от 0 до 60 мин.
, скорость первого автомобиля
Ответ: 15 м/с.
В курсе математики при изучении движения двух тел вводятся понятия «скорость сближения» и «скорость удаления». В первом случае скорости тел суммируются, во втором вычитаются. Эти действия основаны на знаках проекций скоростей движущихся тел. Действия с векторами и их проекциями на оси координат используются как в физике, так и в математике.
6. Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей Vx на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?
Ответ: ___________________________ м.
Эта задача является комбинированной. Для её решения необходимо воспользоваться материалом двух тем: «Определение кинематических величин по графику» и «Относительность движения». Для определения проекций перемещений тел за 8 с необходимо рассчитать площади фигур под графиком.
(м);
(м).
Знак «минус» для показывает, что тела движутся в противоположных направлениях. Поэтому расстояние между ними через 8 с равно сумме модулей перемещений.
(м).
Ответ: 40 м.
Секрет решения:. Самое главное в этой задаче – выяснить, в каких направлениях двигаются тела. Для этого надо уметь извлекать информацию из графических зависимостей, другими словами, надо уметь «читать» графики. Это умения необходимы почти во всех разделах физики.
7. Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 6 км/ч. Река течёт со скоростью 4,5 км/ч. Чему равен модуль скорости катера относительно воды?
Ответ: ___________________________ км/ч
Решение задачи удобно сопроводить чертежом или рисунком. Выберем направление скорости реки вправо. Тогда катеру необходимо держать курс немного левее, чтобы двигаться перпендикулярно береговой линии.
Векторы собственной скорости катера, скорости течения реки и скорости катера относительно береговой линии образуют прямоугольный треугольник. Запишем для него теорему Пифагора:
Ответ: 7,5 км/ч.
Равномерное движение тел по окружности
Необходимая теория: Равномерное движение по окружности
8. Установленная на станке фреза равномерно вращается с частотой 600 оборотов в минуту. Чему равен модуль ускорения точек, находящихся на расстоянии 3 см от оси фрезы? Ответ округлите до целого числа.
Ответ: ___________________________ м/с2.
Так как тело движется равномерно по окружности, то найти требуется центростремительное ускорение. Его можно рассчитать по формуле: Линейная скорость v связана с угловой w соотношением
Подставляя это выражение в первое уравнение и проводя сокращения, получим
При частоте вращения 600 оборотов в минуту тело будет совершать 10 оборотов за секунду.
Проведем расчет:
Ответ: 118 м/с2.
В теме «Равномерное движение тел по окружности» достаточно много формул, которые трудно запоминаются. Из них надо знать базовые, которые относятся к периоду, частоте, линейной скорости, угловой скорости и центростремительному ускорению. Все остальные можно получить через достаточно простые рассуждения и выводы.
9. Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 секунд. Сколько оборотов в секунду делает меньшая шестерня радиусом 10 см?
Ответ: ___________________________ Гц.
Так как шестерни касаются друг друга, это условие говорит о равенстве линейных скоростей этих тел. Выразим скорости вращения через радиусы и периоды обращения.
Приравняем скорости и проведем сокращения.
с учетом того, что период и частота величины обратные, запишем следующее равенство:
Проведем расчет: (Гц).
Ответ: 4 Гц.
В задачах подобного типа всегда надо искать физическую величину, которая является общей для нескольких тел. В данной задаче – это скорость вращения обеих шестерней. Но надо иметь ввиду, что частоты их вращения и угловые скорости различны.
10. Волчок, вращаясь с частотой 20 с-1, свободно падает с высоты 5 м. Сколько оборотов сделает волчок за время падения?
Ответ: ___________________________ оборотов.
Вначале определим время падения волчка с высоты 5 м. Так как он падает свободно, то начальную скорость будет равна 0. Тогда высота и время падения будут связаны формулой отсюда
Проведем расчет времени падения:
(с). Так как волчок вращается с частотой 20
то это означает, что за 1 секунду он делает 20 оборотов. Так как время падения составляет 1 с, то количество оборотов также равно 20.
Ответ: 20.
Секрет решения: Эта задача — комбинированная. В ней связаны два раздела кинематики: «Равноускоренное движение» и «Равномерное движение тел по окружности». Надо знать, что суть формул при движении тел с ускорением по горизонтали или по вертикали под действием силы тяжести не меняется. Главное — не ошибиться со знаками проекций для скорости и ускорения.
Если вы хотите разобрать большее количество заданий — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 1 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
В данной статье рассмотрим темы из раздела кинематики по физике. Мы подробно изучим теоретический материл, основные характеристики и моменты тем, решим подобные задачи, которые могут встретиться на ЕГЭ, а также рассмотрим необходимые для их решения формулы.
Движение по окружности
Начнём с рассмотрения рисунка (рис. 1).
Траекторией движения здесь является окружность. Скоростью называют величину вектора, которая зависит от его направления, а также модуля значения. В некоторых случаях, движение по окружности называют равноускоренным. Например, при движении тела с одной и той же скорость, направление окружности будет постоянно меняться.
Существует также криволинейное движение. Его относят к разным движениям по окружности. Например, забег на стадионе, стрелка от часов и так далее.
Линейная и угловая скорости
Рассмотрим основные характеристики, свойственные линейной и угловой скорости.
Линейную скорость также называют мгновенной. Ей свойственно менять направление в соответствии с касательной по траектории.
Траекторией движения точки является окружность.
Формула, применяемая для вычисления мгновенной скорости: v = 2пR / T, при этом Т – является периодом.
Угловая скорость представляет собой значение, с помощью которого определяют, как изменяется перемещение с течением определённого времени.
Рассмотрим рисунок, а также соответствующие формулы для вычисления (рис. 2).
В данной формуле (рис. 3):
– является угловой скоростью точки (её скорость составляет 1/с);
– обозначают углом поворота вектора;
– является определённым промежутком времени (измеряется в секундах).
Существует формула, которая связывает угловое и центростремительное ускорение (рис. 7).
Перейдём к рассмотрению следующих характеристик, таких как:
– Период вращения;
– Частота вращения;
– Угловое перемещение.
Периодом вращения называют величину, которая определяет время совершения телом одного полного вращения.
Периодом называют скалярную величину. Одна единица периода равна одной секунде.
Период вычисляют по следующей формуле:
T = t / N, T = 1 / v, при этом N – является количество совершаемых оборотов, t – временем их совершения.
Частоту вращения применяют для вычисления частоты совершаемых оборотов за единицу времени.
Частотой является скалярная величина, она обозначается в n ( n = 1 с.^-1).
Частоту вычисляют по следующим формулам:
v = N / t, v = 1 / T.
Угловым перемещением является величина, определяющаяся с помощью угла поворота радиуса, который соединяет центр окружности и точку, в которой находится тело, в соответствии с её начальным положением.
Такую величину обычно измеряют в градусной или радианной мере.
Для закрепления материала рассмотрим примеры задач.
- Тело движется по окружности с ускорением 2,5 м / с^2. Радиус окружности равен 40 метрам.
Найти: линейную скорость движущегося тела.
Решение: а = 2,5 м / с^2, r = 40 м.
a = v^2 / r; v = √ar.
v = √ (2,5 * 40 ) = 10 (м / с).
Ответ: линейная скорость движущегося тела равна 10 метрам в секунду.
- Радиус колеса равен 8 см, линейная скорость точки к оси колеса на 3 см больше точки с линейной скоростью.
Найти: во сколько раз линейная скорость колеса больше линейной скорости точки к его оси вращения.
Решение: r1 = 8 см = 0,08 м, r2 = 5 см = 0,05 м.
u1= 2пr1n1; u2 = 2пr2n2. Делим первое уравнения на две части. У обода колеса будут одинаковые частоты вращения, поэтому n1 = n2.
Получается: u1 / u2 = 2пr1n1 / 2пr2n2 = r1 / r2; u1 / u2 = 0,08 м / 0,05м = 1,6.
Ответ: скорость точки обода в 1,6 раз больше точки, находящейся на 3 см ближе по отношению к оси вращения колеса.
Задачи подобного содержания часто встречается в КИМах заданий ЕГЭ по физике, поэтому рекомендуем подробно их рассмотреть, а также решить дополнительные задачи. Так вы сможете закрепить изученный материал.
Таким образом, мы рассмотрели тему движения точек по окружности, скорости точки, являющиеся угловыми, формулы для вычисления, дополнительные характеристики, а
также примеры решения задач по теме.
Твердое тело и его движение
Переходим к рассмотрению темы твёрдых тел и его видов движения.
Твёрдым телом принято называть объект, у которого при различных воздействиях на него не будет изменять форма. К примеру, если рассматривать две точки, принадлежащие этому телу, то расстояние, находящееся между ними будет являться неизменным.
В данной теме важными моментами будут являться:
– Определение характеристик и описания движения твёрдых тел;
– Определение характеристик и описания движения некоторых точек в пределах твёрдого тела.
Считают, что твёрдое тело двигается в следующих направлениях:
– Поступательном;
– Вокруг оси;
– Плоско;
– Вокруг определённой точки;
– В произвольном направлении.
В ходе подготовки к ЕГЭ по физике, следует учитывать, что в школьной программе рассматривают только вышеописанные виды движения.
Поступательное движение
Итак, рассмотрим тему поступательного движения. Такой вид движения называют поступательным, если на этом теле возможно протянуть прямую, проходящую через две точки. При этом, прямая должна двигаться в параллельном направлении по отношению к своему исходному положению.
Поступательно двигается любое тело, если его движение проходит по прямой линии и все точки на этом теле будут описывать траекторию окружности либо прямой линии.
Разберём несколько примеров поступательного движения:
– Движение отделения шкафа;
– Колесо обозрения (в данном случае это пример криволинейного движения).
В процессе движения, являющегося поступательным, все точки тела описывают равные траектории, а также имеют одну и ту же для всех точек скорость и ускорение.
Вращательное движение
Вращательным движение тела по отношению к оси, являющейся неподвижной называют движение всех точек тела, которые находятся в плоскости и перпендикулярны прямой, которая неподвижна и называется осью вращения, а также описывания центров окружности, находящихся на данной оси.
Данный вид движения характеризуют две точки и прямая, проходящая через данные точки. При этом если прямая является неподвижной, а точки тела двигаются относительно неё, то это движение будет являться вращательным.
Если тело вращается вокруг прямой, то эта прямая будет являться осью вращения.
Примерами тел вращательного движения являются: юла, колёса велосипеда, а также вращение нашей планеты вокруг своей оси.
Для этого вида движения правдивы все формулы, используемые для точки, которая двигается по окружности.
Формула для вычисления:
ε = dω / dt.
При этом, ω = ω ( t ) – является угловой скоростью.
Рассмотрим пример решения задачи по данной теме.
Условие: известно, что изменение угловой скорости является пропорциональным t2, угол исходного поворота равен 2 рад., для этого момента времени t1 = 3, а угловое ускорение ε = – 5п 1 / с^2.
Найти: закон вращения данного тела, совершаемого вокруг оси.
Решение: Обозначим неопределённый коэффициент k, получаем: ω = kt^2.
Далее следует найти ε, возьмём из двух частей неравенства производные по времени: ε = d ω / dt = 2kt.
Затем будем определять k, из условия сказано, что t1 = 3 секундам, значит: ε1 = -5п 1 / с^2.
-5п = 2k * 3 либо k = – 5 / 6 п.
Подставляем k в уравнение: ω = – 5 / 6п^2.
Помним, что ω = d ω / dt.
Умножаем две части на dt: ω = – 5 / 18п^3 + с.
В исходный момент времени t = 0, ω0 = 2 рад, получаем с = 2.
Значит, ω = – 5 / 18п^3 + 2 радиан.
Таким образом, мы закончили рассмотрение раздела кинематики ЕГЭ по физике, рассмотрели три темы, включающие свободное падение, движение точек относительно окружности, виды их скоростей, виды движений твёрдых тел, а также решили задачи по данным темам. Подготовка к сдаче экзамена является важным моментом в завершении школьных программ и закреплении знаний выпускников. Рекомендуем также рассмотреть тренировочные задания ЕГЭ по физике 2020, их вы можете найти на нашем сайте.
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Прямолинейное движение и движение по окружности
Теория к заданию 1 из ЕГЭ по физике
Механическое движение. Относительность механического движения. Система отсчета
Под механическим движением понимают изменение с течением времени взаимного расположения тел или их частей в пространстве: например, движение небесных тел, колебания земной коры, воздушные и морские течения, движение летательных аппаратов и транспортных средств, машин и механизмов, деформации элементов конструкций и сооружений, движение жидкостей и газов и др.
Относительность механического движения
С относительностью механического движения мы знакомы с детства. Так, сидя в поезде и наблюдая за трогающимся с места поездом, стоявшим до этого на параллельном пути, мы часто не можем определить, какой из поездов на самом деле начал двигаться. И здесь сразу следует уточнить: двигаться относительно чего? Относительно Земли, конечно. Потому что относительно соседнего поезда мы начали двигаться независимо от того, какой из поездов начал свое движение относительно Земли.
Относительность механического движения заключается в относительности скоростей перемещения тел: скорости тел относительно разных систем отсчета будут различны (скорость человека, перемещающегося в поезде, пароходе, самолете, будет отличаться как по величине, так и по направлению, в зависимости от того, в какой системе отсчета эти скорости определяются: в системе отсчета, связанной с движущимся транспортным средством, или с неподвижной Землей).
Различными будут и траектории движения тела в разных системах отсчета. Так, например, вертикально падающие на землю капли дождя оставят след в виде косых струй на окне вагона мчащегося поезда. Точно также любая точка на вращающемся пропеллере летящего самолета или спускающегося на землю вертолета описывает окружность относительно самолета и гораздо более сложную кривую — винтовую линию относительно Земли. Таким образом, при механическом движении относительной является также и траектория движения.
Путь, пройденный телом, также зависит от системы отсчета. Возвращаясь все к тому же пассажиру, сидящему в поезде, мы понимаем, что путь, проделанный им относительно поезда за время поездки, равен нулю (если он не передвигался по вагону) или, во всяком случае, намного меньше того пути, который он преодолел вместе с поездом относительно Земли. Таким образом, при механическом движении относительным является также и путь.
Осознание относительности механического движения (т. е. того, что движение тела можно рассматривать в разных системах отсчета) привело к переходу от геоцентрической системы мира Птолемея к гелиоцентрической системе Коперника. Птолемей, следуя наблюдаемому издревле движению Солнца и звезд на небосклоне, в центре Вселенной расположил неподвижную Землю с вращающимися вокруг нее остальными небесными телами. Коперник же считал, что Земля и другие планеты вращаются вокруг Солнца и одновременно вокруг своих осей.
Таким образом, изменение системы отсчета (Земля — в геоцентрической системе мира и Солнце — в гелиоцентрической) привело к гораздо более прогрессивной гелиоцентрической системе, позволяющей решить многие научные и прикладные задачи астрономии и изменить взгляды человечества на Вселенную.
Система координат $X, У, Z$, тело отсчета, с которым она связана, и прибор для измерения времени (часы) образуют систему отсчета, относительно которой рассматривается движение тела.
Телом отсчета называется тело, относительно которого рассматривается изменение положения других тел в пространстве.
Систему отсчета можно выбрать произвольно. При кинематических исследованиях все системы отсчета равноправны. В задачах динамики также можно использовать любые произвольно движущиеся системы отсчета, но удобнее всего инерциальные системы отсчета, так как в них характеристики движения имеют более простой вид.
Материальная точка
Материальная точка — объект пренебрежимо малых размеров, имеющий массу.
Понятие «материальная точка» вводится для описания (с помощью математических формул) механического движения тел. Делается это потому, что описывать движение точки проще, чем реального тела, частицы которого к тому же могут двигаться с разными скоростями (например, при вращении тела или деформациях).
Если реальное тело заменяют материальной точкой, то этой точке приписывают массу этого тела, но пренебрегают его размерами, а заодно пренебрегают различием характеристик движения его точек (скоростей, ускорений и т. д.), если таковое имеется. В каких случаях это можно делать?
Практически любое тело можно рассматривать как материальную точку, если расстояния, проходимые точками тела, очень велики по сравнению с его размерами.
Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении различных точек любой планеты, вызванные ее суточным вращением, не влияют на величины, описывающие годовое движение.
Следовательно, если в изучаемом движении тела можно пренебречь его вращением вокруг оси, такое тело можно представить как материальную точку.
Однако при решении задач, связанных с суточным вращением планет (например, при определении восхода Солнца в разных местах поверхности земного шара), считать планету материальной точкой бессмысленно, так как результат задачи зависит от размеров этой планеты и скорости движения точек ее поверхности.
Материальной точкой правомерно считать самолет, если требуется, например, определить среднюю скорость его движения на пути из Москвы в Новосибирск. Но при вычислении силы сопротивления воздуха, действующей на летящий самолет, считать его материальной точкой нельзя, поскольку сила сопротивления зависит от размеров и формы самолета.
Если тело движется поступательно, даже если его размеры сопоставимы с расстояниями, которые оно проходит, это тело можно рассматривать как материальную точку (поскольку все точки тела движутся одинаково).
В заключение можно сказать: тело, размерами которого в условиях рассматриваемой задачи можно пренебречь, можно считать материальной точкой.
Траектория
Траектория — это линия (или, как принято говорить, кривая), которую описывает тело при движении относительно выбранного тела отсчета.
Говорить о траектории имеет смысл лишь в том случае, когда тело можно представить в виде материальной точки.
Траектории могут иметь разную форму. О форме траектории иногда удается судить по-видимому следу, который оставляет движущееся тело, например, летящий самолет или проносящийся в ночном небе метеор.
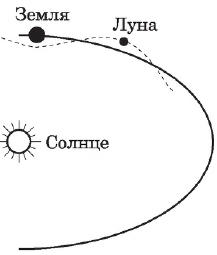
Форма траектории зависит от выбора тела отсчета. Например, относительно Земли траектория движения Луны представляет собой окружность, относительно Солнца — линию более сложной формы.
При изучении механического движения в качестве тела отсчета, как правило, рассматривается Земля.
Способы задания положения точки и описание ее движения
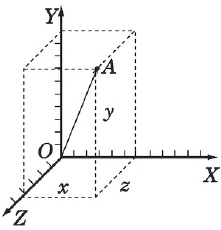
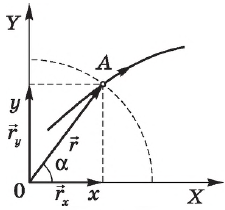
Положение точки в пространстве задается двумя способами: 1) с помощью координат; 2) с помощью радиус-вектора.
Положение точки с помощью координат задается тремя проекциями точки $х, у, z$ на оси декартовой системы координат $ОХ, ОУ, OZ$, связанные с телом отсчета. Для этого из точки А необходимо опустить перпендикуляры на плоскости $YZ$ (координата $х$), $ХZ$ (координата $у$), $ХУ$ (координата $z$) соответственно. Записывается это так: $А(х, у, z)$. Для конкретного случая, $(х=6, у=10.2, z= 4.5$), точка $А$ обозначается $А(6; 10; 4.5)$.
Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси ($х$ на ось $ОХ$ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат $О$ и лежащая на диагонали параллелепипеда, и будет искомой точкой $А$.
Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: $ОХ$ и $ОУ$. Тогда положение точки на плоскости определяют двумя координатами $х$ и $у$.
Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.
Задание положения точки $А$ с помощью радиус-вектора осуществляется соединением точки $А$ с началом координат $О$. Направленный отрезок $ОА = r↖<→>$ называется радиус-вектором.
Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.
Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций $r_x, r_у, r_z$ на оси координат $ОХ, ОY, OZ$, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости имеем:
Здесь $r=|r↖<→>|$ — модуль радиус-вектора $r↖<→>, r_x$ и $r_y$ — его проекции на оси координат, все три величины — скаляры; хжу — координаты точки А.
Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.
Вектор $r↖<→>$ можно также разложить на составляющие по осям $Х$ и $Y$, т. е. представить в виде суммы двух векторов:
Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус-вектором.
Способы описания движения точки
В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.
При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:
Уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.
При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:
Уравнение представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений равносильно заданию одного векторного уравнения.
Для каждого случая движения вид уравнений будет вполне определенным. Если траекторией движения точки является прямая линия, движение называется прямолинейным, а если кривая — криволинейным.
Перемещение и путь
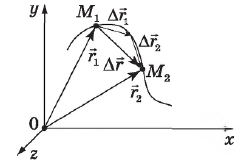
Перемещение в механике — это вектор, соединяющий положения движущейся точки в начале и в конце некоторого промежутка времени.
Понятие вектора перемещения вводится для решения задачи кинематики — определить положение тела (точки) в пространстве в данный момент времени, если известно его начальное положение.
На рис. вектор $<М_1М_2>↖<->$ соединяет два положения движущейся точки — $М_1$ и $М_2$ в моменты времени $t_1$ и $t_2$ соответственно и, согласно определению, является вектором перемещения. Если точка $М_1$ задана радиус-вектором $r↖<→>_1$, а точка $М_2$ — радиус-вектором $r↖<→>_2$, то, как видно из рисунка, вектор перемещения равен разности этих двух векторов, т. е. изменению радиус-вектора за время $∆t=t_2-t_1$:
Сложение перемещений (например, на двух соседних участках траектории) $∆r↖<→>_1$ и $∆r↖<→>_2$ осуществляется по правилу сложения векторов:
Путь — это длина участка траектории, пройденного материальной точкой за данный промежуток времени. Модуль вектора перемещения в общем случае не равен длине пути, пройденного точкой за время $∆t$ (траектория может быть криволинейной, и, кроме того, точка может менять направление движения).
Модуль вектора перемещения равен пути только при прямолинейном движении в одном направлении. Если направление прямолинейного движения меняется, модуль вектора перемещения меньше пути.
При криволинейном движении модуль вектора перемещения также меньше пути, т. к. хорда всегда меньше длины дуги, которую она стягивает.
Скорость материальной точки
Скорость характеризует быстроту, с которой происходят любые изменения в окружающем нас мире (движение материи в пространстве и времени). Движение пешехода по тротуару, полет птицы, распространение звука, радиоволн или света в воздухе, вытекание воды из трубы, движение облаков, испарение воды, нагрев утюга — все эти явления характеризуются определенной скоростью.
При механическом движении тел скорость характеризует не только быстроту, но и направление движения, т. е. является векторной величиной.
Скоростью $υ↖<→>$ точки называется предел отношения перемещения $∆r↖<→>$ к промежутку времени $∆t$, в течение которого это перемещение произошло, при стремлении $∆t$ к нулю (т. е. производной $∆r↖<→>$ по $t$):
Составляющие вектора скорости по осям $X, Y, Z$ определяются аналогично:
Определенное таким образом понятие скорости называют также мгновенной скоростью. Это определение скорости справедливо для любых видов движения — от криволинейного неравномерного до прямолинейного равномерного. Когда говорят о скорости при неравномерном движении, под ней понимают именно мгновенную скорость. Из этого определения непосредственно вытекает векторный характер скорости, поскольку перемещение — векторная величина. Вектор мгновенной скорости $υ↖<→>$ всегда направлен по касательной к траектории движения. Он указывает направление, по которому происходило бы движение тела, если бы с момента времени $t$ на него прекратилось действие любых других тел.
Средняя скорость
Средняя скорость точки вводится для характеристики неравномерного движения (т.е. движения с переменной скоростью) и определяется двояко.
1. Средняя скорость точки $υ_<ср>$ равна отношению всего пройденного телом пути $∆s$ ко всему времени движения $∆t$:
При таком определении средняя скорость — скаляр, т. к. пройденный путь (расстояние) и время — величины скалярные.
Такой способ определения дает представление о средней скорости движения на участке траектории (средней путевой скорости).
2. Средняя скорость точки равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло:
Средняя скорость перемещения — величина векторная.
Для неравномерного криволинейного движения такое определение средней скорости не всегда позволяет определить даже приблизительно реальные скорости на пути движения точки. Например, если точка двигалась по замкнутой траектории в течение некоторого времени, то перемещение ее равно нулю (но скорость явно отличалась от нуля). В этом случае лучше пользоваться первым определением средней скорости.
В любом случае следует различать эти два определения средней скорости и знать, о какой из них идет речь.
Закон сложения скоростей
Закон сложения скоростей устанавливает связь между значениями скорости материальной точки относительно различных систем отсчета, движущихся друг относительно друга. В нерелятивистской (классической) физике, когда рассматриваемые скорости малы по сравнению со скоростью света, справедлив закон сложения скоростей Галилея, который выражается формулой:
где $υ↖<→>_2$ и $υ↖<→>_1$ — скорости тела (точки) относительно двух инерциальных систем отсчета — неподвижной системы отсчета $K_2$ и системы отсчета $K_1$ движущейся со скоростью $υ↖<→>$ относительно $K_2$.
Формула может быть получена путем сложения векторов перемещений.
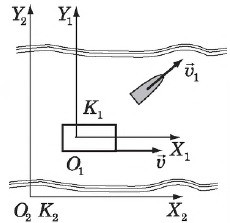
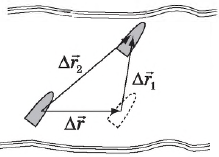
Для наглядности рассмотрим движение лодки со скоростью $υ↖<→>_1$ относительно реки (система отсчета $K_1$), воды которой движутся со скоростью $υ↖<→>$ относительно берега (система отсчета $K_2$).
Векторы перемещений лодки относительно воды $∆r↖<→>_1$, реки относительно берега $∆r↖<→>$ и суммарный вектор перемещения лодки относительно берега $∆r↖<→>_2$ изображены на рис..
Поделив обе части уравнения на интервал времени $∆t$, получим:
В проекциях вектора скорости на оси координат уравнение имеет вид:
Проекции скоростей складываются алгебраически.
Относительная скорость
Из закона сложения скоростей следует, что если два тела движутся в одной и той же системе отсчета со скоростями $υ↖<→>_1$ и $υ↖<→>_2$, то скорость первого тела относительно второго $υ↖<→>_<12>$ равна разности скоростей этих тел:
Так, при движении тел в одном направлении (обгон) модуль относительной скорости равен разности скоростей, а при встречном движении — сумме скоростей.
Ускорение материальной точки
Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.
Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖<→>$ по $t$):
Составляющие $a↖ <→>(а_х, а_у, а_z)$ равны соответственно:
Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории.
В соответствии с этим проекцию ускорения $а_х$ на касательную к траектории называют касательным, или тангенциальным ускорением, проекцию $a_n$ на нормаль — нормальным, или центростремительным ускорением.
Касательное ускорение определяет величину изменения численного значения скорости:
Нормальное, или центростремительное ускорение характеризует изменение направления скорости и определяется по формуле:
где R — радиус кривизны траектории в соответствующей ее точке.
Модуль ускорения определяется по формуле:
При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с 2 и называют «метр на секунду в квадрате».
Равномерное прямолинейное движение
Движение точки называется равномерным, если за любые равные промежутки времени она проходит равные пути.
Например, если автомобиль за каждую четверть часа (15 мин) проходит 20 км, за каждые полчаса (30 мин) — 40 км, за каждый час (60 мин) — 80 км и т. д., то такое движение считается равномерным. При равномерном движении численная величина (модуль) скорости точки $υ$ — величина постоянная:
Равномерное движение может происходить как по криволинейной, так и по прямолинейной траектории.
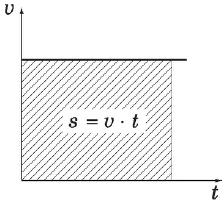
Закон равномерного движения точки описывается уравнением:
где $s$ — расстояние, измеренное вдоль дуги траектории, от некоторой точки на траектории, принятой за начало отсчета; $t$ — время точки в пути; $s_0$ — значение $s$ в начальный момент времени $t=0$.
Путь, пройденный точкой за время $t$, определяется слагаемым $υt$.
Равномерное прямолинейное движение — это движение, при котором тело перемещается с постоянной по модулю и направлению скоростью:
Скорость равномерного прямолинейного движения — величина постоянная и может быть определена как отношение перемещения точки к промежутку времени, в течение которого это перемещение произошло:
Модуль этой скорости
по смыслу есть расстояние $s=|∆r↖<→>|$, пройденное точкой за время $∆t$.
Скорость тела при равномерном прямолинейном движении — это величина, равная отношению пути $s$ ко времени, за которое этот путь пройден:
Перемещение при прямолинейном равномерном движении (по оси X) можно рассчитать по формуле:
где $υ_x$ — проекция скорости на ось X. Отсюда закон прямолинейного равномерного движения имеет вид:
Если в начальный момент времени $x_0=0$, то
График зависимости скорости от времени — прямая, параллельная оси абсцисс, а пройденный путь — это площадь под этой прямой.
График зависимости пути от времени — прямая линия, угол наклона которой к оси времени $Ot$ тем больше, чем больше скорость равномерного движения. Тангенс этого угла равен скорости.
Равномерное движение по окружности.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
Частота обращения — это величина, обратная периоду:
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1 ).
 |
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
Сопоставляя формулы (1) и (3) , получаем связь линейной и угловой скоростей:
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1 , что
Но из формулы (2) имеем: . Следовательно,
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5) :
С учётом формул (5) имеем:
Полученные формулы (6) можно записать в виде одного векторного равенства:
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1 ). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
Выразим угловую скорость из (4)
и подставим в (8) . Получим ещё одну формулу для центростремительного ускорения:
источники:
http://examer.ru/ege_po_fizike/teoriya/pryamolinejnoe_dvizhenie_i_dvizhenie_po_okruzhnosti
http://ege-study.ru/ru/ege/materialy/fizika/ravnomernoe-dvizhenie-po-okruzhnosti/