На уроке рассматривается 14 задание, решение и объяснение ЕГЭ по информатике
Содержание:
- Объяснение заданий 14 ЕГЭ по информатике
- Перевод числа из любой системы счисления в десятичную
- Особенности при переводах в разные системы счисления
- Решение заданий 14 ЕГЭ по информатике
- Определите наибольшее/наименьшее значение x, y
- Сколько цифр или сумма цифр
- Найти основание системы счисления и уравнения
14-е задание: «Операции в системах счисления»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание позиционных систем счисления
До ЕГЭ 2021 года — это было задание № 16 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Основные ошибки связаны с невнимательностью при выполнении арифметических действий
в недесятичных системах счисления. Например, вычитания единицы в ситуации типа: 10100002 – 1»
ФГБНУ «Федеральный институт педагогических измерений»
С основами темы можно ознакомиться в теории к заданию 1.
Перевод числа из любой системы счисления в десятичную
Чтобы перевести, например, 10045N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:
Особенности при переводах в разные системы счисления
Некоторые правила, которые нужно знать, при работе с системами счисления:
- последняя цифра (крайняя справа) в записи числа в системе счисления с основанием
N– представляет собой остаток от деления этого числа наN:
710 = 1112 7/2 = остаток 1
N – это остаток от деления этого числа на N², и так далее:710 = 1112 112=310 7/22 = остаток 310 (112)
10N записывается как единица и N нулей:
2N в двоичной системе записывается как единица и N нулей:3N записывается в троичной системе в виде единицы и N нулей:a; общее правило:10N-1 записывается как N девяток:2N-1 в двоичной системе записывается как N единиц:3N-1 записывается в троичной системе как N двоек:aN-1 в системе счисления с основанием a записывается как N старших цифр этой системы, то есть, цифр (a-1)10N-10M = 10M * (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:2N – 2K при K < N в двоичной системе записывается как N – K единиц и K нулей:
Решение заданий 14 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Определите наибольшее/наименьшее значение x, y
14_14:
Операнды арифметического выражения записаны в системе счисления с основанием 15.
82x19₁₅ – 6x073₁₅
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net:
|
||
| Python: | ||
| С++: |
Ответ: 7806
Сколько цифр или сумма цифр
14_12:
Значение арифметического выражения
43∙7103 – 21∙757 + 98
записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
Результат: 276
14_1:
Значение арифметического выражения:
21024 + 464 — 64
записали в системе счисления с основанием 2.
Сколько цифр «1» содержится в этой записи?
Типовые задания для тренировки
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Существует правило:
- Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:
2N = 10..02(1 единица и N нулей)
21024 + (22)64 - 26 = 21024 + 2128 - 26
10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0 - запомним единицу
2N — 2K = 1…1 (N - K единиц)0…0(K нулей)
10..0000000 - 128 нулей - 1000000 _________________________ 11..1000000 - 122 единицы и 6 нулей
122 + 1 = 123 единицы
Результат: 123
Также можно посмотреть видео решения 14 задания ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_3: 14 задание. Демоверсия ЕГЭ 2018 информатика:
Значение арифметического выражения:
4910 + 730 – 49
записали в системе счисления с основанием 7.
Сколько цифр «6» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням 7:
720 + 730 - 72
730 + 720 - 72
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
730 = 10..0
30
0 + (20 - 2) = 18
Результат: 18
Подробное решение 14 задания демоверсии ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_2:
Значение арифметического выражения:
4500 + 3*42500 + 16500 — 1024
записали в системе счисления с основанием 4.
Сколько цифр «3» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
Результат: 496
Подробное решение данного 14 задания ЕГЭ по информатике можно посмотреть на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_5:
Значение арифметического выражения: 81024 + 832 – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням восьмерки:
65 = 64 + 1 = 82 + 80;
81024 + 832 - (82 + 80); 81024 + 832 - 82 - 80
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
81024 = 10..0
1024
3.-2n = -2n+1 + 2n
! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)
-82 = -83 + 82
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)
Получаем:
81024 + 832 - 83 + 82- 80
0 + (32 - 3) + (2 - 0) = 31
Результат: 31
14_13:
Сколько значащих нулей в двоичной записи числа 4350 + 8340 – 2320 – 12?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- По возможности приведем каждое слагаемое к степеням 2. Получим:
4350 + 8340 – 2320 – 12
(22)350 + (23)340 - 2320 - 3*22 = (22)350 + (23)340 - 2320 - 12 = 2700 + 21020 - 2320 - (23 + 22)
21020 + 2700 - 2320 - 23 - 22
-2n = -2n+1+2n и преобразуем выражение:21020 + 2700 - 2321+ 2320- 24 + 23 - 22
21020 -> один не ноль 2700 - 2321 -> 379 не нулей 2320- 24 -> 316 не нулей 23 - 22 -> один не ноль Итого: 1+ 379+316 +1 = 697
1021 - 697 = 324
Результат: 324
Найти основание системы счисления и уравнения
14_7:
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
Типовые задания для тренировки
✍ Решение:
- Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:
1.
13 | 3
12 4 | 3
1 3 1
1
1310 = 1113
2.
23 | 3
21 7 | 3
2 6 2
1
2310 = 2123
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
Ответ: 13
✍ Решение:
- Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):
204N+1 = 204N + 2616 1 2 3
1.
210
204N+1
По формуле получаем:
2*(N+1)2 + 0*(N+1)1 + 4*(N+1)0 =
= 2*(N2 + 2N + 1) + 0 + 4 = 2N2 + 4N + 6
2.
210
204N
По формуле получаем:
2*N2 + 0*N1 + 4*N0 =
= 2N2 + 4
3. 2616 = 3810
2N2 + 4N + 6 = 2N2 + 4 + 38; 4N = 36; N = 9
Результат: 9
✍ Решение:
- Вместо обозначения искомой системы счисления введем неизвестное x:
144x + 24x = 201x
144 + 24 = 201 1*x2 + 4*x1 + 4*x0 + 2*x1 + 4*x0 = 2*x2 + 0*x1 + 1*x0
x2 - 6x - 7 = 0
D = b2 - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7
Ответ: 7
14_9:
В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.
Типовые задания для тренировки
✍ Решение:
- Вспомним правило:
- Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:
Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X
94 / x = некоторое число и остаток 3 и 68 / x = некоторое число и остаток 3
91/x 65/x
91 - 65 = 26 65 - 26 = 39 39 - 26 = 13 26 - 13 = 13
Ответ: 13
14_10:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:
X = *516 = *0*8
Сколько чисел соответствуют условию задачи?
Типовые задания для тренировки
✍ Решение:
- Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:
1. *516
* | 5 16
* * * * | 0 1 0 1 2
2. *0*8
* | 0 | * 8
* * *|0 0 0|* * * 2
* * 0 0 0 1 0 1
1. 01000101 2. 10000101 3. 11000101
Ответ: 3
Предлагаем посмотреть видео решения данного 14 задания ЕГЭ (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_4:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
Типовые задания для тренировки
✍ Решение:
- Так как 75 должно оканчиваться на 13, то имеем два общих случая:
1. 7510 = 13N 2. 7510 = ...13N (число оканчивается на 13)
1 случай:
75|N N|1 отсюда имеем => 75 - N = 3; т.е. N = 72 3
2 случай:
75|N 72|y отсюда имеем => 75 = Ny + 3, где N - целое, неотриц. 3
75|N 72| y |N => y = Nz + 1, где z - целое, неотриц. 3 y-1|z 1
75 = Ny + 3 y = Nz + 1
75 = N (Nz + 1) + 3; 75 = N2z + N + 3; 75 = N2z + N
z = (72 - N)/N2
72 - 5 / 52 = 67 / 25 не делится, - не подходит!
75 | 4
72 | 18| 4
3 16| 2
2 => не подходит! должна быть единица
75 | 6
72 | 12| 6
3 12| 1
0 => не подходит! должна быть единица
75 | 7
70
5 => не подходит! должна быть 3
75 | 8
72 | 9| 8
3 8| 1
1 => подходит!
Результат: 8,72
Видеоразбор решения (аналитический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_11:
Выражение 25*325 записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.
✍ Решение:
-
Рассмотрим каждый сомножитель отдельно.
- Первый сомножитель:
25 = 32 Переведем в троичную систему счисления (делением на 3, переписываем остатки). Результат: 3210 = 10123
325 = 10..0{25 нулей}3
1000 x 1012 = ---- 2000 1000 0000 1000 ------- 1012000
Ответ: «0»=26, «1»=2, «2»=1
Смотрите видео разбора на нашем канале (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 5**36 + 5**24 - 25 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('4'))
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 22.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.
Примеры:
54 (в десятичной системе) — это 100005 (в пятеричной системе)
72 (в десятичной системе) — это 1007 (в семеричной системе)
29 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 — 52
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
Теперь от получившегося числа нужно отнять 52 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 168 × 420 — 45 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 16**8 * 4**20 - 4**5 - 64 s='' while f>0: s = s + str(f%4) f = f // 4 print(s.count('3'))
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 — 45 — 64 =
= (42)8 × 420 — 45 — 43 =
= 416 × 420 — 45 — 43 =
= 436 — 45 — 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 436 — 45.
Теперь от этого числа нужно отнять 43 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
1) Переведём число 17 в троичную систему.
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени — это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Задача (Основание системы)
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 22 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
Получается неравенство:
338 > N2 — 1
N2 < 339
N — положительное целое число. Тогда:
N < √339 ≈ 18
N ≤ 18
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
Ответ: 1
Задача (Закрепление материала)
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
for i in range(3, 24): if 23%i==2: print(i)
Ответ: 3, 7, 21
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
Задача (Новый тип, Статград окт 2022)
В выражении 1xBAD16 + 2CxFE16 x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.
Решение:
Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.
Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.
for x in range(0, 16): a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4 b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4 if (a+b)%15==0: print(x, (a+b)//15)
Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.
В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.
Получается 18341
Ответ: 18341
Задача(Новый тип, закрепление)
(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x17 + 3×10817
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
Решим задание с помощью предыдущего шаблона на языке Python.
for x in range(0, 17): a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4 b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4 if (a+b)%11==0: print(x, (a+b)//11)
Ответ: 95306
Задача (Новый тип, две переменные)
(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.
M = 2y23x515, N = 67x9y13
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.
Решение:
Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.
for A in range(1, 5000): for x in range(0, 13): for y in range(0, 13): M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5 N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4 if (M+A)%N==0: print(A)
Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.
Если выполняется условие задачи, то нам интересно такое A при котором это произошло.
В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.
Ответ: 1535
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение
Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу
Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break
Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».
И спасибо Вам за этот сайт!)
ЕГЭ информатика 14 задание разбор, теория, как решать.
Позиционные системы счисления. Кодирование чисел. Системы счисления, (П) — 1 балл
Е14.55 неизвестная цифра из алфавита 15-ричной системы счисления
Операнды арифметического выражения записаны в системе счисления с основанием 15. 123×515 + 1×23315 В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в …
Читать далее
Е14.54 Сколько чётных цифр встречается в этой записи
Значение выражения 5 ∙ 7298 + 7 ∙ 8112 + 316 — 171 записали в системе счисления с основанием 9 без незначащих нулей. Сколько чётных цифр встречается в этой записи? Ответ: СтатГрад Вариант ИН2110402 30.03.2022 – задание №14
Читать далее
Е14.53 Значение арифметического выражения 6*512^180+7*64^181+3*8^184+5*8^125-65 записали
Значение арифметического выражения 6*512180+7*64181+3*8184+5*8125-65 записали в системе счисления с основанием 64. Сколько значащих нулей содержится в этой записи? Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №14 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е14.52 Какая цифра чаще всего встречается в этой записи?
Значение выражения 5 ∙ 3438 + 4 ∙ 4912 + 714 – 98 записали в системе счисления с основанием 7 без незначащих нулей. Какая цифра чаще всего встречается в этой записи? Ответ: СтатГрад Вариант ИН2110301 08.02.2022 – задание №14
Читать далее
Е14.51 N^25 — 2N^13 + 10 записали в системе счисления с основанием N
Значение арифметического выражения: N25 — 2N13 + 10 записали в системе счисления с основанием N. Определите основание системы счисления, если известно, что сумма разрядов в числе, представленном в этой системе счисления, равна 75? Ответ: «Некрыловские варианты» от Евгения Джобса — Вариант 6
Читать далее
Е14.50 125^200 — 5^x + 74 содержит ровно 100 цифр «4» в пятеричной записи числа
При каком наименьшем введённом значении x запись выражения 125200 — 5x + 74 содержит ровно 100 цифр «4» в пятеричной записи числа? «Некрыловские варианты» от Евгения Джобса — Вариант 5
Читать далее
Е14.49 Сколько разных цифр встречается в этой записи?
Значение выражения 436 + 3 ∙ 420 + 415 + 2 ∙ 47 + 49 записали в системе счисления с основанием 16. Сколько разных цифр встречается в этой записи? СтатГрад Вариант ИН2110101 27.10.2021– задание №14
Читать далее
Е14.48 3*4^38+2*4^23+4^20+3*4^5+2*4^4+1 записали в системе счисления с основанием 16
Значение арифметического выражения 3*438+2*423+420+3*45+2*44+1 записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи? Источник: Демонстрационный вариант ЕГЭ по информатике 2022 г. задания №14
Читать далее
Е14.47 4^14+64^16–81 записали в системе счисления с основанием 4
Значение арифметического выражения: 414 + 6416 — 81 записали в системе счисления с основанием 4. Сколько цифр «0» содержится в этой записи? Ответы: Источник: «05.04.2021 ЕГЭ 100БАЛЛОВ, Иосиф Дзеранов»
Читать далее
Е14.46 Значение арифметического выражения: 97 + 321 – 8 записали
Значение арифметического выражения: 97 + 321 – 8 записали в системе счисления с основанием 3. Найдите сумму цифр в этой записи. Ответ запишите в десятичной системе. Ответ: Тренировочный вариант от 16.11.2020 «Евгений Джобс»
Читать далее
Автор материалов — Лада Борисовна Есакова.
В этой задаче используется, в основном, описание алгоритмов на псевдокоде (условном алгоритмическом языке, включающем в себя и элементы языка программирования, и элементы обычного естественного языка).
Основные конструкции псевдокода описаны перед текстом задачи.
Исполнитель чертежник
Пример 1.
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b).
Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, -3) переместит Чертёжника в точку (6, -1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).
Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, n>1):
НАЧАЛО
сместиться на (60, 100)
ПОВТОРИ n РАЗ
сместиться на (a, b)
сместиться на (33, 44)
КОНЕЦ ПОВТОРИ
сместиться на (13, 200)
сместиться на (-1, 60)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Решение:
В результате выполнения алгоритма Чертежник переместится
по оси х на:
60 + n*a + n*33 + 13 – 1
по оси y на:
100 + n*b + n*44 + 200 + 60
Известно, что в результате перемещения Чертежник вернулся в исходную точку, т.е. перемещение по оси х равно нулю, и перемещение по оси y равно нулю:
60 + n*a + n*33 + 13 – 1 = 0
100 + n*b + n*44 + 200 + 60 = 0
Т.е.
n*(a + 33) = -72
n*(b + 44) = -360
Наибольшее n – это наибольший общий делитель чисел -72 и -360. Это число 72.
Ответ: 72
Исполнитель робот
Пример 2.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно (по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 22
2) 19
3) 15
4) 12
Решение:
В данной программе РОБОТ сначала проверяет, свободна ли клетка справа или снизу от него. Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом цикле пока у правой стороны клетки, в которой находится РОБОТ, нет стены, он продолжает двигаться вправо. Как только это условие перестанет выполняться, он переходит ко второму действию внутри цикла. Второе действие, заключается в следующем: РОБОТ передвигается на одну клетку вниз. После чего возвращается к началу внешнего цикла.
Проверив последовательно все клетки по правилу движения РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи равно 15 (вся первая строчка, весь столбец F, клетки D2, E2, D4, D6, E4).
Правильный ответ указан под номером 3.
Ответ: 3
Исполнитель редактор
Пример 3.
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150. Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (222) ИЛИ нашлось (888)
ЕСЛИ нашлось (222)
ТО заменить (222, 
ИНАЧЕ заменить (888, 2)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Решение:
Обозначим строку из 68 восьмерок — 68«8»,
строку из двойки и 65 восьмерок – 1«2»65«8» и т.д.
Отработаем 4 первых цикла программы:
68«8» → 1«2»65«8» → 2«2»62«8» → 3«2»59«8» → 60«8»
В результате количество восьмерок уменьшилось на 8. Не сложно понять, что строка будет уменьшаться на 8 восьмерок каждые 4 итерации. В результате останется строка из 4 восьмерок. Доработаем программу:
…→ 4«8» → 1«2»1«8» = 28
Ответ: 28
Исполнитель черепашка
Пример 4.
Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды:
Вперед n, где n – целое число, вызывающее передвижение черепашки на n шагов в направлении движения.
Направо m, где m – целое число, вызывающее изменение направления движения на m градусов по часовой стрелке.
Запись Повтори 5 [Команда1 Команда2] означает, что последовательность команд в скобках повторится 5 раз.
Черепашке был дан для исполнения следующий алгоритм:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120]
Какая фигура появится на экране?
Решение:
Последовательность действий Вперед 40 Направо 90 рисует отрезок длиной 40 шагов, а затем меняет направление на 90 градусов по часовой стрелке. Тогда последовательность Повтори 4 [Вперед 40 Направо 90] нарисует квадрат, а направление вернется в исходное.
Затем выполняется команда Направо 120, она изменит направление на 120 градусов от исходного.
Если повторить все рассмотренные действия 5 раз:
Повтори 5 [Повтори 4 [Вперед 40 Направо 90] Направо 120], то будет 5 раз нарисован квадрат. Причем каждый следующий повернут вокруг вершины относительно предыдущего на 120 градусов. Не сложно заметить, что 4-й квадрат будет нарисован поверх первого (120*3 = 360, сделан поворот на целый круг, возврат в исходное положение), а 5-й поверх второго.
Результат изображен под номером 3.
Ответ: 3
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №14. Выполнение алгоритма.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
ЕГЭ по информатике 2022 — Задание 14 (Чемпионская подготовка)
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 5 36 + 5 24 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Первый способ. (С помощью Питона)
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 4.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.

Примеры:
5 4 (в десятичной системе) — это 100005 (в пятеричной системе)
7 2 (в десятичной системе) — это 1007 (в семеричной системе)
2 9 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
5 36 + 5 24 — 5 2
Посчитаем 5 36 + 5 24 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
Теперь от получившегося числа нужно отнять 5 2 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 16 8 × 4 20 — 4 5 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Первый способ. (С помощью Питона)
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
16 8 × 4 20 — 4 5 — 64 =
= (4 2 ) 8 × 4 20 — 4 5 — 4 3 =
= 4 16 × 4 20 — 4 5 — 4 3 =
= 4 36 — 4 5 — 4 3
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 4 36 — 4 5 .
Теперь от этого числа нужно отнять 4 3 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
1) Переведём число 17 в троичную систему.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
Теперь переведём эти числа в десятичную систему.
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y? Ответ записать в виде целого числа.
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x 0 + 2 × x 1 + 2 × x 2 = 5 × y 0 + 0 × y 1 + 4 × y 2
Любое число в нулевой степени — это 1. Значит, 5 × x 0 = 5 × y 0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x 2 = 4y 2
x + x 2 = 2y 2
x(1 + x) = 2y 2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
x (1 + x) = 2 × 6 2 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 2 2 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
338 > N 2 — 1 N 2
N — положительное целое число. Тогда:
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
Информатика егэ 14 задание уравнение
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.
Составим уравнение: где n — основание этой системы счисления. Исходя из уравнения,
Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).
Основание системы счисления равно 610 = 203.
Корни квадратного уравнения: 8 и −10. Следовательно, основание системы счисления равно 8.
Переведём все числа в десятичную систему счисления:
Составим новое уравнение и решим уже его:
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с
Для каждого x вычисляем значение и решаем уравнение
, причем нас интересуют только натуральные
Для и
нужных решений нет, а для
получаем
так что
Ответ:
Задание 14 ЕГЭ-2019 по информатике: теория и практика
В предстоящем ЕГЭ не появилось никаких изменений по сравнению с прошлым годом.
Возможно, вам также будут интересны демоверсии ЕГЭ по математике и физике.
О нововведениях в экзаменационных вариантах по другим предметам читайте в наших новостях.
Демоверсия КИМ ЕГЭ-2019 по информатике не претерпела никаких изменений по своей структуре по сравнению с 2018 годом. Это значимо упрощает работу педагога и, конечно, уже выстроенный (хочется на это рассчитывать) план подготовки к экзамену обучающегося.
Мы рассмотрим решение предлагаемого проекта (на момент написания статьи пока еще ПРОЕКТА) КИМ ЕГЭ по информатике.
Часть 1
Ответами к заданиям 1–23 являются число, последовательность букв или цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Задание 14
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды «заменить»(v, w) не меняет эту строку.
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
выполняется, пока условие истинно.
выполняется команда1 (если условие истинно).
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 82 идущих подряд цифр 1? В ответе запишите полученную строку.
ПОКА нашлось (11111) ИЛИ нашлось (888)
ЕСЛИ нашлось (11111)
ТО заменить (11111, 88)
ЕСЛИ нашлось (888)
ТО заменить (888, 
Решение
82 единицы условно можно представить как 16 групп по 5 единиц, а также одну группу из двух единиц. Первый вызов оператора условия дает нам 16 групп пар из восьмерок – это 32 восьмерки или 10 групп по три восьмерки, а также еще одна свободная пара восьмерок. Очевидно, что последние две единички так и останутся не затронутыми исполнителем. А 12 оставшихся восьмерок, сгруппированные по три, – это уже 4 восьмерки. Еще одна итерация – остается 2 восьмерки и 2 единички.
Ответ: 8811.
Заместитель генерального директора по ИКТ АНОО «Дом знаний», преподаватель по программированию Яндекс.Лицея (ДГУНХ, Махачкала), учитель высшей категории, финалист Всероссийского конкурса «Учитель года России 2010»
источники:
http://inf-ege.sdamgia.ru/test?theme=248
http://rosuchebnik.ru/material/razbor-zadaniya-14-ege-2019-po-informatike-i-ikt/
ЕГЭ-2023 по информатике. Разбор задания №14
Составил:
учитель информатики
МОУ Подосинковской СОШ
Казаров С.Р.
Кодирование чисел. Системы счисления
- Прямое сложение в системах счисления
- Операции в одной системе счисления
- Операции в разных системах счисления с одной переменной
- Операции в разных системах счисления с двумя переменными
Прямое сложение в системах счисления
Сколько единиц содержится в двоичной записи значения выражения: 8 2020 + 4 2017 + 26 – 1?
Прямое сложение в системах счисления
Решение.
Преобразуем немного выражение, получим:
2 6060 + 2 4034 + 25
2 6060 = 100..(всего 6060 нулей)..00 2
2 4034 = 100..(всего 4034 нулей)..00 2
25 10 = 11001 2
В двоичной записи результат будет выглядеть так:
100..(всего 2025 нулей)..00100..(всего 4029 нулей)..0011001
Всего 5 единиц.
Прямое сложение в системах счисления
Решение на языке Python
x = 8**2020 + 4**2017 + 26 — 1
s = ‘ ‘
while x != 0:
s += str(x % 2)
x //= 2
s = s[::-1]
print(s.count(«1»))
Прямое сложение в системах счисления
Значение арифметического выражения: 125 + 25 3 + 5 9 – записали в системе счисления с основанием 5. Сколько значащих нулей содержит эта запись?
Прямое сложение в системах счисления
Решение.
Последовательно рассмотрим данное выражение.
Рассмотрим первое слагаемое 125=5 в кубе =1000_5 .
Рассмотрим второе слагаемое: 25 в кубе = 5 в степени левая круглая скобка 6 правая круглая скобка = 1000000_5..
Рассмотрим третье слагаемое: 5 в степени левая круглая скобка 9 правая круглая скобка = 100…00_5 — на конце 9 нулей.
Результат сложения первых двух чисел: 5 в кубе плюс 5 в степени левая круглая скобка 6 правая круглая скобка = 1001000_5.
На последнем шаге получаем: 1000000000 плюс 1001000=1001001000 .
Нетрудно увидеть, что всего 7 значащих нулей.
Ответ: 7
Прямое сложение в системах счисления
Решение на языке Python
x = 125 + 25**3 + 5**9
s = ‘ ‘
while x != 0:
s += str(x % 5)
x //= 5
s = s[::-1]
print(s.count(«0»))
Операции в одной системе счисления
Операнды арифметического выражения записаны в системе счисления с основанием 19:
321×419 + 498×919
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 23. Для найденного значения x вычислите частное от деления значения арифметического выражения на 23 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в одной системе счисления
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 23 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789ABCDEFGHI’:
t = int(‘321’ + x + ‘4’, 19) + int(‘498’ + x + ‘9’, 19)
if t % 23 == 0:
print(t // 23)
exit
Ответ: 43100.
Операции в одной системе счисления
Числа M и N записаны в системе счисления с основанием 9 соответственно.
M = 842×59, N = 8×7259
В записи чисел переменной x обозначена неизвестная цифра из алфавита девятеричной системы счисления. Определите наименьшее значение натурального числа A, при котором существует такой x, что M + A кратно N.
Операции в одной системе счисления
При помощи цикла for будем перебирать числа A и x (в соответствии в заданной системой счисления). Затем переведём числа M и N в десятичную систему счисления. Проверим кратность суммы M и A на N и выведем наименьшее A на экран.
Решение на языке Python
for A in range(1, 1000):
for x in ‘012345678’:
M = int(‘842’ + x + ‘5’, 9)
N = int(‘8’ + x + ‘725’, 9)
if (M + A) % N == 0:
print(A)
exit
Ответ: 387.
Операции в разных системах счисления с одной переменной
Операнды арифметического выражения записаны в системе счисления с основаниями 18 и 12:
28×218 + 93×512
В записи чисел переменной x обозначена неизвестная цифра из алфавита десятичной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 133. Для найденного значения x вычислите частное от деления значения арифметического выражения на 133 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с одной переменной
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 133 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789’:
t = int(’28’ + x + ‘2’, 18) + int(’93’ + x + ‘5’, 12)
if t % 133 == 0:
print(t // 133)
break
Ответ: 229.
Операции в разных системах счисления с одной переменной
Операнды арифметического выражения записаны в системе счисления с основаниями 13 и 18:
xA0413 + 1Dx318
В записи чисел переменной x обозначена неизвестная цифра из алфавита десятичной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 184. Для найденного значения x вычислите частное от деления значения арифметического выражения на 184 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с одной переменной
При помощи цикла for будем перебирать x в соответствии в заданной системой счисления. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 184 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
for x in ‘0123456789A’:
t = int(‘ ‘ + x + ‘A04’, 13) + int(‘1D’ + x + ‘3’, 18)
if t % 184 == 0:
print(t // 184)
break
Ответ: 124.
Операции в разных системах счисления с двумя переменными
Операнды арифметического выражения записаны в системах счисления с основаниями 15 и 16:
90x4y15 + 91xy216
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 56. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 56 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с двумя переменными
При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 56 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
result_search = [ ]
for x in ‘0123456789ABCDE’:
for y in ‘0123456789ABCDE’:
t = int(’90’ + x + ‘4’ + y, 15) + int(’91’ + x + y + ‘2’, 16)
if t % 56 == 0:
result_search.append(t)
if result_search:
print(min(result_search) // 56)
Операции в разных системах счисления с двумя переменными
Операнды арифметического выражения записаны в системах счисления с основаниями 7 и 9:
yx3207 + 1x3y39
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите значения x и y, при которых значение данного арифметического выражения будет наименьшим и кратно 181. Для найденных значений x и y вычислите частное от деления значения арифметического выражения на 181 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Операции в разных системах счисления с двумя переменными
При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 181 и выведем частное от деления значения арифметического выражения.
Решение на языке Python
result_search = [ ]
for x in ‘0123456’:
for y in ‘0123456’:
t = int(y + x + ‘320’, 7) + int(‘1’ + x + ‘3’ + y + ‘3’, 9)
if t % 181 == 0:
result_search.append(t)
if result_search:
print(min(result_search) // 181)
Ответ: 148.
В презентации использовались материалы с сайтов
https://inf-ege.sdamgia.ru/
https://kpolyakov.spb.ru/
https://fipi.ru/
Выполнения алгоритмов для исполнителя робот
Исполнитель чертёжник
№1. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 раз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−6, −4)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −1)
2) Сместиться на (1, 1)
3) Сместиться на (−4, −2)
4) Сместиться на (2, 1)
№2. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (3, 3) Сместиться на (1,−2)
Конец
Сместиться на (−8, 12)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−2, −4)
2) Сместиться на (4,−13)
3) Сместиться на (2, 4)
4) Сместиться на (−8, −16)
№3. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (3, 9)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (3, 4)
2) Сместиться на (−5, −10)
3) Сместиться на (−9, −12)
4) Сместиться на (−3, −4)
№4. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−9, −6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −3)
2) Сместиться на (4, 3)
3) Сместиться на (−2, −1)
4) Сместиться на (2, 1)
№5. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 paз
Команда1 Сместиться на (3, 3) Сместиться на (1, −2)
Конец
Сместиться на (4, −6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (6, −2)
2) Сместиться на (−8, 5)
3) Сместиться на (−12, 4)
4) Сместиться на (−6, 2)
№6. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (−4, −12)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (1,−2)
2) Сместиться на (12, 4)
3) Сместиться на (2, 11)
4) Сместиться на (−1, 2)
№7. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 4 paз
Команда1 Сместиться на (3, 2) Сместиться на (2, 1)
Конец
Сместиться на (−12, −8)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−8, −4)
2) Сместиться на (−2, −1)
3) Сместиться на (7, 5)
4) Сместиться на (2, 1)
№8. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Команда1 Сместиться на (3, 3) Сместиться на (1, −2)
Конец
Сместиться на (−6, 9)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (−6, −12)
2) Сместиться на (2, −10)
3) Сместиться на (2, 4)
4) Сместиться на (−2, −4)
№9. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 2 paз
Команда1 Сместиться на (1, 3) Сместиться на (1, −2)
Конец
Сместиться на (2, 6)
После выполнения этого алгоритма Чертёжник вернулся
в исходную точку. Какую команду надо поставить вместо команды Команда1?
1) Сместиться на (− 6, − 
2) Сместиться на (3, 4)
3) Сместиться на (− 4, − 7)
4) Сместиться на (− 3, − 4)
№10. Исполнитель Чертёжник перемещается
на координатной плоскости, оставляя след в виде линии. Чертёжник может
выполнять команду Сместиться на (a, b) (где a,
b — целые числа), перемещающую Чертёжника из точки с координатами (x,
у) в точку с координатами (x + а, у + b). Если числа a,
b положительные, значение соответствующей координаты
увеличивается; если отрицательные, уменьшается.
Например, если Чертёжник находится в точке с координатами (4,
2), то команда Сместиться на (2, −3) переместит
Чертёжника в точку (6, −1).
Запись
Повтори k раз
Команда1 Команда2 КомандаЗ
Конец
означает, что последовательность команд Команда1
Команда2 КомандаЗ повторится k раз.
Чертёжнику был дан для исполнения следующий алгоритм:
Повтори 3 paз
Сместиться на (−2, −1) Сместиться на (3, 2) Сместиться
на (2,1) Конец
На какую одну команду можно заменить этот алгоритм,
чтобы Чертёжник оказался в той же точке, что и после выполнения алгоритма?
1) Сместиться на (−9, −6)
2) Сместиться на (6, 9)
3) Сместиться на (−6, −9)
4) Сместиться на (9, 6)
Остановка в заданой клетке. циклы с оператором пока
№1. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно >
ПОКА < снизу свободно >
вниз
КОНЕЦ ПОКА
ПОКА < справа свободно >
вправо
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 14
2) 17
3) 19
4) 21
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому внутреннему циклу. В этом
цикле пока у нижней стороны клетки в которой находится РОБОТ нет стены
он продолжает двигаться вниз. Как только это условие перестанет выполняться
он переходит ко второму внутреннему циклу. Этот внутренний цикл аналогичен
первому, только теперь проверяется отсутствие стены у правой стороны
клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 19.
Правильный ответ указан под номером 3.
№2. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Клетка в лабиринте может быть чистая или закрашенная.
Закрашенные клетки на рисунке выделены серым цветом.
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды – это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ <условие>
ТО команда
КОНЕЦ ЕСЛИ
выполняется команда только, если условие истинно.
В противном случае ничего не происходит.
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно>
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 22
3) 26
4) 30
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле, пока снизу клетки в которой находится РОБОТ нет стены, он продолжает
двигаться вниз. Как только это условие перестанет выполняться, он переходит
ко второму действию внутри цикла. Второе действие, заключается в следующем:
РОБОТ передвигается на одну клетку вправо, до тех пор, пока справа свободно.
После чего возвращается к началу внешнего цикла.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся. Проверив все клетки
по выведенному нами правилу движения РОБОТА выясняем, что число
клеток, удовлетворяющих условию задачи равно 26.
Правильный ответ указан под номером 3.
№3. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Клетка в лабиринте может быть чистая или закрашенная.
Закрашенные клетки на рисунке выделены серым цветом.
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
4 |
|||||||
|
5 |
|||||||
|
6 |
|||||||
|
A |
B |
C |
D |
E |
F |
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды – это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ <условие>
ТО команда
КОНЕЦ ЕСЛИ
выполняется команда только, если условие истинно.
В противном случае ничего не происходит.
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА<справа свободно ИЛИ снизу свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 21
3) 24
4) 27
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока справа клетки в которой находится РОБОТ нет стены он продолжает
двигаться вправо. Как только это условие перестанет выполняться он
переходит ко второму циклу. Он, заключается в следующем: РОБОТ передвигается
на одну клетку вниз, до тех пор, пока снизу свободно.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 21.
№4. Исполнитель РОБОТ умеет перемещаться
по прямоугольному лабиринту, начерченному на плоскости, разбитой
на клетки. Между соседними по сторонам клетками может стоять стена.
Система команд исполнителя РОБОТ содержит восемь
команд. Четыре команды — это команды перемещения:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если
на пути РОБОТа окажется стена, он разрушится.
Четыре команды проверяют отсутствие стены у каждой
стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкциях ПОКА условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ.
Начало формы
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <снизу свободно ИЛИ справа
свободно>
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 8
2) 12
3) 17
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока снизу клетки в которой находится РОБОТ нет стены он продолжает
двигаться вниз. Как только это условие перестанет выполняться он переходит
ко второму действию цикла. Второе действие, заключается в следующем:
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла. У робота есть возможность разбиться: например,
стартовав из любой клетки столбца F робот разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 12.
Правильный ответ указан под номером 2.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКАснизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 22
2) 19
3) 15
4) 12
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вправо. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ передвигается на одну
клетку вниз. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток А6,B6,C6. Проверив
все клетки по выведенному нами правилу движения РОБОТА выясняем,
что число клеток, удовлетворяющих условию задачи равно 15 (вся первая
строчка, весь столбец F, клетки D2, E2, D4, D6, E4).
Правильный ответ указан под номером 3.
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКАснизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 7
2) 12
3) 17
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ передвигается на одну
клетку вправо. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток С1,Е1,А3.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 7 (В5,С5,В6,С6,D6,E6,F6).
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия.
Команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно)
или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка А1)?
НАЧАЛО
ПОКА слева свободно ИЛИ сверху
свободно
ЕСЛИ слева свободно
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 13
2) 15
3) 21
4) 27
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной. В данной программе РОБОТ поступает следующим
образом: сперва РОБОТ проверяет, свободна ли клетка слева или сверху
от него. Если это так, то РОБОТ переходит к первому действию внутри
цикла. В этом цикле если у левой стороны клетки, в которой находится
РОБОТ, нет стены, он двигается влево, в противном случае он перемещается
вверх. После этого возвращается к началу внешнего цикла. Проанализировав
эту программу, приходим к выводу, что РОБОТ не может разбиться.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 21: A1-A6, A6-F6, A1-D1, E3, F3, D2-F2, B2, C2.
Правильный ответ указан под номером 3.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия. Команды-приказы: вверх,вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно. В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно)
или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
вправо
КОНЕЦ ПОКА
КОНЕЦ
1) 10
2) 13
3) 16
4) 20
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка снизу или справа от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, далее делает один шаг вправо. После этого возвращается
к началу внешнего цикла.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 13: все клетки столбца E, D3−D6, C4, C5.
Правильный ответ указан под номером 2.
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия. Команды-приказы: вверх,вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
вправо
КОНЕЦ ПОКА
вниз
КОНЕЦ ПОКА
КОНЕЦ
1) 6
2) 10
3) 13
4) 16
Пояснение.
В данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка снизу или справа от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вправо, далее делает один шаг вниз. После этого возвращается
к началу внешнего цикла.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 16.
Правильный ответ указан под номером 4.
нестандартные задачи
№1. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
МАШИНКА (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 10
2) 14
3) 3
4) 22
Пояснение.
Начав движение из любой клетки столбца А, клеток
В7, В8, С7, С8 Машинка разобьется, выполняя команду вправо. Стартовав
из клеток В1−В3, Машинка уцелеет. Начав движение из любой клетки первых
двух строк, начиная со столбца С и до столбца I, Машинка разобьется.
Стартовав из любой клетки столбца J, Машинка разобьется, выполняя команду
вверх. Начав движение из любой клетки столбца K, L, M, N Машинка разобьется,
выполняя команду вправо.
Проанализировав «пещеру» (участок лабиринта в центре,
из которого только один выход), приходим к выводу, что Машинка не
разобьется, стартовав из столбцов D и E, H, I. В каждом из них по три
клетки, а в столбце I — 2. Следовательно, ответ 3 + 9 + 2 = 14.
Правильный ответ указан под номером 2.
№2. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 12
2) 13
3) 15
4) 17
Пояснение.
Стартовав из любой клетки столбцов A, B, D, I, K, M, N,
O и клеток F1−F2, G1−G2, I2−N2 кораблик разобьётся, выполнив команду
вверх. Начав из любой клетки столбца С клетки E8 и клеток F4-F8, I4-I8, J4,
G4 и H4, кораблик не разобьётся. Таким образом, число клеток, стартовав
из которых кораблик не разбивается, равно 17.
Правильный ответ указан под номером 4.
№3. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку. При попытке передвижения на любую
серую клетку КОРАБЛИК разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 5
2) 4
3) 3
4) 2
Пояснение.
Эффективным приёмом решения является проверка клеток
группами. Начав движение из любой клетки столбца А, клеток В7, В8 Машинка
разобьется, выполняя команду вверх. Стартовав из любой клетки первой
строки, Машинка разобьется, выполняя команду вверх. Начав движение
из любой клетки столбцов C, D, E, G, H, J, K, L, M, I Машинка разобьется,
выполняя команду вверх.
Начав движение из клетки F8 Машинка не разобьется.
Начав движение из клеток N7, N8, O7, O8 Машинка не разобьется.
Таким образом, правильный ответ указан под номером 1.
№4. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для удобства
идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
вверх
влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Эффективным приёмом решения является проверка клеток
группами. Если Кораблик начнет движение из клеток H6, I6, D7, D8 он не
разобьется. Начав движение из любой другой клетки, Кораблик разобьется,
выполняя последние две команды: вверх, влево.
Правильный ответ указан под номером 4.
№5. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <справа свободно> вправо
ПОКА <слева свободно> влево
вверх
влево
КОНЕЦ
1) 10
2) 9
3) 12
4) 11
Пояснение.
Разбиться Кораблик может только при выполнении команд
«вверх» и «влево». Начав из любой клетки строк 1, 3, 4, 5,
7, столбца А и клеток E6−J6 кораблик разобьётся, выполняя команду
влево. Стартовав из клеток С2, E2, G2, I2, K2, M2, O2, O4, O6, O8 кораблик
уцелеет.
Правильный ответ указан под номером 1.
№6. Исполнитель КОРАБЛИК «живет» в ограниченном
прямоугольном водоеме-лабиринте, разделенном на клетки и изображенном
на рисунке (вид сверху). Серые клетки — скалистые берега, светлые — свободное
пространство, безопасное для передвижения КОРАБЛИКА. По краю водоема-лабиринта
также находятся скалы с нанесенными на них номерами и буквами для
удобства идентификации клеток.
Система команд исполнителя КОРАБЛИК:
При выполнении любой из этих команд КОРАБЛИК перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
КОРАБЛИК (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку КОРАБЛИК
разбивается о скалы.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную. ниже программу,
КОРАБЛИК не разобьется?
НАЧАЛО
ПОКА <слева свободно> влево
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 0
2) 5
3) 15
4) 25
Пояснение.
Разбиться Кораблик может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки строк 1, 3 и
клеток A3−A7, С3−С7, G5−O5 кораблик разобьётся, выполняя команду вверх.
Стартовав из любой клетки строки 8, кроме клетки O8 и клеток A2, C2, E2,
G2, I2, K2, M2, E6−J6, I4−K4 кораблик уцелеет.
Правильный ответ указан под номером 4.
№7. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободо> вниз
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 1
2) 13
3) 21
4) 40
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки рядов столбцов
А, C, O и клеток B8, D1, K1−L1, J3−J4, I4−I6, машинка разобьётся, выполняя
команду вправо. Начав из любой клетки столбцов E, F, G, M и клеток H8,
I8, J6−J8, L3−L8, I1−I2 машинка не разобьётся.
Правильный ответ указан под номером 4.
№8. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <слева свободно> влево
вверх
вправо
КОНЕЦ
1) 10
2) 13
3) 15
4) 17
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Начав из любой клетки столбцов A, G,
H, I, O, и клеток B2−F2, D4, J4−J6, K5−K6, L6, L4, машинка разобьётся, выполняя
команду вправо. Стартовав из клеток B4−B6, C4−C5, N4−N6, М4−М5 машинка
не разобьётся.
Правильный ответ указан под номером 1.
№9. Исполнитель
МАШИНКА «живет» в ограниченном прямоугольном лабиринте на клетчатой
плоскости, изображенном на рисунке. Серые клетки — возведенные
стены, светлые — свободные клетки, по которым МАШИНКА может свободно
передвигаться. По краю поля лабиринта также стоит возведенная стенка
с нанесенными номерами и буквами для идентификации клеток в лабиринте.
Система команд исполнителя
МАШИНКА:
При выполнении
любой из этих команд МАШИНКА перемещается на одну клетку соответственно
(по отношению к наблюдателю): вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды
проверяют истинность условия отсутствия стены у каждой стороны той
клетки, где находится МАШИНКА (также по отношению к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие>
команда
выполняется,
пока условие истинно, иначе происходит переход на следующую строку.
При попытке передвижения
на любую серую клетку МАШИНКА разбивается о стенку.
Сколько клеток приведенного
лабиринта соответствуют требованию, что, стартовав в ней и выполнив
предложенную ниже программу, МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно>
вниз
ПОКА <слева свободно>
влево
вверх
влево
КОНЕЦ
1) 1
2) 7
3) 17
4) 21
Пояснение.
Разбиться Машинка
может только при выполнении команд «вверх» и «влево».
Начав из любой клетки столбцов A, C, E, G, H, J, O и клеток B8, D1, F7 − F8,
I1 − I2, L1, L3 − L4, N1 машинка разобьётся, выполняя команду влево. Стартовав
из любой клетки столбца M, клеток I1, I2, I4 − I6, L6 − L8, K7 машинка не
разобьётся.
Правильный
ответ указан под номером 3.
№10. Исполнитель МАШИНКА «живет» в ограниченном
прямоугольном лабиринте на клетчатой плоскости, изображенном на рисунке.
Серые клетки — возведенные стены, светлые — свободные клетки, по которым
МАШИНКА может свободно передвигаться. По краю поля лабиринта также
стоит возведенная стенка с нанесенными номерами и буквами для идентификации
клеток в лабиринте.
Система команд исполнителя МАШИНКА:
При выполнении любой из этих команд МАШИНКА перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится МАШИНКА (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
При попытке передвижения на любую серую клетку МАШИНКА
разбивается о стенку.
Сколько клеток приведенного лабиринта соответствуют
требованию, что, стартовав в ней и выполнив предложенную ниже программу,
МАШИНКА не разобьется?
НАЧАЛО
ПОКА <снизу свободно> вниз
ПОКА <справа свободно> вправо
вверх
вправо
КОНЕЦ
1) 0
2) 7
3) 1
4) 3
Пояснение.
Разбиться Машинка может только при выполнении команд
«вверх» и «вправо». Стартовав из любой клетки из столбца
А, машинка разобьется на последнем шаге, аналогично для клеток С7, С8
и А8 − J8. Начав движение из любой клетки с С1 по С5 машинка не разобьется,
аналогично для клеток I1, I2 (см. рисунок).
Правильный ответ указан под номером 2.
Остановка в заданной клетке, циклы с операторами ПОКА и ЕСЛИ
№1.
Система команд исполнителя РОБОТ, «живущего» в прямоугольном
лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа
и 4 команды проверки условия. Команды-приказы: вверх, вниз, влево, вправо.
При выполнении любой из этих команд РОБОТ перемещается на одну клетку
соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если РОБОТ начнёт движение
в сторону находящейся рядом с ним стены, то он разрушится, и программа
прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ: сверху
свободно, снизу свободно, слева свободно, справа
свободно. Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно. В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно). В конструкциях
ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И,
ИЛИ, НЕ.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <снизу свободно ИЛИ справа свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ЕСЛИ <снизу свободно>
ТО вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 12
2) 15
3) 18
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у правой стороны клетки, в которой находится РОБОТ, нет стены,
он продолжает двигаться вправо. Как только это условие перестанет выполняться,
он переходит ко второму действию внутри цикла. Второе действие, заключается
в следующем: РОБОТ проверяет, есть ли стена у нижней стороны клетки,
в которой он находится, и если снизу свободно, РОБОТ передвигается
на одну клетку вниз. После чего возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу, что РОБОТ будет
двигаться вправо или вниз, пока у него есть такая возможность. РОБОТ при
данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 18.
№2. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, включает в себя 4
команды-приказа и 4 команды проверки условия.
Команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Другие 4 команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка А1)?
НАЧАЛО
ПОКА < слева свободно ИЛИ сверху свободно >
ЕСЛИ < слева свободно >
ТО влево
ИНАЧЕ вверх
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 8
2) 12
3) 17
4) 21
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка сслева или сверху от него,
если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока слева клетки в которой находится РОБОТ нет стены он продолжает
двигаться влево. В противном случае он двигается вверх.
Проверив все клетки группами выясняем, что число клеток,
удовлетворяющих условию задачи равно 21.
№3. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции. Если РОБОТ начнёт движение в сторону находящейся рядом с
ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 19
3) 20
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому условию. По этому условию,
пока у нижней стороны клетки в которой находится РОБОТ нет стены, он
продолжает двигаться вниз. Как только это условие перестанет выполняться,
он переходит ко второму условию. Это условие аналогично первому,
только теперь проверяется отсутствие стены у правой стороны клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Видно, что существует всего 2 места, в которых робот
может остановиться: нужная нам 6F и 3F. Робот может прийти в клетку 3F
только если он находится в области 1B:3F и клетках 1A и 2A, количество
клеток в этой области равно 17. Общее количество клеток лабиринта
равна 36, следовательно, 36 − 17 = 19.
Правильный ответ указан под номером 2.
№4. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх , вниз
, влево
, вправо
.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА справа свободно
ТО
вправо
КОНЕЦ ПОКА
ЕСЛИ снизу свободнo
ТО
вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 18
2) 19
3) 20
4) 21
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет свободна ли клетка справа или снизу от него,
если это так, то РОБОТ переходит к первому условию. По этому условию,
пока у правой стороны клетки в которой находится РОБОТ нет стены, он
продолжает двигаться вправо. Как только это условие перестанет выполняться,
он переходит ко второму условию. Это условие аналогично первому,
только теперь проверяется отсутствие стены у нижней стороны клетки.
Проанализировав эту программы приходим к выводу,
что РОБОТ будет двигаться вправо или вниз, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Видно, что существует всего 2 места, в которых робот
может остановиться: нужная нам 6F и 6C. Робот может прийти в клетку 6С,
только если он находится в области 2А:6С, количество клеток в этой области
равно 15. Общее количество клеток лабиринта равно 36, следовательно,
36 − 15 = 21.
Правильный ответ указан под номером 4.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦl
1) 18
2) 24
3) 27
4) 30
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ будет двигаться вниз или вправо, пока у него есть такая возможность.
РОБОТ при данной программе никогда не разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 30 (все клетки за исключением E1:F3).
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют истинность
условия отсутствия стены у каждой стороны той клетки, где находится
РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦl
1) 6
2) 14
3) 18
4) 30
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
вначале РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Поэтому РОБОТ будет двигаться вправо или вниз, пока у
него есть такая возможность. РОБОТ при данной программе никогда не
разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 14.
Ответ: 2.
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх вниз
влево
вправо
Четыре команды проверяют
истинность условия отсутствия стены у каждой стороны той клетки, где
находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие
истинно) или команда2 (если условие ложно)
В конструкциях ПОКА и ЕСЛИ условие может
содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические
операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в данной клетке и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно
ПОКА снизу свободно
вниз
КОНЕЦ ПОКА
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 6
2) 10
3) 13
4) 18
Пояснение.
Один из главных приёмов в решении этой задачи — проверять
клетки группами, а не по одной.
При данной программе РОБОТ поступает следующим образом:
вначале РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле пока у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он продолжает двигаться вниз. Как только это условие перестанет
выполняться, он переходит ко второму действию внутри цикла. Второе
действие, заключается в следующем: РОБОТ проверяет, есть ли стена у
правой стороны клетки, в которой он находится, и если справа свободно,
РОБОТ передвигается на одну клетку вправо. После чего возвращается к
началу внешнего цикла.
Поэтому РОБОТ будет двигаться вправо или вниз, пока у
него есть такая возможность. РОБОТ при данной программе никогда не
разобьётся.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 13 (вся шестая строчка, клетки A, B четвертой и пятой строчки, клетки
C, D, E пятой строчки).
Ответ: 3.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд.
Четыре команды — это команды-приказы:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то
он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ снизу свободно
ТО вниз
ИНАЧЕ вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 16
2) 20
3) 25
4) 28
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, в противном случае он перемещается вправо.
После этого возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток C1, A5, C5.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 16 (весь столбец F, E1-E5, клетки D1, D2, D3, D4, D5).
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно (по отношению к наблюдателю): вверх
↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой стороны той клетки, где находится РОБОТ (также по отношению
к наблюдателю):
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие >
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ < условие >
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа
свободно
ЕСЛИ справа свободно
ТО вправо
ИНАЧЕ вниз
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 19
2) 22
3) 25
4) 28
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у правой стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вправо, в противном случае он перемещается
вниз. После этого возвращается к началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ может разбиться. Например, стартовав из клеток А4, B4, C6.
Проверив все клетки по выведенному нами правилу движения
РОБОТА, выясняем, что число клеток, удовлетворяющих условию задачи
равно 22 (вся первая и пятая строчка, весь столбец F, клетки D2-D4, E2-E4,
F2 и. т. д.).
№10. Система команд исполнителя РОБОТ,
«живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит
из 8 команд. Четыре команды −
При выполнении любой из этих команд РОБОТ перемещается
на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия
стены у каждой
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда 1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2
(если условие ложно).
В конструкциях ПОКА и ЕСЛИ условие может содержать команды
проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.
Если РОБОТ начнёт движение в сторону находящейся
рядом с ним стены, то он разрушится, и программа прервётся.
Сколько клеток лабиринта соответствуют требованию,
что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет
и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА снизу свободно ИЛИ справа свободно ЕСЛИ
снизу свободно
ТО
вниз
КОНЕЦ ЕСЛИ
ЕСЛИ справа свободно
ТО
вправо
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
1) 12
2) 16
3) 20
4) 24
Пояснение.
При данной программе РОБОТ поступает следующим образом:
сперва РОБОТ проверяет, свободна ли клетка справа или снизу от него.
Если это так, то РОБОТ переходит к первому действию внутри цикла. В этом
цикле если у нижней стороны клетки, в которой находится РОБОТ, нет
стены, он двигается вниз, в противном случае, если у правой стороны
клетки нет стены, он перемещается вправо. После этого возвращается к
началу внешнего цикла.
Проанализировав эту программу, приходим к выводу,
что РОБОТ не может разбиться.
Проверив все клетки по выведенному нами правилу движения
РОБОТА выясняем, что число клеток, удовлетворяющих условию задачи
равно 12 (клетки А4-6, B4-6, C5-6, D5-6, E6, F6).
Правильный ответ указан под номером 1.
Остановка в клетке, из которой начатодвижение
№1. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
одну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА < снизу свободно > вниз
ПОКА < слева свободно > влево
ПОКА < сверху свободно > вверх
ПОКА < справа свободно > вправо
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Программа заканчивается
командой «ПОКА < справа свободно > вправо», следовательно,
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка справа (условие 1). Этому
условию удовлетворяют все клетки правой стенки лабиринта и еще пять
клеток кроме нее.
Предпоследняя команда: «ПОКА < сверху свободно
> вверх», значит у клетки в которой он прекратит выполнение
должно быть ограничение стенкой сверху. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться на одной строчке с клеткой, с которой
он начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего две:
Г3 и Д1, если нумеровать цифрами сверху вниз, а буквами слева направо.
Представив себе движение робота в том случае когда он стартует из этих
клеток, увидим, что в них он и вернется.
Правильный ответ указан под номером 2.
№2. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <справа свободно> вправо
ПОКА <снизу свободно> вниз
ПОКА <слева свободно> влево
ПОКА <сверху свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <сверху свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка сверху (условие 1).
Этому условию удовлетворяют все клетки верхней стенки лабиринта и
еще пять клеток кроме нее.
Предпоследняя команда: «ПОКА <слева свободно>
влево», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой слева. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одном столбце с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего две:
А1 и Б2 если нумеровать цифрами сверху вниз, а буквами слева направо.
И клетка, из которой движение невозможно начать Д4.
Правильный ответ указан под номером 3.
№3. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вверх
ПОКА <слева свободно> влево
ПОКА<снизу свободно> вниз
ПОКА<справа свободно> вправо
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <справа свободно> вправо», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка справа (условие 1). Этому
условию удовлетворяют все клетки правой стенки лабиринта и еще пять
клеток кроме нее. Предпоследняя команда: «ПОКА<снизу свободно>
вниз», следовательно, у клетки в которой он прекратит выполнение
должно быть ограничение стенкой снизу. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одной строке с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего три:
Е6, Е5 и Б2, если нумеровать цифрами сверху вниз, а буквами слева направо.
Правильный ответ указан под номером 3.
№4. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
од-ну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА < условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА<снизу свободно> вниз
ПОКА<справа свободно> вправо
ПОКА<сверху свободно> вверх
ПОКА<слева свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА<слева свободно> влево», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева (условие 1). Этому
условию удовлетворяют все клетки левой стенки лабиринта и еще восемь
клеток кроме нее.
Предпоследняя команда: «ПОКА<сверху свободно>
вверх», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой сверху. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одной строке с клеткой, с которой он
начал движение (условие 2). Клеток, удовлетворяющих условиям 1 и 2,
всего три: В1, А1 и А3, если нумеровать цифрами сверху вниз, а русскими
буквами слева направо.
Правильный ответ указан под номером 3.
№5. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на
од-ну клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> влево
ПОКА <сверху свободно> вверх
ПОКА <справа свободно> вправо
ПОКА <снизу свободно> вниз
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <снизу свободно> вниз», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка снизу. Этому условию удовлетворяют
все клетки нижней стенки лабиринта и еще шесть клеток кроме нее.
Предпоследняя команда: «ПОКА <справа свободно>
вправо», значит у клетки в которой он прекратит выполнение должно
быть ограничение стенкой справа. Кроме того, робот, прекратив выполнение
этой команды, должен оказаться в одном столбце с клеткой, с которой он
начал движение (условие 2).
Клеток, удовлетворяющих условиям 1 и 2, всего одна:
Г5, если нумеровать цифрами сверху вниз, а буквами слева направо.
Правильный ответ указан под номером 1.
№6. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию 1.
Обратим внимание, что возможны зацикливания, например, если начать
движение из клетки А6, если нумеровать цифрами сверху вниз, а буквами
слева направо.
Ответ: одна клетка Г1.
№7. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию 1.
Обратим внимание, что возможны зацикливания, например, если начать
движение из клетки А1, если нумеровать цифрами сверху вниз, а буквами
слева направо.
Ответ: две клетки Д1 и В2.
№8. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вниз
ПОКА <снизу свободно> вправо
ПОКА <справа свободно> вверх
ПОКА <сверху свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Так как программа заканчивается командой «ПОКА
<сверху свободно> влево», для того, чтобы робот остановился в
той же клетке, с которой он начал движение, необходимо, чтобы у этой
клетки была стенка сверху. Этому условию удовлетворяют все клетки верхней
стенки лабиринта и еще пять клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию.
Обратите внимание, что возможны зацикливания, например, если начать
движение из клетки Д1 (если нумеровать цифрами сверху вниз, а русскими
буквами слева направо).
Ответ: две клетки Г4 и А2.
№9. Система команд исполнителя РОБОТ, «живущего»
в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <сверху свободно> вправо
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо, чтобы РОБОТ остановился в
той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <слева свободно> вверх», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка слева. Этому условию удовлетворяют
все клетки левой стенки лабиринта и еще семь клеток кроме нее.
Проверим каждую клетку, удовлетворяющую условию. Обратите
внимание, что возможны зацикливания, например, если начать движение
из клетки из любой клетки левой стенки.
Ответ: две клетки: Д1 и В2, если нумеровать цифрами
сверху вниз, а буквами слева направо.
№10. Система команд исполнителя РОБОТ,
«живущего» в прямоугольном лабиринте на клетчатой плоскости:
При выполнении этих команд РОБОТ перемещается на одну
клетку соответственно: вверх, вниз, влево, вправо.
Четыре команды проверяют истинность условия отсутствия
стены у той клетки, где находится РОБОТ:
|
сверху |
снизу |
слева |
справа |
Цикл
ПОКА <условие> команда
выполняется, пока условие истинно, иначе происходит
переход на следующую строку.
Сколько клеток лабиринта соответствуют требованию,
что, выполнив предложенную программу, РОБОТ остановится в той же клетке,
с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вниз
ПОКА <снизу свободно> вправо
ПОКА <справа свободно> вверх
ПОКА <сверху свободно> влево
КОНЕЦ
1) 1
2) 2
3) 3
4) 4
Пояснение.
Выясним, что необходимо для того, чтобы РОБОТ остановился
в той же клетке, с которой он начал движение. Так как программа заканчивается
командой «ПОКА <сверху свободно> влево», следовательно
для того, чтобы робот остановился в той же клетке, с которой он начал движение,
необходимо, чтобы у этой клетки была стенка сверху. Этому условию удовлетворяют
все клетки верхней стенки лабиринта и еще шесть клеток кроме нее. Проверим
каждую клетку, удовлетворяющую условию. Обратим внимание, что возможны
зацикливания, например, если начать движение из клетки А1, Б1, если
нумеровать цифрами сверху вниз, а буквами слева направо.
Ответ: три клетки В1, А2 и Д3.

















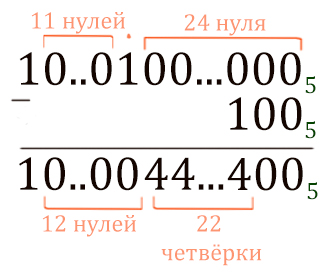
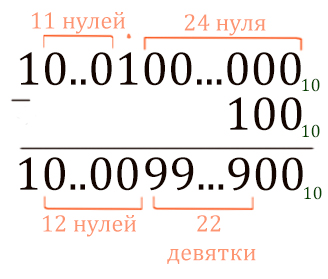
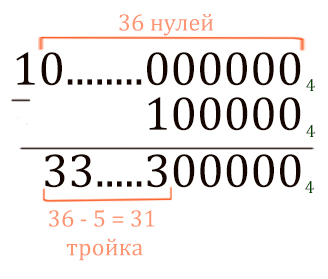


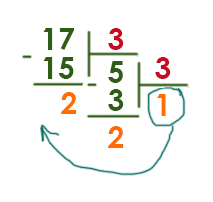

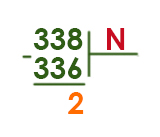
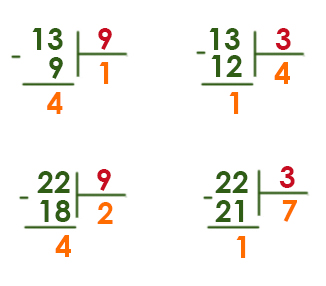













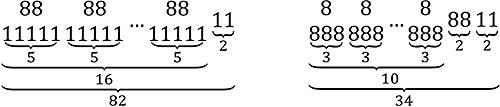




![Прямое сложение в системах счисления Решение на языке Python x = 8**2020 + 4**2017 + 26 - 1 s = ‘ ' while x != 0: s += str(x % 2) x //= 2 s = s[::-1] print(s.count(](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img4.jpg)


![Прямое сложение в системах счисления Решение на языке Python x = 125 + 25**3 + 5**9 s = ‘ ' while x != 0: s += str(x % 5) x //= 5 s = s[::-1] print(s.count(](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img7.jpg)









![Операции в разных системах счисления с двумя переменными При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 56 и выведем частное от деления значения арифметического выражения. Решение на языке Python result_search = [ ] for x in '0123456789ABCDE': for y in '0123456789ABCDE': t = int('90' + x + '4' + y, 15) + int('91' + x + y + '2', 16) if t % 56 == 0: result_search.append(t) if result_search: print(min(result_search) // 56)](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img17.jpg)

![Операции в разных системах счисления с двумя переменными При помощи цикла for будем перебирать x и y в соответствии в заданными системами счислений. Затем переведём все числа в десятичную систему счисления и найдём их сумму, записав полученное значение в переменную. Проверим кратность переменной на 181 и выведем частное от деления значения арифметического выражения. Решение на языке Python result_search = [ ] for x in '0123456': for y in '0123456': t = int(y + x + '320', 7) + int('1' + x + '3' + y + '3', 9) if t % 181 == 0: result_search.append(t) if result_search: print(min(result_search) // 181) Ответ: 148.](https://fsd.multiurok.ru/html/2023/01/11/s_63be65aaa3546/img19.jpg)





















