ЕГЭ.
Прототипы задания №3.
Вариант
1.
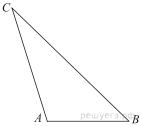
1. Найдите площадь треугольника,
изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см.
рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
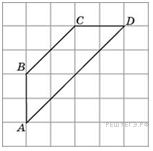
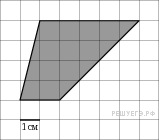
3. Найдите площадь четырехугольника,
изображенного на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
4. Найдите площадь трапеции,
изображенной на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
5. Найдите площадь
четырехугольника, вершины которого имеют координаты (8;0), (9;2), (1;6),
(0;4).
6. Точки O(0,0),
,
,
являются
вершинами четырехугольника. Найдите ординату точки P пересечения его
диагоналей.
7. Найдите
площадь параллелограмма, если две его стороны равны 25 и 1, а угол между ними
равен .
ЕГЭ.
Прототипы задания №3.
Вариант
2.
1. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите площадь четырехугольника,
изображенного на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите площадь трапеции,
изображенной на клетчатой бумаге с размером клетки
1
см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

4. Найдите площадь треугольника,
вершины которого имеют координаты (1;6), (9;6), (9;9).
5. Найдите площадь параллелограмма,
если две его стороны равны 45 и 10, а угол между ними равен .
6. Найдите (в см2)
площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1
см (см. рис.). В ответе запишите .
7. Найдите диагональ
квадрата, если его площадь равна 648.
ЕГЭ.
Прототипы задания №3.
Вариант
3.
1. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите площадь
четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите площадь трапеции,
изображенной на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
4. Найдите (в см2)
площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1
см (см. рис.). В ответе запишите .
5. Найдите площадь
треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).
6. Найдите площадь параллелограмма,
если две его стороны равны 29 и 2, а угол между ними равен .
7. Найдите диагональ квадрата, если
его площадь равна 800.
ЕГЭ.
Прототипы задания №3.
Вариант
4.
1. Найдите площадь
треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите площадь
четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите площадь трапеции,
изображенной на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
4. Найдите (в см2)
площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1
см (см. рис.). В ответе запишите .
5. Найдите площадь трапеции,
изображенной на рисунке.
6. Найдите
диагональ квадрата, если его площадь равна 1012,5.
7. Найдите
площадь параллелограмма, если две его стороны равны 43 и 10, а угол между ними
равен .
ЕГЭ.
Прототипы задания №3.
Вариант
5.
1. Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите
площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1
см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите
площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
4. Найдите
площадь квадрата, вершины которого имеют координаты (4;3), (10;3), (10;9),
(4;9).
5. Найдите
ординату середины отрезка, соединяющего точки A и B
.
6. Угол при
вершине, противолежащей основанию равнобедренного треугольника, равен .
Боковая сторона треугольника равна 3. Найдите площадь этого треугольника.
7. Площадь
прямоугольника равна 54. Найдите его большую сторону, если она на 3 больше
меньшей стороны.
ЕГЭ.
Прототипы задания №3.
Вариант
6.
1.
Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.

2. площадь
трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите
(в см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .
4. Найдите
площадь прямоугольника, вершины которого имеют координаты (1;1), (10;1),
(10;7), (1;7).
5. Найдите
диагональ квадрата, если его площадь равна 180,5.
6. Найдите
площадь параллелограмма, если две его стороны равны 32 и 2, а угол между ними
равен .
7. Периметр
прямоугольника равен 30, а площадь равна 14,5. Найдите диагональ этого
прямоугольника.
ЕГЭ.
Прототипы задания №3.
Вариант
7.
1. Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите
площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите (в
см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .
4. Найдите
площадь четырехугольника, вершины которого имеют координаты (8;0), (10;8),
(2;10), (0;2).
5. Периметр
треугольника равен 90, а радиус вписанной окружности равен 14. Найдите площадь
этого треугольника.
6. Основания равнобедренной
трапеции равны 12 и 18, а ее площадь равна 60. Найдите периметр трапеции.
7. Точки O(0,0),
,
,
являются
вершинами четырехугольника. Найдите ординату точки P пересечения его
диагоналей.
ЕГЭ.
Прототипы задания №3.
Вариант
8.
1. Точки O(0, 0), A(6,
8), C(0, 6) и B являются вершинами параллелограмма. Найдите
ординату точки B.
2. Найдите площадь трапеции,
изображенной на клетчатой бумаге с размером клетки 1 см 1 см
(см. рис.). Ответ дайте в квадратных сантиметрах.
3. Найдите площадь трапеции,
вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6).
4. Найдите диагональ квадрата,
если его площадь равна 0,5.
5. Найдите площадь параллелограмма,
если две его стороны равны 48 и 3, а угол между ними равен .
6. Угол при вершине, противолежащей
основанию равнобедренного треугольника, равен . Боковая сторона
треугольника равна 14. Найдите площадь этого треугольника.
7. Найдите
площадь закрашенной фигуры на координатной плоскости.
ЕГЭ.
Прототипы задания №3.
Вариант
9.
1. Найдите (в
см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .
2. Найдите
площадь трапеции, изображенной на рисунке.
3. Найдите
диагональ квадрата, если его площадь равна 512.
4. Периметр
прямоугольника равен 10, а площадь равна 4,5. Найдите диагональ этого
прямоугольника.
5. Сторона
прямоугольника относится к его диагонали, как , а другая сторона
равна 35. Найдите площадь прямоугольника.
6. Точки (0,
0), (10, 8),
(2, 6) и
являются вершинами
параллелограмма. Найдите абсциссу точки .
7. Найдите
ординату точки пересечения прямой, заданной уравнением , с осью Oy.
ЕГЭ.
Прототипы задания №3.
Вариант
10.
1. Найдите (в см2)
площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1
см (см. рис.). В ответе запишите .
2. Найдите
площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;6),
(5;6).
3. Найдите
диагональ квадрата, если его площадь равна 392.
4. Сторона
прямоугольника относится к его диагонали, как , а другая сторона
равна 42. Найдите площадь прямоугольника.
5. Найдите
площадь ромба, если его высота равна 2, а острый угол .
6. Найдите
абсциссу точки пересечения прямых, заданных уравнениями и
.
7. Найдите
площадь кольца, ограниченного концентрическими окружностями, радиусы которых
равны и
.
ЕГЭ.
Прототипы задания №3.
Вариант
11.
1. Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см. Ответ дайте в квадратных сантиметрах.
2. Найдите (в
см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .
3. Найдите
площадь параллелограмма, изображенного на рисунке.

4. Найдите
площадь закрашенной фигуры на координатной плоскости.
5. Найдите диагональ
квадрата, если его площадь равна 760,5.
6. Найдите
площадь параллелограмма, если две его стороны равны 6 и 11, а угол между ними
равен .
7. Периметр
прямоугольника равен 64, а площадь равна 31,5. Найдите диагональ этого
прямоугольника.
ЕГЭ.
Прототипы задания №3.
Вариант
12.
1. Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см. Ответ дайте в квадратных сантиметрах.
2. Найдите
(в см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .

3. Две
стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора .
4. Найдите
площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2),
(8;4), (1;9).
5. Найдите
диагональ квадрата, если его площадь равна 968.
6. Найдите
площадь параллелограмма, если две его стороны равны 39 и 2, а угол между ними
равен .
7. Периметр
треугольника равен 88, а радиус вписанной окружности равен 10. Найдите площадь
этого треугольника.
ЕГЭ.
Прототипы задания №3.
Вариант
13.
1. Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см. Ответ дайте в квадратных сантиметрах.
2. Найдите (в
см2) площадь фигуры, изображенной на клетчатой бумаге с
размером клетки 1 см 1 см (см. рис.). В ответе
запишите .
3. Найдите
площадь параллелограмма, изображенного на рисунке.
4. Найдите
площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно
16 и 20.
5. Периметр
треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь
этого треугольника.
6. Найдите
площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая
сторона составляет с основанием угол 45.
7. Точки O(0,
0), B(8, 2), C(2, 6) и A являются вершинами
параллелограмма. Найдите абсциссу точки A.
ЕГЭ.
Прототипы задания №3.
Вариант
14
1.
Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см. Ответ дайте в квадратных сантиметрах.
2. Найдите
площадь четырехугольника, вершины которого имеют координаты (1;7), (4;5),
(4;7), (1;9).
3. Найдите
площадь закрашенной фигуры на координатной плоскости.
4. Найдите
площадь параллелограмма, если две его стороны равны 49 и 4, а угол между ними
равен .
5. Найдите
площадь ромба, если его высота равна 15, а острый угол .
6. Основания
трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований
трапеции угол 150. Найдите площадь трапеции.
7. Периметр
треугольника равен 84, а радиус вписанной окружности равен 5. Найдите площадь
этого треугольника.
ЕГЭ.
Прототипы задания №3.
Вариант
15.
1.
Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1
см. Ответ дайте в квадратных сантиметрах.
2. Найдите
диагональ квадрата, если его площадь равна 544,5.
3. Найдите
площадь параллелограмма, если две его стороны равны 19 и 11, а угол между ними
равен .
4. Основания
равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите
площадь трапеции.
5. Найдите
абсциссу точки пересечения прямой, заданной уравнением , с осью Ox.
6.
Найдите
площадь четырехугольника, вершины которого имеют координаты (4, 2), (8, 4), (6,
8), (2, 6).
7. Найдите
площадь треугольника, вершины которого имеют координаты ,
,
.
Ответы:
|
вариант |
№ задания |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
6 |
12 |
6 |
10,5 |
20 |
7 |
12,5 |
|
2 |
6 |
16 |
14 |
12 |
225 |
0,75 |
36 |
|
3 |
7,5 |
9 |
11 |
1 |
25,5 |
29 |
40 |
|
4 |
6 |
4 |
32,5 |
3,5 |
9 |
45 |
215 |
|
5 |
22,5 |
5 |
13 |
36 |
6,5 |
2,25 |
9 |
|
6 |
40,5 |
35 |
2,25 |
54 |
19 |
32 |
14 |
|
7 |
18 |
28 |
5,625 |
68 |
630 |
40 |
6 |
|
8 |
2 |
21 |
30 |
1 |
72 |
49 |
24 |
|
9 |
8 |
9 |
32 |
4 |
2940 |
8 |
3 |
|
10 |
17,5 |
35 |
28 |
252 |
4 |
1,2 |
12 |
|
11 |
9 |
2 |
6 |
90 |
39 |
33 |
31 |
|
12 |
18 |
12 |
10 |
14 |
44 |
39 |
440 |
|
13 |
9 |
40 |
6 |
96 |
304 |
16 |
10 |
|
14 |
18 |
6 |
32 |
98 |
450 |
42 |
210 |
|
15 |
4,5 |
33 |
104,5 |
160 |
2 |
20 |
6 |
Данный материал рассчитан на его использование при контроле знаний по темам на уроках геометрии, а так же при подготовке к ЕГЭ. Задания самостоятельных работ выбраны из открытого банка задач ЕГЭ.
Скачать:
Предварительный просмотр:
Вариант 2
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 75.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 90.
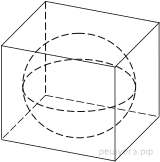
- Цилиндр описан около шара. Объем цилиндра равен 99. Найдите объем шара.
- Цилиндр описан около шара. Объем шара равен 76. Найдите объем цилиндра
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 67.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 124. Найдите объем конуса.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 45. Найдите объем шара.
Вариант 1
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 84.
- Цилиндр описан около шара. Объем цилиндра равен 45. Найдите объем шара.
- Цилиндр описан около шара. Объем шара равен 80. Найдите объем цилиндра.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 62.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 36. Найдите объем конуса.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 7. Найдите объем шара.
Предварительный просмотр:
Вариант 1
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 5. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
- Площадь поверхности куба равна 882. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 12. Площадь поверхности параллелепипеда равна 576. Найдите его диагональ.
- Если каждое ребро куба увеличить на 4, то его площадь поверхности увеличится на 240. Найдите ребро куба.
- Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 8, а площадь поверхности равна 416.
- Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,2 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 5 и 8. Найдите его площадь поверхности.
- Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 17 раз?
- Диагональ куба равна 37. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 42 и 24. Диагональ параллелепипеда равна 58. Найдите площадь поверхности параллелепипеда.
Вариант 2
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 6. Площадь поверхности этого параллелепипеда равна 138. Найдите третье ребро, выходящее из той же вершины.
- Площадь поверхности куба равна 648. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 12. Площадь поверхности параллелепипеда равна 192. Найдите его диагональ.
- Если каждое ребро куба увеличить на 2, то его площадь поверхности увеличится на 144. Найдите ребро куба.
- Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь поверхности равна 930.
- Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,8 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 7 и 9. Найдите его площадь поверхности.
- Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 23 раза?
- Диагональ куба равна 41. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 84 и 21. Диагональ параллелепипеда равна 91. Найдите площадь поверхности параллелепипеда.
Предварительный просмотр:
- В цилиндрический сосуд налили
воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Чему равен объем детали? Ответ выразите в
.
- В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 14.
- Объем конуса равен 112. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
- Объем первого цилиндра равен 48 м3. У второго цилиндра высота в 3 раза больше, а радиус основания — в 4 раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
- Радиус основания цилиндра равен 7, высота равна 2. Найдите площадь боковой поверхности цилиндра, деленную на
.
- Площадь большого круга шара равна 5. Найдите площадь поверхности шара.
- Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 16 раз?
- В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 2,5 раза. Чему равен объем детали? Ответ выразите в литрах.
- Найдите объем V конуса, образующая которого равна 7 и наклонена к плоскости основания под углом 30
. В ответе укажите
.
- Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6 раз?
- Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 26 раз?
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 129.
- Во сколько раз увеличится объем шара, если его радиус увеличить в одиннадцать раз?
- Высота конуса равна 2, образующая равна 4. Найдите его объем, деленный на
.
- Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен
. Вычислите объем конуса, деленный на
.
- Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 30. Найдите его объем, деленный на
.
- Длина окружности основания цилиндра равна 6, высота равна 3. Найдите площадь боковой поверхности цилиндра.
- Длина окружности основания конуса равна 7, образующая равна 8. Найдите площадь боковой поверхности конуса.
- Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 35 раз?
- Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?
- Высота конуса равна 40, образующая равна 50. Найдите площадь его полной поверхности, деленную на
.
- Площадь полной поверхности конуса равна 100. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса
- Объем одного шара в 512 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
- Радиусы двух шаров равны 15 и 36. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
- Радиус основания конуса равен 24, высота равна 18. Найдите площадь полной поверхности конуса, деленную на
.
- Площадь осевого сечения цилиндра равна 47. Найдите площадь боковой поверхности цилиндра, деленную на
.
- Объем шара равен 18432
. Найдите площадь его поверхности, деленную на
.
- Цилиндр описан около шара. Объем цилиндра равен 69. Найдите объем шара.
- Цилиндр описан около шара. Объем шара равен 72. Найдите объем цилиндра.
- Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 41.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 112. Найдите объем конуса.
- Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 23. Найдите объем шара.
- Длина окружности основания цилиндра равна 11. Площадь боковой поверхности равна 121. Найдите высоту цилиндра.
- В сосуде, имеющем форму конуса, уровень жидкости достигает
высоты. Объём жидкости равен 49 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
- Радиусы трех шаров равны 1, 6 и 8. Найдите радиус шара, объем которого равен сумме их объемов.
Предварительный просмотр:
Вариант 1
- Найдите квадрат расстояния между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите расстояние между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 5. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
- Площадь поверхности куба равна 882. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 12. Площадь поверхности параллелепипеда равна 576. Найдите его диагональ.
- Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 8, а площадь поверхности равна 416.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3, 5 и 8. Найдите его площадь поверхности.
- Диагональ куба равна 37. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 42 и 24. Диагональ параллелепипеда равна 58. Найдите площадь поверхности параллелепипеда.
Вариант 2
- Найдите квадрат расстояния между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите расстояние между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 6. Площадь поверхности этого параллелепипеда равна 138. Найдите третье ребро, выходящее из той же вершины.
- Площадь поверхности куба равна 648. Найдите его диагональ.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 12. Площадь поверхности параллелепипеда равна 192. Найдите его диагональ.
- Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь поверхности равна 930.
- Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 7 и 9. Найдите его площадь поверхности.
- Диагональ куба равна 41. Найдите площадь его поверхности.
- Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 84 и 21. Диагональ параллелепипеда равна 91. Найдите площадь поверхности параллелепипеда.
Предварительный просмотр:
Пирамида 1 вариант
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а
. Найдите площадь боковой поверхности.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 168 . Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 168 . Найдите длину отрезка
.
- Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
- Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
- Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 36 раз?
- Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.
- Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 24 и высота равна 16.
- Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 3 раза?
- Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.
Предварительный просмотр:
Вариант 2
- В цилиндрический сосуд налили
воды. Уровень жидкости оказался равным 6 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 3 см. Чему равен объем детали? Ответ выразите в
.
- В цилиндрическом сосуде уровень жидкости достигает 486 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
- Объем первого цилиндра равен 14 м3. У второго цилиндра высота в 3 раза больше, а радиус основания — в 2 раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
- Радиус основания цилиндра равен 10, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на
.
- В цилиндрический сосуд, в котором находится 8 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,1 раза. Чему равен объем детали? Ответ выразите в литрах.
- Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
- Длина окружности основания цилиндра равна 2, высота равна 7. Найдите площадь боковой поверхности цилиндра.
- Площадь осевого сечения цилиндра равна 2. Найдите площадь боковой поверхности цилиндра, деленную на
.
- Длина окружности основания цилиндра равна 7. Площадь боковой поверхности равна 7. Найдите высоту цилиндра.
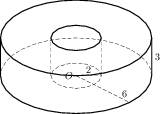
- Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
1)

- Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
1)

Вариант 1
- В цилиндрический сосуд налили
воды. Уровень жидкости оказался равным 6 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 3 см. Чему равен объем детали? Ответ выразите в
.
- В цилиндрическом сосуде уровень жидкости достигает 162 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 9 раз больше диаметра первого? Ответ выразите в сантиметрах.
- Объем первого цилиндра равен 88 м3. У второго цилиндра высота в 3 раза больше, а радиус основания — в 4 раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
- Радиус основания цилиндра равен 4, высота равна 5. Найдите площадь боковой поверхности цилиндра, деленную на
.
- В цилиндрический сосуд, в котором находится 4 литра воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,3 раза. Чему равен объем детали? Ответ выразите в литрах.
- Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
- Длина окружности основания цилиндра равна 5, высота равна 3. Найдите площадь боковой поверхности цилиндра.
- Площадь осевого сечения цилиндра равна 26. Найдите площадь боковой поверхности цилиндра, деленную на
.
- Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 8. Найдите высоту цилиндра.
- Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
1)

- Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
1)

Предварительный просмотр:
Вариант 1
- Площадь большого круга шара равна 39. Найдите площадь поверхности шара
- Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 25 раз?
- Во сколько раз увеличится объем шара, если его радиус увеличить в четыре раза?
- Объем одного шара в 1000 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
- Радиусы двух шаров равны 20 и 48. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
- Объем шара равен 12348
. Найдите площадь его поверхности, деленную на
.
- Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
Вариант 2
- Площадь большого круга шара равна 4. Найдите площадь поверхности шара.
- Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 37 раз?
- Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?
- Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
- Радиусы двух шаров равны 16 и 30. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
- Объем шара равен 26244
. Найдите площадь его поверхности, деленную на
.
- Радиусы трех шаров равны 15, 20 и 25. Найдите радиус шара, объем которого равен сумме их объемов.
Предварительный просмотр:
Вариант 1
- Объем конуса равен 70. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
- Найдите объем V конуса, образующая которого равна 13 и наклонена к плоскости основания под углом 30
. В ответе укажите
.
- Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 15 раз?
- Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 33 раза?
- Высота конуса равна 2, образующая равна 10. Найдите его объем, деленный на
.
- Диаметр основания конуса равен 12, а угол при вершине осевого сечения равен
. Вычислите объем конуса, деленный на
.
- Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 120. Найдите его объем, деленный на
.
- Длина окружности основания конуса равна 3, образующая равна 8. Найдите площадь боковой поверхности конуса.
- Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 24 раза?
- Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 30 раз?
- Высота конуса равна 15, образующая равна 17. Найдите площадь его полной поверхности, деленную на
.
- Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
- Площадь полной поверхности конуса равна 96. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
- В сосуде, имеющем форму конуса, уровень жидкости достигает
высоты. Объём жидкости равен 120 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
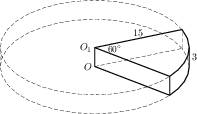
- Найдите объем V части конуса, изображенной на рисунке. В ответе укажите
.



Вариант 2
- Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
- Найдите объем V конуса, образующая которого равна 26 и наклонена к плоскости основания под углом 30
. В ответе укажите
.
- Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6,5 раза?
- Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 30 раз?
- Высота конуса равна 3, образующая равна 4. Найдите его объем, деленный на
.
- Диаметр основания конуса равен 18, а угол при вершине осевого сечения равен
. Вычислите объем конуса, деленный на
.
- Конус получается при вращении равнобедренного прямоугольного треугольника ABC вокруг катета, равного 3. Найдите его объем, деленный на
.
- Длина окружности основания конуса равна 2, образующая равна 3. Найдите площадь боковой поверхности конуса.
- Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 39 раз?
- Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 2 раза?
- Высота конуса равна 16, образующая равна 34. Найдите площадь его полной поверхности, деленную на
.
- Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
- Площадь полной поверхности конуса равна 88. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
- В сосуде, имеющем форму конуса, уровень жидкости достигает
высоты. Объём жидкости равен 4 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
- Найдите объем V части конуса, изображенной на рисунке. В ответе укажите
.
1)


Предварительный просмотр:
Вариант 3
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а
. Найдите площадь боковой поверхности.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 126 . Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 228 . Найдите длину отрезка
.
- Стороны основания правильной четырехугольной пирамиды равны 90, боковые ребра равны 51. Найдите площадь поверхности этой пирамиды.
- Стороны основания правильной шестиугольной пирамиды равны 60, боковые ребра равны 34. Найдите площадь боковой поверхности этой пирамиды.
- Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 15 раз?
- Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 10 и высота равна 12.
- Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 24 и высота равна 9.
- Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 1,5 раза?
- Ребра тетраэдра равны 30. Найдите площадь сечения, проходящего через середины четырех его ребер
Вариант 4
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной четырехугольной пирамиде
точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а
. Найдите площадь боковой поверхности.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 108 . Найдите длину отрезка
.
- В правильной треугольной пирамиде
— середина ребра
,
— вершина. Известно, что
, а площадь боковой поверхности равна 174 . Найдите длину отрезка
.
- Стороны основания правильной четырехугольной пирамиды равны 30, боковые ребра равны 17. Найдите площадь поверхности этой пирамиды.
- Стороны основания правильной шестиугольной пирамиды равны 210, боковые ребра равны 111. Найдите площадь боковой поверхности этой пирамиды.
- Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 37 раз?
- Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 24 и высота равна 16.
- Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 40 и высота равна 15.
- Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2,5 раза?
- Ребра тетраэдра равны 16. Найдите площадь сечения, проходящего через середины четырех его ребер.
Предварительный просмотр:
Вариант 1
- Найдите квадрат расстояния между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите расстояние между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
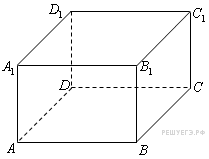
- Найдите расстояние между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
- Найдите квадрат расстояния между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
- Найдите расстояние между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Вариант 2
- Найдите квадрат расстояния между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите расстояние между вершинами
и
прямоугольного параллелепипеда, для которого
,
,
.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите угол
прямоугольного параллелепипеда, для которого
,
,
. Ответ дайте в градусах.
- Найдите расстояние между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
- Найдите квадрат расстояния между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
- Найдите расстояние между вершинами
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
По теме: методические разработки, презентации и конспекты
- Мне нравится
|
Вариант 1 |
|
Найдите высоту трапеции |
5. Задание 8 Два садовода, имеющие прямоугольные участки размерами 35 м на 40 м с общей границей, договорились и сделали общий прямоугольный пруд размером 20 м на 14 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода? |
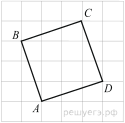
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°. |
6. Задание 13 Найдите объем многогранника, вершинами которого являются точки |
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника. |
7. Задание 15 На клетчатой бумаге с клетками размером 1 см |
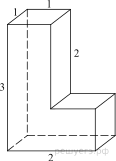
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
8. Задание 16 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. |
|
Вариант 2 |
|
На клетчатой бумаге с размером клетки |
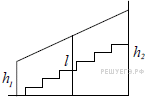
Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил относительно земли равна 1,5 м, а наибольшая h2 равна 2,5 м. Ответ дайте в метрах. |
Площадь треугольника ABC равна4. DE — средняя линия. Найдите площадь треугольника CDE. |
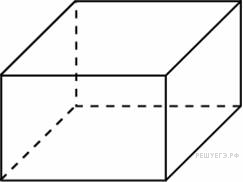
Аквариум имеет форму прямоугольного параллелепипеда с размерами 60 см × 20 см × 50 см. Сколько литров составляет объём аквариума? В одном литре 1000 кубических сантиметров. |
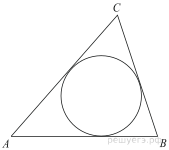
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь. |
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. |
|
Вариант 3 |
|
Найдите высоту треугольника |
Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах. |
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне? |
Плоскость, проходящая через три точки A, B и C, разбивает куб на два многогранника. Сколько граней у многогранника, у которого больше граней? |
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6. |
Найдите косинус угла . В ответе укажите значение косинуса, умноженное на |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. |
|
Вариант 4 |
|
На клетчатой бумаге с размером клетки 1 |
Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Размеры дома, расположенного на участке и также имеющего форму прямоугольника, — 9 м × 6 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах. |
В треугольнике ABC угол A равен 30°, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах. |
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах. |
Сторона правильного треугольника равна |
Хорда |
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). |
Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда. |
ОТВЕТЫ
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Вариант 1 |
2 |
24 |
6 |
18 |
1260 |
10 |
14 |
5 |
|
Вариант 2 |
40 |
1 |
30 |
76 |
2 |
60 |
12 |
3 |
|
Вариант 3 |
5 |
6 |
2 |
92 |
120 |
7 |
-2 |
24 |
|
Вариант 4 |
2,5 |
38 |
0,5 |
110 |
1146 |
8000 |
105 |
48 |
2 сентября 2017
В закладки
Обсудить
Жалоба
Комплект самостоятельных работ для подготовки к ЕГЭ по математике
Материал содержит по три самостоятельные работы по алгебре и геометрии. Количество вариантов от 6 до 10. Количество заданий в работе — от 4 до 12.
Автор: Полякова Ольга Ивановна.
sr-math.doc
1
вариант
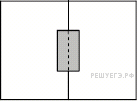
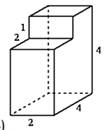
1.Найдите площадь поверхности многогранника, изображённого
на рисунке (все двугранные углы – прямые).
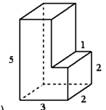
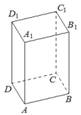
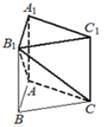
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны
длины рёбер: AB=6, AD=8, AA1=21. Найдите синус угла между прямыми A1D1 и AC.
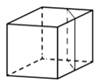
вершинами которого являются точки A, D1, A1, B, C1, B1 прямоугольного
параллелепипеда ABCDA1B1C1D1, у которого AB=3, AD=4, AA1=5
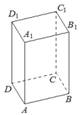
отсекаемой от куба
плоскостью, проходящей
через середины двух рёбер, выходящих из одной
вершины, и
параллельной третьему ребру, выходящему из этой же
вершины, равен 1,5.
Найдите объём куба.
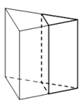
призма ABCDA1B1C1D1, площадь
основания которой равна 6, а боковое ребро равно 6. Найдите
объём многогранника, вершинами
которого являются точки A, B, C, A1, B1.
6. Площадь боковой поверхности треугольной призмы равна
47.
Через среднюю линию основания призмы проведена плоскость, параллельная
боковому ребру. Найдите площадь боковой
поверхности отсечённой
треугольной призмы.
7. Через среднюю линию основания треугольной призмы, объём
которой равен 48, проведена плоскость, параллельная боковому ребру. Найдите
объём отсечённой треугольной призмы.
8. Дана правильная треугольная призма ABCA1B1C1, площадь
основания которой равна 7, а боковое ребро равно 9. Найдите объём многогранника,
вершинами которого являются точки A, C, A1, B1, C1.
2 вариант
1. 1.Найдите площадь поверхности многогранника,
изображённого на рисунке (все двугранные углы – прямые).
2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны
длины рёбер: AB=28, AD=16, AA1=12. Найдите синус угла между прямыми DD1 и B1C.
3. Найдите объём многогранника, вершинами которого являются
точки A, D1, A1, B, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у
которого AB=4, AD=3, AA1=8.
объём треугольной призмы, отсекаемой 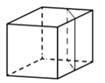
него плоскостью, проходящей через середины двух рёбер,
выходящих из
одной вершины, и параллельной третьему ребру, выходящему из
этой же вершины.
5. Дана правильная четырёхугольная призма ABCDA1B1C1D1,
площадь основания которой
равна 6, а боковое ребро равно 7. Найдите
объём многогранника, вершинами
которого являются точки A, B, C, A1, B1.
6. Через среднюю линию основания треугольной призмы
проведена плоскость,
параллельная боковому ребру. Площадь боковой поверхности 
треугольной призмы равна 43. Найдите площадь
боковой поверхности исходной
призмы.
7. Через среднюю линию основания треугольной призмы, объём
которой равен 56, проведена плоскость, параллельная боковому ребру. Найдите
объём отсечённой треугольной призмы.
8. Дана правильная треугольная призма ABCA1B1C1, площадь
основания которой равна 4, а боковое ребро равно 6. Найдите объём
многогранника, вершинами которого являются точки B, C, A1, B1, C1.
Вариант 1
Вариант 2
1. 
1. 
2.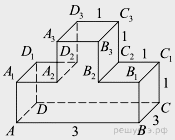
и
.
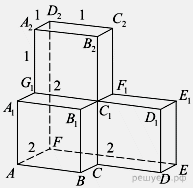
2.
3.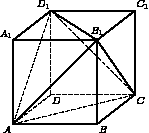
равен
Найдите объем треугольной пирамиды
3. 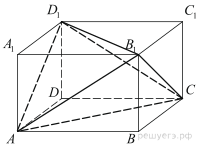
равен 2,7. Найдите объем треугольной пирамиды
4. Найдите объем многогранника, вершинами которого являются точки ,
,
,
прямоугольного параллелепипеда
, у которого
,
,
4. Найдите объем многогранника, вершинами которого являются точки ,
,
,
,
прямоугольного параллелепипеда
, у которого
,
,
|
Вариант 1 1. Периметр прямоугольника равен 42, а площадь 108. Найдите большую сторону прямоугольника. 2. В треугольнике ABC угол C равен 90°, AC = 16, 3 4. В треугольнике ABC угол A равен 40° , внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах. 5. В прямоугольном треугольнике ABC угол С равен |
Вариант 2 1. Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника . 2. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 3. Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 25. 4. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88. 5. В остроугольном треугольнике ABC угол A равен |
|
Вариант 3 1. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника. 2. Найдите большую диагональ ромба, сторона которого равна 3. Угол ACO равен 4. В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах. 5 |
Вариант 4 1. Площадь прямоугольника равна 54. Найдите его большую сторону, если она на 3 больше меньшей стороны. 2. Одна сторона треугольника равна радиусу описанной окружности. Найдите острый угол треугольника, противолежащий этой стороне. Ответ дайте в градусах 3. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции. 4. В треугольнике ABC угол C равен 90°, CH – высота, 5. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 45. Найдите площадь этого треугольника. |
|
Вариант 5 1. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника. 2. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции. 3. Найдите вписанный угол, опирающийся на дугу, которая составляет 4 5. Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса |
Вариант 6 1. Площадь параллелограмма ABCD равна 14. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма. 2. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла. 3. Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30°. Найдите сторону AB этого треугольника. 4. В тупоугольном треугольнике ABC 5 |
|
Вариант 7 1. Найдите хорду, на которую опирается угол 30°, вписанный в окружность радиуса 28. 2. Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20. Найдите высоту трапеции. 3 4. Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма. 5. В треугольнике ABC угол C равен 90°, высота CH равна 4, BC = 8. Найдите |
Вариант 8 1. Найдите площадь ромба, если его диагонали равны 15 и 6. 2. Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника. 3. Угол ACB равен 4. В треугольнике ABC угол C равен 90 °, 5 |















































































































































































































 .
.









 .
.



 .
. 



 .
.  .
. 





 .
.