Егэ уравнение сферы

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

  • что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
  • что такое шар и его элементы;
  • уравнение сферы;
  • формула для нахождения площади поверхности сферы;
  • взаимное расположение сферы и плоскости;
  • теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Определение

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Определение

Круг – это часть плоскости, ограниченная окружностью.

Определение

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Уравнение сферы

– уравнение сферы радиуса R и центром С(x0; y0; z0).

Определение

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Определение

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Определение

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Дополнительная литература:

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

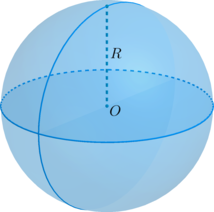
Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Определение

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Определение

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС2=R2, то есть координаты точки М удовлетворяют уравнению:

.

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Определение

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Решение:

Площадь круга вычисляется по формуле: Sкр=πR2.

Площадь поверхности шара вычисляется по формуле: Sсф=4πR2. Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

Ответ: 36

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Решение:

Площадь сферы равна Sсф=4πR2. То есть Sсф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r2 =100, то есть r=10.

Ответ: 10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Решение:

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

p=0,5(AB+BC+AC)=21

S=84.

С другой стороны, S=p·r.

Отсюда r=4.

Теперь найдем расстояние от центра шара до секущей плоскости.

Используем соотношение:

h=3.

Ответ: 3.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Решение:

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

По условию задачи R=10.

Используем соотношение:

h=6.

Ответ: 6.

Источник

Урок геометрии в 11 классе «Решение задач по теме «Объем шара, площадь сферы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

План – конспект урока геометрии в 11 классе

Тема: « Решение задач по темам «Объем шара и его частей», «Площадь сферы».

Тип урока: Урок закрепления изученного материала

-сформировать умения применять формулы объёма шара, площади шара при решении задач.

-создать условия для развития на уроке психологических качеств учащихся: интеллекта, мышления, памяти, внимания;

-обеспечить условия для развития познавательных процессов, для формирования общеучебных и специальных умений, совершенствованию мыслительных операций;

-создать условия для развития коммуникативной культуры.

-обеспечить условия для формирования положительного отношения к знаниям, к процессу учения.

1.Образовательные (формирование познавательных УУД):

· применять формулы объёма шара, площади шара при решении задач.

· Анализировать полученные результаты

· Моделировать решение задачи с помощью плана

2. Воспитательные (формирование коммуникативных и личностных УДД):

· Познавательный интерес и навыки взаимоконтроля, взаимопроверки

· Коммуникативные способности во время работы в парах, группах

· Понимание ответственности за индивидуальную деятельность и деятельность работы в паре

· Положительный эффект настойчивости для достижения цели

3.Развивающие (формирование регулятивных УУД:

· Анализировать, сравнивать, обобщать, делать выводы

· Участвовать во взаимоконтроле, самоконтроле, вносить предложения.

· Осуществлять рефлексию своей деятельности

Оборудование: 1. Компьютер (с видеопроектором).

I. Организационный момент

У : Посмотрите на эти механические часы (висят в классе). Что будет, если мы уберем 1 деталь? Так же и знания человека состоят из маленьких «деталей». И только, когда эти «детали» собраны вместе и не упущена ни одна, тогда знания начинают действовать и их можно применить в жизни. То, что мы узнаем на уроке сегодня и являются такими «деталями» наших знаний. Девиз нашего урока

«Мудрым никто не родился, а научился» C лайд №1

— Как понимаете эти слова?

— Сегодня продолжим путь к мудрости

У : С проверки домашнего задания и с повторения того, что мы уже с вами знаем.

II. Проверка домашнего задания

Задача № 723. Сколько кожи пойдет на пошивку футбольного мяча радиуса 10 см? (На швы добавить 8% от площади поверхности мяча).

Решение: S сферы =4П R 2 ; S = 4П* 10 2 =400П(см 2 )

1% S составляют 0,01* 400П=4П (см 2 ).

8% S составляют 8*4П = 32П(см 2 ).

Ответ: 1357 (см 2 ) Слайд №2

Формулируем тему урока: » Решение задач по темам «Объем шара и его частей», «Площадь сферы». Слайд №3

Поставьте каждый для себя цель урока. Слайд №4

Учащиеся сообщают, какие цели они для себя выбирают. Приходим к общему мнению. Записывают дату, тему в тетрадь, определяют цель урока

I II. Актуализация знаний учащихся

1. Теоретический диктант (с последующей взаимопроверкой).(Работа в паре)

Вписать в текст недостающие по смыслу слова.

1) Всякое сечение шара плоскостью есть круг. Центр этого круга есть . перпендикуляра, опущенного из центра шара на секущую плоскость.

2) Центр шара является его . симметрии.

3) Осевое сечение шара есть .

4) Линия пересечения двух сфер есть .

5) Плоскости, равноудаленные от центра, пересекают шар по. кругам.

6) Около любой правильной пирамиды можно описать сферу, причем ее центр лежит на . пирамиды.

(высоте, основание, плоскостью, центром, круг, равным, перпендикулярен, окружность, касания)

1) Любая диаметральная плоскость шара является его . симметрии.

2) Осевое сечение сферы есть .

3) Центр шара, описанного около правильной пирамиды, лежит на . пирамиды.

4) Радиус сферы, проведенной в точку касания сферы и плоскости . к касательной плоскости.

5) Касательная плоскость имеет с шаром только одну общую точку — точку.

6) В любую правильную пирамиду можно вписать сферу, причем ее центр лежит на . пирамиды.

(высоте, основание, плоскостью, центром, круг, равным, перпендикулярен, окружность, касания)

Взаимопроверка Слайд №5

Ответы (на экране):

Вариант I Вариант II

1) основание, 1) плоскостью,

2) центром, 2) окружность,

3) круг, 3) высоте,

4) окружность, 4) перпендикулярен,

5) равным, 5) касания,

6) высоте. 6) высоте.

2. Опрос теоретический

Что такое сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор.

IV .Закрепление теоретического материала

1. Индивидуальная работа по карточкам.

Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. Найдите объем шара.

Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара, равного 20 см?

Демонстрация решений по карточкам с последующим обсуждением. Выставление оценок.

1.Объем шара радиуса R равен V .

Найдите: объем шара радиуса: а)2 R ; б) 0,5 R .

(Ответ: а) 32/3П R ; б) 1/6 П R 3 )

2. Чему равен объем шарового сектора, если радиус окружности основания равен 60 см, а радиус шара – 75 см?

(Ответ: 112,5П см 3 , или 450П см 3 ).

3. Самостоятельная работа с последующей проверкой ответов.

1. На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9 см. Найдите объем шара и площадь его поверхности.

2. Сфера радиуса 3 имеет центр в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости О XY . Найдите объем шара, ограниченного данной сферой.

(Ответы: 1) 4500 П см 3 , 900П см 2 ; 2) ( x -4) 2 +( y +2) 2 +( z +1) 2 =9; 36П)

Взаимооценка труда учащихся:

Кто из ребят, по вашему мнению, работал лучше всех на уроке?

Что вам понравилось на уроке? Можно ли сказать, что вы стали чуть мудрее?

Сегодня на уроке вы работали активно, старательно, участвовали в обсуждении плана решения задач, высказывали своё мнение.

Проанализируйте все этапы урока, цели которые вы ставил перед собой. Оцените свое эмоциональное состояние от участия в работе на уроке. Поднимите карточку красного цвета, если вы не поняли тему урока, желтую- если вы не совсем уверены, зеленую – если вы хорошо усвоили новый материал.

VI . Домашнее задание. Слайд №6

1. Повторить п. 82-84, формулы п. 82-84.

2. Просмотреть решения задач предыдущих уроков.

3. Решить задачи.

№1 Объем шара равен 36п см 3 . Найдите его радиус.

№2 Объемы двух шаров относятся как 8:1. Найдите отношения их радиусов.

№3 В шар вписан куб со стороной а. Найдите объем шара.

Спасибо за урок!! До свидания.

1) Всякое сечение шара плоскостью есть круг. Центр этого круга есть . ……………..перпендикуляра, опущенного из центра шара на секущую плоскость.

2) Центр шара является его . симметрии.

3) Осевое сечение шара есть .

4) Линия пересечения двух сфер есть .

5) Плоскости, равноудаленные от центра, пересекают шар по. кругам.

6) Около любой правильной пирамиды можно описать сферу, причем ее центр лежит на . ……………….пирамиды.

1) Любая диаметральная плоскость шара является его . симметрии.

2) Осевое сечение сферы есть .

3) Центр шара, описанного около правильной пирамиды, лежит на . пирамиды.

4) Радиус сферы, проведенной в точку касания сферы и плоскости . к касательной плоскости.

5) Касательная плоскость имеет с шаром только одну общую точку — точку.

6) В любую правильную пирамиду можно вписать сферу, причем ее центр лежит на . пирамиды.

Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. Найдите объем шара.

Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара, равного 20 см?

Самостоятельная работа с последующей проверкой ответов.

1. На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9 см. Найдите объем шара и площадь его поверхности.

2. Сфера радиуса 3 имеет центр в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости О XY . Найдите объем шара, ограниченного данной сферой.

3. Решить задачи.

№1 Объем шара равен 36п см 3 . Найдите его радиус.

№2 Объемы двух шаров относятся как 8:1. Найдите отношения их радиусов.

№3 В шар вписан куб со стороной а. Найдите объем шара.

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Преподавание математики в школе в условиях реализации ФГОС

  • Сейчас обучается 35 человек из 22 регионов

Курс повышения квалификации

Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

«Домашнее обучение. Лайфхаки для родителей»

  • Для всех учеников 1-11 классов
    и дошкольников
  • Интересные задания
    по 16 предметам

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 859 027 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

  • 09.03.2017
  • 424
  • 0
  • 09.03.2017
  • 933
  • 2
  • 09.03.2017
  • 911
  • 3
  • 09.03.2017
  • 919
  • 5
  • 09.03.2017
  • 524
  • 0
  • 09.03.2017
  • 1301
  • 2

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 09.03.2017 10371
  • DOCX 36.7 кбайт
  • 347 скачиваний
  • Рейтинг: 5 из 5
  • Оцените материал:

Настоящий материал опубликован пользователем Лацис Лидия Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

  • На сайте: 5 лет и 2 месяца
  • Подписчики: 0
  • Всего просмотров: 14432
  • Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

«Формирование экологического мировоззрения у обучающихся»

«Искусство детям — увлекательно и просто: Египет»

«Study skills – живи для учения, учись для жизни»

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минобрнауки выделило более 590 тысяч бюджетных мест на 2023-24 учебный год

Время чтения: 2 минуты

Тысячи учителей в Австралии вышли на забастовку

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Задания из сборника.Для подготовки к ЕГЭ. Шар.
материал для подготовки к егэ (гиа, геометрия, 11 класс) по теме

Этот документ содержит основные задания из части.В-11.Для успешной сдачи экзамена рекомендую решить самим или с помощью учителя! Успехов!

Скачать:

Вложение Размер
shar_ege.docx 76.92 КБ

Предварительный просмотр:

1.Площадь большого круга шара равна 1. Найдите площадь поверхности шара.

2. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

3.Площадь большого круга шара равна 17. Найдите площадь поверхности шара.

4.Площадь большого круга шара равна 5. Найдите площадь поверхности шара.

5.Площадь большого круга шара равна 29. Найдите площадь поверхности шара.

6.Площадь большого круга шара равна 38. Найдите площадь поверхности шара.

  1. Прямоугольный параллелепипед описан около сферы радиуса 6,5. Найдите его объем.
  1. Прямоугольный параллелепипед описан около сферы радиуса 9,5. Найдите его объем.
  2. Прямоугольный параллелепипед описан около сферы радиуса 12. Найдите его объем.
  3. Прямоугольный параллелепипед описан около сферы радиуса 0,5. Найдите его объем.
  4. Прямоугольный параллелепипед описан около сферы радиуса 11. Найдите его объем.
  5. Прямоугольный параллелепипед описан около сферы радиуса 8. Найдите его объем.
  1. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
  1. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 16 раз?
  2. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 15 раз?
  3. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 25 раз?
  1. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 11 раз?
  1. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
  1. Около шара описан цилиндр, площадь поверхности которого равна 69. Найдите площадь поверхности шара.
  2. Около шара описан цилиндр, площадь поверхности которого равна 99. Найдите площадь поверхности шара
  3. Около шара описан цилиндр, площадь поверхности которого равна 114. Найдите площадь поверхности шара.
  4. Около шара описан цилиндр, площадь поверхности которого равна 66. Найдите площадь поверхности шара.
  5. Около шара описан цилиндр, площадь поверхности которого равна 111. Найдите площадь поверхности шара.
  1. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  1. Радиусы двух шаров равны 24 и 32. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  2. Радиусы двух шаров равны 20 и 48. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  3. Радиусы двух шаров равны 15 и 36. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  4. Радиусы двух шаров равны 21 и 28. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  5. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
  1. Вершина A куба со стороной является центром сферы, проходящей через точку . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
  2. Вершина A куба со стороной является центром сферы, проходящей через точку . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину .
  3. Вершина A куба со стороной является центром сферы, проходящей через точку . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
  4. Вершина A куба со стороной является центром сферы, проходящей через точку . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину .
  5. Вершина A куба со стороной является центром сферы, проходящей через точку . Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину .
  1. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь части поверхности шара, лежащей внутри куба. В ответе запишите .
  2. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите
  3. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите
  4. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите
  5. Середина ребра куба со стороной является центром шара радиуса . Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите .

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

  • что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
  • что такое шар и его элементы;
  • уравнение сферы;
  • формула для нахождения площади поверхности сферы;
  • взаимное расположение сферы и плоскости;
  • теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x0; y0; z0).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

.

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: Sкр=πR 2 .

Площадь поверхности шара вычисляется по формуле: Sсф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна Sсф=4πR 2 . То есть Sсф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

Задачи для подготовки к ЕГЭ «Сфера. Площадь сферы»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Задачи для подготовки к ЕГЭ

«Шар. Площадь поверхности шара»

№1 Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

№2 Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

№3 Ра­ди­у­сы двух шаров равны 6 и 8. Най­ди­те ра­ди­ус шара, пло­щадь по­верх­но­сти ко­то­ро­го равна сумме пло­ща­дей по­верх­но­стей двух дан­ных шаров.

№4Пло­щадь по­верх­но­сти шара равна 24. Най­ди­те пло­щадь боль­шо­го круга шара.

№5 Даны два шара с ра­ди­у­са­ми 5 и 1. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти второго?

№6 Шар впи­сан в ци­линдр. Пло­щадь пол­ной по­верх­но­сти ци­лин­дра равна 18. Най­ди­те пло­щадь по­верх­но­сти шара.

№7 Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Об­ра­зу­ю­щая ко­ну­са равна 7 Най­ди­те ра­ди­ус сферы.

№8 Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

№1 Пло­щадь боль­шо­го круга шара равна 1. Най­ди­те пло­щадь по­верх­но­сти шара.

№2 Дано два шара. Радиус первого шара в 60 раз больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

№3Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

№4 Площадь поверхности шара равна 12. Найдите площадь большого круга шара.

№5 Даны два шара с ра­ди­у­са­ми 8 и 4. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти второго?

№6 Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 6. Найдите площадь поверхности шара.

№7 Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Об­ра­зу­ю­щая ко­ну­са равна Най­ди­те ра­ди­ус сферы.

№8 Шар впи­сан в ци­линдр. Пло­щадь по­верх­но­сти шара равна 30. Най­ди­те пло­щадь пол­ной по­верх­но­сти ци­лин­дра.

источники:

http://nsportal.ru/shkola/geometriya/library/2014/01/03/zadaniya-iz-sbornikadlya-podgotovki-k-ege-shar

http://resh.edu.ru/subject/lesson/4034/conspect/

http://infourok.ru/zadachi-dlya-podgotovki-k-ege-sfera-ploschad-sferi-3964242.html

Источник

8. Геометрия в пространстве (стереометрия)


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Задачи по теме «Сфера и шар»

(blacktriangleright) Сфера – это множество точек пространства, находящихся на одинаковом расстоянии от заданной точки (O) (называемой центром сферы).

(blacktriangleright) Шар – это сфера вместе со своей внутренностью.

Основные формулы (где (R) – радиус сферы или шара):

(blacktriangleright) площадь сферы ({large{S=4pi R^2}})

(blacktriangleright) объем шара ({large{V=dfrac{4}{3}pi R^3}})


Задание
1

#1878

Уровень задания: Равен ЕГЭ

Объем шара равен (displaystyle frac{36}{sqrtpi}). Чему будет равна площадь поверхности шара, если его радиус увеличить на (displaystyle frac{6}{sqrtpi})?

(displaystyle V_{text{шара}} = frac{4}{3}pi R^3 = frac{36}{sqrtpi}) (Rightarrow) (displaystyle R = frac{3}{sqrtpi}). Радиус нового шара равен: (displaystyle R_{text{нов.}} = R + frac{6}{sqrtpi} = frac{9}{sqrtpi}). Тогда найдем площадь поверхности: (displaystyle {S_{text{пов.}} = 4pi R_{text{нов.}}^2 = 4pi left(frac{9}{sqrtpi}right)^2 = 4pifrac{81}{pi} = 324}.)

Ответ: 324


Задание
2

#1877

Уровень задания: Равен ЕГЭ

Во сколько раз объем шара больше объема сегмента, высота которого равна половине радиуса?

Необходимо объем шара разделить на объем соответствующего сегмента, высота которого равна (H = frac{1}{2}R)

[frac{V_{text{шара}}}{V_{text{сегм.}}} = frac{frac{4}{3}pi R^3}{pi left(frac{1}{2}Rright)^2left(R — frac{1}{3}left(frac{1}{2}Rright)right)} = frac{frac{4}{3}pi R^3}{frac{5}{24}pi R^3} = frac{4}{3} cdot frac{24}{5} = frac{32}{5} = 6,4.]

Ответ: 6,4


Задание
3

#2674

Уровень задания: Сложнее ЕГЭ

Имеются две сферы (S_1) и (S_2), про которые известно, что радиус первой сферы в (2) раза больше, чем радиус второй сферы. Кроме того, сфера (S_2) целиком находится внутри сферы (S_1). Пусть объём шара, ограниченного второй сферой, равен (V_2), а объём тела, заключённого между сферами, равен (V). Найдите (V : V_2).

Пусть (V_1) – объём шара, ограниченного первой сферой. Так как радиус (S_1) в два раза больше, чем радиус (S_2), то (V_1 : V_2 = 8) .

[V = V_1 — V_2 = 8V_2 — V_2 = 7V_2,,] следовательно, (V : V_2 = 7).

Ответ: 7


Задание
4

#2306

Уровень задания: Сложнее ЕГЭ

Площадь поверхности шара равна (frac{37}{pi}). На расстоянии (frac1{2pi}) от центра шара проведена плоскость. Найдите длину полученной в сечении окружности.

Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то

[4pi R^2=dfrac{37}{pi} quad Rightarrow quad R^2=dfrac{37}{4pi^2}]

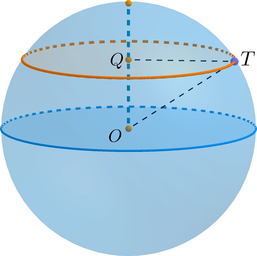
По условию задачи (OQ=frac1{2pi}). Рассмотрим (triangle OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.

Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{37}{4pi^2}-dfrac1{4pi^2}=dfrac{9}{pi^2}
quad Rightarrow quad r=dfrac3{pi}]

Таким образом, длина окружности сечения равна [C=2pi
r=2picdotfrac3{pi}=6.]

Ответ: 6


Задание
5

#2307

Уровень задания: Сложнее ЕГЭ

Площадь поверхности шара равна (64). На расстоянии (frac3{2sqrt{pi}}) от центра шара проведена плоскость. Найдите площадь полученного сечения.

Т.к. площадь поверхности сферы ищется по формуле (S=4pi R^2), то

[4pi R^2=64 quad Rightarrow quad R^2=dfrac{64}{4pi}]

По условию задачи (OQ=frac3{2sqrt{pi}}). Рассмотрим (triangle
OQT): он прямоугольный ((angle OQT=90^circ)), гипотенуза (OT=R), катет (QT) равен радиусу (r) окружности сечения.

Таким образом, по теореме Пифагора [QT^2=r^2=OT^2-OQ^2=dfrac{64}{4pi}-dfrac9{4pi}=dfrac{55}{4pi}]

Таким образом, площадь сечения равна

[S=picdot r^2=picdot dfrac{55}{4pi}=dfrac{55}4=13,75.]

Ответ: 13,75


Задание
6

#951

Уровень задания: Сложнее ЕГЭ

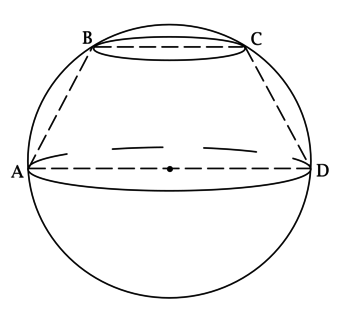
Центр большего основания усечённого конуса совпадает с центром сферы, а окружность его меньшего основания лежит на сфере. Отрезки (BC) и (AD) – диаметры меньшего и большего оснований этого усечённого конуса соответственно, (BCparallel AD), [S_{ABCD} = dfrac{210}{sqrt[3]{pi^2}},qquadqquad dfrac{r}{R} = dfrac{1}{sqrt{15}},] где (R) и (r) – радиусы большего и меньшего оснований усечённого конуса соответственно, (angle ADC = 45^circ). Найдите объём шара, ограниченного данной сферой.

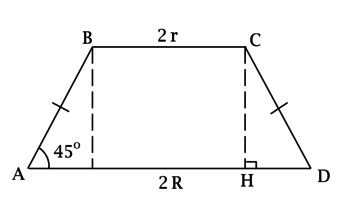
Рассмотрим (ABCD): т.к. (BCparallel AD), то (ABCD) – трапеция. Так как (AB) и (CD) – образующие усечённого конуса, то (AB = CD) и трапеция (ABCD) – равнобедренная.

Построим (CHperp AD). Так как (angle ADC = 45^circ), то (triangle CHD) – равнобедренный и (CH = HD).
[HD = dfrac{AD — BC}{2} = R — r,qquadqquad S_{ABCD} = dfrac{BC + AD}{2}cdot CH = (R + r)(R — r) = R^2 — r^2 = dfrac{210}{sqrt[3]{pi^2}},] но (r = dfrac{R}{sqrt{15}}), тогда [R^2left(1-dfrac{1}{15}right) = dfrac{210}{sqrt[3]{pi^2}}qquadRightarrowqquad R = dfrac{15}{sqrt[3]{pi}}qquadRightarrowqquad V_{text{шара}} = dfrac{4}{3}pi R^3 = dfrac{4}{3}cdotpicdotdfrac{15^3}{pi} = 4500.]

Ответ: 4500


Задание
7

#3114

Уровень задания: Сложнее ЕГЭ

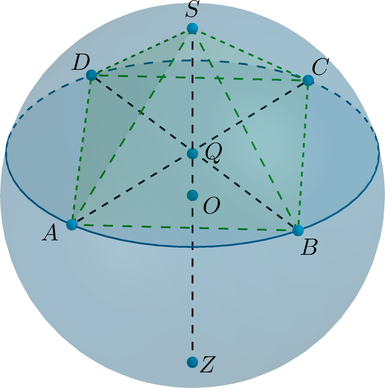
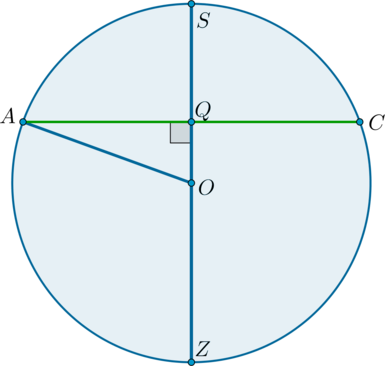
Дан шар, диаметр которого равен (9). Плоскость (alpha) пересекает диаметр (SZ) шара под углом (90^circ) и делит его точкой пересечения в отношении (1:2), считая от вершины (S). Найдите объем пирамиды с вершиной в точке (S), в основании которой лежит квадрат, вписанный в сечение шара плоскостью (alpha).

Пусть (O) – центр шара, (Q) – точка пересечения (SZ) и плоскости (alpha). Пусть (SABCD) – пирамида, объем которой нужно найти.
Рассмотрим сечение шара плоскостью (ASC).

Так как (SQ:QZ=1:2), то (SQ:SZ=1:3), следовательно, (SQ:SO=2:3), следовательно, (OQ:SO=1:3). Тогда [AQ=sqrt{AO^2-OQ^2}=sqrt{AO^2-left(dfrac13AOright)^2}=dfrac{2sqrt2}3AO
=dfrac{2sqrt2}3cdot dfrac92=3sqrt2] Следовательно, (AC=6sqrt2). Следовательно, (AB=AC:sqrt2=6).
Также [SQ=dfrac23SO=dfrac23cdot dfrac92=3] Заметим, что (SQ) – высота пирамиды, так как (SQperp alpha). Следовательно, [V=dfrac13cdot SQcdot AB^2=36.]

Ответ: 36

Задачи по стереометрии, в которых требуется произвести расчет объема сферы и измерение других неизвестных параметров, встречаются в ЕГЭ каждый год. Это означает, что знать основные формулы и уметь оперативно находить правильный ответ должны выпускники с разным уровнем подготовки. Понимая принцип решения задач ЕГЭ, в которых требуется вычислить объем или, к примеру, площадь сферы, старшеклассники смогут выполнять упражнения с любым количеством действий и при этом получить достаточно высокие баллы по итогам прохождения экзаменационного испытания.

Базовая информация

  • Сферой называется поверхность, которая состоит из множества точек пространства. Все они располагаются на одинаковом расстоянии от точки О. Она является центром сферы.
  • Геометрическое тело, которое ограничено сферой, называется шаром. Его осевое сечение представляет собой круг. Радиус последнего равен радиусу шара.
  • Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в n2 раз, а объем — в n3 раз.

Занимайтесь с образовательным порталом «Школково» для качественной подготовки к экзамену!

Проблема поиска необходимой информации встает перед старшеклассниками достаточно остро. Не всегда школьный учебник оказывается под рукой. А поиск базовых формул для вычисления площади, объема шара и других неизвестных параметров бывает достаточно трудоемким даже в онлайн-режиме.

Наш образовательный проект поможет сэкономить время и эффективно подготовиться к сдаче экзаменационного испытания. Мы предлагаем учащимся и их преподавателям выстроить процесс подготовки к ЕГЭ от простого к сложному. Такой подход позволит старшеклассникам понять, какие темы требуют более детального изучения, и улучшить имеющиеся знания.

Базовая информация, которую стоит повторить еще до выполнения задач на нахождение объема шара, представлена в разделе «Теоретическая справка». Материал, подготовленный опытными преподавателями «Школково», поможет вам восполнить пробелы в знаниях без помощи репетитора.

Чтобы задачи ЕГЭ по теме «Шар» или, например, по теме «Цилиндр», не вызывали затруднений, мы предлагаем также потренироваться в выполнении соответствующих упражнений. Множество заданий разной степени сложности вы найдете в разделе «Каталог». Каждое упражнение содержит подробный алгоритм решения. Попрактиковавшись в режиме онлайн и поняв принцип нахождения правильного ответа, школьники смогут без труда вычислить объем сферы.

При необходимости любое задание можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему.

Выполнять онлайн-задания на нахождение площади боковой сферы могут не только школьники из столицы, но и выпускники из других российских городов.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Егэ текст про рыбалку
  • Егэ умскул история 20 век
  • Егэ умножение логарифмов
  • Егэ ударения песня скачать
  • Егэ углубленная математика пробник

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии