Умножение логарифмов
1 случай. .
Доказательство. Используя частный случай формулы перехода к новому основанию (свойство 11), будем иметь:
Что и требовалось доказать.
Например. .
2 случай. При умножении нескольких логарифмов с разными основаниями выражение также можно в некоторых случаях упростить, перейдя к логарифмам с одним основанием по формуле перехода
Примеры решения задач
| Задание | Найти значение выражения |
| Решение | Приведем все логарифмы к одному основанию, например, 3: |
После сокращения будем иметь:
3 случай. Произведение логарифмов с одинаковыми основаниями также можно иногда преобразовать, основываясь на свойствах логарифма.
Основные свойства логарифмов
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.
Сложение и вычитание логарифмов
Рассмотрим два логарифма с одинаковыми основаниями: log a x и log a y . Тогда их можно складывать и вычитать, причем:
- log a x + log a y = log a ( x · y );
- log a x − log a y = log a ( x : y ).
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!
Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Задача. Найдите значение выражения: log3 135 − log3 5.
Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.
Вынесение показателя степени из логарифма
Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:
- log a x n = n · log a x ;
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Задача. Найдите значение выражения: log7 49 6 .
Избавимся от степени в аргументе по первой формуле:
log7 49 6 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:
[Подпись к рисунку]
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.
Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
Пусть дан логарифм log a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:
[Подпись к рисунку]
В частности, если положить c = x , получим:
[Подпись к рисунку]
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Задача. Найдите значение выражения: log5 16 · log2 25.
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 2 4 = 4log5 2; log2 25 = log2 5 2 = 2log2 5;
А теперь «перевернем» второй логарифм:
[Подпись к рисунку]
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Задача. Найдите значение выражения: log9 100 · lg 3.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
[Подпись к рисунку]
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
[Подпись к рисунку]
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
- n = log a a n
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Вторая формула — это фактически перефразированное определение. Она так и называется: .
В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».
Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что log25 64 = log5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
[Подпись к рисунку]
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂
Логарифмическая единица и логарифмический ноль
В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.
- log a a = 1 — это . Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
- log a 1 = 0 — это . Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a 0 = 1 — это прямое следствие из определения.
Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Умножение логарифмов
1 случай. 

2 случай. При умножении нескольких логарифмов с разными основаниями выражение также можно в некоторых случаях упростить, перейдя к логарифмам с одним основанием по формуле перехода
Логарифмом положительного числа
по основанию
называется показатель степени, в которую надо возвести
, чтобы получить
:
Например,
т.е
т. е.
т. е.
Логарифм единицы по любому основанию равен нулю.
Понятие логарифма. Примеры с решением
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример 1:
Найдите число 



б) Поскольку 

Пример 2:
Вычислите: а) 


Свойства логарифмов
Логарифм произведения и сумма логарифмов Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел. 
Пример 3:
Вычислите: a) 




Возможно вам будут полезны данные страницы:
Пример 4:
Найдите значение выражения: 
Логарифм частного двух положительных чисел равен разности логарифмов этих чисел.

Пример 5:
Вычислите: 
Пример 6:
Вычислите: 
Логарифм степени и произведение числа и логарифма
Логарифм степени положительного числа равен произведению показателя степени и логарифма этого числа.
Пример 7:
Вычислите: а) 



Решение: а) 



Пример 8:
Упростите: a) 


Пример 9:
Вычислите: а) 




Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
9. Преобразование числовых и буквенных выражений
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Числовые логарифмические выражения
Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
Таким образом, верно основное логарифмическое тождество [Large{{color{royalblue}{a^t=b quadLeftrightarrowquad
log_a{b}=t}}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).
(blacktriangleright) Если (a,b,c) – числа, удовлетворяющие ограничениям: (a,b,c>0, ane 1), то справедливы следующие формулы:
[begin{array}{|ccc|}
hline textbf{(1)} log_a1=0&&textbf{(2)} log_aa=1\
&&\
textbf{(3)} log_{a^n}{b^m}=frac mnlog_ab&&textbf{(4)}
a^{log_bc}=c^{log_ba}\
&&\
textbf{(5)} log_a{bc}=log_ab+log_ac&&textbf{(6)}
log_a{dfrac bc}=log_ab-log_ac\
&&\
textbf{(7)} log_abcdot log_bc=log_ac & text{или}
&textbf{(7′}) log_bc=dfrac{log_ac}{log_ab}\
&&\
hline
end{array}]
Заметим, что при выполнении ограничений данные формулы верны в обе стороны!
Некоторые частные случаи, которыми удобно пользоваться:
(blacktriangleright) Частные случаи формул (3) и (4): [m=log_a{a^m} text{и} b=a^{log_ab}]
С помощью первой формулы нагляднее видно, как заменить число на логарифм по нужному основанию:
(4=log_2{2^4}=log_2{16});
а с помощью второй – как заменить число на степень с нужным основанием:
(4=3^{log_34}).
(blacktriangleright) Частные случаи формул (7) и (7’): [log_abcdot log_ba=1 text{и}
log_ab=dfrac1{log_ba}]
Пример:
(log_3{25}+dfrac2{log_{frac15}3}={small{text{(применили}}}
{small{text{ формулу}}}
(2))=log_3{25}+2log_3{dfrac15}=log_3{25}+log_3{dfrac1{25}}=log_3{left(25cdotdfrac1{25}right)}=0)
Задание
1
#553
Уровень задания: Равен ЕГЭ
Найдите значение выражения ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right)).
По определению логарифма (log_{17}289) – это степень, в которую надо возвести 17, чтобы получить 289. Таким образом, (log_{17}289 = 2). Аналогично можно сделать вывод, что [log_{500}dfrac{1}{500} = -1.] Итого: ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right) = -2).
Ответ: -2
Задание
2
#554
Уровень задания: Равен ЕГЭ
Найдите значение выражения (16^{log_{2}5}).
Так как (a^{log_{b}c} = c^{log_{b}a}), то (16^{log_{2}5} = 2^{4 cdot log_{2}5} = 2^{log_{2}5^4} = 2^{log_{2}625} = 625^{log_{2}2} = 625^1 = 625).
Ответ: 625
Задание
3
#555
Уровень задания: Равен ЕГЭ
Найдите значение выражения (log_{81}243).
По свойствам логарифма (log_{81}243 = log_{3^4}3^5 = dfrac{5}{4}log_{3}3 = dfrac{5}{4} = 1,25).
Ответ: 1,25
Задание
4
#556
Уровень задания: Равен ЕГЭ
Найдите значение выражения (log_{11}242 — log_{121}4).
По свойствам логарифма [log_{121}4 = log_{11^2}4 = 0,5log_{11}4 = log_{11}(4^{0,5}) = log_{11}2.] Тогда (log_{11}242 — log_{121}4 = log_{11}242 — log_{11}2 = log_{11}dfrac{242}{2} = log_{11}121 = log_{11}11^2 = 2log_{11}11 = 2).
Ответ: 2
Задание
5
#557
Уровень задания: Равен ЕГЭ
Найдите значение выражения (log_{0,7}20 — log_{0,7}14).
По свойствам логарифма [log_{0,7}20 — log_{0,7}14 = log_{0,7}dfrac{20}{14} = log_{frac{7}{10}}dfrac{10}{7} = -1,] ведь по определению логарифма (log_{frac{7}{10}}dfrac{10}{7}) – это степень, в которую надо возвести (dfrac{7}{10}), чтобы получить (dfrac{10}{7}).
Ответ: -1
Задание
6
#558
Уровень задания: Равен ЕГЭ
Найдите значение выражения (dfrac{log_{15}1000}{log_{225}{10^4}}).
По свойствам логарифма [dfrac{log_{15}1000}{log_{225}{10^4}} = dfrac{log_{15}1000}{0,5log_{15}{10^4}} = dfrac{log_{15}1000}{log_{15}{(10^4})^{0,5}} = dfrac{log_{15}1000}{log_{15}{10^2}} = log_{100}1000 = log_{10^2}10^3 = dfrac{3}{2}log_{10}10 = dfrac{3}{2} = 1,5.]
Ответ: 1,5
Задание
7
#559
Уровень задания: Равен ЕГЭ
Найдите значение выражения (log_{7}144 cdot log_{12}343).
По свойствам логарифма [log_{7}144 cdot log_{12}343 = log_{7}(12^2) cdot log_{12}(7^3) = 2cdot 3 cdot log_{7}12 cdot log_{12}7 = 6 cdot log_{7}12 cdot log_{12}7 = 6cdotlog_{7}7 = 6,] потому что (log_{a}bcdotlog_{b}c = log_{a}c).
Ответ: 6

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Умножение логарифмов
Умножение логарифмов может быть выполнено в отдельных случаях с привлечением тех или иных свойств логарифмов. Готовой формулы для умножения логарифмов нет.
Например, два логарифма, у которых основание и выражение под знаком логарифма меняются местами — взаимно обратные числа:
Примеры.
При умножении нескольких логарифмов с разными основаниями можно попытаться перейти к логарифмам с одинаковым основанием по формуле
Пример.
Найти значение выражения:
Решение:
Приведём все логарифмы к одинаковому основанию. Удобнее всего перейти к основанию 10 (короче запись)
Сократив дробь, приходим к частному двух логарифмов по одинаковому основанию и переходим от частного логарифмов к одному логарифму
По формуле
(Вариант — сразу же во всех логарифмах перейти к основанию 2).
Умножение логарифмов с одинаковыми основаниями также можно попытаться изменить, используя свойства логарифмов.
Примеры.
Вычислить:
По формуле квадрата суммы
Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.
Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.
И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.
Дробно-рациональные выражения. Формулы сокращенного умножения
Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета
Если вам встретится такое задание на ЕГЭ – значит, повезло!
1. Найдите значение выражения
Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.
Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.
Ответ: 100.
2. Найдите значение выражения
Ответ: 20.
Корни и степени. Иррациональные выражения
Темы для повторения: Арифметический квадратный корень.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен
.
.
3. Вычислите .
Применили одну из формул сокращенного умножения.
Ответ: 8.
4. Вычислите:
Упростим множители:
Ответ: 8.
Действия со степенями
Темы для повторения:
Вспомним правила действий со степенями.
5. Найдите значение выражения: при
Применили формулу частного степеней
Ответ: 256.
6. Вычислите
Ответ: 2.
7. Вычислите , если
.
Спокойно, не пугаемся. И конечно, не спешим подставлять значение Сначала упростим выражение.
Ответ: 4,5.
8. Вычислите
Применили формулу для произведения степеней:
Ответ: 12.
9. Вычислите
Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.
Ответ: 3.
Логарифмические выражения
Темы для повторения:
Логарифмы
Логарифм положительного числа по основанию
— это показатель степени, в которую надо возвести
, чтобы получить
.
.
При этом > 0,
> 0,
Основные логарифмические формулы:
Основное логарифмическое тождество:
Логарифм произведения равен сумме логарифмов:
Логарифм частного равен разности логарифмов:
Формула для логарифма степени:
Формула перехода к новому основанию:
10. Вычислите: .
Снова формула перехода к другому основанию.
, поэтому
11. Найдите , если
.
12. Найдите значение выражения .
13. Найдите значение выражения .
.
14. Найдите значение выражения .
Тригонометрия. Формулы тригонометрии и формулы приведения
Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.
15. Вычислите:
16. Найдите , если
и
.
Т.к. , то
17. Найдите , если
и
Т.к. , то
18. Найдите значение выражения:
Применили формулу приведения.
19. Упростите выражение:
Применили формулу приведения.
20. Найдите , если
.
21. Вычислите , если
Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?
Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти .
Другие типы заданий
Темы для повторения:
Модуль числа.
Что такое функция.
22. Найдите значение выражения
при
.
Запомним:
.
Если , то
и
.
При этом и
.
При получаем:
.
Ответ: 2.
23. Найдите значение выражения
при
.
При получим:
Ответ: 12.
24. Найдите , если
, при
.
Что такое ? Это функция, каждому числу ставящая в соответствие число
. Например,
;
Тогда:
Заметим, что .
Значит, при
.
25. Найдите , если
, при
.
— функция, каждому числу b ставящая в соответствии число
.
Тогда при
, и значение выражения
равно 1.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023

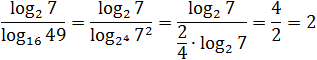


 по основанию
по основанию 
 называется показатель степени, в которую надо возвести
называется показатель степени, в которую надо возвести  Например,
Например,  т.е
т.е 
 т. е.
т. е. 
 т. е.
т. е. 
 Логарифм единицы по любому основанию равен нулю.
Логарифм единицы по любому основанию равен нулю. 















