| 1. | Задание 1. Найди признаки | 1 Б. |
| 2. | Задание 2. Выбери верные суждения | 2 Б. |
| 3. | Задание 3. Поиск соответствия | 2 Б. |
| 4. | Задание 4. Найди верные признаки | 2 Б. |
| 5. | Задание 5. Определи верные суждения | 2 Б. |
| 6. | Задание 6. Установи соответствие | 2 Б. |
| 7. | Задание 7. Найди правильные ответы | 2 Б. |
| 8. | Задание 8. Выбери верные суждения | 2 Б. |
| 9. | Задание 9. Анализ статистической информации | 1 Б. |
| 10. | Задание 10. Определи верные суждения | 2 Б. |
| 11. | Задание 11. Найди правильные ответы | 2 Б. |
| 12. | Задание 12. Выбери верные позиции | 1 Б. |
| 13. | Задание 13. Поиск соответствия | 2 Б. |
| 14. | Задание 14. Выбери верные суждения | 2 Б. |
| 15. | Задание 15. Установи соответствие | 2 Б. |
| 16. | Задание 16. Разбери жизненную ситуацию | 2 Б. |
ЕГЭ обществознание – 210 мин. (3,5 ч.) Вариант №1
Часть 1 (28 баллов)
1. Ниже приведён перечень терминов. Все они, за исключением двух, относятся к институтам гражданского общества.
1) профсоюзы; 2) суды; 3) семья; 4) парламент; 5) местное самоуправление; 6) университеты.
2. Выберите верные суждения о качествах человека как личности и запишите цифры, под которыми они указаны.
1) Качества человека как личности проявляются, прежде всего, в особенностях мышления и памяти.
2) Человеку как личности, прежде всего, свойственно приобретение социальных качеств.
3) Человека как личность в первую очередь характеризует протекание процессов психики.
4) Качества человека как личности проявляются, прежде всего, в его участии в жизни общества.
5) Человека как личность в первую очередь характеризуют унаследованные качества.
3.
Установите соответствие между отличительными признаками и видами деятельности, которые они иллюстрируют: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ОТЛИЧИТЕЛЬНЫЕ ПРИЗНАК
А) направленность на практически полезный результат
Б) формирование знаний и умений, развитие мышления
В) побудительный мотив деятельности заключается не в её результате, а в самом процессе деятельности
Г) все средства специально направлены на изменение субъекта деятельности
|
А |
Б |
В |
Г |
Д |
Д) особенностью деятельности является условная ситуация
ВИД ДЕЯТЕЛЬНОСТИ
1) труд 2) игра 3) учение
4.
К произведениям элитарной (высокой) культуры искусствоведы относят классическую музыку: органные произведения Баха, скрипичную музыку Вивальди, концерты для фортепиано с оркестром Рахманинова. Что позволяет искусствоведам сделать такой вывод?
1) самовыражение и свобода творчества авторов
2) сложность восприятия произведений неподготовленным слушателем
3) установка на следование образцу, который перенимается от предшествующих поколений.
4) высокая степень обобщения коллективного опыта
5) стереотипизация отражения человеком реального мира в музыке
6) ориентация музыки на широкую аудиторию
5.
Выберите верные суждения об источниках финансирования бизнеса и запишите цифры, под которыми они указаны.
1) Наращивание объёмов внешнего финансирования бизнеса повышает степень контроля собственника за предприятием.
2) Наиболее распространённой формой финансирования является банковский кредит.
3) Внутреннее финансирование бизнеса не сопряжено с дополнительными расходами, связанными с привлечением капитала.
4) К внутренним источникам финансирования бизнеса относится сдача в аренду неиспользуемых активов фирмы.
5) Финансирование частного бизнеса не может носить государственный характер.
6.
Установите соответствие между характеристиками и видами ценных бумаг: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ХАРАКТЕРИСТИКА
А) ценная бумага, закрепляющая право её держателя на получение от эмитента в предусмотренный ею срок номинальной стоимости и зафиксированного в ней процента от этой стоимости или имущественного эквивалента
Б) ценная бумага, в которой содержится распоряжение плательщика своему банку уплатить получателю указанную в ней сумму денег в течение срока ее действия.
В) держатель этой ценной бумаги имеет право на получение дивидендов.
Г) денежный документ, удостоверяющий внесение средств на определенное время, имеющий обычно фиксированную ставку процента
|
А |
Б |
В |
Г |
Д |
Д) ценная бумага, из суммы номиналов которой складывается уставный капитал коммерческой организации
ВИД ЦЕННЫХ БУМАГ
1) акция 2) облигация 3) сберегательный сертификат 4) чек
7. Алексей T. приобрёл 5% акций ПАО «Вихрь». Какие права приобрёл Алексей Т. как новый акционер компании? Запишите цифры, под которыми они указаны.
1) право вести от имени компании предпринимательскую деятельность
2) право на получение части прибыли компании
3) право на участие в формировании органов управления компании
4) право самостоятельно распоряжаться имуществом компании
5) право на получение части имущества компании в случае банкротства
6) право представлять компанию в налоговых и судебных органах
8.
Выберите верные суждения об этнической общности и запишите цифры, под которыми они указаны.
1) Древнейшей формой этнической общности является народность.
2) Обязательными признаками этнической общности является общность языка и религии.
3) Обязательным условием формирования этнической общности является общность территории.
4) Этнические общности отличаются устойчивостью.
5) Один и тот же человек может причислять себя к нескольким этническим общностям.
9.
|
Деньги |
35,3% |
|
Образование, профессия |
31,4% |
|
Получить от жизни больше удовольствий |
20,7% |
|
Деловая карьера |
19,6% |
|
Любовь |
11,6% |
Интернет-изданием был проведён опрос среди молодых людей крупных городов страны Z на тему: «Распределение основных ценностей молодых людей». Полученные результаты (в % от числа опрошенных) представлены в таблице. Найдите в приведённом списке выводы, которые можно сделать на основе данных таблицы, и запишите цифры, под которыми они указаны.
1) Приоритетным для молодых людей является достижение материального благополучия в жизни.
2) Большинство опрошенных считают, что получение профессионального образования необходимо молодому поколению.
3) Примерно пятая часть опрошенных связывают основные ценности с удачной деловой карьерой.
4) Половина опрошенных не связывает стремление получать удовольствие
от жизни с получением образования и профессии.
5) Профессиональное образование интересует в качестве основных ценностей примерно треть опрошенных.
10. Выберите верные суждения о функциях гражданского общества и запишите цифры, под которыми они указаны.
1) Стимулирование общественно полезной деятельности граждан.
2) Защита границ и обеспечение общественного порядка.
3) Участие в формировании органов демократического правового социального государства.
4) Организация общественного контроля за соблюдением правил добросовестной конкуренции.
5) Разрешение экономических споров между хозяйствующими субъектами.
11. Партия «Союз за правду» приняла участие в региональных выборах в стране М. Какие из приведённых фактов позволяют определить, что «Союз за правду» является массовой партией, объединяющей сторонников социал-демократической идеологии?
1) Партия имеет чёткую иерархическую структуру.
2) В партии нет строгого постоянного членства.
3) Сторонники партии выступают за сохранение традиций и незыблемости моральных и религиозных принципов.
4) Программа партии содержит постулат о приоритете индивидуальных прав человека над интересами общества.
5) Лидер партии пропагандирует активную социальную политику государства.
6) Партия ведёт систематическую работу с избирателями.
12. Что из перечисленного ниже относится к политическим правам (свободам) гражданина РФ? Запишите цифры, под которыми они указаны.
1) обращение в органы государственной власти 2) доступ к государственной службе
3) защита Отечества 4) участие в управлении делами государства
5) получение квалифицированной юридической помощи
13. Установите соответствие между государственными полномочиями и функциями и субъектами высшей судебной власти РФ, которые их реализуют: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ПОЛНОМОЧИЯ И ФУНКЦИИ
A) осуществляет надзор за деятельностью судов общей юрисдикции
Б) разрешает споры о компетенции между высшими государственными органами субъектов РФ
B) дает разъяснения по вопросам судебной практики
Г) разрешает споры о компетенции между высшими органами федеральной власти
|
A |
Б |
В |
Г |
Д |
Д) дает толкование Основного закона страны
СУБЪЕКТЫ СУДЕБНОЙ ВЛАСТИ РФ
1) Конституционный 2) Верховный Суд РФ
14. Выберите верные суждения об отраслях права. Запишите цифры, под которыми они указаны.
1) Гражданское право относится к совокупности отраслей публичного права.
2) Составные части системы права, сгруппированные по предмету своего регулирования, составляют отрасль права.
3) Конституционное право закрепляет и регулирует наиболее важные, фундаментальные и исходные государственные отношения.
4) Административное право регулирует сферу управленческой, исполнительно-распорядительной деятельности государственных органов, общественных организаций, должностных лиц.
5) Гражданское право регулирует отношения по осуществлению правосудия при разрешении споров по семейным, трудовым и иным делам.
15. Установите соответствие между примерами и мерами юридической ответственности в РФ: к каждой позиции, данной в первом столбце, подберите соответствующую позицию из второго столбца.
ПРИМЕРЫ
|
A |
Б |
В |
Г |
Д |
А) возмещение убытков Б) предупреждение В) дисквалификация
Г) взыскание неустойки Д) замечание
МЕРЫ ЮРИДИЧЕСКОЙ ОТВЕТСТВЕННОСТИ В РФ
1) способы защиты гражданских прав 2) дисциплинарные взыскания 3) административные наказания
16. В отношении Михаила Романова возбуждено уголовное дело по обвинению в причинении тяжкого вреда здоровью. При каких условиях Михаил НЕ подлежит уголовной ответственности? Запишите цифры, под которыми указаны соответствующие условия.
1) Вред причинён в состоянии аффекта.
2) Вред причинён в состоянии необходимой обороны.
3) Вред причинён в состоянии крайней необходимости.
4) Вред причинён в состоянии алкогольного опьянения
5) Вред причинён в состоянии невменяемости.
6) Вред причинён в силу стечения тяжёлых жизненных обстоятельств.
Часть 2 (30 б.)
Прочитайте текст и выполните задания 17-20.
Исследование процесса зарождения малого предпринимательства в отечественной экономике выявило наличие противоречивой ситуации. С одной стороны, в России уже имеются все формальные предпосылки для его успешного развития. Приняты соответствующие федеральные законы и многочисленные подзаконные акты о государственной поддержке малых предприятий. Создана необходимая инфраструктура в лице государственных агентств и фондов, ассоциаций предпринимателей. Имеется рынок резервной рабочей силы, включая высококвалифицированных рабочих и дипломированных специалистов. Важность развития малого предпринимательства подтверждена выступлениями государственных деятелей, политиков, руководителей крупнейших банков и корпораций, ведущих ученых.
С другой стороны, фактическое состояние малого предпринимательства представителями всех заинтересованных сторон оценивается как крайне неудовлетворительное. В России наблюдается ярко выраженная неразвитость данного сектора экономики. В свете реформирования экономической системы и все еще не доведенного до конца перехода к рыночной модели, малым предприятиям следует уделять особое внимание. Чрезмерная концентрация производства в Советском Союзе стала одной из главных причин упадка малых городов, разорения десятков тысяч сел и деревень. Переселение десятков миллионов людей в крупные города создало неразрешимую проблему жилья, бытового и культурно-массового обслуживания, транспорта, экологии, преступности. Развитие малых предприятий необходимо России для становления эффективной и стабильной экономики, но надежды, которые возлагались на малый бизнес в конце 1980-х — начале 1990-х годов, пока полностью не оправдываются.
Предприниматель, деятельность которого направлена на получение прибыли, в свою очередь, удовлетворяет различные экономические потребности государства. Необходимо подчеркнуть основные характеристики, позволяющие малому бизнесу динамично развиваться, что подчеркивает важность развития данного сектора для общества. К ним относятся: быстрое реагирование на конъюнктуру; решение социальных вопросов, например возможность быстро создавать новые рабочие места; противодействие монополизму в экономике; активизация структурной перестройки экономики.
Таким образом, трудно переоценить значимость развития малого бизнеса для нашей страны. Оно способно коренным образом и без существенных капитальных вложений расширить производство многих потребительских товаров и услуг (в первую очередь для малообеспеченного большинства населения) с использованием местных источников сырья, решить проблему занятости, ускорить научно- технический прогресс и составить позитивную альтернативу криминальному бизнесу.
17. Автор приводит ряд негативных последствий, которые возникли в результате чрезмерной концентрации производства в условиях административно-командной экономики. Укажите три из них.
18. В тексте упомянуты ключевые понятия социально-гуманитарных наук. Используя обществоведческие знания,
— укажите не менее трёх основных признаков понятия «предпринимательство»;
— объясните связь названных автором характеристик предпринимательства. (Объяснение может быть дано в одном или нескольких распространённых предложениях.)
19. Какова, на ваш взгляд, позиция автора в оценке возможностей развития малого бизнеса в решении экономических проблем в России? По каким положениям текста вы это определили? (Укажите любые два положения-аргумента.) Приведите пример решения конкретной экономической проблемы с помощью малого бизнеса.
20. Автор видит сильные и слабые стороны малого бизнеса. Опираясь на знания курса, назовите три позиции, по которым малый бизнес уступает крупному бизнесу.
21. На графике изображено изменение ситуации на потребительском рынке бытовых холодильников и морозильников в стране Z. Кривая спроса переместилась из положения D в положение D1 при неизменном предложении S. (На графике P —цена товара; Q —количество товара).
К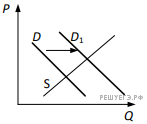
Что могло вызвать изменение спроса? Укажите любое одно обстоятельство (фактор) и объясните его влияние на спрос. (Объяснение должно быть дано применительно к рынку, указанному в тексте задания.)
Как изменятся предложение и равновесная цена на данном рынке, если при прочих равных условиях вырастут цены на аккумуляторы искусственного холода для бытовых холодильников и морозильников?
22. После очередной ссоры с соседями совершеннолетний дееспособный гражданин России Н. К. Сидоров, будучи в состоянии алкогольного опьянения, поджёг соседский дом и надворные постройки. Как оказалось, в сарае спал гражданин Е. Л. Кузьмин, который длительное время нигде не работал и не имел определённого места жительства (бездомный). Во время пожара Е. Л. Кузьмин погиб. Н. К. Сидоров предстал перед судом. Правонарушение какого типа (вида) совершил Н. К. Сидоров? К какому виду юридической ответственности он будет привлечён? В чём заключается принцип справедливости при назначении наказания? Н. К. Сидоров считает, что состояние алкогольного опьянения будет учтено судом в качестве обстоятельства, смягчающего наказание. Прав ли гражданин Сидоров? (Свой ответ объясните.)
23. Конституция Российской Федерации устанавливает основы гражданства РФ. На основе положений Конституции Российской Федерации приведите три объяснения этой характеристики.
(Каждое объяснение должно быть сформулировано как распространённое предложение с опорой на конкретное положение Конституции Российской Федерации.
Обратите внимание на то, что правильное выполнение задания не требует указания в ответе номеров соответствующих статей Конституции и дословного воспроизведения их содержания.)
24.
Используя обществоведческие знания, составьте сложный план, позволяющий раскрыть по существу тему «Внутренняя политика РФ». План должен содержать не менее трех пунктов, из которых два или более детализированы в подпунктах.
25.
Используя обществоведческие знания, факты общественной жизни и личный социальный опыт, выполните задания, ответьте на вопрос.
1) Обоснуйте необходимость проведения социальной политики в РФ. (Обоснование должно быть дано с опорой на обществоведческие знания в нескольких связанных между собой распространённых предложениях, раскрывать причинно-следственные и(или) функциональные связи.)
2) Какие конкретные меры предпринимаются в РФ для поддержки семьи, материнства и детства? (Назовите любые три меры.)
3) Для каждой из них приведите по одному примеру, иллюстрирующему реализацию данной меры. (Каждый пример должен быть сформулирован развёрнуто. В совокупности примеры должны иллюстрировать три различных меры.)
КЛЮЧИ Вариант №1
|
1 |
24 (1) |
6 |
24131 (2) |
11 |
156 (2) |
|
2 |
24 (2) |
7 |
235 (2) |
12 |
124 (1) |
|
3 |
13232 (1) |
8 |
345 (2) |
13 |
21211 (2) |
|
4 |
12 (2) |
9 |
135 (1) |
14 |
234 (2) |
|
5 |
234 (2) |
10 |
134 (2) |
15 |
13312 (2) |
|
16 |
235 (2) |
17. (2) В ответе могут быть названы следующие факты:
− проблемы жилья;
− проблемы бытового и культурно-массового обслуживания;
− транспортные проблемы;
− нарушение экологии;
− преступность.
18 (2)
1) Основные признаки понятия «предпринимательство»:
— самостоятельная деятельность;
— наличие риска;
— направлена на получение прибыли и др.
2) Предприниматель ведет деятельность с целью получения прибыли, что является основной характеристикой предпринимательства. Тем не менее, из данной характеристики выражаются несколько производных функций: удовлетворение социальных потребностей государства, создание рабочих мест. Таким образом, предприниматель, реализуя свои собственные цели, помогает удовлетворять потребности государства.
19. (3) Правильный ответ должен содержать:
1) позицию автора: «Трудно переоценить значимость развития малого бизнеса для нашей страны» (автор видит большие возможности);
2) два авторских положения, доказывающих широкие возможности малых предприятий в решении экономических проблем:
а) решить проблему занятости;
б) ускорить научно-технический прогресс;
в) составить альтернативу криминальному бизнесу;
3) пример: в небольшом поселке Х., на сохранившейся инфраструктуре обанкротившегося колхоза, было открыто фермерское хозяйство, куда смогли устроиться работать многие местные жители, что решило проблему занятости для сельского населения. (Решение проблемы занятости населения.)
20 (3)
Автор видит сильные и слабые стороны малого бизнеса. Опираясь на знания курса, назовите три позиции, по которым малый бизнес уступает крупному бизнесу.
Пояснение.
В ответе могут быть приведены следующие недостатки малого бизнеса:
− высокий риск капитальных вложений, как следствие, сложности с привлечением крупных инвестиций;
− ограниченные возможности привлечения профессионалов: юристов, экономистов, дизайнеров, программистов и др.;
− ограниченные возможности рекламы, как результат, слабая конкурентоспособность по сравнению с крупными фирмами производящими аналогичный товар;
− ограниченные возможности роста и развития бизнеса, вызванные сложностью с привлечением крупных инвестиций.
21. (3)
1. Ответ на первый вопрос: равновесная цена увеличилась.
2. Ответ на второй вопрос (одно обстоятельство (фактор) с объяснением влияния), например: на изменение спроса повлиял рост доходов потребителей, которые могут позволить себе чаще менять бытовую технику.
3. Ответ на третий вопрос: при росте цен на аккумуляторы искусственного холода (комплектующие детали) предложение упадёт, а равновесная цена вырастет.
22. (4)
Пояснение.
1. Ответ на первый вопрос: преступление.
2. Ответ на второй вопрос: уголовная ответственность.
3. Ответ на третий вопрос: наказание и иные меры уголовно-правового характера, применяемые к лицу, совершившему преступление, должны быть справедливыми, то есть соответствовать характеру и степени общественной опасности преступления, обстоятельствам его совершения и личности виновного. Никто не может нести уголовную ответственность дважды за одно и то же преступление.
4. Ответ на четвертый вопрос: гражданин Сидоров не прав. Согласно статье 23 Уголовного кодекса РФ лица, совершившие преступление в состоянии алкогольного опьянения, подлежат уголовной ответственности. Алкогольное опьянение не относится к обстоятельствам, смягчающим наказание.
23. (3) Пояснение.
Могут быть приведены такие подтверждения:
1) в Конституции закреплено, что гражданство Российской Федерации приобретается и прекращается в соответствии с федеральным законом, является единым и равным независимо от оснований приобретения.;
2) в Конституции закреплено, что каждый гражданин Российской Федерации обладает на ее территории всеми правами и свободами и несет равные обязанности, предусмотренные Конституцией Российской Федерации.;
3) в Конституции закреплено, что гражданин Российской Федерации не может быть лишен своего гражданства или права изменить его.;
24 (4)
Пояснение.
Один из вариантов плана раскрытия данной темы.
1. Понятие внутренней политики государства.
2. Приоритетные направления внутренней политики государства в области экономики:
а) совершенствование налогообложения;
б) поддержка малого бизнеса;
в) законотворческая деятельность в области предпринимательского права.
3. Основные направления социальной политики государства:
а) защита материнства и детства;
б) пенсионная реформа;
в) поддержка социально незащищенных групп инвалидов;
г) национальный проект «Здоровье».
4. Развитие науки и образования:
а) национальный проект «Образование;
б) «Сколково»;
в) национальный проект «Наука»
5. Другие направления политики государства.
6. Внутренняя политика России: результаты и перспективы.
25 (6)
- 13.09.2022
Первый тренировочный вариант ЕГЭ 2023 по русскому языку на основе демоверсии ЕГЭ 2023 от ФИПИ.
В 2023 году были изменения по некоторым предметам, поэтому обязательно ознакомьтесь со списком изменений, если еще не смотрели.
- Посмотреть демоверсию 2023 по русскому языку + изменения
Тестовый вариант создан по кодификатору и спецификации ФИПИ ЕГЭ 2023 и в полном соответствии со всеми изменениями демоверсии ЕГЭ 2023. В конце варианта указаны ответы ко всем задания первой и второй части теста. Вариант был опубликован и проводился 12 сентября 2022 года.
Автор-составитель: Проект ЕГЭ 100 БАЛЛОВ https://vk.com/ege100ballov
- Другие тренировочные варианты ЕГЭ по русскому языку
Есть вопросы? Пишите в комментариях ниже!
Некоторые задания из тренировочной работы №1
Задание 9
Укажите варианты ответов, в которых во всех словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
- п..рламент, симв..л, разг…раться
- ч..стота (колебаний), ч..рующий, тр..вянистый
- зам..рев (от страха), ф..дерация, коф..ин
- в..ртуоз, бл..стеть, одр..хлевший
- возр..ждение, с..бачий, зерк..ло
Задание 13
Определите предложение, в котором НЕ с выделенным словом пишется СЛИТНО. Раскройте скобки и выпишите это слово.
- (НЕ)ЗНАЯ броду, не суйся в воду.
- Сергей выдал себя (НЕ)ТЕРПЕЛИВЫМ жестом.
- Встреченный нами солдат был (НЕ)КТО иной, как лейтенант Крамаренко.
- Присмотрись, (НЕ)ПРИЯТЕЛЬ ли твой впереди нас?
- В избушке ночевать было отнюдь (НЕ)БЕЗОПАСНО.
Задание 20
Расставьте знаки препинания: укажите все цифры, на месте которых в предложении должны стоять запятые.
Автор знал (1) что (2) если его роман будет высоко оценен критиками (3) то его обязательно заметят (4) и весь тираж книги раскупят за несколько месяцев.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Тренировочные варианты «Школково». Уровень составитель ЕГЭ
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Авиабилет стоит (12000) рублей. Двум пассажирам из группы в десять человек была сделана скидка в (6%). Сколько в сумме отдали эти (10) пассажиров за перелёт?
Билет со скидкой стоит (12000 cdot (1 — 0,06) = 11280) рублей. Из группы в десять человек двое летели со скидкой, остальные восемь платили по (12000) рублей за билет. В сумме эти (10) пассажиров отдали (12000 cdot 8 + 11280 cdot 2 = 118560) рублей.
Ответ: 118560
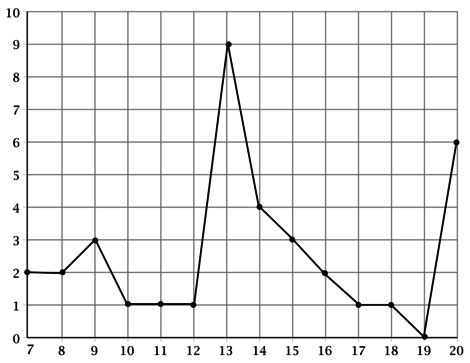
На рисунке жирными точками показано количество конфет, съеденных Лерой с (7) по (20) день диеты. По горизонтали указывается день от начала диеты, по вертикали – количество съеденных конфет в соответствующий день. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, через сколько дней после начала диеты Лера в первый раз за указанный промежуток времени съела в день (3) конфеты.
По рисунку видно, что в первый раз за данный период Лера съела (3) конфеты через (9) дней после начала диеты.
Ответ: 9
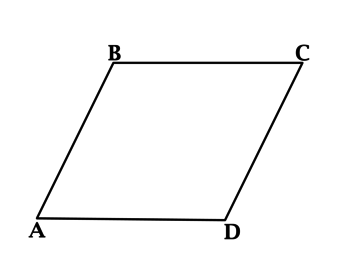
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна (10). Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Из множества натуральных чисел от (21) до (30) наугад выбирают одно число. Какова вероятность того, что оно делится на (3) или на (13)?
Так как вероятности выбора любого числа из данного множества одинаковы, то искомая вероятность есть просто отношение количества чисел из данного множества, которые делятся на (3) или на (4), к количеству всевозможных чисел из данного множества.
Так как число от (21) до (30) не может одновременно делиться на (3) и на (13), то события ( )“число делится на (3)”( )и( )“число делится на (13)”( ) несовместны.
В данном множестве на (3) делятся: (21), (24), (27), (30), а на (13) делятся: (26). Всего в множестве натуральных чисел от (21) до (30) имеется (10) чисел, тогда вероятность того, что наугад взятое из них делится на (3) или на (13) равна [dfrac{5}{10} = 0,5.]
Ответ: 0,5
Найдите сумму корней уравнения
[begin{aligned}
pi x — dfrac{1}{pi} x^3 — 2pi + dfrac{2}{pi} x^2 = 0,
end{aligned}]
если известно, что все они различны.
Перепишем уравнение по убыванию степеней переменной:
[-dfrac1{pi}x^3+dfrac2{pi}x^2+pi x-2pi=0.]
По теореме Виета для уравнения третьей степени (ax^3 + bx^2 + cx + d
= 0) сумма его корней (при учёте того, что все они различны) равна (-dfrac{b}{a}), следовательно, сумма корней рассматриваемого уравнения равна [-dfrac{frac{2}{pi}}{-frac{1}{pi}} = 2.]
Ответ: 2
В параллелограмме (ABCD): (AB = 6), (BC = 5), (sin{angle A} + sin{angle B} + sin{angle C} + sin{angle D} = 3,24). Найдите площадь параллелограмма (ABCD).
В параллелограмме противоположные углы равны, а односторонние углы в сумме составляют (180^{circ}).
Так как (sin{(pi — alpha)} = sin{alpha}), то (sin{angle A} + sin{angle B} + sin{angle C} + sin{angle D} = 4 sin{angle A}), откуда находим (sin{angle A} = 0,81).
Площадь параллелограмма равна произведению двух его непараллельных сторон на синус угла между ними, тогда [S_{ABCD} = 6cdot 5cdot 0,81 = 24,3.]
Ответ: 24,3
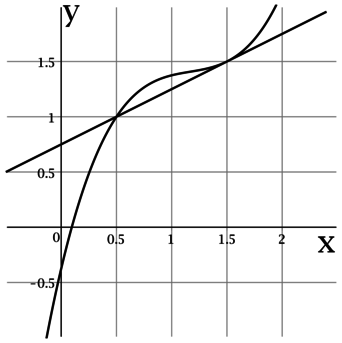
На рисунке изображены график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_0). Найдите значение производной функции (f'(x)) в точке (x_0).
Производная функции (f(x)) в точке (x_0) равна тангенсу угла наклона касательной к графику (f(x)) в точке ((x_0; f(x_0))).
По рисунку видно, что касательная проходит через точки ((0,5; 1)) и ((1,5; 1,5)), тогда тангенс угла наклона касательной составляет (0,5 : 1 = 0,5), следовательно, (f'(x_0) = 0,5).
Ответ: 0,5
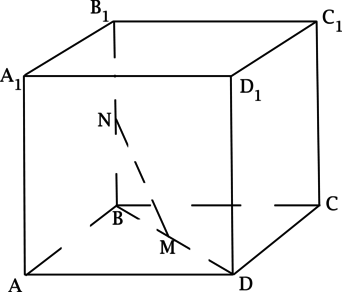
(ABCDA_1B_1C_1D_1) – куб. Точка (N) – середина ребра (BB_1), а точка (M) – середина отрезка (BD). Найдите (mathrm{tg}^2, alpha), где (alpha) – угол между прямой, содержащей (MN) и плоскостью ((A_1B_1C_1D_1)). Ответ дайте в градусах.
(NM) – средняя линия в треугольнике (DBB_1), тогда (NM parallel B_1D) и (alpha) равен углу между (B_1D) и плоскостью ((A_1B_1C_1D_1)).
Так как (DD_1) – перпендикуляр к плоскости (A_1B_1C_1D_1), то (B_1D_1) проекция (B_1D) на плоскость ((A_1B_1C_1D_1)) и угол между (B_1D) и плоскостью ((A_1B_1C_1D_1)) есть угол между (B_1D) и (B_1D_1).
Пусть ребро куба (x), тогда по теореме Пифагора [B_1D_1^2 = x^2 + x^2qquadRightarrowqquad B_1D_1 = xsqrt{2},] аналогично по теореме Пифагора [B_1D = xsqrt{3}.] В треугольнике (B_1D_1D) тангенс угла между (B_1D) и (B_1D_1) равен (dfrac{DD_1}{B_1D_1} = dfrac{1}{sqrt{2}}), откуда (mathrm{tg}^2, alpha = dfrac{1}{2}).
Ответ: 0,5
Найдите значение выражения ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right)).
По определению логарифма (log_{17}289) – это степень, в которую надо возвести 17, чтобы получить 289. Таким образом, (log_{17}289 = 2). Аналогично можно сделать вывод, что [log_{500}dfrac{1}{500} = -1.] Итого: ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right) = -2).
Ответ: -2
Совершенный газ описывается законом Менделеева-Клапейрона: (pV = nu RT), где (p) – давление в паскалях, (V) – объем в (м^3), (nu) – количество вещества в молях, (T) – температура в кельвинах, (R) – универсальная газовая постоянная, равная (8,31, Дж/(Кcdot моль)). В какое минимальное число раз надо увеличить температуру совершенного газа, чтобы при неизменном давлении его объем вырос не менее, чем в (5) раз?
Обозначим начальные параметры с индексом (0). При увеличении объема не менее чем в (5) раз имеем: [nu R T geqslant 5pV_0 = 5nu R T_0,] откуда (T geqslant 5T_0), то есть чтобы чтобы при неизменном давлении газа его объем вырос не менее чем в (5) раз надо увеличить его температуру минимум в (5) раз.
Ответ: 5
На озере расположены пристани А и В. Расстояние между пристанями равно (90, км). Моторная лодка проплыла от А до В с постоянной скоростью, после чего сразу отправилась обратно со скоростью на (5, км/ч) больше прежней. На середине пути из В в А лодка замедлилась и поплыла со скоростью на (2,5, км/ч) меньшей, чем по дороге из А в В. В результате лодка затратила на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость лодки на пути из А в В. Ответ дайте в км/ч.
Пусть (v, км/ч) – скорость лодки по пути от А до В, тогда
(dfrac{90}{v}, ч) – время, затраченное лодкой на путь из А в В,
(dfrac{45}{v + 5}, ч) – время, затраченное лодкой на первую половину пути из В в А,
(dfrac{45}{v — 2,5}) – время, затраченное лодкой на вторую половину пути из В в А.
Так как в итоге лодка проплыла из В в А за такое же время, как и из А в В, то: [dfrac{90}{v} = dfrac{45}{v + 5} + dfrac{45}{v — 2,5},] откуда (v = 10, км/ч).
Ответ: 10
Найдите точку локального максимума функции
(y = (x + 1)cdot e^{-x + sqrt{2}} + e^{2}).
1) (y’ = e^{-x + sqrt{2}} — (x + 1)cdot e^{-x + sqrt{2}} = -xcdot e^{-x + sqrt{2}}).
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-xcdot e^{-x + sqrt{2}} = 0qquadLeftrightarrowqquad x = 0] (так как (e^{t} > 0) при любом (t)). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 0) – точка локального максимума функции (y).
Ответ: 0
a) Решите уравнение
[begin{aligned}
sin(2x) — 2sqrt{3}cos^2x-4sin x + 4sqrt{3}cos x = 0.
end{aligned}]
б) Найдите все его корни, принадлежащие промежутку (left[pi; dfrac{5pi}{2}right]).
а) ОДЗ: (x) – произвольное.
По формуле синуса двойного угла: [2sin xcdotcos x — 2sqrt{3}cos^2x-4sin x + 4sqrt{3}cos x = 0.] Сгруппируем первое и третье слагаемые, а также второе и четвертое:
[begin{aligned}
2sin x(cos x — 2) — 2sqrt{3}cos x(cos x — 2) = 0qquadLeftrightarrowqquad (cos x — 2)(sin x — sqrt{3}cos x) = 0.
end{aligned}]
Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл: [cos x = 2qquad text{или}qquad sin x — sqrt{3}cos x = 0.] Так как (-1 leqslantcos xleqslant 1), то (cos x = 2) не подходит.
[sin x — sqrt{3}cos x = 0.] Так как те (x), при которых (cos x = 0) не могут быть решениями, то на (cos x) можно разделить: [mathrm{tg}, x = sqrt{3}.]
Решения уравнения (mathrm{tg}, x = a) имеют вид (x = mathrm{arctg}, a + pi k), где (kinmathbb{Z}), следовательно,
решения уравнения (mathrm{tg}, x = sqrt{3}) имеют вид (x = dfrac{pi}{3} + pi k, kinmathbb{Z}).
б) [pi leqslant dfrac{pi}{3} + pi k leqslant dfrac{5pi}{2}qquadLeftrightarrowqquad dfrac{2}{3} leqslant k leqslant dfrac{13}{6},] но (kinmathbb{Z}), тогда подходят (x) при (k = 1) и (k = 2): (x = dfrac{4pi}{3}) и (x = dfrac{7pi}{3}).
Ответ:
а) (dfrac{pi}{3} + pi k, kinmathbb{Z}).
б) (dfrac{4pi}{3}), (dfrac{7pi}{3}).
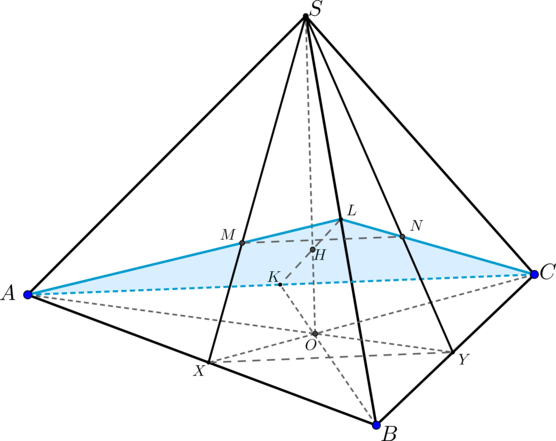
Дана правильная треугольная пирамида (SABC) с вершиной (S). Проведите плоскость через середину ребра (AC) и точки пересечения медиан граней (ASB) и (CSB). Найдите площадь сечения пирамиды этой плоскостью, если (AB=21, AS=12sqrt2).
1) Пусть(K) – середина (AC), (SX, AL) – медианы грани (ASB), (CL,
SY) – медианы грани (CSB), (ALcap SX=M, CLcap SY=N). (SO) – высота пирамиды.
Найдем сечение пирамиды плоскостью (MNK).
Т.к. пирамида правильная, то (triangle SXY) – равнобедренный, (SM=SN=dfrac{2}{3}SX Rightarrow MNparallel XY Rightarrow
MNparallel (ABC)). Таким образом, плоскость (MNK) содержит прямую (MN), параллельную (ABC), следовательно, плоскость (MNK) пересечет плоскость (ABC) по прямой, параллельной (MN) (если это не так, то линия пересечения этих плоскостей (lcap MN=E Rightarrow Ein
(ABC)) и (Ein MN Rightarrow MN) не может быть параллельна ((ABC))).
Прямая, проходящая через точку (K) и параллельная (MN) (или (XY)) – это (AC). Следовательно, сечением является равнобедренный треугольник (ALC).
2) Пусть (LKcap SO=H). Тогда по теореме о трех перпендикулярах (HKperp AC) как наклонная ((HOperp (ABC), OKperp AC) как проекция). Следовательно, и (LKperp AC).
Тогда (S_{ALC}=dfrac{1}{2}ACcdot LK).
Рассмотрим (triangle SKB: BK=ABcdot
dfrac{sqrt3}{2}=dfrac{21sqrt3}{2} Rightarrow cos
B=dfrac{7sqrt3}{12sqrt2}).
Тогда по теореме косинусов для (triangle KLB):
(KL^2=dfrac{729}{4} Rightarrow KL=dfrac{27}{2})
Значит, (S_{ALC}=dfrac{567}{4}).
Ответ:
(dfrac{567}{4}).
Решите неравенство
[begin{aligned}
125^x + 7cdot 25^x + 12cdot 5^x + log_5 15625leqslant 25^x + 5^x
end{aligned}]
ОДЗ: (x) – произвольный.
Так как (log_5 15625 = log_5 5^6 = 6), то исходное неравенство равносильно неравенству
[begin{aligned}
125^x + 6cdot 25^x + 11cdot 5^x + 6leqslant 0
end{aligned}]
Сделаем замену (5^x = t > 0):
[begin{aligned}
t^3 + 6t^2 + 11t + 6leqslant 0
end{aligned}]
Можно угадать корень левой части последнего неравенства: (t = -1). Знание корня многочлена позволяет поделить его столбиком на (t — t_0), где (t_0) – его корень, тогда [begin{array}{rr|l}
t^3+6t^2+11t+6&&negthickspaceunderline{qquad t+1 qquad}\
underline{t^3+ t^2} phantom{000000000}&&negthickspace t^2 + 5t + 6\[-3pt]
5t^2 + 11t,phantom{000}&&\
underline{5t^2 + 5t,}phantom{000}&&\[-3pt]
6t + 6 &&\
underline{6t + 6}&&\[-3pt]
0&&\
end{array}]
Таким образом, последнее неравенство равносильно
[begin{aligned}
(t + 1)(t^2 + 5t + 6)leqslant 0qquadLeftrightarrowqquad (t + 1)(t + 2)(t + 3)leqslant 0,
end{aligned}]
то есть оно не выполняется при (t > 0), следовательно, ответ: [xinvarnothing,.]
Ответ:
(varnothing)
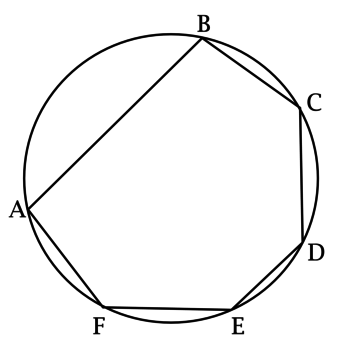
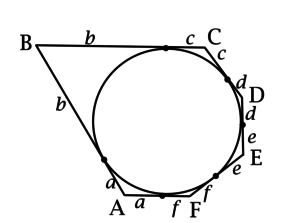
(ABCDEF) – выпуклый шестиугольник, про который известно, что (angle A > 120^circ), (angle Bleqslant 70^circ), (angle C geqslant 130^circ), (angle E geqslant 110^circ).
а) Докажите, что около хотя бы одного из четырёхугольников (ABCD), (ACDE) и (ACDF) нельзя описать окружность.
б) Найдите периметр (ABCDEF), если (AB + CD + EF = 11).
а) Если около четырёхугольника (ABCD) можно описать окружность, то она будет описанной и для треугольника (ACD).
Если около четырёхугольника (ACDE) можно описать окружность, то она будет описанной и для треугольника (ACD).
Если около четырёхугольника (ACDF) можно описать окружность, то она будет описанной и для треугольника (ACD).
Так как около треугольника можно описать ровно одну окружность, то описанные около четырёхугольников (ABCD), (ACDE) и (ACDF) окружности должны совпасть, следовательно, тогда шестиугольник (ABCDEF) также будет вписанным.
Таким образом, достаточно показать, что около (ABCDEF) нельзя описать окружность.
Пусть шестиугольник (ABCDEF) – вписанный, тогда
[begin{aligned}
&angle A + angle C + angle E = 0,5cdotsmile BCDEF + 0,5cdotsmile BAFED + 0,5cdotsmile FABCD =\
&= 0,5(360^circ — smile BAF) + 0,5(360^circ — smile BCD) + 0,5(360^circ — smile FED) =\
&= 540^circ — 0,5(smile BAF + smile BCD + smile FED) = 360^circ,
end{aligned}]
но (angle A + angle C + angle E > 360^circ), следовательно, около (ABCDEF) нельзя описать окружность, откуда следует, что около хотя бы одного из четырёхугольников (ABCD), (ACDE) и (ACDF) нельзя описать окружность.
б)
Пользуясь тем, что отрезки касательных к окружности, проведённых из одной точки, равны, обозначим длины отрезков касательных, проведённых из точки (A), через (a), длины отрезков касательных, проведённых из точки (B), через (b) и т.д.
[11 = AB + CD + EF = a + b + c + d + e + f = 0,5cdot P_{ABCDEF},] откуда (P_{ABCDEF} = 22).
Ответ:
б) (22).
Елена решила сделать вклад в банк в размере (351,000) рублей под целое число (y %) годовых. Какую наибольшую годовую ставку ей может предложить банк, чтобы к началу третьего года сумма на счете Елены не превысила (1,092,000) рублей? Известно, что Елена планирует в конце первого и второго годов дополнительно после начисления процентов вносить на счет треть от суммы, имеющейся на счете на начало текущего года.
Составим таблицу, обозначив за (t=dfrac{100+y}{100}, A=351,000): [begin{array}{|l|c|c|c|}
hline text{Год} & text{Сумма на счете} & text{Сумма на счете} & text{Сумма на счете}\
& text{до начисления }% & text{после начисления }% & text{после дополнительного взноса} \
hline &&&\
1 & A & t A & t A+dfrac{1}{3}A\
&&&\
hline &&&\
2 & tA+dfrac{1}{3}A & tleft(tA+dfrac{1}{3}Aright) & tleft(tA+dfrac{1}{3}Aright)+dfrac{1}{3}left(tA+dfrac{1}{3}Aright) \
&&&\
hline
end{array}]
Таким образом, на начало третьего года на счете у Елены будет та же сумма, которая была на счете на конец второго года после начисления процентов и после внесения второго дополнительного взноса, т.е.
(tleft(tA+dfrac{1}{3}Aright)+dfrac{1}{3}left(tA+dfrac{1}{3}Aright)).
Необходимо, чтобы (t(tA+dfrac{1}{3}A)+dfrac{1}{3}(tA+dfrac{1}{3}A) leqslant 1,092,000)
Заметим, что (1,092,000=dfrac{28cdot 351,000}{9}=dfrac{28}{9}A
Rightarrow) неравенство примет вид:
(3t^2+2t-9 leqslant 0 Rightarrow t leqslant
dfrac{2sqrt7-1}{3}), т.к. (t>0).
Значит, ( y leqslant dfrac{200}{3}(sqrt7-2))
Оценим (dfrac{200}{3}(sqrt7-2)):
(2645<sqrt{7000000}<2646 Rightarrow\
2645<1000sqrt7<2646 Rightarrow\
0,645<sqrt7-2<0,646 Rightarrow\
\
43<dfrac{200}{3}(sqrt7-2)<dfrac{129,2}{3})
Таким образом, т.к. (dfrac{129,2}{3}=43dfrac{1}{15}), наибольшее целое (y=43 %).
Ответ:
(43%).
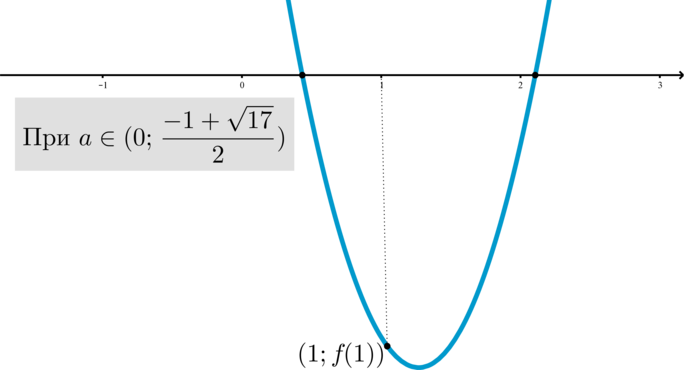
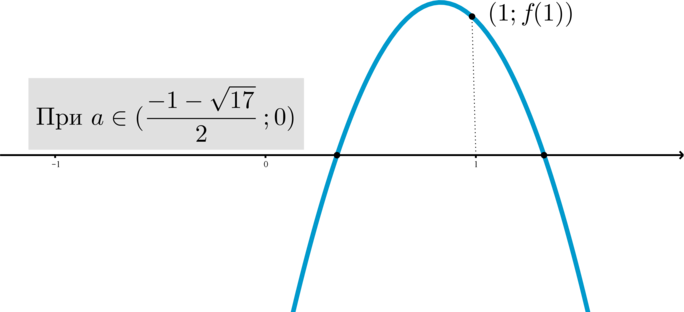
Найдите все значения параметра (a), при каждом из которых ровно один корень уравнения [ax^2+4x+a+1=0] больше (1).
Рассмотрим два случая:
1) (a=0). Тогда уравнение становится линейным и (x=-dfrac{1}{4}). Это значения параметра нам не подходит.
2) (ane 0). Тогда уравнение является квадратным.Его дискриминант (D=4(4-a^2-a)).
а) Если (D=0 Rightarrow a=dfrac{-1pm sqrt{17}}{2} Rightarrow) уравнение (ax^2+4x+a+1=0) имеет один корень (x=-dfrac{2}{a}).
При (a=dfrac{-1+ sqrt{17}}{2}) это корень (x=-dfrac{4}{sqrt{17}-1}<0<1), следовательно, это значение параметра не подходит.
При (a=dfrac{-1- sqrt{17}}{2}) это корень (x=dfrac{4}{sqrt{17}+1}=dfrac{4(sqrt{17}-1)}{sqrt{17}^2-1^2}=dfrac{sqrt{17}-1}{4}<1),
следовательно, это значение параметра также не подходит.
б) Если (D>0 Rightarrow ain left(dfrac{-1- sqrt{17}}{2}
;dfrac{-1+ sqrt{17}}{2} right) Rightarrow) уравнение (ax^2+4x+a+1=0) имеет два корня.
Графиком функции (f(x)=ax^2+4x+a+1) при каждом фиксированном (a) является парабола,
причем при (ain left(0;dfrac{-1+ sqrt{17}}{2}right)) ветви направлены вверх, при (ain left(dfrac{-1- sqrt{17}}{2};0right)) ветви направлены вниз:
Для того, чтобы уравнение имело ровно один корень больше (1), нужно:
[left[
begin{gathered}
begin{aligned}
&begin{cases}
0<a<dfrac{-1+ sqrt{17}}{2}\
f(1)<0
end{cases}\[5pt]
&begin{cases}
dfrac{-1- sqrt{17}}{2}<a<0\
f(1)>0
end{cases}
end{aligned}
end{gathered}
right. quad Longrightarrow quad -dfrac{5}{2}<a<0]
Ответ:
(ain left(-dfrac{5}{2};0right)).
Докажите, что среди любых (n+1) натуральных чисел найдутся два, разность которых делится на (n).
Всего при делении на (n) существует (n) различных остатков, а так как чисел (n+1), то по принципу Дирихле найдутся (2) числа с одинаковыми остатками, следовательно, их разность будет делиться на (n).
Ответ:
Доказательство

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Тренировочный вариант №1 базового ЕГЭ