На уроке рассматривается решение 13 задания ЕГЭ по информатике
Содержание:
- Объяснение заданий 13 ЕГЭ по информатике
- Графы. Поиск количества путей
- Решение заданий 13 ЕГЭ по информатике
13-е задание: «Информационные модели»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
До ЕГЭ 2021 года — это было задание № 15 и № _ ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование указаний в условии задания, что путь должен включать (или не включать) заданные промежуточные вершины»
ФГБНУ «Федеральный институт педагогических измерений»
Графы. Поиск количества путей
- Если в город
Rиз городаAможно добраться только из городовX,YиZ, то количество различных путей из городаAв городRравно сумме числа различных путей проезда изAвX, изAвYи изAвZ, то есть: - где NR — это количество путей из вершины
Aв вершинуR - Число путей не бесконечно, исключением является только граф, в котором есть циклы – замкнутые пути.
- Часто задачи с графами целесообразней решать с конца.
NR = NX + NY + NZ
Решение заданий 13 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
13_1:
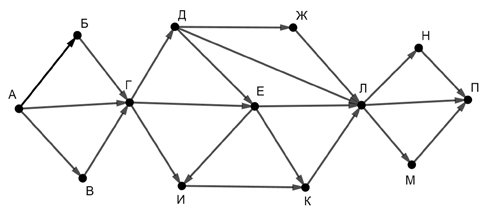
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят «мимо» вершины Г или до которых от пункта А можно дойти, минуя вершину Г:
- Вершина В удалена, т.к. возможны только следующие траектории движения через этот пункт (которые НЕ проходят через пункт Г):
- 1. А — Б — В — И — М
- 2. А — Б — В — Е — И — М
- 3. А — Б — В — Е — М
- 4. А — Б — В — Е — К — М
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = Е
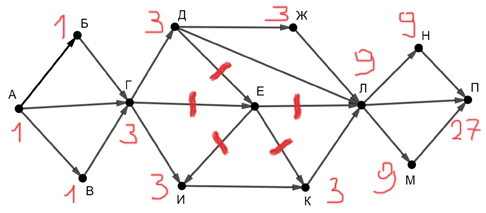
Е = Г + Ж
Г = Б + А + Д = 1 + 1 + 1 = 3
Ж = Г = 3
К = Е + Ж
Теперь возвращаемся, подставляя найденные значения: ↑
Е = Г + Ж = 3 + 3 = 6
Ж = Г = 3
И = Е = 6 (получили из последующих шагов)
К = Е + Ж = 6 + 3 = 9
М = И + Е + К = 6 + 6 + 9 = 21
Результат: 21
Видео ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_2:
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей, ведущих из города А в город М и не проходящих через город Г?

✍ Решение:
- Удалим ребра, которые проходят через вершину Г:
- Теперь посчитаем результаты по оставшимся вершинам:
М = И + Е + К
-----
И = В + Е
В = 1
Е = В + Ж
Ж = 1
Теперь возвращаемся, подставляя найденные значения: ↑
Е = В + Ж = 1 + 1 = 2
И = В + Е = 1 + 2 = 3
К = Е = 2
М = И + Е + К = 3 + 2 + 2 = 7
Результат: 7
Подробное решение данного 13 задания в видеоуроке:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13 задание. Демоверсия ЕГЭ 2018 информатика:
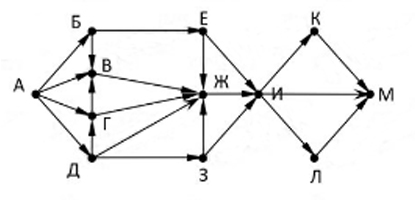
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
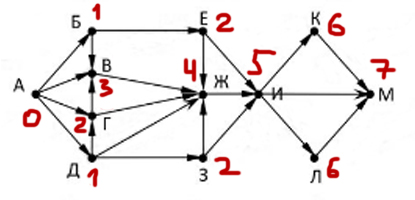
Сколько существует различных путей из города А в город М, проходящих через город Ж?

✍ Решение:
Результат: 20
Подробное решение 13 задания демоверсии ЕГЭ 2018 года смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
13_4:
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Какова длина самого длинного пути из города А в город М?
Длиной пути считать количество дорог, составляющих этот путь.

✍ Решение:
Моделирование и компьютерный эксперимент
Общая структура деятельности по созданию компьютерных моделей
Объект (лат. objectum — предмет) — это некоторая часть окружающего мира, рассматриваемая как единое целое. Все, что человек изучает, использует, производит, является объектом. Каждый объект имеет имя, что позволяет отличить один объект от другого (например, стол, атом, город Москва, ураган Катрин и т. п.). Конкретизировать объект можно с помощью параметров. Параметры — это признаки, которые характеризуют какое-либо свойство объекта. Они могут быть количественные (рост, вес, возраст, размер и т. п.) и качественные (форма, материал, цвет, запах, вкус и т. п.). Очень часто можно наблюдать смену состояний объекта в течение времени и, как результат, изменение параметров объекта. Говорят, что происходит некоторый процесс. Переход объекта из одного состояния в другое происходит при воздействии на него других объектов.
Модель (лат. modulus — мера; франц. modele — образец) — искусственно созданный объект в виде схем, чертежей, логико-математических знаковых формул, компьютерной программы, физической конструкции, который, будучи аналогичен (подобен, сходен) исследуемому объекту (явлению, процессу, устройству, сооружению, механизму, конструкции), отображает и воспроизводит в более простом, уменьшенном виде структуру, свойства, взаимосвязи и отношения между элементами исследуемого объекта, непосредственное изучение которого связано с какими-либо трудностями, большими затратами средств и энергии или просто недоступно, и тем самым облегчает процесс изучения информации об интересующем нас предмете.
Исследуемый объект по отношению к модели является оригиналом (образцом, прототипом). Модели могут создаваться как из однородного с оригиналом материала (например, макет деревянного сооружения можно сделать тоже из дерева), так и из материала, совершенно отличного от материала оригинала (например, бумажная модель самолета). Кроме того, модели могут быть нематериальными, или абстрактными (например, математическая модель самолета, компьютерная модель электрической сети).
Моделирование — это исследование каких-либо объектов (конкретных или абстрактных) на моделях. Объектом моделирования может быть объект, явление или процесс.
При создании модели стараются отразить наиболее существенные свойства объекта, а несущественные свойства отбрасываются. Например, на глобус наносятся океаны и моря, материки и крупные острова, а маленькие озера и островки на него не попадают: в масштабе глобуса они будут просто не видны.
Человек постоянно занимается моделированием, поскольку модели, упрощая объекты и явления, помогают человеку понять реальный мир. Более того, любая наука начинается с разработки простых и адекватных моделей.
Кроме материальных (предметных) моделей (игрушки, глобуса, макета дома…), существуют нематериальные — абстрактные модели: описания, формулы, изображения, схемы, чертежи, графики и т. д. С помощью математических формул описываются, например, арифметические операции, соотношения геометрии, законы движения и взаимодействия тел (S = Vt, F = mа) и многое другое. Химические формулы помогают представить молекулярный состав химических веществ и реакции, в которые они вступают. Пользуясь таблицами, графиками, диаграммами можно отображать различные закономерности и зависимости реального мира.
Все абстрактные модели не имеют физического воплощения. Абстрактные модели, которые можно представить с помощью набора знаков (геометрических фигур, символов, фрагментов текста), — это знаковые модели. Любую знаковую модель можно изобразить на бумаге. Чтобы построить знаковую модель, нужно представлять значение знаков и знать правила их преобразования. Абстрактная модель, прежде чем оформиться в виде знаковой модели, сначала рождается в голове человека. Она может передаваться человека к человеку в устной форме. В таких случаях модель еще не является знаковым образом, поскольку не имеет вида чертежа, формулы, текста. Модель в голове человека существует в форме мысленных представлений (мысленная модель). Модели, полученные в результате умозаключений, называются вербальными (лат. verbalis — устный). Вербальными называются также модели, изложенные в разговорной форме. Таким образом, все абстрактные модели можно разделить на знаковые и вербальные.
Представленная классификация моделей самая простая. Она основана на делении моделей по способу представления. Возможны и другие классификации, — например, по предметному признаку: физические, химические модели, модели строительных конструкций, различных механизмов и т. д.
Если модель формулируется таким образом, что ее можно обработать на компьютере, то она называется компьютерной. Компьютерная модель — это модель, реализуемая с помощью программных средств.
Компьютерные модели обычно различают по программному обеспечению, которое применяется при создании и работе с моделью. Для обработки компьютерных моделей используются существующие программные приложения (математические пакеты, электронные таблицы, графические редакторы и т. д.) либо разрабатываются оригинальные программы с помощью языков программирования (Ваsic, Раsсаl, Dеlpi, С++ и др.).
Моделирование с использованием компьютера предоставляет неизмеримо больше возможностей, чем простое моделирование с помощью реальных предметов или материалов. Например, применение компьютера для раскроя (листового металла, ткани и пр.) позволяет снизить до минимума потери материала. Поиск оптимального решения этой задачи с помощью шаблонов потребует значительно больше времени и средств.
Этапы создания модели
Моделирование — творческий процесс, и разложить его на какие-либо этапы и шаги очень сложно. Многие модели и теории рождаются как соединение опыта и интуиции ученого или специалиста. Однако решение большинства конкретных задач все же можно представить поэтапно.
Моделирование, в том числе компьютерное, начинается с постановки задачи. На этом этапе формулируется задача и требования, которые предъявляются к решению. Постановка задачи заключается, прежде всего, в ее описании. Задача может быть описана на обыденном языке — например, в форме вопроса «что будет, если… ?» или «как сделать, чтобы… ?». Математическую задачу описывают с помощью формул и знаков, а инженерная, экономическая задача может быть описана с помощью различных схем, графиков.
При постановке задачи нужно отразить (или хотя бы понять) цель или мотив создания модели. Одни модели создаются, чтобы разобраться в устройстве или составе того или иного объекта. Другие модели направлены на изучение возможностей управления объектом. Третьи модели ставят целью предсказать поведение объекта (задачи прогнозирования). На этапе постановки задачи полезным оказывается предварительный анализ объекта. Разложение объекта на составляющие, выяснение связей между ними позволяет уточнить постановку задачи.
За постановкой задачи следует этап разработки модели. На этом этапе необходимо выделить существенные факторы, т. е. выяснить основные свойства описываемого объекта, правильно определить связи между ними и с другими объектами окружающего мира. Анализ информации, по возможности, должен быть разносторонним и полным. Те факторы, которые оказались несущественными, могут быть отброшены.
После того как сформулированы основные свойства разрабатываемой модели, определены исходные данные и желаемый результат, наступает очень важный момент — составление алгоритма решения задачи.
При разработке компьютерной модели весьма существенным будет выбор программного обеспечения, с помощью которого выполняется моделирование. Программное обеспечение должно позволять эффективно решать задачи, подобные той, которая рассматривается. Например, для создания рисунка на компьютере нужно выбрать тот или иной графический редактор (какой именно — зависит от требуемого формата файла и приемов, которые необходимо применять при рисовании). Чтобы решить систему уравнений, нужно воспользоваться языками программирования Basic, Pascal или каким-либо другим или же использовать для решения математические пакеты. Программная среда должна соответствовать поставленной задаче — только в этом случае задача может быть успешно решена. Выбор программного обеспечения и составление алгоритма — это взаимосвязанные действия. Возможно, что для решения поставленной задачи придется разработать собственную компьютерную программу.
Когда модель разработана, можно приступать к наиболее интересному этапу — компьютерным экспериментам. В ходе этих экспериментов проверяется работа модели, а также выполняются необходимые расчеты или преобразования, ради которых и создавалась модель.
Проверка модели осуществляется обычно с помощью ее тестирования. При тестировании проверяется разработанный алгоритм функционирования модели. В качестве теста задаются исходные данные, для которых заранее известен ответ. Если ответ, полученный при тестировании, совпадает с известным ответом, а тест составлен правильно, то считается, что модель работает корректно. В противном случае нужно искать и устранять причины расхождений. Все эти действия называются отладкой модели.
После выполнения тестирования и отладки можно приступать непосредственно к моделированию. Технология моделирования может заключаться в расчете модели при различных наборах входных данных, различных параметрах.
Завершается компьютерное моделирование анализом результатов. Материалом для анализа являются результаты компьютерных экспериментов. Поэтому эксперименты должны быть проведены таким образом, чтобы получить достоверный результат. Анализ результатов может привести к необходимости уточнения модели, т. е. к повторному выполнению второго этапа и всех последующих этапов.
Этапы компьютерного моделирования можно представить в виде таблицы.
| 1. ПОСТАНОВКА ЗАДАЧИ | Описание |
| Мотивация | |
| Предварительный анализ |
| 2. РАЗРАБОТКА МОДЕЛИ | Выделение существенных факторов |
| Составление алгоритма | |
| Выбор программного обеспечения | |
| Программирование |
| 3. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ | Тестирование модели |
| Отладка модели | |
| Расчет модели при различных входных данных |
Представление и считывание данных в разных типах информационных моделей
(схемы, карты, таблицы, графики и формулы)
Многообразие объектов предполагает использование огромного количества инструментов для реализации и описания этих моделей. Для исследования большинства объектов не обязательно создавать материальные модели. Если ясно представлять цель исследования, то часто достаточно иметь нужную информацию и представить ее в оптимальной форме. В этом случае речь идет о создании информационной модели. Информационные модели — это абстрактные модели, поскольку, как известно, информация — это нематериальная категория.
Информационная модель — это целенаправленно отобранная информация об объекте, представленная в некоторой форме.
Простейшими примерами информационных моделей являются различные загадки, в которых описываются свойства, по которым нужно угадать название объекта («Летом серый, зимой белый»; «Зимой и летом одним цветом»). К информационным моделям можно отнести тексты справочных изданий, энциклопедий.
Формы представления информационных моделей могут быть различными. Наиболее известны следующие формы:
- в виде сигналов;
- устная, словесная;
- символьная (числа, текст, символы);
- табличная;
- схемы, карты;
- графики.
Один и тот же объект, в зависимости от поставленной цели, можно представить несколькими информационными моделями, отличающимися набором параметров и способом их представления. Рассмотрим примеры анализа информации для модели, представленной в табличной форме.
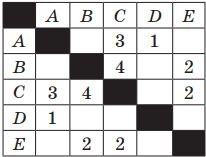
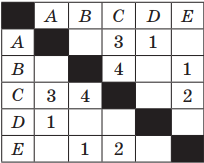
Пример 1. Таблица стоимости перевозок между станциями A, B, C, D, E построена следующим образом: числа, стоящие в ячейках на пересечении строк и столбцов, означают стоимость проезда между соответствующими соседними станциями. Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями. Если на пересечении строки и столбца пусто, то станции не являются соседними. Выбрать таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6».
Решение. Прежде всего, нужно отметить, что данные в таблицах симметричны относительно главной диагонали, т. е. проезд из А в В стоит столько же, сколько и из В в А.
Рассмотрим первую таблицу. Выберем все возможные варианты проезда из А в В и соответственно подсчитаем стоимости: AC(3) + CB(4); AC(3) + CE(2) + EB(2)
Примечание. В скобках указана стоимость проезда.
Стоимость, как первого, так и второго варианта маршрута равна 7.
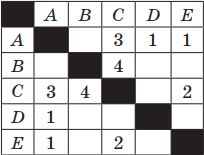
Аналогично поступим для второй таблицы: AC(3) + CB(4); AE(1) + EC(2) + CB(4).
Как и в случае с предыдущей таблицей, стоимость как первого, так и второго варианта маршрута равна 7.
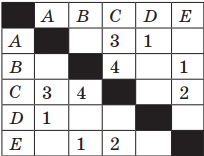
Выписываем все варианты для третьей таблицы: AC(3) + CB(4); AC(3) + CE(2) + EB(1).
Стоимость последнего варианта маршрута равна 6.
Ответ: таблица номер 3 содержит маршрут из А в В, стоимость которого не превышает 6.
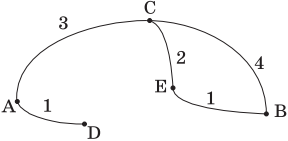
Пример 2. Для заданной информационной модели, записанной в форме таблицы, построить модель в виде схемы. В ячейках на пересечении строк и столбцов таблицы указана стоимость проезда между соседними станциями. Пустые ячейки означают, что станции не являются соседними.
Решение. Отметим точку A, она должна быть соединена с C и D. Отмечаем точки C и D и соединяем их с точкой А дугами; над каждой дугой указываем стоимость проезда. Точка С должна быть соединена, кроме А, с точками В и Е. Точка D является соседней только с А. Точка В должна быть соединена, кроме С, с точкой Е. В результате можно получить следующую схему:
Математические модели (графики, исследование функций)
Знаковые модели принято делить на математические и информационные.
Математическая модель — это знаковая модель, сформулированная на языке математики и логики. Это система математических соотношений — формул, уравнений, неравенств, графиков и т. д., отображающих связи различных параметров объекта, системы объектов, процесса или явления.
Над элементами математической модели можно выполнять определенные математические преобразования. Например, в модели нахождения наименьшего числа выполняются операции сравнения, а в модели вычисления корня уравнения — различные арифметические операции. С помощью математических моделей описываются решения различных инженерных задач, многие физические процессы (движение планет, автомобиля и т. п.); технологические процессы (сварка, плавление металла и т. п.). Графики, таблицы, диаграммы позволяют отображать различные закономерности и зависимости реального мира. Например, модель развития эпидемии можно описать как с помощью формул, так и с помощью графика. Полет снаряда, выпущенного из орудия, можно математически смоделировать с помощью известных формул движения, затем построить график движения снаряда — баллистическую кривую, которая отображает реальный полет снаряда. Математически изменяя параметры снаряда или характеристики движения, можно изучать, например, вопросы увеличения дальности или высоты полета и т. п.
Как известно, не все математические задачи можно решить аналитически, т. е. получить решение в виде формул. Значительно больше задач, которые решаются приближенно, с заданной точностью, т. е. с использованием численных методов. Реализация приближенных расчетов на компьютерах позволяет повысить точность и скорость расчетов.
В настоящее время расчеты для большинства математических моделей проводят на компьютерах, используя специальные прикладные программные комплексы, которые позволяют:
- в несколько раз сократить время проведения исследований;
- уменьшить количество участников эксперимента;
- повысить точность и достоверность эксперимента, а следовательно, увеличить контроль;
- за счет средств графической визуализации, например анимации, получить реальную «картинку»;
- повысить качество и информативность эксперимента за счет увеличения числа контролируемых параметров и более точной обработки данных. На экране компьютера возможно, например, формирование целой системы приборов, которые будут отслеживать изменение параметров объекта.
Построение и использование информационных моделей реальных процессов (физических, химических, биологических, экономических)
Моделирование занимает центральное место в исследовании объекта. Компьютеры дают широкие возможности для постановки компьютерных экспериментов. Компьютерное моделирование позволяет воссоздать явления, которые в реальных условиях воспроизвести невозможно. Это, например, движение материков, эффекты землетрясений и наводнений, рождение сверхновых звезд, изменение направлений морских подводных течений и т. д. При изучении этих явлений на помощь приходят компьютеры и компьютерные программы, причем последние составляются квалифицированными программистами совместно с различными специалистами: физиками, географами, биологами, медиками и др.
Компьютерное моделирование используется также при описании и расчете экспериментов, которые выполнять в реальности не следует. Это, например, модели ядерного взрыва, пожара на предприятии, столкновения на железной дороге, военных действий и т. д. С помощью компьютерных моделей можно с достаточной точностью описать детали этих катастроф и спрогнозировать последствия.
Построение моделей позволяет осознанно принимать решения по усовершенствованию имеющихся объектов и созданию новых, изменению процессов управления ими. И, как следствие, наблюдается изменение окружающего нас мира.
Примеры информационных компьютерных моделей для различных отраслей знаний приведены в таблице.
| Физика | Моделирование движения на плоскости и в пространстве, моделирование различного вида колебаний, процесса расщепления атомного ядра; моделирование работы двигателя, турбины и т. п.; моделирование магнитных, электрических явлений и т. д. |
| Химия | Моделирование строения молекул; моделирование процесса взаимодействия веществ; моделирование отдельных этапов химического производства; моделирование процессов нагревания или остывания различных тел и т. п. |
| Биология | Моделирование развития биологического объекта в зависимости от условий (например, климатических); моделирование побочных действий лекарственных препаратов; моделирование процесса распространения эпидемий; моделирование при решении задач генетики; различные модели изменения численности популяций и т. д. |
| Экономика | Моделирование работы предприятия, банка, отрасли экономики или экономики в целом; моделирование процесса миграции трудовых ресурсов, кризисных явлений в экономике и т. д. |
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
Источник: Демонстрационная версия ЕГЭ—2016 по информатике.
2
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта Г в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.
3
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 45 | 10 | |||||
| П2 | 45 | 40 | 55 | ||||
| П3 | 15 | 60 | |||||
| П4 | 10 | 40 | 20 | 35 | |||
| П5 | 15 | 55 | |||||
| П6 | 55 | 60 | 20 | 55 | 45 | ||
| П7 | 35 | 45 |
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
4
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 50 | ||||
| П3 | 10 | 65 | 8 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 50 | 65 | 22 | 50 | 40 | ||
| П7 | 8 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
5
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | |
| П1 | 40 | 15 | |||||
| П2 | 40 | 35 | 48 | ||||
| П3 | 10 | 65 | 11 | ||||
| П4 | 15 | 35 | 22 | 33 | |||
| П5 | 10 | 50 | |||||
| П6 | 48 | 65 | 22 | 50 | 40 | ||
| П7 | 11 | 33 | 40 |
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину дороги из пункта Б в пункт Д. В ответе запишите целое число.
Пройти тестирование по этим заданиям
Сегодня разберём одно из самых лёгких заданий из ЕГЭ по информатике — задание 13. Вы с похожим типом задач могли встретится на экзамене в 9 классе по информатике.
Приступим к практическим тренировкам решения 13 задания ЕГЭ по информатике 2022.
Задача (Стандартная)
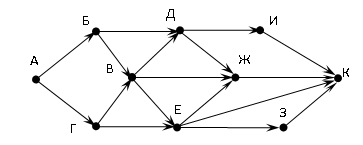
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение:
Нужно подсчитать количество путей от начальной точки А до конечной точки К.
Будем использовать специальную технику для решения 13 задания из ЕГЭ по информатике 2022
Техника:
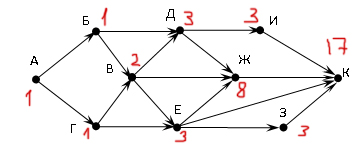
Ставим 1 (единицу) возле начальной точки A. Далее, просматриваем ближайшие точки и анализируем, сколько входит стрелок в эти точки. В точку Б «перетекает» 1 из точки А. В точку Г тоже входит одна стрелка из точки А. Значит, тоже в эту точку «перетекает» 1 из А.
В точку В входят две стрелки. Значит, в точку В «втекает» сумма двух точек, из которых выходят эти стрелки! Получается 1 + 1 = 2.
И продолжаем в том же духе.
Число в конечной точке показывает правильный ответ!
Ответ: 17
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих
через город Ж?
Решение:
Отличие этой задачи от предыдущей заключается в том, что пути, которые будем засчитывать, обязательно должны проходить через пункт Ж. Чтобы выполнить это условие, зачеркнём стрелку из пункта Е в пункт И. Так же зачеркнём стрелку из пункта З в пункт И. По этим стрелкам ходить нельзя, т.к. если мы по ним пойдём, не будет пройден пункт Ж.
Основная техника же решения будет такой же, как и в прошлой задаче.
Ответ: 51
Продолжаем отработку 13 задания ЕГЭ по информатике 2022
Задача (Избегаемая вершина)
На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П
Сколько существует различных путей из пункта А в пункт П, не проходящих через пункт Е?
Решение:
Такая же задача, как и предыдущие две, только здесь, при построении путей, мы не должны проходить через точку E.
Зачеркнём те дороги, которые поведут наши пути через пункт E.
Далее, применим старый метод, который использовали ранее.
Получается ответ 27.
Ответ: 27
Рассмотрим задачу, которая была на реальном экзамене по информатике в этом году.
Задача (ЕГЭ по информатике, 2020, Москва)
На рисунке — схема дорог, связывающих города А, Б, В, Г, Е, Ж, К, Л, М. По каждой дороге можно двигаться в одном направлении, указанном стрелкой. Какая наибольшая длина пути из А в М ?
Решение:
В этой задаче отличается вопрос от привычного нахождения количества путей. Здесь нужно найти наибольшую длину пути из начального пункта в конечный.
Возле начальной точки ставим число 0.
Смотрим сколько входит в узел стрелок. Выбираем стрелку, которая идёт из узла с наибольшим числом. При переходе по стрелочке добавляем 1.
Число, которое получится возле конечной точки и будет ответом. В этой задачке стрелок получилось 7, это и будет ответ.
Ответ: 7
Аннотация:
10 задач для решения задания на подсчёт количества путей в графе с ограничениями. Для удобства, кроме презентации, дан текстовый вариант заданий.
Для решения данного типа задания ученик должен уметь представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)

Автор: Никитенко Евгений Игоревич
Место работы: МБОУ СОШ №10 п. Гирей
Добавил: Игоревич
Уважаемые коллеги! Автор ждёт Ваши отзывы! Оставьте своё мнение о разработке!
Всего комментариев: 0
Хотите готовиться со мной к ЕГЭ?
Пишите: ydkras@mail.ru
Немного обо мне.
В задаче 13 ЕГЭ по информатике требуется подсчитать число путей из одного узла в другой.
Вот типичная задача (заимствована из демонстрационного варианта ФИПИ по информатике 2022 г.):
«На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.Сколько существует различных путей из города А в город М, проходящих через город В?»
Как решать подобные задачи программным путем? Прежде всего надо уметь представлять информацию о графе в форме, удобной для компьютерной обработки. В языке Питон есть очень удобный тип данных для нашей цели: словарь или ассоциативный массив. Это совокупность пар «ключ-значение».
Сначала подготовим исходные данные для заполнения словаря. Создадим текстовый файл, строки которого устроены следующим образом: первая буква строки — это один из городов, а следующие буквы — список городов, в которые можно попасть из данного города.
Для данного графа файл будет таким:
АБВГД
БВЕ
ВЖЗ
ГВЗ
ДГЗ
ЕЖИ
ЖИ
ЗЖИ
ИКЛ
КМ
ЛМ
М
При составлении этого файла необходимо быть очень аккуратным, ничего не упустить и ничего не перепутать и, конечно, не употреблять латинские буквы вместо русских. Последняя строка говорит, что город М существует, но из него нет дорог. (Если мы опустим эту строку, то это может привести к ошибке выполнения в некоторых задачах.)
Напишем фрагмент программы, которая введет этот файл и создаст словарь. описывающий граф:
a={}
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(a)
Вначале создается пустой словарь (словари заключаются в фигурные скобки). Затем файл с описанием графа читается построчно, и первый символ строки используется как ключ, а остальные — как значение, соответствующее данному ключу. Добавление в словарь — это просто присваивание элементу словаря с некоторым ключом значения. Если такой элемент уже существует, то значение будет перезаписано, в противном случае будет создан новый элемент. Метод strip удаляет пробелы и символы конца строки в начале строки и её конце — это нужно, чтобы убрать символы конца строки. Проверка len(s)>0 нужна, чтобы не обрабатывать пустые строки (если они окажутся в файле, это вызовет обибку выполнения). Первый символ каждой строки, т.е. s[0], используется как ключ в словаре, а хвост строки (все символы, кроме первого) — как значение, связанное с этим ключом.
Для контроля распечатаем словарь:
{‘А’: ‘БВГД’, ‘Б’: ‘ВЕ’, ‘В’: ‘ЖЗ’, ‘Г’: ‘ВЗ’, ‘Д’: ‘ГЗ’, ‘Е’: ‘ЖИ’, ‘Ж’: ‘И’, ‘З’: ‘ЖИ’, ‘И’: ‘КЛ’, ‘К’: ‘М’, ‘Л’: ‘М’, ‘М’: »}
Теперь всё готово для того, чтобы написать программу, которая ищет решение.
Простой случай — подсчёт количества путей
Сначала решим более протую задачу: подсчитаем число путей из А в М без каких-либо дополнительных ограничений.
Для этого напишем рекурсивную функцию ways:
def ways(start,end,karta):
if start==end: return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta)
return r
Функция подсчитывает число путей из города start в город end. Граф дорог задается в параметре karta, который должен быть словарем с описанной выше структурой.
Если значения start и end совпадают, то мы уже находимся в городе, в который должны попасть, и функция возвращает 1. Если же мы ещё не добрались до пункта назначения, то функция вызывает сама себя для каждого города, куда можно попасть из текущего города, и суммирует число путей из каждого города до конечного пункта.
Число путей из города А в город М — это результат вычисления функции ways(‘А’,’М’,a). Разумеется, буквы ‘А’ и ‘М’ в параметрах функции должны быть русскими, а не латинскими.
Приведём программу полностью:
def ways(start,end,karta):
if start==end: return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta)
return r
a={}
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(ways(‘А’,’М’,a))
Ограничения на маршрут: запрещенные города и города, обязательные для посещения
Выше был рассмотрен самый простой вариант задачи 13: подсчет числа путей без каких-либо ограничений. Но очень часто требуется считать лишь маршруты, которые проходят через какой-то город и/или не должны проходить через другой город.
Вначале решим задачу с городом, обязательным для посещения. Вспомним, что в задаче, приведенной в начале этой заметки, требуется, чтобы маршруты проходили через город В.
Подсчитаем число маршрутов от А до В, а затем от В до М. Любой маршрут первого этапа можно комбинировать с маршрутом второго этапа, поэтому общее число маршрутов — это произведение числа маршрутов первого этапа на число маршрутов второго этапа. Таким образом, задача решается заменой последней строки в приведенной выше программе на строку
print(ways(‘А’,’В’,a)*ways(‘В’,’М’,a))
Если какой-то город запрещен для посещения, то можно найти сперва общее число маршрутов от начального пункта до конечного, затем — число маршрутов, которые проходят через данный город. Число маршрутов, которые не проходят через этот город, равно разности общего числа маршрутов и числа маршрутов, проходящих через данный город.
Так, найти число маршрутов, которые не проходят через город В в приведенной выше задаче, можно с помощью выражения
print(ways(‘А’,’М’,a) — ways(‘А’,’В’,a)*ways(‘В’,’М’,a))
Другой способ рещения задачи с избегаемым городом — доработать нашу функцию ways, добавив в неё возможность исключать из рассмотрения определённые города.
Функция может выглядеть, например, так:
def ways(start,end,karta,zapret):
if start in zapret: return 0
if start==end: return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta,zapret)
return r
В нее добавлен новый параметр zapret — это символьная строка, содержащая города, маршруты через которые не учитываются. Если символ start содержится в этой строке, то функция возвращает 0. Строка zapret может состоять более чем из одного символа: в этом случае будут учтены только те маршруты, которые не проходят через любой из городов, перечисленных в этой строке.
Число маршрутов из А в М, не проходящих через город В, можно найти так:
def ways(start,end,karta,zapret):
if start in zapret: return 0
if start==end: return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta,zapret)
return r
a={}
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(ways(‘А’,’М’,a,’В’))
Можно также пользоваться этой функцией, чтобы найти число маршрутов, проходящих через город В. Для этого вычтем из общего числа маршрутов число таких, которые через этот город не проходят:
print(ways(‘А’,’М’,a,»)-ways(‘А’,’М’,a,’В’))
(Если параметр zapret — это пустая строка, то ограничений на подсчет маршрутов нет.)
Обязательный и избегаемый города
Если требуется, чтобы маршрут обязательно проходил через какой-либо город и не проходил через другой, то можно решить задачу, разбив путь на два этапа, как было описано ранее. На каждом этапе мы задаем запрещенный город в параметре zapret.
Можно также вычесть из числа маршрутов, которые не проходят через «запрещённый» город, число маршрутов, которые не проходят как через «запрещённый», так и через «обязательный» город.
Оба способа использованы в приводимой ниже программе. В ней вычисляется число маршрутов, которые проходят через город В, но не проходят через город Ж:
def ways(start,end,karta,zapret):
if start in zapret: return 0
if start==end: return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta,zapret)
return r
a={}
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(ways(‘А’,’В’,a,’Ж’)*ways(‘В’,’М’,a,’Ж’))
print(ways(‘А’,’М’,a,’Ж’)-ways(‘А’,’М’,a,’ВЖ’))
В некоторых задачах ограничение формулируется примерно так: «сколько существует маршрутов, проходящих либо через город В, либо через город З, либо через оба эти города?» Решение простое: следует из общего числа маршрутов вычесто число маршрутов, которые не проходят ни через В, ни через З:
print(ways(‘А’,’М’,a,»)-ways(‘А’,’М’,a,’ВЗ’))
Ещё один вариант ограничения — найти число маршрутов, которые проходят либо через пункт В, либо через пункт З, но не через оба этих пункта одновременно. Можно сложить число маршрутов, проходящих через В и не проходящих через З, с числом маршрутов, проходящих через З и не проходящих через В. Можно также найти число маршрутов, проходящих дибо через В, либо через З, либо через В и З, а потом вычесть из него число маршрутов, проходящих как через В, так и через З.
Ограничения на длину маршрута
В некоторых задачах требуется, чтобы определенным ограничениям удовлетворяла и длина маршрута (т.е. количество городов, через которые проходит маршрут).
Так, вопрос может быть таким: «Сколько существует маршрутов из А в М, проходящих ровно через семь городов, считая А и М?»
Доработаем нашу функцию ways с тем, чтобы она хранила текущий маршрут. Дополним её новым параметром trassa, в котором будем хранить маршрут. Когда мы достигнем города назначения, то проверим длину маршрута. Если она такая, какая требуется, то мы засчитываем рашение (возвращаем 1), в противном случае — нет (возвращаем 0).
Вот полная программа, решающая эту задачу:
def ways(start,end,karta,zapret,trassa):
trassa=trassa+start
if start in zapret: return 0
if start==end:
if len(trassa)==7: return 1
else: return 0
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta,zapret,trassa)
return r
a={}
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(ways(‘А’,’М’,a,»,»))
Так как нам требовалась только длина маршрута, то можно было бы обойтись не строкой, а целой переменной. Но строка, хранящая маршрут, дает большую гибкость: можно, анализировать эту строку и, например, принимать только те маршруты, которые проходят по участку В-Ж. (if ‘ВЖ’ in trassa).
Самый длинный или самый короткий путь
Иногда требуется выяснить, какова длина самого длинного или самого короткого пути. Задачу можно решить, фиксируя длину пути в момент достижения пункта назначения.
Решим задачу нахождения длины самого длинного и самого короткого пути:
def ways(start,end,karta,zapret,trassa):
global l,L
trassa=trassa+start
if start in zapret: return 0
if start==end:
if len(trassa)>L: L=len(trassa)
if len(trassa)<l: l=len(trassa)
return 1
r=0
for i in range(len(karta[start])): r += ways(karta[start][i],end,karta,zapret,trassa)
return r
a={}
l=1000
L=0
f=open(‘in.txt’)
for s in f:
s=s.strip()
if len(s)>0: a[s[0]]=s[1:]
print(ways(‘А’,’М’,a,»,»))
print(l,L)
Команда global l,L в функции ways дает доступ к внешним переменным l и L, в которых вычисляется минимальная и blog/loadingмаксимальная длина пути.
Нужно обращать внимание на формулировку вопроса в задачах о длине пути. Данная программа вычисляет число городов, через который проходит путь, включая начальный и конечный города. Если же требуется найти число дорог, по которым надо проехать, то оно, очевидно, на единицу меньше числа городов. Так, данная программа дает ответ, что самый короткий путь содержит 6 городов, а самый длинный — 9. Соответственно, минимальное число дорог — это 5, а максимальное — 8.
Стоит ли овчинка выделки?
У дочитавших до этого места может возникнуть вопрос: а нужно ли всё это? Ведь такие задачи можно решать на листке бумаги. Автор не берется ответить на этот вопрос. Попробуйте найти ответ сами. Решите одну и ту же задачу вручную и на компьютере — и определите, какой способ будет для вас проще и быстрее. Удачи вам!
(c) Ю.Д.Красильников, 2022 г
ЕГЭ информатика 13 задание разбор, теория, как решать.
Поиск путей в графе, (П) — 1 балл
Е13.26 ненулевой длины, которые начинаются и заканчиваются в городе Е
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе Е, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не …
Читать далее
Е13.25 из пункта А в пункт С, проходящих ровно через один из пунктов Ж и М
На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И , К , Л , М , Н , П, Р , С . П о к аждой д ороге м ожно п ередвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих …
Читать далее
Е13.24 из города А в город Л, проходящих через город 3
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л, проходящих через город 3? Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание …
Читать далее
Е13.23 Сколько существует различных путей из пункта А в пункт С, проходящих через пункты Е и М
На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И , К , Л , М , Н , П, Р , С . По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункты Е и М? …
Читать далее
Е13.22 Сколько существует различных путей из города Г в город Т, не проходящих через Л?
Сколько существует различных путей из города Г в город Т, не проходящих через Л? На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Ответ: Тренировочный вариант №1 от 13.09.2021 «ЕГЭ 100БАЛЛОВ»
Читать далее
Е13.21 Какова длина самого короткого пути из города А в город М
Какова длина самого короткого пути из города А в город М? Длиной пути считать количество дорог, составляющих этот путь. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Ответ: Источник: «03.05.2021 ЕГЭ 100БАЛЛОВ, …
Читать далее
Е13.20 Какова длина самого длинного пути из города А в город М
Какова длина самого длинного пути из города А в город М? Длиной пути считать количество дорог, составляющих этот путь. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Ответы: Источник: «19.04.2021 ЕГЭ 100БАЛЛОВ, …
Читать далее
Е13.19 Какова длина самого длинного пути из города А в город Л?
Какова длина самого длинного пути из города А в город Л? На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Какова длина самого длинного пути из города А в город Л? Длиной пути считать количество дорог, …
Читать далее
Е13.18 проходящих через пункт Г или через пункт Е, но не через оба этих пункта
проходящих через пункт Г или через пункт Е, но не через оба этих пункта. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город …
Читать далее
Е13.17 различных путей пункта А в пункт Н, проходящих через пункт Е
Сколько существует различных путей из пункта А в пункт Н, проходящих через пункт Е? На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Ответ: Тренировочный вариант от 09.11.2020 «Евгений Джобс»
Читать далее