Всего: 319 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
Добавить в вариант
В электронной таблице значение формулы =СРЗНАЧ(А4:С4) равно 5. Чему равно значение формулы СУММ(А4:D4), если значение ячейки D4 равно 6? Пустых ячеек в таблице нет.
В электронной таблице значение формулы =СРЗНАЧ(Е2:Е4) равно 3,
чему равно значение формулы =СУММ(Е2:Е5), если значение ячейки Е5 равно 5? Пустых ячеек в таблице нет.
В электронной таблице значение формулы =СУММ(А7:С7) равно 9. Чему равно значение формулы =CPЗHAЧ(A7:D7). если значение ячейки D7 равно 3? Пустых ячеек в таблице нет.
В электронной таблице значение формулы =СУММ(В2:В4) равно 6. Чему равно значение формулы =СРЗНАЧ(В2:В5), если значение ячейки В5 равно 14? Пустых ячеек в таблице нет.
В электронной таблице значение формулы =CPЗHAЧ(A3:D4) равно 5. Чему равно значение формулы =СРЗНАЧ(АЗ:С4), если значение формулы =CУMM(D3:D4) равно 4? Пустых ячеек в таблице нет.
В электронной таблице значение формулы =CPЗHAЧ(C2:D5) равно 4. Чему равно значение формулы =CУMM(C5:D5), если значение формулы =CPЗHAЧ(C2:D4) равно 5? Пустых ячеек в таблице нет.
Дан фрагмент электронной таблицы.
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 7 | … | 4 | 5 |
| 2 | =B2+C2+D2 | =C2 | =(A1–D1)*(B1-3) | =(A1–D1)*C1 |
Какое целое число должно быть записано в ячейке B1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:D2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
Дан фрагмент электронной таблицы.
| А | B | C | D | |
|---|---|---|---|---|
| 1 | 9 | … | 2 | 5 |
| 2 | =B2+C2+D2 | =C2 | =(A1–D1)*(B1-5) | =(A1–D1)*C1 |
Какое целое число должно быть записано в ячейке B1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:D2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3. Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 4 | 2 | |
| 2 | =2*(A1–C1) | =(2*B1+A1)/4 | =C1-1 |
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку?
Источник: Яндекс: Тренировочная работа ЕГЭ по информатике. Вариант 1.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 2 | 44 | |
| 2 | =С1 − В1*В1*5 | =(В1*В1+С1)/А1 | =C1−20 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона А1 :С2 имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 20 | 48 | |
| 2 | =С1 − В1*В1*5 | =(В1*В1+С1+3)/А1 | =C1−45 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку?
Известно, что все значения диапазона А1 :С2 имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 7 | =А1*3 | |
| 2 | =(В1 − А1)/3 | =В1 − C1 | =В2+А1 |
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, положительны.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 5 | =А1*3 | |
| 2 | =(В1 − А1)/3 | =В1 − С1 | =В2+А1 |
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, положительны.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 20 | 48 | |
| 2 | =С1-В1*В1*5 | =2*(В1*В1*В1+3)/А1 | =С1-15*В1 |
Какое число должно быть записано в ячейке В1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона А1:С2 имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 20 | 35 | |
| 2 | =С1-2*В1*В1 | =(В1*В1*В1-4)/А1 | =С1-8*В1 |
Какое число должно быть записано в ячейке В1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона А1:С2 имеют один и тот же знак.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 3 | 5 | |
| 2 | =(C1+3)/(A1-1) | =(B1+3)/(C1+3) | =(4*C1+6)/(A1+2) |
Какое целое число должно быть записано в ячейке С1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 1.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 4 | 5 | |
| 2 | =(C1+3)/(A1+4) | =B1/(C1-3) | =(A1+1)/(2*C1-2*B1) |
Какое целое число должно быть записано в ячейке С1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 2.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 4 | 3 | |
| 2 | =(C1+2)/(A1+4) | =2*A1/(C1+2) | =3/(C1-B1) |
Какое целое число должно быть записано в ячейке С1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Сибирь. Вариант 1.
Дан фрагмент электронной таблицы:
| A | B | C | |
| 1 | 2 | 2 | |
| 2 | =B2 | =(B1-2)/A1 | =B2+C1 |
Какое целое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 1.
Всего: 319 1–20 | 21–40 | 41–60 | 61–80 | 81–100 …
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 9 задания. Объясняется тема о работе в электронных таблицах и базах данных.
Содержание:
- ЕГЭ по информатике 9 задания объяснение
- Анализ диаграмм и графиков в электронных таблицах
- Типы ссылок в ячейках
- Построение диаграмм
- Тренировочные задания 9 ЕГЭ по информатике и их решение
- Встроенные функции в электронных таблицах
- Задания с диаграммами (задания прошлых лет для тренировки)
9-е задание: «Электронные таблицы»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение обрабатывать числовую информацию в электронных таблицах
До ЕГЭ 2021 года — определенные типы этого задания были заданием № 7 ЕГЭ
Ниже рассмотрены наиболее часто встречающиеся функции и их смысл. Наводите курсор на пример для просмотра ответа.
Таблица: Наиболее часто используемые функции
| русский | англ. | действие | синтаксис |
|---|---|---|---|
| СУММ | SUM | Суммирует все числа в интервале ячеек | СУММ(число1;число2) |
| Пример: | |||
| =СУММ(3; 2) =СУММ(A2:A4) |
|||
| СЧЁТ | COUNT | Подсчитывает количество всех непустых значений указанных ячеек | СЧЁТ(значение1, [значение2],…) |
| Пример: | |||
| =СЧЁТ(A5:A8) | |||
| СРЗНАЧ | AVERAGE | Возвращает среднее значение всех непустых значений указанных ячеек | СРЕДНЕЕ(число1, [число2],…) |
| Пример: | |||
| =СРЗНАЧ(A2:A6) | |||
| МАКС | MAX | Возвращает наибольшее значение из набора значений | МАКС(число1;число2; …) |
| Пример: | |||
| =МАКС(A2:A6) | |||
| МИН | MIN | Возвращает наименьшее значение из набора значений | МИН(число1;число2; …) |
| Пример: | |||
| =МИН(A2:A6) | |||
| ЕСЛИ | IF | Проверка условия. Функция с тремя аргументами: первый аргумент — логическое выражение; если значение первого аргумента — истина, то результатом выполнения функции является второй аргумент. Если ложно — третий аргумент. | ЕСЛИ(лог_выражение; значение_если_истина; значение_если_ложь) |
| Пример: | |||
| =ЕСЛИ(A2>B2;»Превышение»;»ОК») | |||
| СЧЁТЕСЛИ | COUNTIF | Количество непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СЧЁТЕСЛИ(диапазон, критерий) |
| Пример: | |||
| =СЧЁТЕСЛИ(A2:A5;»яблоки») | |||
| СУММЕСЛИ | SUMIF | Сумма непустых ячеек в указанном диапазоне, удовлетворяющих заданному условию. | СУММЕСЛИ (диапазон, критерий, [диапазон_суммирования]) |
| Пример: | |||
| =СУММЕСЛИ(B2:B25;»>5″) |
Анализ диаграмм и графиков в электронных таблицах
Типы ссылок в ячейках
Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.
- Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:
- Имена ячеек в абсолютной формуле не меняются при переносе или копировании ячейки с формулой в другое место таблицы.
- Для указания того, что не меняется столбец, ставится знак
$перед буквой столбца. Для указания того, что не меняется строка, ставится знак$перед номером строки: - В смешанных формулах меняется только относительная часть:
Относительная адресация:
имя столбца вправо на 1
номер строки вниз на 1
Абсолютная адресация:
имена столбцов и строк при копировании формулы остаются неизменными
Смешанные формулы
Построение диаграмм
- Диаграммы используются для наглядного представления табличных данных.
- Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
- Так, круговая и кольцевая диаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
- Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.
- Типы диаграмм Линейчатая и Гистограмма (на левом рис.), а также График и Точечная (на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

Егифка ©:
* Некоторые изображения, представленные в изложении теоретического материала, заимствованны с сайта К. Полякова
Тренировочные задания 9 ЕГЭ по информатике и их решение
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Встроенные функции в электронных таблицах
9_00: 9 задание. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением.
В ответе запишите только целую часть получившегося числа.
Типовые задания для тренировки
9_01: Задание 1:
Задание выполняется с использованием прилагаемых файлов
Найдите разность между максимальным и минимальным числом в диапазоне C48:Y360. В ответе запишите только целую часть числа.
✍ Решение:
-
Добавим формулы в пустые ячейки:
- Ячейка A502
= МАКС(C48:Y360) - Ячейка B502
= МИН(C48:Y360) - любая пустая ячейка
=A502-B502 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 920
9_02: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл 9-J1.xls электронной таблицы, содержащей вещественные числа – показатели высот над уровнем моря географических точек.
Найдите среднее значение всех отрицательных показателей и максимальное положительное значение.
В качестве ответа укажите целую часть суммы найденных значений.
✍ Решение:
- Перейдите в пустую ячейку (например,
АО1). - Поскольку для вычисления среднего арифметического используется дополнительное условие (только отрицательные показатели), то проще использовать формулу
СРЗНАЧЕСЛИ. Внесите формулу в заготовленную ячейку:
=СРЗНАЧЕСЛИ(A1:AN500;"<0")
Здесь условие обязательно должно быть в кавычках.
МАКСЕСЛИ.AO2:=МАКСЕСЛИ(A1:AN500;A1:AN500;">0")
АО3:=СУММ(AO1;AO2)
Получилось 502,531856
Ответ: 502
9_03: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл 9-j2.xl s электронной таблицы, содержащей вещественные числа – успеваемость учеников школ города по учебным дисциплинам за четвертую четверть.
Найдите школы с максимальным и минимальным средними показателями.
В качестве ответа укажите два числа – номера найденных школ, сначала с наименьшим показателем, затем с наибольшим.
✍ Решение:
- Поскольку средние значения по дисциплинам расставлены по столбцам, то необходимо выполнить вычисление общего среднего арифметического по каждой школе в каждом столбце.
- Для этого в пустой ячейке
B18для школы №1 напишите формулу вычисления среднего арифметического:
=СРЗНАЧ(B2:B16)
B20 и введите формулу:=ЕСЛИ(МАКС($B$18:$AI$18)=B18;B1;"")
$), иначе при копировании диапазон изменится, а нам этого не надо.B21 и введите формулу:=ЕСЛИ(МИН($B$18:$AI$18)=B18;B1;"")
Ответ: 32 8
9_04: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры и её средним арифметическим значением в первой половине дня (до 12:00 включительно).
В ответе запишите только целую часть получившегося числа.
✍ Решение:
-
Добавим формулы в пустые ячейки:
- Ячейка A94
= МАКС(B2:N92)= 35,6 - Ячейка A95
=СРЗНАЧ(B2:N92)= 21,4 - любая пустая ячейка
=A94-A95= 14,2 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 14
9_05: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным значением температуры в апреле и её средним арифметическим значением во второй половине дня (с 12:00) за тот же период.
В ответе запишите только целую часть получившегося числа.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только за апрель (04 месяц). Для поиска среднего арифметического значения учтем также, что время должно быть с 12.00, то есть со столбца N:
- Ячейка A94
= МАКС(B2:Y31)= 26,0 - Ячейка A95
= СРЗНАЧ(N2:Y31)= 21,0 - любая пустая ячейка
=A94-A95= 5,0 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 5
9_06: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите разность между максимальным и минимальным значением температуры среди измерений, сделанных в 17:00.
В ответе запишите только целую часть получившегося числа, округлять не нужно.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только за 17.00, то есть со столбца S:
- Ячейка A94
=МАКС(S2:S92)= 37,8 - Ячейка A95
=МИН(S2:S92)= 22,4 - любая пустая ячейка
=A94-A95= 15,4 - Оставляем только целую часть (отсекаем дробную, не округляя число).
Ответ: 15
9_07: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте сумму средних арифметических значений температур в 16:00 и в 23:00.
Округлите полученное число до целого и запишите его в ответ.
✍ Решение:
-
Добавим формулы в пустые ячейки. Возьмем значения ячеек только в 16.00, то есть со столбца R и в 23.00, то есть со столбца Y:
- Ячейка A94
=СРЗНАЧ(R2:R92)= 29,9 - Ячейка A95
=СРЗНАЧ(Y2:Y92)= 20,8 - любая пустая ячейка
=A94+A95= 50,7 - После округления получаем 51.
- Можно также решить данное задание, записав все в одну строку:
= СРЗНАЧ(R2:R92)+СРЗНАЧ(Y2:Y92)
Ответ: 51
9_08: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Найдите результат деления суммы всех значений температуры на максимальное значение.
В ответе запишите только целую часть получившегося числа, округлять не нужно.
✍ Решение:
-
Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от
- Ячейка A94
=МАКС(B2:Y92)= 38,0 - Ячейка A95
=СУММ(B2:Y92)= 51807,0 - любая пустая ячейка (поделим сумму на максимальное значение)
=A95/A94= 1363,3 - Оставляем только целую часть = 1363.
B2 до Y92 (B2:Y92):
Ответ: 1363
9_09: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
Посчитайте чему будет равно самое часто встречаемое значение температуры и среднее арифметическое значений температуры за всё время измерений. Найдите разницу между самым встречаемым значением и средним арифметическим значением.
В ответе запишите только целую часть числа (разницы).
✍ Решение:
-
Добавим формулы в пустые ячейки. Используем в формулах вcю таблицу, то есть диапазон ячеек от
- Для более достоверных расчетов будем использовать числа с тремя знаками после десятичной запятой. Воспользуемся кнопкой
- Ячейка A94
=СРЗНАЧ(B2:Y92)= 23,721 - Ячейка A95
=МОДА(B2:Y92)= 25,700 - любая пустая ячейка
=A95-A94= 1,979 - Оставляем только целую часть = 1.
B2 до Y92 (B2:Y92):
Для нахождения наиболее часто встречаемого значения используется функция МОДА ()
Ответ: 1
9_14: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-0.xls (в заголовке задания), содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев.
В каком количестве измерений температура оказалась выше 25 градусов?
✍ Решение:
- Поскольку нам необходимо посчитать количество, то будем использовать функцию
СЧЁТ(). Но так как считать надо количество измерений температуры выше 25 градусов, то нужно использовать функцию с критерием, а именно,СЧЁТЕСЛИ(). - Введите формулу в любую пустую ячейку:
=СЧЁТЕСЛИ(B2:Y92;">25")
Обратите внимание, что так как с условием сравнивается диапазон, а не единственная ячейка, то само условие необходимо разместить в кавычках.
Ответ: 942
9_15: Задание:
Задание выполняется с использованием прилагаемых файлов
Откройте файл электронной таблицы 9-j5.xls, содержащей вещественные числа – количество баллов, которое набрали участники тестирования. В первой строке указаны дисциплины, во второй – максимальный балл за тест по дисциплине, в левом столбце – фамилии участников. Считается, что тест пройден, если участник тестирования набрал больше 60% от максимального балла. В качестве ответа укажите, сколько участников тестирования прошли больше трёх тестов.
✍ Решение:
- Для начала будем сравнивать максимальный балл * 0,6 с баллом, набранным участником. Если балл участника больше, будем ставить в ячейку цифру
1, иначе —0. - В ячейку
B35введем формулу:
=ЕСЛИ(B4>B$2*0,6;1;0)
О включительно (последний столбец с данными).ЕСЛИ().А35:=ЕСЛИ(СУММ(B35:O35)>3;1;"")
B64.Ответ: 18
9_16: Задание:
Задание выполняется с использованием прилагаемых файлов
В электронной таблице в файле 9-j10.xls хранятся вещественные числа – результаты ежечасного измерения скорости ветра на протяжении трех месяцев.
Найдите количество дней, когда максимальная скорость ветра составляла не менее 90% от максимального значения за весь период.
✍ Решение:
- Сначала найдем максимальную скорость ветра за весь период. Введем формулу в ячейку
AB2:
=МАКС(B2:Y91)
AB2. Будем использовать функцию СЧЁТЕСЛИ(), так как считаем при условии.=СЧЁТЕСЛИ($Z$2:$Z$91;">="&AB2*0,9)
Обратите внимание, что в условии используются кавычки, но для добавления к условию рассчитанного значения в ячейке AB2, необходимо «приклеить» это значение с помощью знака &
Ответ: 80
Также можно посмотреть некоторые аналогичные задания ОГЭ
Задания с диаграммами (задания прошлых лет для тренировки)
9_7:
Задан фрагмент электронной таблицы:
Как изменится значение ячейки C3, если после ввода формул переместить содержимое ячейки B2 в B3?
(«+1» означает увеличение на 1, «-1» означает уменьшение на 1):
Варианты:
1) -2
2) -1
3) 0
4) +1
✍ Решение:
-
Проанализируем данные электронной таблицы до перемещения:
- В ячейке C2 будет находиться число 4, так как функция СЧЁТ подсчитывает количество непустых ячеек указанного диапазона.
- В ячейке С3 будет находиться число 3:
(1 + 2 + 2 + 6 + 4) / 5 = 3
Теперь посмотрим, что произойдет после перемещения:
(1 + 2 + 2 + 3) / 4 = 2
(нужно не забывать, что функция СРЗНАЧ не учитывает пустые ячейки, поэтому ячейка B2 не учтена).
Результат: 2
Подробное решение задания на видео:
📹 YouTube здесь (теоретическое решение)
📹 Видеорешение на RuTube здесь (теоретическое решение)
Задание:
В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3.
Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?
✍ Решение:
- Функция СРЗНАЧ предназначена для вычисления среднего арифметического значения указанного диапазона ячеек. Т.е. в нашем случае среднее значение ячеек C2, C3, C4, C5.
- Результат функции
=СРЗНАЧ(С2:С5)задан по условию, подставим его в формулу:
(C2 + C3 + C4 + C5)/4 = 3
x / 4 = 3
x = 3 * 4 = 12 -> C2 + C3 + C4 + C5 = 12
=СУММ(С2:С4). Зная значение в ячейке С5, вычтем его из полученной суммы и найдем ответ:C2 + C3 + C4 = C2 + C3 + C4 + C5 - C5 =
= 12 - 5 = 7
Результат: 7
Подробное решение смотрите на видео:
📹 YouTube здесь
Рассмотрим еще один пример решения 9 задания ЕГЭ по информатике:
9_10:
Дан фрагмент электронной таблицы:
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
✍ Решение:
- Круговая диаграмма отображает доли отдельных частей в общей сумме. В нашем случае в диаграмме отражаются результаты вычисления формул в ячейках А2:С2
- По диаграмме можно судить о том, что, скорее всего, полученные значения в формулах во всех ячейках должны быть равны (секторы диаграммы визуально равны).
- Получим выражения из формул ячеек, подставив вместо С1 -> x:
А2: х + 2 В2: 8/2 = 4 С2: х * 2
2 * х = 4 => x = 2
Результат: 2
Детальный разбор можно посмотреть в видеоуроке решения данного 9 задания ЕГЭ по информатике:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
9_11:
Задан фрагмент электронной таблицы:
Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:C2 соответствовала рисунку:

✍ Решение:
- По диаграмме можно судить только о следующем: если она не перевернута, то значения в ячейках A2 и B2 должны быть равны, а значение ячейки C2 — в два раза больше каждой из них.
- Поскольку у нас неизвестны значения двух ячеек, то обозначим B1 за x, а C1 за y.
- Подставим неизвестные в формулы и получим:
- Исходя из первого пункта, получаем:
A2 = B2 = C2/2
4y = x - y 2 * 4y = x - y + 4
8y = 5y - y + 4 -> y = 1
Результат: 5
Подробное теоретическое решение смотрите на видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь (теоретическое решение)
9_12:
Дан фрагмент электронной таблицы в режиме отображения формул:
После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.
Значениям D2:D6 соответствует график:
Варианты:
1) А 2) Б 3) В 4) Г
✍ Решение:
- Копирование диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 буквально означает выделение диапазона АЗ:ЕЗ и протягивание маркера копирования до конца указанного блока ячеек.
- Поскольку нас интересует только столбец D, то посмотрим, что там за формула, и что с ней произойдет при копировании:
- в ячейке D3 значение зависит от ячейки A3 и оно равно 2;
- при копировании формулы столбец остается тот же (D), поэтому и в формуле буквы остаются теми же (D и A), а вот строки копируются вниз, т.е. цифры в формуле увеличиваются на единицу при движении вниз на каждую строку; соответственно, нас интересуют еще ячейки A4, A5, A6;
- формулы ячеек A4, A5, A6 зависят от ячеек столбца B, поэтому рассмотрим получившиеся при копировании формулы столбцов A и B:
- Теперь вычислим значения в этих столбцах:
- Получаем точки по столбцу D: 1, -1, -1, -7, -15, что соответствует графику Г (ответ 4)
Результат: 4
Разбор задания смотрите на видео:
📹 YouTube здесьздесь (теоретическое решение)
9_13:
Дан фрагмент электронной таблицы:
Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, положительные.
✍ Решение задания 7:
- На изображенной диаграмме (если она преднамеренно не перевернута) секторы соответствуют указанному диапазону ячеек при движении по часовой стрелке с «севера на юг»: т.е. А2 — синий сектор, B2 — красный и т.п. Таким образом, делаем следующий вывод:
А2 = B2 = 2 * C2 = 2 * D2
B2 = 2 * D2 2(x + 5) = x + 21 2x - x = 21 - 10 x = 11
Результат: 11
Видеоразбор задания:
📹 YouTube здесьздесь (теоретическое решение)
Девятое задание из ЕГЭ по информатике нового формата 2021 основывается на работе с таблицами Excel.
Это задание выполняется на компьютере в новом формате ЕГЭ 2021 года. Будет выдан файл Excel, по которому нужно получить правильный ответ и записать его в бланк заданий.
Если Вам урок удобнее смотреть в видеоформате, то можете перейти на ролик по 9 заданию из ЕГЭ по информатике 2021 на Youtube. Подписывайтесь на канал!
Здесь имеется столбец «Продукт». Другие столбцы: «Жиры», «Белки», «Углеводы», «Калорийность» – это характеристики этих продуктов.
В Excel можно каждой ячейке задавать какие-нибудь формулы. Например, пусть в ячейке F2 будет писаться СУММА из ячеек B2 (Жиры) и С2 (Белки).
Кликаем по ячейке F2, а затем на значок «вставить функцию».
Появится окно «Вставка функции«. Здесь все функции разбиты на категории: Финансовые, математические, логические и т.д. По умолчанию стоит категория «10 недавно используемых функций». В этой категории уже есть нужная нам функция СУММ. Выбираем её и кликаем «ОК». (Основная категория для функции СУММ является «математические»)
Появляется окно для функции СУММ.
Если мы напишем в поле Число1: «B2:E2» ,– то у нас суммируются три ячейки: B2, C2, E2. Таким образом, мы задали интервал.
Можно суммировать и вниз, т.е. ячейки одного столбца (B2:B1001).
Чтобы просуммировать отдельные ячейки, без интервала – необходимо уже использовать поле Число2.
Нам нужно просуммировать два числа: значение ячейки B2 и значение С2. Значит, пишем в поле Число1
— B2, а в поле Число2 — C2.
Нажимаем «Ок». Теперь у нас в ячейке F2 сумма значений ячеек B2 и С2.
Примечание 1: Мы могли сделать данную операцию с помощью интервала. Для этого нужно было написать в поле Число1: B2:C2.
Примечание 2: Так же мы могли суммировать и без вставки функции. Для этого нужно кликнуть по ячейке F2 и затем в поле, на которое показывает стрелка на рисунке, вписать формулу: «=B2+C2«. И нажать «Enter».
Необходимо подвести мышку к нижнему правому углу ячейки с формулой, чтобы появился чётный крестик:
И нажав левую кнопку мыши, тянем вниз. Таким образом, у нас формула распространится на весь столбец.
При изменении данных в ячейках столбцов В и С – значения в ячейках столбца F меняется автоматически.
Примерные задачи 9 задания ЕГЭ по информатике 2021
Задача (Среднее значение с условием)
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике и информатике. Каков средний балл по информатике среди участников тестирования, получивших зачётные баллы по этому предмету (т.е. не менее 44 баллов)?
В ответе округлить число до двух знаков после запятой.
Решение:
Для решения этой задачи будем использовать функцию =СРЗНАЧЕСЛИ().
Кликнем в свободную ближайшую ячейку E2. Здесь мы хотим получить ответ на задачу. Нажмём на кнопку «Вставить функцию«, выберем категорию «статистические«, а затем выберем функцию СРЗНАЧЕСЛИ.
В диапазоне нужно указать все ячейки с числами столбца «Информатика» (Столбец D). Значит, напишем: D2:D273 (Чтобы понять сколько строчек в таблице, нужно прокрутить всю таблицу до самого конца вниз.). В условии напишем: >=44 (Т.к. мы должны считать среднее значение для тех ячеек, где число не меньше 44).
Нажимаем «ОК» и получаем в ячейке E2 число 68,60851064. Нам его нужно округлить до 2 знаков после запятой. Воспользуемся инструментом в программе Excel для округления.
Найдём кнопки «Уменьшить разрядность» и «Увеличить разрядность«. Их можно применять к выделенной ячейке.
Уменьшим разрядность до 2 знаков. Получается число 68,61. Это и будет ответ!
Примечание 1: Если мы хотим найти среднее значение без условия, есть функция СРЗНАЧ.
Примечание 2: СРЗНАЧЕСЛИ (СРЗНАЧ)- это и есть среднее арифметическое значение.
Ответ: 68,61
Посмотрим ещё один важный пример 9 задания ЕГЭ по информатике нового формата 2021.
Задача (Количество с условием)
Откройте файл электронной таблицы, содержащей данные о сотрудниках одного из предприятий города Москвы. Сколько человек в таблице имеют возраст меньше 30 лет, и их вес превышает 100 кг?
В ответе напишите одно целое число.
Решение:
Сначала поставим 1 в столбце F в тех строчках, которые удовлетворяют нашему условию: человек имеет возраст меньше 30 лет, и его вес превышает 100 кг. Если строчка не удовлетворяет условию, значит, в ячейке столбца F поставим 0.
Сначала настроим формулу для одной строчки, а затем формулу распространим на весь столбец.
Кликаем по ячейке F2. Нажимаем на кнопку «Вставить функцию«. Выбираем функцию ЕСЛИ из категории «Логические«.
В поле «Лог_выражение» задаём условие : И(C2>100; E2<30). Т.к. сначала мы задаём формулу для второй строки, то пишем ячейки C2 и E2. Мы написали условие нашей задачи для второй строки. Столбец C — отвечает за Вес, а столбец E — за возраст.
В условии ставим вначале союз «И«, т.к. одновременно два условия должны выполняться. Если бы в задаче говорилось, что мы должны подсчитать количество строчек, где хотя бы одно условие сработало, тогда бы поставили союз «ИЛИ«.
В поле «Значение_если_истина» ставим 1. В поле «Значение_если_ложь» ставим 0. Нажимаем «ОК».
Получилось, что в ячейке F2 высветился ноль. Значит, первый сотрудник не удовлетворяет условию задачи.
Теперь распространим формулу на весь столбец F. Подводим мышку к ячейке F2 к правому нижнему углу. Когда появился чёрный крестик, нажимаем левую кнопку мыши и тянем вниз, распространяя формулу на весь столбец.
Где-то будут получатся нули, а где-то единицы. Всё зависит от характеристик сотрудника.
После того, как формула будет распространена на весь столбец F, нам нужно посчитать количество единиц в столбце F. Это количество и покажет число сотрудников, которые подходят под условие задачи.
Воспользуемся функцией СУММ. Кликнем по ячейке G2. Именно здесь получим ответ. Затем нажмём на кнопку «Вставить функцию» и выберем СУММ из категории «Математические«.
В поле Число1 зададим интервал F2:F301 (Ведь всего у нас 301 строчка в таблице).
Нажимаем «ОК» и получаем в ячейке G2 ответ на нашу задачу. В ответе напишем 14.
Примечание: Для подчёта количества с условием можно использовать функцию СЧЁТЕСЛИ. Попробуйте решить с помощью неё самостоятельно.
Ответ: 14
Продолжаем тренироваться решать 9 задания из ЕГЭ по информатике нового формата 2021.
Задача (Наименьшее значение + условие ИЛИ)
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Чему равна наименьшая сумма баллов по математике и информатике среди школьников, получивших более 50 баллов по математике или информатике?
В ответе запишете целое число.
Решение:
В начале нужно выписать отдельно сумму баллов по математике и информатике для тех школьников, которые подходят под условие.
Выпишем сумму двух предметов, для удовлетворяющих условию строчек, в столбец F, с помощью функции ЕСЛИ.
В начале нужно задать формулу для одной ячейки F2. Кликаем по ячейке F2, нажимаем на кнопку «Вставить функцию«, выбираем функцию ЕСЛИ.
В поле «Лог_выражение» пишем: ИЛИ(C2>50; D2>50). В поле «Значение_если_истина«: C2+D2. В поле «Значение_если_ложь«: «» (Пустые двойные кавычки).
Важно: Здесь мы в поле «Значение_если_ложь» должны поставить пустые двойные кавычки, ведь, если поставить ноль, тогда, при поиске минимального значения будем находить всегда этот ноль. Мы ноль ставим в это поле только тогда, когда ищем количество строчек, ведь, тогда мы суммируем единицы, а ноль при суммировании не влияет на результат.
Нажимаем «ОК», и в ячейке F2 получается число 160. Это говорит о том, что первая строчка удовлетворяет условию задачи. И теперь в ячейке F2 лежит сумма баллов по математике и информатике для первого учащегося.
Распространим данную формулу на весь столбец F.
В основном получатся числа, но где-то ячейки останутся пустыми. Это значит, что эти строчки не подошли под условие задачи.
Теперь нужно с помощью функции МИН найти минимальное значение в столбце F.
Кликаем по ячейке G2, нажимаем «Вставить функцию«, выбираем функцию МИН из категории «Статистические«.
В поле Число1 пишем диапазон столбца F: F2:F273.
Получаем ответ 75.
Ответ: 75
Продолжаем оттачивать навыки работы с электронными таблицами в 9 задании из ЕГЭ по информатике нового формата 2021.
Задача (Среднее значение + сложное условие)
Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Каков средний балл по математике обучающихся, набравших не менее 60 баллов по информатике?
В ответе запишите только целую часть получившегося числа.
Решение:
Эту задачу решим двумя способами.
1 Способ
В этом способе решения будем снова использовать функцию СРЗНАЧЕСЛИ.
Кликаем по ячейке F2 и вставляем функцию СРЗНАЧЕСЛИ из категории «Статистические«.
Т.к. столбец, по которому мы будем проверять условие, отличается от того, по которому нужно искать среднее значение, то мы напишем следующие параметры:
В поле «Диапазон» пишем: D2:D273 (Это диапазон, который участвует в условии).
В поле «Условие«: >=60 (Это само условие, которое работает в диапазоне, написанный выше).
В поле «Диапазон_усреднения«: C2:C273 (Это диапазон, для которого будет найдено среднее арифметическое значение. Будут участвовать только те строчки, которые прошли условие).
Если последнее поле остаётся пустым, то среднее значение ищется по первому полю.
Нажимаем «ОК», и получаем число 60,0301205. Округлим это число до целых, получим число 60.
2 Способ
Этот способ подходит и для более запутанных ситуаций.
Для строчек, где выполняется условие задачи, перенесём значения столбца С в столбец F.
Кликаем в ячейку F2, нажимаем кнопку «Вставить функцию«, выбираем функцию Если.
Сначала нужно записать формулу для одной строки.
В поле «Лог_выражение» пишем: D2>=60 (Условие того, что человек набрал не менее 60 баллов по информатике)
В поле «Значение_если_истина» пишем: C2 (Переносим само значение столбца математики. Именно впоследствии мы должны найти среднее значение баллов по математике).
В поле «Значение_если_ложь» пишем: «» (Пустые кавычки. Нельзя писать ноль, иначе мы сильно занизим реальное среднее значение).
Нажимаем «ОК». Получается число 81 в ячейке F2.Оно перенеслось из ячейки C2, ведь значение по информатике больше 60 для этой строчки.
Распространяем формулу на весь столбец.
В строках, которые не удовлетворяют условию задачи, будут пустые ячейки.
Когда столбец готов, легко найти среднее значение для столбца F.
Кликаем в ячейку G2 и вставляем функцию СРЗНАЧ. В этой функции указываем диапазон F2:F273.
Получается число 60,0301205. Округляем его до целых, получается число 60.
Ответ: 60
Не редкий гость в примерных задачах 9 задания из ЕГЭ по информатике 2021.
Задача (Найти проценты)
Откройте файл электронной таблицы, содержащей данные о количестве белков, жиров и углеводов для различных продуктов. Сколько процентов от общего числа составили продукты, у которых более 10 г белка?
В ответе напишите одно целое число.
Решение:
Задачи на проценты обычно сводятся к нахождению количества.
Найдём сколько продуктов, у которых белка более 10 г.
Кликаем по полю E2. Применим функцию СЧЕТЕСЛИ из категории «Статестические«.
Диапазон указываем: C2:C1001 (Столбец белка).
В поле критерий пишем: >10.
Нажимаем кнопку «ОК». В поле E2 получается число 373.
Чтобы найти проценты, нужно это количество, которое мы нашли, разделить на всё количество продуктов и умножить на сто.
Кликаем по верхнему полю («строка формул»):
Дописываем: =СЧЁТЕСЛИ(C2:C1001;»>10″)/1000 * 100
Всего у нас 1000 наименований продуктов. Строчек 1001, но начинаются продукты со второй строчки. Поэтому делим на 1000 (1001 — 1). Умножаем на 100, чтобы найти проценты.
Нажимаем Enter. Получается число 37,3. Округлим до целого числа, ответом будет 37.
Ответ: 37
В следующей примерной задаче 9 задания ЕГЭ по информатике 2021 будем комбинировать уже изученные приёмы.
Задача (Комбинируем приёмы)
Откройте файл электронной таблицы, содержащей вещественные числа – ведомость продуктового магазина. Наценкой товара считается разность между закупочной ценой и ценой реализации. Прибыль – количество проданных товаров, умноженное на значение наценки. Найдите товар с наценкой выше среднего значения, который принесет максимальную прибыль после его полной продажи.
В качестве ответа укажите одно число – полученную после продажи найденного товара прибыль. Ответ округлите до целых чисел.
Сначала нужно найти среднее значение наценки. Запишем наценку в столбце E.
Запишем формулу сначала для одной ячейки E2. Кликаем по ячейки E2, затем кликаем по верхнему полю («строка формул») и пишем: =C2-B2.
Примечание: Формула начинается со знака «равно»!
Нажимаем Enter. Получается число 9,42.
Подводим курсор мышки к правому нижнему углу. После появления чёрного крестика, нажимаем левую кнопку мышку и тянем вниз. Тем самым распространим формулу на весь столбец.
Найдём среднее значение наценки, которая находится в столбце E.
Кликаем по ячейке F2, затем на кнопку «Вставить функцию«, выбираем СРЗНАЧ. Диапазон указываем: E2:E100. Нажимаем «ОК» и получаем число 58,25. Это и есть среднее значение для наценки.
Теперь напишем в столбец G прибыль, но только для тех товаров, у которых наценка выше среднего значения.
Сначала запишем формулу для одной строчки. Кликаем по ячейки G2, нажимаем «Вставить функцию«, выбираем ЕСЛИ.
В поле «Лог_выражение» пишем: E2>58,25. Если наценка выше среднего, то будем считать прибыль.
Т.к. в столбце E все числа имеют не более двух знаков после запятой и число 58,25 тоже имеет два знака после запятой, то мы не получим ошибок из-за округления среднего значения.
В поле «Значение_если_истина» : E2 * D2 (Умножаем наценку на количество проданных товаров. Получаем прибыль).
В поле «Значение_если_ложь«: «» (Пустые кавычки. Ведь мы потом будем искать максимальное значение для прибыли, для товаров, у которых наценка выше среднего значения).
Нажимаем «ОК». Получается в G2 пустое окошко. Значит, для этого товара наценка не выше среднего значения.
Распространим формулу на весь столбец G. Где-то окажутся числа, а где-то пустые ячейки.
Кликнем по ячейке H2 и найдём с помощью функции МАКС (категория «Статистические») максимальную прибыль, в диапазоне указав: G2:G100. Округлив до целых, в ячейке H2 получается ответ 10185.
Примечание: Мы могли при составлении условия E2>58,25 использовать название ячейки F2 вместо числа 58,25. Но тогда нужно её «зацементировать» т.е. E2>$F$2 (Использовать абсолютную адресацию). Если мы всё-таки решили написать число, то нужно следить, чтобы точность была одинаковая у среднего значения, и у тех ячеек, которые мы сравниваем с этим средним значением.
Ответ: 10185
Последнее. Если в задаче говорится о значении по абсолютной величине, т.е. о значении по модулю, то нужно использовать конструкцию ABS(). Например, разница по абсолютной величине двух ячеек A2 и B2 равна ABS(A2-B2). Это можно использовать при составлении формул.
Так же при подготовке к 9 заданию может быть полезна статья, которая была написана под старый формат ЕГЭ по информатике.
На этом всё. Комбинируйте приёмы, которые мы рассмотрели в этом уроке при подготовке к 9 заданию из ЕГЭ по информатике нового формата 2021. Удачи!
В решение заданий демо-версии используется язык программирования Python.
|
Задание 1. Анализ информационных моделей На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта D в пункт В и из пункта F в пункт A. В ответе запишите целое число. |
На графе расставим веса вершин. Далее 2 и 7 вершины ведут нас к 5, значит А это 5, оставшаяся «тройка» это вершина Е под номером 6. Сумма дорог BD + AF = 53 + 5 = 58 Ответ: 58 |
||||||||||||||||||
|
Задание 2. Построение таблиц истинности логических выражений Миша заполнял таблицу истинности логической функции F F= ¬(y → x) v (z→ w) v ¬z , но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z. В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Функция задана выражением ¬x v y, зависящим от двух переменных, а фрагмент таблицы имеет следующий вид. В этом случае первому столбцу соответствует переменная y, а второму столбцу – переменная x. В ответе следует написать yx. |
¬(y → x) v (z→ w) v ¬z=0. Следовательно y → x =1, z→ w=0, z=1. Значит третий столбец z. z→ w=0, значит w=0, и это может быть только 4 столбец. y → x =1, следовательно из второй строки мы видим, что первый столбец может быть только у, а второй х.
Решение на Python Ответ: YXZW |
||||||||||||||||||
Задание 3. Базы данных. Файловая система В прикрепленном файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в На рисунке приведена схема указанной базы данных. Используя информацию из приведённой базы данных, определите общий вес |
На третьем листе книги применим фильтр по району и получим ID четырех магазинов. На втором листе применим фильтр по товару и получим ID товара. На первом листе применим фильтры по ID товара и ID магазинов и типу операции. Все даты попадают в интервал от 1 до 8 июня. Получим: Поступило в продажу 710 упаковок. В упаковке 0,5 кг. Получим 355 кг. Ответ: 355 |
||||||||||||||||||
|
Задание 4. Кодирование и декодирование информации По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код,удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трёх оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков? |
Ответ: 14 |
||||||||||||||||||
|
Задание 5. Анализ и построение алгоритмов для исполнителей На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему 1. Строится двоичная запись числа N. Полученная таким образом запись является двоичной записью искомого числа R.Например, для исходного числа 610 = 1102 результатом является число |
Минимальное R, большее 40, это 41. ИЛИ программное решение Ответ: 16
|
||||||||||||||||||
|
Задание 6. Определение результатов работы простейших алгоритмов Исполнитель Черепаха действует на плоскости с декартовой системой координат. Черепахе был дан для исполнения следующий алгоритм: Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует 5 команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд n (где n– целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова; Назад n (где n– целое число), вызывающая передвижение в противоположном голове направлении; Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке, Налево m (где m– целое число), вызывающая изменение направления движения на m градусов против часовой стрелки. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Определите, сколько точек с целочисленными координатами будут находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения. |
Сначала нужно построить фигуру. Далее мы находим уравнения прямых, которыми ограничена фигура и решаем ИЛИ Ответ: 1 задание — 38, 2 задание — 128 |
||||||||||||||||||
|
Задание 7. Кодирование и декодирование информации. Передача информации Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайт. В ответе запишите только целое число, единицу измерения писать не нужно. |
I = ν ⋅ i ⋅ t ⋅ k, где ν — частота дискретизации (Гц), i — разрешение (бит), t — время (с), k — количество дорожек (1 -моно, 2- стерео, 4 — квадро) I1 = ν ⋅ i ⋅ t I2 = 3,5 · 28 = 98 Ответ: 98 |
||||||||||||||||||
|
Задание 8. Перебор слов и системы счисления Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечётная цифра не стоит рядом с цифрой 6. |
* * * * * — пятизначное число. 6 * * * * — вариантов 3 ⋅ 7 ⋅ 7 ⋅ 7 = 1029 Ответ: 2961 |
||||||||||||||||||
Задание 9. Работа с таблицами Файл с данными Откройте файл электронной таблицы, содержащей в каждой строке шесть натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия: |
Для решения этой задачи понадобится 10 вспомогательных столбцов. Сначала мы посчитаем количество повторяющихся чисел в каждой строке. Затем сумму каждой строки диапазона H:M. Если повторений нет, то эта сумма равна 6. Далее мы найдем среднее арифметическое неповторяющихся значений. Затем найдем сумму повторяющихся значений. Затем проверим соблюдение двух условий. И подсчитаем количество строк, в которых соблюдаются оба условия. Ответ: 2241 |
||||||||||||||||||
Задание 10. Поиск символов в текстовом редакторе Файл с данными Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует. |
В текстовом редакторе используем инструмент найти (по умолчанию он не учитывает регистр, в расширенном поиске есть кнопка больше, где можно проверить настройки). Ищем слово целиком. Ставим галочку учитывать регистр. Слово теперь со строчной буквы встречается 45 раз. Ответ: 45 |
||||||||||||||||||
|
Задание 11. Вычисление количества информации При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байт. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством бит. Определите объём памяти (в Кбайт), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайт. |
I = K · i, N = 2 i ID : ****….**** – всего 250 различных символов в наборе N = 10 + 1650 = 1660, 1024<1660<2048, 2048 = 211, значит для кодирования одного символа нужно 11 бит. IID = 250 · 11 = 2750 бит = 343,75 байт ≈ 344 байт – отводится на идентификатор целое число байт I65536 = 65536 ⋅ 344 = 22544384 байта = 22016 Кбайт– всего Ответ: 22016 |
||||||||||||||||||
|
Задание 12. Выполнение алгоритмов для исполнителей Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр. А) заменить (v, w). Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Б) нашлось (v). Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется. Цикл выполняется, пока условие истинно. В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно). В конструкции ЕСЛИ условие выполняется команда 1 (если условие истинно) или команда 2 (если условие ложно). Дана программа для Редактора: |
def pr(n): #функция определяет простое ли число for n in range(100): #перебираем n if ‘>2’ in s: if ‘>0’ in s: sum_s = 0 Ответ: 5 |
||||||||||||||||||
|
Задание 13. Поиск путей в графе На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. |
Начнем подсчет из вершины Е налево через В и возвращаемся в Е через Л. Ответ: 21 |
||||||||||||||||||
|
Задание 14. Кодирование чисел. Системы счисления Операнды арифметического выражения записаны в системе счисления с основанием 15. |
for x in range(15): if n%14 == 0: Ответ: 8767 |
||||||||||||||||||
|
Задание 15. Преобразование логических выражений На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение |
def deli(n,m): for A in range(1,1000): if Ok: Ответ: 94 |
||||||||||||||||||
|
Задание 16. Рекурсивные алгоритмы Алгоритм вычисления значения функции F(n), где n – натуральное число, |
F(2023) = 2023! = 2023 ⋅ 2022! F(2023)/F(2020) = (2023 ⋅ 2022 ⋅ 2021 ⋅ 2020!)/2020! = 2023 ⋅ 2022 ⋅ 2021 = = 8266912626 Ответ: 8266912626 |
||||||||||||||||||
Задание 17. Проверка на делимость Файл с данными В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых |
f= open(’17.txt’) k = 0 for i in p: for i in range(1,len(p)): #Осторожно, скобки! print(k,PP) Ответ: 180 190360573 |
||||||||||||||||||
Задание 18. Робот-сборщик монет Файл с данными Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз — в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клетке маршрута Робота. Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную. Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.Пример входных данных:
Для указанных входных данных ответом должна быть пара чисел 41 и 22. |
Сначала скопируем таблицу рядом, начиная со столбца АА, можно уменьшить ширину столбца до 4-5. Ячейка АА1=А1. Ячейка АВ1 = АА1+В1, протягиваем ее до АТ1. Ячейка АА2 = АА1 + А2, протягиваем ее до АА20. Далее ячейка АВ2 = В2+МАКС(АА2;АВ1), протягиваем ее на весь оставшийся диапазон, копируем только значения, не трогая стен. Справа от стен формулы повторяют крайний левый рял, столбец АА, снизу от стен формулы копируют верхнюю строку 1. Далее делаем замену всех формул МАКС на МИН. Ответ: 1099 1026 |
||||||||||||||||||
|
Задание 19. Выигрышная стратегия. Задание 1 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу из 129 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 128. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. |
При значениях S < 64 у Пети есть возможность сделать такой ход, что Ваня не сможет выиграть своим первым ходом. При значении S = 64 Петя своим первым ходом может получить 65 или 128 камней в куче. Во всех случаях Ваня увеличивает количество камней в куче в два раза и выигрывает своим первым ходом. Ответ: 64 |
||||||||||||||||||
|
Задание 20. Выигрышная стратегия. Задание 2 Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
Найденные значения запишите в порядке возрастания. |
Значение S должно быть меньше 64, поскольку иначе Ваня сможет выиграть своим первым ходом. Ответ: 32 63 |
||||||||||||||||||
|
Задание 21. Выигрышная стратегия. Задание 3 Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
Если найдено несколько значений S, в ответе запишите минимальное из них. |
Ответ: 62 |
||||||||||||||||||
|
Задание 22. Многопроцессорные системы В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно. |
В независимых процессах время считается от 0, Ответ: 17 |
||||||||||||||||||
|
Задание 23. Анализ программы с циклами и условными операторами Исполнитель преобразует число на экране. |
def f(x, y): print (f(1,10) * f(10, 35)) Ответ: 98 |
||||||||||||||||||
Задание 24. Анализ программы с циклами и условными операторами Файл с данными Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная |
f=open(’24.txt’) PP = [‘CA’, ‘CO’, ‘DA’, ‘DO’, ‘FA’, ‘FO’] for i in range(1, len(p), 2): Ответ: 95 |
||||||||||||||||||
|
Задание 25. Анализ программы с циклами и условными операторами Назовём маской числа последовательность цифр, в которой также могут Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка. |
Самый простой способ использовать библиотеку fnmatch. или так полным перебором: y = {»,’0′,’00’,’000′} for x in range (1000): Ответ: 162139404 80148 |
||||||||||||||||||
Задание 26. Анализ программы с циклами и условными операторами В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. |
|||||||||||||||||||
Задание 27. Анализ программы с циклами и условными операторами У медицинской компании есть N пунктов приёма биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приёма и вскрывается только в лаборатории. Файл А Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приёма биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов. |
Ответ: 51063 5634689219329 |
Автор материалов — Лада Борисовна Есакова.
Microsoft Excel (в дальнейшем просто — Excel) — это программа выполнения расчетов и управления так называемыми электронными таблицами.
Excel позволяет выполнять сложные расчеты, в которых могут использоваться данные, расположенные в разных областях электронной таблицы и связанные между собой определенной зависимостью. Для выполнения таких расчетов в Excel существует возможность вводить различные формулы в ячейки таблицы. Excel выполняет вычисления и отображает результат в ячейке с формулой.
Важной особенностью использования электронной таблицы является автоматический пересчет результатов при изменении значений ячеек. Excel также может строить и обновлять графики, основанные на введенных числах.
Адрес ячейки в электронных таблицах состоит из имени столбца и следующего за ним номера строки, например, C15.
Для написания формул используют адреса ячеек и знаки арифметических операций (+, -, *, /, ^). Формула начинается знаком =.
В Excel предусмотрены стандартные функции, которые могут быть использованы в формулах. Это математические, логические, текстовые, финансовые и другие функции. Однако, на экзамене Вам могут встретиться только самые простые функции: СЧЕТ (количество непустых ячеек), СУММ (сумма), СРЗНАЧ (среднее значение), МИН (минимальное значение), МАКС (максимальное значение).
Диапазон ячеек обозначается следующим образом: A1:D4 (все ячейки прямоугольника от A1 до D4.
Адреса ячеек бывают относительными, абсолютными и смешанными.
Они по-разному ведут себя при копировании формулы из ячейки в ячейку.
Относительная адресация:
Если в ячейке B2 мы напишем формулу =D1+3, то таблица воспримет это как «взять значение ячейки на две правее и на одну выше текущей, и прибавить к нему 3».
Т.е. адрес D1 воспринимается таблицей, как положение относительно ячейки, куда вводится формула. Такой адрес называется относительным. При копировании такой формулы в другую ячейку, таблица автоматически пересчитает адрес относительно нового расположения формулы:
Абсолютная адресация:
Если нам не нужно, чтобы адрес пересчитывался при копировании формулы, мы можем его «закрепить» в формуле — поставить знак $ перед буквой и индексом ячейки: =$D$1+3. Такой адрес называется абсолютным. Такая формула не будет изменяться при копировании:
Смешанная адресация:
Если же мы хотим, чтобы при копировании формулы автоматически пересчитывался, к примеру, только индекс ячейки, а буква оставалась неизменной, мы можем «закрепить» в формуле только букву (или наоборот): =$D1+3. Такой адрес называется смешанным. При копировании формулы будет меняться только индекс в адресе ячейки:
Электронные таблицы. Копирование формул.
Пример 1.
В ячейке C2 записана формула =$E$3+D2. Какой вид приобретет формула, после того как ячейку C2 скопируют в ячейку B1?
1) =$E$3+C1 2) =$D$3+D2 3) =$E$3+E3 4) =$F$4+D2
Решение:
Место расположения формулы меняется с C2 на B1, т.е. формула сдвигается на одну ячейку влево и на одну ячейку вверх (буква «уменьшается» на единицу и индекс уменьшается на единицу). Значит, так же изменятся все относительные адреса, а абсолютные (закрепленные знаком $) останутся неизменными:
=$E$3+С1.
Ответ: 1
Пример 2.
В ячейке В11 электронной таблицы записана формула. Эту формулу скопировали в ячейку А10. В результате значение в ячейке А10 вычисляется по формуле х—Зу, где х — значение в ячейке С22, а у — значение в ячейке D22. Укажите, какая формула могла быть написана в ячейке В11.
1) =C22-3*D22 2) =D$22-3*$D23 3) =C$22-3*D$22 4) =$C22-3*$D22
Решение:
Проанализируем поочередно каждую формулу:
Место расположения формулы меняется с B11 на A10, т.е. буква «уменьшается» на 1 и индекс уменьшается на 1.
Тогда при копировании формулы изменятся следующим образом:
1) =B21-3*C21
2) =C$22-3*$D22
3) =B$22-3*C$22
4) =$C21-3*$D21
Условию задачи соответствует формула 2).
Ответ: 2
Электронные таблицы. Определение значения формулы.
Пример 3.
Дан фрагмент электронной таблицы:
|
А |
В |
С |
D |
|
|
1 |
1 |
2 |
3 |
|
|
2 |
4 |
5 |
6 |
|
|
3 |
7 |
8 |
9 |
В ячейку D1 введена формула =$А$1*В1+С2, а затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?
1) 10 2) 14 3) 16 4) 24
Решение:
Место расположения формулы меняется с D1 на D2, т.е. буква не меняется, а индекс увеличивается на 1.
Значит, формула примет вид: =$А$1*В2+С3. Подставим в формулу числовые значения ячеек:1*5+9=14. Правильный ответ указан под номером 2.
Ответ: 2
Пример 4.
В электронной таблице значение формулы =СРЗНАЧ(A6:C6) равно (-2). Чему равно значение формулы =СУММ(A6:D6), если значение ячейки D6 равно 5?
1) 1 2) -1 3) -3 4) 7
Решение:
По определению среднего значения:
СРЗНАЧ(A6:C6) = СУММ(A6:С6)/3 = -2
Значит, СУММ(A6:С6) = -6
СУММ(A6:D6) = СУММ(A6:С6)+D6 = -6+5 = -1
Ответ: 2
Электронные таблицы и диаграммы.
Пример 5.
Дан фрагмент электронной таблицы в режиме отображения формул.
После выполнения вычислений построили диаграмму по значениям диапазона A1:D1. Укажите полученную диаграмму:
Решение:
Вычислим по формулам значения ячеек A1:D1.
B1 = 3-2 =1
A1 = 2-1 =1
C1 = 1+2 =3
D1 = 1*3 =3
Этим данным соответствует диаграмма 3.
Ответ:3
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задача №7. Электронные таблицы. Абсолютная и относительная адресация. Графики и диаграммы.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Анализ диаграмм и
электронных таблиц
Разбор заданий № 07 ЕГЭ (11 кл)
Проверяемые элементы содержания: знание технологии обработки информации в электронных таблицах
и методов визуализации данных с помощью диаграмм и графиков.
(базовый уровень, время – 3 мин)
Что нужно знать:
|
Электронная таблица[1] |
|
|
вычисления с данными, представленными в |
|
|
бумажные таблицы. |
|
|
Электронные таблицы представляют собой удобный инструмент |
|
|
вычислений. Решения многих вычислительных |
|
|
математическое моделирование |
|
|
математических формул в электронных |
|
|
между различными |
|
|
В формулах используются ссылки на ячейки: можно сослаться |
|
|
используя её адрес. |
|
|
Виды адресации: |
|
|
● относительная (A1); |
|
|
● абсолютная ($A$1); |
|
|
● смешанная ($A1 или A$1) |
|
|
При относительной адресации ссылка |
|
|
копировании меняется в зависимости от |
|
|
конфигурация (взаиморасположение) |
|
|
(диапазоном ячеек), на |
|
|
Абсолютная |
|
|
зафиксировать адрес |
|
|
При смешанной |
|
|
на строку (или столбец) изменяется в |
|
|
при копировании. Смешанный тип ссылок это и |
|
|
вместе взятые. Этот вид |
|
|
Примечание: знак $ используется для обозначения абсолютной адресации. |
|
Информационные ресурсы:
1.
Теория: Относительные, абсолютные и смешанные ссылки
2.
Соответствие команд Excel и OOo Calc: https://wiki.openoffice.org/wiki/Соответствие_команд_Excel_и_OOo_Calc
3.
Задания для тренировки: ЕГЭ−2020, информатика: задания, ответы, решения. Обучающая система «РЕШУ ЕГЭ» Дмитрия Гущина.
4. Онлайн-тесты
Константина Полякова для подготовки к ЕГЭ:
B7-1
— Адресация в электронных таблицах,
B7-2
— Диаграммы в электронных таблицах (решение задания № 5)
Задание № 7 (ДЕМО
ЕГЭ-2020 ФИПИ)
|
Дан |
|
формула. При копировании адреса ячеек в |
|
стало числовое значение |

Решение:
1) При
копировании формулы из ячейки B3 в ячейку C2 относительные адреса в формуле
изменяются:
a) номер
столбца увеличивается на 1,
b) номер
строки уменьшается на 1.
2) B3
=A$2+D$3 → C2 =B$2+E$3
3) C2
= 20 + 30000 = 30020 Ответ: 30020
Задание № 7 (ДЕМО
ЕГЭ-2019 ФИПИ)
|
Дан фрагмент электронной таблицы. Из ячейки C3 в ячейку D4 была скопирована |
|
формула. При копировании адреса ячеек в |
|
стало числовое значение |
|
|
Решение:
1) При
копировании формулы из ячейки C3 в ячейку D4
относительные адреса в формуле изменяются:
a) номер
столбца увеличивается на 1,
b) номер
строки увеличивается на 1.
2) C3
=$B$3+D2 → D4 =$B$3+E3
3) D4
= 400 + 700 = 1100
Ответ: 1100
Задание № 7 (ДЕМО ЕГЭ-2018
ФИПИ)
|
Дан |
|
формула. При копировании адреса ячеек в |
|
стало числовое значение |
|
|
Решение:
4) При
копировании формулы из ячейки B3 в ячейку A4
относительные адреса в формуле изменяются:
a) номер
столбца уменьшается на 1,
b) номер
строки увеличивается на 1.
5) B3
=$C2+D$3 → A4 =$C3+C$3
6) A4
= 300 + 300 = 600 Ответ: 600
Решение задания № 5 (Онлайн-тест К.
Полякова)
|
Коле нужно с помощью электронных таблиц построить |
|
от 10 до 49. Для этого сначала в диапазоне В1:К1 он записал числа от 0 до |
|
диапазоне А2:А5 |
|
двузначного числа (А2 — число десятков; В1 — число единиц), после чего скопировал |
|
её во все ячейки диапазона B2:К5. В итоге получил таблицу двузначных чисел. Какая |
|
формула была |
Решение:
1) 
=A2*10+B1 – формула двузначного числа;
2) для
увеличения числа десятков копируем формулу вниз по столбцу, т.е. в первом
слагаемом увеличивается номер строки, а номер столбца остаётся неизменным
($A2);
3) для
увеличения числа единиц копируем формулу вправо по строке, т.е. во втором
слагаемом увеличивается номер столбца, а номер строки остаётся неизменным
(B$1);
4) В
результате в ячейке B2 имеем следующую формулу: =$A2*10+B$1
Ответ: =$A2*10+B$1
Разбор заданий № 7. СтатГрад. Подготовка к ЕГЭ 2019[2]
Вариант 1
|
Дан фрагмент |
|
|
|
Какое целое число |
|
построенная по значениям |
|
Известно, что все |

1) Из
анализа диаграммы имеем следующее соотношение секторов круга: 1:1:2:4;
2) Из
анализа таблицы имеем: B2=C2; A2>D2. ⇒
B2:C2:D2:A2 ≡ 1:1:2:4.
3) D2
= 8; A2 = 2•C2 + 8 = 16 ⇒ C2 = 4
4) 2•(B1-3)
= 4, B1 — 3 = 2, B1 = 5
Ответ: 5
Вариант 2
|
Дан фрагмент |
|
|
|
Какое целое число |
|
построенная по значениям |
|
Известно, что все |

1) Из
анализа диаграммы имеем следующее соотношение секторов круга: 1:1:2:4;
2) Из
анализа таблицы имеем: B2=C2; A2>D2. ⇒
B2:C2:D2:A2 ≡ 1:1:2:4.
3) D2
=(A1-D1)*C1 = (9-5)•2 = 8 ⇒ C2 =
4.
4) (A1-D1)*(B1-5)
= 4
4•(B1-5) = 4; B1-5 = 1; B1 = 6.
Ответ: 6
Вариант 3
|
В ячейки электронной |
|
|
|
В ячейку A5 записали |
|
ячейку B1. Какое число |
Решение:
A5 =$C6+E$3 → B1 =$C2+F$3; B1 = 11 + 42 = 53 Ответ: 53
Вариант 4
|
В ячейки электронной |
|
|
|
В ячейку A4 записали формулу = $E5 + B$4. После этого |
|
ячейку B1. Какое число |
Решение:
A4 =$E5+B$4 → B1 =$E2+C$4; B1 = 31 + 13 = 44 Ответ: 44
Вариант 5
|
В ячейки электронной |
|
|
|
В ячейку B3 записали |
|
ячейку A1. Какое число |
Решение:
B3 =$D6+F$4 → A1 =$D4+E$4; A1 = 333 + 600 = 933 Ответ: 933
Вариант 6
|
В ячейки электронной |
|
|
|
В ячейку A6 записали формулу = $C5 + D$4. После этого |
|
ячейку B3. Какое число |
Решение:
A6 =$C5+D$4 → B3 =$C2+E$4; B3 = 100 + 600 = 700 Ответ: 700
Разбор заданий № 7. ЕГЭ 2020. Информатика. Ушаков Д.М. 10
тренировочных вариантов[3]
Вариант № 1
|
При работе с |
|
Какой вид приобретёт |
Решение:
1.
C3 → D2: номер столбца увеличился на 1, а номер строки уменьшился
на 1.
2.
=$B3+C$2 → =$B2+D$2 Ответ: =$B2+D$2
Вариант № 2
|
Дан фрагмент |
||||||
|
A |
B |
C |
D |
|||
|
1 |
3 |
5 |
4 |
|||
|
2 |
=D1+B1 |
1 |
2 |
|||
|
3 |
=C$2+$C3 |
6 |
7 |
|||
|
Чему станет равным значение ячейки A2, если в неё |
||||||
|
B3? |
Решение:
1.
B3 → A2: номер столбца уменьшился на 1 и номер строки уменьшился
на 1.
2.
=C$2+$C3 → =B$2+$C2
3.
B2 =D1+B1; B2 = 4+3 = 7
4.
A2 = 7+1 = 8 Ответ: 8
Вариант № 3
|
|
Решение:
1)
Из анализа диаграммы имеем следующее соотношение секторов круга:
1:3:3:1;
2)
Из анализа таблицы имеем: A2 = 1; B2 = 3; C2 = 3
3)
A2:B2:C2:D2 ≡ 1:3:3:1 ⇒
D2 = 1
4)
(B1+C2)/6 = 1; (B1+3)/6 = 1; B1 = 3 Ответ:
3
|
Дан фрагмент |
||||||
|
A |
B |
C |
D |
|||
|
1 |
6 |
|||||
|
2 |
=D2-B1 |
=B1/2 |
=A1-B2 |
=A1+B1/2 |
||
|
Какое число |
||||||
|
построенная после выполнения вычислений |
||||||
|
диапазона ячеек A2:D2, соответствовала рисунку? |
 Вариант № 4
Вариант № 4
Решение:
1)
Из анализа диаграммы имеем следующее соотношение секторов круга:
3:1:1:1;
2)
Из анализа таблицы имеем: D2 =A1+B1/2 = A1+B2;
A2 = (A1+B1/2) — B1 = A1-B1/2 = A1-B2; C2 = A1-B2;
3)
A2 = C2; D2 > A2 в 3 раза ⇒
D2 = 3•A2;
4)
A1+B1/2 = 3•(A1-B1/2); 6+B1/2 = 3•(6-B1/2)
5)
B1/2+3•(B1/2) = 12; 2•B1 = 12; B1 = 6 Ответ: 6
Вариант № 5
Решение:
1)
Из анализа диаграммы имеем следующее соотношение секторов круга:1:3:3:1
2)
Из анализа таблицы имеем: A2
= 1; B2 = 3; D2 = 1 ⇒ C2 = 3;
3)
Составим уравнение: (B1+3)/2 = 3; B1 = 3 Ответ: 3
Вариант № 6
|
При работе с |
|
Какой вид приобретёт |
Решение:
1.
E5 → D3: : номер
столбца уменьшился на 1, а номер строки уменьшился на 2.
2. =$C3-B$3
→ =$C1-A$3 Ответ:
=$C1-A$3
Вариант № 7
|
Дан фрагмент |
||||||
|
A |
B |
C |
D |
|||
|
1 |
3 |
5 |
4 |
|||
|
2 |
10 |
=C$3+B3 |
1 |
2 |
||
|
3 |
20 |
=C$2+$C3 |
6 |
7 |
||
|
Чему станет равным значение ячейки A1, если в неё |
||||||
|
B2? |
Решение:
1. B2
→ A1: номер столбца уменьшился на
1 и номер строки уменьшился на 1.
2. =C$3+B3
→ =B$3+A2 3. B3 = C2 + C3 = 1 + 6 = 7;
4. A1 = B3 + A2 = 7 + 10 = 17 Ответ: 17
|
Дан фрагмент |
||||||
|
A |
B |
C |
D |
|||
|
1 |
3 |
5 |
||||
|
2 |
=(A1+C1)/4 |
=C1-1 |
=A2/2 |
=B1/2 |
||
|
Какое число должно быть |
||||||
|
построенная после |
||||||
|
значениям диапазона |
 Вариант № 8
Вариант № 8
Решение:
1) Из анализа диаграммы имеем
следующее соотношение секторов круга:1:1:2:4
2) Из анализа таблицы имеем: A2 =
2; B2 = 4; C2 = 1 ⇒ D2 = 1; 3)
Составим уравнение: B1/2 = 1; B1 = 2. Ответ: 2
Вариант № 9
|
Дан фрагмент |
|
|||||
|
A |
B |
C |
D |
|||
|
1 |
3 |
5 |
||||
|
2 |
=C1-A1 |
=A2*2 |
=A1+2 |
=B1-B2 |
||
|
Какое число должно быть |
||||||
|
выполнения вычислений |
||||||
|
соответствовала рисунку? |
Решение:
1) Из анализа диаграммы имеем
следующее соотношение столбцов: 2:4:5:3 2) Из анализа таблицы имеем: A2 = 2; B2 = 4; C2 = 5 ⇒ D2 = 3; 3) Составим уравнение: B1-B2 =
3; B1 = 7. Ответ: 7
Вариант № 10
|
Дан фрагмент |
|
|||||
|
A |
B |
C |
D |
|||
|
1 |
3 |
7 |
||||
|
2 |
=(B1-D2)/5 |
=C1-A1 |
=A1-2 |
=C2*3 |
||
|
Какое число должно быть |
||||||
|
выполнения вычислений |
||||||
|
соответствовала рисунку? |
Решение:
1) Из анализа диаграммы имеем
следующее соотношение столбцов: 2:4:1:3 2) Из анализа таблицы имеем: A2 = ?; B2 = 4; C2 = 1; D2 = 3 ⇒ A2 = 2; 3) Составим уравнение:
(B1-3)/5 = 2; B1-3 =10; B1 = 13. Ответ: 13






















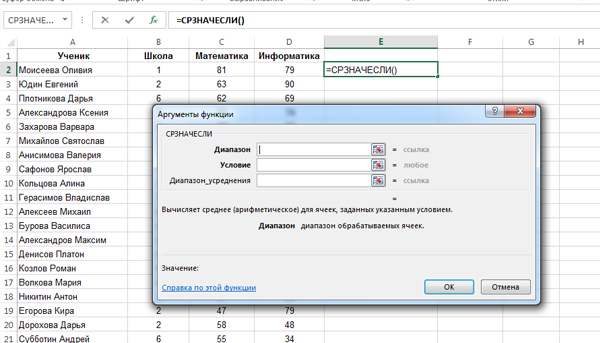
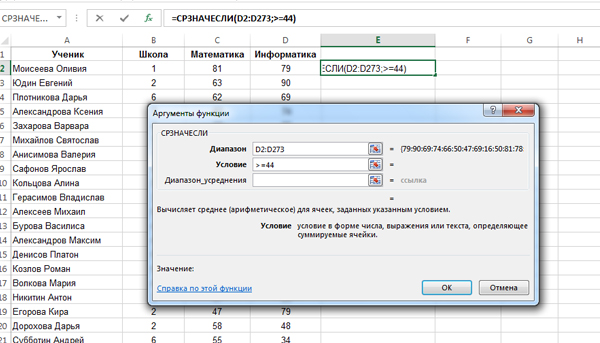
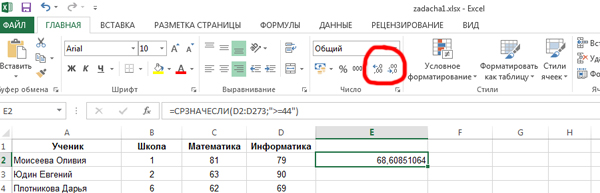
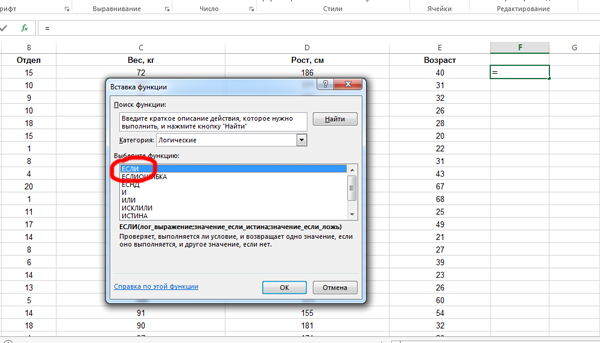
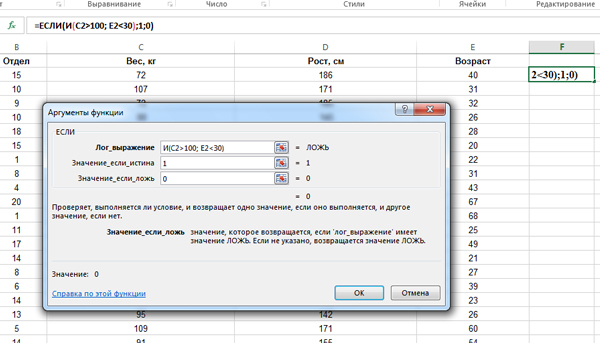
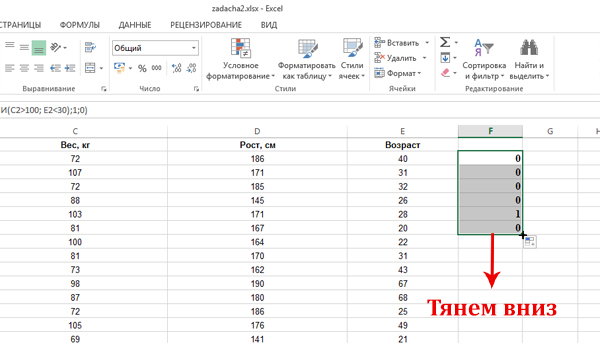
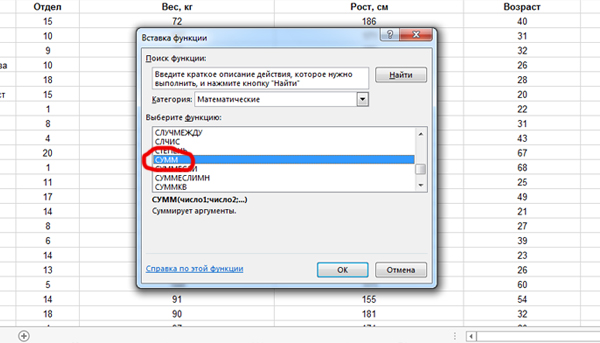
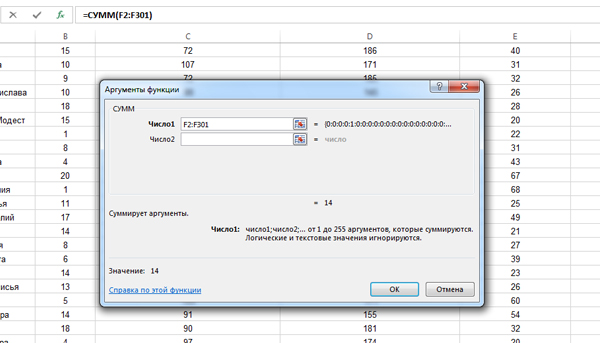
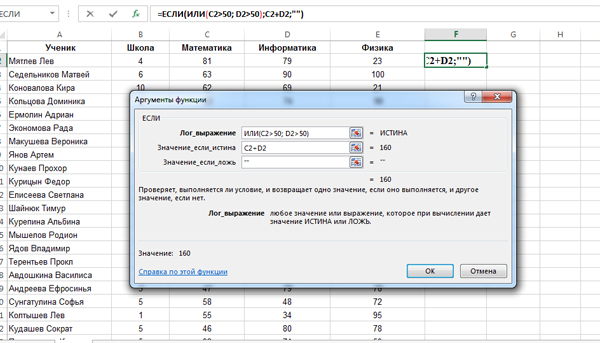
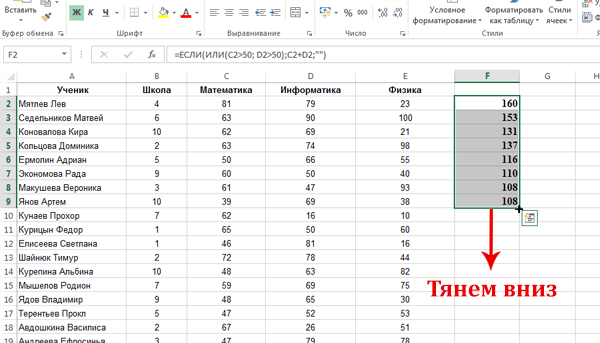
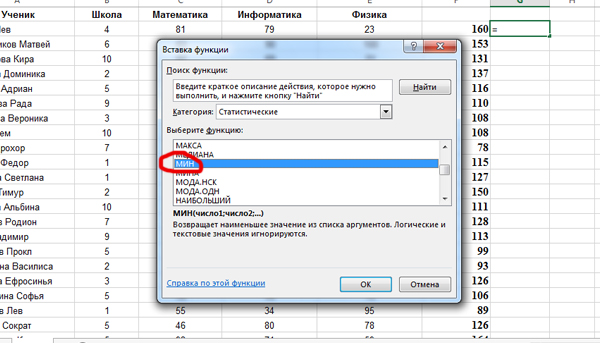
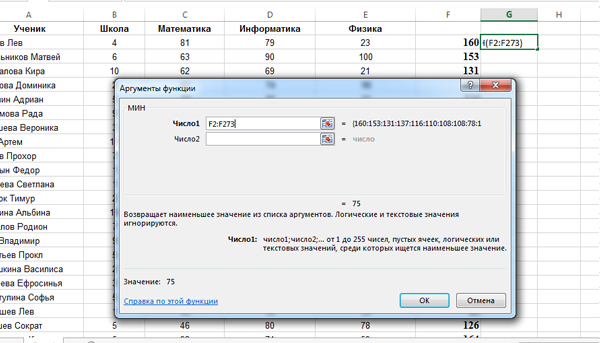
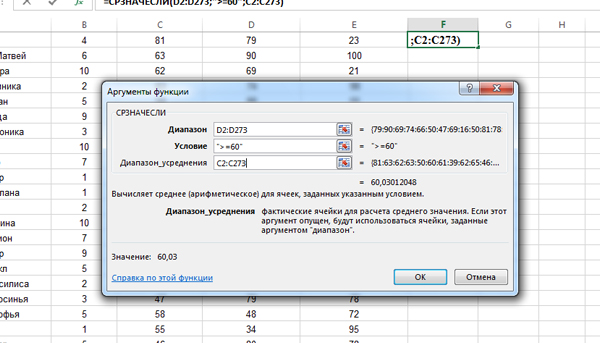
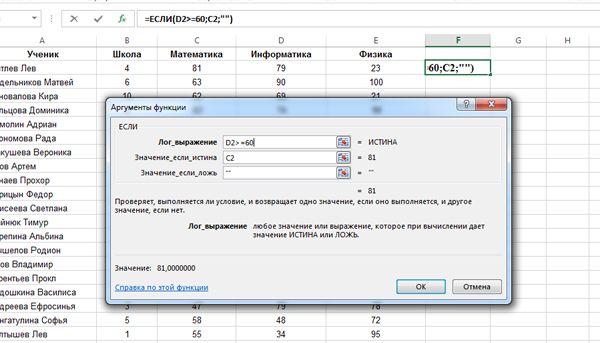
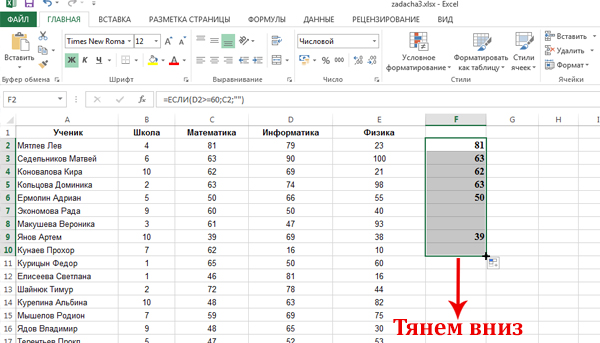
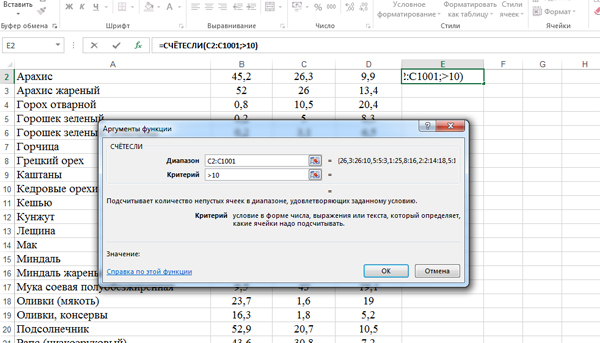
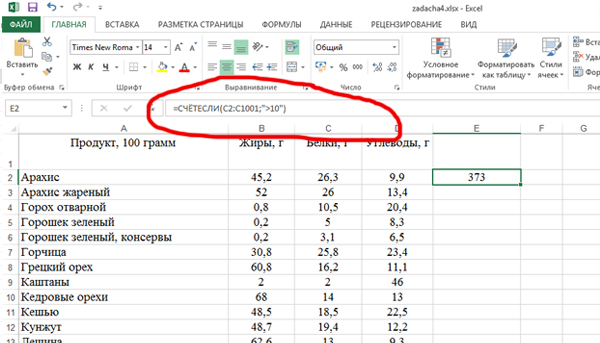
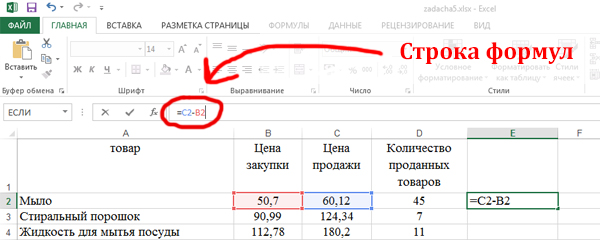
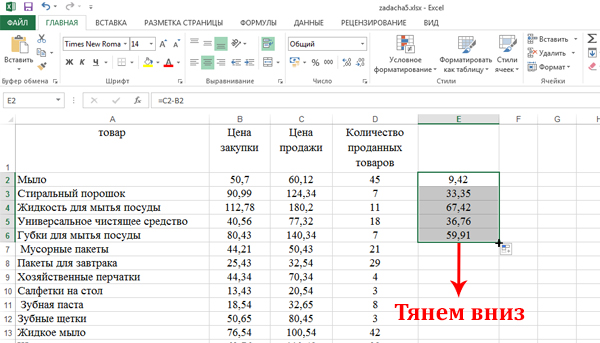
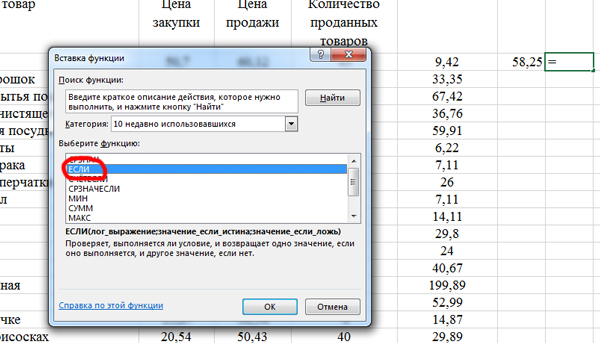
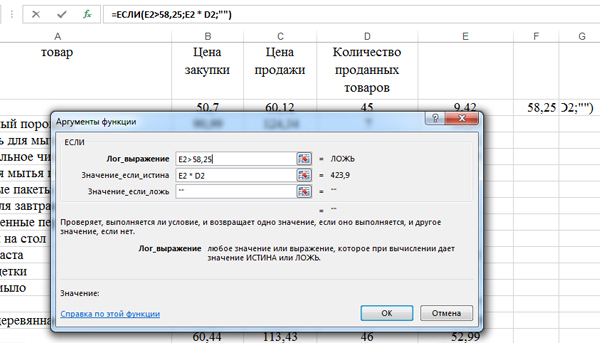
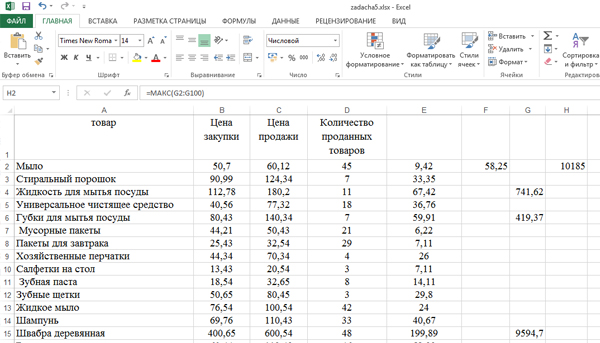


















 Вариант № 4
Вариант № 4 
 Вариант № 8
Вариант № 8 
