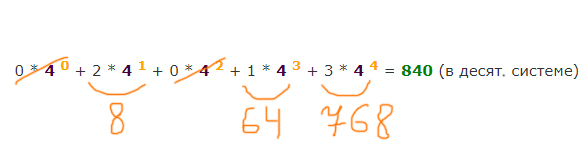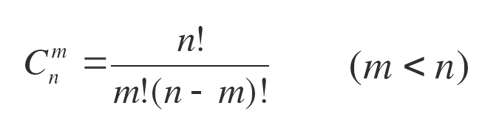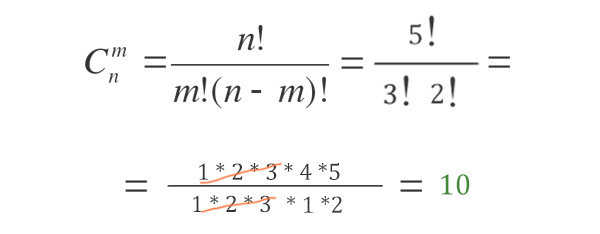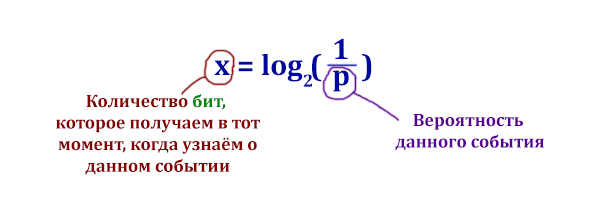Егэ по информатике факториал - Помощь в подготовке к экзаменам и поступлению

Факториалом натурального числа n (обозначается n!) называется произведение всех натуральных чисел от 1 до n. Например, 4! = 1 · 2 · 3 · 4 = 24.

Дано целое положительное число A. Необходимо найти минимальное натуральное K, для которого K! ≥ A.

Для решения этой задачи ученик написал программу, но, к сожалению, его программа неправильная.

Ниже эта программа для Вашего удобства приведена на пяти языках программирования.

Бейсик	Python
DIM A, K, F AS INTEGER INPUT A K = 0 F = 1 WHILE F <= A     K = K + 1     F = F * K WEND PRINT K END	a = int(input()) k = 0 f = 1 while f <= a:     k += 1     f *= k print(k)
Паскаль	Алгоритмический язык
var a, k, f: integer; begin     read(a);     k := 0;     f := 1;     while f <= a do begin         k := k + 1;         f := f * k     end;     writeln(k) end.	алг нач     цел a, k, f     ввод a     k := 0     f := 1     нц пока f <= a         k := k + 1         f := f * k     кц     вывод k кон
Си++
#include using namespace std; int main(){     int a, k, f;     cin >> a;     k = 0;     f = 1;     while (f <= a) {         ++k;         f *= k;     }     cout << k;     return 0; }

Последовательно выполните следующее.

1.  Напишите, что выведет эта программа при вводе A = 6.

2.  Назовите минимальное A, большее 10, при котором программа выведет неверный ответ.

3.  Найдите в программе все ошибки (их может быть одна или несколько).

Для каждой ошибки выпишите строку, в которой она допущена, и приведите эту же строку в исправленном виде.

Достаточно указать ошибки и способ их исправления для одного языка программирования.

Обратите внимание: Вам нужно исправить приведённую программу, а не написать свою. Вы можете только заменять ошибочные строки, но не можете удалять строки или добавлять новые. Заменять следует только ошибочные строки: за исправления, внесённые в строки, не содержащие ошибок, баллы будут снижаться.

Источник

16-е задание: «Вычисление рекуррентных выражений»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 9 минут.

Проверяемые элементы содержания: Вычисление рекуррентных выражений

До ЕГЭ 2021 года — это было задание № 11 ЕГЭ

Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ

Содержание:

Решение по рекуррентной формуле
Что вернет функция. Сколько символов «звездочка». Какова сумма чисел
С каким аргументом?
Не актуально для компьютерного ЕГЭ!

Решение по рекуррентной формуле

16_13:

Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1; G(1) = 1;
F(n) = F(n–1) + 3·G(n–1), при n >=2 
G(n) = F(n–1) - 2·G(n–1), при n >=2

Чему равна сумма цифр значения F(18)?

Ответ: 46

Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function F(n: integer): integer; forward;
function G(n: integer): integer; forward;
 
function F(n: integer): integer;
begin
  if n = 1 then
    F := 1  // или result := 1
  else if n >= 2 then
    F := F(n - 1) + 3 * G(n - 1)
    // или result := F(n - 1) + 3 * G(n - 1)
end;
 
function G(n: integer): integer;
begin
  if n = 1 then
    G := 1  // или result := 1
  else if n >= 2 then
    G := F(n - 1) - 2 * G(n - 1)
    // или result := F(n - 1) - 2 * G(n - 1)
end;
 
begin
  var res := F(18);
  var s := 0;
  while res > 0 do
  begin
    s := s + (res mod 10);
    res := res div 10;
  end;
  print(s)
end.

Питон:

def F( n ):
    if n == 1: 
        return 1
    elif (n >= 2):
        return F(n-1)+3*G(n-1)
def G( n ):
    if n == 1: 
        return 1
    elif (n >= 2):
        return F(n-1)-2*G(n-1)
 
res = F(18)
s = 0
while res > 0:
    s += res%10
    res = res // 10
print(s)

C++:

16_1:

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1
F(n) = F(n–1) * (n + 2), при n > 1

Ответ: 840

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET (решение №1):

function F(n: integer): integer;
begin
  if n = 1 then
    F := 1
  else if n > 1 then
    F := F(n - 1) * (n + 2)
end;
 
begin
  print(F(5))
end.

PascalABC.NET (решение №2):

function F(n:integer):integer:=
 n=1 ? 1
 :  F(n-1) * (n+2);
 
begin
  print(F(5))
end.

Питон:

def F( n ):
    if n == 1: 
        return 1
    elif (n > 1):
        return F(n-1)*(n+2)
print (F(5))

C++:

✎ Решение теоретическое (методом с конца к началу):

Из условия задания мы имеем рекуррентную формулу: F(n–1) * (n + 2) и условие остановки рекурсии: n > 1.
Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 5:

F(5) = F(4) * 7

Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(1) (при котором «сработает» остановка рекурсии). Получим:

F(5) = F(4) * 7
       F(4) = F(3) * 6
              F(3) = F(2) * 5
                     F(2) = F(1) * 4
                              1

На F(2) необходимо остановиться, так как действует условие остановки рекурсии: формула работает для n > 1. Также учтем, что по условию F(1) = 1.
Теперь с конца к началу перепишем все получившиеся сомножители и перемножим их:

1 * 4 * 5 * 6 * 7 = 840

16_2:

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(0) = 1, F(1) = 1
F(n) = 2 * F(n–1) + F(n-2), при n > 1

Чему равно значение функции F(6)? В ответе запишите только целое число.

Ответ: 99

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET (решение №2):

function F(n:integer):integer;
begin
  if (n = 0) or (n = 1) then result:=1
  else if n>1 then result:=2*F(n-1) + F(n-2);
end;
begin
  print(F(6))
end.

✎ Решение 1. Теоретическое (метод решения с начала к концу):

Из условия задания мы имеем рекуррентную формулу: 2 * F(n–1) + F(n-2) и условие остановки рекурсии: n > 1.
Из заданной рекуррентной формулы видим, что функция зависит от предыдущей функции (F(n–1)) и от пред-предыдущей функции (F(n-2)).
Так как первые два значения заданы (F(0) = 1, F(1) = 1), то можно построить таблицу последующих значений, двигаясь к числу 6:

n	0	1	2	3	4	5	6
F(n) ^{2*F(n – 1)+F(n — 2)}	1	1	2*1+1 =3	2*3+1 =7	2*7+3 =17	2*17+7 =41	2*41+17 =99

Таким образом, получаем, что при вызове функции F(6) результатом будет число 99

✎ Решение 2. Теоретическое (метод решения с конца к началу):

Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 6:

F(6) = 2*F(5) + F(4)

Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(2) (F(1) и F(0) известны из условия задачи). Получим:

F(6) = 2*F(5) + F(4)
       F(5) = 2*F(4) + F(3)
              F(4) = 2*F(3) + F(2)
                     F(3) = 2*F(2) + F(1)
                              F(2) = 2*F(1) + F(0) = 2*1+1 = 3
                                        1       1

Теперь с конца к началу перепишем все получившиеся значения функций:

F(6) = 2*F(5) + F(4) = 2*41 + 17 = 99
       F(5) = 2*F(4) + F(3) + 2*17+7 = 41 ↑
              F(4) = 2*F(3) + F(2) = 2*7+3 = 17 ↑
                     F(3) = 2*F(2) + F(1) = 2*3+1 = 7 ↑
                              F(2) = 2*F(1) + F(0) = 2*1+1 = 3 ↑  
                                        1       1

📹 Видео (теоретическое)

Видеорешение на RuTube здесь

16_10:

Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1; G(1) = 1;
F(n) = F(n–1) – G(n–1), 
G(n) = F(n–1) + 2*G(n–1), при n >= 2

Чему равно значение величины F(5)/G(5)?
В ответе запишите только целое число.

Типовые задания для тренировки

Ответ: -2

Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function F(n: integer): integer; forward;
function G(n: integer): integer; forward;
 
function F(n:integer):integer;
begin
  if n = 1 then result:=1
  else if n>=2 then result:=F(n-1) - G(n-1);
end;
 
function G(n:integer):integer;
begin
  if n = 1 then result:=1
  else if n>=2 then result:=F(n-1) + 2*G(n-1);
end;
begin
  print(F(5)/G(5))
end.

✎ Решение теоретическое:

Решим задание с вызова функций F(5) и G(5). Будем получать формулы последовательно для F(5), F(4), …, F(1), G(5), G(4), …, G(1). Дойдя до известных значений F(1) = 1 и G(1) = 1, подставим их в полученные формулы:

F(5) = F(4) – G(4)
G(5) = F(4) + 2*G(4)
	F(4) = F(3) – G(3)  
	G(4) = F(3) + 2*G(3) 
		F(3) = F(2) – G(2) 
		G(3) = F(2) + 2*G(2) 
			F(2) = F(1) – G(1) 
			G(2) = F(1) + 2*G(1) 
                               F(1) = 1; G(1) = 1;

F(2) = F(1) – G(1) = 1 - 1 = 0
G(2) = F(1) + 2*G(1) = 1 + 2 = 3
F(3) = F(2) – G(2) = 0 - 3 = -3
G(3) = F(2) + 2*G(2) = 0 + 6 = 6
F(4) = F(3) – G(3) = -3 - 6 = -9 
G(4) = F(3) + 2*G(3) = -3 + 12 = 9
F(5) = F(4) – G(4) = -9 - 9 = -18
G(5) = F(4) + 2*G(4) = -9 + 18 = 9

Итого:

F(5)/G(5) = -18/9 = -2

Что вернет функция. Сколько символов «звездочка». Какова сумма чисел

16_9:

Что вернет функция F, если ее вызвать с аргументом 6?

Паскаль:

function f(a:word):longword;
begin
  if a>0 then
    f := f(a-1)*a;
  else
    f:=1;
end;

Бейсик:

FUNCTION F(a)
  IF a > 0 THEN
     F = F(a - 1) * a
  ELSE
     F = 1;
  END IF
END FUNCTION

Python:

def F(a):
    if a > 0:
        return F(a - 1) * a
    else:
        return 1

С++:

int F(int a);
int F(int a) {
  if (a > 0)
    return F(a - 1) * a;
  else
    return 1;
}

Ответ: 720

Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

function f(a:word):longword;
begin
  if a>0 then
    f := f(a-1)*a
  else
    f:=1;
end;
begin
  print(f(6))
end.

✎ Решение теоретическое:
Рассмотрим алгоритм функции:

Если аргумент функции, т.е. a, равен единице, то функция возвращает в программу значение 1, иначе вызывается функция с аргументом a — 1 и результат этой функции умножается на a.
Это рекурсивный алгоритм вычисления факториала числа. Чтобы удостовериться в этом, выполним трассировку функции с аргументом = 6:

F(6):
6 > 0, то F(5)*6
F(5):
5 > 0, то F(4)*5
F(4):
4 > 0, то F(3)*4
F(3):
3 > 0, то F(2)*3
F(2):
2 > 0, то F(1)*2
F(1): 
1 > 0, то F(0)*1
F(0):
0 > 0 - нет, то F(0) = 1

Теперь подставляем значения, двигаясь вверх по прописанному алгоритму:
F(1)= F(0)*1 = 1*1 = 1
F(2)= F(1)*2 = 1*2 = 2
F(3)= F(2)*3 = 2*3 = 6
F(4)= F(3)*4 = 6*4 = 24
F(5)= F(4)*5 = 24*5 = 120
F(6)= F(5)*6 = 120*6 = 720

Т.е. 6! = 720

16_3:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(18)?

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
 
procedure F(n: integer);
begin
  write('*');
  if n > 10 then F(n - 2) else G(n);
end;
 
procedure G(n: integer);
begin
  write('**');
  if n > 0 then F(n - 3);
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  PRINT "*"
  IF n > 10 THEN
     F(n - 2)
  ELSE
     G(n)
  END IF
END SUB
SUB G(n)
  PRINT "**"
  IF n > 0 THEN
     F(n - 3)
  END IF
END SUB

Python:

def F(n):
  print("*")
  if n > 10:
    F(n - 2)
  else:
    G(n)
def G(n):
  print("**")
  if n > 0:
    F(n - 3)

С++:

void F(int n) {
  std::cout << "*";
  if (n > 10) {
    F(n - 2);
  }
  else {
    G(n);
  }
}
void G(int n) {
  std::cout << "**";
  if (n > 0)
    F(n - 3);
}

Типовые задания для тренировки

Ответ: 19

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var k:=0; // объявление глобальной переменной-счетчика 
procedure F(n: integer);
begin
  write('*');
  k+=1; // увеличение счетчика
  if n > 10 then F(n - 2) else G(n);
end;
 
procedure G(n: integer);
begin
  write('**');
  k+=2;// увеличение счетчика
  if n > 0 then F(n - 3);
end;
begin
 f(18);
 print(k) // вывод счетчика
end.

✎ Решение теоретическое:

Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:
*
F(n - 2) при n > 10
G(n) при n <= 10

Для G:
**
F(n - 3) при n > 0

✎ Способ 1:

Выпишем последовательность вызовов процедур, начиная с указанного в задании F(18):

F(18) -> F(16) -> F(14) -> F(12) -> F(10) -> G(10) -> 
F(7) -> G(7) -> F(4) -> G(4) -> F(1) -> G(1) -> F(-2) -> G(-2)

Обратим внимание, что независимо от условия процедура F выводит на экран одну *, а процедура G выводит две *. Посчитаем для последовательности вызовов итоговую сумму звездочек: 9F + 5G = 9*1 + 5*2 = 19

Результат: 19

✎ Способ 2:

Рассмотрим пошагово выполнение программы при вызове F(18):

1 шаг: F(18)
       *    F(16)
2 шаг:      *    F(14)
3 шаг:           *    F(12)
4 шаг:                *    F(10)
5 шаг:                     *    G(10)
6 шаг:                          **   F(7)
7 шаг:                                *  G(7)
8 шаг:                                   **  F(4)
9 шаг:                                       *    G(4)
10 шаг:                                           **   F(1)
11 шаг:                                                *   G(1)
12 шаг:                                                    **   F(-2)
13 шаг:                                                         *   G(-2)
14 шаг:                                                             **

Посчитаем количество звездочек: 19

📹 Видео (аналитическое решение)

Видеорешение на RuTube здесь

16_12:

Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(5)?

Паскаль:

procedure F(n: integer);
begin
 writeln('*');
 if n > 0 then begin
   F(n-2);
   F(n div 2);
   F(n div 2);
 end
end;

Бейсик:

DECLARE SUB F(n)
SUB F(n)
  PRINT '*'
  IF n > 0 THEN
     F(n - 2)
     F(n  2)
     F(n  2)
  END IF
END SUB

Python:

def F(n):
  print('*')
  if n > 0:    
    F(n-2)
    F(n // 2)
    F(n // 2)

С++:

void F(int n) {
  std::cout << ″*″;
  if (n > 0) {
    F(n - 2);
    F(n / 2);
    F(n / 2);
  }
}

Ответ: 34

Показать решение:

В начале каждого вызова независимо от условия на экран выводится «звездочка». Кроме того, если условие n > 0 истинно, то функция вызывается еще три раза с разными аргументами. Таким образом, каждая функция выводит на экран либо одну звездочку (если условие ложно), либо 4 звездочки если условие истинно.
Схематично рассмотрим вызов каждой функции, начиная с функции F(5). Дойдя до F(0), для которой условие будет ложно, будем подставлять полученное количество «звездочек», двигаясь опять к F(5):

F(5) = одна '*', F(3), F(2), F(2)
F(3) = одна '*', F(1), F(1), F(1)
F(2) = одна '*', F(0), F(1), F(1)
F(1) = одна '*', F(-1), F(0), F(0)
F(0) = одна '*' = 1  (условие ложно)
F(-1) = одна '*' = 1 (условие ложно)
---
Движение обратно:
F(1) = одна '*', F(-1), F(0), F(0) = 1 + 1 + 1 + 1 = 4 '*'
F(2) = одна '*', F(0), F(1), F(1) = 1 + 1 + 4 + 4 = 10 '*'
F(3) = одна '*', F(1), F(1), F(1) = 1 + 4 + 4 + 4 = 13 '*'
F(5) = одна '*', F(3), F(2), F(2) = 1 + 13 + 10 + 10 = 34 '*'

16_4:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
 
procedure F(n: integer);
begin
  writeln(n);
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  if n > 0 then F(n);
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  PRINT n
  IF n MOD 2 = 0 THEN
     F(n  2)
  ELSE
     G ( (n - 1)  2)
  END IF
END SUB
SUB G(n)
  PRINT n
  IF n > 0 THEN
     F(n)
  END IF
END SUB

Python:

def F(n):
  print(n)
  if n % 2 == 0:
    F(n // 2)
  else:
    G((n - 1) // 2)
def G(n):
  print(n)
  if n > 0:
    F(n)

С++:

void F(int n) {
  std::cout << n << endl;
  if (n % 2 == 0) {
    F(n / 2);
  }
  else {
    G((n - 1) / 2) ;
  }
}
void G(int n) {
  std::cout << n << endl;
  if (n > 0)
    F(n);
}

Типовые задания для тренировки

Ответ: 40

Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var sum:=0; // сумматор
procedure F(n: integer);
begin
  writeln(n);
  sum+=n; // добавляем число в сумматор
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  sum+=n; // добавляем число в сумматор
  if n > 0 then F(n);
end;
begin
  F(17);
  print('sum =',sum)
end.

✎ Решение теоретическое:

Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:
n
F(n div 2) при n - четное (n mod 2 = 0)
G((n - 1) div 2) при n - нечетное

Для G:
n
F(n) при n > 0

Выпишем последовательность вызовов процедур, начиная с указанного в задании F(17).
Обратим внимание, что независимо от условия как процедура F выводит на экран n, так и процедура G выводит n.

F(17) -> n - нечетное, G(8) вывод 17
G(8) -> F(8)                вывод 8
F(8) -> n - четное, F(4)    вывод 8
F(4) -> n - четное, F(2)    вывод 4 
F(2) -> n - четное, F(1)    вывод 2
F(1) -> n - нечетное, G(0)  вывод 1
G(0)                        вывод 0

Сумма:

17 + 8 + 8 + 4 + 2 + 1 + 0 = 40

16_5:

Ниже записаны две рекурсивные функции (процедуры): F и G.
Чему будет равно значение, вычисленное при выполнении вызова F(6)?

Паскаль:

function F(n: integer):integer; forward;
function G(n: integer):integer; forward;
function F(n:integer):integer;
begin
 if (n > 2) then
 F:= F(n - 1) + G(n - 2)
 else F:= n;
end;
function G(n:integer):integer;
begin
 if (n > 2)then
 G:= G(n - 1) + F(n -2)
 else G:= n+1;
end;

Бейсик:

FUNCTION F(n)
  IF n > 2 THEN
     F = F(n - 1) + G(n - 2)
  ELSE
     F = n;
  END IF
END FUNCTION 
FUNCTION G(n)
  IF n > 2 THEN
     G = G(n - 1) + F(n -2)
  ELSE
     G = n+1;
  END IF
END FUNCTION

Python:

def F(n):
    if n > 2:
        return F(n - 1) + G(n - 2)
    else:
        return n
def G(n):
    if n > 2:
        return G(n - 1) + F(n - 2)
    else:
        return n+1

С++:

int F(int n);
int G(int n);
int F(int n) {
  if (n > 2)
    return F(n - 1) + G(n - 2);
  else
    return n;
}
int G(int n) {
  if (n > 2)
    return G(n - 1) + F(n - 2);
  else
    return n + 1;
}

Типовые задания для тренировки

Ответ: 17

✍ Показать решение:

Результат:

📹 Видео (аналитическое решение)

Видеорешение на RuTube здесь

С каким аргументом?

16_8:

Вызов представленной ниже рекурсивной функции приводит к появлению на экране чисел и точек. С каким минимальным натуральным аргументом а нужно вызвать эту функцию, чтобы в результате на экране появилось 5 точек (не обязательно подряд, между точками могут встречаться числа)?
Паскаль:

function gz(a:integer):integer;
var p:integer;
begin
  if a<1 then begin 
   gz:=1; exit; 
  end;
  if a mod 3=0 then begin
   write('...');
   p:=gz(a div 3)+gz(a div 4);
  end
  else begin
    write('.');
    p:=gz(a div 4);
  end;
  write(p);
  gz:=2; 
end;

Ответ: 6

✍ Показать решение:

✎ Решение с использованием программирования:

PascalABC.NET:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
var sum:=0; // сумматор
procedure F(n: integer);
begin
  writeln(n);
  sum+=n; // добавляем число в сумматор
  if n mod 2  =0 then F(n div 2) 
  else G((n - 1) div 2);
end;
 
procedure G(n: integer);
begin
  writeln (n); 
  sum+=n; // добавляем число в сумматор
  if n > 0 then F(n);
end;
begin
  F(17);
  print('sum =',sum)
end.

Результат: 6

📹 Видео (аналитическое)
📹 Видеорешение на RuTube здесь (аналитическое)

Не актуально для компьютерного ЕГЭ!

Все числа, которые будут напечатаны на экране, в том же порядке

Демоверсия ЕГЭ 2018 информатика:

Ниже на пяти языках программирования записан рекурсивный алгоритм F.
Паскаль:

procedure F(n: integer);
begin
if n > 0 then
begin
  write(n);
  F(n - 3);
  F(n div 3)
end
end;

Бейсик:

SUB F(n)
  IF n > 0 THEN
     PRINT n
     F(n - 3)
     F(n  3)
  END IF
END SUB

Python:

def F(n):
  if n > 0:
     print(n)
     F(n - 3)
     F(n // 3)

С++:

void F(int n){
  if (n > 0){
    std::cout <<n;
    F(n - 3);
    F(n / 3);
  }
}

Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(9). Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Похожие задания для тренировки

Ответ: 9631231

✍ Показать решение:

В данном фрагменте программы рекурсивная процедура вызывает саму себя дважды.
Благодаря условию, находящемуся в процедуре (if n > 0 — условие остановки рекурсии), обеспечивается выход из рекурсии и не происходит «зацикливания».
Выполнение процедур закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 0 перестанет работать (т.е. когда параметр процедуры n станет <= 0).
div — целочисленное деление, т.е., например:

5 div 2 = 2
1 div 2 = 0

Отобразим пошагово выполнение каждой процедуры, двигаясь сверху вниз и оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

   F(9)
1: 9  F(6)    (9 - 3 = 6)
2:     6   F(3)    (6 - 3 = 3)
3:          3    F(0)    (3 - 3 = 0, условие не работает)
4:         F(1)  (3 div 3 = 1)
5:          1    F(-2)    (1 - 3 = -2, условие не работает)
6:         F(0)    (1 div 3 = 0, условие не работает)
7:    F(2) (6 div 3 = 2)
8:     2   F(-1)    (2 - 3 = -1, условие не работает)
9:    F(0)    (2 div 3 = 0, условие не работает)
10:F(3)  (9 div 3 = 3)
11:3  F(0)     (3 - 3 = 0, условие не работает) 
12:F(1)  (3 div 3 = 1)   
13: 1   F(-2)     (1 - 3 = -2, условие не работает)

Выделены те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.
Перепишем по порядку все выводимые на экран числа сверху вниз: 9631231

📹 Видео 1 способ
📹 Видеорешение на RuTube здесь

📹 Видео 2 способ
📹 Видеорешение на RuTube здесь

16_7:

Ниже записан рекурсивный алгоритм F. Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(130).
Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Паскаль:

procedure F(n: integer);
begin
  if n > 1 then
  begin
    write(n);
    F(n div 10);
    F(n - 40)
   end
end;

Бейсик:

SUB F(n)
  IF n > 1 THEN
     PRINT n
     F(n  10)
     F(n - 40)
  END IF
END SUB

Python:

def F(n):
  if n > 1:
     print(n)
     F(n // 10)
     F(n - 40)

С++:

void F(int n){
  if (n > 1){
    std::cout <<n;
    F(n / 10);
    F(n - 40);
  }
}

Ответ: 1301390950510

✍ Показать решение:

В данном фрагменте программы рекурсивная процедура F вызывает саму себя дважды.
В процедуре находится условие if n > 1 — условие остановки рекурсии, благодаря которому обеспечивается выход из рекурсии и не происходит «зацикливания».
Выполнение фрагмента программы закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 1 перестанет работать (т.е. когда параметр процедуры n станет <= 1).
div — целочисленное деление, т.е., например:

5 div 3 = 1
1 div 3 = 0

Выполним трассировку кода процедуры: двигаться будем пошагово сверху вниз, оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

   F(130) 130  
1: ➥  F(13) (130 div 10 = 13) 13
2:           ➥ F(1) условие не работает! 1 ≤ 0
3:           ➥ F(-27) условие не работает! -27 ≤ 0
4: ➥  F(90) (130 - 40 = 90) 90        
5:           ➥ F(9) (90 div 10 = 9) 9
6:                    ➥ F(0) условие не работает! 0 ≤ 0
7:                    ➥ F(-31) условие не работает! -31 ≤ 0
8:           ➥  F(50) (90 - 40 = 50) 50
9:                     ➥  F(5) (50 div 10 = 5) 5
10:                              ➥ F(0) условие не работает! 0 ≤ 0
11:                              ➥ F(-35) условие не работает! -35 ≤ 0
12:                    ➥  F(10) (50 - 40 = 10) 10
13:                              ➥ F(1) условие не работает! 1 ≤ 0
14:                              ➥ F(-30) условие не работает! -30 ≤ 0

Выделены красным цветом те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.
Перепишем сверху вниз все выводимые на экран числа: 1301390950510

Результат: 1301390950510

📹 Видео

📹 Видеорешение на RuTube здесь

16_11:

Определите, что выведет на экран программа при вызове F(5).

Паскаль:

procedure F(n: integer); forward;
procedure G(n: integer); forward;
procedure F(n: integer);
begin
  if n > 2 then
   begin
    write(n);
    F(n - 1);
    G(n - 2);
   end
  else
    write(n+2);
end;
procedure G(n: integer);
begin
  write(n);
  if n > 2 then
   begin
    G(n - 1);
    F(n - 2);
   end;
end;

Бейсик:

DECLARE SUB F(n)
DECLARE SUB G(n)
SUB F(n)
  IF n > 2 THEN
     PRINT n
     F(n - 1)
     G(n - 2)
  ELSE
     PRINT n+2
  END IF
END SUB
SUB G(n)
  PRINT n
  IF n > 2 THEN
     G(n - 1)
     F(n - 2)
  END IF
END SUB

Python:

def F(n):
    if n > 2:
        print(n, end='')
        F(n - 1)
        G(n - 2)
    else:
        print(n+2, end='')
 
def G(n):
    print(n, end='')
    if n > 2:
        G(n - 1)
        F(n - 2)

С++:

void G(int n);
void F(int n) {
	if (n > 2) {
	  std::cout << n;
	  F(n - 1);
	  G(n - 2);		
	  }
	else
	  std::cout << n+2;
}
void G(int n) {
	std::cout << n;
	if (n > 2) {
	  G(n - 1);
	  F(n - 2);
	  } 
}

Типовые задания для тренировки

Ответ: 543412323

Показать решение:

При истинности условия функция F также, как и функция G «запускает» еще две функции: функция F: 1)F(n — 1) и 2)G(n — 2), а функция G: 1)G(n — 1) и 2)F(n — 2).
Рассмотрим последовательно алгоритм работы функций, нумеруя вызовы функций. Для удобства будем делать отступы для каждой функции. Таким образом, для вызова каждой функции должно быть два внутренних вызова:

F(5) = 5 (на экране)
1) F(n - 1), т.е. F(4)
    F(4) = 4(на экране)
    1) F(n - 1), т.е. F(3)
           F(3) = 3(на экране)
           1) F(n - 1), т.е. F(2)
                  F(2) = n + 2 = 4 (на экране) (блок else)
           2) G(n - 2), т.е. G(1)
   	          G(1) = 1 (на экране)
    2) G(n - 2), т.е. G(2)
	   G(2) = 2 (на экране)
2) G(n - 2), т.е. G(3)
    G(3) = 3 (на экране)
    1)G(n - 1), т.е. G(2)
           G(2) = 2 (на экране)
    2) F(n - 2), т.е. F(1)
           F(1) = n + 2 = 3 (на экране) (блок else)

Перепишем сверху вниз все цифры, выведенные на экран:

543412323

Источник

Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.

Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.

Задача (Классика)

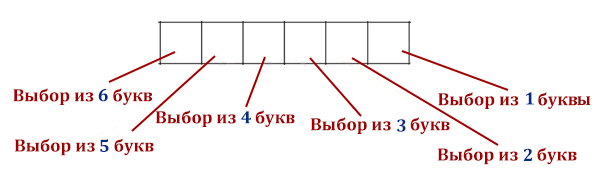
Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:

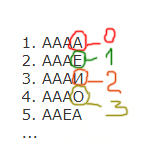
1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…

Запишите слово, стоящее на 248-м месте от начала списка.

Решение:

Обозначим условно А — 0, Е — 1, И — 2, О — 3.

Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.

Теперь запишем список с помощью цифр.

1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…

Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.

Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.

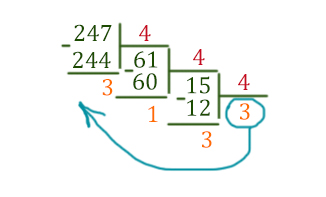
Переведём число 247 в четверичную систему!

Получилось число 3313₄ в четверичной системе. Сделаем обратное декодирование в буквы. Таким образом, ответ будет ООЕО.

Ответы: ООЕО

Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.

Задача (Классика, Другая вариация)

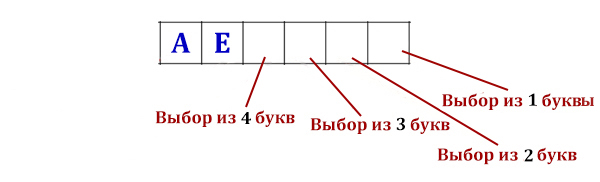
Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:

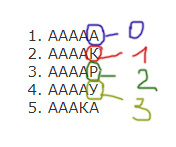
1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА

Решение:

Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.

У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.

1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……

Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!

Получили число в четверичной системе 31020₄. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 31020₄ из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.

Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу 840 нужно прибавить 1, и в ответе будет 841

Ответ: 841

Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)

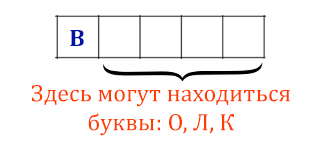
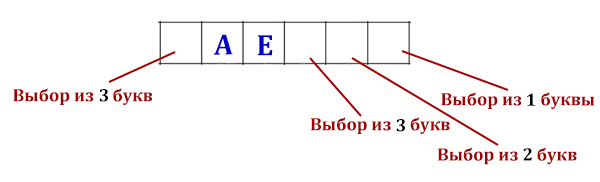
Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И,
записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.

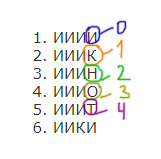
1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…

Под каким номером в списке идёт первое слово, которое начинается
с буквы О?

Решение:

Закодируем буквы цифрами.

Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.

Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 3000₅. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.

Теперь, как в предыдущей задаче, переведём число 3000₅ из пятеричной системы в десятичную.

0 * 5 ⁰ + 0 * 5 ¹ + 0 * 5 ² +
3 * 5 ³ = 375 (в десят. системе)

Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.

Ответ: 376

Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)

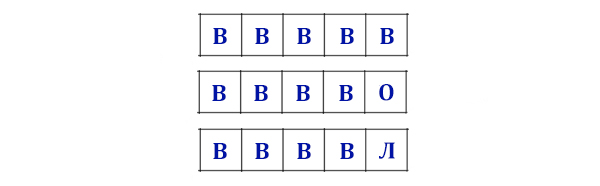
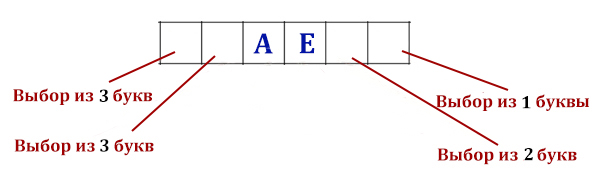
Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К,
причём буква В используется в каждом слове ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или
не встречаться совсем. Словом считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?

Решение:

Для начала решим вводную подзадачу.

Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или
не встречаться совсем. Сколько можно составить 5-буквенных слов ?

Т.е буквы могут повторяться!

Например

Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.

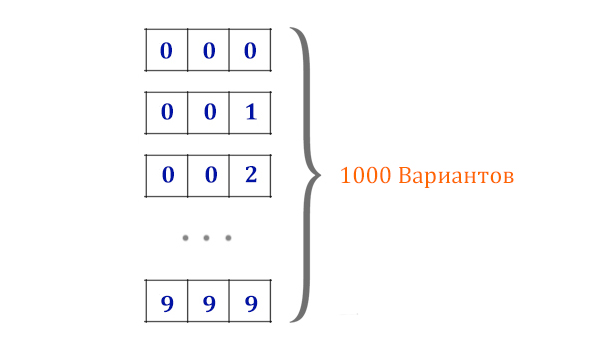
Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?

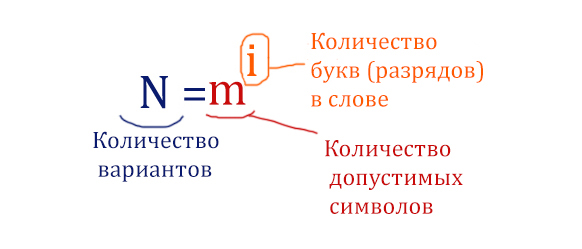
Выведем общую формулу для количества вариантов, когда символы могут повторяться!

Для трёхразрядных чисел от 000 до 999:

N = 10³ = 1000 вариантов.

Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).

N = 4⁵ = 1024 вариантов.

Вернёмся к изначальной задаче. Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!

Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).

N = 3⁴ = 81 комбинация.

Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.

Таким образом, окончательный ответ будет:

N = 81 * 5 = 405 различных вариантов.

Ответ: 405

Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!

Задача(Закрепление формулы)

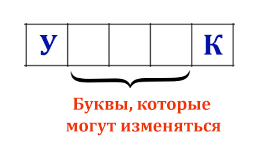
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?

Решение:

Применим главную формулу 8 задания из ЕГЭ по информатике

N = mⁱ = 6³ = 216

Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.

В ответе будет 216.

Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!

Ответ: 216

Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)

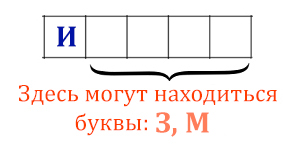
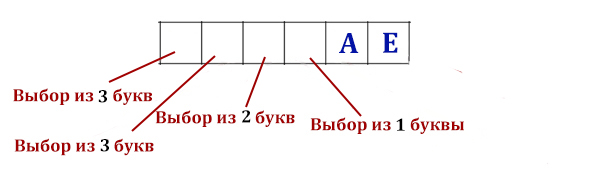
Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А,
причём в каждом слове есть ровно одна гласная буква и она встречается
ровно 1 раз. Каждая из допустимых согласных букв может встречаться
в слове любое количество раз или не встречаться совсем. Словом считается
любая допустимая последовательность букв, не обязательно осмысленная.
Сколько существует таких слов, которые может написать Вася?

Решение:

Рассмотрим количество вариантов, когда гласная И стоит в первом месте!

Подсчитаем количество слов с помощью супер-формулы

N = mⁱ = 2⁴ = 16

Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.

Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.

Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160

Ответ: 160

Отработаем главную формулу 8 задания из ЕГЭ по информатике.

Задача (Развиваем понимание формулы!)

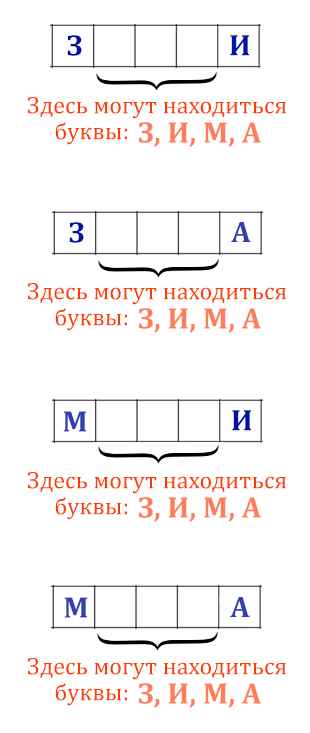
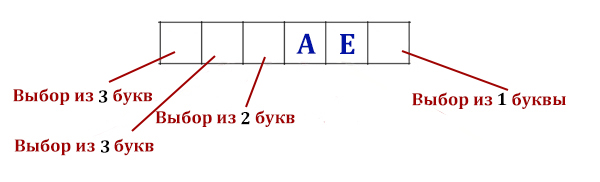
Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Решение:

Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная

Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.

N = mⁱ = 4³ = 64

Длина изменяющихся ячеек равна 3, а количество возможных букв 4.

Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256

Ответ: 256

Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.

Задача (Другой метод решения!!)

Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?

Решение:

Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!

Решим вводную подзадачу (без дополнительных ограничений).

Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .

Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!

N = 6 * 5 * 4 * 3 * 2 * 1 = 720

Вернёмся к изначальной задаче!

В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.

N = 5 * 5 * 4 * 3 * 2 * 1 = 600

В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.

Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ

Узнаем количество вариантов в каждом таком случае.

N1 = 4 * 3 * 2 * 1 = 24

На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.

N2 = 3 * 3 * 2 * 1 = 18

Аналогично предыдущему случаю.

N3 = 3 * 3 * 2 * 1 = 18

N4 = 3 * 3 * 2 * 1 = 18

N5 = 3 * 3 * 2 * 1 = 18

Всего слов с сочетанием АЕ будет

24 + 18 + 18 + 18 + 18 = 96

Значит, всего слов, которые удовлетворяют условию задаче будет

N = 600 — 96 = 504

Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 6³ = 216

Ответ: 504

Задача (Закрепления «метода умножения»)

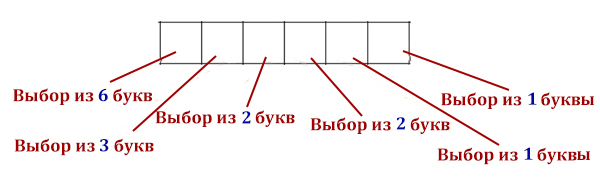
Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?

Решение:

Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».

На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.

Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.

N = 6 * 3 * 2 * 2 * 1 * 1 = 72

Ответ: 72

Задача (Азбука Морзе)

Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?

Решение:

Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.

У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.

Подсчитаем общее количество вариантов.

N = 2³ + 2⁴ = 8 + 16 = 24 комбинаций.

Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать

Ответ: 24

Задача (Обратная предыдущей)

Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?

Решение:

Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.

N = 4^x = 300

Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4^x больше 300.

4⁵ = 1024

Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!

Ответ: 5

Задача (Важная!)

Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?

Решение:

На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.

Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.

n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).

Восклицательный знак — это факториал!

Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»

Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.

Ответ: 10

Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.

Задача (Главная формула + сочетания)

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?

Решение:

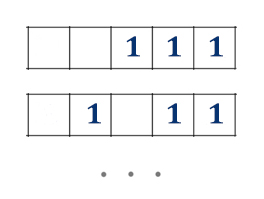
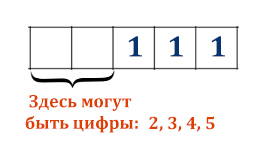
В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!

Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики. Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.

Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.

Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.

N = mⁱ = 4² = 16

Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160

Ответ: 160

Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.

Задача (Таблица соревнований)

Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?

Решение:

Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.

	1 команда	2 команда	3 команда	…	20 команда
1 дисциплина	1	—	1	…	3
2 дисциплина	—	2	1	…	2
…	…	…	…	…	…
10 дисциплина	1	1	2	…	—

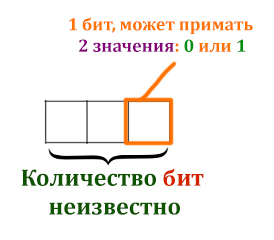
В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.

Сделав рисунок, задача обрела привычные очертания.

Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.

N = mⁱ = 2ⁱ = 4

i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)

Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.

Всего ячеек = 20 * 10 = 200

Тогда вся таблица будет весит:

V = 2 бита * 200 = 400 бит.

Ответ: 400

Формула Шеннона

Задача (Формула Шеннона)

В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

Решение:

Данную задачу нужно решать по формуле Шеннона

Найдём вероятность p того, что вытащили чёрный шарик.

p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + = 8 / 32 = 1 /4

p = 1 / 4

Применим формулу Шеннона.

x = log₂(4)
2^x = 4

x = 2 бита

Ответ: 2

Доброго времени суток ! Помогите пожалуйста решить задачу .) Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?

В закрытом ящике находится 32 карандаша, некоторые из них синего цвета. Наугад вынимается один карандаш. Сообщение «этот карандаш – НЕ синий» несёт 4 бита информации. Сколько синих карандашей в ящике?
Был бы очень рад , если вы разберете и эту задачку

Добрый день. Полностью разобрал этот номер, но наткнулся на один интересный пример. Объясните доступным языком, пожалуйста. На решу егэ вообще не понял их решение:

Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Т должна входить в код не менее одного раза, а буква Й — не более одного раза. Сколько различных кодов может составить Тимофей? (ответ: 8006)

Добрый день! Подскажите пожалуйста, как решить следующую задачу: Сколько существует чисел, шестнадцатеричная запись которых содержит 3 цифры, причём все цифры различны и никакие две чётные и две нечётные цифры не стоят рядом.

Петя составляет семибуквенные слова перестановкой букв слова АССАСИН. Сколько всего различных слов может составить Петя? Мое решение: 21 вариант с буквой А, 35- с буквой С, и 4 на буквы И и Н. Всего 60 и умножаем на 7. Получается 420. Не уверена, что применила верный алгоритм. Прокомментируйте, пожалуйста, решение

Можете заказать решение задачи через раздел «связь».

В Задаче (Другой метод решения!!) допущена ошибка в решении, ведь 24 + 18 + 18 + 18 + 18 = 114,значит N = 600 — 114 = 486!

Добрый день! Помогите пожалуйста решить задачку
Сколько чисел длиной 6 можно составить, если известно, что цифры идут в порядке убывания, при этом четные и нечетные цифры чередуются?

У меня только один вопрос. Почему в школах на уроках информатики вместо действительно полезного изучения какого нибудь языка программирования, заставляют заниматься вот этой вот ересью и решать какое по счету слово напишет Вася? Я могу только составить в ответ на это только слова которые нельзя здесь писать. От таких знаний и занятий ни один ребенок не захочет стать программистом, потому что это непонятно, и неизвестно зачем уметь решать такие задачи. Я сам программист с 10 летним стажем не смог объяснить ребенку как решать некоторые задачи и самое главное, я не знаю зачем дети должны уметь это решать.

Дмитрий, согласен с Вами. Особенно 11 задание и формула Шеннона. Надо либо излагать задание корректно, либо исключить вообще: «В корзине лежат черные и белые шары. Среди них 18 черных шаров. Сообщение о том, что достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?» — для двух состояний достаточно одного бита.

marvell special for u

c = 0
from itertools import*
for i in permutations(‘МАТВЕЙ’, r=6):
i = ».join(i)
if i[0] != ‘Й’ and i.count(‘АЕ’) == 0:
print(i)
c += 1
print(c)

Источник

В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.

Рекурсивные функции с возвращаемыми значениями

Задание 6 (ИНФ-11 ЕГЭ 2023_ДЕМО)

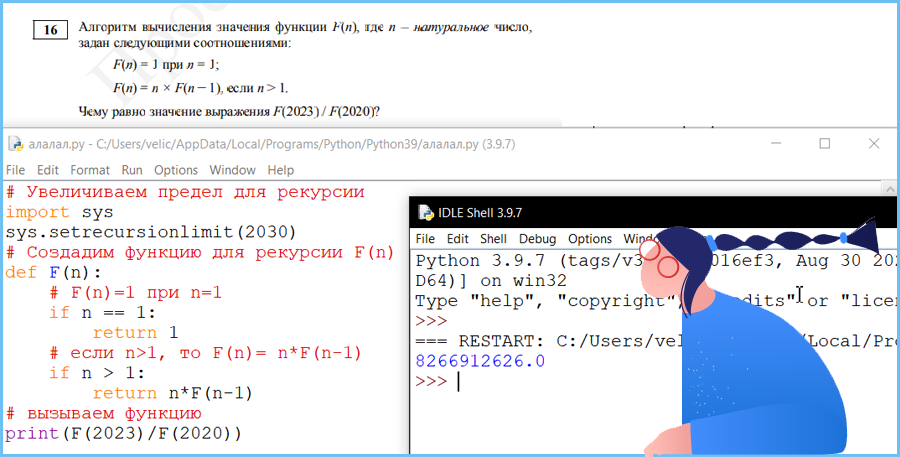
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?

Вариант программы 1

Лимит рекурсии по умолчанию в Python является 1000, вы получите ошибку « RecursionError: максимальная глубина рекурсии превышена в сравнении »
Это может быть исправлено, увеличивая предел рекурсиона в Python, ниже – фрагмент о том, как вы можете увеличить предел рекурсии.

import sys
sys.setrecursionlimit(2030)

Вариант программы 2

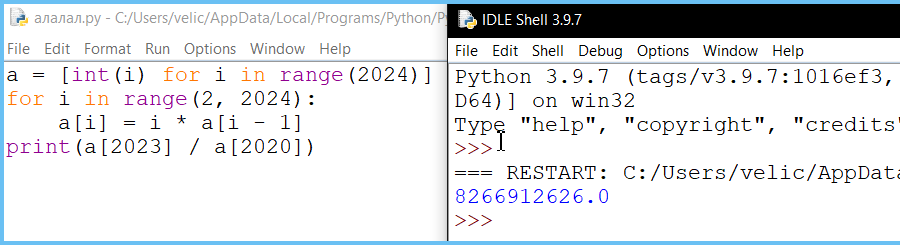
Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Решу ЕГЭ)

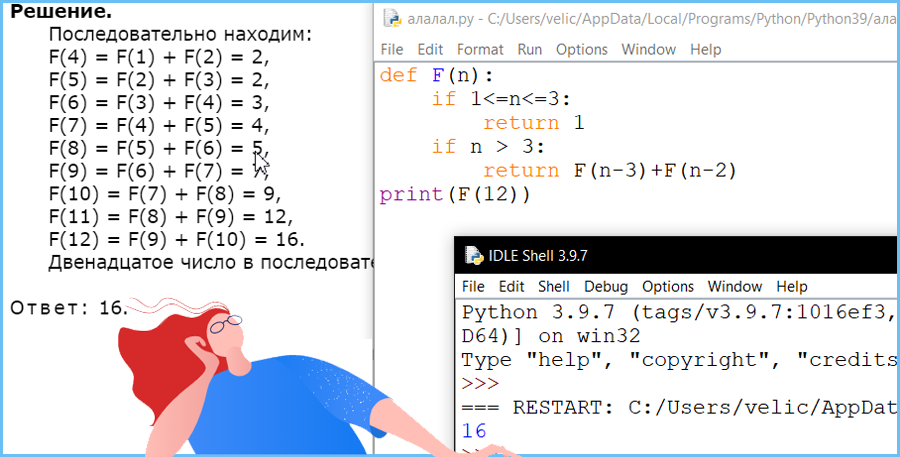
Последовательность чисел Падована задается рекуррентным соотношением:

F(1) = 1

F(2) = 1

F(3) = 1

F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное число.

Чему равно двенадцатое число в последовательности Падована?

В ответе запишите только натуральное число.

Задание 6 (Решу ЕГЭ)

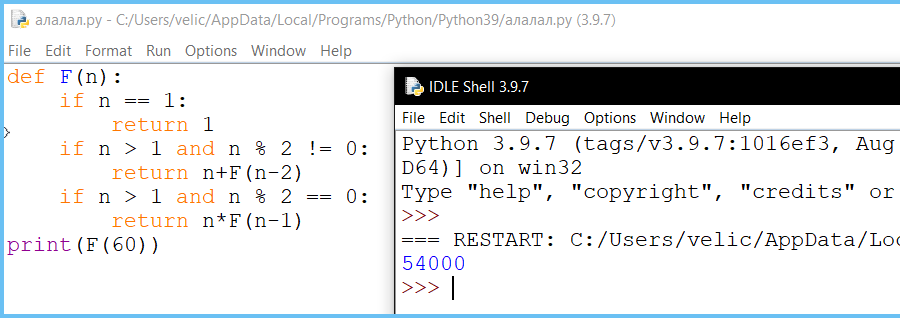
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(1) = 1;

F(n) = n + F(n − 2), если n — нечётно, и n > 1;

F(n) = n × F(n − 1), если n — чётно.

Чему равно значение функции F(60)?

Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Решу ЕГЭ)

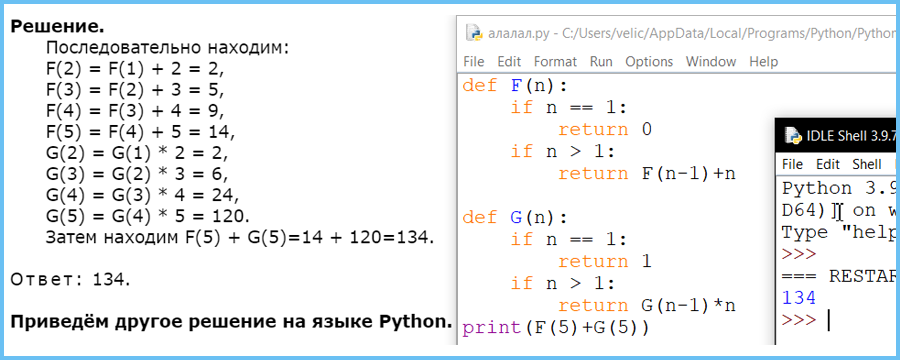
Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 0

F(n) = F(n–1) + n, при n >1

G(1) = 1

G(n) = G(n–1) * n, при n >1

Чему равно значение функции F(5) + G(5)?

В ответе запишите только натуральное число.

Сложные задачи

Задание 6 (Поляков ЕГЭ)

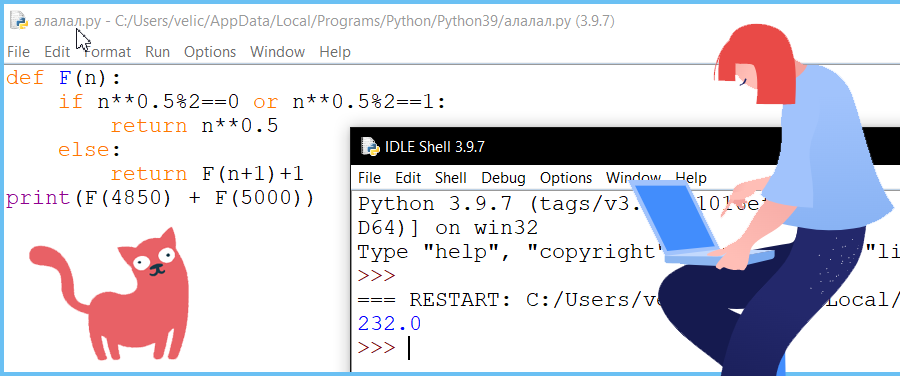
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = sqrt(n), если sqrt(n) – натуральное число,
F(n) = F(n + 1) + 1, если sqrt(n) – дробное число.
Чему равно значение выражения F(4850) + F(5000)?

При делении натурального числа на 2 мы получаем в остатке (%) или 0 или 1 (чётные и нечётные числа), таким образом проверяем, если корень дает четное или нечётное целое число, то выводим корень этого числа во всех остальных случаях применяет функцию F(n+1)+1
sqrt(n) запишем как n**0.5, что бы не подключать дополнительный математический модуль из библиотеки

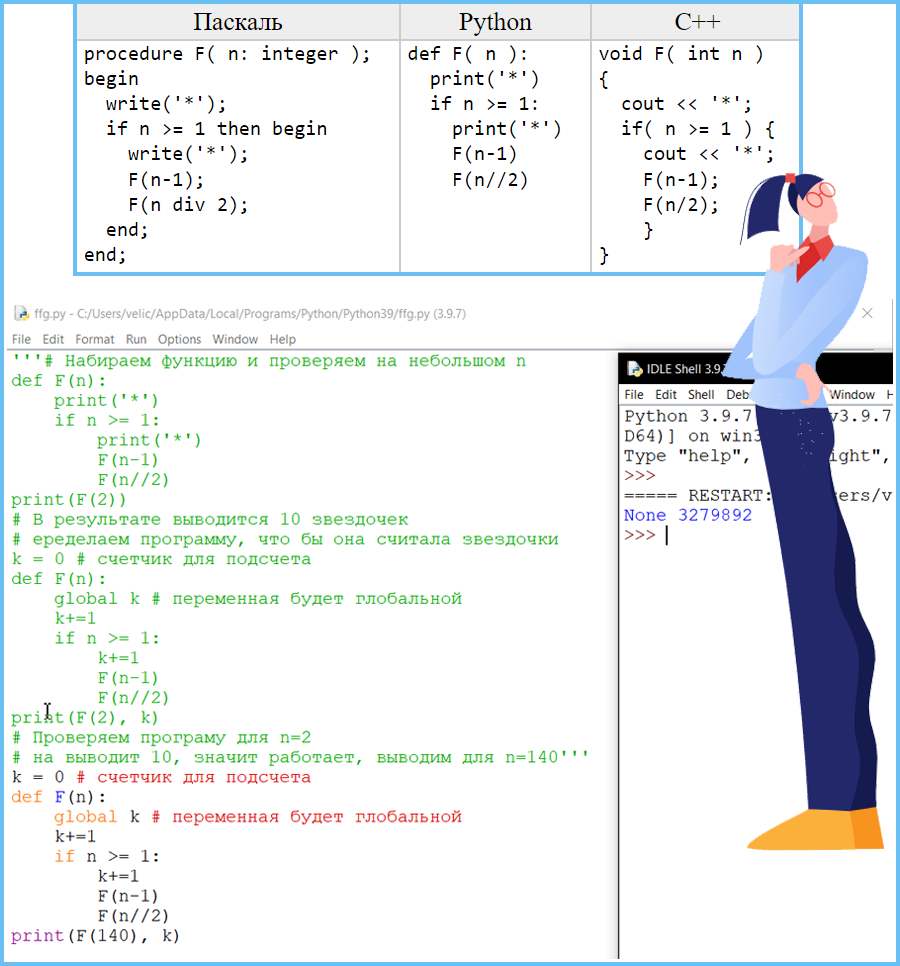
Задание 6 (Поляков ЕГЭ)

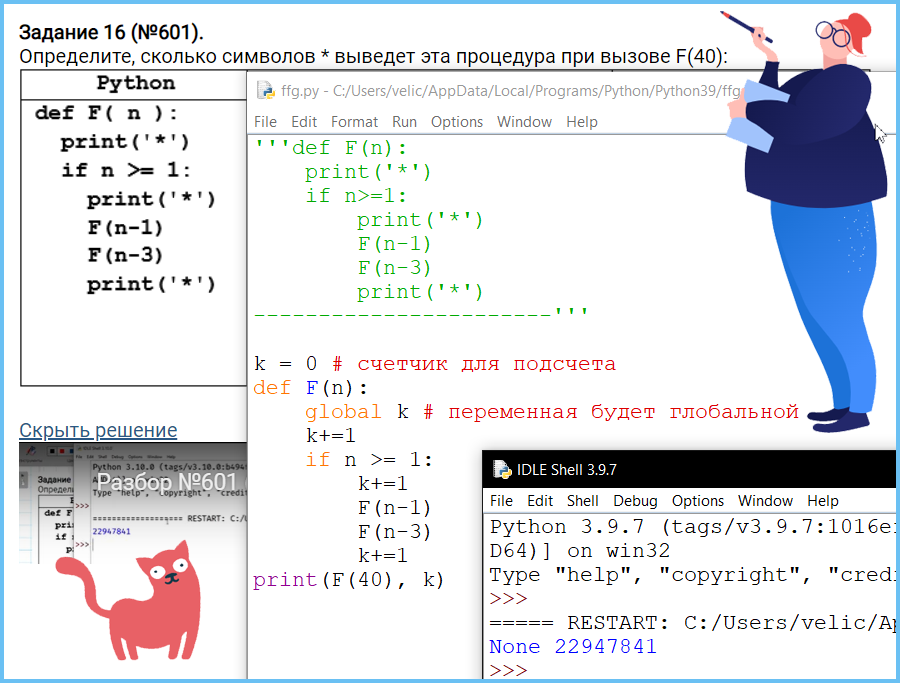
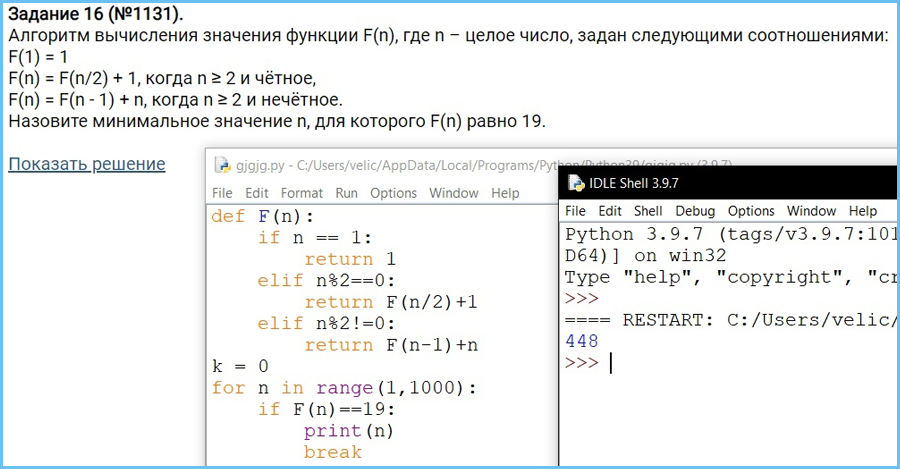
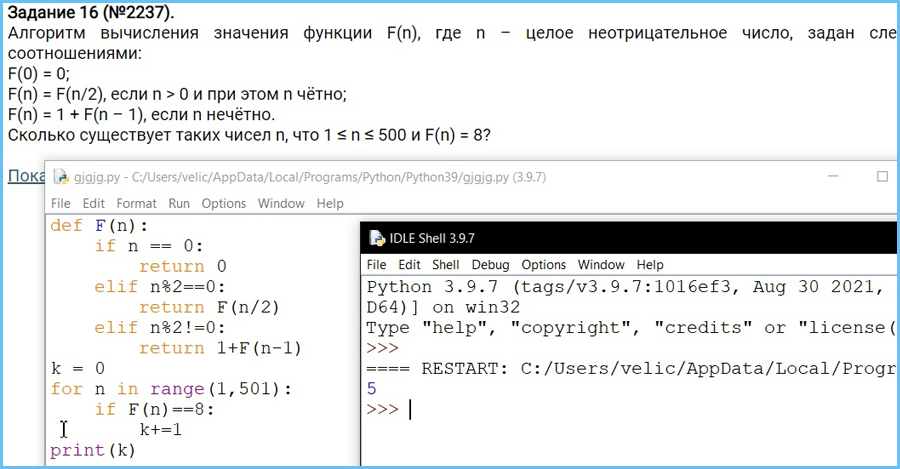
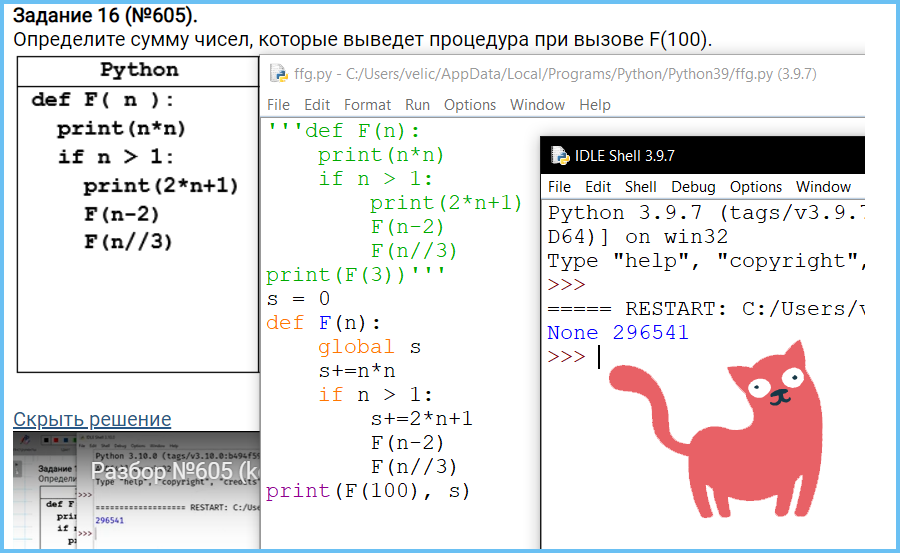
Определите, сколько символов * выведет эта процедура при вызове F(140):

Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Поляков ЕГЭ)

(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n!, если n ≥ 5000,
F(n) = 2 · F(n + 1) / (n + 1), если 1 ≤ n < 5000.
Чему равно значение выражения 1000 · F(7) / F(4)?
Примечание.
Факториал числа n, который обозначается как n!, вычисляется по формуле n!=1·2·…·n.

Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для проведения вычислений с вещественными числами (числами с плавающей точкой).

Для использования этих функций в начале программы необходимо подключить модуль, что делается командой import:
# программный код
import math
num1 = math.sqrt(2) # вычисление корня квадратного из двух
Как можно заметить из примера выше, для вызова функции мы вынуждены указывать название модуля и символ точки. С другой стороны, если функции используются достаточно часто, то такой вызов (постоянное указание названия модуля и символа точки) может усложнить программу и сделать её менее читабельной. Для того, чтобы не указывать название модуля и символ точки при вызове функций, мы пишем следующий код:

# программный код
from math import *
Если нужно использовать только некоторые функции модуля, то мы можем импортировать только их следующим образом:
from math import sqrt, ceil, factorial

ещё не решила)

Источник

№1. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(2) = 3

F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n >2

Чему равно значение функции F(5)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(2) * 3 + F(1) * 2 = 11,

F(4) = F(3) * 4 + F(2) * 3 = 53,

F(5) = F(4) * 5 + F(3) * 4 = 309.

№2. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(2) = 3

F(n) = F(n−1) * F(n−2) + (n−2), при n > 2

Чему равно значение функции F(5)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(2) * F(1) + 1 = 4,

F(4) = F(3) * F(2) + 2 = 14,

F(5) = F(4) * F(3) + 3 = 59.

№3. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(2) = 2

F(n) = 2 * F(n–1) + (n – 2) * F(n–2), при n >2

Чему равно значение функции F(6)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = 2 * F(2) + (3 – 2) * F(1) = 5,

F(4) = 2 * F(3) + (4 – 2) * F(2) = 14,

F(5) = 2 * F(4) + (5 – 2) * F(3) = 43,

F(6) = 2 * F(5) + (6 – 2) * F(4) = 142.

№4. Последовательность чисел Фибоначчи
задается рекуррентным соотношением:

F(1) = 1

F(2) = 1

F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.

Чему равно восьмое число в последовательности Фибоначчи?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(1) + F(2) = 2,

F(4) = F(2)
+ F(3) = 3,

F(5) = F(3)
+ F(4) = 5,

F(6) = F(4)
+ F(5) = 8,

F(7) = F(5)
+ F(6) = 13,

F(8) = F(6) + F(7) = 21.

Восьмое число в последовательности Фибоначчи равно
21.

№5. Последовательность чисел Фибоначчи
задается рекуррентным соотношением:

F(1) = 1

F(2) = 1

F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.

Чему равно девятое число в последовательности Фибоначчи?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(1) + F(2) = 2,

F(4) = F(2)
+ F(3) = 3,

F(5) = F(3)
+ F(4) = 5,

F(6) = F(4)
+ F(5) = 8,

F(7) = F(5)
+ F(6) = 13,

F(8) = F(6) + F(7) = 21,

F(9) = F(7) + F(8) = 34.

Девятое число в последовательности Фибоначчи
равно 34.

№6. Последовательность чисел трибоначчи
задается рекуррентным соотношением:

F(1) = 0

F(2) = 1

F(3) = 1

F(n) = F(n–3) + F(n–2) + F(n–1), при n >3, где n – натуральное
число.

Чему равно девятое число в последовательности трибоначчи?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(4) = F(1) + F(2) + F(3) = 2,

F(5) = F(2)
+ F(3) + F(4) = 4,

F(6) = F(3)
+ F(4) + F(5) = 7,

F(7) = F(4)
+ F(5) + F(6) = 13,

F(8) = F(5) + F(6) + F(7) = 24,

F(9) = F(6) + F(7) + F(8) = 44.

Девятое число в последовательности трибоначчи
равно 44.

№7. Последовательность чисел трибоначчи
задается рекуррентным соотношением:

F(1) = 0

F(2) = 1

F(3) = 1

F(n) = F(n–3) + F(n–2) + F(n–1), при n >3, где n – натуральное
число.

Чему равно одиннадцатое число в последовательности
трибоначчи?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(4) = F(1) + F(2) + F(3) = 2,

F(5) = F(2)
+ F(3) + F(4) = 4,

F(6) = F(3)
+ F(4) + F(5) = 7,

F(7) = F(4)
+ F(5) + F(6) = 13,

F(8) = F(5)
+ F(6) + F(7) = 24,

F(9) = F(6)
+ F(7) + F(8) = 44,

F(10) =
F(7) + F(8) + F(9) = 81,

F(11) = F(8) + F(9) + F(10) = 149.

Одиннадцатое число в последовательности трибоначчи
равно 149.

№8. Последовательность чисел Люка задается
рекуррентным соотношением:

F(1) = 2

F(2) = 1

F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.

Чему равно восьмое число в последовательности Люка?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(1) + F(2) = 3,

F(4) = F(2)
+ F(3) = 4,

F(5) = F(3)
+ F(4) = 7,

F(6) = F(4)
+ F(5) = 11,

F(7) = F(5)
+ F(6) = 18,

F(8) = F(6) + F(7) = 29.

Восьмое число в последовательности Люка равно 29.

№9. Последовательность чисел Люка задается
рекуррентным соотношением:

F(1) = 2

F(2) = 1

F(n) = F(n–2) + F(n–1), при n >2, где n – натуральное
число.

Чему равно десятое число в последовательности Люка?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(1) + F(2) = 3,

F(4) = F(2)
+ F(3) = 4,

F(5) = F(3)
+ F(4) = 7,

F(6) = F(4)
+ F(5) = 11,

F(7) = F(5)
+ F(6) = 18,

F(8) = F(6) + F(7) = 29,

F(9) = F(7) + F(8) = 47,

F(10) = F(8) + F(9) = 76.

Десятое число в последовательности Люка равно 76.

№10. Последовательность чисел Падована
задается рекуррентным соотношением:

F(1) = 1

F(2) = 1

F(3) = 1

F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное
число.

Чему равно десятое число в последовательности Падована?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(4) = F(1) + F(2) = 2,

F(5) = F(2)
+ F(3) = 2,

F(6) = F(3)
+ F(4) = 3,

F(7) = F(4)
+ F(5) = 4,

F(8) = F(5)
+ F(6) = 5,

F(9) = F(6) + F(7) = 7,

F(10) = F(7) + F(8) = 9.

Десятое число в последовательности Падована равно
9.

Вызов рекурсивных процедур

№1. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
SUB F(n) PRINT n IF n < 5 THEN F(n + 1) F(n + 3) END IF END SUB	def F(n): print(n) if n < 5: F(n + 1) F(n + 3)
Паскаль	Алгоритмический язык
procedure F(n: integer); begin writeln(n); if n < 5 then begin F(n + 1); F(n + 3) end end	алг F(цел n) нач вывод n, нс если n < 5 то F(n + 1) F(n + 3) все кон
Си
void F(int n) { printf(«%dn», n); if (n < 5) { F(n + 1); F(n + 3); } }

Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(1)?

Пояснение.

Первым действием процедура F(1) выведет число 1.
Далее процедура F(1) вызовет процедуру F(n + 1), в результате
выполнения которой на экране появится число n + 1 = 2. Процедура
F(2) вызовет процедуру F(3), которая выведет на экран число 3 и вызовет
процедуру F(4), которая выведет на экран число 4 и вызовет F(5), которая
выведет на экран число 5.

После этого управление вернётся к процедуре F(4), которая
начнёт выполнять следующий шаг своего алгоритма, т. е. обратиться
к процедуре F(n + 3) = F(7). Процедура F(7) выведет на экран число 7.
Далее управление вернётся к процедуре F(3). Рассуждая аналогично приходим
к выводу, что процедура F(3) дополнительно выведет на экран число 6,
процедура F(2) — 5.

Последним действием процедуры F(1) будет вызов процедуры
F(n + 3) = F(4), которая выведет на экран числа 4, 5, 7.

Таким образом, на экране будут числа 1, 2, 3, 4, 5, 7, 6,
5, 4, 5, 7. Их сумма равна 49.

Ответ: 49.

№2. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
SUB F(n) IF n > 2 THEN F = F(n — 1) +F(n-2) ELSE F = 1 END IF END SUB	def F(n): if n > 2: return F(n-1)+ F(n-2) else: return 1
Паскаль	Алгоритмический язык
procedure F(n: integer): integer; begin if n > 2 then F := F(n — 1) + F(n — 2) else F := 1; end;	алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := 1 все кон
Си
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return 1; }

Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(5)?

Пояснение.

Значение, вычисленное алгоритмом при вызове F(5)
равно:

F(5)= F(4) + F(3) = F(3) + F(2) + F(2) + F(1) = F(2) + F(1)
+1 + 1 + 1 = 5.

Ответ: 5.

№3. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
SUB F(n) IF n > 2 THEN F = F(n — 1) +F(n-2) ELSE F = 1 END IF END SUB	def F(n): if n > 2: return F(n-1)+ F(n-2) else: return 1
Паскаль	Алгоритмический язык
procedure F(n: integer): integer; begin if n > 2 then F := F(n — 1) + F(n — 2) else F := 1; end;	алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := 1 все кон
Си
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return 1; }

Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(6)?

Пояснение.

Значение, вычисленное алгоритмом при вызове F(6)
равно:

F(6)= F(5)
+ F(4) = F(4) + F(3) + F(3) + F(2) = F(3) + F(2) + 2(F(2) + F(1)) + 1 =

= F(2) + F(1) + 1 + 2 · 2 + 1= 8.

Ответ: 8.

№4. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
SUB F(n) PRINT n IF n > 0 THEN F(n — 1) F(n — 3) END IF END SUB	def F(n): print(n) if n > 0: F(n — 1) F(n — 3)
Паскаль	Алгоритмический язык
procedure F(n: integer); begin writeln(n); if n > 0 then begin F(n — 1); F(n — 3) end end	алг F(цел n) нач вывод n, нс если n > 0 то F(n — 1) F(n — 3) все кон
Си
void F(int n) { printf(«%dn», n); if (n > 0) { F(n — 1); F(n — 3); } }

Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(5)?

Пояснение.

Первым действием процедура F(5) выведет число 5 и вызовет
процедуры F(4) и F(2).

Далее процедура F(2) выведет на экран число 2 и вызовет
процедуры F(1) и F(−1). Процедура F(1) выведет на экран число 1 и вызовет
процедуры F(0) и F(−2). Функция F(0) выведет на экран число 0. Функции
F(−1) и F(−2) выведут на экран числа −1 и −2.

Процедура F(4) выведет число 4 и вызовет процедуры
F(3) и F(1). Процедура F(1) выведет на экран цифры 1, 0 и −2. Процедура
F(3) выведет число 3 и вызовет процедуры F(2) и F(0). Процедура F(2)
выведет на экран цифры 2, 1, −2, −1 и 0, а процедура F(0) выведет число
0.

В итоге на экране появятся числа 5, 4, 3, 2, 1, 0, −2,
−1, 0, 1, 0, −2, 2, 1, 0, −2, −1.

Сумма чисел будет равна 11.

Ответ: 11.

№5. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
SUB F(n) PRINT n IF n > 1 THEN F(n — 1) F(n — 3) END IF END SUB	def F(n): print(n) if n > 1: F(n — 1) F(n — 3)
Паскаль	Алгоритмический язык
procedure F(n: integer); begin writeln(n); if n > 1 then begin F(n — 1); F(n — 3) end end	алг F(цел n) нач вывод n, нс если n > 1 то F(n — 1) F(n — 3) все кон
Си
void F(int n) { printf(«%dn», n); if (n > 1) { F(n — 1); F(n — 3); } }

Чему равна сумма всех чисел, напечатанных на экране при
выполнении вызова F(6)?

Пояснение.

На первом шаге процедура F(6) выведет число 6 и вызовет
процедуры F(5) и F(3).

На втором шаге процедуры F(5) и F(3) выведут числа 5 и
3 и вызовут процедуры F(4), F(2), F(2) и F(0).

На третьем шаге будут выведены числа 4, 2, 2 и 0; вызваны
процедуры F(3), F(1), F(1), F(−1), F(1), F(−1).

На четвёртом шаге будут выведены числа 3, 1, 1, −1, 1,
−1; вызваны процедуры F(2) и F(0).

На пятом шаге будут выведены числа 2, 0 и вызваны процедуры
F(1), F(−1).

На шестом шаге будут выведены числа 1 и −1.

Найдём сумму выведенных чисел:

6 + 5 + 3 + 4 + 2 + 2+ 0 + 3 + 1 + 1 + (−1) + 1 + (−1) + 2 +
0 + 1 + (−1) = 28.

Ответ: 28.

№6. Ниже на пяти языках программирования
записан рекурсивный алгоритм F.

Бейсик	Python
FUNCTION F(n) IF n > 2 THEN F = F(n — 1) + F(n-2) ELSE F = n END IF END FUNCTION	def F(n): if n > 2: return F(n-1)+ F(n-2) else: return n
Паскаль	Алгоритмический язык
function F(n: integer): integer; begin if n > 2 then F := F(n — 1) + F(n — 2) else F := n; end;	алг цел F(цел n) нач если n > 2 то знач := F(n — 1)+F(n — 2) иначе знач := n все кон
Си
int F(int n) { if (n > 2) return F(n-1) + F(n-2); else return n; }

Чему будет равно значение, вычисленное алгоритмом
при выполнении вызова F(5)?

Пояснение.

Значение, вычисленное алгоритмом при вызове F(5)
равно:

F(5)= F(4) + F(3) = F(3) + F(2) + F(2) + F(1) = F(2) + F(1)
+2 + 2 + 1 = 8.

Ответ: 8.

Алгоритмы опирающиеся на одно предидущеезначение

№1. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) =
F(n–1) * n, при n >1

Чему равно значение функции F(5)? В ответе запишите
только натуральное число.

Пояснение.

Последовательно находим: F(2) = F(1) * 2 = 2, F(3) =
F(2) * 3 = 6, F(4) = F(3) * 4 = 24, F(5) = F(4) * 5 = 120.

Примечание

Использование функции позволяет вычислить так называемый
факториал числа n — произведение натуральных чисел от 1 до n.
Тем самым, F(5) = 1 * 2 * 3 * 4 * 5 = 120.

№2. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 3

F(n) =
F(n–1) * (n–1), при n
>1

Чему равно значение функции F(6)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(2) = F(1) * 1 = 3,

F(3) = F(2) * 2 = 6,

F(4) = F(3) * 3 = 18,

F(5) = F(4) * 4 = 72,

F(6) = F(5) * 5 = 360.

№3. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) =
5*F(n–1) + 3*n, при n
>1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(2) = 5 * F(1) + 3 * 2 = 11,

F(3) = 5 * F(2) + 3 * 3 = 64,

F(4) = 5 * F(3) + 3 * 4 = 332.

№4. Алгоритм вычисления значения функции
F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * F(n–1) − F(n–1) * n + 2 * n, при n >1

Чему равно значение функции F(4)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(2) = F(1) * F(1) − F(1) * 2 + 2 * 2 = 3,

F(3) = F(2) * F(2) − F(2) * 3 + 2 * 3 = 6,

F(4) = F(3) * F(3) − F(3) * 4 + 2 * 4 = 20.

№5. Алгоритм вычисления значения функции
F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 0

F(n) =
F(n–1) + n, при n >1

G(1) = 1

G(n) =
G(n–1) * n, при n >1

Чему равно значение функции F(5) + G(5)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(2) = F(1) + 2 = 2,

F(3) = F(2)
+ 3 = 5,

F(4) = F(3)
+ 4 = 9,

F(5) = F(4)
+ 5 = 14,

G(2) = G(1)
* 2 = 2,

G(3) = G(2)
* 3 = 6,

G(4) = G(3) * 4 = 24,

G(5) = G(4) * 5 = 120.

Затем находим F(5) + G(5)=14 + 120=134.

№6. Алгоритм вычисления значения функции
F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = 2 *
G(n–1) + 5 * n, при n
>1

G(1) = 1

G(n) =
F(n–1) + 2 * n, при n
>1

Чему равно значение функции F(4) + G(4)?

В ответе запишите только натуральное число.

Пояснение.

Последовательно находим:

F(2) = 2 * G(1) + 5 * 2 = 12,

G(2) = F(1)
+ 2 * 2 = 5,

F(3) = 2 *
G(2) + 5 * 3 = 25,

G(3) = F(2)
+ 2 * 3 = 18,

F(4) = 2 *
G(3) + 5 * 4 = 56,

G(4) = F(3)
+ 2 * 4 = 33.

Затем находим F(4) + G(4)=56 + 33=89.

№7. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:

F(1) = 1;

F(n) =
F(n-1) * (n+1), при n
>1.

Чему равно значение функции F(4)? В ответе запишите
только натуральное число.

Пояснение.

Последовательно находим:

F(2) = F(1) * 3 = 3,

F(3) = F(2) * 4 = 12,

F(4) = F(3) * 5 = 60.

Ответ: 60.

№8. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:

F(1) = 1;

F(n) =
F(n-1) * (n+1), при n
>1.

Чему равно значение функции F(5)? В ответе запишите
только натуральное число.

Пояснение.

Последовательно находим:

F(2) = F(1) * 3 = 3,

F(3) = F(2) * 4 = 12,

F(4) = F(3) * 5 = 60

F(5) = F(4) * 6 = 360.

Ответ: 360.

№9. Алгоритм вычисления значения функции
F(n). где n — натуральное число, задан следующими соотношениями:

F(1)= 1; F(2)=1;

F(n) = F(n-2) * n при n >2.

Чему равно значение функции F(7)? В ответе запишите
только натуральное число.

Пояснение.

Последовательно находим:

F(3) =3F(1)
= 3, F(4) = 4F(2) = 4, F(5) = 5F(3) = 15, F(6) = 6F(4) = 24, F(7) = 7F(5) =
105.

№10. Алгоритм вычисления значения функции
F(n), где n — натуральное число, задан следующими соотношениями:

F(1) = 1; F(2) = 1;

F(n) = F(n — 2) * (n — 1), при n > 2.

Чему равно значение функции F(7)? В ответе запишите
только натуральное число.

Пояснение.

Последовательно находим:

F(3) = F(1) * 2 = 2,

F(4) = F(2) * 3 = 3,

F(5) = F(3) * 4 = 8,

F(6) = F(4) * 5 = 15,

F(7) = F(5) * 6 = 48.

Источник

Решение по рекуррентной формуле

Что вернет функция. Сколько символов «звездочка». Какова сумма чисел

С каким аргументом?

Не актуально для компьютерного ЕГЭ!

Формула Шеннона

В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.

Рекурсивные функции с возвращаемыми значениями

Задание 6 (ИНФ-11 ЕГЭ 2023_ДЕМО)

Вариант программы 1

import sys sys.setrecursionlimit(2030)

Вариант программы 2

Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Решу ЕГЭ)

Задание 6 (Решу ЕГЭ)

Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Решу ЕГЭ)

Сложные задачи

Задание 6 (Поляков ЕГЭ)

Задание 6 (Поляков ЕГЭ)

Алгоритмы, опирающиеся на несколько предыдущих значений

Задание 6 (Поляков ЕГЭ)

ещё не решила)

Новое и интересное на сайте:

import sys
sys.setrecursionlimit(2030)