Егэ по информатике 2013 - Помощь в подготовке к экзаменам и поступлению

Главная
Пробные и реальные тесты ЕГЭ
ЕГЭ по информатике
Реальные варианты ЕГЭ 2013 по информатике — Центр

28.08.2013

Все настоящие варианты из ЕГЭ по информатике, который проходил в 2013 году.

По некоторым данным эти кимы были доступны для скачивания ещё до проведения егэ.

Разбор и решение этих вариантов поможет будущим выпускникам максимально качественно подготовиться к будущим экзаменам.

В файле задания для региона «Центр».

Смотреть в PDF:

Или прямо сейчас: Скачайте в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

Данный топик предназначен, в принципе, для всех: и для школьников, решивших сдавать информатику, и для олдфагов, уже закончивших школу, дабы посмотреть, каковы нынче задания на ЕГЭ.

Вступление

Да, среди читателей хабра присутствует те, кто в данный момент учится в 11-ом классе и собирается сдавать ЕГЭ по информатике. Я сделал такой вывод, глядя на статистику страницы Хабра в ВК, и предположив, что раз ученик 11-ого класса читает хабр (а он читает, иначе бы не подписался на страницу) => интересуется IT => будет поступать в ВУЗ на IT-специальность => будет сдавать ЕГЭ по информатике.
Вам повезло, если у вас информатика является профильным предметом в школе. Это означает, что в неделю у вас 2-3 урока и изучаете вы предмет достаточно глубоко. Мне же так не повезло и информатика у меня всего 1 час в неделю. К тому же, учителю явно безразлично на то, получаем ли мы (наш класс) хоть какие-нибудь знания или нет. Пример: на уроке нам дают читать темы из учебника, которые надо законспектировать в обязательном порядке, а затем конспект сдать на проверку для получения оценки. Плюс, в «базовом» уровне отсутствуют такие темы как программирование и алгоритмизация.
И как же тогда сдать ЕГЭ?

Нанять репетитора;
Записаться на курсы;
Заняться самообразованием.

Лично я выбрал 3-ий вариант.

ЕГЭ 2013. Демонстрационный вариант

ФИПИ (Федеральный Институт Педагогических Измерений) опубликовал демонстрационный вариант ЕГЭ по информатике на 2013 год.

Демо | Спецификация | Кодификатор | Изменения КИМ ЕГЭ 2013

Согласно списку изменений, принципиальных отличий от ЕГЭ 2012 нет:

Одно задание с кратким ответом по теме «Кодирование текстовой информации» заменено на задание по теме «Рекурсивные алгоритмы» раздела «Элементы теории алгоритмов».
Немного изменена последовательность заданий во второй части работы.

Поэтому для подготовки в данный момент пойдет литература, предназначенная для подготовки к прошлому году.
Но сперва надо разобраться, а к чему собственно готовится?

Структура ЕГЭ

На выполнение работы отводится 235 минут. Всего в ЕГЭ три части: A, B и C. Всего 32 задания. Рекомендуется не более 1,5 часа (90 минут) отвести на выполнение заданий частей 1 и 2, а остальное время – на часть 3.

Часть	Кол-во заданий	Макс. бал	% от макс. бала за всю работу	Тип заданий
A	13	13	32,5	Выбор ответа
B	15	15	37,5	Краткий ответ
C	4	12	40	Развернутый ответ
Итого	32	40	100

Все задания можно разделить на разделы.

Раздел	Кол-во заданий	Макс. бал	% от макс. бала за всю работу
Информация. Кодирование информации	4	4	10
Моделирование и компьютерный эксперимент	2	2	5
Системы счислений	2	2	5
Логика и алгоритмы	6	8	20
Элементы теории алгоритмов	6	7	17,5
Программирование	5	10	25
Архитектура компьютеров и комп. сетей	2	2	5
Технология обработки граф. и звук. информации	1	1	2,5
Обработка числовой информации	2	2	5
Технологии поиска и хранения информации	2	2	5
Итого	32	40	100

В принципе, самой сложной частью, несомненно, является часть C. Хотя в частях A и B также присутствуют задания повышенной сложности. Ключевой особенностью экзамена является то, что решением задач части C является исходный код на любом языке программирования, который, соответственно, надо записать в бланке ответов КИМ, то бишь, на листочке.

Самоподготовка

Ниже я предоставлю свой собственный список материалов, по которым я уже начал подготовку к ЕГЭ. Буду рад, если в комментариях будут предложены ваши источники подготовки.

Интернет-проекты

Сайт и форум Полякова Константина Юрьевича, доктора технических наук и учителя высшей категории. Собственно, нашел этот сайт случайно и изучал еще во время подготовки к ЕГЭ 2012. Радует то, что автор расписывает и раскладывает по полочкам абсолютно все, что касается определенного задания. Для каждого задания один документ в .doc. В общем, оцените сами:
Прошлогодние материалы для подготовки к ЕГЭ по информатике.
Т.к. ключевых отличий от ЕГЭ 2012 нет, то можно смело начать готовиться по этому курсу. Хотя можно и дождаться, когда автор начнет выкладывать курсы по ЕГЭ 2013.

Подготовка в ВКонтакте. Страница ЕГЭ 2013 | Информатика. Да-да, вам не показалось, в ВК есть много тематических групп и страниц, даже посвященных ЕГЭ. На данной странице администраторами выкладываются учебные материалы и задания, которые по желанию решают участники группы. Через n-ое время, выкладывается ответ. Если возникают вопросы, то тебе объяснят либо сами пользователи, либо администраторы: распишут на тетрадки решение, отсканируют/сфотографируют и опубликуют.

Видео лекции по информатике. Три хороших видеоролика, длинной около 2-ух часов каждый.

Заключение

В общем, экзамен по информатика нельзя назвать легким, но и адски сложным тоже не назвать, если готовиться.
Так что, «учиться, учиться и ещё раз учиться», если вам, конечно, интересен предмет.

Источник

ФИПИ ЕГЭ по информатике 2023 2013

НАШ БЛОГ

Последние статьи из нашего блога!

Как успешно сдать ЕГЭ по литературе

Если вы хотите успешно сдать ЕГЭ по литературе, вам стоит пройти курсы подготовки. Какой результат это даст.

Вопросы абитуриентов о поступлении в вуз

Многие школьники теряются в том ворохе вопросов, которые им нужно решить в 11 классе. Школьные занятия, ЕГЭ, выбор вуза – все это пугает выпускника и часто его путает. Как пройти этот непростой этап с честью? Все тщательно спланировать.

Поступить на дистанционное без ЕГЭ

Учиться дистанционно в государственном или частном вузе – это возможность получения официального диплома на удалении от места учебы. Такой формат обучения практикуется далеко не всеми учебными заведениями в РФ. Также правильно она называется заочн…

Источник

Демонстрационный
вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 2 /
39)

Единый государственный экзамен по ИНФОРМАТИКЕ и ИКТ

Пояснения к демонстрационному варианту контрольных
измерительных материалов единого государственного экзамена 2013 года по
ИНФОРМАТИКЕ и ИКТ

При ознакомлении с демонстрационным
вариантом контрольных измерительных материалов ЕГЭ 2013 г. следует иметь в виду,
что задания, включённые в него, не отражают всех вопросов содержания, которые
будут проверяться с помощью вариантов КИМ в 2013 г. Полный перечень вопросов,
которые могут контролироваться на едином государственном экзамене 2013 г., приведён
в кодификаторе элементов содержания и требований к уровню подготовки выпускников
общеобразовательных учреждений для единого государственного экзамена 2013 г. по
информатике и ИКТ.

Назначение демонстрационного
варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой
общественности составить представление о структуре будущих КИМ, количестве заданий,
их форме, уровне сложности. Приведённые критерии оценки выполнения заданий с развёрнутым
ответом, включённые в этот вариант, дают представление о требованиях к полноте
и правильности записи развёрнутого ответа. Эти сведения позволят выпускникам выработать
стратегию подготовки к ЕГЭ по информатике и ИКТ.

Единый государственный экзамен по ИНФОРМАТИКЕ и ИКТ

Демонстрационный
вариант контрольных измерительных
материалов единого государственного экзамена 2013 года по информатике и ИКТ

подготовлен Федеральным государственным
бюджетным научным учреждением

«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»

(2013 — 3 / 39

Демонстрационный
вариант контрольных измерительных материалов для проведения в 2013 году
единого государственного экзамена по ИНФОРМАТИКЕ и ИКТ

Инструкция по выполнению работы

На выполнение экзаменационной работы по информатике
и ИКТ отводится 235 минут. Экзаменационная работа состоит из 3 частей, содержащих
32 задания. Рекомендуем не более 1,5 часов (90 минут) отвести на выполнение заданий
частей 1 и 2, а остальное время – на часть 3.

Часть 1 содержит 13 заданий (А1–А13). К каждому
заданию даётся четыре варианта ответа, из которых только один правильный.

Демонстрационный
вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 4 / 39)

В экзаменационных заданиях используются следующие соглашения.

1. Обозначения для логических связок (операций):

a)
отрицание (инверсия, логическое НЕ) обозначается  (например, А);

b)
конъюнкция (логическое умножение, логическое И) обозначается
/

(например, А / В) либо & (например, А & В);

c)
дизъюнкция (логическое сложение, логическое ИЛИ) обозначается
/

(например, А / В);

d)
следование (импликация) обозначается → (например, А → В);

e)
тождество обозначается ≡ (например, A ≡ B). Выражение A ≡
B истинно тогда и только тогда, когда значения A и B совпадают (либо они оба истинны,
либо они оба ложны);

f)
символ 1 используется для обозначения истины (истинного высказывания);
символ 0 – для обозначения лжи (ложного высказывания).

2.
Два логических выражения, содержащих переменные, называются равносильными
(эквивалентными), если значения этих выражений совпадают при любых значениях переменных.
Так, выражения А → В и (А)
/ В равносильны, а А / В и А / В неравносильны (значения выражений разные,
например, при А = 1, В = 0).

3.
Приоритеты логических операций: инверсия (отрицание), конъюнкция
(логическое умножение), дизъюнкция (логическое сложение), импликация (следование),
тождество. Таким образом, А
/ В / С / D означает то же, что и ((А)
/ В) / (С / D).

Возможна
запись А / В / С вместо (А / В) / С. То же относится и к дизъюнкции: возможна
запись А / В / С вместо (А / В) / С.

4.
Обозначения Мбайт и Кбайт используются в традиционном для информатики
смысле – как обозначения единиц измерения, чьё соотношение с единицей «байт» выражается
степенью двойки.

Часть 2 состоит из 15 заданий с кратким ответом
(В1–В15). К этим заданиям Вы должны самостоятельно сформулировать и записать ответ.

Часть 3 состоит из 4 заданий(С1–С4). Для
выполнения заданий этой части Вам необходимо написать развёрнутый ответ в произвольной
форме.

Все бланки ЕГЭ заполняются яркими чёрными
чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.

При выполнении заданий Вы можете пользоваться
черновиком. Обращаем Ваше внимание на то, что записи в черновике не будут учитываться
при оценивании работы.

Советуем выполнять задания в том порядке,
в котором они даны. Для экономии времени пропускайте задание, которое не удаётся
выполнить сразу, и переходите к следующему. Если после выполнения всей работы у
Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Баллы, полученные Вами за выполненные задания,
суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее
количество баллов.

Желаем
успеха!

(2013 — 5 / 39

Часть 1

При выполнении
заданий этой части в бланке ответов № 1 под номером выполняемого Вами задания
(А1–А13) поставьте знак «×» в клеточке, номер которой соответствует номеру
выбранного Вами ответа.

Сколько
единиц в двоичной записи десятичного числа 255?

1) 1                                                                                              2)
2                                                                                         3)
7                                                                                        4)
8

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 6 / 39)

Для групповых операций
с файлами используются маски имён файлов. Маска представляет собой последовательность
букв, цифр и прочих допустимых в именах файлов символов, в которых также могут
встречаться следующие символы.

Символ «?» (вопросительный знак) означает ровно один произвольный
символ.

Символ «*» (звездочка)
означает любую последовательность символов произвольной длины, в том числе
«*» может задавать и пустую последовательность.

В каталоге находится 6 файлов: asc.wma casting.wmv last.wma
pasta.wmvx pasta.wri

vast.wma

Определите, по какой из перечисленных
масок из этих 6 файлов будет отобрана указанная группа файлов:

casting.wmv last.wma pasta.wmvx vast.wma

1)
?as*.wm?

2)
*as?.wm*

3)
?as*.wm*

4)
?as*.w*

Автомат получает на вход
два двузначных шестнадцатеричных числа. В этих числах все цифры не превосходят
цифру 6 (если в числе есть цифра больше 6, автомат отказывается работать). По
этим числам строится новое шестнадцатеричное число по следующим правилам.

1.
Вычисляются два шестнадцатеричных числа – сумма старших разрядов
полученных чисел и сумма младших разрядов этих чисел.

2.
Полученные два шестнадцатеричных числа записываются друг за другом
в порядке возрастания (без разделителей).

Пример. Исходные числа: 66, 43. Поразрядные суммы: A,
9. Результат: 9A.

Определите, какое из предложенных чисел может быть результатом
работы автомата.

                1) 9F                                                                                 2)
911                                                                           3)
42                                                                                 4)
7A

Между населёнными пунктами A, B, C, D, E, F построены дороги,
протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает,
что прямой дороги между пунктами нет.)

	A	B	C	D	E	F
A		3
B	3		7	4	7
C		7			5
D		4			2
E		7	5	2		3
F					3

Определите длину кратчайшего пути между пунктами A и F (при
условии, что передвигаться можно только по построенным дорогам).

1) 11                                                                                       2)
12                                                                                  3)
13                                                                                4)
18

Дан фрагмент таблицы истинности выражения F.

x1	x2	x3	x4	x5	x6	x7	F
1	1	0	1	1	1	1	0
1	0	1	0	1	1	0	0
0	1	0	1	1	0	0	1

Каким из приведённых ниже выражений может быть F?

1)
¬x1 / x2 / ¬x3 / x4 / x5
/ ¬x6 / ¬x7

2)
¬x1 / x2 / ¬x3 / x4 / ¬x5
/ ¬x6 / x7

3)
x1 / ¬x2 / x3 / ¬x4 / x5
/ x6 / ¬x7

4)
x1 / ¬x2 / x3 / ¬x4 / ¬x5
/ x6 / ¬x7

(2013 — 7 / 39

Ниже представлены две таблицы из базы данных. Каждая строка
таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация
представлена значением поля ID в соответствующей строке таблицы 1. Определите на
основании приведённых данных фамилию и инициалы внучки Петровой С.М.

	Таблица 1			Таблица 2
ID	Фамилия_И.О.	Пол	ID_Родителя	ID_Ребёнка
25	Жвания К.Г.	Ж	25	134
49	Черняк А.П.	М	76	49
62	Петрова М.Н.	Ж	76	123
76	Ильченко Т.В.	Ж	82	76
82	Петрова С.М.	Ж	82	96
96	Басис В.В.	Ж	102	76
102	Ильченко В.И.	М	102	96
123	Павлыш Н.П.	Ж	134	49
134	Черняк П.Р.	М	134	123
…	…	…	…	…

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 8 / 39)

Производится одноканальная
(моно) цифровая звукозапись. Значение сигнала фиксируется 48 000 раз в секунду,
для записи каждого значения используется 32 бит. Запись длится 4 минуты, её результаты
записываются в файл, сжатия данных не производится. Какая из приведённых ниже
величин наиболее близка к размеру полученного файла?

               1) 44 Мбайт                                          2)
87 Мбайт                                           3)
125 Мбайт                                    4)
175 Мбайт

Для кодирования некоторой
последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный
двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность.
Вот этот код: А – 00, Б – 01, В – 100, Г – 101, Д – 110. Можно ли сократить для
одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать
однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант
ответа.

1)
для буквы Д – 11

2)
это невозможно

3)
для буквы Г – 10

4)
для буквы Д – 10

На числовой прямой даны два отрезка: P = [2, 10] и Q = [6,
14].

Выберите такой отрезок A, что формула

( (x  А) → (x  P) ) / (x  Q)

тождественно истинна, то
есть принимает значение 1 при любом значении переменной х.

                                                                                                                                                 1)
[0, 3]       2) [3, 11]                                    3)
[11, 15]                                          4)
[15, 17]

В некоторой стране
автомобильный номер длиной 5 символов составляют из заглавных букв (задействовано
30 различных букв) и любых десятичных цифр в любом порядке.

Каждый такой номер в
компьютерной программе записывается минимально возможным и одинаковым целым количеством
байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым
и минимально возможным количеством бит).

Определите объём памяти, отводимый этой программой для записи

50 номеров.

1)
100 байт

2)
150 байт

3)
200 байт

4)
250 байт

1) Басис В.В.

2) Ильченко Т.В.

3) Павлыш Н.П.

4) Петрова М.Н.

Дан фрагмент электронной таблицы.

	А	В	С	D
1	1	2	3
2	5	4	= $A$2 + B$3
3	6	7	= A3 + B3

Чему станет равным значение ячейки D1, если в неё скопировать
формулу из ячейки С2?

Примечание: знак $ обозначает абсолютную адресацию.

1)
18

2)
12

3)
14

4)
17

(2013 — 9 / 39

В программе описан одномерный целочисленный массив A с индексами
от 0 до 10. Ниже представлен фрагмент этой программы, записанный на разных языках
программирования, в котором значения элементов массива сначала задаются, а затем
меняются.

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 10 / 39)

Система команд исполнителя РОБОТ, «живущего» в прямоугольном
лабиринте на клетчатой плоскости, включает в себя 4 команды-приказа и 4 команды
проверки условия. Команды-приказы:

При выполнении любой из этих
команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево
←, вправо →.

Если РОБОТ начнёт движение в сторону находящейся рядом с ним
стены, то он разрушится, и программа прервётся.

Другие 4 команды проверяют
истинность условия отсутствия стены у каждой стороны той клетки, где находится
РОБОТ:

сверху
свободно

снизу свободно

слева свободно

справа свободно

Цикл

ПОКА условие

последовательность
команд

КОНЕЦ ПОКА

выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2

КОНЕЦ ЕСЛИ

выполняется команда1 (если условие истинно) или команда2
(если условие ложно).

Сколько клеток лабиринта
соответствуют требованию, что, начав движение в ней и выполнив предложенную программу,
РОБОТ уцелеет и остановится в закрашенной клетке (клетка А1)?

НАЧАЛО

ПОКА слева свободно ИЛИ сверху свободно

ЕСЛИ слева свободно 3 ТО
влево ₄

ИНАЧЕ вверх

КОНЕЦ
ЕСЛИ ⁵

КОНЕЦ ПОКА 6

КОНЕЦ ^{A B C D E F}

               1) 8                                                                                         2)
12                                                                                 3)
17                                                                                 4)
21

Бейсик	Паскаль
FOR i=0 TO 10 A(i)=i-1 NEXT i FOR i=1 TO 10 A(i-1)=A(i) NEXT i A(10)=10	for i:=0 to 10 do A[i]:=i-1; for i:=1 to 10 do A[i-1]:=A[i]; A[10]:=10;
Си	Алгоритмический язык
for (i=0;i<=10;i++) A[i]=i-1; for (i=1;i<=10;i++) A[i-1]=A[i]; A[10]=10;	нц для i от 0 до 10 A[i]:=i-1 кц нц для i от 1 до 10 A[i-1]:=A[i] кц A[10]:=10

Как изменятся элементы этого массива после выполнения фрагмента
программы?

1) все элементы,
кроме последнего, окажутся равны между собой

2) все элементы
окажутся равны своим индексам

3) все элементы,
кроме последнего, будут сдвинуты на один элемент вправо

4) все элементы,
кроме последнего, уменьшатся на единицу

(2013 — 11 / 39

Часть 2

Ответом к заданиям
этой части (В1–В15) является число, последовательность букв или цифр. Впишите
ответы сначала в текст работы, а затем перенесите их в бланк ответов № 1
справа от номера соответствующего задания, начиная с первой клеточки, без
пробелов, запятых и других дополнительных символов. Каждую букву
или цифру пишите в отдельной клеточке в соответствии с приведёнными в бланке
образцами.

У исполнителя Арифметик две команды, которым присвоены номера:

1.
прибавь 2,

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 12 / 39)

Определите значение переменной
c
после выполнения следующего фрагмента программы (записанного ниже на
разных языках программирования). Ответ запишите в виде целого числа.

Бейсик	Паскаль
a = 30 b = 14 a = a – 2 * b IF a > b THEN c = b + 2 * a ELSE c = b — 2 * a ENDIF	a := 30; b := 14; a := a – 2 * b; if a > b then c := b + 2 * a else c := b — 2 * a;
Си	Алгоритмический
a = 30; b = 14; a = a – 2 * b; if (a > b) c = b + 2 * a; else c = b — 2 * a;	a := 30 b := 14 a := a – 2 * b если a > b то c := b + 2 * a иначе c := b — 2 * a все

Ответ: ___________________________.

Дан фрагмент электронной таблицы.

	A	B	C
1	2	4
2	= (B1 – A1)/2	= 2 – A1/2	= (C1 – A1)*2 – 4

Какое целое число должно быть записано в ячейке      C1,
         чтобы построенная         после выполнения              вычислений
        диаграмма по значениям       диапазона             ячеек      A2 : С2
соответствовала рисунку?

Известно, что все
значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

Ответ: ___________________________.

2. умножь
на 3.

Первая из них увеличивает число на экране на 2, вторая утраивает его. Например,
21211 – это программа умножь на 3 прибавь 2 умножь на 3 прибавь 2
прибавь 2, которая преобразует число 1 в число 19.

Запишите порядок команд в программе преобразования числа
3 в число 69, содержащей не более 5 команд, указывая лишь номера команд. Если
таких программ более одной, то запишите любую из них.

Ответ:
___________________________.

(2013 — 13 / 39

Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи,
задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков
пунктуации и т. д.) можно закодировать, используя код азбуки Морзе длиной не
менее четырёх и не более пяти сигналов (точек и тире)?

Ответ:
___________________________.

Определите, что будет напечатано в результате выполнения программы
(записанной ниже на разных языках программирования).

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 14 / 39)

Алгоритм
вычисления значения функции F(n), где n – натуральное число, задан
следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * n, при n >1

Чему равно значение функции F(5)?

В ответе запишите только натуральное число.

Ответ: ___________________________.

Запись десятичного числа
в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой
0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?

Ответ: ___________________________.

Ниже на четырёх языках
записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа:
a и b. Укажите наименьшее из таких чисел x, при вводе которых
алгоритм печатает сначала 2, а потом 21.

Бейсик	Паскаль
DIM X, A, B AS INTEGER INPUT X A=0: B=1 WHILE X > 0 A = A+1 B = B*(X MOD 10) X = X 10 WEND PRINT A PRINT B	var x, a, b: integer; begin readln(x); a:=0; b:=1; while x>0 do begin a:=a+1; b:=b*(x mod 10); x:= x div 10 end; writeln(a); write(b); end.
Си	Алгоритмический
#include<stdio.h> void main() { int x, a, b; scanf(«%d», &x); a=0; b=1; while (x>0){ a=a+1; b=b*(x%10); x= x/10; } printf(«%dn%d», a, b); }	алг нач
цел x, a, b
ввод x
a:=0; b:=1
нц пока x>0
a:=a+1
b:=b*mod(x,10) x:=div(x,10) кц вывод a, нс, b
кон

Ответ: ___________________________.

Бейсик	Паскаль
DIM N, S AS INTEGER N = 0 S = 0 WHILE S <= 35 N = N + 1 S = S + 4 WEND PRINT N	var n, s: integer; begin n := 0; s := 0; while s <= 35 do begin n := n + 1; s := s + 4 end; write(n) end.
Си	Алгоритмический
#include<stdio.h> void main() { int n, s; n = 0; s = 0; while (s <= 35) { n = n + 1; s = s + 4; } printf(«%d», n); }	алг нач цел n, s n := 0 s := 0 нц пока s <= 35 n := n + 1 s := s + 4 кц вывод n кон

Ответ:
___________________________.

(2013 — 15 / 39

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д,
Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Л?

Ответ:
___________________________.

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 16 / 39)

В терминологии сетей
TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса
узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети.
Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается
в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

По заданным IP-адресу узла и маске определите
адрес сети.

IP-адрес узла: 217.19.128.131

Маска: 255.255.192.0

При записи ответа выберите
из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в нужном
порядке соответствующие им буквы, без использования точек.

A	B	C	D	E	F	G	H
0	16	19	64	128	131	192	217
Пример. Пусть искомый IP-адрес: 192.168.128.0, и дана таблица
A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде:
HBAF

Ответ: ___________________________.

В языке запросов поискового
сервера для обозначения логической операции «ИЛИ» используется символ «|», а для
логической операции «И» – символ «&».

В таблице приведены запросы
и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу
Эсминец?

Считается, что все запросы
выполнялись практически одновременно, так что набор страниц, содержащих все искомые
слова, не изменялся за время выполнения запросов.

Ответ: ___________________________.

Документ объёмом 20 Мбайт можно передать с одного компьютера
на другой двумя способами.

А. Сжать архиватором, передать архив по каналу связи, распаковать.

Б. Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если:

•
средняя скорость передачи данных по каналу связи составляет 2²⁰
бит в секунду;

•
объём сжатого архиватором документа равен 20% исходного;  время, требуемое на сжатие документа,
– 5 секунд, на распаковку – 1 секунда?

В ответе напишите букву А, если быстрее способ А, или Б, если
быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд
один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды,
в ответе нужно написать Б23.

Единиц измерения «секунд», «сек.», «с.» к ответу добавлять не
нужно.

Ответ:
___________________________.

(2013 — 17 / 39

У исполнителя Удвоитель две команды, которым присвоены номера:

1. прибавь
1,

2.
умножь на 2.

Первая из них увеличивает на 1 число на экране, вторая удваивает
его.

Программа для Удвоителя – это последовательность команд.

Сколько есть программ, которые число 3 преобразуют в число
23?

Ответ:
___________________________.

Определите, какое число будет напечатано в результате выполнения
следующего алгоритма (для Вашего удобства алгоритм представлен на четырёх языках).

Демонстрационный вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс.
(2013 — 18 / 39)

Сколько существует различных
наборов значений логических переменных x₁, x₂,
x₃, x₄, y₁, y₂y₃, y₄, которые удовлетворяют всем перечисленным
ниже условиям?

(x₁ → x₂) / (x₂
→ x₃) / (x₃ → x₄) = 1

(¬y₁ / y₂) / (¬y₂
/ y₃) / (¬y₃ / y₄) =
1

(y₁ → x₁) / (y₂
→ x₂) / (y₃ → x₃) / (y₄
→ x₄) = 1

В ответе не
нужно перечислять все различные наборы значений переменных x₁,
x₂, x₃, x₄, y₁,
y₂y₃, y₄, при которых выполнена
данная система равенств. В качестве ответа Вам нужно указать количество таких
наборов.

Ответ: ___________________________.

Не забудьте перенести все ответы в
бланк ответов № 1.

Бейсик	Паскаль
DIM A, B, T, M, R AS INTEGER A = -20: B = 20 M = A: R = F(A) FOR T = A TO B IF F(T) < R THEN M = T R = F(T) ENDIF NEXT T PRINT M FUNCTION F(x) F = 3(x-8)(x-8) END FUNCTION	var a,b,t,M,R :integer; Function F(x:integer):integer; begin F := 3(x-8)(x-8) end; begin a := -20; b := 20; M := a; R := F(a); for t := a to b do begin if (F(t)<R) then begin M := t; R := F(t) end end; write(M); end.
Си	Алгоритмический
#include<stdio.h> int F(int x) { return 3(x-8)(x-8); } void main() { int a, b, t, M, R; a = -20; b = 20; M = a; R = F(a); for (t=a; t<=b; t++){ if (F(t)<R) { M = t; R = F(t); } } printf(«%d», M); }	алг нач
цел a, b, t, R, M
a := -20; b := 20 M := a; R := F(a) нц для t от a до b если F(t)< R
то
M := t; R := F(t) все кц вывод M кон алг цел F(цел x)
нач
знач := 3(x-8)(x-8) кон

Ответ:
___________________________.

(2013 — 19 / 39

Часть 3

Для записи ответов
на задания этой части (С1–С4) используйте бланк ответов № 2. Запишите сначала
номер задания (С1, С2 и т. д.), а затем полное решение. Ответы записывайте
чётко и разборчиво.

Требовалось написать программу,
при выполнении которой с клавиатуры считывается координата точки на прямой (x
– действительное число) и определяется принадлежность этой точки одному из выделенных
отрезков В и D (включая границы). Программист торопился и написал программу неправильно.

Бейсик	Паскаль
INPUT x IF x>=-3 THEN IF x<=9 THEN IF x>1 THEN PRINT «не принадлежит» ELSE PRINT «принадлежит» ENDIF ENDIF ENDIF END	var x: real; begin readln(x); if x>=-3 then if x<=9 then if x>1 then write(‘не принадлежит’) else write(‘принадлежит’) end.
Си	Алгоритмический язык
void main(void) { float x; scanf(«%f»,&x); if(x>=-3) if(x<=9) if(x>1) printf(«не принадлежит»); else printf(«принадлежит»); }	алг нач
вещ x
ввод x
если x>=-3 то
если x<=9 то
если x>1 то
вывод ‘не принадлежит’
иначе вывод ‘принадлежит’
все
все
все
кон

(2013 — 21 / 39

Дан целочисленный массив из 30 элементов. Элементы массива могут
принимать целые значения от 0 до 100. Опишите на русском языке или на одном из языков
программирования алгоритм, позволяющий найти и вывести произведение элементов массива,
которые имеют нечётное значение и делятся на 3. Гарантируется, что в исходном массиве
есть хотя бы один элемент, значение которого нечётно и кратно 3.

Исходные данные объявлены так, как показано ниже. Запрещается
использовать переменные, не описанные ниже, но разрешается не использовать часть
из них. Исходные данные всегда подобраны так, что результат произведения не выходит
за пределы объявленных типов данных.

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 22 / 39) случае Вы должны использовать
те же самые исходные данные и переменные, какие были предложены в условии (например,
в образце, записанном на естественном языке).

Два игрока, Петя и Ваня,
играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди,
первый ход делает Петя. За один ход игрок может добавить в кучу один камень
или увеличить количество камней в куче в два раза. Например, имея кучу
из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока,
чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в
тот момент, когда количество камней в куче становится не менее 22. Победителем
считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой
будет 22 или больше камней. В начальный момент в куче было S камней, 1
≤ S ≤ 21.

Будем говорить, что
игрок имеет выигрышную стратегию, если он может выиграть при любых ходах
противника. Описать стратегию игрока – значит описать, какой ход он должен сделать
в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой
ответ.

1.
а) Укажите все такие значения числа S, при которых Петя может
выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите
выигрывающий ход для каждого указанного значения S.

б) Укажите такое значение
S, при котором Петя не может выиграть за один ход, но при любом ходе Пети
Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2.
Укажите два таких значения S, при которых у Пети есть выигрышная
стратегия, причём

–
Петя не может выиграть за один ход, и

–
Петя может выиграть своим вторым ходом, независимо от того, как
будет ходить Ваня.

Для каждого указанного значения S опишите выигрышную стратегию
Пети.

3.
Укажите значение S, при котором:

–
у Вани есть выигрышная стратегия, позволяющая ему выиграть первым
или вторым ходом при любой игре Пети, и

–
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.

Для указанного значения
S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных
при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева
указывайте, кто делает ход, в узлах – количество камней в куче.

Паскаль	Алгоритмический язык
const N=30; var a: array [1..N] of longint; i, j, p: longint; begin for i := 1 to N do readln(a[i]); … end.	алг нач цел N=30 целтаб a[1:N] цел i, j, p нц для i от 1 до N ввод a[i] кц … кон
Бейсик	СИ
N=30 DIM A(N) AS LONG DIM I, J, P AS LONG FOR I = 1 TO N INPUT A(I) NEXT I … END	#include <stdio.h> #define N 30 void main(void){ long a[N]; long i, j, p; for (i=0; i<N; i++) scanf(«%ld», &a[i]); … }
Русский (естественный) язык
Объявляем массив A из 30 элементов. Объявляем целочисленные переменные I, J, P. В цикле от 1 до 30 вводим элементы массива A с 1-го по 30-й. …

В качестве ответа Вам необходимо привести фрагмент программы
(или описание алгоритма на естественном языке), который должен находиться на месте
многоточия. Вы можете записать решение также на другом языке программирования (укажите
название и используемую версию языка программирования, например Free Pascal
2.4) или в виде блок-схемы. В этом

(2013 — 23 / 39

На вход программе подаются сведения о пассажирах, желающих сдать
свой багаж в камеру хранения на заранее известное время до полуночи. В первой строке
сообщается число пассажиров N, которое не меньше 3, но не превосходит 1000; во второй
строке – количество ячеек в камере хранения K, которое не меньше 10, но не превосходит
1000. Каждая из следующих N строк имеет следующий формат:

<Фамилия> <время сдачи багажа> <время освобождения
ячейки>, где <Фамилия> – строка, состоящая не более чем из 20 непробельных
символов; <время сдачи багажа> – через двоеточие два целых числа, соответствующие
часам (от 00 до 23 – ровно 2 символа) и минутам (от 00 до 59 – ровно 2 символа);
<время освобождения ячейки> имеет тот же формат.

<Фамилия> и <время сдачи багажа>, а также <время
сдачи багажа> и <время освобождения ячейки> разделены одним пробелом. Время
освобождения больше времени сдачи.

Демонстрационный
вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 24 / 39)

Система оценивания экзаменационной работы по информатике
и ИКТ

Часть 1

За правильный ответ на каждое задание части 1 ставится 1 балл.

Если
указаны два и более ответов (в том числе правильный), неверный ответ или ответ
отсутствует – 0 баллов.

№ задания	Ответ
A1	4
A2	2
A3	1
A4	3
A5	4
A6	3
A7	1
A8	1
A9	1
A10	2
A11	3
A12	2
A13	4

Часть 2

За правильный
ответ на каждое задание части 2 ставится 1 балл, за неверный ответ или его отсутствие
– 0 баллов.

№ задания	Ответ
B1	11212
B2	10
B3	5
B4	48
B5	9
B6	120
B7	15
B8	37
B9	13
B10	А122
B11	HCEA
B12	2200
B13	22
B14	8
B15	15

Сведения отсортированы в порядке времени сдачи багажа. Каждому
из пассажиров в камере хранения выделяется свободная ячейка с минимальным номером.
Если в момент сдачи багажа свободных ячеек нет, то пассажир уходит, не дожидаясь
освобождения одной из них.

Требуется написать программу (укажите используемую версию языка
программирования, например Borland Pascal 7.0), которая будет выводить на экран
для каждого пассажира номер ему предоставленной ячейки (можно сразу после ввода
данных очередного пассажира). Если ячейка пассажиру не предоставлена, то его фамилия
не печатается.

Пример входных данных:

Иванов
09:45 12:00

Петров
10:00 11:00

Сидоров
12:00 13:12

Результат работы программы на этих входных данных:

Иванов 1

Петров 2 Сидоров 1

(2013 — 25 / 39

Часть
3

КРИТЕРИИ ОЦЕНИВАНИЯ
ЗАДАНИЙ С РАЗВЁРНУТЫМ ОТВЕТОМ

Демонстрационный
вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 26 /
39)

Последовательно выполните следующее.

1.
Перерисуйте и заполните таблицу, которая показывает, как работает
программа при аргументах, принадлежащих различным областям (A, B, C, D и E). Границы
(точки –3, 1, 5 и 9) принадлежат заштрихованным областям (B и D соответственно).

условие не выполнится,
«—» (прочерк), если условие не будет проверяться, «не изв.», если программа ведет
себя по-разному для разных значений, принадлежащих данной области. В столбце
«Программа выведет» укажите, что программа выведет на экран. Если программа ничего
не выводит, напишите «—» (прочерк). Если для разных значений, принадлежащих области,
будут выведены разные тексты, напишите «не изв.». В последнем столбце укажите
«Да» или «Нет».

2.
Укажите, как нужно доработать программу, чтобы не было случаев её
неправильной работы. (Это можно сделать несколькими способами, достаточно указать
любой способ доработки исходной программы.)

Содержание верного ответа и указания по оцениванию (допускаются иные формулировки ответа, не искажающие его смысла)
Элементы ответа: 1.
	Область	Условие 1 (x >= –3)	Условие 2 (x <=9)	Условие 3 (x>1)	Программа выведет	Область обрабатывается верно
A	Нет	—	—	—	Нет
B	Да	Да	Нет	Принадлежит	Да
C	Да	Да	Да	Не принадлежит	Да
D	Да	Да	Да	Не принадлежит	Нет
E	Да	Нет	—	—	Нет

Бейсик	Паскаль
INPUT x IF x>=-3 THEN IF x<=9 THEN IF x>1 THEN PRINT «не принадлежит» ELSE PRINT «принадлежит» ENDIF ENDIF ENDIF END	var x: real; begin readln(x); if x>=-3 then if x<=9 then if x>1 then write(‘не принадлежит’) else write(‘принадлежит’) end.
Си	Алгоритмический язык
void main(void) { float x; scanf(«%f»,&x); if(x>=-3) if(x<=9) if(x>1) printf(«не принадлежит»); else printf(«принадлежит»); }	алг
нач
вещ x
ввод x
если x>=-3 то
если x<=9 то
если x>1 то
вывод ‘не принадлежит’ иначе
вывод ‘принадлежит’ все все
все
кон

Демонстрационный
вариант ЕГЭ 2013 г. ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 28 / 39)

работать хуже, чем раньше, т.е. для всех точек, для которых программа ранее выдавала верный ответ, доработанная программа также должна выдавать верный ответ. 3. Приведённых трёх ограничений недостаточно для описания двух областей (потеряно условие x>=5). Кроме того, необходимо учесть, что области не соединены. Исправлением этой ошибки может быть разбиение области на две части и использование дизъюнкции, либо использование сложной (для выведения) математической конструкции (\|\|x–3\|–4\|≤2), либо использование сложной комбинации каскадных условий. В сложных случаях это действие считается выполненным, если верно определены заштрихованные области, т.е. программа выводит сообщение «принадлежит» для всех точек закрашенных областей, и только для них, для точек вне заштрихованных областей программа выводит «не принадлежит» или не выводит ничего. В работе (во фрагментах программ) допускается наличие отдельных синтаксических ошибок, не искажающих замысла автора решения
Выполнены все три действия	3
Правильно выполнены два действия из трёх (исправлены обе ошибки, но в пункте 1 задания не приведена таблица (либо таблица содержит ошибки в двух и более строках), либо приведена таблица (которая содержит ошибки не более чем в одной строке), но исправлена только одна ошибка программы). При написании операций сравнения допускается одно неправильное использование строгих/нестрогих неравенств (считается несущественной ошибкой, погрешностью записи). Например, вместо «x>=5» используется «x>5»	2
Правильно выполнено только одно действие из трёх, т.е. либо только приведена таблица, которая содержит ошибки в не более чем одной строке, либо таблица не приведена (или приведена и содержит ошибки более чем в одной строке), но исправлена одна ошибка программы. При оценивании этого задания на 1 балл допускается не учитывать корректность работы программ на точках границ областей (вместо нестрогих неравенств в решении были использованы строгие неравенства или наоборот)	1
Все пункты задания выполнены неверно (таблица анализа правильности алгоритма не приведена либо содержит ошибки в двух и более строках, программа не приведена либо ни одна из двух ошибок не исправлена)	0
Максимальный балл	3

(2013 — 27 / 39

2. Возможная доработка (Паскаль):

if (x>=-3) and (x<=1) or (x>=5) and (x<=9) then
write(‘принадлежит’) else write(‘не принадлежит’) Возможны и другие
способы доработки.

Например:

if x>=-3
then if x<=1 then write(‘принадлежит’) else if x>=5
then if x<=9 then write(‘принадлежит’) else

write(‘не
принадлежит’) else

write(‘не принадлежит’)
else

write(‘не
принадлежит’)

Другой пример:

if
abs(abs(x-3)-4)<=2 then write(‘принадлежит’) else

write(‘не
принадлежит’)

Указания по оцениванию

Баллы

Обратите внимание! В задаче требуется выполнить три
действия.

1.
Заполнить таблицу.

2.
Исправить ошибку в условном операторе.

3.
Исправить ошибку, связанную с неправильным набором условий. Баллы
за данное задание начисляются как сумма баллов за верное выполнение каждого действия.
Рассмотрим отдельно каждое действие.

1.
Действие по заполнению таблицы считается выполненным, если в таблице
нет ошибок или ошибки присутствуют только в одной строке.

2.
Неправильное использование условного оператора, в результате чего
при невыполнении первого или второго условия программа не выдавала ничего (отсутствуют
случаи ELSE). Исправлением этой ошибки может быть либо добавление случая ELSE
к каждому условию IF, либо объединение всех условий IF в одно при помощи конъюнкции.

В сложных случаях это действие
считается выполненным, если программа выдает одно из двух сообщений: «принадлежит»
или «не принадлежит» – для любых чисел x, при этом программа не стала

(2013 — 29 / 39

Демонстрационный вариант ЕГЭ 2013 г.
ИНФОРМАТИКА и ИКТ, 11 класс. (2013 — 30 / 39) случае Вы должны использовать
те же самые исходные данные и переменные, какие были предложены в условии (например,
в образце, записанном на естественном языке).

Содержание верного ответа и указания по оцениванию

(допускаются
иные формулировки ответа, не искажающие его смысла)

На языке Паскаль

p := 1;

for i := 1 to
N do

if (a[i] mod
2<>0) and (a[i] mod 3=0) then p := p * a[i]; writeln(p);

На алгоритмическом языке

p := 1

нц для i от 1
до N

если
mod(a[i],2)<>0 и mod(a[i],3)=0

то

p :=
p * a[i]

все кц

вывод p

На языке Бейсик

P = 1

FOR I = 1 TO
N

IF A(I) MOD
6=3 THEN

P = P * A(I)

ENDIF

NEXT I

PRINT P

На языке СИ

p=1;

for (i=0;
i<N; i++)

if (a[i]%2!=0
&& a[i]%3==0) p*=a[i]; printf(«%ld», p);

На естественном языке

Записываем в переменную
P начальное значение, равное 1. В цикле от 1-го элемента до 30-го находим остаток
от деления элемента исходного массива на 2 и на 3. Если остаток от деления на
2 не равен 0 и остаток от деления на 3 равен 0, то считаем произведение данного
элемента массива и значения переменной P или достаточно проверить, что остаток
от деления на 6 равен 3 (см. решение на языке Бейсик). Результат умножения сохраняем
в переменную P. Переходим к следующему элементу массива. После завершения цикла
выводим значение переменной P

Паскаль	Алгоритмический язык
const N=30; var a: array [1..N] of longint; i, j, p: longint; begin for i := 1 to N do readln(a[i]); … end.	алг нач цел N=30 целтаб a[1:N] цел i, j, p нц для i от 1 до N ввод a[i] кц … кон
Бейсик	СИ
N=30 DIM A(N) AS LONG DIM I, J, P AS LONG FOR I = 1 TO N INPUT A(I) NEXT I … END	#include <stdio.h> #define N 30 void main(void){ long a[N]; long i, j, p; for (i=0; i<N; i++) scanf(«%ld», &a[i]); … }
Русский (естественный) язык
Объявляем массив A из 30 элементов. Объявляем целочисленные переменные I, J, P. В цикле от 1 до 30 вводим элементы массива A с 1-го по 30-й. …

Источник

Крылов С. С., Чуркина Т. Е. ЕГЭ-2013. Информатика и ИКТ : типовые экзаменационные варианты : 10 вариантов

ЕГЭ-2013. Информатика и ИКТ : типовые экзаменационные варианты : 10 вариантов / С. С. Крылов, Т. Е. Чуркина. — М. , 2012. — 176 с. — (ЕГЭ-2013. ФИПИ — школе).
Серия «ЕГЭ-2013. ФИПИ — школе» подготовлена разработчиками контрольных измерительных материалов. В сборнике представлены:
• 10 типовых экзаменационных вариантов для подготовки к экзамену 2013 года;
• типовой бланк ответов ЕГЭ;
• ответы к заданиям всех частей экзаменационной работы (1, 2, 3);
• критерии оценивания заданий.
Выполнение заданий типовых экзаменационных вариантов предоставляет учащимся возможность самостоятельно подготовиться к итоговой аттестации, а также объективно оценить уровень своей подготовки.
Учителя могут использовать типовые экзаменационные варианты для организации контроля результатов обучения школьников и интенсивной подготовки учащихся к ЕГЭ.
СОДЕРЖАНИЕ
Введение ……3
Инструкция по выполнению работы…… 4
Вариант 1 ……7
Вариант 2 ……20
Вариант 3 ……33
Вариант 4 …….46
Вариант 5 ……59
Вариант 6 ……72
Вариант 7 ……84
Вариант 8 ……96
Вариант 9 …….108
Вариант 10 ……120
Ответы к заданиям частей А и В ……132
Критерии проверки и оценки выполнения заданий с развёрнутым ответом части С ……134

Источник

Выберите вариант ЕГЭ по предмету Информатика 2013 год

ЕГЭ Информатика 2013 год. Вариант 1

Источник варианта

Демонстрационный вариант ФИПИ.

Как вам удобнее вводить ответы?
1) Обычная форма, ответы возле каждого вопроса
2) Аналог реального бланка ответов, все элементы располагаются на одном бланке, который можно вывести/спрятать

Источник

№2 Издание основано в 1995 г. inf.1september.ru

У Ч Е Б Н О — М Е Т О Д И Ч Е С К И Й Ж У Р Н А Л

Д Л Я У Ч И Т Е Л Е Й И Н Ф О Р М А Т И К И

ЕГЭ-А10:

глаза боятся, а руки делают

“Я вам не

помешаю?” — cпросил ноль единичку

F++F++F

F → F−F++F−F

…Нарисуем —

будем жить ☺

Младший братик AutoCAD’a

1se1septemberptember.ru.ru

ИНФИНФОРМАТИКАОРМАТИКА ПодПодписка:писка: «Роc«Роcпечать»печать» –32291– 32291(бумажна(бумажнаяя версия),версия),191917979 (эле(электронная);ктронная); «Поч«Почтата РосРоссии»сии» – 79– 06790666 (бума(бумажнаяжная версверсия),ия), 1268126844 (эле(электронная)ктронная)

				февраль 2013 / ИНФОРМАТИКА

НА ОБЛОЖКЕ		В НОМЕРЕ

На обложке последнего	3		ПАРА СЛОВ

зимнего номера — сне-
жинки Коха. Классические				Выбирайте выражения… общаясь
			с компьютером ☺
и, возможно, самые из-	4
вестные фрактальные кри-		ЕГЭ
вые. Кто только и как толь-
ко их не строил ☺. Даже в				ЕГЭ-A10: задачи с интервалами
различных курсах для на-	12		ПРОФИЛЬ
чальной школы дети, кото-
рые только познакомились				Помехоуcтойчивое кодирование.
с основами какого-нибудь				Основы
языка (Лого, например),	21		РОССЫПЬ “ЗАЦЕПОК”
уже выводят такие при-
вычные, но такие красивые	48		ЗАНИМАТЕЛЬНЫЕ
снежинки, придуманные в
далеком 1904 году швед-		МАТЕРИАЛЫ ДЛЯ ПЫТЛИВЫХ
ским математиком Хельге				УЧЕНИКОВ И ИХ ТАЛАНТЛИВЫХ
фон Кохом.
			УЧИТЕЛЕЙ

				“В мир информатики” № 184

НА ДИСКЕ

ЭЛЕК ТРОННЫЕ МАТЕРИА ЛЫ:

Презентации к статьям номера

Программа для решения задач ЕГЭ А10

Дистрибутив программы A9CAD к статье “Что нам стоит дом построить”

ИНФОРМАТИК	ПОДПИСНЫЕ ИНДЕКСЫ: по каталогу “Роспечати”: 32291 (бумажная версия), 19179 (электронная версия);
“Почта России”: 79066 (бумажная версия), 12684 (электронная версия)


http://inf.1september.ru	Учебно-методический журнал	ИЗДАТЕЛЬСКИЙ ДОМ	ГАЗЕТА	УЧРЕДИТЕЛЬ:
	для учителей информатики	“ПЕРВОЕ СЕНТЯБРЯ”	ИЗДАТЕЛЬСКОГО ДОМА	ООО “ЧИСТЫЕ ПРУДЫ”
	О с н о в а н в 19 9 5 г.	Главный редактор:	Первое сентября – Е.Бирюкова	Зарегистрировано
	Выходит один раз в месяц	Артем Соловейчик	ЖУРНАЛЫ	ПИ № ФС77-44341
		(генеральный директор)	ИЗДАТЕЛЬСКОГО ДОМА	от 22.03.2011
		Коммерческая деятельность:	Английский язык – А.Громушкина	в Министерстве РФ
	РЕДАКЦИЯ:	по делам печати
	Библиотека в школе – О.Громова
	гл. редактор С.Л. Островский	Константин Шмарковский	Подписано в печать:
	Биология – Н.Иванова
	(финансовый директор)	по графику 15.01.2013,
	редакторы	География – О.Коротова
	Развитие, IT	фактически 15.01.2013
	Е.В. Андреева,	Дошкольное
	Заказ №
	и координация проектов:	образование – Д.Тюттерин
	Д.М. Златопольский	Отпечатано в ОАО “Первая
	Сергей Островский	Здоровье детей – Н.Сёмина
	(редактор вкладки	Образцовая типография”
	(исполнительный директор)	Информатика – С.Островский
	“В мир информатики”)	Филиал “Чеховский Печатный Двор”
		Искусство – М.Сартан
	Реклама, конференции	ул. Полиграфистов, д. 1,
	Дизайн макета И.Е. Лукьянов
	История – А.Савельев
	и техническое обеспечение	Московская область,
	верстка Н.И. Пронская	Классное руководство
	Издательского дома:	г. Чехов, 142300
	корректор Е.Л. Володина	и воспитание школьников –	Сайт www.chpk.ru,
	Павел Кузнецов
	М.Битянова
		E-mail: salеs@chpk.ru,
	секретарь Н.П. Медведева
	Производство:	Литература – С.Волков
	факс 8 (495) 988-63-87
	Фото: фотобанк Shutterstock
	Станислав Савельев	Математика – Л.Рослова	АДРЕС ИЗДАТЕЛЯ:
	Журнал распространяется		Начальная школа – М.Соловейчик
	Административно-	ул. Киевская, д. 24,
	по подписке	Немецкий язык – М.Бузоева
	хозяйственное обеспечение:	Москва, 121165
	Цена свободная	Русский язык – Л.Гончар
	Андрей Ушков	Тел./факс: (499) 249-31-38
	Тираж 21 609 экз.	Спорт в школе – О.Леонтьева
		Отдел рекламы:
	Главный художник:	Технология – А.Митрофанов
	Тел. редакции: (499) 249-48-96
	(499) 249-98-70
	Иван Лукьянов	Управление школой – Е.Рачевский
	E-mail: inf@1september.ru
	http://1september.ru
	Педагогический университет:	Физика – Н.Козлова
	http://inf.1september.ru
	Французский язык – Г.Чесновицкая	ИЗДАТЕЛЬСКАЯ ПОДПИСКА:
		Валерия Арсланьян (ректор)
		Химия – О.Блохина	Телефон: (499) 249-47-58

			Школьный психолог – И.Вачков	E-mail: podpiska@1september.ru

ЕГЭ

ЕГЭ-A10: задачи с интервалами

К.Ю. Поляков,

д. т. н., Санкт-Петербург

	/ ИНФОРМАТИКА
	2013	На фото:

	февраль	штурмовик A10
	Thunderbolt. Столь

		же грозное оружие,
		как и задача A10 ☺

Введение

В демонстрационном варианте конт- рольно-измерительных материалов ЕГЭ по информатике [1] появилась новая задача на математическую логику, которая обещает быть одной из “проблемных” задач на предстоящем ЕГЭ:

Задача 1. На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 16]. Выберите такой отрезок A, что формула

(( x A) →(x P)) (x Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[0, 3]

2)[3, 11]

3)[11, 15]

4)[15, 17]

Эта задача не столько сложная, сколько “закрученная”. Во-первых, с трудом можно представить себе реальную задачу, которая сводится к такой формуле.

Во-вторых, достаточно простая суть скрывается за обилием математических обозначений. Этим недостатком страдает и теоретизированное решение, приведенное в [2], которое трудно воспринимать даже человеку с высшим техническим образованием.

В этой заметке предлагается довольно простой метод решения подобных задач, использующий визуальное представление отрезков на числовой оси.

Прежде чем приступать к решению, приведем некоторые предварительные сведения, которыми должен владеть учащийся.

Рассмотрим интервал P = [2, 10]. Очевидно, что область истинности вы-

ражения P : x P представляет собой отрезок на числовой оси:

Область истинности выражения

P : x P — это объединение интервалов (–∞, 2) и (10, ∞) :

Для решения задач нам будут нужны две операции с интервалами: пересечение (определение общей части двух интервалов) и объединение. Если

ввести высказывание Q : x Q, то пересечение интервалов P и Q определяет область истинности вы-

ражения P Q1 (она выделена желтым цветом):

Действительно, выражение P Q истинно, если x принадлежит обоим отрезкам одновременно.

Объединение отрезков P и Q определяет область

истинности логической суммы P + Q (x принадлежит хотя бы одному из отрезков):

Для преобразования логических выражений нам будет нужна формула, представляющая импликацию через операции “ИЛИ” и “НЕ”2

A →B = A + B

и законы де Моргана:

A B = A + B, A + B = A B.

Решение задачи из демоварианта

Сначала приведем заданное выражение к более понятной форме. Введем логические высказывания

P : x P, Q : x Q и A : x A.

Тогда выражение, заданное в условии, запишется в форме

Z = (A →P)+ Q.

Раскрыв операцию “импликация” через “ИЛИ” и “НЕ”, получаем

Z = A + P + Q.

Это выражение должно быть истинно для любого x, поэтому область истинности выражения Z должна охватывать всю числовую ось. Нам известны отрезки P и Q, они конечны и всю числовую ось перекрыть не могут:

Оставшуюся часть должна перекрыть область

истинности выражения A. Это означает, что A может быть ложно только внутри отрезка [2, 14]; соответственно, выражение A может быть истинно только на этом отрезке. Поэтому правильный ответ — это отрезок, целиком попадающий

1 Далее конъюнкцию (логическое умножение) мы будем обозначать знаком “ ”, а дизъюнкцию (логическое сложение) — знаком “+”. Эти обозначения, в отличие от тех, что применяются в заданиях ЕГЭ, проще воспринимаются и позволяют сразу выявлять аналогии с алгеброй.

2 Черта сверху обозначает отрицание (инверсию) логического выражения.

внутрь отрезка [2, 14]. Проверка заданных вариантов ответа показывает, что верный ответ — 2 (отрезок [3, 11]).

Вариации

В этом разделе мы рассмотрим еще несколько задач на ту же тему, которые теоретически могут встретиться в КИМ.

Задача 2. На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 25]. Выберите такой отрезок A, что формула

(( x A) →(x P)) (x Q)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[0, 15]

2)[10, 25]

3)[2, 10]

4)[15, 20]

Отличие от Задачи 1 состоит в том, что в двух скобках вместо знака “принадлежит” используется “не принадлежит”. Как и раньше, введем логические высказывания

P : x P, Q : x Q и A : x A.

Тогда выражение, заданное в условии, запишется в форме

Z = (A →P)+ Q.

Раскрыв операцию “импликация” через “ИЛИ” и “НЕ”, получаем

Z = A + P + Q.

Поскольку выражение должно быть истинно для любого х, области истинности всех слагаемых

должны перекрыть всю числовую ось. Область P состоит из двух полуосей, (–∞, 2) и (20, ∞): участков числовой оси, которые не входят в отрезок [2, 20], а область Q — это отрезок [15, 25]:

Область истинности выражения A должна перекрывать оставшуюся часть — полуинтервал [2, 15) (открытый справа, потому что точка x = 15 уже перекрыта отрезком Q). Из всех отрезков, приведенных в условии, только отрезок [0, 15] (вариант 1) полностью перекрывает полуинтервал [2, 15), это и есть правильный ответ.

Задача 3. На числовой прямой даны три отрезка: P = [10, 27], Q = [15, 30] и R = [25, 40]. Выберите такой отрезок A, что формула

(( x Q) →(x R)) (x A) (x P)

тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 15]

2)[10, 40]

3)[25, 35]

4)[15, 25]

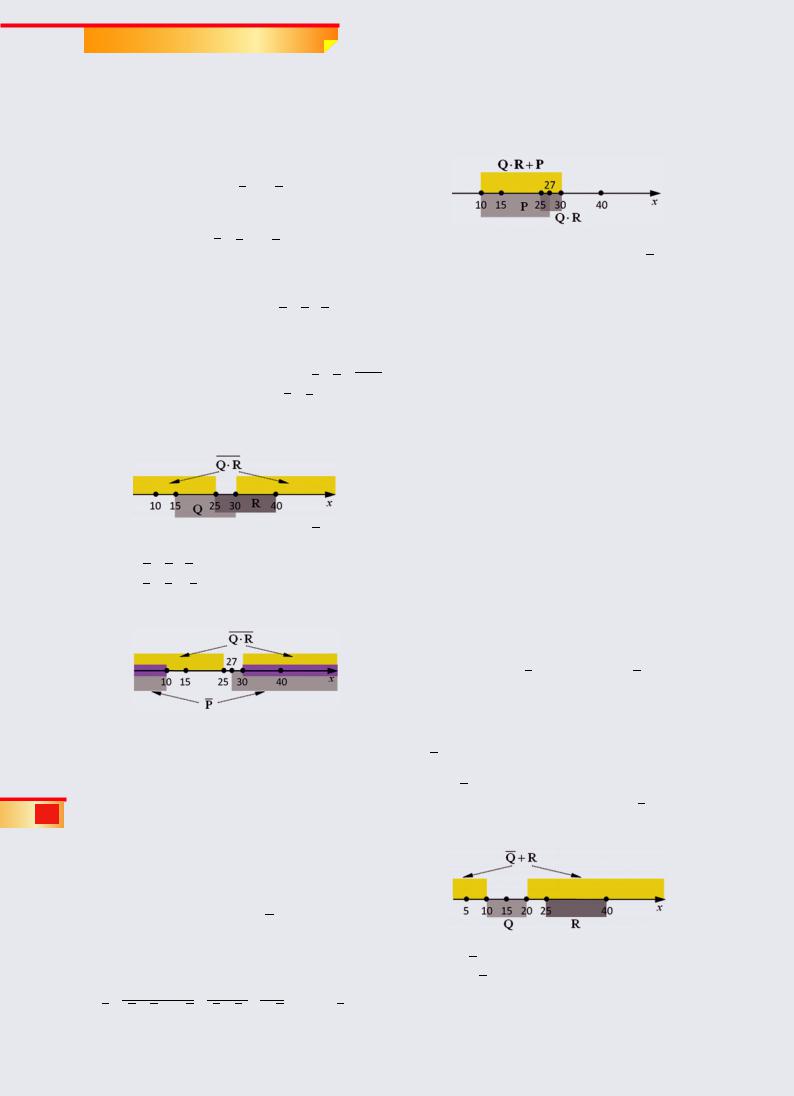
В отличие от предыдущих задач здесь, вопервых, задано три интервала и, во-вторых,

февраль 2013 / ИНФОРМАТИКА

ЕГЭ

требуется, чтобы выражение было тождественно ложно (а не истинно).

Введем логические высказывания

P : x P, Q : x Q, R : x R и A : x A.

Учтем, что в формуле дважды используется знак “ ” (“не принадлежит”), поэтому выражение можно записать в виде:

Z = (Q →R) A P

Представим импликацию через операции “ИЛИ” и “НЕ”:

Z = (Q + R) A P

Это выражение должно быть тождественно ложно при всех х. Поэтому роль неизвестного сомножителя A состоит в том, чтобы обнулить выра-

жение везде, где произведение (Q + R) P равно 1. Поэтому для этих значений x выражение A должно быть равно нулю, а для остальных x его значение не играет роли.

Поскольку по закону де Моргана Q + R = Q R ,

область истинности выражения Q + R — это область вне общей части отрезков Q и R (она показана желтым цветом на рисунке):

Теперь умножим это выражение на P (ему соответствует область вне отрезка [10, 27]), построив

область (Q + R) P; эта область, где одновременно

истинны Q + R и P, выделена на рисунке фиолетовым цветом:

В этой “фиолетовой” области выражение A должно быть обязательно равно 0, и только внутри отрезка [10, 30] может быть истинно. Таким образом, среди ответов нужно найти отрезок, который целиком помещается внутри отрезка [10, 30]. Этому условию удовлетворяет только отрезок [15, 25] (ответ 4).

Возможен еще один подход к решению этой задачи, который фактически сводит ее к предыдущей. Для этого требуется построить обратное выражение, выполнив инверсию сложного выражения по законам де Моргана.

Выражение Z тождественно ложно тогда и только тогда, когда обратное ему, Z, тождественно истинно; таким образом, если выполнить инверсию для Z, мы сведем Задачу 3 к задаче из демоварианта ЕГЭ-2013, разобранной выше.

Используя законы де Моргана, получаем:

Z = (Q + R) A P = (Q + R) + A P = Q R + A + P

Выражение Q · R истинно на общей части (пересечении) отрезков Q и R, то есть на отрезке [25, 30]. Добавляя к этому диапазону отрезок P, получим отрезок [10, 30], где истинно выражение

Q R + P :

Остальную часть числовой оси (при x < 10 и

x > 30) должно перекрыть выражение A , то есть A должно быть ложно вне отрезка [10, 30]. Далее, аналогично предыдущему способу, находим правильный ответ 4 (отрезок [15, 25]).

Задача 4. На числовой прямой даны три отрезка: P = [5, 10], Q = [10, 20] и R = [25, 40]. Выберите такой отрезок A, что выражения

( x A) →(x P) и ( x Q) →(x R)

тождественно равны, то есть принимают одинаковые значения при любом значении переменной х (кроме, возможно, конечного количества точек).

1)[7, 20]

2)[2, 12]

3)[10, 25]

4)[20, 30]

В этой задаче оговорка “кроме, возможно, конечного количества точек” означает, что в некоторых точках — на концах отрезков — заданные выражения могут иметь различные значения.

Введем логические высказывания

P : x P, Q : x Q , R : x R и A : x A . Обозначим буквами два заданных логических

выражения:

Y = A →P , Z = Q →R .

Выразим импликации через операции “ИЛИ” и “НЕ”:

Y = A →P = A + P, Z = Q →R = Q + R

Заметим, что неизвестная величина A входит только в выражение Y. Общая идея состоит в том, чтобы построить на числовой оси область истинности для полностью известного выражения

Z = Q + R , а затем дополнить отрезок P до этой области; это “дополнение” будет соответствовать

области A .

Область истинности выражения Z = Q + R состоит из отрезка R и области вне отрезка Q:

Обратите внимание, что в данном случае область Z = Q + R (она выделена желтым цветом)

совпадает с Q (конечно, так будет не всегда). Теперь рассмотрим область истинности выраже-

ния P (она выделена серым цветом):

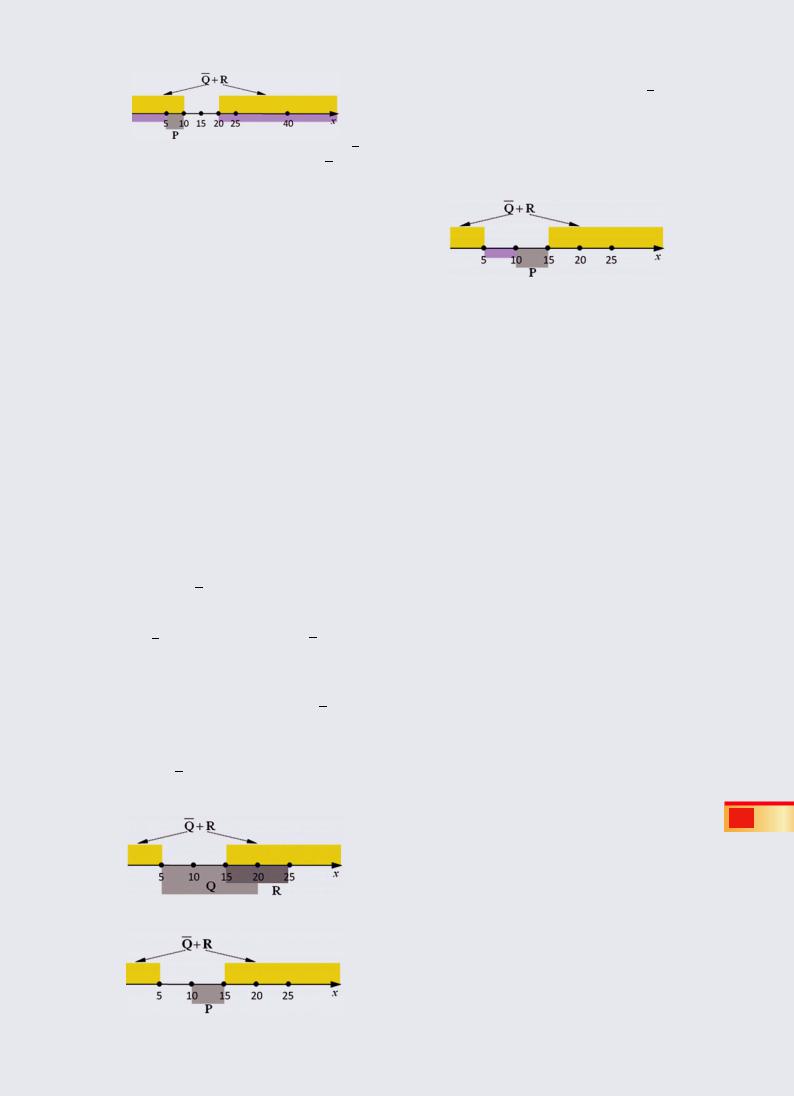
Чтобы область истинности выражения Y = A + P совпала с желтой областью, выражение A должно “перекрыть” всю фиолетовую область (возможно, заходя в область P, но не внутрь отрезка [10, 20]). Поэтому выражение A обязательно должно быть истинно на отрезке [10, 20]; обязательно должно быть ложно на полуосях (–∞, 5) и (20, +∞), а на отрезке [5, 10] его значение может быть любым. Из предложенных вариантов ответов этим требованиям удовлетворяет только отрезок [7, 20] (ответ 1).

Задача 5. На числовой прямой даны три отрезка: P = [10, 15], Q = [5, 20] и R = [15, 25]. Выберите такой отрезок A, что выражения

( x A) →(x P) и ( x Q) →(x R)

принимают разные значения при любом значении переменной х (кроме, возможно, конечного количества точек).

1)[7, 20]

2)[2, 15]

3)[5, 12]

4)[20, 25]

По аналогии с предыдущей задачей, здесь допускается, что заданные функции могут иметь одинаковые значения в отдельных точках — на концах отрезков.

Введем логические высказывания

P : x P , Q : x Q, R : x R и A : x A. Обозначим буквами два заданных логических

выражения:

Y = A →P , Z = Q →R .

Выразим импликации через операции “ИЛИ” и “НЕ”:

Y = A →P = A + P, Z = Q →R = Q + R

Заметим, что неизвестная величина A входит только в выражение Y. Для решения задачи построим на числовой оси область истинности для

полностью известного выражения Z = Q + R, а затем дополним отрезок P до “обратной” области, в которой выражение Z ложно; это “дополнение” будет соответствовать области A.

Область Z = Q + R — это объединение отрезка R и области вне отрезка Q:

Теперь рассмотрим область P (она выделена серым цветом)

Чтобы выполнить заданное условие (противо-

положность значений Y = A + P и Z = Q + R при любых x, за исключением конечного числа точек), область истинности выражения Y = A + P должна совпадать с областью, где выражение Z ложно; для этого выражение A должно “перекрыть” всю фиолетовую область (возможно, заходя в область P), но не должно заходить в “желтую” область:

Из предложенных вариантов ответов этим требованиям удовлетворяет только отрезок [5, 12] (ответ 3).

Задачи для тренировки

Учитывая существующий дефицит литературы по этой теме, приведем несколько задач, которые можно использовать для тренировки. Ответы к этим задачам можно найти на странице http://kpolyakov. narod.ru/school/ege.htm. Кроме того, на диске в приложении к этому номеру размещена программа на языке Python 3, которая решает задачи этого типа.

1. На числовой прямой даны два отрезка: P = [5, 15] и Q = [12, 18]. Выберите такой отрезок A, что формула

((x А) → (x P )) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[3, 11]

2)[2, 21]

3)[10, 17]

4)[15, 20]

2. На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула

((x А) → (x P)) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[3, 11]

2)[6, 10]

3)[8, 16]

4)[17, 23]

3. На числовой прямой даны два отрезка: P = [25, 30] и Q = [15, 20]. Выберите такой отрезок A, что формула

((x А) → (x P)) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 15]

2)[12, 30]

3)[20, 25]

4)[26, 28]

4. На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 30]. Выберите такой отрезок A, что формула

((x А) → (x P)) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

февраль 2013 / ИНФОРМАТИКА

ЕГЭ

1)[0, 15]

2)[3, 20]

3)[10, 25]

4)[25, 40]

5. На числовой прямой даны два отрезка: P = [10, 25] и Q = [0, 12]. Выберите такой отрезок A, что формула

((x А) → (x P)) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 15]

2)[20, 35]

3)[5, 20]

4)[12, 40]

6. На числовой прямой даны два отрезка: P = [10, 20] и Q = [12, 15]. Выберите такой отрезок A, что формула

((x А) → (x P)) (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 15]

2)[20, 35]

3)[5, 20]

4)[12, 40]

7. На числовой прямой даны два отрезка: P = [10, 20] и Q = [5, 15]. Выберите такой отрезок A, что формула

((x P) → (x Q)) (x A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 15]

2)[20, 35]

3)[15, 22]

4)[12, 18]

8. На числовой прямой даны два отрезка: P = [10, 20] и Q = [15, 25]. Выберите такой отрезок A, что формула

((x P) → (x Q)) (x A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[8, 17]

2)[10, 12]

3)[15, 22]

4)[12, 18]

9. На числовой прямой даны два отрезка: P = [10, 40], Q = [5, 15] и R = [35, 50]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 20]

2)[15, 25]

3)[20, 30]

4)[120, 130]

10. На числовой прямой даны три отрезка: P = [0, 20], Q = [5, 15] и R = [35, 50]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[–15, –5]

2)[2, 7]

3)[10, 17]

4)[15, 20]

11. На числовой прямой даны три отрезка: P = [15, 30], Q = [0, 10] и R = [25, 35]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 17]

2)[15, 25]

3)[20, 30]

4)[35, 40]

12. На числовой прямой даны три отрезка: P = [20, 50], Q = [15, 20] и R = [40, 80]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 25]

2)[20, 30]

3)[40, 50]

4)[35, 45]

13. На числовой прямой даны три отрезка: P = [10, 50], Q = [15, 20] и R = [30, 80]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[10, 25]

2)[25, 50]

3)[40, 60]

4)[50, 80]

14. На числовой прямой даны три отрезка: P = [0, 40], Q = [20, 45] и R = [10, 50]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1)[5, 20]

2)[10, 15]

3)[15, 20]

4)[35, 50]

15. На числовой прямой даны два отрезка: P = [5, 15] и Q = [10, 20]. Выберите такой отрезок A, что формула

(x P) (x Q) (x A) тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 7]

2)[8, 15]

3)[15, 20]

4)[7, 20]

16. На числовой прямой даны два отрезка: P = [12, 22] и Q = [7, 17]. Выберите такой отрезок A, что формула

(x P) (x Q) (x A) тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 5]

2)[7, 12]

3)[10, 20]

4)[5, 22]

17. На числовой прямой даны два отрезка: P = [10, 20] и Q = [5, 15]. Выберите такой отрезок A, что формула

((x Q) → (x P)) (x A) тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 6]

2)[5, 8]

3)[7, 15]

4)[12, 20]

18. На числовой прямой даны три отрезка: P = [15, 30], Q = [5, 10] и R = [20, 25]. Выберите такой отрезок A, что формула

((x P) → (x Q)) ((x A) → (x R)) тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 20]

2)[0, 10]

3)[10, 15]

4)[25, 30]

19. На числовой прямой даны три отрезка: P = [15, 30], Q = [5, 10] и R = [10, 20]. Выберите такой отрезок A, что формула

((x P) → (x Q)) (x A) (x R) тождественно ложна, то есть принимает значение 0 при любом значении переменной х.

1)[0, 12]

2)[10, 17]

3)[15, 20]

4)[15, 30]

20. На числовой прямой даны три отрезка: P = [10, 15], Q = [10, 20] и R = [5, 15]. Выберите такой отрезок A, что выражения

(x A) → (x P) и (x Q) → (x R) тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного количества точек).

1)[5, 12]

2)[10, 17]

3)[12, 20]

4)[15, 25]

21. На числовой прямой даны три отрезка: P = [5, 10], Q = [15, 20] и R = [25, 30]. Выберите такой отрезок A, что выражения

1)[5, 10]

2)[15, 20]

3)[10, 20]

4)[15, 25]

22. На числовой прямой даны три отрезка: P = [10, 25], Q = [15, 30] и R = [25, 35]. Выберите такой интервал A, что формулы

(x A) → (x P) и (x Q) → (x R)

тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного количества точек).

1)(10, 12)

2)(0, 10)

3)(5, 15)

4)(15, 25)

23. На числовой прямой даны три отрезка: P = [10, 30], Q = [15, 30] и R = [20, 35]. Выберите такой интервал A, что формулы

1)(10, 25)

2)(15, 20)

3)(15, 30)

4)(5, 20)

24. На числовой прямой даны три отрезка: P = [5, 15], Q = [10, 20] и R = [15, 20]. Выберите такой отрезок A, что выражения

1)[3, 10]

2)[7, 12]

3)[12, 17]

4)[22, 25]

25. На числовой прямой даны три отрезка: P = [5, 25], Q = [5, 15] и R = [10, 20]. Выберите такой отрезок A, что выражения

(x A) → (x P) и (x Q) → (x R) принимают разные значения при любом значении переменной х (за исключением, возможно, конечного количества точек).

1)[5, 12]

2)[10, 18]

3)[18, 25]

4)[20, 35]

Литература

1.Демонстрационный вариант контрольноизмерительных материалов ЕГЭ 2013 года по информатике и ИКТ http://www.ﬁpi.ru/binaries/1384/ inf11.zip.

2.А10. Разбор демонстрационного варианта // Электронный ресурс (http://ege-go.ru/a10/a10- demo/).

Автор благодарит д. ф.-м. н. М.А. Ройтберга за полезные замечания по содержанию статьи.

февраль 2013 / ИНФОРМАТИКА

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вступление

ЕГЭ 2013. Демонстрационный вариант

Структура ЕГЭ

Самоподготовка

Интернет-проекты

Заключение

ФИПИ ЕГЭ по информатике 2023 2013

НАШ БЛОГ

Как успешно сдать ЕГЭ по литературе

Вопросы абитуриентов о поступлении в вуз

Поступить на дистанционное без ЕГЭ

Инструкция по выполнению работы

Часть 1

Часть 2

1. прибавь 1,

Часть 3

КРИТЕРИИ ОЦЕНИВАНИЯ ЗАДАНИЙ С РАЗВЁРНУТЫМ ОТВЕТОМ

Выберите вариант ЕГЭ по предмету Информатика 2013 год

ЕГЭ Информатика 2013 год. Вариант 1

Источник варианта

ЕГЭ-A10: задачи с интервалами

Введение

Решение задачи из демоварианта

Задачи для тренировки

Новое и интересное на сайте:

1. прибавь
1,

КРИТЕРИИ ОЦЕНИВАНИЯ
ЗАДАНИЙ С РАЗВЁРНУТЫМ ОТВЕТОМ