Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
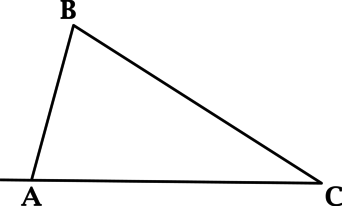
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
Варианты для подготовки к ЕГЭ (задания по геометрии)
Вариант № 1
1. 
2. Электрику ростом 1,8 метра нужно поменять лампочку, закреплённую на стене дома на высоте 4,2 м. Для этого у него есть лестница длиной 3 метра. На каком наибольшем расстоянии от стены должен быть установлен нижний конец лестницы, чтобы с последней ступеньки электрик дотянулся до лампочки? Ответ запишите в метрах.
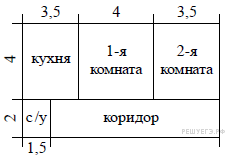
3. 
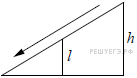
4. 
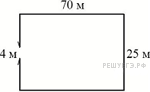
5. 
6.
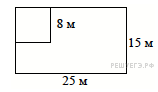
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
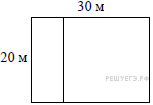
7. 
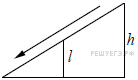
8. 
9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?
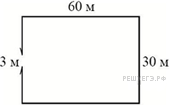
10. 
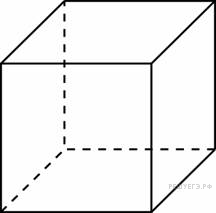
11. 
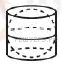
12. 
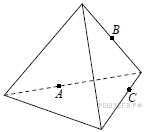
13. 
14. В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину диагонали
.
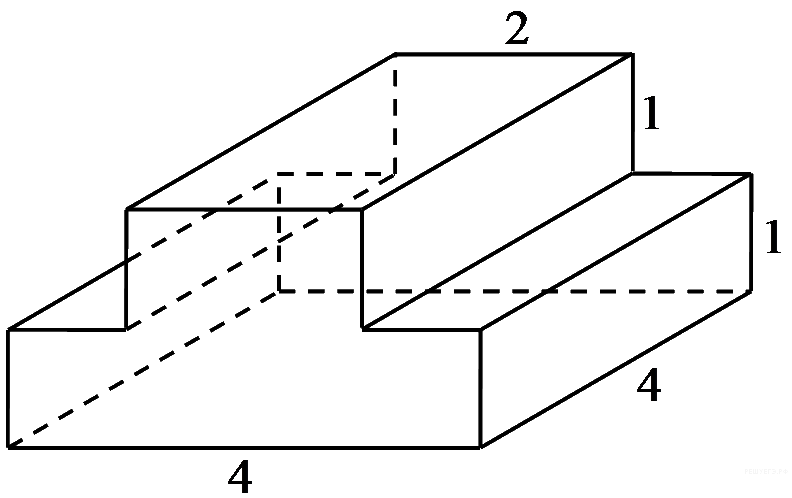
15. 
16.
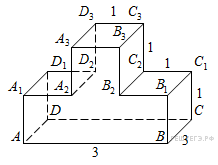
17. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
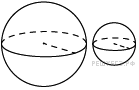
18. 
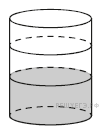
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.
20. 
Ключ Вариант № 1
|
№ п/п |
Ответ |
|
1 |
1400 |
|
2 |
1,8 |
|
3 |
66 |
|
4 |
1 |
|
5 |
186 |
|
6 |
311 |
|
7 |
120 |
|
8 |
1 |
|
9 |
800 |
|
10 |
177 |
|
11 |
24 |
|
12 |
72 |
|
13 |
6 |
|
14 |
27 |
|
15 |
60 |
|
16 |
1200 |
|
17 |
11 |
|
18 |
9 |
|
19 |
2 |
|
20 |
93 |
Вариант № 2
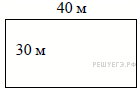
1. 
2. 
3. 
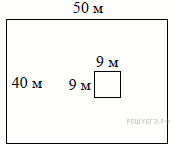
4. Рыболовное хозяйство строит бассейн для разведения рыбы. Бассейн имеет форму прямоугольника со сторонами 4 м и 12 м. В центре бассейна находится техническая постройка, которая имеет форму прямоугольника со сторонами 2 м и 3 м. Найдите площадь оставшейся части бассейна.
5. 
6.
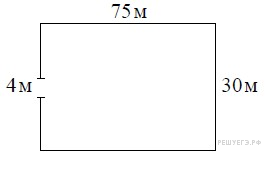
Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 30 м и 75 м. Найдите длину забора (в метрах), которым нужно огородить участок, если в заборе предусмотрен проезд шириной 4 м.
7. 
8. 
9. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
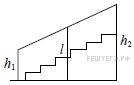
10. 
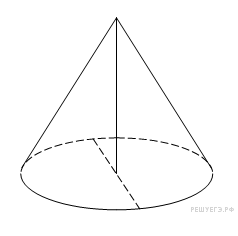
11. 
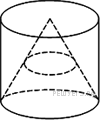
12. 
13.
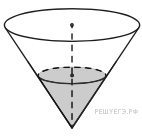
В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
14. 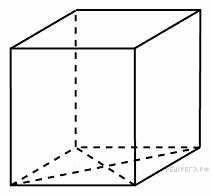
15. 
и
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
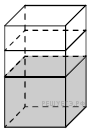
16. 
17. 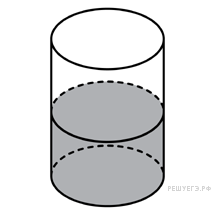
.
18. 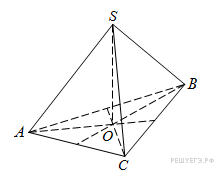
медианы основания
пересекаются в точке
. Площадь треугольника
равна 4; объем пирамиды равен 6. Найдите длину отрезка
.
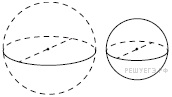
19. 
20.
К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ключ
|
№ п/п |
Вариант № 1 |
Вариант № 2 |
|
1 |
1400 |
100 |
|
2 |
1,8 |
55 |
|
3 |
66 |
40 |
|
4 |
1 |
42 |
|
5 |
186 |
186 |
|
6 |
311 |
206 |
|
7 |
120 |
12 |
|
8 |
1 |
1919 |
|
9 |
800 |
120 |
|
10 |
177 |
1,1 |
|
11 |
24 |
17 |
|
12 |
72 |
63 |
|
13 |
6 |
120 |
|
14 |
27 |
42 |
|
15 |
60 |
11 |
|
16 |
1200 |
3200 |
|
17 |
11 |
2500 |
|
18 |
9 |
4,5 |
|
19 |
2 |
48 |
|
20 |
93 |
13 |
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 1.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
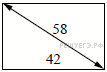
Сторона ромба равна 58, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 240 и 70. Радиус описанной окружности равен 125.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 34°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 58°. Его сторона CA касается окружности. Найдите градусную меру дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 48, средняя линия равна 19. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 88. Найдите радиус описанной окружности этой трапеции.
Проверочная работа по № 1ЕГЭ «Окружность». ВАРИАНТ – 2.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 100, острый угол равен 
2.
Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.
10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 19 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 4
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 72 и 30. Радиус описанной окружности равен 39.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 76, средняя линия равна 6. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 7, описан многоугольник, периметр которого равен 30. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ –3.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 24, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 20 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 4
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 144 и 60. Радиус описанной окружности равен 78.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 88, средняя линия равна 12. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 29. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 4.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 46, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 6
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 288 и 84. Радиус описанной окружности равен 150.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 63. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 5.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 50, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 104, средняя линия равна 20. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 35. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 6.
1.
В окружности с центром O AC и BD — диаметры. Вписанный угол ACB равен 
9.
Сторона ромба равна 94, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 3
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 192 и 56. Радиус описанной окружности равен 100.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 



6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 100, средняя линия равна 18. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 62. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Проверочная работа по № 1 ЕГЭ «Окружность». ВАРИАНТ – 7.
1.
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.
9.
Сторона ромба равна 20, острый угол равен 
2.
Угол ACB равен 

10.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
3.
В треугольнике ABC сторона AB равна 2
11.
Катеты равнобедренного прямоугольного треугольника равны 
4.
Хорда AB делит окружность на две части, градусные величины которых относятся как 
12.
Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.
Найдите высоту трапеции.
5.
Касательные CA и CB к окружности образуют угол ACB, равный 78°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
13.
Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 76°, 101°, 106°, 77°. Найдите угол B этого четырехугольника. Ответ дайте в градусах.
6.
Угол ACO равен 
14.
Радиус окружности, описанной около правильного треугольника, равен 
7.
Сторона правильного треугольника равна 
15.
Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
8.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.
16.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 
Геометрия на плоскости (планиметрия)
Задание
1
#199
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).
Ответ: 106
Задание
2
#200
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).
Ответ: 108
Задание
3
#201
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).
Ответ: 56
Задание
4
#202
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).
Ответ: 40
Задание
5
#203
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).
Ответ: 86
Задание
6
#204
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).
Ответ: 108
Задание
7
#205
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).
Ответ: 71
ЕГЭ Геометрия
14.05.2020.
Тест. Геометрия, 11 класс
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.
Задачи по геометрии : прикладная геометрия. 21 вопрос.
Список вопросов теста
Вопрос 2
Колесо имеет спиц. Найдите величину угла (в градусах), который образуют две соседние спицы.
Вопрос 3
Какой угол (в градусах) образуют минутная и часовая стрелки в ?
Вопрос 5
Кошка ходит по прямоугольной комнате по кругу вдоль стен, пока не пройдёт километр. Стены комнаты имеют длины и
м. Сколько кругов пройдёт кошка?
Вопрос 6
Перила лестницы дачного дома для надежности закреплены посередине вертикальным столбом. Найдите наибольшую высоту перил относительно земли, если наименьшая высота
перил относительно земли равна
м, а высота столба
—
м.
Ответ дайте в метрах.
Вопрос 8
Человек стоит на расстоянии м от столба, на котором висит фонарь, расположенный на высоте
м. Тень человека равна
м.
Какого роста человек (в метрах)?
Вопрос 9
От столба к дому натянут провод длиной м, который закреплён на стене дома на высоте
м от земли (см. рисунок).
Найдите высоту столба, если расстояние от дома до столба равно м.
Ответ дайте в метрах.
Вопрос 10
От столба высотой м к дому натянут провод, который крепится на высоте
м от земли (см. рисунок). Расстояние от дома до столба
м.
Найдите длину провода.
Ответ дайте в метрах.
Вопрос 11
Колесо имеет спиц. Углы между соседними спицами равны.
Найдите величину угла (в градусах), который образуют две соседние спицы.
Вопрос 12
На рисунке показано, как выглядит колесо с 7 спицами.
Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 30°?
Вопрос 13
Перила лестницы дачного дома для надежности закреплены посередине вертикальным столбом.
Найдите высоту этого столба, если наименьшая высота
перил равна
м, а наибольшая
равна
м.
Ответ дайте в метрах.
Вопрос 14
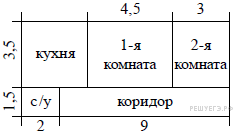
Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3,5 м на 3 м, первая комната — 3,5 м на 5 м, санузел имеет размеры 1,5 м на 2 м, длина коридора 9,5 м.
Найдите площадь всей квартиры (в квадратных метрах).
Вопрос 15
В треугольнике угол
равен
Найдите
Вопрос 16
В прямоугольной трапеции основания равны и
а один из углов равен
Найдите меньшую боковую сторону.
Вопрос 17
Стороны параллелограмма равны 12 и 24. Высота, опущенная на меньшую сторону, равна 18.
Найдите длину высоты, опущенной на большую сторону параллелограмма.
Вопрос 18
Вопрос 19
В треугольнике стороны
и
равны. Внешний угол при вершине
равен 163°.
Найдите угол
Ответ дайте в градусах.
Вопрос 20
В прямоугольном параллелепипеде находится конус, основание которого вписано в основание параллелепипеда, а высота равна высоте параллелепипеда.
Найдите объем параллелепипеда, если радиус основания конуса равен , а высота конуса равна
.
Вопрос 21
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
2 августа 2020
В закладки
Обсудить
Жалоба
Геометрия. Базовый уровень
В презентации представлены типовые задания ЕГЭ по математике базового уровня, блок «Геометрия».
geometri-mb.pptx
geometri-mb.pdf
Автор: Ларионова Наталья Евгеньевна.
Геометрия на ЕГЭ по математике
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
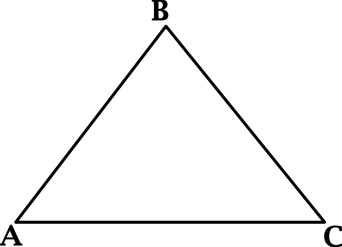
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны
и
сантиметров соответственно. Постройте треугольник
с помощью циркуля и линейки.
б) В треугольнике угол
равен
градусов, сторона
равна
,
равна
. Постройте треугольник
.
в) В треугольнике сторона
равна
, угол
равен
, угол
равен
. Постройте треугольник
.
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
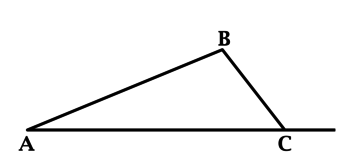
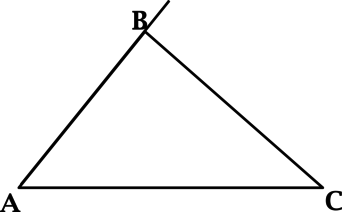
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.
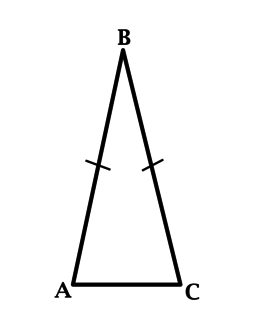
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и
.
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
09.03.2023