Егэ параметр прошлых лет - Помощь в подготовке к экзаменам и поступлению

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи с параметром из ЕГЭ прошлых лет

Задание
1

#6329

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система [begin{cases} (x-2a-2)^2+(y-a)^2=1\
y^2=x^2end{cases}]

имеет ровно четыре решения.

(ЕГЭ 2018, основная волна)

Второе уравнение системы можно переписать в виде (y=pm x). Следовательно, рассмотрим два случая: когда (y=x) и когда (y=-x). Тогда количество решений системы будет равно сумме количества решений в первом и во втором случаях.

1) (y=x). Подставим в первое уравнение и получим: [2x^2-2(3a+2)x+(2a+2)^2+a^2-1=0quad(1)] (заметим, что в случае (y=-x) мы поступим так же и тоже получим квадратное уравнение)
Чтобы исходная система имела 4 различных решения, нужно, чтобы в каждом из двух случаев получилось по 2 решения.
Квадратное уравнение имеет два корня, когда его (D>0). Найдем дискриминант уравнения (1):
(D=-4(a^2+4a+2)).
Дискриминант больше нуля: (a^2+4a+2<0), откуда (ain (-2-sqrt2;
-2+sqrt2)).

2) (y=-x). Получаем квадратное уравнение: [2x^2-2(a+2)x+(2a+2)^2+a^2-1=0quad (2)] Дискриминант больше нуля: (D=-4(9a^2+12a+2)>0), откуда (ain
left(frac{-2-sqrt2}3; frac{-2+sqrt2}3right)).

Необходимо проверить, не совпадают ли решения в первом случае с решениями во втором случае.

Пусть (x_0) – общее решение уравнений (1) и (2), тогда [2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=2x_0^2-2(a+2)x_0+(2a+2)^2+a^2-1] Отсюда получаем, что либо (x_0=0), либо (a=0).
Если (a=0), то уравнения (1) и (2) получаются одинаковыми, следовательно, имеют одинаковые корни. Этот случай нам не подходит.
Если (x_0=0) – их общий корень, то тогда (2x_0^2-2(3a+2)x_0+(2a+2)^2+a^2-1=0), откуда ((2a+2)^2+a^2-1=0), откуда (a=-1) или (a=-0,6). Тогда вся исходная система будет иметь 3 различных решения, что нам не подходит.

Учитывая все это, в ответ пойдут:

[ainleft(dfrac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right)]

Ответ:

(ainleft(frac{-2-sqrt2}3; -1right)cupleft(-1;
-0,6right)cupleft(-0,6; -2+sqrt2right))

Задание
2

#4032

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых система [begin{cases}
(a-1)x^2+2ax+a+4leqslant 0\
ax^2+2(a+1)x+a+1geqslant 0 end{cases}]

имеет единственное решение.

(ЕГЭ 2018, СтатГрад, 19 апреля 2018)

Перепишем систему в виде: [begin{cases}
ax^2+2ax+aleqslant x^2-4\
ax^2+2ax+ageqslant -2x-1
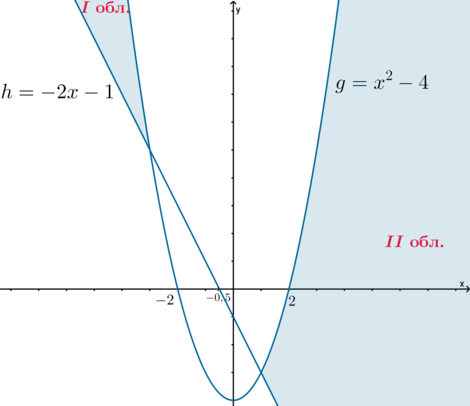
end{cases}] Рассмотрим три функции: (y=ax^2+2ax+a=a(x+1)^2), (g=x^2-4), (h=-2x-1). Из системы следует, что (yleqslant g), но (ygeqslant
h). Следовательно, чтобы система имела решения, график (y) должен находиться в области, которая задается условиями: “выше” графика (h), но “ниже” графика (g):

(будем называть “левую” область областью I, “правую” область – областью II)
Заметим, что при каждом фиксированном (ane 0) графиком (y) является парабола, вершина которой находится в точке ((-1;0)), а ветви обращены либо вверх, либо вниз. Если (a=0), то уравнение выглядит как (y=0) и графиком является прямая, совпадающая с осью абсцисс.
Заметим, что для того, чтобы исходная система имела единственное решение, нужно, чтобы график (y) имел ровно одну общую точку с областью I или с областью II (это значит, что график (y) должен иметь единственную общую точку с границей одной из этих областей).

Рассмотрим по отдельности несколько случаев.

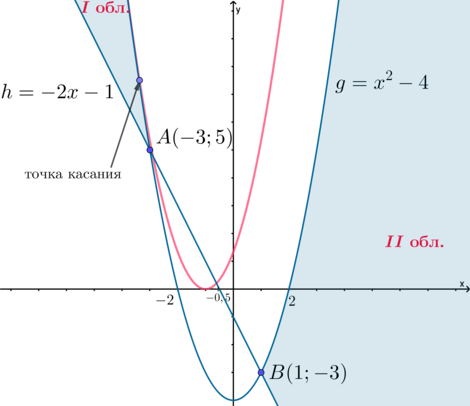
1) (a>0). Тогда ветви параболы (y) обращены вверх. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) касалась границы области I или границы области II, то есть касалась параболы (g), причем абсцисса точки касания должна быть (leqslant
-3) или (geqslant 2) (то есть парабола (y) должна коснуться границы одной из областей, которая находится выше оси абсцисс, раз парабола (y) лежит выше оси абсцисс).

(y’=2a(x+1)), (g’=2x). Условия касания графиков (y) и (g) в точке с абсциссой (x_0leqslant -3) или (x_0geqslant 2): [begin{cases}
2a(x_0+1)=2x_0\
a(x_0+1)^2=x_0^2-4 \
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right. end{cases}
quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} &x_0leqslant -3\
&x_0geqslant 2 end{aligned}end{gathered}right.\[1ex]
a=dfrac{x_0}{x_0+1}\[1ex]
x_0^2+5x_0+4=0 end{cases}] Из данной системы (x_0=-4), (a=frac43).
Получили первое значение параметра (a).

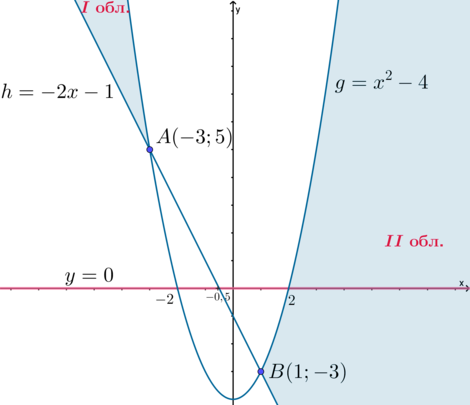
2) (a=0). Тогда (y=0) и видно, что прямая имеет бесконечное множество общих точек с областью II. Следовательно, это значение параметра нам не подходит.

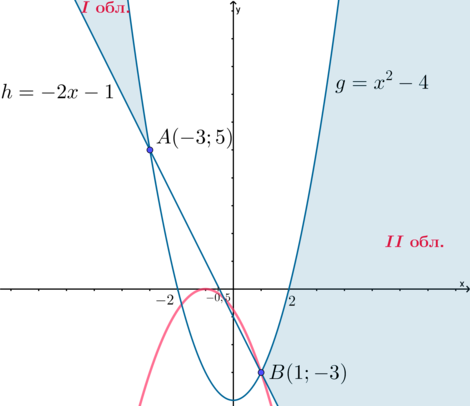
3) (a<0). Тогда ветви параболы (y) обращены вниз. Чтобы у исходной системы было единственное решение, нужно, чтобы парабола (y) имела одну общую точку с границей области II, лежащей ниже оси абсцисс. Следовательно, она должна проходить через точку (B), причем, если парабола (y) будет иметь еще одну общую точку с прямой (h), то эта общая точка должна быть “выше” точки (B) (то есть абсцисса второй точки должна быть (<1)).

Найдем (a), при которых парабола (y) проходит через точку (B): [-3=a(1+1)^2quadRightarrowquad a=-dfrac34] Убеждаемся, что при этом значении параметра вторая точка пересечения параболы (y=-frac34(x+1)^2) с прямой (h=-2x-1) – это точка с координатами (left(-frac13; -frac13right)).
Таким образом, получили еще одно значение параметра.

Так как мы рассмотрели все возможные случаи для (a), то итоговый ответ: [ain left{-dfrac34; dfrac43right}]

Ответ:

(left{-frac34; frac43right})

Задание
3

#4013

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система уравнений [begin{cases}
2x^2+2y^2=5xy\
(x-a)^2+(y-a)^2=5a^4 end{cases}]

имеет ровно два решения.

(ЕГЭ 2018, СтатГрад, 26 января 2018)

1) Рассмотрим первое уравнение системы как квадратное относительно (x): [2x^2-(5y)x+2y^2=0] Дискриминант равен (D=9y^2), следовательно, [x_{1,2}=dfrac{5ypm 3y}4quadRightarrow quad x_1=2y, quad x_2=dfrac12y] Тогда уравнение можно переписать в виде [(x-2y)cdot (2x-y)=0] Следовательно, всю систему можно переписать в виде [begin{cases}
left[begin{gathered}begin{aligned} &y=2x\[1ex]
&y=0,5xend{aligned}end{gathered}right.\[1ex]
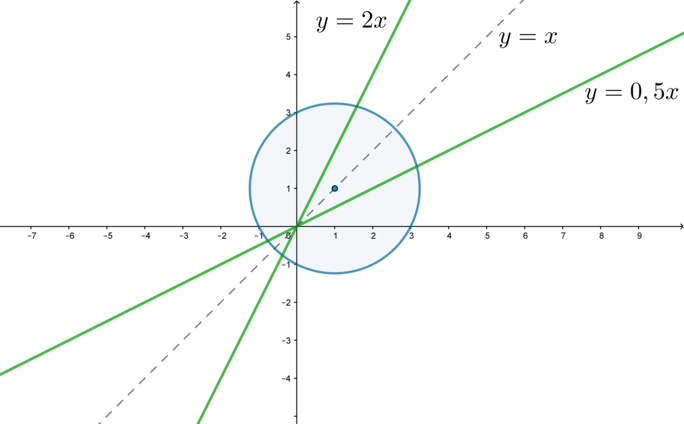
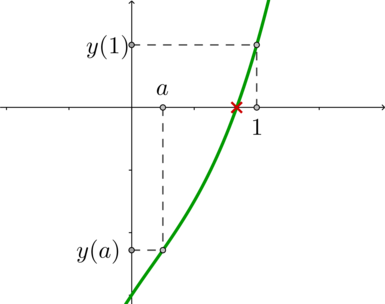
(x-a)^2+(y-a)^2=5a^4end{cases}] Совокупность задает две прямые, второе уравнение системы задает окружность с центром в ((a;a)) и радиусом (R=sqrt5a^2). Чтобы исходное уравнение имело два решения, нужно, чтобы окружность пересекала график совокупности ровно в двух точках. Вот чертеж, когда, например, (a=1):

Заметим, что так как координаты центра окружности равны, то центр окружности “бегает” по прямой (y=x).

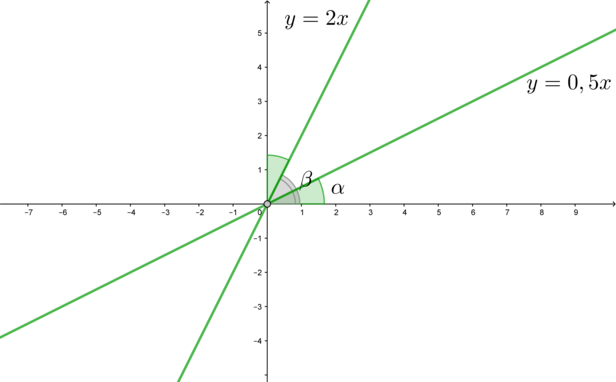
2) Так как у прямой (y=kx) тангенс угла наклона этой прямой к положительному направлению оси (Ox) равен (k), то тангенс угла наклона прямой (y=0,5x) равен (0,5) (назовем его (mathrm{tg},alpha)), прямой (y=2x) – равен (2) (назовем его (mathrm{tg},beta)). Заметим, что (mathrm{tg},alphacdot
mathrm{tg},beta=1), следовательно, (mathrm{tg},alpha=mathrm{ctg},beta=mathrm{tg},(90^circ-beta)). Следовательно, (alpha=90^circ-beta), откуда (alpha+beta=90^circ). Это значит, что угол между (y=2x) и положительным направлением (Oy) равен углу между (y=0,5x) и положительным направлением (Ox):

А так как прямая (y=x) является биссектрисой I координатного угла (то есть углы между ней и положительными направлениями (Ox) и (Oy) равны по (45^circ)), то углы между (y=x) и прямыми (y=2x) и (y=0,5x) равны.
Все это нам нужно было для того, чтобы сказать, что прямые (y=2x) и (y=0,5x) симметричны друг другу относительно (y=x), следовательно, если окружность касается одной из них, то она обязательно касается и второй прямой.
Заметим, что если (a=0), то окружность вырождается в точку ((0;0)) и имеет лишь одну точку пересечения с обеими прямыми. То есть этот случай нам не подходит.
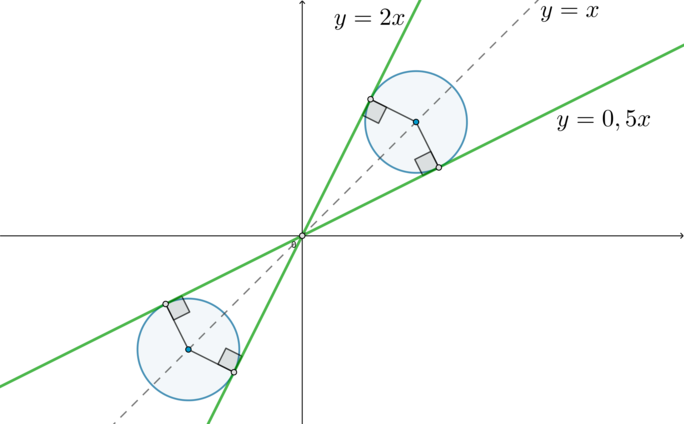
Таким образом, для того, чтобы окружность имела 2 точки пересечения с прямыми, нужно, чтобы она касалась этих прямых:

Видим, что случай, когда окружность располагается в третьей четверти, симметричен (относительно начала координат) случаю, когда она располагается в первой четверти. То есть в первой четверти (a>0), а в третьей (a<0) (но такие же по модулю).
Поэтому рассмотрим только первую четверть.

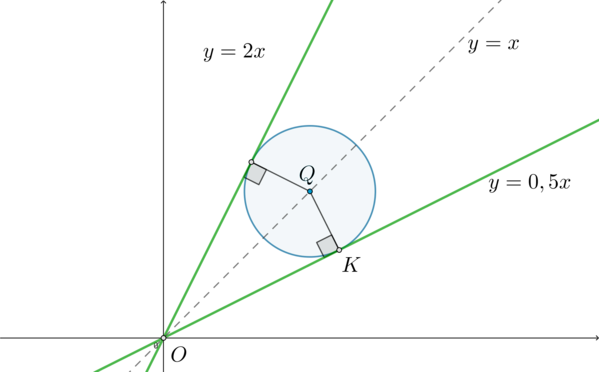
Заметим, что (OQ=sqrt{(a-0)^2+(a-0)^2}=sqrt2a), (QK=R=sqrt5a^2). Тогда [OK=sqrt{2a^2-5a^4}] Тогда [mathrm{tg},angle
QOK=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}] Но, с другой стороны, [mathrm{tg},angle QOK=mathrm{tg},(45^circ-alpha)=dfrac{mathrm{tg},
45^circ-mathrm{tg},alpha}{1+mathrm{tg},45^circcdot
mathrm{tg},alpha}] следовательно, [dfrac{1-0,5}{1+1cdot 0,5}=dfrac{sqrt5a^2}{sqrt{2a^2-5a^4}}
quadLeftrightarrowquad a=pm dfrac15] Таким образом, мы уже сразу получили и положительное, и отрицательное значение для (a). Следовательно, ответ: [ain {-0,2;0,2}]

Ответ:

({-0,2;0,2})

Задание
4

#3278

Уровень задания: Равен ЕГЭ

Найдите все значения (a), для каждого из которых уравнение [25^x-(a+6)cdot 5^x=(5+3|a|)cdot 5^x-(a+6)(3|a|+5)]

имеет единственное решение.

(ЕГЭ 2017, официальный пробный 21.04.2017)

Сделаем замену (t=5^x, t>0) и перенесем все слагаемые в одну часть: [t^2-bigg((a+6)+(5+3|a|)bigg)cdot t+(a+6)(3|a|+5)=0] Получили квадратное уравнение, корнями которого по теореме Виета являются (t_1=a+6) и (t_2=5+3|a|). Для того, чтобы исходное уравнение имело один корень, достаточно, чтобы полученное уравнение с (t) тоже имело один (положительный!) корень.
Заметим сразу, что (t_2) при всех (a) будет положительным. Таким образом, получаем два случая:

1) (t_1=t_2): [a+6=5+3|a| quadLeftrightarrowquad 3|a|=a+1 quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned} & 3a=a+1\
&3a=-a-1 end{aligned} end{gathered} right. \
a+1geqslant 0 end{cases}quadLeftrightarrowquad
left[begin{gathered}begin{aligned} & a=dfrac12\[2ex]
&a=-dfrac14 end{aligned} end{gathered} right.]

2) Так как (t_2) всегда положителен, то (t_1) должен быть (leqslant
0): [a+6leqslant 0 quadLeftrightarrowquad aleqslant -6.]

Ответ:

((-infty;-6]cupleft{-frac14;frac12right})

Задание
5

#3252

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{x^2-a^2}=sqrt{3x^2-(3a+1)x+a}]

имеет ровно один корень на отрезке ([0;1]).

(ЕГЭ 2017, резервный день)

Уравнение можно переписать в виде: [sqrt{(x-a)(x+a)}=sqrt{(3x-1)(x-a)}] Таким образом, заметим, что (x=a) является корнем уравнения при любых (a), так как уравнение принимает вид (0=0). Для того, чтобы этот корень принадлежат отрезку ([0;1]), нужно, чтобы (0leqslant
aleqslant 1).
Второй корень уравнения находится из (x+a=3x-1), то есть (x=frac{a+1}2). Для того, чтобы это число было корнем уравнения, нужно, чтобы оно удовлетворяло ОДЗ уравнения, то есть: [left(dfrac{a+1}2-aright)cdot
left(dfrac{a+1}2+aright)geqslant 0quadRightarrowquad
-dfrac13leqslant aleqslant 1] Для того, чтобы этот корень принадлежал отрезку ([0;1]), нужно, чтобы [0leqslant dfrac{a+1}2leqslant 1
quadRightarrowquad -1leqslant aleqslant 1] Таким образом, чтобы корень (x=frac{a+1}2) существовал и принадлежал отрезку ([0;1]), нужно, чтобы (-frac13leqslant aleqslant 1).
Заметим, что тогда при (0leqslant aleqslant 1) оба корня (x=a) и (x=frac{a+1}2) принадлежат отрезку ([0;1]) (то есть уравнение имеет два корня на этом отрезке), кроме случая, когда они совпадают: [a=dfrac{a+1}2quadRightarrowquad a=1] Таким образом, нам подходят (ain left[-frac13; 0right)) и (a=1).

Ответ:

(ain left[-frac13;0right)cup{1})

Задание
6

#3238

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых уравнение [xsqrt{x-a}=sqrt{6x^2-(6x+3a)x+3a}]

имеет единственный корень на отрезке ([0;1].)

(ЕГЭ 2017, резервный день)

Уравнение равносильно: [xsqrt{x-a}=sqrt{3a(1-x)}] ОДЗ уравнения: [begin{cases} xgeqslant 0\ x-ageqslant 0\3a(1-x)
geqslant 0end{cases}] На ОДЗ уравнение перепишется в виде: [x^3-a(x^2-3x+3)=0]

1) Пусть (a<0). Тогда ОДЗ уравнения: (xgeqslant 1). Следовательно, для того, чтобы уравнение имело единственный корень на отрезке ([0;1]), этот корень должен быть равен (1). Проверим: [1^3-a(1^2-3cdot 1+3)=0 quadRightarrowquad a=1.] Не подходит под (a<0). Следовательно, эти значения (a) не подходят.

2) Пусть (a=0). Тогда ОДЗ уравнения: (xgeqslant 0). Уравнение перепишется в виде: [x^3=0 quadRightarrowquad x=0] Полученный корень подходит под ОДЗ и входит в отрезок ([0;1]). Следовательно, (a=0) – подходит.

3) Пусть (a>0). Тогда ОДЗ: (xgeqslant a) и (xleqslant 1). Следовательно, если (a>1), то ОДЗ – пустое множество. Таким образом, (0<aleqslant 1) и при этих (a) ОДЗ: (aleqslant xleqslant
1). Следовательно, если корень подойдет по ОДЗ, то он попадет и в отрезок ([0;1]).
Рассмотрим функцию (y=x^3-a(x^2-3x+3)). Исследуем ее.
Производная равна (y’=3x^2-2ax+3a). Определим, какого знака может быть производная. Для этого найдем дискриминант уравнения (3x^2-2ax+3a=0): (D=4a(a-9)). Следовательно, при (ain (0;1]) дискриминант (D<0). Значит, выражение (3x^2-2ax+3a) положительно при всех (x). Следовательно, при (ain (0;1]) производная (y’>0). Следовательно, (y) возрастает. Таким образом, по свойству возрастающей функции уравнение (y(x)=0) может иметь не более одного корня.

Следовательно, для того, чтобы корень уравнения (точка пересечения графика (y) с осью абсцисс) находился на отрезке ([a;1]), нужно, чтобы [begin{cases} y(1)geqslant 0\
y(a)leqslant 0 end{cases}quadRightarrowquad ain [0;1]] Учитывая, что изначально в рассматриваемом случае (ain (0;1]), то ответ (ain (0;1]).

Итоговый ответ, полученный объединением ответов во всех трех случаях: [ain [0;1]]

Ответ:

([0;1])

Задание
7

#3267

Уровень задания: Равен ЕГЭ

Найдите все значения (a), при каждом из которых уравнение [sqrt{1-4x}cdot ln(9x^2-a^2)=sqrt{1-4x}cdot ln (3x+a)]

имеет ровно один корень.

(ЕГЭ 2017, основная волна)

Данное уравнение можно переписать как [begin{cases}
sqrt{1-4x}cdot ln dfrac{(3x-a)(3x+a)}{3x+a}=0\[2ex]
3x+a>0end{cases} quadLeftrightarrowquad
begin{cases}
sqrt{1-4x}cdot ln (3x-a)=0\
3x+a>0end{cases}] Система имеет два корня:
1) (x_1=frac14), если он удовлетворяет (3x+a>0) и (3x-a>0): [begin{cases}
dfrac34+a>0\[1ex]
dfrac34-a>0end{cases} quadLeftrightarrowquad
-dfrac34<a<dfrac34]
2) (x_2=frac{a+1}3), если он удовлетворяет (3x+a>0) и (1-4xgeqslant 0): [begin{cases}
a+1+a>0\[1ex]
1-dfrac43a-dfrac43geqslant 0end{cases}quadLeftrightarrowquad
-dfrac12<aleqslant -dfrac14]

Рассмотрим случаи, когда данная система имеет ровно один корень. Пусть (x_1ne x_2), то есть (ane -frac14).
1. Пусть (x_1=frac14) – единственное решение системы.
(x_1) будет корнем, если (-frac34<a<frac34), (x_2) не будет корнем, если (ain
left(-infty;-frac12right]cupleft(-frac14;+inftyright)). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain left(-dfrac34;-dfrac12right]cupleft(-dfrac14;dfrac34right)] 2. Пусть (x_2=frac{a+1}3) – единственное решение системы.
(x_1) не будет корнем, если (ain
left(-infty;-frac34right]cupleft[frac34;+inftyright)), (x_2) будет корнем, если (-frac12<aleqslant -frac14). Пересекая эти значения, а также учитывая, что (ane -frac14), получаем: [ain varnothing]

Пусть (x_1=x_2). Тогда (a=-frac14). Заметим, что при этом значении что (x_1), что (x_2) являются решением, следовательно, оно нам подходит.
Итоговый ответ: [ain left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)]

Ответ:

(ain
left(-dfrac34;-dfrac12right]cupleft[-dfrac14;dfrac34right)
)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите все значения параметра k, при каждом из которых уравнение имеет хотя бы одно решение на интервале

Найдите все значения k, при каждом из которых уравнение

имеет хотя бы одно решение на отрезке

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C).

Определите, при каких значениях параметра a уравнение

имеет ровно два решения.

Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.

Найдите все значения параметра a, при каждом из которых уравнение

имеет корни, но ни один из них не принадлежит интервалу (4; 19).

Найдите все значения параметра a, при каждом из которых уравнение

имеет хотя бы один корень на отрезке [5; 23].

Пройти тестирование по этим заданиям

Источник

22 февраля 2018

В закладки

Обсудить

Жалоба

Задачи с параметрами в ЕГЭ разных лет

ЕГЭ 2018. Досрочная волна

ЕГЭ 2017 (2 июня)

ЕГЭ 2017 (досрочная волна)

ЕГЭ 2016 (основная волна)

ЕГЭ 2015 (досрочная волна)

Демоверсии 2015-2018

Источник

Автор материала — Анна Малкова

Какими были задачи с параметрами на ЕГЭ-2022? На этой странице — обзор всех типов задач №17, предложенных на ЕГЭ по математике в этом году, с полным решением и оформлением.

Напомним, что «параметры» — одна из дорогостоящих задач ЕГЭ. Она оценивается в 4 первичных балла.

Основной темой задач с параметрами на ЕГЭ этого года были модули.

Если вы не помните, что такое модуль числа, — вам сюда.

Способы решения — разные. В одних задачах удобнее графический способ, в других — аналитический.

Мы начнем с тех задач, которые решаются графическим способом. В первых трех, которые мы здесь разбираем, нам встретится уравнение окружности.

Почитать о нем подробно можно здесь.

1. При каких значениях параметра уравнение имеет ровно 4 решения?

Решение:

Вспомним, как решать уравнения вида

$left|Aright|=BLeftrightarrow left{ begin{array}{c}Bge 0 \left[ begin{array}{c}A=B \A=-B end{array}right. end{array}.right.$

Поэтому исходное уравнение равносильно системе:

$left{ begin{array}{c}2x+2age 0 \left[ begin{array}{c}x^2+a^2-6x-4a=2x+2a \x^2+a^2-6x-4a=-2x-2a end{array}right. end{array}.right.$

Получим:

$left{ begin{array}{c}x+age 0 \left[ begin{array}{c}x^2-8x+a^2-6a=0 \x^2-4x+a^2-2a=0 end{array}right. end{array}right.Leftrightarrow left{ begin{array}{c}x+age 0 \left[ begin{array}{c}x^2-8x+16+a^2-6a+9=25 \x^2-4x+4+a^2-2a+1=5 end{array}right. end{array}right.Leftrightarrow$

$Leftrightarrow left{ begin{array}{c}age -x \left[ begin{array}{c}{left(x-4right)}^2+{left(a-3right)}^2=25 \{left(x-2right)}^2+{left(a-1right)}^2=5 end{array}right. end{array}.right.$

Изобразим решения системы в координатах

Уравнение ${left(x-4right)}^2+{left(a-3right)}^2=25$ задает окружность с центром и радиусом 5; уравнение ${left(x-2right)}^2+{left(a-1right)}^2=5$ задает окружность с центром и радиусом sqrt{5} ; при этом должно выполняться условие age -x.

Заметим, что обе окружности проходят через точки O(0;0) и

Найдем, при каких значениях параметра исходное уравнение имеет ровно 4 решения.

При a=-1 прямая a=-1 проходит через точку общую для двух окружностей; уравнение имеет ровно 3 решения.

Если прямая a=a_0 проходит через точку (нижнюю точку окружности ), уравнение также имеет 3 решения.

При этом поскольку разность ординат точек Q и A равна то есть радиусу окружности

При уравнение имеет 4 решения.

Если решений меньше 4.

Если a=0, уравнение имеет ровно 3 решения, т.к. точка O(0; 0) общая для обеих окружностей.

Если прямая a=a_0 проходит через B — верхнюю точку окружности уравнение имеет ровно 3 решения.

В этом случае

При уравнение имеет ровно 4 решения.

Если решений меньше, чем 4.

Объединив случаи, получим ответ.

Ответ:

2. При каких значениях параметра уравнение имеет ровно 2 решения?

Решение:

Раскроем модуль по определению.

$Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}7x-age 0 \{ x}^2-x-7a+a^2-7x+a=0 end{array}right. \left{ begin{array}{c}7x-atextless 0 \{ x}^2-x-7a+a^2+7x-a=0 end{array}right. end{array}right. Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}ale 7x \{ x}^2-8x+a^2-6a=0 end{array}right. \left{ begin{array}{c}atextgreater 7x \{ x}^2+6x+a^2-8a=0 end{array}right. end{array}right. Leftrightarrow$
$Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}ale 7x \{ x}^2-8x+16+a^2-6a+9=25 end{array}right. \left{ begin{array}{c}atextgreater 7x \{ x}^2+6x+9+a^2-8a+16=25 end{array}right. end{array}right. Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}ale 7x \{ (x-4)}^2+({a-3)}^2=25 (1) end{array}right. \left{ begin{array}{c}atextgreater 7x \{ (x+3)}^2+{(a-4)}^2=25 (2) end{array}right. end{array}right.$

Уравнение (1) задает окружность с центром в точке Р (4; 3) и радиусом 5,

уравнение (2) задает окружность с центром в точке Q(-3; 4) и радиусом 5.

Изобразим график совокупности двух систем в системе координат (x;a).

При ale 7x получаем часть окружности (1), лежащую ниже прямой a = 7x;

при получаем часть окружности (2), лежащую выше прямой a = 7x.

Исходное уравнение имеет ровно два различных решения, если прямая ${a = a}_{0 }$ пересекает график совокупности двух систем ровно два раза.

Прямая $a = a{}_{0 },$ проходящая через точку С, пересекает график совокупности двух систем один раз.

Найдем координаты С — самой нижней точки и Е — самой верхней точки правой окружности.

Для этих точек x = 4. Найдем координату a:

${ (4-4)}^2+({a-3)}^2=25; ({a-3)}^2=25; a=-2$ или a=8,

Координаты точек С (4; -2) и Е (4; 8).

Найдем координаты D — самой нижней точки и F — самой верхней точки левой окружности

Для этих точек x = — 3, найдем координату a.

${ (-3 +3)}^2+({a-4)}^2=25; ({a-4)}^2=25; a=-1$ или a=9,

Координаты точек: D (3; 1), F(3; 9).

Точки А и В, в которых пересекаются две окружности, лежат на прямой

a = 7x (так как при a = 7x выражение под модулем равно нулю).

Подставив a = 7x в уравнение окружности (1) ${ (x-4)}^2+({a-3)}^2=25,$ получим:

${ x}^2-8x+{left(7xright)}^2-6cdot 7x=0;$

${50 x}^2-50x=0;$

x = 0 или x = 1.

Получили точки В (0; 0) и А (1; 7).

Прямая $a = a{}_{0 }$ пересекает график совокупности двух систем ровно два раза в следующих случаях:

1) если прямая $a = a{}_{0 }$ проходит выше точки С, но ниже точки D:

2) если прямая $a = a{}_{0 }$ проходит выше точки В, но ниже точки А:

3) если прямая $a = a{}_{0 }$ проходит выше точки Е, но ниже точки F:

Если или то решений нет.

Если a = -2 или a = 9, уравнение имеет ровно одно решение.

Если a = -1 или a = 8, ровно три решения.

Если или ровно четыре решения. Эти случаи нам не подходят.

Ответ: a

3. При каких значениях параметра уравнение

имеет ровно 2 корня?

Решение:

$left|Aright|=BLeftrightarrow left{ begin{array}{c}Bge 0 \left[ begin{array}{c}A=B \A=-B end{array}right. end{array}.right.$

Раскрыв модуль, получим:

$left{ begin{array}{c}left[ begin{array}{c}x^2+a^2-7x+5a=x-a \x^2+a^2-7x+5a=a-x end{array}right. \x-age 0 end{array}right.Leftrightarrow left{ begin{array}{c}left[ begin{array}{c}x^2-8x+a^2+6a=0 \x^2-6x+a^2+4a=0 end{array}right. \x-age 0 end{array}right.Leftrightarrow$
$Leftrightarrow left{ begin{array}{c}left[ begin{array}{c}x^2-8x+16+a^2+6a+9=25 \x^2-6x+9+a^2+4a+4=13 end{array}right. \x-age 0 end{array}Leftrightarrow left{ begin{array}{c}left[ begin{array}{c}{left(x-4right)}^2+{left(a+3right)}^2=25 \{left(x-3right)}^2+{left(a+2right)}^2=13 end{array}right. \x-age 0 end{array}.right.right.$

Решим систему графически в координатах

Прямая a=x — это биссектриса первого и третьего координатных углов.

Неравенство ale x задает полуплоскость, расположенную ниже прямой a=x.

Уравнение ${left(x-3right)}^2+{left(a+2right)}^2=13$ задает окружность omega 1 с центром в точке и радиусом

Уравнение ${left(x-4right)}^2+{left(a+3right)}^2=25$ задает окружность omega 2 с центром в точке и радиусом R=5.

Заметим, что обе окружности проходят через точки О(0; 0) и М(1; 1). В этом легко убедиться, подставив координаты этих точек в уравнения окружностей.

Исходное уравнение имеет ровно 2 корня, если прямая a = a_0 пересекает совокупность двух окружностей ровно в двух точках, лежащих не выше прямой a = x.

Это происходит в следующих случаях:

1) Прямая a = a_0 проходит выше точки А и ниже точки В на рисунке, где А — нижняя точка окружности omega 2, В — нижняя точка окружности omega 1.

2) Прямая a = a_0 проходит выше точки С и ниже точки D на рисунке, где D — верхняя точка окружности omega 2, С — верхняя точка окружности omega 1.

3) Прямая a = a_0 проходит выше точки О(0; 0) и ниже точки М(1;1).

Найдем координаты точек А, В, С, D.

Получим, что

Ответ:

Заметим, что в каждом из уравнений присутствовало выражение — как в уравнении окружности. Именно поэтому становилось понятно, что их можно решить графически в координатах x; a.

Теперь — следующий тип задач. Здесь окружностей уже не будет. Зато будет разложение на множители.

4. При каких значениях параметра уравнение

имеет ровно 4 решения?

Решение:

Раскроем модуль. Уравнение равносильно совокупности двух систем:
$left[ begin{array}{c}left{ begin{array}{c}xtextless 0 \a^2-ax-2x^2-6a-6x=0 end{array}right. \left{ begin{array}{c}xge 0 \a^2-ax-2x^2-6a+12x=0 end{array}right. end{array}.right.$

Упростим по очереди каждую из них.

1) Случай

Найдем дискриминант и корни этого квадратного уравнения.

$D={left(a+6right)}^2-8left(6a-a^2right)=a^2+12a+36-48a+8a^2=$

$9a^2-36a+36=9left(a^2-4a+4right)=9{left(a-2right)}^2ge 0;$

$displaystyle x=frac{-a-6pm 3left(a-2right)}{4};$

$displaystyle x_1=frac{2a-12}{4}=frac{a}{2}-3;$

x_2=-a.

2) Случай xge 0:

В этом случае также найдем дискриминант и корни квадратного уравнения.

$D={left(a-12right)}^2-8left(6a-a^2right)=a^2-24a+144-48a+8a^2=$

$9a^2-72a+144=9left(a^2-8a+16right)=9{left(a-4right)}^2;$

$displaystyle x=frac{12-apm 3left(a-4right)}{4}; x_1=frac{12-a+3a-12}{4}=frac{a}{2};$

$displaystyle x_2=frac{12-a-3a+12}{4}=frac{-4a+24}{4}=6-a.$

Получим:

$displaystyle left{ begin{array}{c}x textless 0 \left[ begin{array}{c}x=frac{a}{2}-3 \x=-a end{array}right. end{array}right.$ или $displaystyle left{ begin{array}{c}xge 0 \left[ begin{array}{c}x=frac{a}{2} \x=6-a end{array}right. end{array}right.$ .

Решим совокупность двух систем графически в координатах

Если ale 0, уравнение имеет меньше 4 решений.

Если age 6, также меньше 4 решений.

Если прямая a=a_0 проходит через точку A или точку B, уравнение имеет ровно 3 решения.

В точке A пересекаются прямые $displaystyle x=frac{a}{2}$ и x=6-a , значит, для этой точки
$displaystyle frac{a}{2}=6-a, a=12-2a, a=4 .$
В точке B пересекаются прямые $displaystyle x=frac{a}{2}-3$ и x=-a , то для точки B:
$displaystyle frac{a}{2}-3=-a ; a-6=-2a; a=2$ .
Уравнение имеет ровно 4 решения, если или или .

Ответ:

Следующие две задачи мы решим (для разнообразия) аналитическим способом.

5. При каких значениях параметра уравнение

имеет меньше 4 решений?

Решение:

Уравнение равносильно совокупности:

$left[ begin{array}{c}left{ begin{array}{c}xge 0 \a^2-4ax-5x^2-6a+6x=0 end{array}right. \left{ begin{array}{c}xtextless 0 \a^2-4ax-5x^2-6a-30x=0 end{array}right. end{array}.right.$

Рассмотрим каждый случай отдельно

1) xge 0;

Каждое из уравнений — квадратное и не может иметь больше 2 корней.

Если уравнение (1) имеет 2 неотрицательных корня, а уравнение (2) имеет 2 отрицательных корня, исходное уравнение имеет ровно 4 решения. Найдем, при каких значениях это происходит, а затем исключим эти значения. Получим случай, когда исходное уравнение имеет менее 4 корней.

Исходное уравнение имеет ровно 4 решения, если уравнение имеет два неотрицательных корня, а уравнение имеет два отрицательных корня.

1 уравнение:

По теореме Виета, $displaystyle x_1+x_2=-frac{b}{a};$

$displaystyle x_1x_2=frac{c}{a}$ для уравнения

При этом

$displaystyle left{begin{matrix}4a-6 textless 0 \ a^2 -6aleq 0\(4a-6)^2-20(6a-a^2)textgreater 0end{matrix}right. Leftrightarrow left{begin{matrix}a textless frac{3}{2} \ a(a-6)leq 0\ 16a^2-48a+36-120a+20a^2textgreater 0end{matrix}right. Leftrightarrow left{begin{matrix}a textless frac{3}{2} \ 0leq aleq 6 \ 36a^2-168a+36 textgreater 0end{matrix}right. Leftrightarrow left{begin{matrix}a textless frac{3}{2} \ 0 leq a leq 6\ 3a^2 -14a+3 textgreater 0.end{matrix}right.$

$displaystyle a=frac{14pm 4sqrt{10}}{6}=frac{7 pm 2sqrt{10}}{3}.$

$displaystyleleft{ begin{array}{c} a textless frac{3}{2} \0le ale 6 \{ 3a}^2-14a+3 textgreater 0 end{array}right. Leftrightarrow left{ begin{array}{c}0le a textless frac{3}{2} \left(a-frac{7+2sqrt{10}}{3}right)left(a-frac{7-2sqrt{10}}{3}right) textgreater 0end{array}.right.$

Оценим $displaystyle frac{7-2sqrt{10}}{3}$ и $displaystyle frac{7+2sqrt{10}}{3}.$

Сравним т.к.

$displaystyle frac{7-2sqrt{10}}{3}textgreater 0,$ также $displaystyle frac{7-2sqrt{10}}{3}textless frac{7-2cdot 3}{3};0textless frac{7-2sqrt{10}}{3}textless frac{1}{3}.$

$displaystyle frac{7+2cdot 3}{3}textless frac{7+2sqrt{10}}{3}textless frac{7+2cdot 4}{3};4textless frac{7+2sqrt{10}}{3}textless 5.$

Получим: $displaystyle 0leq a textless frac{7-2sqrt{10}}{3}.$

2 уравнение:

$left{ begin{array}{c}x_1textless 0 \x_2textless 0 end{array}right.Leftrightarrow left{ begin{array}{c}x_1+x_2textless 0 \x_1x_2textgreater 0 end{array}right.Leftrightarrow left{ begin{array}{c}-left(4a+30right)textless 0 \6a-a^2textgreater 0 end{array}right.Leftrightarrow left{ begin{array}{c}2a+15textgreater 0 \aleft(a-6right)textless 0 end{array}.right.$

При этом т.е. ${left(4a+30right)}^2-20left(6a-a^2right)textgreater 0.$

— верно при всех a.

Получим:

$left{ begin{array}{c}2a+15textgreater 0 \aleft(a-6right)textless 0; end{array}Leftrightarrow 0textless atextless 6.right.$

Исходное уравнение имеет ровно 4 решения, если выполняется система условий:

$displaystyle left{ begin{array}{c}0 leq atextless frac{7-2sqrt{10}}{3} \0textless atextless 6 end{array}right.Leftrightarrow 0textless atextless frac{7-2sqrt{10}}{3}.$ При всех остальных значениях a — меньше четырёх решений. Значит, подходят значения $displaystyle ain left(-infty ;0right]cup [ frac{7-2sqrt{10}}{3};+infty ).$

Ответ: $displaystyle ain left(-infty ;0right]cup [frac{7-2sqrt{10}}{3};+infty).$

6. Найдите все положительные значения a, при каждом из которых уравнение

имеет ровно 4 корня.

Решение:

Раскроем модуль по определению.

$Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}a^2-2ax-3x^2-4a-4x+8x=0 \xge 0 end{array}right. \left{ begin{array}{c}xtextless 0 \a^2-2ax-3x^2-4a-4x-8x=0 end{array}right. end{array}right.Leftrightarrow left[ begin{array}{c}left{ begin{array}{c}a^2-2ax-3x^2-4a+4x=0 \xge 0 end{array}right. \left{ begin{array}{c}xtextless 0 \a^2-2ax-3x^2-4a-12x=0 end{array}right. end{array}right. .$

Мы получили совокупность двух систем. Чтобы исходное уравнение имело ровно 4 корня, нужно, чтобы каждая система имела ровно два решения. Решим каждую из систем отдельно.

1) Первая система:

$left{ begin{array}{c}a^2-2ax-3x^2-4a+4x=0 \xge 0 end{array}right.Leftrightarrow left{ begin{array}{c}xge 0 \3x^2+2left(a-2right)x+4a-a^2=0 end{array}right. .$

Чтобы квадратное уравнение имело два неотрицательных корня, необходимо и достаточно выполнения условий:

$left{ begin{array}{c}Dtextgreater 0 \x_1+x_2textgreater 0 \x_1cdot x_2textgreater 0 end{array}right. .$

Другой способ: можно рассмотреть квадратичную функцию

и воспользоваться условиями: $left{ begin{array}{c}Dtextgreater 0 \x_B textless 0 \fleft(0right)ge 0 end{array}right..$

Найдем дискриминант соответствующего квадратного уравнения.

$4{left(a-2right)}^2-4cdot 3cdot left(4a-a^2right)textgreater 0;$

при этом

Получим:

$left{ begin{array}{c}a^2-4a+1textgreater 0 \a textless 2 \0le ale 4 end{array}.right.$

Корни уравнения

Отсюда

2) Вторая система:

$left{ begin{array}{c}xtextless 0 \a^2-2ax-3x^2-4a-12x=0 end{array}Leftrightarrow left{ begin{array}{c}xtextless 0 \3x^2+2left(a+6right)x+4a-a^2=0 end{array}right.right. .$

Чтобы система имела ровно 2 решения, для квадратичной функции

необходимо и достаточно выполнения условий:

$left{ begin{array}{c}x_Btextless 0 \Dtextgreater 0 \fleft(0right)textgreater 0 end{array}.right.$

$4{left(a+6right)}^2-4cdot 3cdot left(4a-a^2right)textgreater 0;$

— верно для всех

$left{ begin{array}{c}a+6textgreater 0 \4a-a^2textgreater 0 end{array}.right.$

Решение второй системы:

Исходное уравнение имеет ровно 4 различных решения, если

$left{ begin{array}{c}0le atextless 2 - sqrt{3} \0textless atextless 4 end{array}right.Leftrightarrow 0textless atextless 2 - sqrt{3}.$

Ответ:

Как всему этому научиться? Если вы решили освоить тему «Параметры» — не нужно начинать со сложных задач. Вначале — подготовительная работа. Элементарные функции и их графики, базовые элементы для решения задач с параметрами. Кроме того, надо отлично знать методы алгебры: разложение выражений на множители, выделение полных квадратов, решение уравнений и неравенств всех типов и многое другое.

Изучить все это можно на Онлайн-курсе подготовки к ЕГЭ по математике. На нем мы решаем и такие задачи, и более сложные. Изучаем не менее 11 методов решения задач с параметрами. Выпускники Онлайн-курса отлично справились с «параметрами» на ЕГЭ-2022.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи с параметрами на ЕГЭ-2022: модули, окружности, квадратные уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Всё варианты 17 задания математика ЕГЭ Профиль 2022

Всё варианты 17 задания математика ЕГЭ Профиль 2022admin2022-08-03T22:55:27+03:00

Скачать задания в формате pdf.

Задания 13 ЕГЭ по математике профильного уровня 2022 год (параметры)

1) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений

[ left{ {begin{array}{*{20}{c}} {frac{{x,{y^2} — 2,x,y — 4y + 8}}{{sqrt {4 — y} }} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]

имеет ровно три различных решения.

ОТВЕТ: (left( {0;1} right) cup left( {1;4} right).)

2) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений

[ left{ {begin{array}{*{20}{c}} {frac{{x,{y^2} — 3,x,y — 3y + 9}}{{sqrt {x + 3} }} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]

имеет ровно два различных решения.

ОТВЕТ: (left( {0;frac{1}{3}} right] cup left{ 3 right}.)

3) (28.03.2022 досрочная волна) Найдите все значения параметра a, при каждом из которых система уравнений

[ left{ {begin{array}{*{20}{c}} {left( {x,{y^2} — 3,x,y — 3y + 9} right)sqrt {x — 3} = 0,} \ {y = a,x,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,} end{array}} right. ]

имеет ровно три различных решения.

ОТВЕТ: (left( {0;frac{1}{3}} right).)

4) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

({x^2} + {a^2} + x — 7a = left| {,7x + a,} right|)

имеет более двух различных решений.

ОТВЕТ: (left[ { — 1;,0} right] cup left[ {,7;,8} right].)

5) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

({x^2} + {a^2} — 2x — 6a = left| {,6x — 2a,} right|)

имеет два различных решения.

ОТВЕТ: (left( {2 — 2sqrt 5 ;4 — 2sqrt 5 } right) cup left( {0;,6} right) cup left( {2 + 2sqrt 5 ;4 + 2sqrt 5 } right).)

6) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

(left| {{x^2} + {a^2} — 6x — 4a} right| = 2x + 2a)

имеет два различных решения.

ОТВЕТ: (left( { — 2;1 — sqrt 5 } right) cup left( { — 1;,0} right) cup left( {1 + sqrt 5 ;8} right).)

7) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

(left| {{x^2} + {a^2} — 6x — 4a} right| = 2x + 2a)

имеет четыре различных решения.

ОТВЕТ: (left( {1 — sqrt 5 ;, — 1} right) cup left( {0;1 + sqrt 5 } right).)

(02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

({a^2} + 2,a,x — 3{x^2} — 4a — 4x + 8left| x right| = 0)

имеет четыре различных решения.

ОТВЕТ: (left( {0;1} right) cup left( {1;,3} right) cup left( {3;4} right).)

9) (02.06.2022 основная волна) Найдите все значения параметра a, при каждом из которых уравнение

({a^2} — 9{x^2} + 18left| x right| — 9 = 0)

имеет два различных решения.

ОТВЕТ: (left( { — infty ; — 3} right) cup left{ 0 right} cup left( {3;infty } right).)

10) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение

(sqrt {15{x^2} + 6ax + 9} = {x^2} + ax + 3)

имеет ровно три различных решения.

ОТВЕТ: (left[ { — 4;, — 3} right) cup left( { — 3;3} right) cup left( {3;,4} right].)

11) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение

(sqrt {{x^4} — 4{x^2} + {a^2}} = {x^2} + 2x — a)

имеет ровно три различных решения.

ОТВЕТ: (left( { — infty ; — 4} right) cup left( { — 4;0} right).)

12) (27.06.2022 резервная волна) Найдите все значения параметра a, при каждом из которых уравнение

(sqrt x + sqrt {2a — x} = a)

имеет ровно два различных решения.

ОТВЕТ: (left[ {2;,4} right).)

Источник

Задачи с параметром из ЕГЭ прошлых лет

Задачи с параметрами в ЕГЭ разных лет

Всё варианты 17 задания математика ЕГЭ Профиль 2022

Задания 13 ЕГЭ по математике профильного уровня 2022 год (параметры)

Новое и интересное на сайте: