в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 36 1–20 | 21–36
Добавить в вариант
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.
Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503
Задания Д1 B1 № 131
Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Задания Д29 C2 № 9072
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.
Задания Д1 B1 № 5952
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Задания Д1 B1 № 5987
Два камня одновременно бросили из одной точки: первый — вертикально вверх, второй — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?
1) покоится
2) движется по параболе
3) движется равномерно и прямолинейно
4) движется по дуге окружности
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Задания Д2 B2 № 6637
Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?
1) первого закона Ньютона
2) второго закона Ньютона
3) третьего закона Ньютона
4) принципа относительности Галилея
Задания Д2 B2 № 6676
Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?
1) Первого закона Ньютона
2) Второго закона Ньютона
3) Третьего закона Ньютона
4) принципа относительности Галилея
Задания Д1 B1 № 125
Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Задания Д3 B3 № 4412
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса второго бруска равен
1)
2)
3)
4)
Задания Д3 B3 № 4447
Два бруска массой m и
равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском
модуль импульса первого бруска равен
1) mV
2)
3)
4)
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.
Источник: Демонстрационная версия ЕГЭ—2020 по физике.
Задания Д1 B1 № 3357
Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.
Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Всего: 36 1–20 | 21–36
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Относительное движение
Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.
(v) — абсолютная скорость
(vec{u}) — переносная скорость
(v’) — относительная скорость
[vec{v}=vec{u}+vec{v} ‘]
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Так как пассажир идет в том же направлении, что и автобус, то вектора их скоростей складываются, поэтому абсолютная скорость равна [upsilon_{text{абс}}=upsilon_{text{пер}}+upsilon_{text{отн}}=10text{ м/с}+1text{ м/с}=11text{ м/с}]
Ответ: 11
По прямой дороге с постоянной скоростью 100 км/ч едет мотоциклист и в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
[upsilon_{text{отн}}=upsilon_{text{абс}}-upsilon_{text{пер}}=100text{ км/ч}-70text{ км/ч}=30text{ км/ч}]
Ответ: 30
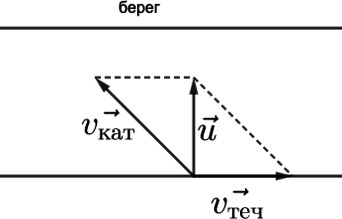
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 8 км/ч. Река течёт со скоростью 6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
Чтобы катер двигался перпендикулярно относительно берега, относительно воды ему надо двигаться под углом. По закону сложения скоростей: [vec{v_{text{абс}}}=vec{v_{text{пер}}}+vec{v_{text{отн}}}] [vec{u}=vec{v_{text{теч}}}+vec{v_{text{кат}}}]
По теореме Пифагора найдем скорость катера относительно воды: [v_{text{кат}}=sqrt{u^2+v_{text{теч}}^2}=sqrt{8^2+6^2}=10 text{ км/ч}]
Ответ: 10
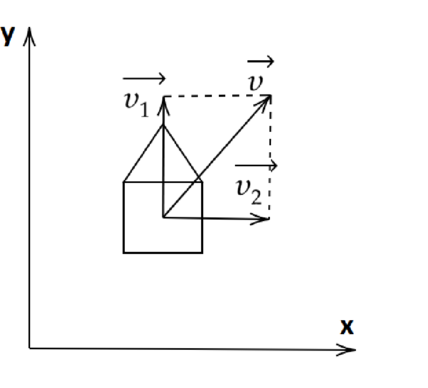
Пассажир зашел в автобус через заднюю дверь. Автобус поехал с постоянной скоростью (upsilon_1=25) м/с, а пассажир пошел к передней части автобуса. Скорость пассажира относительно автобуса равна (upsilon_{2}=3) м/с. С какой скоростью едет автобус относительно пассажира?
Скорость первого тела относительного второго равна скорости второго тела относительно первого и направлена в противоположную сторону. [vec{v}_{text{абс}}=vec{v}_{text{отн}}+vec{v}_{text{пер}}] [vec{v}_{text{1}}=vec{v}_{text{12}}+vec{v}_{text{2}}] [vec{v}_{text{2}}=vec{v}_{text{21}}+vec{v}_{text{1}}] [vec{v}_{text{12}}=-vec{v}_{text{21}}] Таким образом, автобус относительно пассажира едет со скоростью 3 м/с в обратную сторону.
Ответ: 3
Вася идет по прямой дороге со скоростью (upsilon_1=3text{ км/ч}.) Навстречу ему движется грузовик со скоростью (upsilon_2=30text{ км/ч}). С какой скоростью (upsilon_3) (по модулю) должен двигаться велосипедист навстречу Васе, чтобы модули его скорости относительно автомобиля и относительно Васи были одинаковы? Ответ дайте в км/ч.
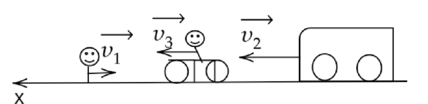
Ответ: 13,5
Пароход плывет по прямой реке. Его скорость относительно реки равна (v_1=5) км/ч и направлена перпендикулярно береговой линии. Река течет со скоростью (v_2=4) км/ч. Чему равен модуль скорости (v) (в км/ч) парохода относительно Земли? Ответ округлите до десятых.
Рассмотрим рисунок: векторы cкорости (v_1) и (v_2) составляют друг с другом угол (90^{circ}). Значит (v) можно найти по теореме Пифагора: [v^2=v_1^2+v_2^2] Отсюда: [v=sqrt{v_1^2+v_2^2}=sqrt{(5text{ км/ч})^2+4text{ км/ч})^2}approx6,4text{ км/ч}]
Ответ: 6,4
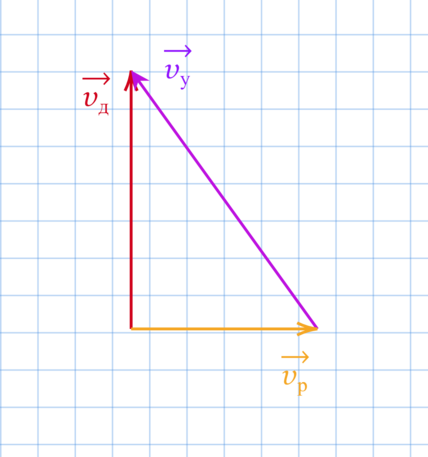
Дейнерис вылетела на драконе Дрогоне из Королевской Гавани в Браавос со скоростью (upsilon_text{д}=43,2) км/ч. Перпендикулярной Ее Величеству Джон Сноу вылетел в Винтерфелл на драконе Рейгале со скоростью (upsilon_text{р}=3,5) м/с. С какой скоростью в м/с они удаляются друг от друга?
Переведем скорость Дрогона в м/с: [upsilon_text{д}=frac{43,2text{ км/ч}cdot1000}{3600}=12text{ м/с}]
Изобразим:
Отсюда видно, что скорость удаления двух драконов (тел) друг от друга — это модуль относительной скорости: [|vec{upsilon}_text{у}|=|vec{upsilon_text{д}}-vec{upsilon_text{р}}|=sqrt{upsilon_text{д}^2+upsilon_text{р}^2}]
Подставим исходные данные: [upsilon_y=sqrt{3,5^2+12^2}=sqrt{156,25}=12,5text{ м/с}]
Ответ: 12,5

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
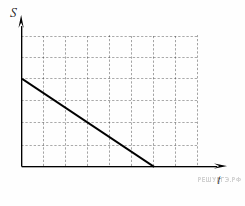
Задание 1 № 101. Может ли график зависимости пути от времени иметь следующий вид?
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем, так что представленный график не может изображать зависимость пути от времени.
Правильный ответ: 2.
Задание 1 № 125. Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Решение.
В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.
Правильный ответ: 1.
Задание 1 № 126. Два автомобиля движутся по прямому шоссе: первый — со скоростью ν, второй — со скоростью -3 ν. Какова скорость второго автомобиля относительно первого?
|
1) |
2) |
3) |
4) |
Решение.
Скорость второго автомобиля относительно первого равна ν2 — ν 1=-3 ν- ν= -4ν
Правильный ответ: 2.
Задание 1 № 131. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды ν . Чему должен быть равен модуль скорости лодки относительно берега?
1)
2)
3)
4)
Решение.
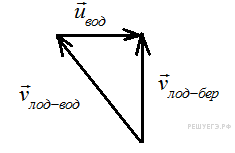
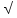
2 способ:
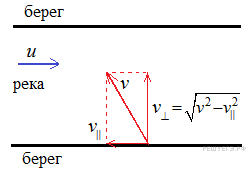
Правильный ответ: 4.
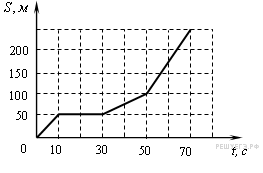
Задание 1 № 133. На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью 5 м/с.
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
.
На других интервалах скорость была иная.
Правильный ответ: 4.
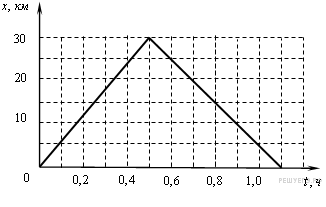
Задание 1 № 134. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке х=0, а пункт Б — в точке х=30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна: 30-0/0,5=60 км/ч.
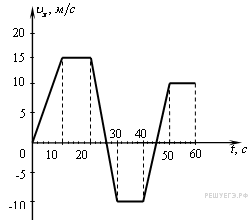
Задание 1 № 138. На рисунке приведен график зависимости проекции скорости тела от времени.
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Задание 1 № 317. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки:. Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение: 0,4 + 0,3 =0,7 м/с.
Задание 1 № 3354. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
|
t, с |
0 |
1 |
2 |
3 |
4 |
5 |
|
x1, м. |
0 |
2 |
4 |
6 |
8 |
10 |
|
x2, м |
0 |
0 |
0 |
0 |
0 |
0 |
|
x3, м |
0 |
1 |
4 |
9 |
16 |
25 |
|
x4, м |
0 |
2 |
0 |
-2 |
0 |
2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
Решение.
Таблица содержит информацию о положениях тел только в отдельные моменты времени. В промежутках между указанными временами тела могли двигаться абсолютно произвольно. Определим тело, скорость которого могла бы быть постоянной и отличной от нуля. При движении с постоянной скоростью координата тела за равные промежутки времени изменяется одинаково. Из таблицы видно, что этому свойству удовлетворяет только первое тело. Значит, скорость первого тела могла быть постоянной и не равной нулю.
Задание 1 № 3357. Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Решение.
Крайняя точка лопасти вертолета двигается по окружности вокруг оси вращения винта. Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
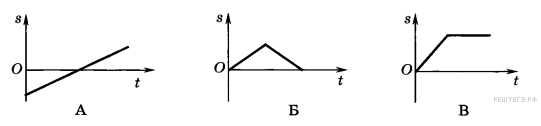
Задание 1 № 3539. На каком из графиков изображена возможная зависимость пройденного пути от времени?
1) А
2) Б
3) В
4) Такой график отсутствует
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Этому требованию удовлетворяет только график В.
Правильный ответ: 3.
Задание 1 № 3540. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: . То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберемся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: . В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через ? тогда весь путь пройденный велосипедистом равен . На первую половину пути велосипедист затратил время . На обратную дорогу — время . Все время пути составило . Окончательно, находим, что средняя путевая скорость велосипедиста равна
.
Задание 1 № 3541. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна . Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: . Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при и равен 20 м.
Ответ: 6 с
Задание 1 № 3544. Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение . Теперь не составляет труда определить координату места встречи:
Задание 1 № 3545.
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от до электрокар двигался в положительном направлении оси . При этом его координата изменилась на . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно . Таким образом, путь, пройденный машинкой за интервал времени от до равен .
Задание 1 № 3548. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1)
2)
3)
4)
Решение.
Обозначим искомую скорость велосипедиста через . Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью , а к автобусу — со скоростью .
Приравняв эти две скорости, находим требуемую скорость велосипедиста:
Правильный ответ: 1.
Задание 1 № 3549. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через , а скорость парохода в стоячей воде — через . Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна . Скорость парохода вверх по течению: . Решая систему из двух этих уравнений, для скорости течения воды имеем .
Задание 1 № 3734.
Материальная точка движется вдоль оси OX. На рисунке представлен график зависимости проекции скорости этой материальной точки на ось OX от времени. Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
1) 1
2) 2
3) 3
4) 4
Решение.
Из графика видно, что проекция скорости материальной точки на ось OX положительна и постоянна, а значит, точка движется равномерно и в положительном направлении оси OX. Единственный график, удовлетворяющий обоим этим требованиям, — это график под номером 1.
Правильный ответ: 1.
Задание 1 № 3783. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями. Модуль скорости первого тела равен . Скорость же второго тела: . Следовательно, скорость второго тела больше скорости первого тела на величину
Задание 1 № 3867.
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
Для тела 2:
Таким образом модуль скорости одного тела относительно другого равен
Задание 1 № 4077. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» связана со скоростью этого тела относительно «подвижной системы отсчёта» и скоростью движения «подвижной с. о.» относительно «неподвижной» при помощи следующего соотношения: В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
Ответ: 11 м/с
Задание 1 № 4186. Координата материальной точки изменяется с течением времени по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1) 1
2) 2
3) 3
4) 4
Решение.
Из зависимости видно, что координата убывает со временем, при этом в начальный момент времени координата равна а в начало координат материальная точка попадает в момент времени: Таким образом, зависимости соответствует график под номером 4.
Правильный ответ: 4.
Задание 1 № 4221. Координата материальной точки изменяется с течением времени по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1)
2)
3)
4)
Решение.
Из зависимости видно, что координата возрастает со временем, при этом в начальный момент времени координата равна , а в момент времени координата равна . Таким образом, зависимости соответствует график под номером 3.
Правильный ответ: 3.
Задание 1 № 4409. По плоскости движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t, и , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид и . Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая .
Правильный ответ: 3
Задание 1 № 4444. По плоскости движутся четыре точечных тела — А,Б В, и Г, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени и можно смотреть как на параметрическое задание прямой на плоскости .
Выразим время из первого уравнения и подставим во второе: . Из рисунка видно, что уравнению соответствует прямая A.
Правильный ответ: 1
Задание 1 № 4934. Два автомобиля движутся по прямому шоссе: первый со скоростью , второй со скоростью относительно шоссе. Скорость первого автомобиля относительно второго равна
1)
2)
3)
4)
Решение.
Скорость первого автомобиля относительно второго равна
.
Правильный ответ: 2.
Механическое движение. Относительность движения
Код ОГЭ 1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости.
Внимание! Это конспект для 9 класса! Чтобы прочитать конспект «Механическое движение» для 7 класса перейдите по ссылке.
Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой считается тело, размеры которого малы по сравнению с другими характерными размерами, встречающимися при решении поставленной задачи.
Траектория – воображаемая линия, вдоль которой движется тело.
Относительность механического движения:
- Механическое движение можно наблюдать только относительно других тел. Тело, относительно которого рассматривается механическое движение, называется телом отсчёта.
- В различных системах отсчёта скорость и перемещение, характеризующие движение одного и того же тела, могут иметь разные модули и направления.
- Координаты тела, траектория движения, путь зависят от выбора системы отсчёта, то есть для одного и того же тела могут быть разными.
Основные физические величины, характеризующие механическое движение
- Путь
– длина траектории. Внимание! Путь не может быть отрицательным!
- Перемещение
– направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением.
Проекция вектора перемещения на координатную ось sx = x – x0 , где х0 – начальная координата тела, х – конечная координата тела.
Модуль вектора перемещения может не совпадать по числовому значению с длиной пути. Его можно рассчитать с помощью проекций вектора перемещения на координатные оси
- Средняя путевая скорость
равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной!
- Вектор средней скорости
равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло:
. В проекциях на координатную ось 0х
. Внимание! Вектор средней скорости сонаправлен с вектором перемещения.
- Мгновенная скорость
– скорость тела в данной точке пространства в данный момент времени.
Внимание! 1). Вектор мгновенной скорости направлен по касательной к траектории движения в каждой её точке. 2). Проекция перемещения на соответствующую координатную ось численно равна площади под графиком зависимости проекции скорости на эту ось от времени.
- Ускорение
– векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло:
. В проекциях на координатную ось
. Физический смысл: численно равно изменению скорости за 1 с.
Конспект урока в 9 классе «Механическое движение. Относительность движения».
Дополнительные материалы (конспекты 7 класса): 1) Механическое движение. Траектория и путь. 2) Прямолинейное движение 3) Неравномерное движение. Средняя скорость. 4) ЗАДАЧИ на движение с решениями.
Следующая тема для 9 класса: «Равномерное прямолинейное движение» (код ОГЭ 1,2).
С данной темы приступаем к повторению первого раздела физики,
который называется «Кинематика». И в начале вспомним основные понятия,
относящиеся к данному разделу, а также поговорим об относительности движения.
Кинематика, как часть механики, была известна еще со времен
Аристотеля. Однако впервые раздел кинематики был четко выделен в курсе
«Физической и экспериментальной механики» генерала Жана-Виктора Понселе,
который читал его в Парижском университете с 1837 по 1848 годы.
Кинематика — это раздел механики, в котором изучают
движение тел, без рассмотрения причин, вызвавших это движение.
Основной задачей кинематики является нахождение
положения тела в произвольный момент времени, если известны его положение,
скорость и ускорение в начальный момент времени.
Наиболее простым видом движения в природе является механическое
движение. Под механическим движением понимают изменение положения
тел (или частей одного тела) друг относительно друга в пространстве с течением
времени.
Простым примером механического движения может служить лодка,
плывущая по реке. Она меняет свое положение относительно берега, деревьев и
человека, находящихся на берегу. И таких примеров можно привести достаточно
много.
Чтобы изучать движение тела, нужно прежде всего уметь
определять это положение. Здесь важно помнить, что положение тела
можно задать только относительно какого-либо другого тела, которое, обычно,
называют телом отсчета. И так, тело отсчета — это тело
(или группа тел), принимаемое в данном случае за неподвижное, относительно
которого рассматривается движение других тел.
Тело отсчета можно выбрать совершенно произвольно. В рассмотренном
примере, им может служить рыбак, стоящий на берегу реки, или деревья, кусты,
береговая линия.
Для описания движения мало выбрать тело отсчета, необходимо
еще указать и систему координат, связав ее с телом отсчета, и способ измерения
времени. Так вот, совокупность тела отсчета, системы координат и способа
измерения времени создают систему отсчета, относительно которой и
рассматривают движение тела.
Положение тела в пространстве можно определить с помощью
радиус-вектора или при помощи координат. Радиус-вектор — это вектор,
который соединяет исследуемую точку и начало координат. Радиус-вектор
обозначается латинской буквой и,
как и любой другой вектор, имеет длину и направление.
Под координатой точки понимают проекцию конца
радиус-вектора на выбранную координатную ось.
Таким образом, для того, чтобы в рассмотренном примере
определить координату точки М, необходимо опустить с конца
радиус-вектора два перпендикуляра — на ось Ox и
ось Oy. Тогда найденные значения x и y и будут являться
координатами точки M.
Еще одно затруднение, с которым можно столкнуться,
при изучении движения тела, это то, что каждое тело имеет определенные размеры,
следовательно, разные его части, разные точки тела находятся в разных местах
пространства. Так как же определить положение всего тела? В общем случае
это сделать трудно. Но оказывается, во многих случаях нет необходимости
указывать положение каждой точки движущегося тела.
Зачем, например, описывать движение каждой точки самолета,
если эти движения ничем не различаются между собой?
Движение тела, при котором все его точки движутся
одинаково, называют поступательным.
Не нужно описывать движение каждой точки тела и
тогда, когда размеры тела малы по сравнению с расстоянием, которое оно
проходит, или по сравнению с расстояниями от него до других тел.
Например, сидя в автомобиле, его нельзя считать
точкой, по отношению к водителю или пассажиру, но, например, автомобиль мал по
сравнению с протяженностью расстояния, которое ему предстоит преодолеть, и
поэтому автомобиль считают точкой при описании его движения.
Так же поступают в астрономии при изучении движений
небесных тел. Планеты, звезды и Солнце, конечно, не малые тела.
Но, например, в сравнении с масштабами нашей
галактики «Млечный путь» и Землю и Солнце мы можем принимать за точку, которая
движется вокруг другой точки — центра галактики.
А можно ли галактику принять за точку?
Конечно же да, но только в случаях рассмотрения ее движения относительно других
галактик или всей Вселенной.
Поэтому говоря в дальнейшем о движении тела, в
действительности будем иметь в виду движение какой-нибудь точки этого тела. Не
надо забывать при этом, что эта точка материальна, то есть она отличается от
обычных тел лишь тем, что она не имеет размеров.
Таким
образом, материальная точка — это тело, размерами которого в данных
условиях движения можно пренебречь.
Линия,
которую описывает движущееся тело в определенной системе координат, называется траекторией.
Например, в идеализированной модели движения Луны вокруг Земли, в системе
отсчета, связанной с Землей, траекторией движения Луны будет являться
окружность.
А
в системе отсчета, связанной с Солнцем это кривая, чем-то напоминающая лепестки
цветка (такую кривую еще называют циклоидой).
Если можно найти длину траектории, которую описало тело за
некоторый промежуток времени, то можно определить путь, пройденный
телом. Обозначается путь малой латинской буквой s.
Следует также помнить, что путь — величина скалярная и всегда
положительная.
В тех случаях, когда траектория движения не известна,
определить положение тела, то есть его координаты, в конце пути нельзя,
даже если известны начальное положение тела и длина пройденного им пути.
Допустим, известно, что некоторое тело начинает двигаться из
точки О и за один час проходит 20 км.
Для ответа на вопрос, где будет находиться тело спустя один
час после его выхода из точки О, не хватает информации о его движении. Ведь
тело могло, например, двигаться прямолинейно в северном направлении и оказаться
в точке А, находящейся на расстоянии 20 км. А могло также, дойдя до
точки B, находящейся на расстоянии 10 км от точки О, повернуть на восток и вернуться в
точку О. При этом пройденный путь также окажется равным 20 км. При
заданном значении пути, тело могло оказаться в любой точке пространства,
ограниченного окружностью, радиуса 20 км.
Чтобы избежать такой неопределенности, для нахождения
положения тела в пространстве в заданный момент времени, была введена
физическая величина, называемая перемещением.
Перемещением тела называют направленный отрезок
прямой, соединяющий начальное положение тела с его конечным положением.
Как видно из рисунка, перемещение тела равно
геометрической разности радиус-векторов тела в начальный и конечный моменты
времени.
Для того, чтобы определить проекцию перемещения на
выбранную координатную ось, необходимо найти координаты тела в начальный и
конечный моменты времени, и найти их разность.
Необходимо отметить, что модуль перемещения не может быть
больше пути.
Знак равенства относится только к случаю прямолинейного
движения, если направление движения не изменяется.
Скорость — это мера механического состояния тела,
которая характеризует быстроту изменения положения тела относительно данной
системы отсчета и является векторной физической величиной.
Известно, что тело в редких случаях движется с неизменной
скоростью, поэтому для характеристики такого движения было введено понятие
средней скорости. И так, средняя скорость — это векторная физическая
величина, численно равная отношению перемещения к промежутку времени, за
который оно произошло, и направленная вдоль перемещения.
Так же в физике различают понятие мгновенной скорости,
то есть скорости тела в данный момент времени или в данной точке траектории.
Она равна пределу, к которому стремится средняя скорость за бесконечно малый
промежуток времени.
– это производная от радиус-вектора по времени.
Следует помнить, что мгновенная скорость всегда направлена
по касательной к траектории движения тела, а в
случае прямолинейного движения совпадает с ней.
Следующей важной характеристикой движения является ускорение.
Ускорение — это векторная физическая величина, характеризующая быстроту
изменения скорости. Оно показывает, на какую величину изменяется скорость тела
за единицу времени.
Среднее ускорение — векторная физическая величина,
численно равная отношению изменения скорости ко времени, за который оно
произошло.
где —
это производная от скорости по времени.
Для того, чтобы найти направление вектора среднего ускорения,
необходимо найти направление вектора изменения скорости. Для этого параллельным
переносом совмещают начало вектора начальной скорости с началом вектора
конечной скорости и строят их разность.
Вектор среднего ускорения направлен параллельно вектору
скорости в сторону вогнутости траектории.
Важно запомнить, что, зная траекторию
движения тела, можно определить направление вектора его скорости,
но не ускорения. Ведь направление ускорения определяется направлением
равнодействующей сил, действующих на тело.
На рисунке изображен автомобиль. Что можно сказать о данном
автомобиле: движется он или покоится? Однозначного ответа нет. Ведь не известно,
относительно чего рассматривать его движение.
А вот так?
Здесь можно сказать, что автомобиль движется относительно
дороги.
А что можно сказать о водителе данного автомобиля: он
движется или покоится?
В данном примере оба ответа будут правильными, ведь
относительно дороги водитель действительно движется вместе с автомобилем, а
относительно автомобиля он покоится.
А что можно сказать о траектории его движения? И опять здесь
нет однозначного ответа.
Так как в разных системах отсчета будут
различны вид траектории, значение скорости и других величин! В этом и
заключается относительность движения.
Вот еще один пример. Два велосипедиста на велосипеде-тандеме
движутся по проселочной дороге. Движутся ли они относительно друг друга?
Правильный ответ — «нет», так как положение их тел
относительно друг друга не меняется с течением времени.
А вот еще один классический пример. Мальчик переходит с кормы
на нос лодки, которая сама движется по течению реки. Когда мальчик доходит до
носа лодки, отсчет времени прекращают. Каково перемещение мальчика относительно
берега реки?
Для ответа на этот вопрос необходимо определить перемещение
мальчика, относительно лодки.
И перемещение лодки относительно берега, за этот промежуток
времени.
Тогда очевидно, что перемещение мальчика относительно
берега будет равно геометрической сумме перемещений мальчика относительно
лодки, и лодки, относительно берега.
Таким образом, если тело одновременно участвует в
нескольких движениях, то результирующее перемещение точки равно векторной
сумме перемещений, совершаемых ею в каждом из движений. В этом состоит
установленный экспериментально принцип независимости движений.
Основные выводы:
В рамках данной темы были повторены основные понятия кинематики,
поговорили о механическом движении тел и способах его описания. А также
разобрались с понятием относительности механического движения.