В этом разделе представлен тематический классификатор задачной базы. Вы можете прорешать все задания по интересующим вас темам.
| Тема | Кол-во заданий в базе |
Кол-во решенных заданий |
Из них решено правильно |
Проверить себя |
|---|
| Задания 2. Чтение графиков и диаграмм | 48 / 88 | 0 / 0 | 0 / 0 | |||||||
|
| Задания 3. Квадратная решётка, координатная плоскость | 110 / 134 | 0 / 0 | 0 / 0 | |||||||
|
| Задания 4. Начала теории вероятностей | 83 / 114 | 0 / 0 | 0 / 0 | |
| Задания 5. Простейшие уравнения | 72 / 125 | 0 / 0 | 0 / 0 | ||
|
| Задания 7. Производная и первообразная | 58 / 127 | 0 / 0 | 0 / 0 | |||||||
|
| Задания 9. Вычисления и преобразования | 214 / 254 | 0 / 0 | 0 / 0 | |||||||||||||||||||||||||||||||||||||||||||||||
|
| Задания 10. Задачи с прикладным содержанием | 71 / 134 | 0 / 0 | 0 / 0 | |||||||||||||||||||||||||||
|
| Задания 11. Текстовые задачи | 95 / 161 | 0 / 0 | 0 / 0 | ||
|
| Задания 12. Наибольшее и наименьшее значение функций | 159 / 218 | 0 / 0 | 0 / 0 | |||||||||||||||||
|
| Задания 13 (C1). Уравнения | 177 / 319 | 0 / 0 | 0 / 0 | |||||||
|
| Задания 14 (C2). Стереометрическая задача | 232 / 364 | 0 / 0 | 0 / 0 | ||||||||||||||||||||||
|
| Задания 15 (C3). Неравенства | 354 / 422 | 0 / 0 | 0 / 0 | ||
|
| Задания 16 (C4). Планиметрическая задача | 219 / 349 | 0 / 0 | 0 / 0 | |||||||
|
Задания 17 (C5). Финансовая математика |
129 / 155 | 0 / 0 | 0 / 0 | |
| Задания 18 (C6). Задача с параметром | 191 / 282 | 0 / 0 | 0 / 0 | |||||||||||||||||
|
Задания 19 (C7). Числа и их свойства |
169 / 270 | 0 / 0 | 0 / 0 |
Теория к №19 |
||||||||||||||||
|
Дополнительные задания для подготовки по математике
| Задания Д1. Выбор оптимального варианта | 35 / 106 | 0 / 0 | 0 / 0 | ||||||||||||
|
| Задания Д2. Планиметрия: вычисление длин и площадей | 117 / 117 | 0 / 0 | 0 / 0 | |||||||||||||||||
|
| Задания Д3. Планиметрия: задачи, связанные с углами | 220 / 236 | 0 / 0 | 0 / 0 | |||||||
|
| Задания Д4. Задачи с прикладным содержанием | 2 / 2 | 0 / 0 | 0 / 0 | ||
|
| Задания Д5 C1. Сложные уравнения, системы уравнений | 184 / 186 | 0 / 0 | 0 / 0 | |||||||||||||||||
|
| Задания Д6 C2. Сложная стереометрия | 133 / 133 | 0 / 0 | 0 / 0 | |||||||
|
| Задания Д7 C3. Сложные неравенства | 50 / 50 | 0 / 0 | 0 / 0 | ||
|
| Задания Д8 C3. Простые системы неравенств | 105 / 181 | 0 / 0 | 0 / 0 | ||||||||||||
|
| Задания Д9 C3. Сложные неравенства и системы неравенств | 105 / 108 | 0 / 0 | 0 / 0 | ||||||||||||
|
| Задания Д10 C4. Сложная планиметрия | 136 / 136 | 0 / 0 | 0 / 0 | |||||||||||||||||
|
| Задания Д11 C5. Сложные практические задачи | 53 / 53 | 0 / 0 | 0 / 0 | ||
|
| Задания Д12 C6. Сложные уравнения, неравенства, системы с параметром | 144 / 144 | 0 / 0 | 0 / 0 | ||||||||||||
|
| Задания Д13 C7. Сложные задания на числа и их свойства | 158 / 158 | 0 / 0 | 0 / 0 | ||||||||||||
|
Дополнительные материалы подготовки к профильному ЕГЭ по математике:
Текстовые задачи:
1.Движение по прямой Теория и задания >>> Задания с решением >>>
Курс состоит из трёх главных аспектов:
- теоретическая часть с разбором характерных заданий и заданиями для закрепления;
- видео-разборы типичных заданий ЕГЭ;
- проверочные работы для контроля усвоения материала.
Задания сформированы по темам, начиная с самых простых, и заканчивая более сложными.
Все формулы.pdf
Вейцман Л.Р., Вейцман Р.Л. «Геометрия: основные сведения школьного курса»
1. Графики и диаграммы
(1) Графики и диаграммы.pdf
2. Простейшие текстовые задачи
(2) Простейшие текстовые задачи.pdf
3. Простейшие уравнения
(3) простейшие уравнения.pdf
4. Вычисления и преобразования
(4) Вычисления и преобразования.pdf
5. Задачи с прикладным содержанием
(5) Задачи с прикладным содержанием.pdf
6. Текстовые задачи
(6) Текстовые задачи.pdf
7. Теория вероятностей
(7) теория вероятностей.pdf
8. Квадратная решётка
(8) квадратная решетка.pdf
9. Планиметрия
(9) планиметрия.pdf
10. Тригонометрия Ч.1
(10) Тригонометрия Ч.1.pdf
(10) Тригонометрия Ч.2
(10) Тригонометрия Ч.2.pdf
23 ноября 2012
Сегодня мы разберем очень простой и — не побоюсь этого слова — красивый прием, с помощью которого составляется уравнение плоскости в задаче C2 из ЕГЭ по математике. Урок разделен на две части: теоретическую (что такое определитель и как его считать) и практическую (как с помощью определителя находить уравнение плоскостей). Те, кому не терпится, могут сразу перейти ко второй части — «Уравнение плоскости через определитель».
Если вы до сих пор не сталкивались с определителями, не расстраивайтесь — сегодня мы разберем все, что надо знать об этих объектов для решения задачи C2. А если кто-то из учителей (особенно на пробниках) будет возникать, мол, этого нет в школьной программе, пошлите их читать учебник Калинина «Геометрия 10—11 классы». В этой замечательной книге (довольно объёмной и содержательной, между прочим) все подробно расписано на стр. 450. Итак, поехали!
Что такое матрица и определитель
В этом уроке не будет строгих определений из высшей математики. Потому что они крайне сложны для понимания. Лучше определим их вот как:
- Матрица — это просто таблица, заполненная числами. Матрицы бывают квадратными (когда количество строк совпадает с количеством столбцов) и прямоугольными (когда не совпадает);
- Определитель — это число, которое находится по специальному алгоритму из чисел, записных в квадратной матрице. У каждого размера матрицы свой алгоритм. Для прямоугольных матриц определитель найти нельзя.
Примеры квадратных матриц размером 2×2, 3×3 и 4×4:
Примеры прямоугольных матриц 2×3, 3×2 и даже 4×1:
Как видите, матрицы бывают разных размеров и обозначаются квадратными скобкам. Внутри них могут стоять совершенно разные числа, в т.ч. отрицательные и нули. Но для решения задачи C2 нам потребуются только квадратные матрицы размером 3×3. Например, такие:
Как считать определитель 3-го порядка
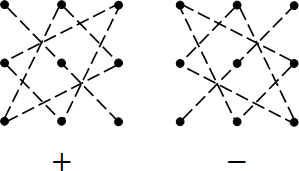
Теперь разберемся с определителями. Чаще всего их обозначают буквой d (от слова determinant). Поскольку нас интересуют только матрицы 3×3, учимся считать определители именно для них. Процедура выглядит довольно просто. Взгляните на картинку:
Что это за пентаграммы? На первом рисунке мы берем три числа, лежащие на диагонали, и перемножаем их. Затем берем другие тройки чисел, лежащие в вершинах треугольников, и тоже перемножаем их между собой. В результате всех этих махинаций мы получим три числа, которые надо сложить (поэтому внизу левой картинки стоит знак плюс).
Теперь разбираемся со второй картинкой. Здесь мы снова берем и перемножаем три числа, но уже на другой диагонали. Так же мы снова берем два треугольника и перемножаем числа, стоящие в их углах (отдельно для каждого треугольника). Полученные три числа опять складываем, а результат вычитаем из первого числа (поэтому внизу справа стоит знак минус).
На первый взгляд, без бутылки не разберешься. Но на практике такие определители считаются очень быстро. Некоторые даже умудряются считать их устно. Чтобы убедиться в этом, давайте попробуем найти пару определителей.
Задача. Найдите определитель квадратной матрицы:
Перемножаем числа. стоящие на первой диагонали (выходит из левого верхнего угла):
1 · 5 · 9 = 45
Теперь перемножаем числа, стоящие в вершинах треугольников на первом рисунке. Каждую тройку надо считать отдельно:
2 · 6 · 7 = 84;
3 · 4 · 8 = 96.
Осталось сложить полученные числа:
45 + 84 + 96 = 225
Итак, для первого рисунка (отмеченного знаком плюс) мы получили число a = 225.
Переходим ко второй диагонали набору треугольников. Эта диагональ начинается из правого верхнего угла матрицы. Имеем:
3 · 5 · 7 = 105
Выписываем числа из двух оставшихся треугольников:
2 · 4 · 9 = 72;
1 · 6 · 8 = 48;
Осталось выполнить последние шаги — сложить эти три числа, а полученное число (назовем его b) вычесть из числа a = 225, найденного ранее:
b = 105 + 72 + 48 = 225;
d = a − b = 225 − 225 = 0.
Получили число d = 0 — это и есть определитель.
Задача. Найдите определитель квадратной матрицы:

В этот раз не будем подробно расписывать каждый шаг. Запишем только то, что действительно надо писать в решении. А именно:
a = 1 · (−2) · 5 + 2 · 3 · 0 + 3 · (−1) · 4 = −10 + 0 − 12 = −22;
b = 3 · (−2) · 0 + 2 · (−1) · 5 + 1 · 3 · 4 = 0 − 10 + 12 = 2;
d = a − b = −22 − 2 = −24.
Вот и все! Число d = −24 — это ответ.
Задача. Найдите определитель квадратной матрицы:

Снова запишем только вычисления:
a = 1 · 6 · (−2) + 0 · 1 · 0 + (−1) · 3 · (−3) = −12 + 0 + 9 = −3;
b = (−1) · 6 · 0 + 1 · 1 · (−3) + 0 · 3 · (−2) = 0 − 3 + 0 = −3;
d = a − b = −3 − (−3) = −3 + 3 = 0.
Из первой и последней задачи следует, что определитель матрицы вполне может равняться нулю. Это свойство как раз и потребуется для решения задачи C2. Точнее, для того, чтобы быстро составлять уравнения плоскостей.
Ну и как составлять эти уравнения? Ответ смотрите во второй части — «Уравнение плоскости через определитель».
Смотрите также:
- Задача C2: уравнение плоскости через определитель
- Видеоурок по задачам C2: уравнение плоскости через определитель
- Сложные выражения с дробями. Порядок действий
- Комбинированные задачи B12
- Как быстро запомнить таблицу синусов и косинусов
- ЕГЭ 2022, задание 6. Касательная к графику функции
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Муниципальное
общеобразовательное бюджетное учреждение
«Средняя
общеобразовательная школа №3» г. Соль-Илецка
проект
Координатный
метод решения
стереометрических
задач
на
Едином Государственном Экзамене.
Матрицы
и определители в школе.
2014
г.
Введение
На
уроках математики нам не хватает времени, чтобы больше узнать о роли
математических наук в жизни человека и их связи с различными областями
жизнедеятельности, об истории возникновении и развитии этой науки, ученых и их
достижениях, и что очень важно в настоящее время, о нестандартных методах
решения задач. В результате мы часто задаемся вопросом: «Зачем мы изучаем
математику? Существуют ли более совершенные методы решения? И почему мы их не
изучаем в школьной программе?».
Мы
провели исследование по теме «Методы решения стереометрических задач» и хотели
узнать, так ли важна эта тема в жизни старшеклассников.
Чтобы
ответить на эти вопросы, мы:
·
изучили теорию вопроса;
·
встретились с учителями математики города
и района, выпускниками прошлых лет, студентами математических вузов,
преподавателями университета, учащимися 11 классов;
·
обработали результаты, полученные в ходе
опроса;
·
просмотрели научные газеты и журналы,
чтобы найти ответ на вопрос «Есть ли подобная информация в периодической
печати?».
Выяснили
что, учителям и старшеклассникам часто приходится решать стереометрические задачи
нестандартными методами, применяя теоретические знания из курса высшей
математики, конкретно по теории пределов, элементам высшей алгебры (матрицы,
определители), аналитической геометрии.
Вышеперечисленные
разделы математики изучаются в нашей школе на факультативах и кружках, что
помогло нам быстро и комфортно сориентироваться в данных областях
математической науки.
В
результате работы над проектом мы научились оформлять выводы, делать
презентацию, проводить опрос, отбирать задачи математического содержания,
встречающиеся в быту и повседневной жизни, из сборников ЕГЭ и располагать их по
темам, распределять работу между собой, оформлять брошюру.
Задачи
части «С» Единого государственного экзамена по стереометрии в последнее время
большей частью посвящены вычислению расстояний и углов в пространстве. Около 30%
выпускников приступало к решению задачи С2 на ЕГЭ 2010-2012 гг. Так в 2010 году
процент приступивших к выполнению составил 30%, в 2011 году – 33,1%, а в 2012
году – 29%. Задание С2 оценивается в 2 балла. В 2010 году от 1 до 2 баллов за
задачу С2 смогли получить 11,6% участников экзамена, в 2011 – 13,9%, а в 2012 –
5,53%.
Полное
решение каждой задачи состоит из теоретической части, заключающейся в
обосновании взаимного расположения элементов заданной стереометрической
конфигурации, и вычислительной части. При проверке задачи С2 выставление
баллов производится в соответствии со следующими критериями:
·
Обоснованно получен верный ответ – 2
балла;
·
Решение содержит обоснованный переход к
планиметрической задаче, но получен неверный ответ или решение не закончено – 1
балл;
·
Решение не соответствует ни одному из
критериев, перечисленных выше – 0 баллов.
На
наш взгляд данные критерии оценивания задачи С2 очень жестки, так как многие
учащиеся решают стереометрические задачи нестандартными методами, порой
собственными методами, и получают обоснованно верные решения и ответы.
Следует
отметить, что при решении задачи координатным или векторным методами выпускник
должен получить правильный ответ, и только тогда его решение будет оценено в 2
балла. В противном случае его решение не соответствует приведенным критериям и
будет оценено в 0 баллов.
Визитная карточка проекта
|
ФИО |
Альбрехт Мукашев |
|
Место |
МОБУ |
|
ФИ |
Савченко Борисов |
|
Место |
МОБУ |
|
Предметный |
Математика |
|
Тема проекта |
«Координатный стереометрических на |
|
Вид проекта |
Информационный По По По |
|
Цели |
· · · · |
|
Задачи |
1. 2. «Координатный метод решения стереометрических задач на Едином Государственном |
|
Этапы |
1. 2. 3. 4. 5. |
|
Реальность |
Данный |
|
Краткое описание выполненного проекта |
Реализуя проектную идею, ученики собрали и систематизировали информацию по |
|
Презентация |
Проект |
Особенности реализации проекта
На
уроке проектной деятельности проведено тестирование учащихся 11 класса с целью
выявления наиболее заинтересованных ребят для работы над проектом. Им
поставлена задача: собрать и систематизировать материал по теме «Координатный
метод решения стереометрических задач на Едином Государственном Экзамене»;
подготовить небольшую компьютерную презентацию.
Ход
выполнения проекта
Какие методы и приемы
работы были освоены учащимися в работе над проектом
Анализ литературы, рефлексивный анализ
собственной деятельности и т.д. Приемы умственной деятельности: анализ,
конкретизация, обобщение, сравнение, выявление существенного.
Приемы работы:
·
консультации
с учителем;
·
поиск
недостающей информации в информационном поле и у руководителя проекта;
·
работа в сети
Интернет;
·
работа в
программах Microsoft Office,
PowerPoint (для создания презентации) и Microsoft
Office Word (для создания
письменного варианта проекта).
Описание затруднений
учителя, учащихся, возникших в процессе выполнения проекта и путей их
разрешения
На этапе сбора и обработки информации у авторов
проекта возникли трудности при структурировании собранного материала, отбора
наиболее существенного и значимого. Также при создании презентации участникам
было сложно выбрать основную информацию и представить её на слайдах в сжатой
форме.
ХОД ПРОЕКТА:
1. ЭТАП
— изучение и анализ результатов ЕГЭ по математике по определению темы проекта;
— постановка задач, определение состава групп, определение возможных способов
решения поставленных задач
2. ЭТАП
— обсуждение собранного материала;
— разработка сценария основной части проекта.
3. ЭТАП
— форматирование и печать брошюры
— подготовка компьютерной презентации проекта
— оформление проекта.
4. ЭТАП
— защита проекта с демонстрацией подготовленного материала.
— оформление результатов проекта.
Оглавление.
1.Введение.
2.Основная часть.
3.Заключение.
4.Список используемой литературы.
Цели:
·
образовательные: продолжение работы по формированию устойчивого интереса к
математике; сформировать у учащихся основные ИКТ-компетентности: умения и
навыки исследовательской, проектной деятельности; работать над повышением
мотивации школьников к изучению математики на основе межпредметной интеграции и
проектной деятельности; развитие навыков самостоятельного получения информации,
формирование умения отбирать и структурировать материал, добиваться лучших
результатов на ЕГЭ по математике.
·
воспитательные: создание условий для
отношений сотрудничества между учащимися, формирование таких качеств личности,
как познавательная активность, самостоятельность, упорство в достижении
поставленной цели.
·
развивающие: развитие творческих
способностей учащихся (воображения, наблюдательности, памяти), монологической
речи, самоанализа и рефлексии; способности выявлять причинно – следственные
связи, развитие логического мышления.
Вид проекта: исследовательский,
практико–ориентированный, групповой, межпредметный, среднесрочный.
Проблема: «Научиться
решать стереометрические задачи нестандартными методами для повышения
познавательного интереса в математике и качества знаний выпускников школ?
Почему многие «боятся? задачи С2 ЕГЭ математика?»
Девиз
проекта: «Слишком много переживаем. Слишком
серьезно воспринимаем. Надо относиться ко всему проще. Но с умом. Без нервов.
Главное – думать. И не делать глупостей.»
Основная
часть
Задача 1. На
единичном кубе ABCDA1B1C1D1
найдите угол между прямыми AB1 и BC1.

Введем
прямоугольную систему координат, так как показано на рисунке, и найдем
координаты точек, а затем и координаты векторов AB1 и BC1.
Теоретическая часть.
Понятие вектора. Проекции вектора
Направленные отрезки принято
называть также геометрическими векторами или просто векторами. Вектор как
направленный отрезок мы будем по—прежнему записывать в тексте двумя большими
латинскими буквами с общей чертой наверху при условии, что первая из них
обозначает начало, вторая — конец вектора. Наряду с этим мы будем также
обозначать вектор одной малой латинской буквой полужирного шрифта, которая на
чертежах ставится у конца стрелки, изображающей вектор (см. чертеж), где
изображён вектор а с началом А и концом В). Начало
вектора часто будет называться также его точкой приложения.
Векторы называются
равными, если они имеют одинаковые длины, лежат на параллельных
прямых или на одной прямой и направлены в одну сторону.
Число, равное длине вектора
(при заданном масштабе), называется его модулем. Модуль вектора а
обозначается символом |а| или а. Если |а|
= 1, то вектор a называется единичным.
Единичный вектор, имеющий
одинаковое направление с данным вектором а, называется
ортом вектора а и обозначается обычно символом а0.
Проекцией вектора на ось и называется
число, равное величине отрезка оси и,
где точка А1 является проекцией на ось и точки
А, а B1 — проекцией
точки В.
Проекция вектора на ось и обозначается
символом: при Если вектор
обозначен символом а, то его проекцию на ось и принято обозначать: приa.
Проекция вектора а на
ось и выражается через его модуль и угол наклона
к оси и формулой
(1)
Проекции произвольного
вектора а на оси некоторой заданной системы координат в дальнейшем
обозначаются буквами X, Y, Z. Равенство
означает, что числа X, Y, Z
являются проекциями вектора на координатные оси.
Проекции вектора на
координатные оси называют также его (декартовыми) координатами. Если даны две
точки M1(x1 ; у1 ; z1 ) и
М2(x2 ; у2 ; z2),
являющиеся соответственно началом и концом вектора а, то
его координаты X, Y, Z определяются по формулам
,
,
Формула (2)
позволяет по координатам вектора определить его модуль.
Если —
углы, которые составляет вектор а с координатными осями
(черт, 41), то называются
направляющими косинусами вектора а.
Вследствие формулы
(1) ,
,
.
Отсюда и из формулы (2)
следует, что . Последнее равенство
позволяет определить один из углов если
известны два других.
1. Вычислить модуль
вектора а — {6; 3; — 2}.
2. Даны две координаты
вектора Х=4, У= —12. Определить его третью координату Z при
условии, что .
3. Даны точки А(3; —1; 2)и В(— 1; 2; 1).Найти
координаты векторов и
.
4. Определить точку N, с которой
совпадает конец вектора а = {3; —1; 4}, если его начало
совпадает с точкой М (I; 2; —3).
5. Определить начало вектора
а = {2; —3; —1}, если его конец совпадает с точкой (1; —1; 2).
6. Дан модуль вектора и углы
= 45°,
= 60°,
=120°.
Вычислить проекции вектора а на координатные оси.
7. Вычислить направляющие
косинусы вектора а ={12; —15; —16}.
8. Вычислить направляющие
косинусы вектора
9. Может ли вектор
составлять с координатными осями следующие углы: 1) =
45°, = 60°,
= 120°;
2) = 45°,
=135°,
= 60°; 3)
= 90°,
=150°;
= 60°?
10. Может ли вектор составлять с двумя координатными осями следующие
углы: 1) = 30°,
= 45°;
2) = 60°,
= 60°;
3) = 150°,
= 30°?
11. Вектор составляет с
осями Ох и Oz углы =120° и
= 45°. Какой угол он составляет с осью Оу?
11. Вектор а составляет
с координатными осями Ох и Оу углы =
60°, = 120°. Вычислить его координаты при
условии, что .
Скалярное произведение векторов
Скалярным произведением двух векторов называется число,
равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов а, b
обозначается символом аb (порядок записи сомножителей
безразличен, т. е. аb = bа).
Если угол между векторами а, b обозначить
через , то их скалярное произведение
можно выразить формулой .
(1)
Скалярное произведение векторов а, b
можно выразить также формулой
, или
Из формулы (1) следует, что ab > 0,
если — острый угол, ab <
0, если угол — тупой; ab = 0 в
том и только в том случае, когда векторы a и b
перпендикулярны (в частности, ab = 0, если a = 0
или b = 0).
Скалярное произведение аа называется
скалярным квадратом вектора и обозначается символом а2.
Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его
модуля:
Если векторы а и b заданы своими
координатами:
, и
,
то их скалярное произведение может быть вычислено по формуле
.
Отсюда следует необходимое и достаточное условие перпендикулярности
векторов:
.
Угол между векторами
и
даётся формулой , или в координатах,
Проекция произвольного вектора S = {X;
Y; Z} на какую—нибудь ось и определяется формулой При S
= Se, где е — единичный вектор, направленный по
оси и. Если даны углы ,
,
,
которые ось и составляет с координатными осями, то и для вычисления проекции вектора S
может служить формула при 5 = X cos α + Y cos β
+ Z cos γ.
1. Векторы а и
b образуют угол ;
зная, что |а| = 3, |b| = 4, вычислить: 1)
аb; 2) а2; 3) b2;
4) (а + b)2; 5) (3а
— 2b) (а + 2b); 6) (а
—b)2; 7) (3а + 2b)2.
2. Векторы а
и b взаимно перпендикулярны; вектор с образует с ними
углы, равные , зная, что |а| = 3, |b
| = 5, |c| = 8, вычислить: 1) (3а — 2b) (b + 3с);
2) (а + b + c)2; 3) (а + 2b— 3с)2.
3. Доказать справедливость
тождества
(а + 6)2 + (а — 6)2
= 2(a2 + b2)
и выяснить его геометрический смысл.
Определители
второго порядка.
Пусть
дана квадратная таблица из четырех чисел ,
,
,
:

Число называется
определителем второго порядка, соответствующего таблице (1). Этот определитель
обозначается символом 
имеем

Числа ,
,
,
называются
элементами определителя. Говорят, что элементы ,
лежат
на главной диагонали определителя, ,
— на
побочной. Таким образом, определитель второго порядка равен разности между
произведениями элементов, лежащих на главной и побочной диагоналях. Например,
.
Рассмотрим
систему двух уравнений
,
(3)
с
двумя неизвестными x, y. (Коэффициенты ,
,
,
и свободные
члены ,
предположим
данными.) Введем обозначения



Определитель ,
составленный из коэффициентов при неизвестных системы (3), называется
определителем этой системы. Определитель получается
путем замены элементов первого столбца определителя свободными
членами системы (3); определитель при
помощи замены свободными членами системы (3) элементов его второго столбца.
Если , то система
(3) имеет единственное решение; оно определяется формулами
,
.
Если и при
этом хотя бы один из определителей ,
отличен
от нуля, то система (3) совсем не имеет решений (как говорят, уравнения этой
системы несовместны).
Если
же , но
также , то система
(3) имеет бесконечно много решений (в этом случае одно из уравнений системы
есть следствие другого).
Пусть
в уравнениях системы (3) ; тогда
система (3) будем иметь вид:
,
. (6)
Система
уравнений вида (6) называется однородной; она всегда имеет нулевое
решение; x=0, y=0. Если , то это
решение является единственным; если же , т о система
(6), кроме нулевого, имеет бесконечно много других решений.
|
1 |
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Решить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решить |
|
|
|
|
|
|
|
|
|
|
|
|
Определители третьего порядка
Пусть дана квадратная таблица из девяти чисел a1, а2, а3, b1, b2, b3,

Определителем третьего порядка, соответствующим таблице
(1), называется число, обозначаемое символом
и определяемое равенством

Числа a1, а2, а3,
b1, b2, b3, с1, с2,
с3 называются элементами определителя. Элементы a1, b2, с3 расположены на диагонали определителя,
называемой главной; элементы а3, b2, с1, составляют его побочную
диагональ. Для практики вычислений полезно заметить, что первые три слагаемые в
правой части равенства (2) представляют собой произведения элементов
определителя, взятых по три так, как показано различными пунктирами на
нижеприводимой схеме слева.
Чтобы получить следующие три члена правой части равенства (2),
нужно перемножить элементы определителя по три так, как показано различными
пунктирами на той же схеме справа, после чего у каждого из
найденных произведений изменить знак.
В задачах 2 (а-ж) требуется вычислить определители третьего
порядка.
а). 

в) 
г). 

ж). 
Общее уравнение плоскости. Уравнение плоскости,
проходящей через данную
точку и имеющей данный
нормальный вектор
В декартовых координатах
каждая плоскость определяется уравнением первой степени и каждое уравнение
первой степени определяет плоскость.
Всякий (не равный нулю)
вектор, перпендикулярный к данной плоскости, называется её нормальным вектором.
Уравнение
А(х — xо) +
В(у — yо) + С(z — zz0)
= 0 (1)
определяет плоскость, проходящую через точку М0(х0;
у0; z0) и имеющую нормальный вектор п = {А; В; С}.
Раскрывая в уравнении (1)
скобки и обозначая число —Ах0 — Ву0,—Сz0 буквой
D представим его в виде:
Ах + By + Cz + D = 0.
Это уравнение называется общим
уравнением плоскости
может быть представлено в следующем виде:

1. Составить уравнение
плоскости, которая проходит через точку M1(2; 1; —1) и имеет
нормальный вектор n ={1, —2; 3}.
2. Составить уравнение плоскости, которая проходит через начало
координат и имеет нормальный вектор п = {5; 0; —3}.
3. Точка Р (2; —1; —1) служит основанием перпендикуляра, опущенного
из начала координат на плоскость. Составить уравнение этой плоскости.
4. Даны две точки М1(3;
—1; 2) и М2(4; —2; —1). Составить уравнение плоскости, проходящей
через точку М1 перпендикулярно к вектору .
5. Составить уравнение
плоскости, проходящей через точку M1(3; 4; —5)
параллельно двум векторам a1 = {3; 1; —1} и a2
= {1; —2; 1}.
6. Составить уравнение плоскости, проходящей через точки M1(2;
— 1; 3) и М2(3; 1; 2) параллельно вектору а = {3; — 1;
—4}.
Практическая часть: решение конкретных задач С2 ЕГЭ
математика.
Задача 1. В правильной
треугольной призме ABCA1B1C1,
все ребра которой равны 1, найдите косинус угла между плоскостями ACB1
и BA1C1.

Заключение.
Мы
считаем, что целесообразно включить в школьный курс математики изучение таких разделов,
как матрицы и определители, уравнение прямых и плоскостей. На наш взгляд методы
решения стереометрических задач при помощи высшей алгебры и аналитической
геометрии позволит многим учащимся получить высокие баллы на Едином
Государственном Экзамене.
Но самое
главное – это интерес к изучению геометрии и решению задач. Подстегивает, то,
что мы и все учащиеся нашей школы хотим изучать математику, хотим решать задачи
более совершенными методами, хотим знать больше, чем нам положено в рамках
школьной программы.
Мы очень
рады, тому что мы и все ребята познаем математические тайны с большим
интересом. Наверное, после этого проекта, мы с ребятами, найдем другие новые
методы решения задач, и по другим предметам.
Желаем
всем математических побед.
Список
использованной литературы
1.
Д.В .Клетеник «Сборник задач по аналитической
геометрии», изд. 15. Москва, Наука, Физматлит, 1998. — ISBN 5-02-015080-0.
2.
В.С. Щипачев «Высшая математика», изд. 4.
Москва, Высшая школа, 1998.
3.
А. Н. Канатников «Аналитическая
геометрия», 2-е изд. — М.: Изд-во
МГТУ им. Н.Э. Баумана, 2000.— 388 с.
4.
Умнов А.Е. «Аналитическая
геометрия и линейная алгебра» , 3-е изд., испр. и доп. — М.: МФТИ, 2011.
— 543 с.
5.
Бортаковский А.С., Пантелеев А.В.
«Аналитическая геометрия в примерах и задачах», М.: Высшая школа, 2005. — 496 с.
6.
Письменный Д.Т., Конспект лекций
по высшей математике: полный курс. 9-е изд. — М.: 2009. — 608 с.
7.
Черкасов
А.Н, Введение в высшую математику. ., М.: Наука, 1964. — 244 с.
Задача 3. Начала теории вероятностей
Задача 3. Начала теории вероятностей
Задача 4. Вероятности сложных событий
Задача 4. Вероятности сложных событий
Задача 5. Простейшие уравнения
Задача 5. Простейшие уравнения
Задача 6. Вычисления и преобразования
Задача 6. Вычисления и преобразования
Задача 7. Производная и первообразная
Задача 7. Производная и первообразная
Задача 8. Задачи с прикладным содержанием
Задача 8. Задачи с прикладным содержанием
Задача 9. Текстовые задачи
Задача 9. Текстовые задачи
Задача 10. Графики функций
Задача 10. Графики функций
Задача 11. Наибольшее и наименьшее значение функций
Задача 11. Наибольшее и наименьшее значение функций

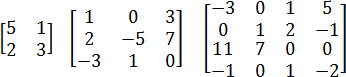
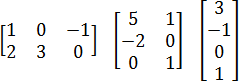
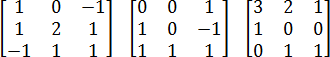
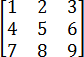
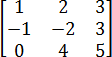
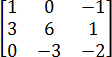






 ;
;








