Каталог заданий.
Вписанные окружности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 1 № 27624
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Аналоги к заданию № 27624: 56807 56809 56811 56813 56815 56817 56819 56821 56823 56825 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
2
Тип 1 № 27625
Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Аналоги к заданию № 27625: 56857 56859 56861 56863 56865 56867 56869 56871 56873 56875 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 1 № 27640
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Аналоги к заданию № 27640: 57407 512328 512370 57409 57411 57413 57415 57417 57419 57421 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.4 Окружность и круг, 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
4
Тип 1 № 27907
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Аналоги к заданию № 27907: 53121 53123 53125 53127 53129 53131 53133 53135 53137 53139 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
5
Тип 1 № 27908
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Аналоги к заданию № 27908: 53171 53173 53175 53177 53179 53181 53183 53185 53187 53189 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.1.7 Вписанная окружность и описанная окружность правильного многоугольника, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник- описанным около этой окружности.
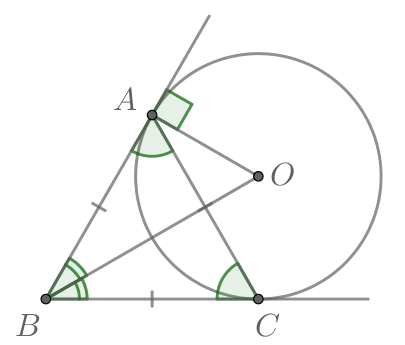
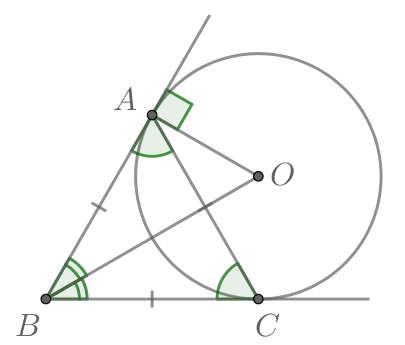
В любой треугольник можно вписать окружность. Центром вписанной окружности (точка $О$) является точка пересечения биссектрис внутренних углов треугольника.
$OD$ – это радиус $(r)$ вписанной окружности
$r={2S_{ABC}}/{a+b+c}$
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
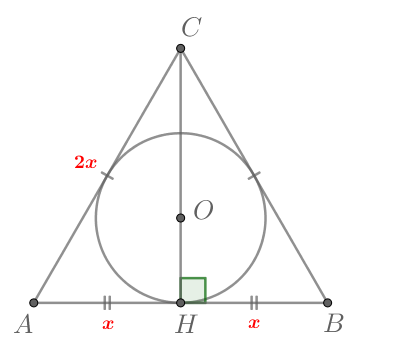
В равнобедренном треугольнике вписанная окружность точкой касания делит основание пополам
В равностороннем треугольнике радиус вписанной окружности равен трети высоты данного треугольника.
$r={h}/{3}$
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Пример:
В прямоугольном треугольнике $АВС$ катет и гипотенуза соответственно равны $8$ и $10$. Найдите радиус окружности, вписанной в этот треугольник.
Решение:
В прямоугольном треугольнике радиус вписанной окружности равен:
$r={a+b-c}/{2}$, где $а$ и $b$ – это катеты, $с$ – гипотенуза.
Нам неизвестен один из катетов, найдем его по теореме Пифагора:
$a^2+b^2=c^2$
$8^2+b^2=10^2$
$64+b^2=100$
$b^2=100-64$
$b^2=36$
$b=6$
Теперь подставим все величины в формулу нахождения радиуса вписанной окружности в прямоугольном треугольнике:
$r={6+8-10}/{2}={4}/{2}=2$
Ответ: $2$
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
В трапеции и ромбе центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов, радиус вписанной окружности равен половине высоты.
$r={h}/{2}$
В квадрате радиус вписанной окружности равен половине стороны.
$r={a}/{2}$
Площадь любого многоугольника можно найти как произведение полупериметра на радиус вписанной окружности.
$S={P∙r}/{2}$
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник- вписанным в эту окружность.
Около любого треугольника можно описать окружность, причем только одну. Центром описанной окружности является точка $(О)$ пересечения серединных перпендикуляров к сторонам треугольника.
$ОА$ — радиус описанной окружности $(R)$
В равностороннем треугольнике радиус описанной окружности равен две трети высоты данного треугольника.
$R={2h}/{3}$
Центр описанной окружности может находиться в различных положениях относительно треугольника:
1. В остроугольном треугольнике центр описанной окружности лежит внутри треугольника.
2. В тупоугольном треугольнике центр описанной окружности лежит снаружи треугольника.
3. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.
$R={c}/{2}$
Радиус описанной окружности можно найти как:
$R={a}/{2sinA}={b}/{2sinB}={c}/{2sinC};$
$R={a∙b∙c}/{4S}$, где $S$ — это площадь заданного треугольника.
Около четырехугольника не всегда можно описать окружность. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.
$R={d}/{2}$
Только вокруг равнобедренной трапеции можно описать окружность.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Связь между сторонами правильного n-угольника и радиусами описанной и вписанной окружностей:
$АВ=an$ — сторона правильного многоугольника
$R$ — радиус описанной окружности
$r$ — радиус вписанной окружности
$n$ — количество сторон и углов
$a_n=2∙R∙sin{180°}/{n};$
$r=R∙cos{180°}/{n};$
$a_n=2∙r∙tg{180°}/{n}.$
Углы в окружности:
1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается
$∠О=∪BmA$
2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается
$∠B={∪AmC}/{2}$
3. Угол между хордой и касательной равен половине дуги, заключенной внутри него.
$∠B={∪BmC}/{2}$
Теория к заданию 6 ЕГЭ профильной математики
ПЛАНИМЕТРИЯ. Центральные и вписанные углы. Касательная, хорда, секущая. Вписанные и описанные окружности (теория к заданию 6 ЕГЭ профильной математики)
Учим и применяем формулы и теоремы.
Автор: Лариса Алькаева. Репетитор по математике
Из материала:
Отрезок, соединяющий две точки на окружности, называется хордой.
Самая большая хорда проходит через центр окружности и называется диаметром.
Центральный угол — угол, вершина которого лежит в центре окружности.
Центральный угол равен дуге, на которую опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Подготовка к ЕГЭ «Вписанные и описанные окружности»
Вписанные и описанные окружности
В
Окружность называется вписанной в многоугольник , если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.
Не во всякий многоугольник можно вписать окружность.
Площадь многоугольника, в который вписана окружность можно найти по формуле 
з


Отсюда радиус вписанной окружности равен
Е
В любой треугольник можно вписать окружность, притом только одну. Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.
Радиус вписанной окружности равен 
О
Окружность называется описанной около многоугольника , если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника. Радиус вычисляется как радиус окружности, описанной около треугольника, определенного любыми тремя вершинами данного многоугольника:
Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 
∠ 


О
Радиус описанной окружности вычисляется по формулам:


где 

Найдите радиус окружности, вписанной в квадрат со стороной 16.
Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.
Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности.
В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.
Угол A четырехугольника ABCD , вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Стороны четырехугольника ABCD AB , BC , CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Точки A , B , C , D , расположенные на окружности, делят эту окружность на четыре дуги AB , BC , CD и AD , градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD . Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD . Ответ дайте в градусах.
Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.
Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.
Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Описанная окружность
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
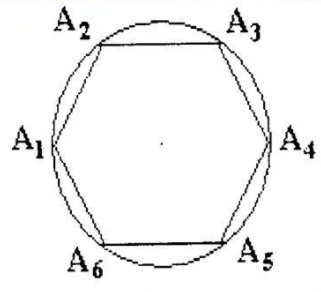
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.
Вписанная окружность
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.
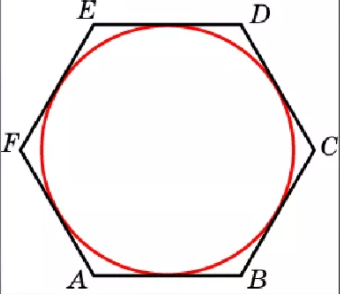
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.
Вписанный и описанный треугольники
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
В любой треугольник можно вписать окружность: 
Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Вписанный и описанный четырехугольники
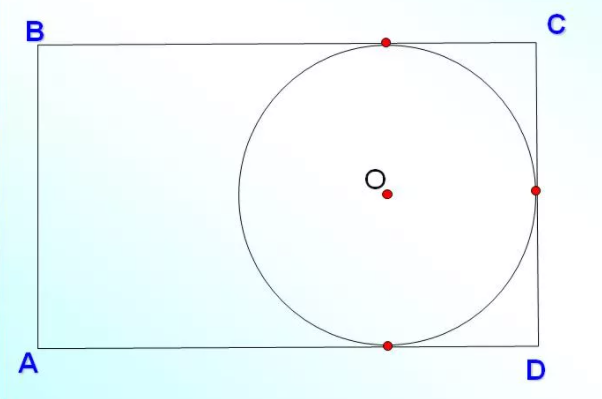
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.
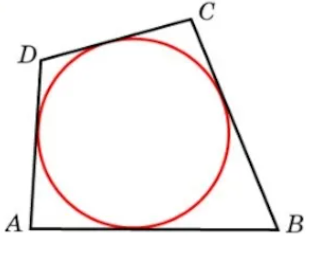
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.
На рисунке выполняется данное условие, то есть AD + BC=DC + AB
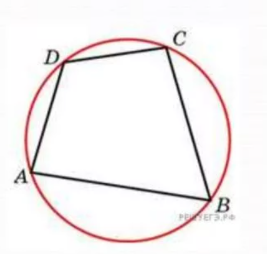
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.
На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.
источники:
http://infourok.ru/podgotovka-k-ege-vpisannie-i-opisannie-okruzhnosti-2253189.html
http://spadilo.ru/opisannaya-i-vpisannaya-okruzhnost/
ЕГЭ Профиль №3. Вписанные окружности
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Вписанные окружности
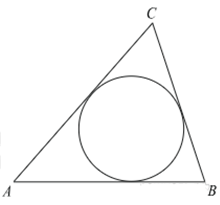
| Задача 1. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
Ответ
ОТВЕТ: 6. |
 |
| Задача 2. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
Ответ
ОТВЕТ: 24. |
 |
| Задача 3. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 3. |
 |
| Задача 4. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Ответ
ОТВЕТ: 22. |
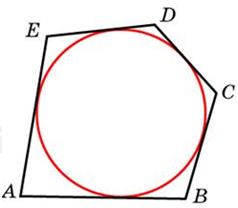 |
| Задача 5. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Ответ
ОТВЕТ: 30. |
 |
| Задача 6. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Ответ
ОТВЕТ: 1. |
 |
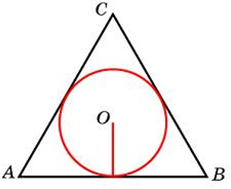
| Задача 7. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.
Ответ
ОТВЕТ: 2. |
 |
| Задача 8. Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Ответ
ОТВЕТ: 18. |
 |
| Задача 9. Сторона правильного треугольника равна (sqrt 3 ). Найдите радиус окружности, вписанной в этот треугольник.
Ответ
ОТВЕТ: 0,5. |
 |
| Задача 10. Радиус окружности, вписанной в правильный треугольник, равен (frac{{sqrt 3 }}{6}). Найдите сторону этого треугольника.
Ответ
ОТВЕТ: 1. |
 |
| Задача 11. Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
Ответ
ОТВЕТ: 0,25. |
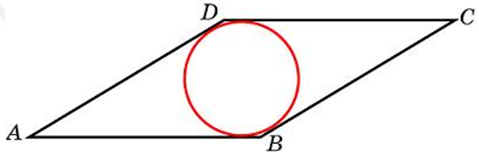 |
| Задача 12. Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Ответ
ОТВЕТ: 8. |
 |
| Задача 13. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt 3 ).
Ответ
ОТВЕТ: 2. |
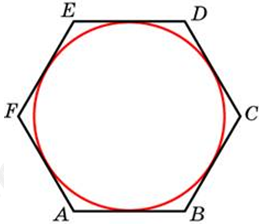 |
| Задача 14. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt 3 ).
Ответ
ОТВЕТ: 1,5. |
 |
| Задача 15. Катеты равнобедренного прямоугольного треугольника равны (2 + sqrt 2 ). Найдите радиус окружности, вписанной в этот треугольник.
Ответ
ОТВЕТ: 1. |
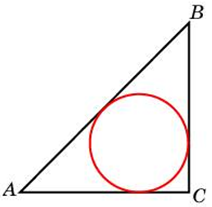 |
| Задача 16. В треугольнике ABC (AC = 4,;;BC = 3,) угол C равен 90°. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 1. |
 |
| Задача 17. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Ответ
ОТВЕТ: 1,5. |
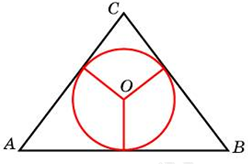 |
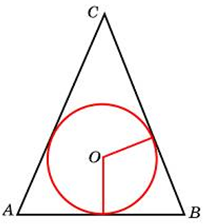
| Задача 18. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Ответ
ОТВЕТ: 22. |
 |
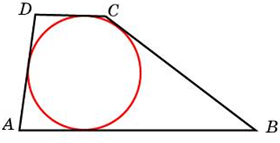
| Задача 19. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Ответ
ОТВЕТ: 4. |
 |
| Задача 20. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Ответ
ОТВЕТ: 10. |
 |
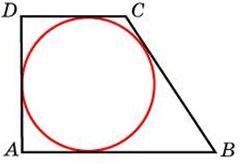
| Задача 21. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Ответ
ОТВЕТ: 2. |
 |
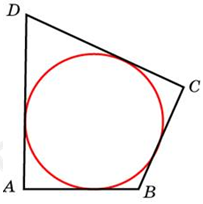
| Задача 22. В четырехугольник ABCD вписана окружность, (AB = 10,;;CD = 16.) Найдите периметр четырехугольника.
Ответ
ОТВЕТ: 52. |
 |
| Задача 23. В четырехугольник ABCD вписана окружность, (AB = 10,) (BC = 11) и (CD = 15.) Найдите четвертую сторону четырехугольника.
Ответ
ОТВЕТ: 14. |
 |
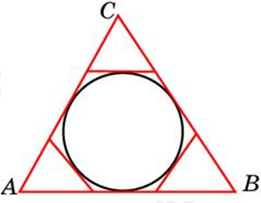
| Задача 24. К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Ответ
ОТВЕТ: 24. |
 |
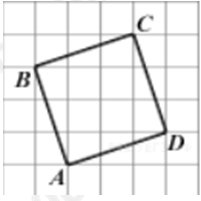
| Задача 25. Найдите радиус r окружности, вписанной в четырехугольник ABCD. Считайте, что стороны квадратных клеток равны 1. В ответе укажите (rsqrt {10} ).
Ответ
ОТВЕТ: 5. |
 |
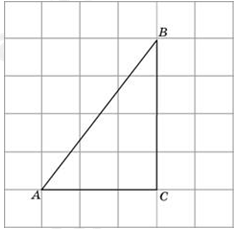
| Задача 26. Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
Ответ
ОТВЕТ: 1. |
 |
Тема 1.
Геометрия на плоскости (планиметрия)
1
.
17
Окружность: вписанная в многоугольник или угол
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
геометрия на плоскости (планиметрия)
1.01Треугольник: внутренние и внешние углы
1.02Треугольник: высота, биссектриса, медиана
1.03Треугольник: задачи на подобие
1.04Прямоугольный треугольник и теорема Пифагора
1.05Треугольник: площадь и периметр
1.06Параллелограмм и его свойства
1.07Параллелограмм и свойство его биссектрисы
1.08Прямоугольник и его свойства
1.09Ромб и его свойства
1.10Квадрат и его свойства
1.11Трапеция и ее свойства
1.12Равнобедренная трапеция
1.13Окружность: центральный и вписанный углы
1.14Окружность: углы, образованные хордами, секущими, касательными
1.15Окружность: отрезки хорд, секущих, касательных
1.16Окружность: описанная около многоугольника
1.17Окружность: вписанная в многоугольник или угол
1.18Длина окружности или дуги и площадь круга или сектора
1.19Правильный шестиугольник и его свойства
1.20Площадь многоугольника: различные формулы
1.21Внешние углы многоугольника и тригонометрия
1.22Решение треугольника и других фигур с помощью тригонометрии
1.23Теорема синусов и теорема косинусов
1.24Координатная плоскость
1.25Векторы: сложение, вычитание, координаты
1.26Задачи на клетчатой бумаге
Решаем задачи
Радиус окружности, вписанной в ромб, равен Найдите сторону ромба, если один из его углов равен
Боковые стороны трапеции, описанной около окружности, равны и
Найдите среднюю линию трапеции.
Показать ответ и решение
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны. Следовательно, сумма
оснований трапеции равна сумме боковых сторон, то есть равна Так как средняя линия трапеции равна полусумме
оснований, то ответ:
Острый угол ромба равен радиус вписанной в этот ромб окружности равен
Найдите сторону ромба.
Радиус окружности, вписанной в правильный треугольник, равен Найдите сторону этого треугольника.
Сторона правильного треугольника равна Найдите радиус окружности, вписанной в этот треугольник.
Показать ответ и решение
1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также
являются высотами и медианами. Пусть — точка касания окружности со стороной
(то есть
— радиус).
Следовательно, (как часть высоты) и
(как часть медианы, так как медианы точкой пересечения делятся в
отношении считая от вершины).
Если то
следовательно,
тогда
2 способ.
Площадь правильного треугольника со стороной равна
Тогда по формуле
где
— полупериметр,
— радиус вписанной окружности, имеем:
К окружности, вписанной в треугольник проведены три касательные, параллельные сторонам треугольника. Периметры
отсеченных треугольников равны и
Найдите периметр треугольника
Показать ответ и решение
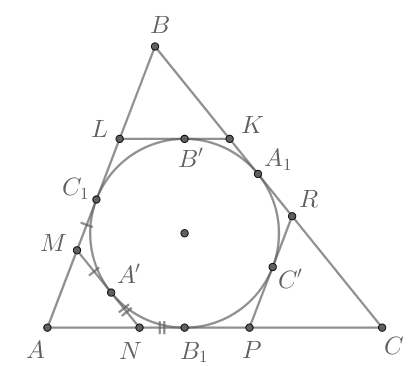
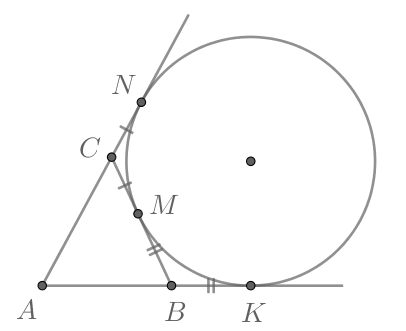
Рассмотрим рисунок. Пусть –= точки касания сторон треугольника
с окружностью.
— точки на
окружности, через которые проведены касательные параллельно сторонам треугольника. Получились треугольники
Пусть
Так как отрезки касательных, проведенных из одной точки к окружности, равны, то
Следовательно,
Аналогично для других треугольников:
Следовательно,
Около окружности, радиус которой равен описан прямоугольный треугольник, гипотенуза которого равна
Найдите
периметр этого треугольника.
Показать ответ и решение
Рассмотрим прямоугольный треугольник (
),
Пусть
— центр вписанной в него окружности. Пусть
также — точки касания на сторонах
соответственно.
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то
Заметим также, что радиусы и
перпендикулярны
и
соответственно (как радиусы, проведенные в точку
касания). Следовательно, — прямоугольник (четырехугольник, имеющий три прямых угла). Но т.к. его смежные стороны
равны, то это – квадрат. Следовательно,
Тогда периметр треугольника равен:
Показать ответ и решение
Пусть — центр окружности.
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
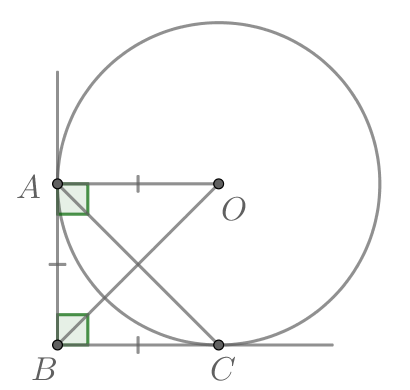
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник является равнобедренным, то есть
Т.к. отрезки касательных, проведенных из одной точки к
окружности, равны, то Следовательно, по теореме Пифагора
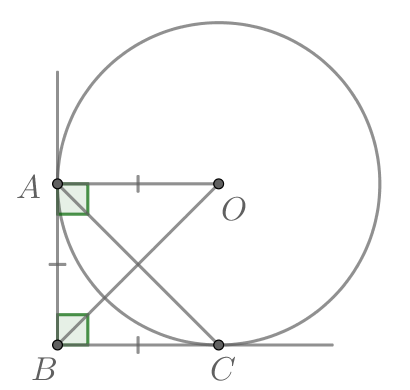
Показать ответ и решение
Пусть — центр окружности.
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник является равнобедренным, то есть
Т.к. отрезки касательных, проведенных из одной
точки к окружности, равны, то Следовательно, площадь прямоугольного треугольника
равна
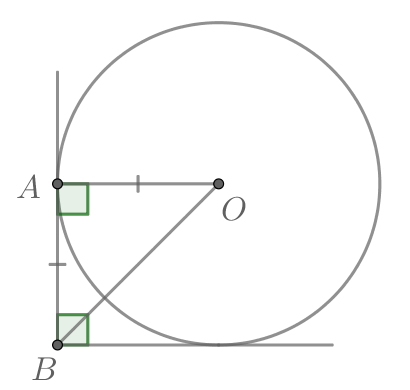
Показать ответ и решение
Обозначим одну из точек касания окружности и сторон угла за Пусть также
— центр окружности. То есть необходимо
найти
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда прямоугольный
треугольник является равнобедренным, то есть
По теореме Пифагора:
Показать ответ и решение
Обозначим точки касания окружности и сторон угла за и
Тогда известно, что
Пусть также
— центр
окружности.
Тогда — радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Рассмотрим треугольник он равнобедренный (
как отрезки касательных, проведенных из одной точки),
следовательно,
Таким образом, он равносторонний, следовательно,
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда из прямоугольного
треугольника
В треугольник вписана окружность с центром в точке
причем
Найдите
треугольника
Ответ
дайте в градусах.
Показать ответ и решение
Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то — биссектрисы углов
соответственно. Следовательно,
Также
Следовательно,
Боковые стороны равнобедренного треугольника равны основание равно
Найдите радиус вписанной окружности.
Показать ответ и решение
Известно, что для любого треугольника где
— полупериметр,
— радиус вписанной окружности. В нашем случае по
формуле Герона (полупериметр )
Следовательно,
В треугольнике
угол
равен
Найдите радиус вписанной окружности.
Показать ответ и решение
Известно, что для любого треугольника где
— полупериметр,
— радиус вписанной окружности.
В нашем случае
Гипотенуза по теореме Пифагора равна следовательно,
Сторона ромба равна острый угол равен
Найдите радиус окружности, вписанной в этот ромб.
Показать ответ и решение
Для любого многоугольника, в который можно вписать окружность, верно где
— полупериметр, а
— радиус
вписанной окружности.
где — сторона ромба,
— его угол.
Следовательно,
Полупериметр ромба равен Тогда
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как Найдите
большую сторону этого четырехугольника, если известно, что его периметр равен
Показать ответ и решение
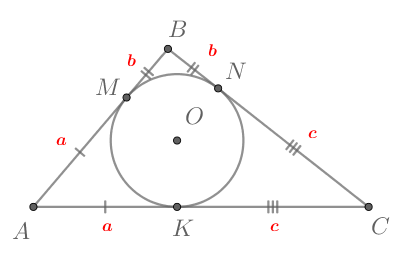
Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны.
Следовательно, четвертая сторона равна Тогда можно составить уравнение:
(большая сторона равна )
В ромб со стороной вписана окружность. Найдите радиус этой окружности, если площадь ромба равна
Показать ответ и решение
Пусть дан ромб
— центр окружности, вписанной в этот ромб. Т.к. центр окружности, вписанной в
многоугольник, лежит на пересечении биссектрис его углов, то — точка пересечения диагоналей ромба (т.к. они являются
биссектрисами углов ромба). Пусть — точка касания окружности со стороной
Тогда
— радиус окружности.
Рассмотрим треугольники и
Они подобны по двум углам. Следовательно,
Т.к. площадь ромба равна полупроизведению диагоналей, то
Отсюда Следовательно,
Показать ответ и решение
Обозначим точки касания окружности и сторон угла за и
Тогда известно, что
Пусть также
— центр
окружности. То есть необходимо найти
— радиус окружности, причем
(т.к.
— касательная, а радиус, проведенный в точку касания,
перпендикулярен касательной).
Рассмотрим треугольник он равнобедренный (
как отрезки касательных, проведенных из одной точки),
следовательно,
Таким образом, он равносторонний, следовательно,
Т.к. окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, то есть Тогда из прямоугольного
треугольника
Показать ответ и решение
Рассмотрим рисунок:
Т.к. отрезки касательных, проведенных из одной точки, равны, то
Таким образом,
периметр
Следовательно,
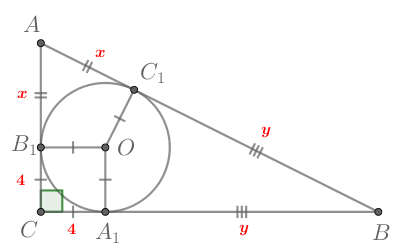
Показать ответ и решение
1) Пусть в треугольнике
Таким образом, наибольшей стороной будет или
или
Т.к. отрезки касательных, проведенных из одной точки к окружности, равны, то
(где
— точки касания).
Таким образом, из условия следует, что
Решая систему из этих двух уравнений, находим,
что
2) Заметим, что полупериметр данного треугольника равен а площадь по формуле Герона
равна
Тогда по формуле (площадь равна полупериметру, умноженному на радиус вписанной окружности) имеем:
откуда Следовательно,
Значит, большая сторона равна
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Окружность, вписанная в многоугольник или угол
Окружность называется вписанной в выпуклый многоугольник/угол, если она касается всех сторон этого многоугольника/угла.
Тогда многоугольник/угол называется описанным около окружности.
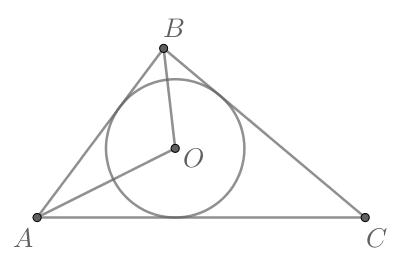
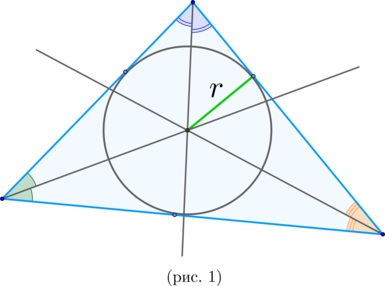
(blacktriangleright) В любой треугольник можно вписать окружность. Ее центр лежит на пересечении биссектрис треугольника (рис. 1).
Площадь описанного треугольника ищется по формуле [{Large{S_{triangle}=pcdot r}},]
где (p) – полупериметр.
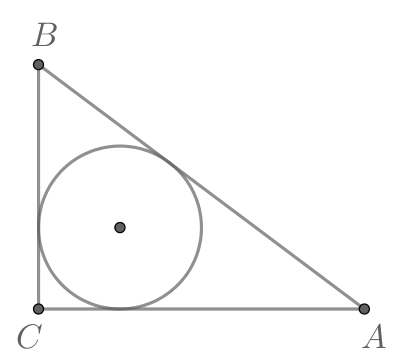
(blacktriangleright) Если в прямоугольный треугольник вписана окружность, (a, b) – катеты, (c) – гипотенуза, (r) – радиус этой окружности, то верна формула: [{large{r=dfrac{a+b-c}2}}] 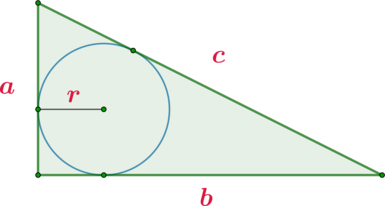
(blacktriangleright) Если в выпуклый четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
И наоборот: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность (рис. 2).
Центр вписанной окружности лежит на пересечении биссектрис углов.
Площадь описанного четырехугольника ищется по формуле
[{large{S_{text{опис.4-к}}=pcdot r}},]
где (p) – полупериметр.
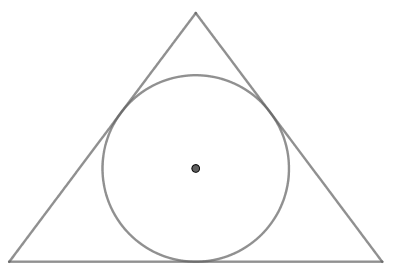
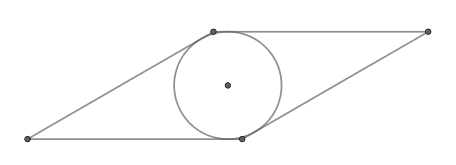
(blacktriangleright) Если в параллелограмм вписана окружность, то он – ромб (рис. 3).
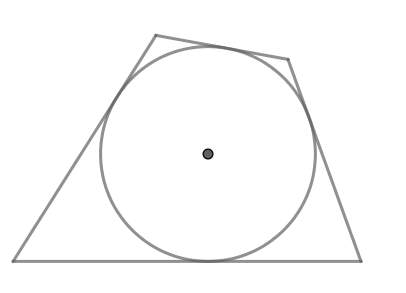
(blacktriangleright) Если в прямоугольник вписана окружность, то он – квадрат (рис. 4).
(blacktriangleright) Если в угол вписана окружность, то ее центр лежит на биссектрисе этого угла (рис. 5).
Задание
1
#3106
Уровень задания: Равен ЕГЭ
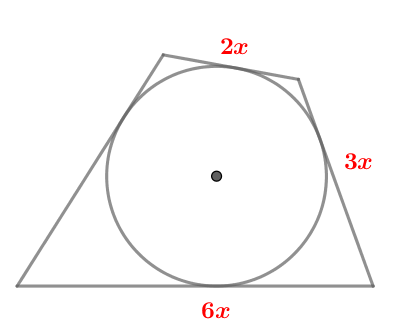
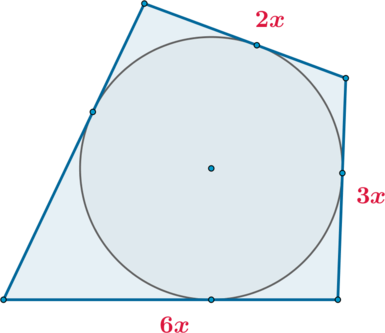
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как (2:3:6). Найдите большую сторону этого четырехугольника, если известно, что его периметр равен (54).
Рассмотрим рисунок. Так как четырехугольник описан около окружности, то суммы его противоположных сторон равны. Следовательно, четвертая сторона равна ((2x+6x)-3x=5x). Тогда можно составить уравнение: [2x+3x+6x+5x=54quadLeftrightarrowquad 6x=20,25] (большая сторона равна (6x))
Ответ: 20,25
Задание
2
#652
Уровень задания: Равен ЕГЭ
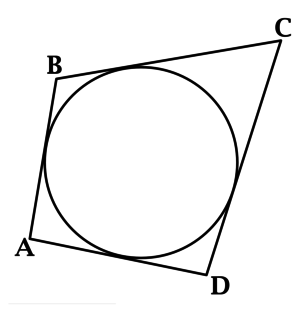
В четырёхугольник (ABCD) вписана окружность, (AB = 3,5), (AD = 4), (BC = 6,5). Найдите длину (CD).
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны:
(AB + CD = AD + BC), откуда получаем (3,5 + CD = 4 + 6,5), значит, (CD = 7).
Ответ: 7
Задание
3
#2375
Уровень задания: Равен ЕГЭ
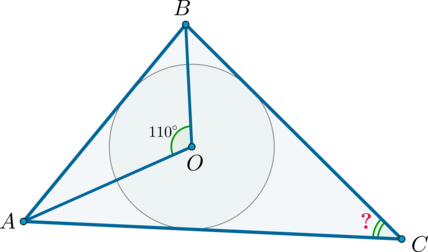
В треугольник (ABC) вписана окружность с центром в точке (O), причем (angle AOB=110^circ). Найдите (angle C) треугольника (ABC). Ответ дайте в градусах.
Т.к. центр вписанной окружности лежит на пересечении биссектрис углов треугольника, то (AO, BO) – биссектрисы углов (A, B) соответственно.
Следовательно, (angle BAO+angle
ABO=180^circ-110^circ=70^circ).
Также (angle A+angle B=2cdot (angle BAO+angle ABO)=140^circ), следовательно, (angle C=180^circ-(angle A+angle
B)=180^circ-140^circ=40^circ).
Ответ: 40
Задание
4
#3569
Уровень задания: Равен ЕГЭ
Боковые стороны равнобедренного треугольника равны (5), основание равно (6). Найдите радиус вписанной окружности.
Известно, что для любого треугольника (S_{triangle}=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности.
В нашем случае по формуле Герона (полупериметр (p=8)) (S_{triangle}=sqrt{8cdot 3cdot 3cdot 2}=4cdot 3=12). Следовательно, [r=dfrac Sp=dfrac{12}{0,5(5+5+6)}
= 1,5]
Ответ: 1,5
Задание
5
#3560
Уровень задания: Равен ЕГЭ
Около окружности, радиус которой равен (3), описан многоугольник, периметр которого равен (20). Найдите его площадь.
Так как для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности, то [S=dfrac{20}2cdot 3=30]
Ответ: 30
Задание
6
#3561
Уровень задания: Равен ЕГЭ
Сторона правильного треугольника равна (sqrt3). Найдите радиус окружности, вписанной в этот треугольник.
1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также являются высотами и медианами. Пусть (H) – точка касания окружности со стороной (AB) (то есть (OH) – радиус). Следовательно, (OHperp AB) (как часть высоты) и (OH=frac13CH) (как часть медианы, так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины).
Если (AC=2x=sqrt3), то (AH=x), следовательно, (CH=sqrt{4x^2-x^2}=xsqrt3), тогда [OH=dfrac13cdot CH=dfrac13cdot sqrt3cdot dfrac{sqrt3}2=0,5]
2 способ.
Площадь правильного треугольника со стороной (a) равна (S=dfrac{sqrt3}4a^2). Тогда по формуле (S=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности, имеем: [r=dfrac Sp=dfrac{frac{sqrt3}4cdot (sqrt3)^2}{0,5(sqrt3+sqrt3+sqrt3)}
=0,5]
Ответ: 0,5
Задание
7
#3562
Уровень задания: Равен ЕГЭ
Радиус окружности, вписанной в правильный треугольник, равен (dfrac{sqrt3}6). Найдите сторону этого треугольника.
1 способ.
Центр вписанной окружности лежит на пересечении биссектрис. Так как треугольник правильный, то его биссектрисы также являются высотами и медианами. Пусть (H) – точка касания окружности со стороной (AB) (то есть (OH) – радиус). Следовательно, (OHperp AB) (как часть высоты) и (OH=frac13CH) (как часть медианы, так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины).
Если (AC=2x), то (AH=x), следовательно, (CH=sqrt{4x^2-x^2}=xsqrt3), тогда [dfrac{sqrt3}6=OH=dfrac13cdot CH=dfrac{sqrt3}3xquadRightarrowquad
x=dfrac12quadRightarrowquad AC=2x=1]
2 способ.
Площадь правильного треугольника со стороной (a) равна (S=dfrac{sqrt3}4a^2). Тогда по формуле (S=pcdot r), где (p) – полупериметр, (r) – радиус вписанной окружности, имеем: [dfrac{sqrt3}4a^2=dfrac{3a}2cdot rquadRightarrowquad a=2sqrt3r=1]
Ответ: 1
На этапе подготовки к ЕГЭ старшеклассники повторяют базовые определения и формулы, в том числе и по теме «Окружность, вписанная в многоугольник или угол». Достаточно подробное изучение данного раздела планиметрии осуществляется, как правило, в средней школе. В связи с этим необходимость повторения основных формул и понятий по теме «Окружность, вписанная в угол или многоугольник» на этапе подготовки к ЕГЭ возникает у многих выпускников. Поняв принцип решения подобных заданий, старшеклассники смогут рассчитывать на получение достаточно высоких баллов по итогам сдачи единого государственного экзамена.
Готовьтесь к ЕГЭ вместе с образовательным порталом «Школково»
Занимаясь перед прохождением аттестационного испытания, многие старшеклассники сталкиваются с проблемой поиска базовых понятий и формул для нахождения радиуса окружности, вписанной в правильный многоугольник, и других параметров. Далеко не всегда их легко найти в Интернете, как и, например, задачи на правильный шестиугольник. А школьного учебника может просто не оказаться под рукой в нужное время. Для того чтобы ликвидировать пробелы в знаниях по этому и другим математическим разделам, обратитесь к образовательному проекту «Школково». На нашем сайте представлен весь необходимый материал, изложенный доступно и понятно. Какими свойствами обладает окружность, вписанная в угол и многоугольник, и какие формулы необходимо знать для успешного решения задач по данной теме? Ответы на эти и другие вопросы вы найдете на сайте «Школково» в разделе «Теоретическая справка».
Чтобы подготовка к единому госэкзамену была действительно эффективной, рекомендуем также попрактиковаться в решении соответствующих задач. Большая база заданий представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
31
Май 2013
Категория: 01 Геометрия
01. Вписанная окружность
2013-05-31
2022-09-11
Задача 1. Периметр треугольника равен а радиус вписанной окружности равен
Найдите площадь этого треугольника.
Решение: + показать
Задача 2. Площадь треугольника равна а радиус вписанной окружности равен
Найдите периметр этого треугольника.
Решение: + показать
Задача 3. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна
Решение: + показать
Задача 4. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Решение: + показать
Задача 5. Радиус окружности, вписанной в правильный треугольник, равен Найдите сторону этого треугольника.
Решение: + показать
Задача 6. Около окружности, радиус которой равен описан многоугольник, периметр которого равен
Найдите его площадь.
Решение: + показать
Задача 7. В четырехугольник вписана окружность,
Найдите периметр четырехугольника.
Решение: + показать
Задача 8. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
Решение: + показать
Задача 9. Сторона ромба равна острый угол равен
˚. Найдите радиус вписанной окружности этого ромба.
Решение: + показать
Задача 10. Найдите высоту трапеции, в которую вписана окружность радиуса
Решение: + показать
Задача 11. Боковые стороны трапеции, описанной около окружности, равны и
Найдите среднюю линию трапеции.
Решение: + показать
Задача 12. Периметр прямоугольной трапеции, описанной около окружности, равен ее большая боковая сторона равна
Найдите радиус окружности.
Решение: + показать
Задача 13. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Решение: + показать
Задача 14. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Решение: + показать
Задача 15. Катеты равнобедренного прямоугольного треугольника равны Найдите радиус окружности, вписанной в этот треугольник.
Решение: + показать
Задача 16. В треугольнике стороны
угол
равен
°. Найдите радиус вписанной окружности.
Решение: + показать
Задача 17. Боковые стороны равнобедренного треугольника равны основание равно
Найдите радиус вписанной окружности.
Решение: + показать
Задача 18. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны и
считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение: + показать
Задача 19. К окружности, вписанной в треугольник проведены три касательные. Периметры отсеченных треугольников равны
Найдите периметр данного треугольника.
Решение: + показать
Вы можете пройти тест по теме «Окружность и многоугольник»
Автор: egeMax |
комментариев 12