Регистрация Форум Текущее время: 10 мар 2023, 22:13 Сообщения без ответов | Активные темы Страница 1 из 2 [ Сообщений: 15 ] На страницу 1, 2 След. Начать новую тему»> Ответить Тренировочный вариант №413
Тренировочный вариант №413
Страница 1 из 2 [ Сообщений: 15 ] На страницу 1, 2 След. Текущее время: 10 мар 2023, 22:13 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|
На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023
Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы Решение и ответы на задачи на официальном сайте источника онлайн.
Вариант 413 и вариант 414 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, а
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d0%bb%d0%b0%d1%80%d0%b8%d0%bd-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-413-%d0%b8-414-%d0%b5%d0%b3%d1%8d-2023-%d0%bf%d1%80%d0%be%d1%84%d0%b8%d0%bb%d1%8c-%d0%bf%d0%be-%d0%bc%d0%b0%d1%82%d0%b5%d0%bc/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Диагностические и тренировочные варианты СтатГрад ЕГЭ База по математике с ответами
22.09.2016
10101-22.09.2016
10102-22.09.2016
10103-22.09.2016
10104-22.09.2016
10105-22.09.2016
10106-22.09.2016
10107-22.09.2016
10108-22.09.2016
20.12.2016
10201-20.12.2016
10202-20.12.2016
10203-20.12.2016
10204-20.12.2016
10205-20.12.2016
10206-20.12.2016
10207-20.12.2016
10208-20.12.2016
26.01.2017
10301-26.01.2017
10302-26.01.2017
10303-26.01.2017
10304-26.01.2017
10305-26.01.2017
10306-26.01.2017
10307-26.01.2017
10308-26.01.2017
06.03.2017
10601-06.03.2017
10602-06.03.2017
10603-06.03.2017
10604-06.03.2017
10605-06.03.2017
10606-06.03.2017
10607-06.03.2017
10608-06.03.2017
21.04.2017
10701-06.03.2017
10702-06.03.2017
10703-06.03.2017
10704-06.03.2017
10705-06.03.2017
10706-06.03.2017
10707-06.03.2017
10708-06.03.2017
21.09.2017
10101-21.09.2017
10102-21.09.2017
10103-21.09.2017
10104-21.09.2017
10105-21.09.2017
10106-21.09.2017
10107-21.09.2017
10108-21.09.2017
21.12.2017
10201-21.12.2017
10202-21.12.2017
10203-21.12.2017
10204-21.12.2017
10205-21.12.2017
10206-21.12.2017
10207-21.12.2017
10208-21.12.2017
25.01.2018
10301-25.01.2018
10302-25.01.2018
10303-25.01.2018
10304-25.01.2018
10305-25.01.2018
10306-25.01.2018
10307-25.01.2018
10308-25.01.2018
06.03.2018
10401-06.03.2018
10402-06.03.2018
10403-06.03.2018
10404-06.03.2018
10405-06.03.2018
10406-06.03.2018
10407-06.03.2018
10408-06.03.2018
18.04.2018
10501-18.04.2018
10502-18.04.2018
10503-18.04.2018
10504-18.04.2018
10505-18.04.2018
10506-18.04.2018
10507-18.04.2018
10508-18.04.2018
20.09.2018
10101-20.09.2018
10102-20.09.2018
10103-20.09.2018
10104-20.09.2018
10105-20.09.2018
10106-20.09.2018
10107-20.09.2018
10108-20.09.2018
20.12.2018
10201-20.12.2018
10202-20.12.2018
10203-20.12.2018
10204-20.12.2018
10205-20.12.2018
10206-20.12.2018
10207-20.12.2018
10208-20.12.2018
24.01.2019
10301-24.01.2019
10302-24.01.2019
10303-24.01.2019
10304-24.01.2019
10305-24.01.2019
10306-24.01.2019
10307-24.01.2019
10308-24.01.2019
13.03.2019
10401-13.03.2019
10402-13.03.2019
10403-13.03.2019
10404-13.03.2019
10405-13.03.2019
10406-13.03.2019
10407-13.03.2019
10408-13.03.2019
19.04.2019
10501-19.04.2019
10502-19.04.2019
10503-19.04.2019
10504-19.04.2019
10505-19.04.2019
10506-19.04.2019
10507-19.04.2019
10508-19.04.2019
17.05.2019
10501-17.05.2019
10502-17.05.2019
10503-17.05.2019
10504-17.05.2019
10505-17.05.2019
10506-17.05.2019
10507-17.05.2019
10508-17.05.2019
25.09.2019
1910101-25.09.2019
1910102-25.09.2019
1910103-25.09.2019
1910104-25.09.2019
1910105-25.09.2019
1910106-25.09.2019
1910107-25.09.2019
1910108-25.09.2019
18.12.2019
1910201-18.12.2019
1910202-18.12.2019
1910203-18.12.2019
1910204-18.12.2019
1910205-18.12.2019
1910206-18.12.2019
1910207-18.12.2019
1910208-18.12.2019
29.01.2020
1910301-29.01.2020
1910302-29.01.2020
1910303-29.01.2020
1910304-29.01.2020
1910305-29.01.2020
1910306-29.01.2020
1910307-29.01.2020
1910308-29.01.2020
06.02.2020 (10 класс)
1900201-06.02.2020
1900202-06.02.2020
1900203-06.02.2020
1900204-06.02.2020
1900205-06.02.2020
1900206-06.02.2020
1900207-06.02.2020
1900208-06.02.2020
12.02.2020 (10 Триклассгонометрия)
1900401-12.02.2020
1900402-12.02.2020
11.03.2020
1910401-11.03.2020
1910402-11.03.2020
1910403-11.03.2020
1910404-11.03.2020
1910405-11.03.2020
1910406-11.03.2020
1910407-11.03.2020
1910408-11.03.2020
04.02.2020 (10 класс Теория вероятностей и статистика)
1900501-02.04.2020
1900502-02.04.2020
15.04.2020 (10 класс Итоговая уровневая работа)
1900601-15.04.2020
1900602-15.04.2020
22.04.2020
1910501-22.04.2020
1910502-22.04.2020
1910503-22.04.2020
1910504-22.04.2020
1910505-22.04.2020
1910506-22.04.2020
1910507-22.04.2020
1910508-22.04.2020
30.09.2020
2010101-30.09.2020
2010102-30.09.2020
2010103-30.09.2020
2010104-30.09.2020
2010105-30.09.2020
2010106-30.09.2020
2010107-30.09.2020
2010108-30.09.2020
16.12.2020
2010201-16.12.2020
2010202-16.12.2020
2010203-16.12.2020
2010204-16.12.2020
2010205-16.12.2020
2010206-16.12.2020
2010207-16.12.2020
2010208-16.12.2020
28.09.2021
2110101-28.09.2021
2110102-28.09.2021
2110103-28.09.2021
2110104-28.09.2021
2110105-28.09.2021
2110106-28.09.2021
2110107-28.09.2021
2110108-28.09.2021
15.12.2021
2110201-15.12.2021
2110202-15.12.2021
2110203-15.12.2021
2110204-15.12.2021
2110205-15.12.2021
2110206-15.12.2021
2110207-15.12.2021
2110208-15.12.2021
27.01.2022
2100101-27.01.2022
2100102-27.01.2022
2100103-27.01.2022
2100104-27.01.2022
2100105-27.01.2022
2100106-27.01.2022
2100107-27.01.2022
2100108-27.01.2022
16.02.2022
2110301-16.02.2022
2110302-16.02.2022
2110303-16.02.2022
2110304-16.02.2022
2110305-16.02.2022
2110306-16.02.2022
2110307-16.02.2022
2110308-16.02.2022
15.03.2022
2110401-15.03.2022
2110402-15.03.2022
2110403-15.03.2022
2110404-15.03.2022
2110405-15.03.2022
2110406-15.03.2022
2110407-15.03.2022
2110408-15.03.2022
28.04.2022
2110501-28.04.2022
2110502-28.04.2022
2110503-28.04.2022
2110504-28.04.2022
2110505-28.04.2022
2110506-28.04.2022
2110507-28.04.2022
2110508-28.04.2022
18.05.2022
2100301-18.05.2022
2100302-18.05.2022
2100303-18.05.2022
2100304-18.05.2022
2100305-18.05.2022
2100306-18.05.2022
2100307-18.05.2022
2100308-18.05.2022
28.09.2022
2210101-28.09.2022
2210102-28.09.2022
2210103-28.09.2022
2210104-28.09.2022
2210105-28.09.2022
2210106-28.09.2022
2210107-28.09.2022
2210108-28.09.2022
13.12.2022
2210201-13.12.2022
2210202-13.12.2022
2210203-13.12.2022
2210204-13.12.2022
2210205-13.12.2022
2210206-13.12.2022
2210207-13.12.2022
2210208-13.12.2022
08.02.2023 (10 класс)
2200101-08.02.2023
2200102-08.02.2023
2200103-08.02.2023
2200104-08.02.2023
2200105-08.02.2023
2200106-08.02.2023
2200107-08.02.2023
2200108-08.02.2023
28.02.2023
2210301-28.02.2023
2210302-28.02.2023
2210303-28.02.2023
2210304-28.02.2023
2210305-28.02.2023
2210306-28.02.2023
2210307-28.02.2023
2210308-28.02.2023
Задание 1
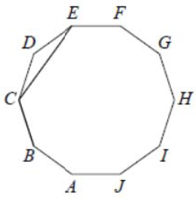
ABCDEFGHIJ — правильный десятиугольник. Найдите угол ВСЕ. Ответ дайте в градусах.
Ответ: 126
Скрыть
Вокруг любого правильного многоугольника можно описать окружность.
Центральный угол EOB равен $$frac{360^{circ}}{10}cdot3=108^{circ}$$.
Тогда большая дуга EB равна $$360^{circ}-108^{circ}=252^{circ}$$.
Угол BCE опирается на ту же дугу EB, но является вписанным, поэтому равен половине дуги EB, т. е. $$126^{circ}$$.
Задание 2
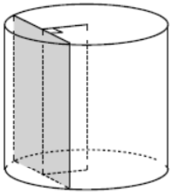
Радиус основания цилиндра равен 10, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 8. Найдите площадь этого сечения.
Ответ: 216
Скрыть
Для удобства введем буквенные обозначения: О – центр основания цилиндра, DA и СВ – образующие цилиндра, ОН – расстояние от оси до сечения.
Сечение представляет собой прямоугольник, площадь которого равна произведению двух его смежных сторон, а именно:
S = АВ · DA
DA – образующая цилиндра, следовательно DA = 18,
Найдем АВ. Для этого рассмотрим треугольник ОНА. Данный треугольник прямоугольный (с прямым углом Н). Так же в треугольнике известны катет ОН = 8 и гипотенуза OA = 10 (ОА – радиус основания).
По теореме Пифагора найдем катет, АН:
АН2 = ОА2 — ОН2 = 102 – 82 = 36
АН = 6
АВ = АН + ВН, так как АН = ВН = 6, то
АВ = 6 + 6 = 12
Осталось найти площадь сечения:
S = АВ · DA = 12 · 18 = 216 – площадь сечения
Задание 3
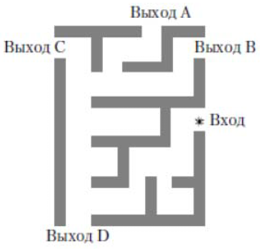
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу D.
Ответ: 0,25
Скрыть
$$P(A)=frac{1}{2}cdotfrac{1}{2}=frac{1}{4}=0,25$$
Задание 4
Турнир по настольному теннису проводится по олимпийской системе в несколько туров: если в туре участвует чётное число игроков, то они разбиваются на случайные игровые пары. Если число игроков нечётно, то с помощью жребия выбираются случайные игровые пары, а один игрок остаётся без пары и не участвует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из турнира, а победители и игрок без пары, если он есть, выходят в следующий тур, который проводится по таким же правилам. Так продолжается до тех пор, пока не останутся двое, которые играют между собой финальный тур, то есть последнюю партию, которая выявляет победителя турнира. Всего в турнире участвует 25 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придётся сыграть друг с другом?
Ответ: 0,08
Скрыть
Пусть $$n$$ — число участников.
Всего возможных пар игроков:
$$binom{2}{n}=frac{n!}{2!cdot(n-1)!}=frac{n(n-1)}{2}$$.
Значит, вероятность, что в какой-то одной любой игре будет нужная нам пара игроков:
$$(frac{n(n-1)}{2})^{-1}=frac{2}{n(n-1)}$$.
Так как изначально было $$n$$ игроков и ровно один после каждой игры выбывает, то всего игр будет:
$$n-1$$.
Так как во всех играх вероятность выпадения нужной нам пары игроков одинакова, то искомая вероятность:
$$frac{2}{n(n-1)}cdot(n-1)=frac{2}{n}$$.
$$P(A)=frac{2}{25}=0,08$$
Задание 5
Решите уравнение $$tgfrac{pi(x+1)}{3}=-sqrt{3}$$. В ответе укажите наименьший положительный корень.
Ответ: 1
Скрыть
$$tgfrac{pi(x+1)}{3}=-sqrt{3}Rightarrowfrac{pi(x+1)}{3}=-frac{pi}{3}+pi nRightarrow x+1=-1+3nRightarrow x=-2+3n$$
$$left{begin{matrix} -2+3n>0\ nto min \ nin Z end{matrix}right.Rightarrowleft{begin{matrix} n>frac{2}{3}\ nto min\ nin Z end{matrix}right.Rightarrow n=1:quad x=-2+3cdot1=1$$
Задание 6
Найдите значение выражения $$7cos(pi+beta)-2sin(frac{pi}{2}+beta)$$, если $$cosbeta=-frac{1}{3}$$.
Ответ: 3
Скрыть
$$7cos(pi+beta)-2sin(frac{pi}{2}+beta)=-7cosbeta-2cosbeta=-9cosbeta=-9cdot(-frac{1}{3})=3$$
Задание 7
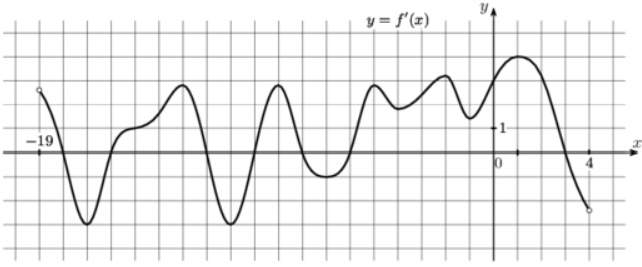
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x)$$, определенной на интервале (-19;4). Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку [-17;-1].
Ответ: 3
Скрыть
На графике производной точка минимума — точка пересечения оси Ox при возрастании графика.
$$-16; -10; -6Rightarrow 3$$ точки
Задание 8
Скорость колеблющегося на пружине груза меняется по закону $$v(t)=5sin(pi t)$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 2,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,67
Скрыть
$$5sinpi tgeq2,5$$
$$sinpi tgeq0,5$$
$$frac{pi}{6}+2pi nleqpi tleqfrac{5pi}{6}+2pi n$$
Так как просят в течении первой секунды, то $$n=0$$
$$frac{1}{6}leq tleqfrac{5}{6}$$
$$tau=frac{frac{5}{6}-frac{1}{6}}{1}=frac{2}{3}approx0,67$$
Задание 9
Учебный самолет летел со скоростью 800 км/час. Когда ему осталось пролететь на 90 км больше, чем он пролетел, пилот увеличил скорость до 900 км/час. Средняя скорость на всем пути оказалась равной 850 км/час. Какое расстояние (в км) пролетел самолет всего?
Ответ: 1530
Скрыть
Решение сводится к составлению линейного уравнения. Если принять за $$x$$ расстояние полета с начальной скоростью, тогда:
$$frac{x+x+90}{850}=frac{x}{800}+frac{x+90}{900}$$, т.е. мы уравняли время полета всего расстояния.
Решение (без вычислений НОЗ) приводит нас к такому «упрощенному» виду уравнения:
$$1440000x + 64800000 = 1445000x + 61200000$$ или
$$3600000 = 5000x$$ откуда
имеем $$x = 720, x + 90 = 810$$, а весь путь самолета $$= 1530$$ км.
Задание 10
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ: 10
Скрыть
Верхний проходит через $$(-1;4)$$ и $$(-3;3)$$. Тогда:
$$left{begin{matrix} 4=-1k+b\ 3=-3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} 1=2k\ 4=-0,5+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=0,5\ b=4,5 end{matrix}right.$$
$$y=0,5x+4,5$$
Нижний через $$(1;-4)$$ и $$(3;-1)$$. Тогда:
$$left{begin{matrix} -4=k+b\ -1=3k+b end{matrix}right.Leftrightarrowleft{begin{matrix} 3=2k\ -4=1,5+b end{matrix}right.Leftrightarrowleft{begin{matrix} k=1,5\ b=-5,5 end{matrix}right.$$
$$y=1,5x-5,5$$
Тогда:
$$0,5x+4,5=1,5x-5,5Rightarrow x=10$$
Задание 11
Найдите наименьшее значение функции $$y=x^5-80x$$ на отрезке [-4;-1].
Ответ: -704
Скрыть
$$y’=5x^4-80$$
$$5x^4-80=0$$
$$5x^4=80$$
$$x^4=16$$
$$x=pm2$$
$$x=2$$ — точка минимума по методу интервалов, но она не попадает в отрезок, проверяем значения концов отрезка.
$$y(-1)=79$$
$$y(-4)=-1024+320=-704$$
Задание 12
А) Решите уравнение $$tg2x=2cos2xcdotctg x$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-pi;frac{pi}{2}]$$
Ответ: А)$$pmfrac{pi}{6}+frac{2pi n}{3},nin Z$$ Б)$$-frac{5pi}{6};-frac{pi}{2};-frac{pi}{6};frac{pi}{6};frac{pi}{2}$$
Задание 13
Дан куб ABCDA1B1C1D1 с ребром длины 1. Точка Р — середина A1D1, точка Q делит отрезок АВ1 в отношении 2:1, считая от вершины А, R — точка пересечения отрезков ВС1 и В1С.
А) Найдите площадь сечения куба плоскостью PQR.
Б) Найдите отношение, в котором плоскость сечения делит диагональ АС1 куба.
Ответ: А) $$frac{sqrt{5}}{2}$$ Б) $$frac{2}{1}$$
Задание 14
Решите неравенство: $$8+log_{sqrt{x}}8leq4log_xsqrt{17x^2-2}$$
Ответ: $$(sqrt{frac{2}{17}};frac{1}{2sqrt{2}}],(1;sqrt{2}]$$
Задание 15
В июне 2025 года Анна Михайловна планирует взять кредит в банке на 3 года. Условия его. возврата таковы:
— в январе каждого года долг увеличивается на 10 % от суммы долга на конец предыдущего года;
— в период с февраля по июнь каждого из 2026 и 2027 годов необходимо выплатить часть долга, причём платёж 2027 года в 1,5 раза больше платежа предыдущего года;
— в период с февраля по июнь 2028 года выплачивается оставшаяся сумма по кредиту, равная 2 679 600 рублей.
Найдите сумму кредита, если сумма всех платежей составит 9 179 600 рублей.
Ответ: 7,6 млн
Задание 16
Первая окружность проходит через вершины А и В треугольника АВС и пересекает стороны АС и ВС в точках D и Е соответственно. Вторая окружность проходит через точки D и Е и пересекает продолжения сторон ВС и АС за вершину С в точках М и N соответственно.
А) Докажите, что прямая MN параллельна прямой АВ.
Б) Прямые MD и NE вторично пересекают первую окружность в точках Х и Y соответственно. Найдите ее радиус, если AX=XY=2, а АВ=4.
Ответ: 2
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых неравенство
$$-1leqsin xcdot(a-cos2x)leq1$$
верно при всех действительных значениях $$x$$.
Ответ: $$[1-frac{3}{sqrt[3]{2}};0]$$
Задание 18
В записи натурального числа $$n$$ сделаем замену цифр. Если цифра $$a > 0$$, то заменяем её на цифру $$(10 — a)$$, а если $$a = 0$$, то её не меняем. Обозначим полученное число через $$n^*$$.
А) Может ли быть $$n=10n^*$$?
Б) Какое наибольшее значение может принимать отношение $$frac{n}{n^*}$$?
В) Если $$n$$ делится на $$n^*$$, то чему может быть равно отношение $$frac{n}{n^*}$$?
Ответ: А) нет, Б) 9, В) 1;4;5;9
Пробные варианты ЕГЭ 2023 по математике (база) из различных источников.
Изменения в содержании КИМ отсутствуют.
Пробные варианты ЕГЭ 2023 по математике (база)
| Автор: Ширяева Е.А. | |
| Варианты 1-2 | ответы |
| Варианты 3-4 | ответы |
| Варианты 5-6 | |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| math100.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| yagubov.ru | |
| вариант 36 (декабрь) | yagubov23-ma-baza-var36 |
| вариант 35 (ноябрь) | yagubov23-ma-baza-var35 |
| вариант 34 (октябрь) | yagubov23-ma-baza-var34 |
| вариант 33 (сентябрь) | yagubov23-ma-baza-var33 |
| вариант 32 (август) | yagubov23-ma-baza-var32 |
Экзаменационная работа включает в себя 21 задание.
На выполнение работы отводится 3 часа (180 минут).
Все бланки ЕГЭ заполняются яркими чёрными чернилами.
Допускается использование гелевой или капиллярной ручки.
При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Связанные страницы:
Пробные варианты ЕГЭ 2023 по математике профильного уровня
Сборник задач по стереометрии для 10-11 классов
Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022
Тест по теме «Производная» 11 класс алгебра с ответами
Основные тригонометрические тождества и формулы
Контакты
ул. Чернышевского, д. 17, офис 33, Казань, Республика Татарстан, 420000, Россия
- +7 (920) 298-89-20
Меню
- Онлайн-тестирование
- Видеоуроки
- Библиотека школьной литературы
- Методический материал
- Сочинения
- Правообладателям

© 2015 — 2023 «Пять с Плюсом». Все права защищены




 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема