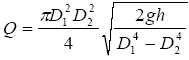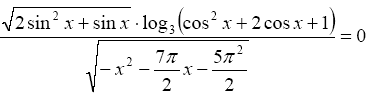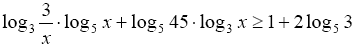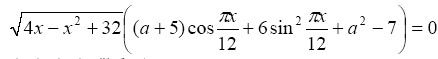Ответы на тренировочный вариант №189 профильного ЕГЭ
А. Ларин: Тренировочный вариант № 189.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Решите уравнение:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В четырехугольной пирамиде SABCD (четырехугольник в основании выпуклый) боковые ребра SA, SB и SC попарно перпендикулярны и имеют длину 3. Длина SD равна 9. Найдите
а) угол наклона ребра SD к плоскости основания.
б) наибольшее возможное при этих условиях значение объема пирамиды SABCD.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В правильный треугольник со стороной a вписан круг. В этот круг вписан правильный треугольник, в который вписан круг и так далее.
а) Доказать, что площади кругов образуют геометрическую прогрессию.
б) Найдите сумму площадей всех кругов.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
В банке купили монеты достоинством 1 дол., 1 евро и 1 фунт стерлингов. Всего 100 монет. Цена монет на день покупки составляла: 1 дол. — 32 руб., 1 евро — 40 руб., 1 фунт стерлингов — 50 руб. На всю покупку затратили 3930 руб. Какое максимальное количество долларов могло быть куплено?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях a уравнение
имеет ровно 4 решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Заданы три бесконечных целочисленных возрастающих арифметических прогрессий, разность которых 3, 5 и 7, каждая из которых содержит хотя бы одно отрицательное число. Натуральное число «n» назовем хорошим, если оно принадлежит всем прогрессиям.
а) Доказать, что существует хотя бы одно хорошее число.
б) Можно ли утверждать, что для любых прогрессий существует хорошее число на отрезке [100; 200]?
в) Можно ли утверждать, что для любых прогрессий существует хорошее число на отрезке [200; 400]?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Задание 1
Найдите значение выражения $$15*(frac{1}{3})^{2}-3frac{2}{3}$$
Ответ: -2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$15*(frac{1}{3})^{2}-3frac{2}{3}=$$$$15*frac{1}{9}-frac{11}{3}=$$$$5*frac{1}{3}-frac{11}{3}=$$$$frac{5-11}{3}=-2$$
Задание 2
Для квартиры площадью 62 кв. м заказан натяжной потолок белого цвета. Стоимость материалов с учётом работ по установке натяжных потолков приведена в таблице.
|
Цвет потолка |
Цена в рублях за 1 м2 (в зависмости от площали помещения) |
|||
|
до 10 м2 |
от 11 до 30 м2 |
от 31 до 60 м2 |
свыше 60 м2 |
|
|
белый |
1200 |
1000 |
800 |
600 |
|
цветной |
1350 |
1150 |
950 |
750 |
Какова стоимость заказа, если действует сезонная скидка в 5%?
Варианты ответа
1. 37200 рублей
2. 45000 рублей
3. 35340 рублей
4. 47120 рублей
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем стоимость за 62 м2: 600* 62=37200 рублей
Найдем скидку:37200*0,05=1860 рублей
Итого: 37200-1860=35340 рублей, что соответствует 3 варианту ответа
Задание 3
На координатной прямой отмечены числа x, y, z
Какая из разностей отрицательна?
Варианты ответа
1. z-x
2. z-y
3. y-x
4. ни одна из них
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Учтем,что x0; z-y>0; y-x>0. Получили, что нет ни одного отрицательного значения, следовательно, ответом будет вариант 4
Задание 4
Найдите значение выражения $$frac{26}{(5sqrt{13})^{2}}$$
Ответ: 0,08
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{26}{(5sqrt{13})^{2}}=$$$$frac{26}{25*13}=frac{2}{25}=0,08.$$
Задание 5
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1,2 B – в 9 часов, 0,8 B-19 ч. 19-9=10(ч)
Задание 6
Решите уравнение $$(5-x)^{2}=(11-x)^{2}$$
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(5-x)^{2}=(11-x)^{2}$$ $$(5-x-(11-x))(5x+(11-x))=0$$ $$-6*(16-2x)-0$$ $$16-2x-0$$ $$x=8$$
Задание 7
В начале года число абонентов телефонной компании «Юг» составляло 1 миллион 200 тысяч человек, а в конце года их стало 1 миллион 584 тысячи человек. На сколько процентов увеличилось за год число абонентов этой компании?
Ответ: 32
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1,2 млн.-100% 1,584 млн.-x% $$x=frac{1,584 *100}{1,2}=1,32*100=132$$% 132-100=32%- изменение
Задание 8
На диаграмме показано содержание питательных веществ в творожных сырках. Определите по диаграмме содержание каких веществ превосходит 30%
*к прочему относятся вода, витамины и минеральные вещества
Варианты ответа
1. белки
2. жиры
3. углеводы
4. прочее
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
30% — сектор немного меньший, чем треть круга. Следовательно, более 30% составляют вещества из категории «прочее», то есть ответ будет под пунктом 4
Задание 9
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 2, но не дойдя до отметки 5.
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
С 2 до 5 сектор составляет $$frac{5-2}{12}$$ круга. Т.е. и вероятность будет $$frac{3}{12}=0,25$$
Задание 10
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
КОЭФФИЦИЕНТЫ
1) k<0, b<0
2) k>0, b>0
3) k>0, b<0
В таблице под каждой буквой укажите соответствующий номер.
Ответ: 231
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
k>0-возрастает ,k<0-убывает,b>0- Oy пересекает над Ox, b<0-под Ox,тогда А2 Б3 В1.
Задание 11
Дана арифметическая прогрессия: 12, 9, 6,… . Какое число стоит в этой последовательности на 6-м месте?
Ответ: -3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$a_{1}=12 $$. Найдем разность арифметической прогрессии: $$d=9-12=-3$$ Найдем 6ой член данной прогрессии: $$a_{6}=12-3(6-1)=12-15=-3.$$
Задание 12
Найдите значение выражения $$frac{a-7b}{a}:frac{7b^{2}-ab}{a^{2}}$$, при $$a=-9;b=6$$
Ответ: 1,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{a-7b}{a}:frac{7b^{2}-ab}{a^{2}}=$$$$frac{a-7b}{a}*frac{a^{2}}{b(7b*a)}=$$$$-frac{a}{b}=-frac{-9}{6}=1,5.$$
Задание 13
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой $$t_{f}=1,8t_{c}+32$$ , где tc — температура в градусах Цельсия, tf — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует − 85 градусов по шкале Цельсия?.
Ответ: -121
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$t_{F}=1,8*(-85)+32=-153+32=-121$$
Задание 14
Укажите промежуток, являющийся решением системы неравенств $$left{begin{matrix} 3x-9<0\ 2-3x>-10 end{matrix}right.$$
Варианты ответа
- $$(-infty ;+infty )$$
- $$(-infty ;4)$$
- $$(3 ;4 )$$
- $$(-infty ;3 )$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$left{begin{matrix}3x-9<0\2-3x>-10end{matrix}right.Leftrightarrow$$$$ left{begin{matrix}3x<9\2+10>3xend{matrix}right.Leftrightarrow$$$$ left{begin{matrix}x<3\x<4end{matrix}right.Rightarrow xin (-infty ;3 )$$
Данный ответ соответствует 4 варианту.
Задание 15
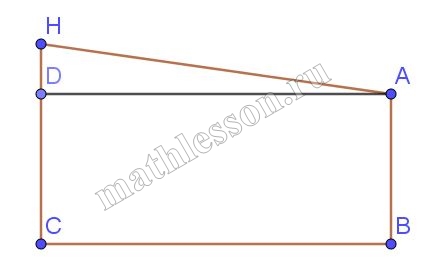
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
DC=AB=3; AD=BC=8;
Тогда из $$Delta HAD: HD=sqrt{10^{2}-8^{2}}=6$$
HC=HD+DC=9.
Задание 16
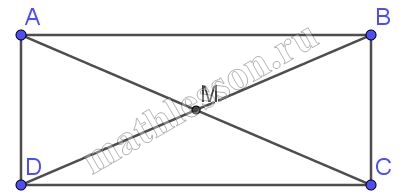
Диагональ прямоугольника образует угол 52 с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Ответ: 76
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$angle ADM=angle DAM=52$$
Из $$Delta AMB :angle M=180-2*52=76.$$
Задание 17
В треугольнике ABC BM – медиана и BH –высота. Известно, что AC=42 и BC=BM. Найдите AH.
Ответ: 31,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$BC=BMRightarrow Delta BMC$$-равнобедренный $$Rightarrow BH$$-медиана $$Rightarrow MH=HC=frac{1}{2}MC=frac{1}{2}*frac{1}{2}AC.$$ Т.е. $$MH=frac{1}{4}*42=10,5 ; AM=21Rightarrow AH=31,5.$$
Задание 18
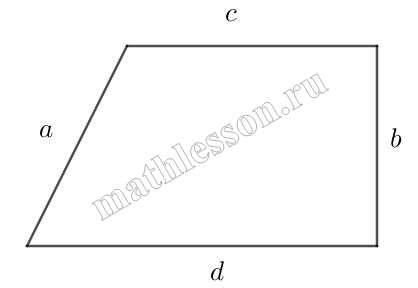
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Раз вписана окружность , то a+b=c+d=18
2) $$m=frac{c+d}{2}=9$$- средняя линия
Задание 19
Катеты прямоугольного треугольника равны $$3sqrt{11}$$ и 1. Найдите синус наименьшего угла этого треугольника.
Ответ: 0,1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)$$angle A<angle B$$, т.к. $$CB<AC$$
2)Найдем $$AB=sqrt{(3sqrt{11})^{2}+1^{2}}=sqrt{100}=10.$$
3) $$sin angle A =frac{CB}{AB}=frac{1}{10}=0,1.$$
Задание 20
Какие из следующих утверждений верны?
1. Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2. Сумма противолежащих углов параллелограмма равна 180°
3. Сумма углов тупоугольного треугольника равна 180°.
Ответ: 13
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. верно 2. неверно( они равны) 3.верно
Задание 21
Найдите значение выражения: $$frac{sqrt{97+56sqrt{3}}}{sqrt{7+4sqrt{3}}}*sqrt{7+4sqrt{3}}$$
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{sqrt{97+56sqrt{3}}}{sqrt{7+4sqrt{3}}}*sqrt{7-4sqrt{3}}$$ Выделим полный квадрат из $$97 +56sqrt{3}$$ $$left{begin{matrix}a^{2}+b^{2} =97\2ab=56sqrt{3}end{matrix}right.Leftrightarrow$$$$left{begin{matrix}a^{2}+b^{2}=97(1)\ab=28 sqrt{3}end{matrix}right.$$ $$28sqrt{3}=2*2*7*sqrt{3}$$, пусть a = 7 , тогда $$b=4sqrt{3}.$$ Выполним выполнение равенства(1): $$7^{2}+(4sqrt{3})^{2}=49+48=97$$ –верно, тогда $$97+56*sqrt{3}=(7+4sqrt{3})^{2}.$$ Получим: $$sqrt{frac{(7+4sqrt{3})^{2}}{7+4sqrt{3}}*(7-4sqrt{3})}=$$$$sqrt{(7+4sqrt{3})(7-4sqrt{3})}=sqrt{49-48}=1.$$
Задание 22
Одновременно из пунктов А и С в пункт В отправляются два туриста. Через 4 часа они прибыли в пункт В. Второй турист каждый километр проходил на 3 минуты быстрее первого, так как путь от С до В на 4 км длиннее пути от А до В. Найдите скорость первого туриста.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x км –путь , тогда x+4 км-CB. Пусть y кмч –скорость первого, z кмч – скорость второго: $$left{begin{matrix}frac{x+4}{z}=4 & & \frac{x}{y}=4& & \frac{1}{y}-frac{1}{z}=frac{3}{60} & &end{matrix}right.Leftrightarrow$$$$left{begin{matrix}z=frac{x+4}{4} & & \y=frac{x}{4} & & \frac{4}{x}-frac{4}{x+4}=frac{1}{20} & &end{matrix}right.$$ $$frac{4x+16-4x}{x^{2}+4x}=frac{1}{20}Leftrightarrow$$ $$frac{16}{x^{2}+4x}=frac{1}{20}Leftrightarrow$$ $$x^{2}+4x-320=0$$ $$left{begin{matrix}x_{1}+x_{2}=-4 & & \x_{1}x_{2}=-320& &end{matrix}right.Leftrightarrow$$$$left{begin{matrix}x_{1}=-20 & & \x_{2}=16& &end{matrix}right.$$ $$y=frac{16}{4}=4$$
Задание 23
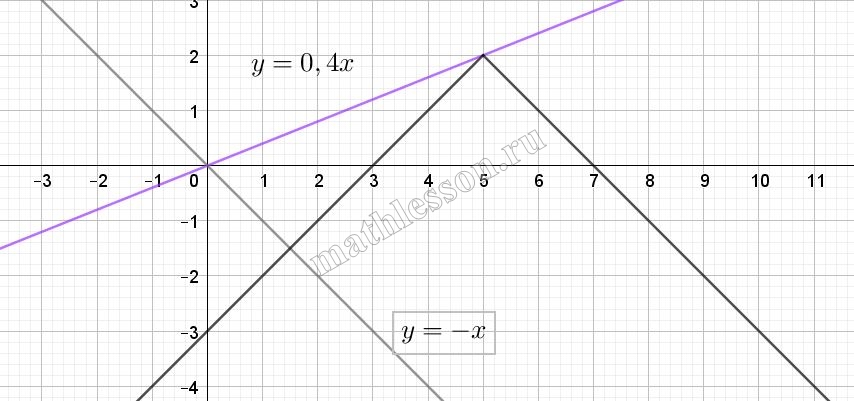
Найдите все значения k при которых прямая у = kx пересекает в двух точках ломаную, заданную условиями:$$left{begin{matrix}x-3,x<5\ 7-x,xgeq 5end{matrix}right.$$
Ответ: (-1; 0,4)
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y=left{begin{matrix}x-3, x<5 & & \7-x, xgeq 5& &end{matrix}right.$$
Начертим график данной функции :
При a>0 до момента , когда пройдет поезд (5;2) (прямая розового цвета) : $$2=5*kRightarrow k=0,4$$, то есть $$kin [0; 0,4)$$.
При a<0, пока не станет параллельна (прямая серого цвета) прямой y=7-x, то есть $$ain (-1; 0)$$ Итог (-1; 0,4)
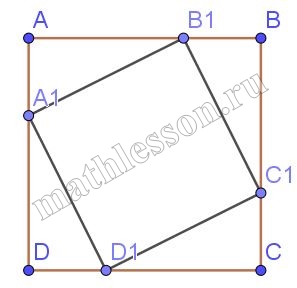
Задание 24
В квадрат, площадью 24 см2 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найдите площадь прямоугольника.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) Пусть $$angle B_{1}C_{1}B=alpha$$ , тогда $$angle D_{1}C_{1}C=90-alpha$$ , тогда $$angle C_{1}D_{1}C=alpha$$ .
Рассуждая аналогично получим :
$$angle B_{1}C_{1}B=angle C_{1}D_{1}C =angle DA_{1}D_{1}=angle A_{1}B_{1}A=alpha$$ , следовательно , $$angle B_{1}C_{1}Bsim angle C_{1}D_{1}C sim angle DA_{1}D_{1}sim angle A_{1}B_{1}A$$
2)т.к. $$B_{1}C_{1}:C_{1}D_{1}=1:3$$,то пусть $$B_{1}B=xRightarrow CC_{1}=3x, BC_{1}=y$$, тогда $$CD_{1}=3y.$$
3) т.к. $$A_{1}B_{1}=C_{1}D_{1}$$ и $$B_{1}C_{1}=A_{1}D_{1}$$ и все треугольники подобны , то $$Delta A_{1}B_{1}A=Delta C_{1}D_{1}C$$ и $$Delta B_{1}C_{1}B=Delta DA_{1}D_{1}$$ следовательно $$DD_{1}=x$$
4) из п. 3 получили, что $$BC=y+3x$$ и $$CD=x+3y$$, тогда
$$y+3x=x+3yRightarrow x=y$$
5)$$AC=sqrt{S_{ABCD}}=sqrt{24}$$
$$frac{BC_{1}}{CC_{1}}=frac{1}{3}Rightarrow$$$$ BC_{1}=frac{sqrt{24}}{4}Rightarrow$$$$CC_{1}=frac{3sqrt{24}}{4}$$
6) $$Delta B_{1}BC_{1}$$: $$B_{1}C_{1}=sqrt{(frac{sqrt{24}}{4})^{2}+(frac{sqrt{24}}{4})^{2}}=sqrt{3}.$$Тогда $$C_{1}D_{1}=3sqrt{3}.$$
7)$$S_{A_{1}B_{1}C_{1}D_{1}}=3sqrt{3}*sqrt{3}=9$$
Задание 25
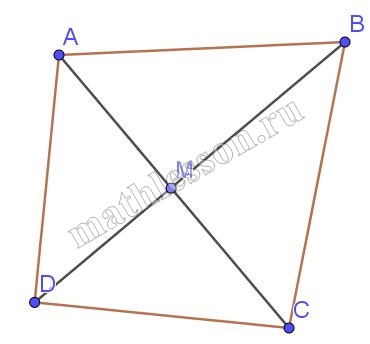
В выпуклом четырёхугольнике АВСD углы ACB и ADB равны. Докажите, что углы ABD и ACD также равны.
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) $$angle AMD=angle BMC$$(вертикальные) $$angle ADB=angle ACB$$(по условию) $$Rightarrow Delta AMB sim Delta BMC$$ и $$frac{AM}{MB}=frac{MD}{MC}(1)$$
2) $$angle AMB=angle DMC$$ (вертикальные) с учетом равенства (1) получим $$Delta AMB sim Delta DMCRightarrow angle ABD=angle ACD$$
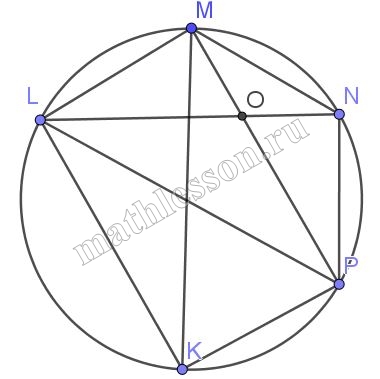
Задание 26
Точки K, L, M, N, P расположены последовательно на окружности радиуса $$2sqrt{2}$$ . Найдите площадь треугольника KLM, если LM || KN, KM || NP, MN || LP, а угол LOM равен 45, где О – точка пересечения хорд LN и MP
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1) $$LMleft | right | KNRightarrow angle LMK=angle MKN$$(накрест лежащие)$$Rightarrow cup LK=cup MN$$(вписанные углы равны)
$$MK left | right |NPRightarrow angle MKN=angle KNPRightarrow cup KP=cup MN=cup LK.$$
$$LPleft | right | MNRightarrow angle LPM=angle PMNRightarrow cup LM=cup NP.$$
2)Пусть $$cup KL=alpha$$ и $$cup LM=beta .$$
$$angle LOM=angle NOP$$(вертикальные) ,но т.к.
$$cup LM=cup NP$$, то $$angle LOM-frac{cup LM+cup PN}{2}=beta =45$$
3)$$Delta LPK : LK=2R sin LPK= 2R sin 45$$
$$Delta LPM: LM=2R sin LPM =2R sin 22,5$$
$$S_{Delta LKM}=frac{1}{2} *LK*LM* sin KLM=$$$$frac{1}{2} *2R sin 22,5 * sin (90+22,5)=$$$$2R^{2}* sin 22,5 * cos 22,,5 * sin 45=R^{2}* sin^{2} 45=4$$
Вопрос B1 #3779
Заработная плата футболиста составляет 1 млн. 200 тыс. долларов в год. Налог на заработную плату составляет 13%. После выплаты налогов 8% от оставшейся суммы он выплатил агенту, 270 тыс. рублей составил штраф за неспортивное поведение и 200 тыс. руб. – штраф за нарушение спортивного режима. Оставшиеся деньги он получил наличными. Найти размер выплаченных футболисту денег (в рублях), если 1 доллар стоит 60 руб.
Вопрос B2 #3780
На чемпионате Москвы по легкой атлетике провели три полуфинала на 100 м. у мужчин. Были показаны следующие результаты:
В финал проходят по 2 лучших в забеге и еще 2 добавляются по лучшему времени из тех, кто не попал в 2-е лучших в забеге. С каким наихудшим временем спортсмен пробился в финал?
Вопрос B3 #3781
Фигура ограничена дугой АCВ окружности с центром в т.Q (5,-7) и радиусами AQ и BQ. Найти площадь фигуры, если точки имеют следующие координаты: A (2,-10); B (8,-10), C (2;-4). (В ответе записать (S/ pi ))
Вопрос B4 #3782
1 марта в университет на занятия вышли 260 преподавателей и 2580 студентов. На автомобиле приезжают 5% преподавателей и 15% студентов. Найти вероятность того, что угнанная наугад машина принадлежит преподавателю.
Вопрос B5 #3783
Решить уравнение (log_{pi}log_{2}log_{7}x^{2}=0)
В ответе записать корень уравнения или произведение корней, если корней несколько.
Вопрос B6 #3784
В окружности проведены две хорды АВ и CD, пересекающиеся в точке М. Дано:
(frac{AM}{MB}= frac{5}{7}; frac{AM}{MD}= frac{1}{2})
Найти отношение СМ:МD.
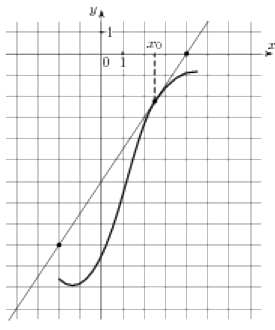
Вопрос B7 #3785
На рисунке изображен график функции (y = f(x)) и касательная к нему в точке с абсциссой (x_{0}) . Найдите значение производной функции (f(x)) в точке (x_{0}) .
Вопрос B8 #3786
Боковые грани SAB и SCD правильной четырехугольной пирамиды SABCD образуют двугранный угол 60°. Ребро основания АВ равно 1. Найти площадь полной поверхности пирамиды.
Вопрос B9 #3787
Найти значение выражения (sqrt{18053^{2}-18047^{2}} cdot sqrt{6})
Вопрос B10 #3788
Из водопроводного крана диаметром (D_{1})см, находящегося на высоте (h) см, тонкой струей вытекает вода. Диаметр струи у поверхности земли равен (D_{2}) см ((D_{2} < D_{1})). Объем воды, вытекающей из крана в единицу времени (Объемный расход (Q)), определяется формулой
где (g=980frac{см}{с^{2}})
Пусть (D_{1} = 0,5 см, D_{2} = 0,2 см, Q=10 pi frac{см^{3}}{c}) .
Найти (h). (Ответ округлить с точностью до 1дм.)
Вопрос B11 #3789
Найдите двузначное натуральное число, если известно, что разность между самим числом и утроенной суммой его цифр равна 7, а при делении произведения цифр на их сумму в частном получается 2 и в остатке 1.
Вопрос B12 #3790
Найдите точку максимума функции (frac{4x^{2}+9}{x})
Вопрос B13 #3791
Решить уравнение:
Вопрос B14 #3792
В четырехугольной пирамиде SABCD (четырехугольник в основании выпуклый) боковые ребра SA, SB и SC попарно перпендикулярны и имеют длину 3. Длина SD равна 9. Найдите
а) угол наклона ребра SD к плоскости основания.
б) наибольшее возможное при этих условиях значение объема пирамиды SABCD.
Вопрос B15 #3793
Решите неравенство:
Вопрос B16 #3794
В правильный треугольник со стороной a вписан круг. В этот круг вписан правильный треугольник, в который вписан круг и так далее.
а) Доказать, что площади кругов образуют геометрическую прогрессию.
б) Найдите сумму площадей всех кругов.
Вопрос B17 #3795
В банке купили монеты достоинством 1 дол., 1 евро и 1 фунт стерлингов. Всего 100 монет. Цена монет на день покупки составляла: 1 дол. – 32 руб., 1 евро – 40 руб., 1 фунт стерлингов – 50 руб. На всю покупку затратили 3930 руб. Какое максимальное количество долларов могло быть куплено?
Вопрос B18 #3796
При каких значениях a уравнение
имеет ровно 4 решения?
Вопрос B19 #3797
Заданы три бесконечных целочисленных возрастающих арифметических прогрессий, разность которых 3, 5 и 7, каждая из которых содержит хотя бы одно отрицательное число. Натуральное число «n» назовем хорошим, если оно принадлежит всем прогрессиям.
а) Доказать, что существует хотя бы одно хорошее число.
б) Можно ли утверждать, что для любых прогрессий существует хорошее число на отрезке [100; 200]?
в) Можно ли утверждать, что для любых прогрессий существует хорошее число на отрезке [200; 400]?
ЕГЭ по математике, Вариант № 189, 11 класс, 2010.
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий. Часть 1 содержит 12 заданий с кратким ответом (В1–В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1–С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Примеры.
1. Тетрадь стоит 20 рублей. Какое наибольшее число таких тетрадей можно будет купить на 550 рублей после понижения цены на 25%?
2. На рисунке жирными точками показана цена алюминия на момент закрытия биржевых торгов во все рабочие дни с 4 по 17 марта 2008 года. По горизонтали указываются числа месяца, по вертикали – цена тонны алюминия в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена алюминия на момент закрытия торгов была наибольшей.
3. В треугольнике ABC угол C равен 90° , AB = 30, AC = 24. Найдите sin A.
4. Строительной фирме нужно приобрести 78 кубометров пенобетона у одного из трех поставщиков. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице.
5. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q =160 −10 p . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за месяц r = q ⋅ p составит не менее 550 тыс. руб.
6. Перед каждым из чисел 14, 15, …, 20 и 4, 5, …, 8 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
7. В треугольнике ABC AB =1 3, BC = 2 , CA=1 2. Точка D лежит на прямой BC так, что BD:DC =1 :3. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F . Найдите длину отрезка EF .
8. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 80 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа позже автомобилиста. Ответ дайте в км/ч.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ по математике, Вариант № 189, 11 класс, 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ по математике, Вариант № 189, 11 класс, 2010 — pdf — depositfiles.
Скачать книгу ЕГЭ по математике, Вариант № 189, 11 класс, 2010
— pdf — Яндекс.Диск.
Дата публикации: 31.05.2013 17:44 UTC
Теги:
математика :: ЕГЭ по математике :: 11 класс
Следующие учебники и книги:
- ЕГЭ 2010, Математика, Задача B4, Рабочая тетрадь, Смирнов В.А., Семенов А.Л., Ященко И.В.
- ЕГЭ 2013, Математика, 30 типовых вариантов заданий, Семенов А.Л., Ященко И.В.
- Геометрия, Все типы заданий ГИА и ЕГЭ, Решаем задачи повторяем теорию, Вольфсон Б.И., 2013
- ЕГЭ по математике, Вариант № 190, 11 класс, 2010
Предыдущие статьи:
- ЕГЭ по математике, Вариант № 188, 11 класс, 2010
- ЕГЭ по математике, Вариант № 187, 11 класс, 2010
- ЕГЭ по математике, Вариант № 186, 11 класс, 2010
- ЕГЭ по математике, Вариант № 185, 11 класс, 2010
| Автор | Сообщение | |||||
|---|---|---|---|---|---|---|
|
Заголовок сообщения: Re: Тренировочный вариант №189
|
||||||
|
Решение 18.
_________________ |
|||||
  |
||||||
|
|
||||||
|
ЭТОЯ |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение 19.
_________________ |
|||||
  |
||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение задачи 18. Подробности:
|
|||||
  |
||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Всем здравствуйте! Решение задания 13. Подробности:
|
|||||
  |
||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение задачи 17. Подробности:
|
|||||
  |
||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение задания 15. Подробности:
|
|||||
  |
||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение задания 16. Подробности:
|
|||||
  |
||||||
|
Grigorich |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
№19 Подробности:
|
|||||
  |
||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Решение задания 18. Подробности: Подробности:
Последний раз редактировалось netka 24 мар 2017, 23:35, всего редактировалось 1 раз. |
|||||
  |
||||||
|
Alexander N |
Заголовок сообщения: Re: Тренировочный вариант №189
|
|||||
|
Здравствуйте! Подробности:
Последний раз редактировалось Alexander N 23 мар 2017, 04:01, всего редактировалось 1 раз. |
|||||
  |
||||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
|
Вы не можете начинать темы |
|
|