Егэ математика в колледже

Большинство студентов колледжа могут сдать ЕГЭ уже на первом курсе. Даже если они не успели записаться на экзамен до февраля. Рассказываем, как.

Если программа колледжа включает в себя не только обучение профессии, но и программу по общеобразовательным предметам, то уже в конце первого курса студенты могут сдать ЕГЭ. То есть сэкономить год по сравнению с ровесниками. Проще говоря, если программа в колледже длится от 2.5 лет и больше, а на первом курсе есть русский и математика, можно сдавать ЕГЭ.

Как записаться на ЕГЭ в колледже

Студент колледжа может записаться на ЕГЭ как электронным способом, так и по личному заявлению. Рассмотрим основные варианты.

• Если колледж является частью большой образовательной организации, у которой есть аккредитованное подразделение старшей школы, то он может решать все вопросы через это подразделение. Например, колледж и старшая школа-предуниверсарий подчиняются вузу. В этом случае учащиеся колледжа могут регистрироваться на ЕГЭ от организации. Тогда их будет видеть в системе ответственный за ЕГЭ по школьному подразделению, но ответственности за них нести не будет. Например, он не обязан организовывать сопровождение на экзамен.
• Если колледж является автономным и “своей школы” у него нет, то студент регистрируется на ЕГЭ самостоятельно через электронные сервисы или очно — для этого нужно записаться на прием в РЦОИ. 

Что делать, если опоздал записаться на ЕГЭ

Очень часто студенты колледжа поздно узнают о своем праве сдать ЕГЭ и думают, что опоздали, но это не так. Даже если студент колледжа решил сдать ЕГЭ в феврале и позже, он все еще может подать заявление.

Действовать нужно через описанные службы. Бывает так, что в партнерской школе студенту колледжа отказывают в просьбе зарегистрировать его на ЕГЭ с опозданием. В этой ситуации студент может позвонить на горячую линию РЦОИ и явиться на прием.

В заявлении с просьбой зарегистрировать на экзамен с опозданием нужно указать причину. Недостаток информирования со стороны администрации учебного заведения — достаточная причина.

К заявлению, помимо копии паспорта и СНИЛС, необходимо приложить справку об обучении в колледже, копию аккредитации программ СПО (которые всегда можно найти на сайте), а также копию аттестата за 9 класс. Заверять копию не обязательно, поскольку сам факт приема на программу СПО автоматически означает наличие аттестата.

Зарегистрироваться на ЕГЭ можно и в марте, и в апреле. Следить за местом проведения экзамена нужно в личном кабинете регионального портала государственных услуг или на сайте Госуслуг.

Нужно ли писать итоговое сочинение в колледже

Итоговое сочинение для допуска к сдаче ЕГЭ студентам колледжа писать не нужно. Студент колледжа может по своему желанию зарегистрироваться на итоговое сочинение и написать его. Раньше это имело смысл для получения дополнительных баллов к ЕГЭ при поступлении, однако сейчас это не актуально в подавляющем большинстве вузов. Если все же вуз принимает баллы за итоговое сочинение как баллы за индивидуальные достижения, то можно настаивать на том, чтобы написать сочинение.

Если студент колледжа решил писать итоговое сочинение после того, как его написали во всех школах, то и тут не все потеряно. Дело в том, что для проваливших работу или проболевших существуют резервные дни. С опозданием на итоговое сочинение можно записаться в том же РЦОИ. Тогда студента прикрепят к точке, где проводится итоговое сочинение в резервные дни. Если у колледжа нет партнерской школы, студенту подберут школу по месту жительства.

Как поменять ЕГЭ студенту колледжа

Менять ЕГЭ студенту колледжа нужно так же через партнерскую школу, если она есть, или через РЦОИ. Основанием для решения может быть “изменение планов по выбору специальности для поступления в вуз”.

Если студент колледжа решил не сдавать какой-то из выбранных ранее ЕГЭ, то можно просто не приходить на экзамен. Никаких санкций и наказания за это не последует.

Можно ли поступать в вуз по ЕГЭ сразу после первого курса колледжа

Да, поступать в вуз после первого курса можно. Однако для этого необходимо закрыть первый год обучения без академических задолженностей по общеобразовательным предметам и получить об этом справку.

В идеале, чтобы избежать конфликтных ситуаций и лишних нервов, нужно полноценно закрыть первый курс, дождаться приказа о переводе на второй курс и затребовать его заверенную копию и выписку итоговых оценок. С заверенной копией аккредитации программ СПО, копией о лицензии колледжа, копией приказа и результатами ЕГЭ студент колледжа имеет право подать документы в вуз наравне с выпускниками 11 класса школ.

Как поступать в вуз после колледжа

Поступать по внутренним вузовским экзаменам после первого курса нельзя, только по ЕГЭ. Право поступать по экзаменам, которые вузы проводят самостоятельно, есть только у тех, кто закончил обучение по программе СПО и получил диплом — документ об успешном завершении программы.

Выпускники колледжа могут поступать и по ЕГЭ, и по внутренним экзаменам. Как правило, в собственный вуз выпускники колледжа поступают по внутренним. Во-первых, их к этому готовят, во-вторых, внутренние рекомендации играют роль. В другой вуз, в вуз совсем иного профиля часто проще поступить по ЕГЭ.

Должны ли колледжи готовить к ЕГЭ?

Однозначно нет. Даже школы должны давать среднее образование, а не готовить к экзаменам. Но они это делают, поскольку результаты государственных экзаменов учитываются в рейтинге школ, показывают ее успешность, подтверждают качество образования.

А колледжу готовить к ЕГЭ еще и не выгодно. Колледж не заинтересован терять студентов до окончания обучения. Помешать готовиться к ЕГЭ он не может, но и помогать — не обязан.

Как готовиться к ЕГЭ студенту колледжа

С одной стороны, при обучении в колледже к ЕГЭ готовиться сложно. Приходится осваивать программу среднего профессионального образования, сдавать сессии и еще и готовиться к ЕГЭ.

С другой стороны, довольно часто в колледже подростки становятся более ответственными и самостоятельными за счет нешкольного отношения взрослых и профессиональной атмосферы. Их ровесников-школьников опекают, ограничивают, например, в выходе из школы. А в колледжах более свободная атмосфера и часто более партнерские отношения.

Немаловажно и то, что старшеклассник и ЕГЭ — это понятно и предсказуемо. А подготовка к ЕГЭ в колледже обычно самостоятельное и осознанное решение. Поэтому мотивация выше.

Конечно, студенту колледжа полностью самостоятельно готовиться к экзаменам сложно. Лучше всего записаться на надежные курсы, где умеют работать с сознательными абитуриентами. Для того, чтобы оценить, умеют ли на курсах работать со студентами колледжа, стоит начать с бесплатного пробного урока и понять, подходит ли программа обучения.

Сдавать ЕГЭ в колледже — не обязанность, а право. Оно есть и им стоит воспользоваться просто чтобы оценить свои силы. Если ребенок не уверен в своих силах, стоит для начала сдать бесплатный пробный ЕГЭ. Не исключено, что баллы хотя бы по одному предмету окажутся неплохими и их можно будет приберечь на будущее и досдать на следующий год другие предметы. Помните, что ЕГЭ, которые сдаешь в колледже не сгорят к моменту его окончания. Результатами можно будет воспользоваться, если возникнет желание после колледжа пойти в вуз.

Программа

итогового экзамена по математике

Раменское,

2013 г.

Пояснительная записка

Программа итогового экзамена по математике предназначена для студентов СПО.

Тест является основной формой проверки знаний за курс математики.

Объем теста – 20 заданий.

Продолжительность проведения экзамена – 5 часов.

Программа итогового экзамена по математике

Для успешной подготовки к итоговому экзамену по математике году студентам следует обратить особое внимание на повторение тем, согласно стандарта.

1. Тригонометрия:

Основные формулы тригонометрии. Функции и их графики. Решение тригонометрических уравнений и неравенств.

1. Производная:

Правила вычисления производных. Производная сложной функции. Производная показательной функции. Метод интервалов. Применение производной к исследованию функции.

1. Первообразная:

Основное свойство первообразной. Правила нахождения первообразных.

1. Понятие степени:

Корень n-ой степени и его свойства. Степень с рациональным показателем. Решение иррациональных уравнений.

5. Показательная и логарифмическая функции:

Показательная функция. Решение показательных уравнений и неравенств. Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств. Свойства функций.

6. Стереометрия:

Многогранники. Тела вращения.

Критерии оценки контрольной работы

1 задание:

Степень с рациональным показателем – 1 балл

2 задание:

Степень с рациональным показателем – 1 балл

3 задание:

Свойства логарифмической функции – 1 балл

4 задание:

Основные тригонометрические формулы – 2 балла

5 задание:

Основные тригонометрические формулы–2 балла

6 задание:

Решение тригонометрических уравнений– 1 балл

7 задание:

Решение иррациональных уравнений – 2 балла

8 задание:

Решение показательных уравнений – 2 балла

9 задание:

Метод интервалов — Решение иррациональных уравнений – 1 балл

10 задание:

Свойства тригонометрических функций – 1 балл

11 задание:

Вычисление производных — 1 балл

12 задание:

Нахождение первообразной функции – 1 балл

13 задание:

Решение логарифмических уравнений – 1 балл

14 задание:

Нахождение максимального и минимального значений функции – 2 балла

15 задание:

Свойства тел в стереометрии – 1 балл

16 задание:

Площадь криволинейной трапеции – 3 балла

17 задание:

Построение графика логарифмической функции – 3 балла

18 задание:

Решение показательных неравенств — 3 балла

19 задание:

Многогранники — 3 балла

20 задание:

Тела вращения — 3 балла

Рекомендации для проверки (проведения) экзаменационного теста.

Тест состоит из 20 заданий.

Задания содержат по 4 варианта ответов, причем каждый вопрос имеет только один вариант правильного ответа. Выберите нужный вариант и отметьте соответствующую ячейку в таблицу ответов.

Максимальный балл за тест – 35.

0 – 14 баллов — «2» («неудовлетворительно»)

15 – 19 баллов — «3» («удовлетворительно»)

21 – 29 баллов — «4» («хорошо»)

30 – 35 баллов — «5» («отлично» )

Ответы

Вариант 1

Вариант 2

Вариант 3

Бланк ответов

экзаменационного теста

по математике

Ф.И.О.___________________________________________________

Группа № ________________________

Специальность ____________________

___ вариант.

Вариант 1

1. Вычислите 29 – 15.

1. 2) 43 3) 73 4) 101.

1. Упростите выражение .

1. 5 2) 1 3) 10 4) 0.

3) Упростите выражение – 2.

1) 2) 1 3) 8 4) 20.

4) Найдите значение , если = -0,8 и .

1) -0,6 2) 0,6 3) 0,2 4) 0,36

5) Упростите выражение 7cos²α – 5 + 7sin²α.

1) 1 + cos²α 2) 2 3) -12 4) 12.

6) Решите уравнение = 1.

1)2n, n 2) 3) +2n, n 4) n, n

7) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (35;37) 3) (-2; 4) .

Укажите промежуток, которому принадлежит корень уравнения = 8.

1) [-4;0) 2) [0;1) 3) [-∞;-4) 4) [4;6).

9) Решите неравенство ≤0.

1) (-∞;-2) [) 2) [-2;) ( 1;+∞) 3) (-∞;-2) 4) (-∞;-5) (-2;.

10) Найдите множество значений функции у =– 2.

1) [3;1] 2) (-∞;+∞) 3) [-1;1] 4) [-3;-1].

11) Найдите производную функции f(x) = .

1) -4 2) -8 3) 8 4) .

12) Укажите первообразную функции f(x) = 2х + 4х³ – 1.

1) х² + х⁴ – х 2) 2х² + 4х⁴ 3) 2 + 12х² 4) х²+х⁴.

13) Решите равнение + = .

1) 0 2) 4 3) 9 4) 15.

14) Найдите точки максимума функции у = х³ – 3х² .

1) 0 2) 2 3) -2 4) 3.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 2; 1.

1) 5 2) 10 3) 3 4) 31.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 4 – х², у = 0, х = 0, х = 2.

1) 8 2) 2 3) 5 4) 6.

17) Укажите область определения функции у =.

1) (-∞;0)(2;+∞) 2) (-2;+∞) 3) (2;+∞) 4) (0;2).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 0 2) -1 3) 1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 56дм² и 192дм², а длина их общего ребра 8дм. Найдите объем параллелепипеда.

1) 840 2) 1029 3) 1344 4) 1210.

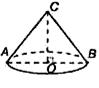
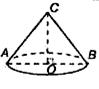
20) Образующая конуса равна 12см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 384 2) 192 3) 24 4) 648.

Вариант 2

1. Вычислите 7 — 3∙.

1. 2) 8 3) -5 4) -17.

1. Упростите выражение .

1) 1,2 2) 5 3) 4) .

3) Упростите выражение + — .

1) 2 +2 2) 7 3) 3 — 6 4) 2.

4) Найдите значение, если = и 0.

1) — 2) 3) 4) .

5) Упростите выражение -3sin²α — 6 – 3cos²α.

1) 1 2) 2cosα 3) cosα + 4) -9 .

6) Укажите промежуток, которому принадлежит корень уравнения = -х.

1) 2) (-;-10) 3) 4) .

7) Решите уравнение = 1.

1) n, n 2) 3) +2n, n 4) n,n.

Укажите промежуток, которому принадлежит корень уравнения = 125.

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≤ 0.

1) (-2;) 2) [-2;2) (;+∞) 3) (-∞;3) 4) (-∞;-2) (].

10) Найдите множество значений функции у = + 4.

1) [3;5] 2) (-∞;+∞) 3) [-1;1] 4) [-5;-3].

11) Найдите производную функции f(x) = .

1) 3 2) 3) -3 4) —.

12) Укажите первообразную функции f(x) = 3х² + 2х -4.

1) х³+ х² — 4х 2) 6х + 2 3) х³+ х² 4) х²+ х – 4х.

13) Решите равнение + =

1) 0 2) 11 3) 3 4) 12.

14) Найдите точку минимума функции у = х² — 1.

1) -1 2) 1 3) -2 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 2; 3; 6.

1) 55 2) 7 3) 49 4) 11.

16) Вычислите площадь фигуры (S), ограниченной линиями у = х³ + 1, у = 0, х = 0, х = 2.

1) 8 2) 5 3) 6 4) 4.

17) Укажите область определения функции у =.

1) (-∞;0)(4;+∞) 2) (-4;+∞) 3) (4;+∞) 4) (0;4).

18) Найдите наименьшее целое решение неравенства – 1 0.

1) 0 2) 1 3) -1 4) 2.

19) Площади двух граней прямоугольного параллелепипеда равны 35см² и 42см², а длина их общего ребра 7см. Найдите объем параллелепипеда.

1) 840 2) 10290 3) 770 4) 210.

20) Образующая конуса равна 24см и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3840 2) 1092 3) 5184 4) 648.

Вариант 3

1) Вычислите 2∙ – 0,9⁰

1)10,9 2) 11 3) 9,1 4) 9.

2) Упростите выражение

1. 2) 2 3) 0,7 4) 36.

3) Упростите выражение — +

1) -1 + 2) -2 3) 0 4) .

4) Найдите значение , если = — и

1) 2) 3) 4)

5) Упростите выражение -4sin²α +5 – 4cos²α

1) 1 2) 1 + 8sin²α 3) 1 + 8cos²α 4) 9.

6) Укажите промежуток, которому принадлежит корень уравнения = -х

1) 2) (-∞;-2) 3) 4) .

7) Решите уравнение = -1

1) 2)0 3) +2n, n 4) n, n

Укажите промежуток, которому принадлежит корень уравнения = 16

1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6).

9) Решите неравенство ≥0

1) (-∞;-8] (; 2) 2) [-8;) ( 2;+∞) 3) (-∞; 2) 4) (-∞;-8) (2; +∞.

10) Найдите множество значений функции у = – 1

1) [-1;1] 2) (-∞;+∞) 3) [-2;0] 4) [0;2].

11) Найдите производную функции f(x) =

1) -18 2) 6 3) 18 4) .

12) Укажите первообразную функции f(x) = 5х⁴ – 2х + 1

1) 5х⁵ – 2х² + 1 2) 20х³ – х 3) х⁴ – 2х + х 4) х⁵ – х² + х.

13) Решите равнение + =

1) 15 2) 5 3) 4 4) 10.

14) Найдите точку максимума функции у = 4х – х⁴

1) 4 2) 2 3) -4 4) 0.

15) Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 6; 6; 7

1) 19 2) 11 3) 121 4) 36.

16) Вычислите площадь фигуры (S), ограниченной линиями у = 1 – х³, у = 0, х = 0, х = 1.

1) 1 2) 3) 4) 1.

17) Укажите область определения функции у =.

1) (-3;+∞) 2) (-∞;0)(3;+∞) 3) (3;+∞) 4) (0;3).

18) Найдите наибольшее целое решение неравенства – 1 0.

1) 1 2) -1 3) 2 4) 0.

19) Площади двух граней прямоугольного параллелепипеда равны 20см² и 45см², а длина их общего ребра 5см. Найдите объем параллелепипеда.

1) 240 2) 120 3) 180 4) 4500.

20) Образующая конуса равна 18дм и составляет с плоскостью основания угол 30⁰. Найдите объем конуса, считая = 3.

1) 3804 2) 2192 3) 2187 4) 6408.

СБОРНИК ТРЕНИРОВОЧНЫХ ЗАДАНИЙ

К ЭКЗАМЕНАМ ПО МАТЕМАТИКЕ В ФОРМАТЕ ЕГЭ

ДЛЯ УЧАЩИХСЯ СПО И НПО

Преобразование степенных и дробно-иррациональных выражений.

1. Степени и корни 

 Степень с целым показателем 

 (n раз, ),

Свойства:

  Корень n-й степени 

  — арифметический корень n-й степени из числа  

Свойства:

В частности,  — арифметический квадратный корень: 

Степень с дробным (рациональным) показателем 

Свойства степени с действительным показателем 

ВЫЧИСЛИТЕ:

;    ;    ;  ;  ;   ;   ;   ;   ;

;    ;   ;  ;  

            ;  ;  ;  

1. Логарифмы. Логарифмические уравнения

ВЫЧИСЛИТЬ:

; ;  ;     ;    ;     ;

1. Показательные неравенства

Неравенство вида

в зависимости от основания эквивалентно следующему:

              при a>1      f(x)>g(x);

 при 0.

Неравенство вида

эквивалентно следующему неравенству:

 при a>1      f(x);

 при 0g(x).

Чтобы пользоваться свойством монотонности показательной функции следует путем надлежащих преобразований добиться одинаковых оснований в левой и правой частях неравенства

РЕШИТЬ НЕРАВЕНСТВА

0,42х+1≥0,16;   5(x2 — 2*x — 1) = 25;    ;    ;  ;  ;

1. Тригонометрические уравнения

 sin x = a

Если | a | > 1, то уравнение sin x = a не имеет корней. (Например, уравнение sin x = 2 не имеет корней
Если | a | ≤ 1, то корни уравнения выражаются формулой x = ( —1)n arcsin a + πn, n ∈ Z.
Частные случаи:
1. sin x = 0 ⇒ x = πn, n ∈ Z.
2. sin x = 1 ⇒ x = π/2 + 2πn, n ∈ Z.
3. sin x = -1 ⇒ x = -π/2 + 2πn, n ∈ Z.

 cos x = a

Если | a | > 1, то уравнение cos x = a не имеет корней. (Например, уравнение cos x = —1,5 не имеет корней)
Если | a | ≤ 1, то корни уравнения выражаются формулой x = ±arccos a + πn, n ∈ Z.
Частные случаи:
1. cos x = 0 ⇒ x = π/2 + πn, n ∈ Z.
2. cos x = 1 ⇒ x = 2πn, n ∈ Z.
3. cos x = -1 ⇒ x = π + 2πn, n ∈ Z.

tg x = a

Уравнение tg x = a имеет корни при любом значении a.

Корни уравнения выражаются формулой x = arctg a + πn, n ∈ Z.

 ctg x = a

Уравнение ctg x = a имеет корни при любом значении a.

Корни уравнения выражаются формулой x = arcctg a + πn, n ∈ Z.

   ;        ;  ;      

1. Производная функции. Исследование функции.

        Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. 

Следствие. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Достаточные признаки монотонности функции.

• Еслиf ‘( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.
• Если f ‘( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.

 Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции.

Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум).

Необходимое условие экстремума. Если x0 — точка экстремума функции f ( x ) и производная f’ существует в этой точке, то f’ ( x0 ) = 0.

Эта теорема — необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке.
Достаточные условия экстремума.

• Если производная при переходе через точку x0 меняет свой знак с плюса на минус, то x0 – точка максимума.
• Если производная при переходе через точку x0 меняет свой знак с минуса на плюс, то x0 – точка минимума.

Найдите наибольшее значение функции y = e2x – 6ex + 3 на отрезке [1; 2]

Найдите наименьшее значение функции 

Найдите точку максимума функции 

Найдите точку минимума функции 

Найдите точку минимума функции 

1. Чтение графиков

 При ответе на вопрос необходимо: использовать приобретенные знания и умения в практической деятельности и повседневной жизни, анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических расчетах; описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках.

На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 7 ноября, а 13 ноября — остальные 4. Сколько рублей потерял бизнесмен в результате этих операций (все операции проводились в момент открытия биржи)?

Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя – чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в Омах), на оси ординат – сила тока в Амперах. Сколько Ампер составляет сила тока в цепи при сопротивлении 2,5 Ом?

На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.

На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году. Ответ дайте в градусах Цельсия.

1. Реальная математика (Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни)

1. В первом банке один фунт стерлингов можно купить за 47,4 рубля. Во втором банке 30 фунтов — за 1446 рублей. В третьем банке 12 фунтов стоят 561 рубль. Какую наименьшую сумму (в рублях) придется заплатить за 10 фунтов стерлингов?
2. В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше 10000 руб., он получает сертификат на 1000 рублей, который можно обменять в том же магазине на любой товар ценой не выше 1000 руб. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель И. хочет приобрести пиджак ценой 9500 руб., рубашку ценой 800 руб. и галстук ценой 600 руб. 

В каком случае И. заплатит за покупку меньше всего: 

1) И. купит все три товара сразу. 

2) И. купит сначала пиджак и рубашку, галстук получит за сертификат. 

      3) И. купит сначала пиджак и галстук, получит рубашку за сертификат. 

4)В ответ запишите, сколько рублей заплатит И. за покупку в этом случае. ? 

   3.     В среднем гражданин А. в дневное время расходует 120 кВт·ч электроэнергии в   месяц, а в ночное время — 185 кВт·ч электроэнергии. Раньше у А. в квартире был установлен однотарифный счетчик, и всю электроэнергию он оплачивал по тарифу 2,40 руб. за кВт·ч. Год назад А. установил двухтарифный счётчик, при этом дневной расход электроэнергии оплачивается по тарифу 2,40 руб. за кВт·ч, а ночной расход оплачивается по тарифу 0,60 руб. за кВт·ч.  В течение 12 месяцев режим потребления и тарифы оплаты электроэнергии не менялись. На сколько больше заплатил бы А. за этот период, если бы не поменялся счетчик? Ответ дайте в рублях. 

4.       Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 28 секунд. Петя загружает файл размером 28 Мб за 24 секунды, а Миша загружает файл размером 38 Мб за 32 секунды. Сколько секунд будет загружаться файл размером 665 Мб на компьютер с наибольшей скоростью загрузки?

             8. Теория вероятности.  (Классическое определение теории вероятности)

Вероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.P(A) = m/n, где m — число благоприятствующих событию A исходов, n –  число всех элементарных равновозможных исходов. Формула представляет собой так называемое классическое определение вероятности по Лапласу, пришедшее из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша. 

1. В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. 
2. На соревнования по метанию ядра приехали 2 спортсмена из Швейцарии, 6 из Великобритании и 2 из Чехии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что спортсмен, который выступает девятым, будет из Чехии. 
3. Фабрика выпускает сумки. В среднем на 180 качественных сумок приходится две сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. 
4. Конкурс исполнителей длится 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что выступление представителя России состоится в третий день конкурса.    
5. В среднем из 150 аккумуляторов, поступивших в продажу, 9 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным. 

ВАРИАНТЫ ВЫПУСКНЫХ ЭКЗАМЕНОВ ЗА КУРС СРЕДНЕЙ ШКОЛЫ
с 1967 до 2008 года

В 1967 был проведён эксперимент, а с 1968 года устные выпускные экзамены по алгебре и началам анализа во всех советских школах стали письменными. С 1967 до начала 70-х годов экзамен состоял из четырёх, затем пяти, а с 1990 года — шести неизвестных заранее задач, составляемых министерством образования. С 2002 по 2008 год этот способ проверки знаний использовался только для учащихся математических и физико-математических классов. Для тех, кто занимался по базовой или гуманитарной программе, в 2001 году был вновь был проведен эксперимент, а с 2002 года проводился экзамен по открытым текстам: вариант состоял из 10 заданий, взятых из заранее опубликованного задачника. Продолжительность экзаменов составляла 5 астрономических часов.

Ниже мы приводим задания выпускных экзаменов по математике, проводившихся в России с 1967 до 2008 год включительно, пока эта форма экзамена не уступила место единому новой, в формате ЕГЭ и ГВЭ. Для базовых, физико-математических и математических классов ежегодно составлялось несколько экзаменационных работ по нескольким часовым поясам, каждая в двух равноценных вариантах. Обозначение 1991-Э1-2 означает второй вариант первой работы 1991 года. Варианты углубленной программы до 1977 года и те, у которых стоит метка «ищем», мы найти не смогли. Если они у вас есть — присылайте.

С 2009 по 2015 год выпускные экзамены из школ были объединены со вступительными экзаменами в вузы и проводились в формате Единого государственного экзамена. С 2016 года ЕГЭ по математике стал проводиться в двух форматах: к прежнему (профильному) экзамену, объединяющему в себе выпускной и вступительный экзамен, добавился экзамен другой структуры и сложности, называвшийся ЕГЭ по базовой математике.

В 2020 году ЕГЭ по базовой математике был отменен (школьники могли выпуститься из школы, не сдавая экзаменов), а в 2021 году экзаменом для выпускников школ, не планирующих поступать в университеты, был ГВЭ — государственный выпускной экзамен. ЕГЭ профильного уровня по-прежнему сочетает в себе функции впускного экзамена из школ и вступительного экзамены в вузы.

Варианты ЕГЭ-профиль, ЕГЭ-база и различные варианты ГВЭ представлены на сайте Решу ЕГЭ.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет №1

1.       
Корни
натуральной степени из числа и их свойства.

2.       
Перпендикуляр
и наклонная.

3.       
Событие,
вероятность события.

4.           
Примеры:

1)
Решить уравнения

2)Найти
предел

5.                
 Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№2

1.    
Степени
с рациональными показателями, их свойства.

2.    
Параллелепипед.
Куб.

3.    
Понятие
о пределе последовательности.

4.    
Примеры:

1)Упростите выражение

cos²x-6+sin²x

2) Найти производную

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№3

1.    
Логарифми
его свойства

2.     Двугранный угол.

3.     Понятие о
производной функции, её геометрический смысл.

4.     Примеры:

1) Найти значение производной функции

f¹(x)
при x=0—1

2) Найти предел

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№4

1.     Радианная
мера угла

2.     Раскрытие
неопределенностей 0/0  и  ∞/∞.

3.     Цилиндр.

4.     Примеры:

1)Вычислите

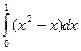
2) Упростите выражение   

cos⁴x—sin⁴x

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№5

1.       
Основные
тригонометрические тождества

2.       
Геометрические преобразования пространства:
параллельный перенос

3.       
Понятие о производной функции

4.       
Примеры

1)Необходимо
выбрать в подарок 4 из 10 имеющихся  книг. Сколькими способами можно это
сделать?

2)
Найти значение производной функции

f¹(x) при x=1

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№6

1.     Геометрический
смысл производной функции

2.     Геометрические
преобразования пространства: симметрия относительно плоскости

3.     Шар и сфера, их
сечения.

4.     Примеры:

1)  
Из 30 участников собрание надо
выбрать председателя и секретаря. Сколькими способами это можно сделать?

2)    Найти
производную

f(x)=xcosx

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№7

1.     Физический смысл
производной функции

2.    
Арксинус, арккосинус, арктангенс
числа

3.    
Формулы
объема куба, прямоугольного параллелепипеда

4.    
Примеры:

1)  Сколько шестизначных чисел (без повторения цифр) можно
составить из цифр 0, 3, 5, 6, 7, 8?

2)  Решите уравнения

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№8

1.    
Функции.Область
определения и множество значений; график функции.

2.     Производные суммы,
разности, произведения, частного.

3.    
Формулы
объема цилиндра

4.     Примеры:

1)   
Сколькими способами 8 человек
могут встать в очередь в театральную кассу?

2)  Вычислить:1)
;  2)

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№9

1.     Исследование
функции по схеме.

2.     Производные
основных элементарных функций.

3.     Формулы
объема куба.

4.     Примеры:

1)     
Вычислить

           2)          3) 

2)    Решить
уравнения

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№10

1.     Действия над
векторами в пространстве

2.     Производные
основных элементарных функций.

3.     Параллелепипед.
Куб.

4.     Примеры:

1)     
Упростить:

(sin²x+tx²xsin²x)ctgx

2)   
Найти
значение выражения

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№11

1.     Перпендикуляр и
наклонная.

2.     Понятие о пределе последовательности.

3.    
Логарифми
его свойства.

4.    
Примеры

1)Вычислите

 5^-4 *
5⁶;                3)   7¹⁰ : 7¹²;                  
5)  (3^-4)^-1;

2)Написать
уравнение касательной к графику  функции в точке с абсциссой x₀

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№12

1.     Корни
натуральной степени из числа и их свойства

2.     Производные суммы,
разности, произведения, частного.

3.     Аксиомы
стереометрии

4.     Примеры:

1)      Вычислите

  4⁴ *4^-3;            
65^-3 : 65^-3;                (8²)^-2
* 8³

2)    В группе 30 студентов. Необходимо выбрать старосту,
заместителя старосты и профорга. Сколько существует способов это сделать?

5. 
Задача :

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№13

1.     Пирамида.
Правильная пирамида.

2.     Показательная
функция, свойства и график.

3.    
Арксинус, арккосинус, арктангенс
числа

4.    
Примеры:

1)   
Вычислить:

  81* 3^-4;                
2)  9^-6 * 9⁵;                      3)   (3^-1)⁵
*27²; 

2)   
Порядок выступления 7 участников конкурса
определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

5.    
Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№14

1.     Шар
и сфера, их сечения

2.     Основные
понятия комбинаторики

3.     Действия над
векторами в пространстве

4.     Примеры

1)   
Вычислить:

 6⁰
: 6^-3   5)   9^-2 :  3^-6;                               6) 
125^-4 : 25^-5

2)     Вычислите

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№15

1.    
Формулы
объема цилиндра

2.    
Степени
с рациональными показателями, их свойства.

3.     Основные
тригонометрические тождества

4.     Примеры:

1)   
Решите уравнение    

sin²x = cosx—
cos²x

2)    
Найти производную

f ¹(x) при x=0 —1

5.     Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№16

1.     Формулы
объема цилиндра, конуса

2.     Исследование
функции по схеме.

3.     Раскрытие
неопределенностей 0/0 

4.     Примеры:

1)   
Вычислите

2)    В шахматном турнире участвуют 16 человек. Сколько
партий должно быть сыграно в турнире, если между любыми двумя участниками
должна быть сыграна одна партия?

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№17

1.     Формулы
объема шара

2.     Раскрытие
неопределенностей ∞/∞.

3.     Параллельный
перенос

4.     Примеры:

1)    Решите
графически 

2) На борту самолёта 12 мест рядом с
запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные
места неудобны для пассажира высокого роста. Пассажир В. высокого роста.
Найдите вероятность того, что на регистрации при случайном выбореместа пассажиру
В. достанется удобное место, если всего в самолёте 300 мест

5.    Задача:

МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ
КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№18

1.    
Формулы
объема куба, прямоугольного параллелепипеда

2.     Радианная мера
угла.

3.    
Логарифмическая
функция, свойства и график

4.    
Примеры:

1)   
Вычислите

2)    
 

Из множества натуральных чисел от 10 до 19 наудачу
выбирают        одно число. Какова вероятность того, что оно делится на 3?

5.     Задача

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№19

1.    
Формулы
объема призмы

2.    
Физический
смысл производной

3.    
Событие,
вероятность события

4.    
Примеры:

1) Напишите
первые пять членов последовательности.

а_n=2ⁿ+1/2ⁿ

2)Решите
уравнение

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№20

1.    
Формулы
объема пирамиды, усеченной пирамиды 

2.    
Геометрический
смысл производной

3.     Степенная
функция,  свойства и график.

4.     Примеры:

1)    Решить уравнения

2)   В
сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос
по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
достанетсявопрос
по ботанике.

5.    Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№21

1.     Площади
поверхностей тел вращения.

2.     Понятие о
производной функции

3.     Функции.Область
определения и множество значений; график функции

4.     Примеры:

1)    Решите уравнения

2)   В
сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос
по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене
билете школьнику
не достанетсявопроса по неравенствам.

5.     Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№22

1.    
Векторы
в пространстве.

2.     Основные
тригонометрические тождества.

3.    
Раскрытие
неопределенностей 0/0.

4.    
Примеры:

1)   
Решить
уравнение

3(x-2)-5=4-(5x-1)

2)   
Исследуйте
функцию и постройте график

f(x)=3x^-1

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№23

1.     Площади
поверхностей тел вращения.

2.     Логарифми его
свойства

3.     Радианная мера
угла.

4.     Примеры:

1)  Решить уравнения

.

2)Исследуйте
функцию и постройте график

f(x)=x²+2

5.    
Задача:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РД

ГБПОУ КОЛЛЕДЖ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Дисциплина«Математика»

Билет
№24

1.     Конус. Усеченный
конус. 

2.    
Корни
натуральной степени из числа и их свойства.      

3.    
Арксинус, арккосинус, арктангенс
числа

4.    
Примеры:

1)    Вычислите

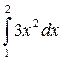
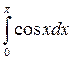
2)   
Первести из градусной меры в радианную

 45⁰,60⁰,36⁰

5.
Задача