Задания
Версия для печати и копирования в MS Word
Тип 1 № 27845
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Спрятать решение
Решение.
Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Ответ: 9.
Аналоги к заданию № 27845: 50931 50933 50935 50937 50939 50941 50943 50945 50947 50949 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.6 Многоугольник. Сумма углов выпуклого многоугольника, 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-13

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Тип 1 № 27845
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
2. Тип 2 № 27215
Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
3. Тип 3 № 500037
Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
4. Тип 4 № 320205
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
5. Тип 5 № 26650
Найдите корень уравнения
6. Тип 6 № 26781
Найдите значение выражения
7. Тип 7 № 119975
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
8. Тип 8 № 27995
Для обогрева помещения, температура в котором поддерживается на уровне через радиатор отопления пропускают горячую воду. Расход проходящей через трубу воды
кг/с. Проходя по трубе расстояние x, вода охлаждается от начальной температуры
до температуры
причeм
где
— теплоeмкость воды,
— коэффициент теплообмена, а
— постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 84 м.
9. Тип 9 № 99602
Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в
10. Тип 10 № 508951
На рисунке изображён график функции Найдите
11. Тип 11 № 77501
Найдите точку минимума функции
12. Тип 12 № 519423
а) Решите уравнение
б) Найдите его корни, принадлежащие отрезку
13. Тип 13 № 520995
В правильном тетраэдре АВСD точка Н — центр грани АВС, а точка М — середина ребра СD.
а) Докажите, что прямые АВ и СD перпендикулярны.
б) Найдите угол между прямыми DН и ВМ.
14. Тип 14 № 514256
Решите неравенство
15. Тип 15 № 517480
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,6 млн рублей?
16. Тип 16 № 517479
В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O1 и O2 соответственно, касающиеся прямой CH в точках M и N соответственно.
а) Докажите, что прямые AO1 и CO2 перпендикулярны.
б) Найдите площадь четырёхугольника MO1NO2, если AC = 20 и BC = 15.
17. Тип 17 № 507743
Найти все значения параметра a, при каждом из которых среди значений функции есть ровно одно целое число.
18. Тип 18 № 517451
На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?
б) Может ли ровно одно число на доске оканчиваться на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Просмотр содержимого документа
«2023 ЕГЭ Январь Математика Вариант 2»
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)
На чтение 1 мин Просмотров 12 Опубликовано 6 марта, 2023
Решение заданий ЕГЭ профильного уровня. Задача 14 Решение и ответы на задачи на официальном сайте источника онлайн.
Презентация открытого занятия для слушателей курсов повышения квалификации. Решение задачи 14 профильного уровня ЕГЭ по математике
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/matematika/library/2019/11/25/reshenie-zadaniy-ege-profilnogo-urovnya-zadacha-14
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Привет! Сегодня повторим геометрическую фигуру параллелограмм и порешаем задачи на эту тему.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
3. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его четырёх сторон.
Признаки параллелограмма:
1. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту.
S = h∙a
C другой стороны, каждая диагональ параллелограмма делит его на два равных треугольника. Применив формулу для площади треугольника через синус угла, получим, что площадь параллелограмма можно вычислить следующим образом:
S = a∙b∙sinα
a и b — стороны, α — величина угола между ними
Так же, разделив двумя диагоналями параллелограмм на 4 треугольника, и использовав вышеуказанную формулу для площади треугольника через синус угла, получается, площадь параллелограмма через диагонали можно представить в виде формулы:
S = ½∙d1∙d2∙sinφ
d1 и d2 — диагонали, φ — величина угла между ними
Эта формула справедлива для любого выпуклого четырёхугольника.
Задачи на параллелограмм.
Задача (Накрест лежащие углы)
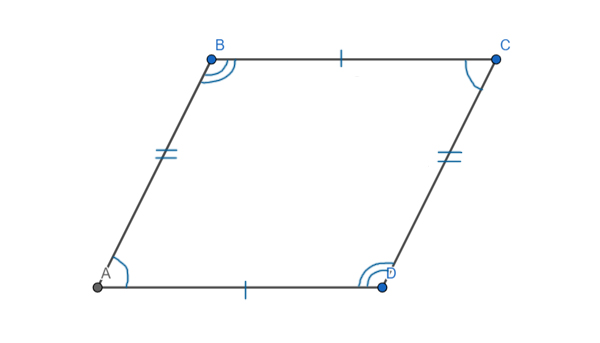
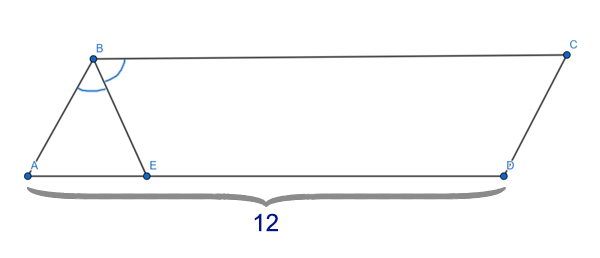
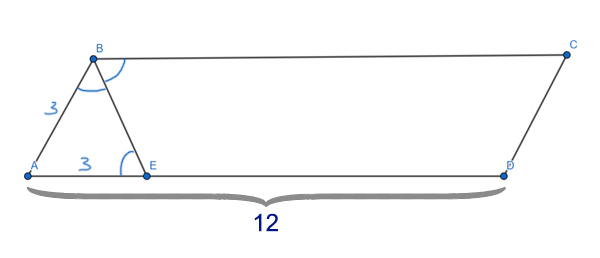
Биссектриса тупого угла ∠ABC параллелограмма ABCD делит противоположную сторону AD в соотношении 1:3, считая от вершины острого угла. Бо́льшая сторона AD равна 12. Найдите периметр параллелограмма.
Решение:
Найдём отрезок AE. Всего отрезок AD содержит 4 части (1+3), а AE — это одна часть. Тогда получается AE = AD/4 = 12/4 = 3.
Углы ∠EBC и ∠BEA равны, т.к. эти углы накрест лежащие при параллельных прямых AD и BC и секущей BE.
Т.к. ∠EBC=∠BEA=∠ABE (Ведь BE — биссектриса), следовательно, треугольник ABE — равнобедренный (два угла равны ∠BEA = ∠ABE). Значит, боковые стороны равны AB=AE=3.
Теперь можно найти и периметр. По 1 свойству параллелограмма AB=DC=3, а так же AD=BC=12.
P=(12+3)*2 = 30
Ответ: 30
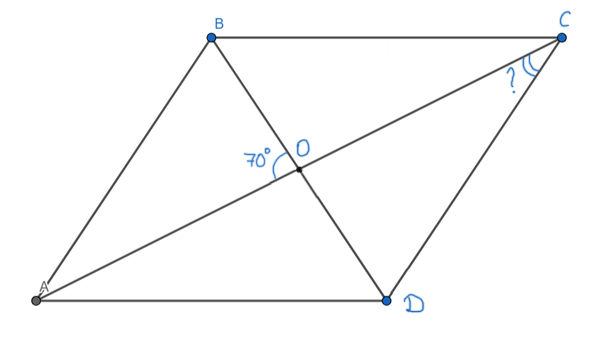
Задача (Свойство диагоналей)
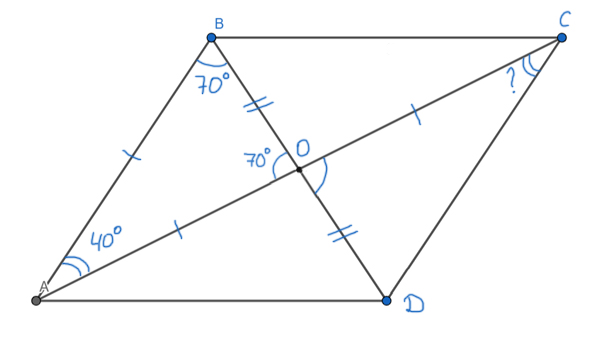
В параллелограмме ABCD диагональ AC вдвое больше, чем сторона AB. Диагонали пересекаются в точке O. Угол ∠AOB=70°. Найдите угол ∠ACD. Ответ запишите в градусах.
Решение:
Воспользуемся свойством параллелограмма. Оно говорит, что диагонали параллелограмма в точке пересечения делятся пополам. Получается AO=OC=AB, т.к. AB — так же половина диагонали AC.
Получается треугольник ABO — равнобедренный. Тогда углы при основании раны ∠AOB= ∠ABO=70°. Т.к сумма углов в треугольнике ABO равна 180°, то ∠BAO = 180° — 70° — 70° = 40°.
Угол ∠BAO = ∠ОСВ (эти углы накрест лежащие при параллельных прямых AB и DC и секущей AC).
Значит, ∠BAO = ∠ОСВ = 40°.
Ответ: 40
Задача (Используем параллельные прямые)
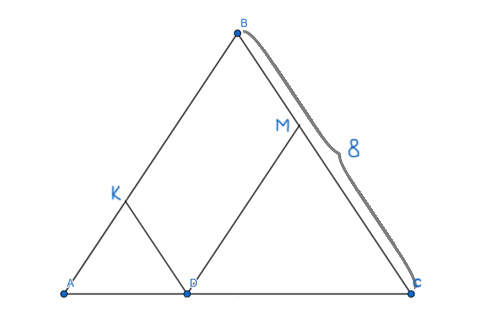
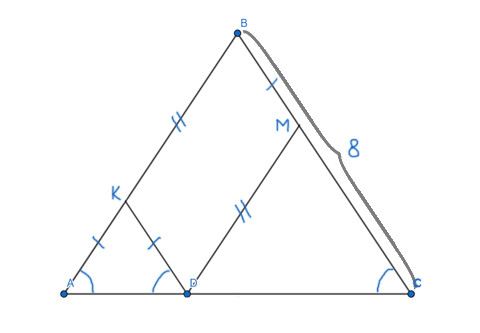
Боковая сторона равнобедренного треугольника равна 8. Из произвольной точки, на основании треугольника, проведены две прямы, параллельные боковым сторонам. Найдите периметр образовавшегося параллелограмма.
Решение:
Углы ∠KDA и ∠BCA являются соответственными при параллельных прямых KD и BC и секущей AC. Значит, они равны ∠KDA=∠BCA.
Получается, что треугольник AKD — равнобедренный. Ведь, ∠BAC=∠BCA (Т.к. это углы при основании в равнобедренном треугольнике ABC) ⇒ ∠BAC = ∠KDA, а если в треугольнике два угла равны, то такой треугольник — равнобедренный.
Чтобы найти периметр параллелограмма, достаточно найти сумму двух его пересекающихся сторон, и затем эту сумму нужно умножить на 2. Сумма двух пересекающихся сторон параллелограмма DKBM как раз равна боковой стороне треугольника ABC. Т.е. KD + KB = AB (АК=КD т.к. треугольник AKD равнобедренный).
PDKBM = 2*(KD + KB) = 2 * AB = 2 * 8 = 16
Ответ: 16
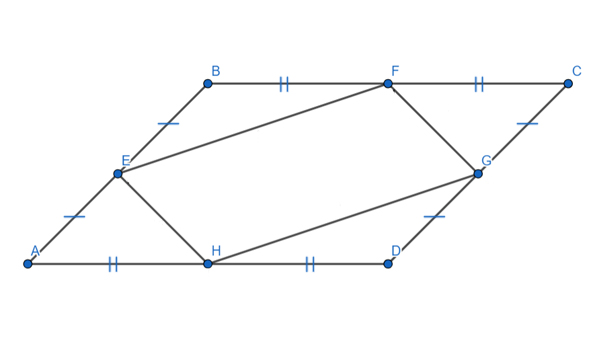
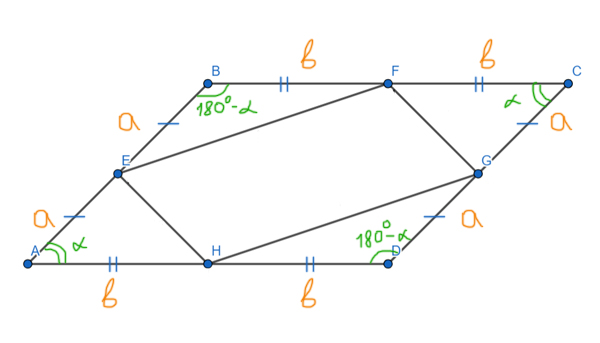
Задача (Два параллелограмма)
Площадь параллелограмма ABCD равна 77. Найдите площадь параллелограмма EFGH, вершинами которого являются середины сторон данного параллелограмма.
Решение:
Обозначим AE=EB=CG=GD=a, BF=FC=AH=HD=b, ∠BAD=∠BCD=α, ∠ABC=∠ADC=180°-α.
Рассмотрим площади четырёх треугольников, которые получились внутри параллелограмма ABCD равны. Используем формулу для площади треугольника через синус угла.
SAEH = ½∙a∙b∙sinα
SEBF = ½∙a∙b∙sin(180°-α)
SFCG = ½∙a∙b∙sinα
SHGD = ½∙a∙b∙sin(180°-α)
Т.к. по формуле приведения sinα = sin(180°-α), то площади всех четырёх треугольников равны.
Площадь параллелограмма ABCD через синус угла α можно представить:
SABCD = AB∙AD∙sinα = 2a∙2b∙sinα = 4∙a∙b∙sinα
Тогда
SABCD — SAEH — SEBF — SFCG — SHGD =
4∙a∙b∙sinα — 4 ∙ (½∙a∙b∙sinα) = 2∙a∙b∙sinα
Получается, что если из площади параллелограмма ABCD вычесть площади четырех получившихся треугольников, то останется ровно половина от изначальной площади. Это и есть площадь параллелограмма EFGH.
SEFGH = ½ ∙ SABCD = ½ ∙ 77 = 38,5
Ответ: 38,5
Задача (Диагонали параллелограмма)
Диагонали параллелограмма равны 12 и 14. Найдите стороны параллелограмма, если их разность равна 4. В ответе запишите сумму двух его разных сторон.
Решение:
Здесь удобно воспользоваться 3 свойством, которое было описано в начале статьи.
Пусть AB=x, а BC=y.
Тогда по 3 свойству:
122 + 142 = x2 + x2 + y2 + y2
А с другой стороны, по условию
x — y = 4
x = 4 + y
Подставляем x в первое уравнение.
340 = 2∙(4+y)2 + 2∙y2
340 = 2∙(16 + 8∙y + y2) + 2∙y2
170 = 16 + 8∙y + y2 + y2
2∙y2 + 8∙y — 154 = 0
Получили квадратное уравнение.
y2 + 4∙y — 77 = 0
D = 16 + 4∙77 = 324
√D = 18
y1 = (-4 + 18)/2 = 7
y2 = (-4 — 18)/2 = -11
Отрицательное число не подходит.
x = 7 + 4 = 11.
Ответ: 18
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.