Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Пример:
Решение любой текстовой задачи можно разделить на несколько основных этапов:
- Работа с условием
- Составление математической модели
- Проверка ответа
Работа с условием
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
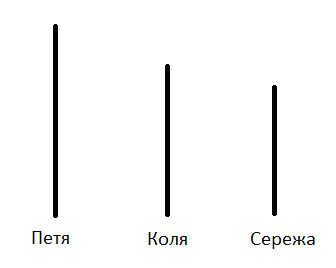
Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?
Иллюстрация:
Из рисунка сразу понятен ответ: Петя выше всех.
Пример.
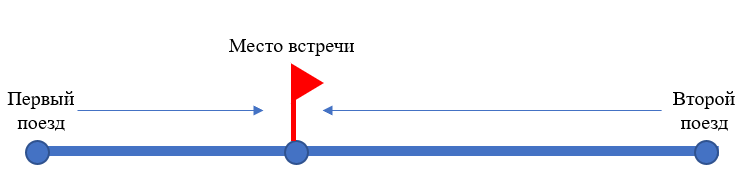
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?
Иллюстрация:
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.
Составим математическую модель:
45х + 55х = 200
100х = 200
х = 2 ч
Ответ: 2 ч.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Математическая модель
Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.
x — число девочек
y — число мальчиков
| Реальная ситуация | Математическая модель |
|---|---|
| В классе поровну мальчиков и девочек | $ { x=y} $ |
| Девочек на 5 больше, чем мальчиков | $ { x=y+5, ; или; x-y=5,; или; x-5=y} $ |
| Мальчиков в 2 раза больше, чем девочек | $ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $ |
| Если в класс перейдут 3 мальчика, то девочек станет в два раза больше | $ { y=2(y+3)} $ |
Алгебраическая зависимость
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.
Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К
Сережа ниже Коли на 10 см: К = С + 10
Подставим в первое уравнение рост Коли: П – 20 = С + 10
Нам нужно найти, на сколько см Петя выше Сережи: П – С
П – 20 = С + 10
П – С = 20 + 10
П – С = 30
Получаем, что Петя выше Сережи на 30 см.
Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4
Вместе ребята сделали 12 снежинок: М + К + Р = 12
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.
Так что же такое один процент?
Процент — это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Пример:
Есть 100 яблок.
$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $
Есть 200 груш
$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.
Пример:
200 груш — 100 %
2 груши — 1 %
Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.
$ frac{200}{2}=frac{100}{1} $
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100
Эту тему мы еще подробно пройдем на курсе.
Рассмотрим несколько примеров работы с процентами в текстовых задачах.
Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов
Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?
Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?
На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:
Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880
Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.
Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.
Пример:
Первый рабочий изготавливает $200$ деталей за время, которое второй рабочий потратит на изготовление $180$ таких же деталей. Найдите производительность первого рабочего, если он изготавливает в минуту на $2$ детали больше, чем второй?
Решение:
Пусть $х$ деталей/мин — производительность второго рабочего, тогда $(х+2)$ деталей/мин — производительность первого рабочего.
Создаем стандартную таблицу и столбец «Производительность»(р) заполняем данными с неизвестными.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $(x+2)$ | ||
| Второй рабочий | $x$ |
Так как первый рабочий изготовил $200$ деталей — это его выполненная работа, у второго рабочего работа равна $180$ деталей.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $200$ | $(x+2)$ | |
| Второй рабочий | $180$ | $x$ |
Третий столбец заполняем по формуле $t={A}/{p}$.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $200$ | $(x+2)$ | ${200}/{(x+2)}$ |
| Второй рабочий | $180$ | $x$ | ${180}/{x}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи время на выполнение работы рабочие затратили одинаковое. Поэтому содержимое третьего столбца приравняем друг к другу.
${200}/{(x+2)}={180}/{x}$
Решим полученное уравнение по свойству пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
$180(х+2)=200х$
Разделим обе части уравнения на $20$
$9(х+2)=10х$
Раскроем скобки и приведем подобные слагаемые
$9х+18=10х$
$х=18$ (деталей в минуту)- производительность второго рабочего.
$(х+2)=18+2=20$ (деталей в минуту)- производительность первого рабочего.
Ответ: $20$
Задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
При совместной работе задачи решаются через производительность.
Производительность при совместной работе равна сумме производительности каждого из рабочих.
$р_{совместная}=р_1+р_2…+р_n$
Пример:
В помощь садовому насосу, перекачивающему $6$ литров воды за $4$ минуты, подключили второй насос, перекачивающий тот же объём воды за $2$ минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать $27$ литров воды?
Решение:
Найдем производительность первого насоса. Работа (А) первого насоса – $6$ литров, время работы $t=4$ минуты.
$р_1={A}/{t}={6}/{4}={3}/{2}$ (литров/минуту)
Найдем производительность второго насоса. Второй насос выполняет тот же объем работы, т.е перекачивает $6$ литров воды. Время работы второго насоса $t=2$ минуты.
$р_2={A}/{t}={6}/{2}=3$(литров/минуту)
Найдем совместную производительность
$р_{совместная}=р_1+р_2={3}/{2}+3={3+6}/{2}={9}/{2}$ (литров/минуту)
Чтобы найти время, за которое оба насоса перекачивают $27$ литров воды, надо всю работу, т.е. $27$ литров разделить на совместную производительность
$t={A}/{p}={27}/{{9}/{2}}={27·2}/{9}=6$ минут.
Ответ: $6$
Процент – это сотая доля числа.
Процент обозначается символом $%$.
- Чтобы найти процент от числа, надо заданное число разделить на 100 и умножить на величину процента. $%$ от $а={а·%}/{100}$.
- Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на $100$.
Задачи на скидки:
Скидка — это понижение цены товара или услуги. Чаще всего скидку указывают в процентах.
Чтобы найти цену товара с учетом скидки необходимо:
- Из $100%$ отнять процент скидки.
- Найти полученный процент от полной стоимости товара.
Пример:
Зимняя куртка стоит $4500$ рублей. Сезонная скидка составляет $20%$. Сколько надо заплатить за куртку с учетом скидки.
Решение:
Найдем, сколько процентов будет стоить куртка, после скидки: $100%-20%=80%$
Посчитаем, сколько составляет 80% от 4500 рублей. Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.
${4500·80}/{100}=3600$ рублей- это цена куртки, после скидки.
Ответ: $3600$
Все для решения текстовых задач ЕГЭ по математике
- 15.08.2016
Представляем вашему вниманию пособие по решению самых часто встречающихся текстовых задач на ЕГЭ.
В этом сборнике дается полная теория и подробные примеры решения всех типов задач, которые могут встретиться на ЕГЭ:
- задачи на движение
- задачи на работу
- задачи на проценты
- задачи на концентрацию
- задачи на прогрессии
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Скачать материал

Скачать материал


- Сейчас обучается 36 человек из 28 регионов


- Сейчас обучается 21 человек из 14 регионов


- Сейчас обучается 165 человек из 48 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ЕГЭ
Решение текстовых задач задач
Профиль №11
составила Шапиева Л.С.
Решение задач является наиболее
характерной и специфической
разновидностью свободного мышления
У.Джеймс -
2 слайд
Текстовые задачи условно можно разбить на следующие основные группы:
Задачи на производительность
задачи на работу
задачи на бассейны и трубы
Задачи на проценты, концентрацию, части и доли
Задачи на проценты и доли
Задачи на концентрацию, смеси и сплавы -
3 слайд
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных тел
Задачи на арифметическую и геометрическую прогрессии -
4 слайд
Алгоритм решения текстовых задач
Ввод переменных, т.е. обозначение буквами x, y, z,… величины, которые требуется найти по условию задачи.
Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения.
Решение уравнений или неравенств.
Проверка полученных решений на выполнение условий задачи. -
5 слайд
Указания к решению текстовых задач
Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины.
Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
В составленных уравнениях надо проверить размерность членов уравнений
В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу. -
6 слайд
Задачи на проценты, концентрацию, части и доли
-
7 слайд
Задачи на проценты и доли
-
8 слайд
Задача №1: Влажность свежескошенной травы 60%, сена – 20%.
Сколько сена получится из 1 т свежескошенной травы?
Решение: 1000 0,4 = 400 кг сухого вещества в траве
80 % — 400 кг
100 % — х кг
х = (100 400):80 = 500 кг
Ответ: 500 кг.
Вода
20 %
Вода
60 %
Сухое
вещество
80 %
Сухое
вещество
40 %
1 т
? кг -
9 слайд
Задача № 2: Яблоки подешевели на 20 %. Сколько яблок можно
теперь купить на те же деньги, на которые раньше покупали
2,8 кг яблок?
Решение:
100 % 2,8 кг
80 % х кг
х = 3,5 кгОтвет: 3,5 кг
-
10 слайд
Задача № 3: Арбуз весил 20 кг и содержал 99 % воды, когда он немного усох, то стал содержать 98 % воды. Сколько теперь весит арбуз?
Решение:
20 0,99 = 19,8 кг воды в арбузе
20 – 19,8 = 0,2 кг сухого вещества
После усыхания 100 98 = 2% — это 0,2 кг
0,2 : 0,02 = 10 кг
Ответ: 10 кг. -
11 слайд
Задача №4: В школьной столовой обед из двух блюд стоит на 40 % дешевле, чем в кафе, расположенном вблизи школы, причем «первое» стоит на 60%, а «второе» – на 30 % дешевле, чем в кафе. Во сколько раз в школьной столовой «второе» стоит дороже, чем «первое»?
Решение: пусть х цена «первого» в кафе, y цена «второго» в кафе, тогда
х+ y 0,4 (х +y) — стоимость в школьной столовой
0,4 х и 0,7 y – стоимость в школьной столовой отдельно каждого блюда
х+ y 0,4 (х +y) = 0,4 х + 0,7 y
0,6х +0,6 y = 0,4 x + 0,7 y
0,2х = 0,1 y
2x = y
х= 0,5y стоимость «первого» в кафе; 0,4 0,5 y = 0,2y стоимость «первого»
в столовой
0,7y : 0,2y = 3,5
то есть второе блюдо в столовой в 3,5 раза дороже
Ответ: 3,5 -
12 слайд
Задача №5: В начале 2009 года мистер Джонс приобрёл по 100 акций компаний А и В. Через год он продал эти акции за сумму на 10 % большую той, что была заплачена им при покупке . При этом акции компании А были проданы на 5 % дороже, а акции компании В – на 20 % дороже, чем были им куплены. Во сколько раз акции компании В стоила дешевле акции компании А при их покупке мистером Джонсом?
Решение: пусть х цена одной акции А, y цена одной акции В
100 х+ 100 y цена купленных акций
100 х + 100 y +0,1 (100x + 100y) – цена акций через год
х + 0,05 х =1,05 х – цена одной акции А через год
y + 0,2y = 1, 2y – цена одной акции В через год
100 х + 100 y +0,1 (100x + 100y) = 100 1,05х + 100 1,2 y
110х + 110 y= 105 x +120 y
5x = 10y
x=2y
то есть акции компании А в 2 раза дороже акций компании В
Ответ: 2 -
13 слайд
Задача №6: Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90 % воды, а изюм содержит 5 % воды.
Вода
90 %
Вода
5 %
Сухое
вещество
10 %
Сухое
вещество
95 %
6 кг
? кг
Решение: 6 0,95 = 5,7 кг сухого вещества в изюме, его количество не изменилось
5,7 кг – 10 %
х кг – 100 %
х = (5,7 100) : 10 = 57 кг изюма
Ответ : 57 -
14 слайд
Задача №7: На аукционе одна картина была продана с прибылью 20%, а другая – с прибылью 50%. Общая прибыль от продажи двух картин составила 30%. У какой картины первоначальная стоимость была выше и во сколько раз?
Ответ: 2
Решение: пусть x стоимость первой картины, y – второй картины.
Прибыль от продажи первой 0,20х , второй – 0,50y.
Общая прибыль 0,30 (x + y)
0,20 х + 0,50y = 0,30 (x + y)
0,20x 0,30x = 0,30 y 0,50y
0,10x = 0,20y -
15 слайд
Задача №8: В четверг акции компании подорожали на некоторое количество процентов, а пятницу подешевели на то же самое количество процентов. В результате они стали стоить на 36 % дешевле, чем при открытии торгов в четверг. На сколько процентов подорожали акции компании в четверг?
1 + 0,01х – (1+0,01х)0,01х = 1 – 0,36
1 + 0,01х – 0,01х+0,0001х2 = 0,64
0,0001х2 = 0,36
х2 = 3600
х1 = 60
х2 = 60 не удов. условию задачи
Ответ: 60 %.Решение:
Четверг – подорожали на х % 1 + 0,01х
Пятница – на столько же подешевели 1 + 0,01х – (1+0,01х)0,01х -
16 слайд
Задача №9: В кувшин налили 3 литра молока 8 % жирности, некоторое количество молока 2 % жирности и тщательно перемешали. Определите сколько литров молока 2 % жирности было налито в кувшин, если известно, что жирность молока, полученного после перемешивания, составила 6 %?
Решение: Пусть х л молока – 2 % жирности
3 0,08 = 0,24 жира в 3 литрах 8 % молока
х 0,02 – жира в х литрах 2 % молока
0,24 + 0,02х = 0,06(3+ х)
0,24 + 0,02х = 0,18 + 0,06х
х = 1,5 лОтвет: 1,5
-
17 слайд
Задача №10: В апреле мобильный телефон стоил на 10 % больше, чем в июле, а в июле он стоил на 15 % больше, чем в декабре. На сколько процентов стоимость телефона в апреле была выше, чем стоимость телефона в декабре?
Решение: пусть х цена в декабре
Апрель – 1,15 х+ 0,11,15х = 1,265х
Июль – 0,15 х + х = 1,15х
Декабрь – х
1,265х х = 0,265х разница в цене между апрелем и декабрем
х – 100 %
0,265 х – y %
y = (0,265х 100) : х = 26,5 %
Ответ: 26,5 -
18 слайд
Задачи на концентрацию, смеси и сплавы
-
19 слайд
Задача №1: В сосуд , содержащий 10 литров 15-процентного водного раствора некоторого вещества добавили 15 литров 10-процентного водного раствора этого же вещества. Сколько процентов составит концентрация получившегося раствора?
+
=
Решение:
10 0,15 = 1,5 л вещества в
первом растворе
15 0,1 = 1,5 л вещества во 2 растворе
1,5 +1,5 = 3 л масса вещества в новом растворе10 + 15 = 25 л масса нового раствора
25 л – 100 %
3 л – х %
х = 12 %
Ответ: 12 -
20 слайд
Задача №2: В емкость содержащую 600 граммов 2 % раствора соли, добавили 1050 граммов воды, некоторое количество соли и тщательно перемешали полученную смесь. Определите, сколько граммов соли было добавлено, если известно, что после перемешивания получился раствор, содержащий 2,5 % соли.
+
=
Решение: пусть х гр. соли добавили
600 0,02 = 12 гр. соли было в емкости
600 +1050 = 1650 гр. масса после добавления воды
1650 + х масса раствора после добавления соли
х +12 масса соли в новом растворе
(1650 + х) 0,025 = х + 12
41,25+ 0,025х = х + 12
х= 30 грОтвет: 30
+ -
21 слайд
Задача №3: В двух бочках содержится сахарный сироп различной концентрации. В первой бочке содержится 150 кг сиропа, а во второй – 250 кг. Если перемешать весь сироп, находящийся в этих бочках, то получится сироп в котором 30 % сахара. А, если смешать равные массы сиропа из каждой бочки, то полученный сироп будет содержать 28 % сахара. Какова масса сахара в (кг), содержащегося в сиропе из второй бочки.
Решение: пусть х% сахара в первом сиропе, y % сахара во втором сиропе
150 + 250 = 400 кг масса нового сиропа
400 0,3 = 120 кг сахара в новом растворе
150 0,01 х + 250 0,01 y = 120
1 кг +1 кг = 2 кг – равные массы
0,01х + 0,01y = 0,28 2
x=20 % , y = 36 %
250 0,36 = 90 кг сахара во втором сиропе
Ответ: 90
+
= -
22 слайд
Задача №4: (ЕГЭ 05.06.14) Имеется два раствора .Первый раствор содержит 10 % соли, второй – 30 % соли. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25 % соли. На сколько килограммов масса первого раствора меньше массы второго раствора.
+
=
Решение: пусть х кг масса первого раствора,
y кг масса второго раствора
х + y = 200 кг масса нового раствора
200 0,25 = 50 кг соли в новом растворе
0,1х масса соли в первом растворе
0,3y масса соли во втором растворе
0,1х + 0,3y соли после смешивания в новом растворе т.е. 50 кг -
23 слайд
Задача №5:
Сколько граммов 30 %-го раствора надо добавить к 80 г 12 %-го раствора этой же соли, чтобы получить 20 %-й раствор соли?Решение.
Пусть надо добавить х г 30 % раствора соли.
Получится (80 + х) г 20 % раствора.
В 80 г 12 % раствора содержится 800,12 г соли
0,3х г соли — в х г 30 % раствора,
0,2(80 + х) г соли — в (80 + х) г 20 % раствора.
Получаем уравнение:
0,3х + 0,1280 = 0,2(80 + х)
0,3 х + 9,6 =16 + 0,2х,
0,3 х 0,2 х = 16 – 9,6,
0,1 х = 6,4,
х = 64.
О т в е т: 64 -
24 слайд
Задача №6: При смешивании первого раствора соли , концентрация которого 40 % ,и второго раствора этой же соли, концентрация которого 48 %, получился раствор с концентрацией 42 %. В каком отношении взяты первый и второй растворы?
40 %
48 %
+
=
42 %
I – 40 % , х масса I , 0,40 х соли в I растворе
II 48 %, y масса II, 0,48y соли во II растворе
0,40х + 0,48 y = 0,42 (x + y)
0,40х + 0,42х = 0,42y + 0,48y
0,02х = 0,06y
х/y = 3/1
Ответ: 3 : 1. -
25 слайд
Задача №7: Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % раствор?
Решение:
Пусть х — количество воды, которое надо добавить.
Новое количество раствора (50 + х) г.
Количество соли в исходном растворе 50 0,08 г.
Количество соли в новом растворе составляет 5 % от (50+ х) г,
т. е. 0,05(50+ х) г.
Так как количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение. Иногда в химии это уравнение называют кратко «баланс по соли».
50 0,08 = 0,05(50+х),
508 = 5(50+х),
80 = 50 + х,
х = 30.
Ответ: 30 -
26 слайд
Задача№ 8: Два слитка, один из которых содержит 35% серебра, а другой 65% , сплавляют и получают слиток массой 30 г, содержащий 47 % серебра. Какова масса каждого из этих слитков.
Решение: Пусть х г масса первого слитка, а y г – второго слитка.
35 %
65 %
x г.
y г.
47 %
Ответ: 18 и 12. -
27 слайд
Задача №9: Если смешать 8 кг и 2 кг растворов серной кислоты разной концентрации , то получим 12 % раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15 % раствор. Определите первоначальную концентрацию каждого раствора.
Решение: x % – концентрация в первом растворе,
y % концентрация во втором растворе
Ответ: 10 и 20. -
28 слайд
Задача №10: Имеются смеси апельсинового и ананасового соков. Первая смесь содержит 40 % апельсинового сока, а вторая – 80 %. Сливаются вместе p л первой смеси и q л второй смеси, а в результате получается 20 л смеси, содержащей 70 % апельсинового сока. Определите p и q.
p
q
40 %
80 %
20 л
70 %
Ответ: 5 и 15. -
29 слайд
Задачи на производительность
-
30 слайд
Задачи на работу обычно содержат следующие величины:
– время, в течение которого производится работа,
– производительность труда, работа, произведенная в единицу времени (возможны и другие обозначения N, W);
– работа, произведенная за время t
Уравнения, связывающее эти три величины:
vt
A
=
v
A
t
=
t
A
v
=
v
A
t -
31 слайд
В другой столбик
внесем
Урожай, собранный каждым звеномПервый столбик – урожайность.
Это условие поможет нам
составить уравнение.
х
х + 5
S, га
1
2
А, ц
урожайность, ц/га
<
на 2 га
875
920
875
х
920
х + 5
1. Одно звено собрало со своего участка 875 ц пшеницы,
а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что
с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом?
875
х
–
920
х+5
= 2
920
х + 5
=
875
х
+ 2
920
х + 5
– 2
875
х
=
1 способ
2 способ
3 способ
Из большей величины вычтем 2, уравняем с меньшей величиной
В новом столбике можно
выразить площадь участков,
для этого
весь урожай : урожайность
Из большей величины вычтем меньшую, разность равна 2
К меньшей величине прибавим 2, уравняем с большей величиной
Это условие поможет ввести х …
Решив, любое из уравнений, мы сразу получим ответ на вопрос задачи, без дополнительных действий. -
32 слайд
Первый столбик – время, необходимое на выполнение работы каждым насосом отдельно.
В другой столбик внесем выполненную работу – это 1 часть
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
х-2
х
1
2
1
1
1
х-2
2. При одновременной работе двух насосов пруд был очищен за
2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если
один из них может эту работу выполнить на 2 ч быстрее другого?
справка
справка
справка
Формула A = vt поможет
нам составить уравнение
Скорость совместной работы находим сложением скоростей
Работа выполнена полностью, т.е. выполнена 1 часть
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
1
х
t
A
v
=
1
х-2
1
х
+
vсовм=
A = 1
t =
1
х-2
1
х
+
= 1
35
12
Реши уравнение самостоятельно -
33 слайд
1
х-4
1
х
+
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
= 5
Первый столбик – время, необходимое на выполнение работы каждой бригадой отдельно.
В другой столбик внесем выполненную работу – это 1 часть
х
х- 4
1
2
1
1
1
х
3. Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, что за 24 ч совместной работы они заасфальтировали 5 таких участков?
справка
справка
справка
Формула A = vt поможет
нам составить уравнение
Скорость совместной работы находим сложением скоростей
За 24ч заасфальтировали 5 участков, т.е. работа составляет 5 частей
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
х- 4
1
t
A
v
=
1
х-4
1
х
+
vсовм=
A = 5
t =
24
24
Реши уравнение самостоятельно -
34 слайд
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
Первый столбик – время, необходимое на заполнение бассейна каждой трубе отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 5
1
2
1
1
1
х
4. Бассейн наполняется через первую трубу на 5 ч быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала первую трубу на 5 ч, а затем вторую на 7,5 ч. За сколько часов наполнится бассейн при совместной работе обеих труб?
справка
справка
Найдем работу, которую выполнит
I труба за 5 ч по формуле A = vt
Найдем работу, которую выполнит
II труба за 7,5 ч по формуле A = vt
Это условие поможет ввести х …
, часть/ч
v
, часть
A
, ч
t
х- 5
1
t
A
v
=
7,5
х
A1=
A2 =
1
х-5
5
1
= 1
= 1
х-5
5
х
7,5
+
Реши уравнение самостоятельно -
35 слайд
В новом столбике можно
выразить производительность (скорость) работы,
для этого
работу : время
Первый столбик – время, необходимое на выполнение всей работы каждой бригаде отдельно.
В другой столбик внесем выполненную работу –
это 1 часть
х
х- 12
1
2
1
1
1
х
5. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила через 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде?
Это условие
поможет
ввести х …
, часть/дн.
v
, часть
A
, дн.
t
х-12
1
t
A
v
=
= 1
= 1
5
справка
справка
справка
По формуле A = vt найдем работу, выполненную за 9дн. I бригадой
Скорость совместной работы находим сложением скоростей
По формуле A = vt найдем работу, выполненную за 5дн. совместно
1
х-12
1
х
+
vсовм=
A =
A =
9
1
х-12
1
х
+
1
х
+
1
х-12
1
х
+
5
1
х
9
Реши уравнение самостоятельно -
36 слайд
Задача №6 : При одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут. Определите, за сколько минут израсходует пачку первый принтер, если известно, что он сделает это на 10 минут быстрее, чем второй.
-
37 слайд
Задача №7: Бассейн наполняется двумя трубами, действующими одновременно, за 2 часа. За сколько часов может наполнить бассейн первая труба, если она, действуя одна, наполняет бассейн на 3 часа быстрее, чем вторая?
-
-
39 слайд
Задача №8: В городе имеются три завода по выпуску рыбных консервов. Первый завод может переработать 50 тонн рыбы за трое суток, второй – 45 тонн за двое суток, а третий – 95 тонн за шесть суток. Определите минимальное время, за которое на этих заводах можно переработать 110 тонн рыбы.
-
40 слайд
Решение:
110 : 55 = 2 сут
Ответ: 2 суток. -
41 слайд
Задача №9: Первый наборщик текста набирает за час 5 страниц текста, второй – 6 страниц, а третий – 7 страниц. Определите, по сколько страниц текста нужно отдать для набора каждому из них, если требуется, чтобы весь текст, объем которого 216 страниц, был набран как можно быстрее.
Решение:
5 + 6 + 7 = 18 частей всего
216 : 18 = 12 страниц 1 часть
12 5 = 60 стр.
12 6 = 72 стр.
12 7 = 84 стр.
Ответ: 60, 72, 84 страницы. -
42 слайд
Задачи на движение
-
43 слайд
Задачи на движение
по прямой (навстречу и вдогонку)
по замкнутой трассе
по воде
на среднюю скорость
протяженных тел -
44 слайд
При решении задач на движение принимают такие допущения:
движение считается равномерным, если нет специальных оговорок;
изменение направления движения и переходы на новый режим движения считаются происходящими мгновенно;
если два тела начинают движение одновременно (если одно тело догоняет другое), то в случае, если или встречаются, каждое тело с момента выхода и до встречи затрачивает одинаковое время; -
45 слайд
всякие переходы на новый режим движения, на новое направление движения считают происходящим мгновенно;
если тела выходят в разное время, то до момента встречи из них затрачивает время больше то, которое выходит раньше;
все величины, как правило, положительные (в природе скорость расстояние и время положительны), поэтому можно смело умножать, делить и возводить в квадрат получающиеся уравнения и неравенства, не делая необходимых в таких случаях оговорок. -
46 слайд
В задачах на движение используются обычно формулы, выражающие законы равномерного движения: S=V·t , где S- пройденное расстояние, V- скорость равномерного движения, t — время движения.
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения задачи её условие формулируется в различных единицах измерения(метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения: -
47 слайд
Движение навстречу:
Движение вдогонку:
Движение по окружности
(замкнутой трассе):
Средняя скорость:
-
48 слайд
Задачи на движение
Встречное движение
v1 v2
t1 t2s1 tвстр s2
s
t1=t2=tвстр. Vсбл=v1+v2 s=vсбл*tсближ
Обьекты, начавшие двигаться навстречу друг другу одновременно, движутся до момента встречи одинаковое время . -
49 слайд
Задача№ 1.Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
1
1
у
х
S,
часть
Велосипедист
Мотоциклист
v,
часть/ч
t,
ч
1
у
1
х
на весь путь
Если в задаче не дано расстояние, очень удобно считать весь путь, как 1 целая часть.
На 3 часа
>
x – у = 3
1
у
1
х
+
навстречу
v
48
60
встречи
t
S
1
1
у
1
х
+
= 1
4
5
1 часть
часть/ч
1
у
1
х
часть/ч
4
5
ч
Ответ: 4 ч -
50 слайд
Движение в одном направлении
v1 v2
t1 t2s s2
s1 vсближ =v1-v2,.s=s1-s2 , s=vсбл*tвстр
-
51 слайд
10 км/ч
Задача№ 2: Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
2
x
3
15 км/ч
Удобно показать на схеме тот момент, когда 1-й вел. был в пути уже 2 ч, а 2-й вел. один час.
t
30 км
10 км
3
1
2
+
t
х – 10
3й и 2й
v,
вдогонку
S,
км
t,
ч
3й и 1й
х – 15
t
3
1
2
+
t
3
1
2
+
(t )
(х – 15)
(х – 10)
t
= 10
= 30
С системой придется потрудиться. При выборе ответа учтем, что скорость 3-го велосипедиста должна быть больше 15. Ответ: 25.
1
2
1
3
Отметим на схеме примерное место встречи 2го и 3го
И примерное место встречи 1го и 3го
t
3
1
2
+
t -
52 слайд
Движение в противоположных направлениях
В таких задачах два тела могут начинать движение в противоположных направлениях из одной точки:
а) одновременно;
б) в разное время.
А могут начинать свое движение из двух разных точек, находящихся на заданном расстоянии, и в разное время.
Общим теоретическим положением для них будет следующее:
v удал. = v1+ v2, где v1 и v2 соответственно скорости первого и второго тел.
(Схематический чертеж строится аналогично предыдущим). -
53 слайд
Задача№ 3. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 72 км. На следующий день он отправился обратно со скоростью на 6 км/ч больше прежней. По дороге он сделал остановку на 6 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
Путь В-А
х
Путь А-В
v,
км/ч
t,
ч
S,
км
72
х
72
х+6
72
=
х+6
Чтобы найти время надо расстояние разделить на скоростьt =
S
v
72
Остановка
6
72
х+6
+ 6 =
72
х
А
В
72 км
6ч
Это условие поможет ввести х …
6 км/ч -
54 слайд
Движение по воде
скорость перемещения лодки V по воде, при скорости течения реки Vр и собственной скорости движения Vс, выражается:
V по течению=Vс+Vр при движении лодки по течению реки.
V против течения=Vс−Vр при движении лодки против течения реки.
Движущийся плот всегда имеет скорость течения реки. -
55 слайд
Задача№ 4:Теплоход проходит по течению реки до пункта назначения 560
км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 56 часов после отплытия из него. Ответ дайте в км/ч.
х–4
По. теч.
Пр. теч.
560
Пусть vсоб. = x
х+4
v,
км/ч
560
S,
км
справка
Это условие поможет ввести х …
Чтобы найти время надо расстояние разделить наскорость
t =
S
v
560
х+4
t,
ч
справка
560
х–4
56ч
Стоянка
8
+ + =
560
х+4
560
х–4
8
56
Чтобы найти скорость по течению надо к собственной скорости прибавить скорость течения
Стоянка длилась 8 ч – это время
также надо учесть
Чтобы найти скорость против течения надо из собственной скорости отнять скорость течения
Ответ: 24 -
56 слайд
движение по замкнутой трассе
-
57 слайд
Если два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v1 и v2 соответственно
(v1 > v2 соответственно), то 1-й велосипедист
приближается ко 2 со скоростью v1 – v2.
В момент, когда 1-й велосипедист
в первый раз догоняет 2-го,
он проходит расстояние на
один круг больше.
Продолжить
Показать
В момент, когда 1-й
велосипедист во
второй раз догоняет
2-го, он проходит
расстояние на два
круга больше и т.д. -
58 слайд
1
2
Задача№ 5: Из одной точки круговой трассы, длина которой равна15 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 60 км/ч, скорость второго равна 80 км/ч. Сколько минут с момента старта пройдет, прежде чем первый автомобиль будет опережать второй ровно на 1 круг?
1 красный
2 зеленый
60
80
v,
км/ч
на 15 км меньше (1 круг)
Уравнение:
Ответ: 45
х получим в часах.
Не забудь перевести в минуты.
t,
ч
х
х
S,
км
60х
80х
Показать -
59 слайд
2
1
Задача№6: Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля.
Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1 автомоб.
2 автомоб.
90
х
v,
км/ч
на 10 км больше (1 круг)
Ответ: 75
t,
ч
2
3
2
3
S,
км
2
3
90
2
3
х
Уравнение:
Показать -
60 слайд
Задача№ 7: Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного
из них на 21 км/ч больше скорости другого?
1 красный
2 синий
х
х+21
v,
км/ч
на 7 км меньше (половина круга)
Уравнение:
Ответ: 20
t получим в часах.
Не забудь перевести в минуты.
t,
ч
t
t
S,
км
tх
t(х+21)
Сколько кругов проехал
каждый мотоциклист
нам не важно. Важно, что синий проехал до точки встречи на половину круга больше, т.е. на 7 км.
Еще способ в комментариях.
Показать -
61 слайд
старт
финиш
2
1
2
1
1
2
2
1
1
2
Пусть полный круг – 1 часть.
Задача№ 8: Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
Показать -
62 слайд
Задача№ 9. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?
на 1 круг больше
Ответ: 10
1 лыжник
2 лыжник
v,
круг/мин
t,
мин
60
60
S,
км
х
х+2
1
1
t,
мин
1 лыжник
2 лыжник
S,
часть
v,
часть/мин
1
х+2
1
х
1
х+2
1
х
60
х
60
х+2
Сначала выразим скорость каждого лыжника. Пусть за х мин 1-й лыжник проходит полный круг. Второй на 2 минуты больше, т.е. х+2.
60
х
60
х+2
– = 1
Это условие поможет ввести х … -
63 слайд
Задача№ 10: Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
1 желтый
2 синий
S,
км
80
х
v,
км/ч
t,
ч
2
3
2
3
2
3
80
2
3
х
на 14 км больше (1 круг)
Уравнение:
Можно было сначала найти скорость вдогонку: 80 – х
Тогда уравнение будет выглядеть так:
v
S
=
t
Ответ: 59
Нажать на кнопку можно несколько раз. Сколько кругов проехал каждый автомобиль нам
не важно. Важно, что желтый автомобиль проехал на 1 круг больше, т.е. на 14 км.
Показать
1
2 -
64 слайд
Задача№ 11: Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз.
Найдите скорость мотоциклиста,
если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
1
6
2
3
2
3
у
1 уравнение:
1
6
х
=
Показать
1 встреча. Велосипедист был до 1 встречи 40 мин (2/3 ч), мотоциклист 10 мин (1/6ч). А расстояние за это время они проехали равное.
-
65 слайд
Задача №12. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км.
Ответ дайте в км/ч.
1 мотоцик.
2 велосип.
S,
км
х
у
v,
км/ч
t,
ч
1
2
1
2
1
2
у
на 30 км больше (1 круг)
2 уравнение:
Ответ 80
1
2
х
Искомая величина – х
Показать (2)
2 встреча. Велосипедист и мотоциклист были в пути
до 2-й встречи 30 мин (1/2 ч).
А расстояние за это время мотоциклист проехал на 1 круг больше.
-
66 слайд
Задача №13. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
минутная
часовая
х
S,
круг
v,
круг/ч
t,
ч
1
1
12
х
1х
1
12
х
на круга больше
2
3
3
1х – =
1
12
х
2
3
3
Ответ: 240 мин
2
3
1
3
В первый раз минутной стрелке надопройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
2
3
на круга больше
2
3
3 -
67 слайд
6
12
1
2
9
11
10
8
7
4
5
3
Показать (4)
В первый раз минутной стрелке надопройти на круга больше, чтобы догнать минутную стрелку.
Во 2-й раз – еще на 1 круг больше.
В 3-й раз – еще на 1 круг больше.
В 4-й раз – еще на 1 круг больше.Всего
2
3
на круга больше
2
3
3
Проверка
Другой способ – в комментариях. -
68 слайд
Задачи на движение протяженных тел
В задачах на движение протяжных тел требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда проезжающего мимо
придорожного столба
идущего параллельно путям пешехода
лесополосы определенной длины
другого двигающегося поезда
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Если поезд движется мимо протяженной лесополосы, то он проходит расстояние равное сумме длины самого поезда и лесополосы. -
69 слайд
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Пройденное расстояние = длине поезда
Решение. Зная скорость движения v = 80 км/ч и время, за которое он проезжает мимо столба t = 36 с, можно найти длину поезда как пройденное расстояние по формуле:
vt
S
=
1 мин
1 с
1ч
: 60
: 60
* 60
* 60
: 60
: 60
Выразим время в часах
* 1000
Задача № 1 -
70 слайд
Задача № 2 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Пройденное расстояние = длине поезда + длина лесополосы
Решение. Зная скорость движения v = 60 км/ч и время, за которое он проезжает мимо лесополосы t = 1 мин, можно найти расстояние, которое прошел поезд (длина лесополосы + длина поезда).
vt
S
=
1 мин
1 с
1ч
: 60
: 60
* 60
* 60
: 60
Выразим время в часах -
71 слайд
Задача № 3 Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
400 м
Решим задачу с помощью уравнения
x
S
x+400
t
v
60000 м/ч
, м
, ч
, м/ч
v
S
=
t -
72 слайд
При решении задач на движение двух тел часто очень
удобно считать одно тело неподвижным, а другое — приближающимся к нему со скоростью, равной сумме скоростей
этих тел (при движении навстречу) или разности скоростей
(при движении вдогонку). Такая модель помогает разобраться
с условием задачи.
Задача № 4 По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Воспользуемся предложенной моделью -
73 слайд
2
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение. Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью v (м/мин) , равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние
120 м
400 м
600 м
80 м
1200 м
t
S
v
=
* 60
: 1000
+
+
+
1 -
74 слайд
Задача № 6 По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
* 1000
: 60
Скорость вдогонку (на сколько скорость пассажирского поезда больше скорости товарного) -
75 слайд
Задача № 7 По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
600 м
Решим задачу с помощью уравнения
x
S
x+600
t
v
1000 м/мин
, м
, мин
, м/мин
v
S
=
t -
76 слайд
Задача № 8 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
* 1000
Скорость навстречу друг другу
(сумма скоростей при движении навстречу друг другу)
: 60
: 60 -
77 слайд
Задача № 9 По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
700 м
Решим задачу с помощью уравнения
x
S
x+700
t
v
100000 м/ч
, м
, ч
, м/ч
v
S
=
t -
78 слайд
Задача № 10 Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает
мимо идущего параллельно путям со скоростью 6 км/ч
навстречу ему пешехода за 30 секунд. Найдите длину поезда
в метрах.
*1000
: 60
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной сумме скоростей пешехода и поезда (скорость навстречу друг другу). Сам пешеход не имеет «протяженной» длины (если бы это была колонна солдат, то мы бы учли это).
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу) -
79 слайд
Задача № 11 Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает
мимо идущего в том же направлении параллельно
путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите
длину поезда в метрах.
*1000
: 60
Выразим время в минутах
Решение. Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной разности скоростей пешехода и поезда. Пешеход не имеет «протяженной» длины.
Скорость навстречу друг другу (сумма скоростей при движении навстречу друг другу) -
80 слайд
Чтобы определить среднюю скорость при неравномерном движении, надо весь пройденный путь разделить на все время движения:
Задачи на нахождение
средней скорости -
-
82 слайд
Задача №12: Автомобиль двигался 3,2ч по шоссе со скоростью 90км/ч, затем 1,5ч по грунтовой дороге со скоростью 45км/ч, наконец, 0,3ч по проселочной дороге со скоростью 30км/ч. Какова средняя скорость движения автомобиля на всем пути?
Средняя скорость движения определяется по формуле: -
83 слайд
3. Определим все время движения:
2. Определим весь путь:
.
90
3,2
=
288
(км)
(км)
67,5
45
1,5
=
.
288 + 67,5 + 9 =
(км)
9
30
=
0,3
.
3,2 + 1,5 + 0,3 =
1. Определим длину каждого участка пути:
364,5
(км)
5
(ч)
4. Найдем среднюю скорость движения:
364,5 : 5 =
72,9
(км/ч)
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 681 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 31.10.2019
- 153
- 0
- 31.10.2019
- 197
- 2
- 31.10.2019
- 118
- 0
- 31.10.2019
- 153
- 2




Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы менеджмента в туризме»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс повышения квалификации «Международные валютно-кредитные отношения»
-
Курс повышения квалификации «Информационная этика и право»
7 сентября 2017
В закладки
Обсудить
Жалоба
Теория к заданиям первой части ЕГЭ по математике
Задачи 1-12 профильного уровня.
→ Решение задач на проценты: 1.pdf
→ Чтение графиков: 2.pdf
→ «Теория вероятностей»: 4.pdf
→ «Уравнения»: 5.pdf
→ Планиметрия: 6.pdf
→ «Производная»: 7.pdf
→ «Стереометрия»: 8.pdf
→ «Преобразование выражений»: 9.pdf
→ Задачи с физическим содержанием: 10.pdf
→ Движение. Работа. Смеси. Прогрессия: 11.pdf
→ Максимум (минимум) функции. Наибольшее (наименьшее): 12.pdf
Авторы: Александр и Наталья Крутицких | matematikalegko.ru
Текстовые задачи в профильном уровне ЕГЭ по математике
Короткова Елена Владиславовна
Санкт-Петербург
Текстовые задачи являются важной составляющей школьного курса математики, поэтому наличие таких задач в ЕГЭ оправдано и необходимо для оценки общей математической подготовки выпускников. Предложенные для решения на экзамене задачи стандартные. И особых вопросов эти задания вызывать не должны.
Однако изучение текстовых задач происходит в основной школе, рассматриваются они недостаточно основательно, поэтому приобретённые в основной школе навыки и знания решения таких задач со временем теряются. Для того чтобы успешно справляться с этими заданиями, необходимо в ходе подготовки к ЕГЭ повторить классификации задач, а также систематизировать знания по математике.
Все текстовые задачи можно условно классифицировать по типам: задачи на числовые зависимости; задачи, связанные с понятием процента; задачи на «движение», «концентрацию смесей и сплавов», «работу» и т. д.
По методу решения задачи делятся на задачи решаемые: арифметическим методом, алгебраическим методом и геометрическим методом.
Арифметический метод. Решить задачу арифметическим методом значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу можно решить различными арифметическими способами.
Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств).
При решении задач алгебраическим методом основная деятельность учащегося сосредотачивается на первом этапе решения задачи: на разборе условия задачи при составлении уравнений или неравенств по условию задачи.
Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
Геометрический метод. Он состоит в том, что решение задачи сопровождается наглядным представлением, иногда доказательство или решение видно из наглядной картины. Под геометрическим методом решения алгебраических задач понимается метод решения, заключающийся в использовании геометрических представлений (изображений), законов геометрии и элементов аналитических методов (уравнений или неравенств), систем уравнений, арифметических выражений и др.
Рассмотрим один из распространенных типов задач – задачи на работу.
Эти задачи содержат в себе информацию о выполнении некоторой работы несколькими субъектами (рабочими, насосами, механизмами и т. п.). Объём работы в таких задачах обычно не указывается и не является искомым, а также предполагается, что выполняемая работа проводиться равномерно, т. е. с постоянной производительностью для каждого субъекта.
В задачах на работу, системы уравнений содержат следующие величины:
Эти три величины связаны соотношением
Обычно величина выполняемой работы нас не интересует, поэтому удобнее принимать объём всей работы за единицу, т. е. 
Исследуя прототипы из Открытого Банка задач ЕГЭ по математике на движение и производительность, нельзя не заметить, что все задачи данного типа можно разделить на две группы – задачи на «детали» и задачи на «трубы». Для каждой из них составим общие модели решения типовых задач, которые знать будет очень полезно.
В задачах «на детали» за неизвестные, как правило, надо принимать производительность – её роль такова же, как роль скорости в задачах на движение.
Правила решения задач на работу очень просты.
, то есть работа= производительность
время. Из этой формулы легко найти t или v.
- Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Заполнен бассейн (один). Построено здание (одно). А вот если речь идет о количестве кирпичей, воды или деталей — работа как раз и равна этому количеству.
- Если трудятся двое и более объектов (два экскаватора, два завода…) — их производительности складываются.
- В качестве переменной удобно взять именно производительность.
Рассмотрим применение алгебраического метода решения таких задач на практике.
Задача. На изготовление 16 деталей первый мастер затрачивает на 6 часов меньше, чем второй мастер на изготовление 40 таких же деталей. Известно, что первый за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй мастер?
1 способ. Примем за х время работы одного из мастеров.
Решение:
Пусть 
|
Работа (детали) |
Производительность (дет/час) |
Время, (ч) |
|
|
Первый мастер |
16 |
|
|
|
Второй мастер |
40 |
|
|
Зная, что первый мастер за час делает на 3 детали больше, чем второй, составим и решим уравнение.
Таким образом, второй мастер делает 40:8=5 деталей в час.
Ответ: 5 деталей в час.
2 способ. Примем за х производительность одного из рабочих.
Решение:
Пусть 

|
Работа, (детали) |
Производительность, (дет/час) |
Время, (ч) |
|
|
Первый мастер |
16 |
|
|
|
Второй мастер |
40 |
|
|
Зная, что первый мастер на выполнение работы затрачивает на 6 часов меньше, чем второй мастер, составим и решим уравнение.
Таким образом, второй мастер делает 5 деталей в час.
Ответ: 5 деталей в час.
Из приведенных решений видно, что выбор неизвестных не влияет на ответ задачи, но от этого зависит длина решения. Поэтому при решении задачи, выбирать неизвестные стоит исходя из условия. Чем меньше действий предстоит совершить, тем быстрее решается задача. А это очень большое преимущество на экзамене.
В задачах «на трубы» модель решения схожа с задачами «на работу». Разница лишь в том, что здесь производительность трубы – это объём жидкости, протекающей через неё за единицу времени. Иногда в подобных задачах за неизвестные необходимо одновременно принять и объём бассейна, производительность труб, время наполнения и слива бассейна каждой трубой. Из-за большого количества неизвестных задача на первый взгляд может показаться очень трудной и нерешаемой, но это не так. Рассмотрим пример решения задачи.
Задача. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 110 литров она заполняет на 1 минуту быстрее, чем первая труба?
Решение:
Пусть 
|
Объём резервуара (л) |
Скорость заполнения |
Время заполнения (м) |
|
|
Первая труба |
110 |
|
|
|
Вторая труба |
110 |
|
|
Зная, что вторая труба заполняет резервуар на 1 минуту быстрее, чем первая труба, составим и решим уравнение.

Таким образом, вторая труба пропускает 11 литров воды в минуту.
Ответ: 11 литров воды в минуту.
Решая задачи «на работу», нужно принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе.
В заключении можно сделать некоторые выводы и дать рекомендации, которые необходимо знать при сдаче ЕГЭ.
При решении любых текстовых задач нужно обращать особое внимание на единицы измерения – в течение всего решения они обязательно должны быть одинаковыми.
Для преобразования условия задачи в математическую модель математические знания практически не нужны – необходим здравый смысл. Очень важно обязательно сформулировать, используя переменные, что необходимо найти, т. к. переменных может быть намного больше, чем уравнений, где все их найти просто невозможно.
Решая уравнения нужно помнить, что в текстовых задачах все величины, как правило, положительны, т. к. в природе отрицательных скоростей и расстояний не существует. Это даёт право на умножение, деление и на возведение в квадрат получающиеся уравнения и неравенства.
Решая задачи «на работу», очень выгодно принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе.
Список литературы:
1. Ерина Т.М. Алгебра. Текстовые задачи — Москва, МГТУ «МАМИ»,2004
2. Методика преподавания математики в средней школе: общая методика А.Я. Блох и другие, Москва, Просвещение, 1985.
3.Турецкий Е.Н., Фридман Л.М. -Как научиться решать задачи, Москва, Просвещение, 1989
4. Решение текстовых задач. http://schoolcollection.edu.ru/catalog/res/d92c7ae3-a9f1-4ff3-afb0-e1f1783fee48/?from=8f5d7210-86a6-11da-a72b-0800200c9a66&.
5. Презентационные подходы в решении текстовых задач. http://school-collection. edu.ru/.
Все или почти все текстовые задачи идут по одной проверенной схеме. Сначала естественно, нужно прочитать текст самой задачи, затем нарисовать к ней рисунок. Рисунок приобретает особое значение особенно тогда, когда ты совсем не понимаешь, что происходит.
✅ После этого на рисунок добавляем известные данные, условия для заданий и обозначаем за неизвестную то, что просят найти в задаче. Затем строим таблицу: в первый столбец вносим известные данные, во второй добавляем неизвестную, а третий всегда считаем по формуле. По условию задачи составляем уравнение и решаем его, чтобы найти неизвестную. Вот и все!
Осталось потренироваться на конкретной задаче! Не откладывай решение задач надолго 😌
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!