Каталог заданий
Задания 10. Графики функций. Гиперболы
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 10 № 508951
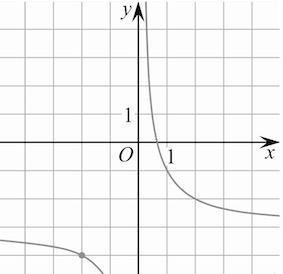
На рисунке изображён график функции
Найдите
Аналоги к заданию № 508951: 508971 508952 508953 508954 508955 508956 508957 508958 508959 508960 … Все
Источник: А. Ларин: Тренировочный вариант № 110.
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 10 № 508961
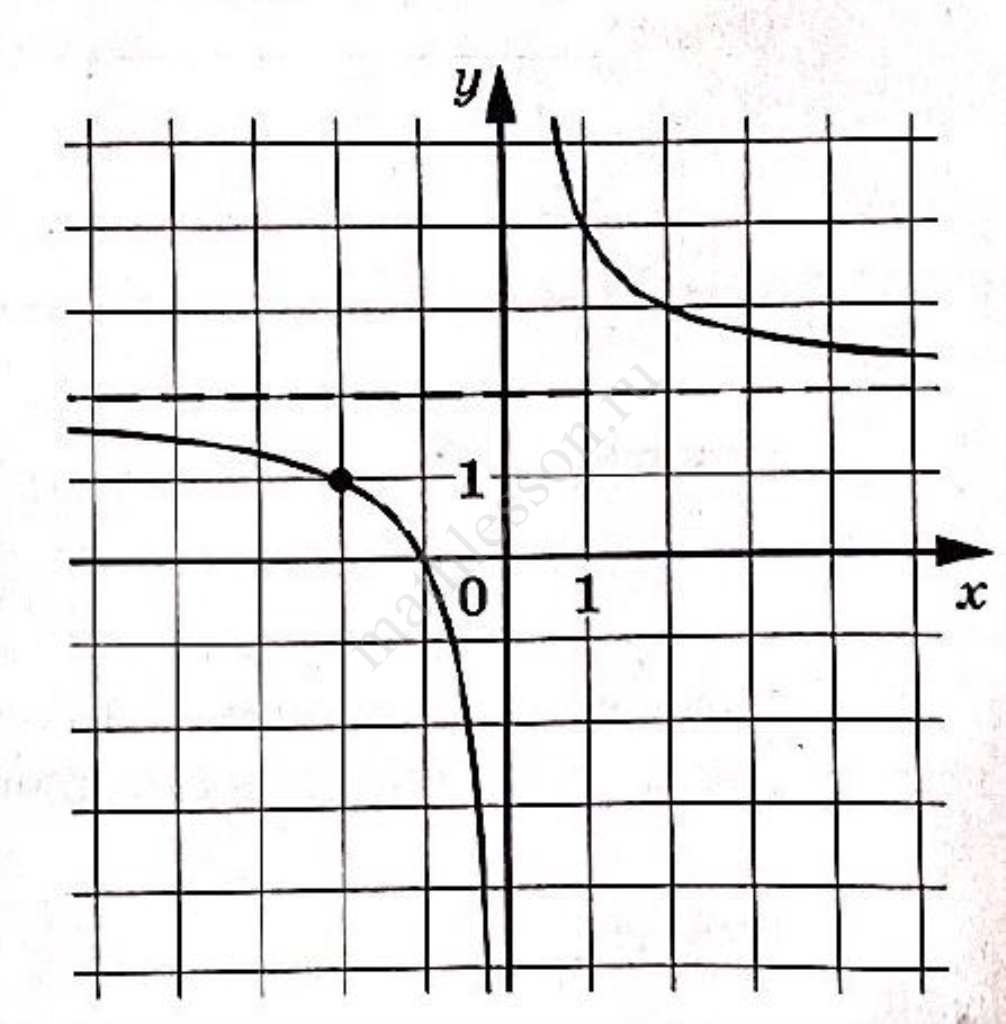
На рисунке изображён график функции
Найдите, при каком значении x значение функции равно 0,8.
Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 10 № 564197
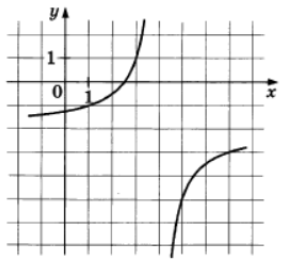
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 10 № 564198
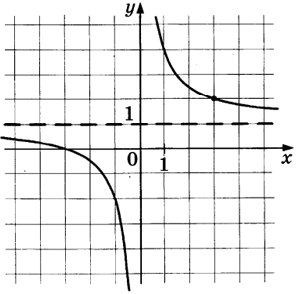
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 10 № 564199
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите
Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
ЕГЭ Профиль №9. Гипербола
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Гипербола
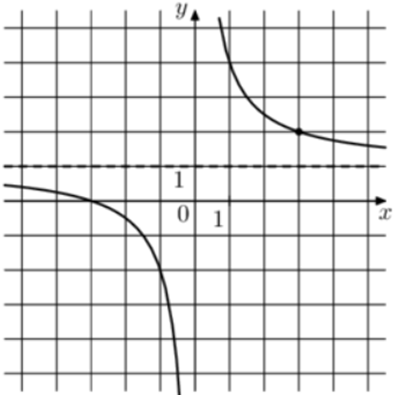
| Задача 1. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( { — 12} right).)
Ответ
ОТВЕТ: 0,75. |
 |
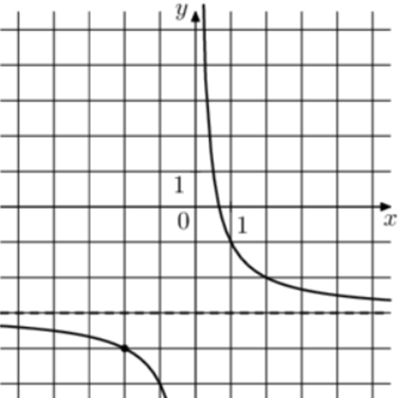
| Задача 2. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {50} right).)
Ответ
ОТВЕТ: — 2,96. |
 |
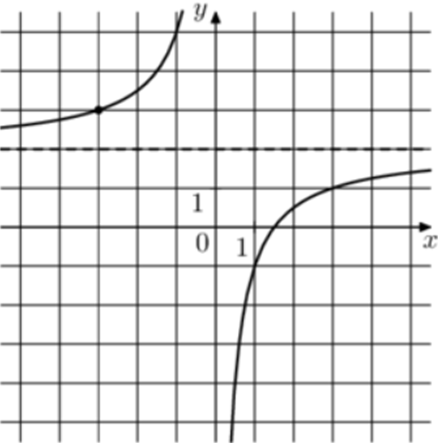
| Задача 3. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {7,5} right).)
Ответ
ОТВЕТ: 1,6. |
 |
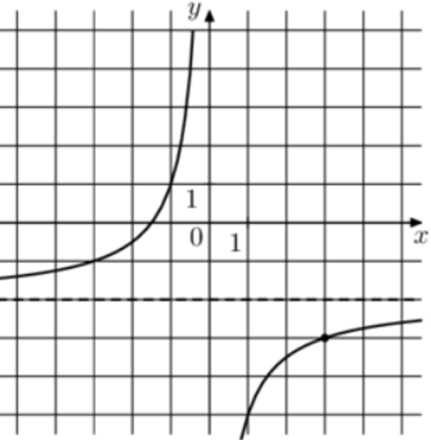
| Задача 4. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {0,25} right).)
Ответ
ОТВЕТ: — 14. |
 |
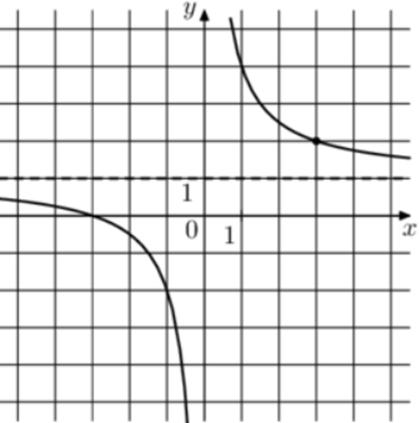
| Задача 5. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,8.
Ответ
ОТВЕТ: — 15. |
 |
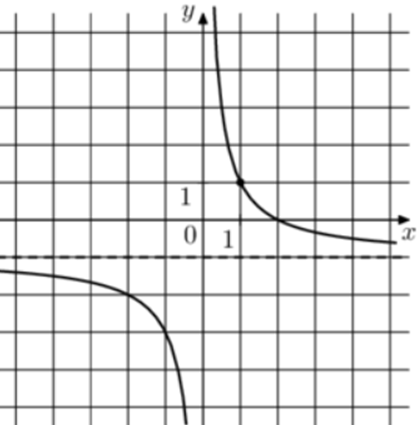
| Задача 6. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 19.
Ответ
ОТВЕТ: 0,1. |
 |
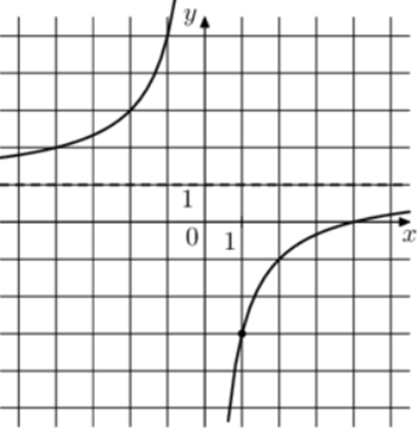
| Задача 7. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,75.
Ответ
ОТВЕТ: 16. |
 |
| Задача 8. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно ( — 9,5.)
Ответ
ОТВЕТ: 0,4. |
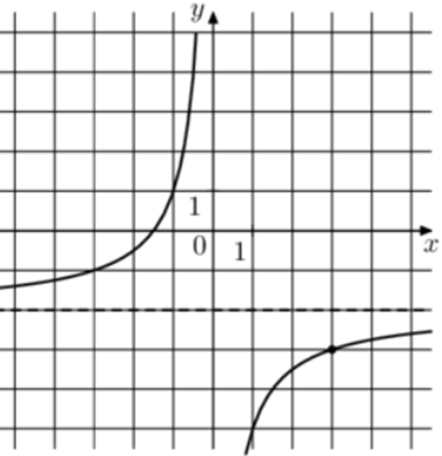 |
| Задача 9. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {19} right).)
Ответ
ОТВЕТ: 0,15. |
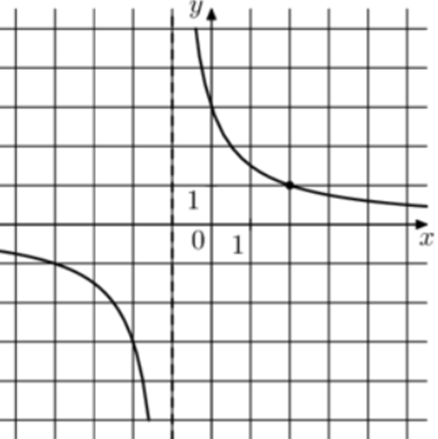 |
| Задача 10. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( { — 4frac{2}{3}} right).)
Ответ
ОТВЕТ: — 0,75. |
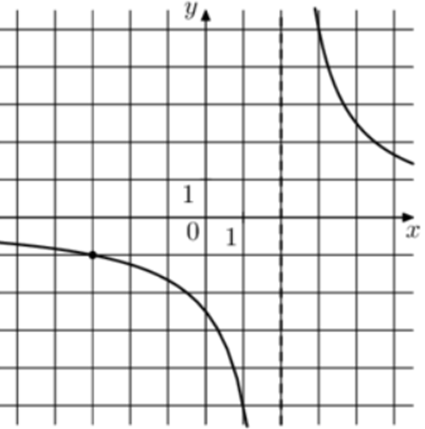 |
| Задача 11. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {18} right).)
Ответ
ОТВЕТ: — 0,1. |
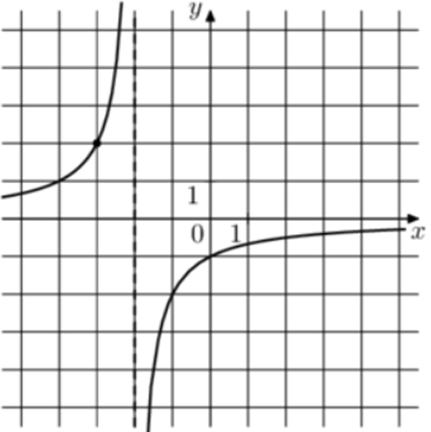 |
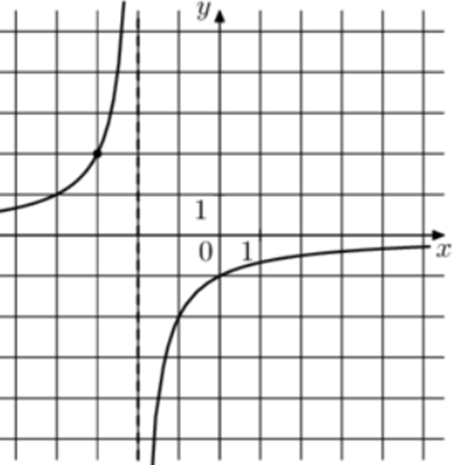
| Задача 12. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {6frac{1}{3}} right).)
Ответ
ОТВЕТ: — 0,24. |
 |
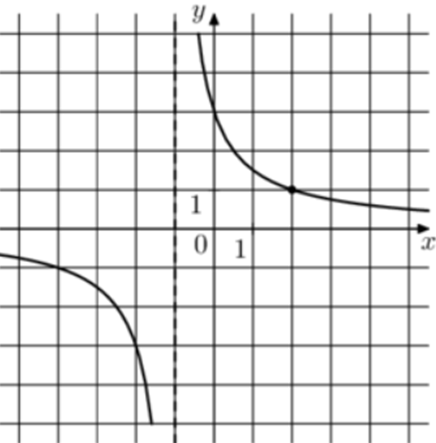
| Задача 13. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: 14. |
 |
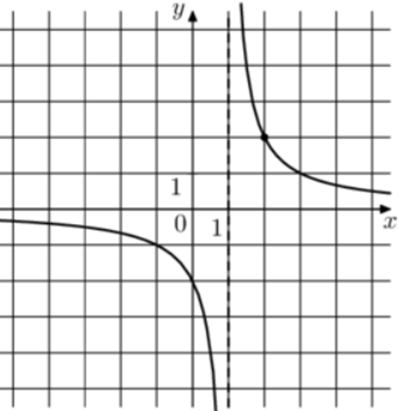
| Задача 14. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,08.)
Ответ
ОТВЕТ: — 24. |
 |
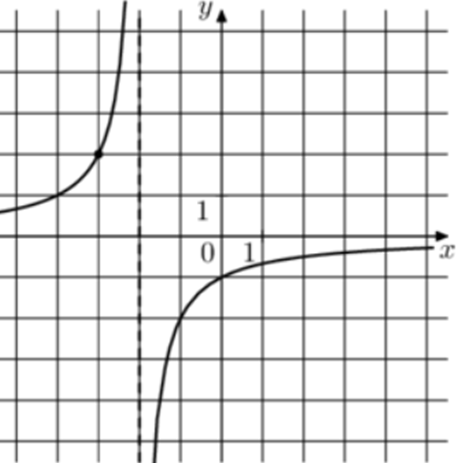
| Задача 15. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,04.)
Ответ
ОТВЕТ: 48. |
 |
| Задача 16. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: — 29. |
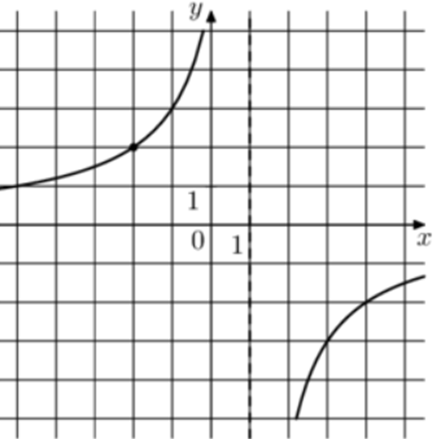 |
| Задача 17. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 1. |
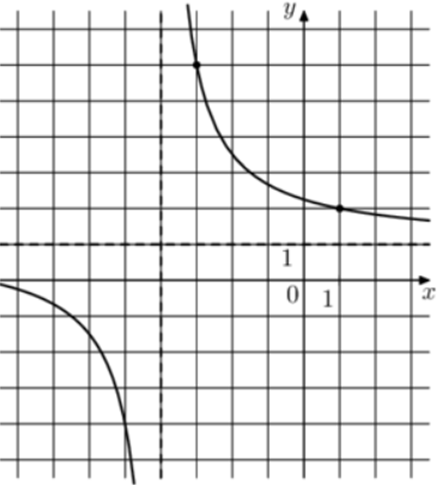 |
| Задача 18. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
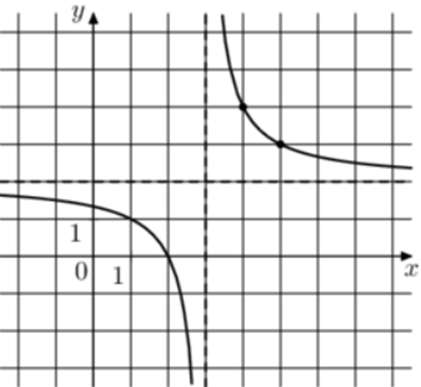 |
| Задача 19. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
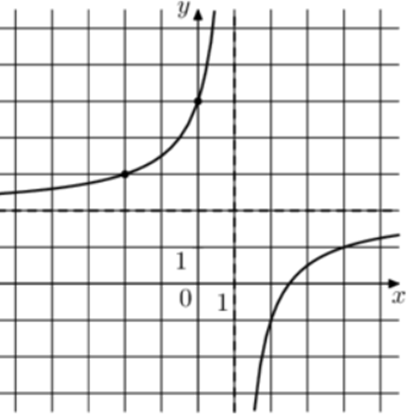 |
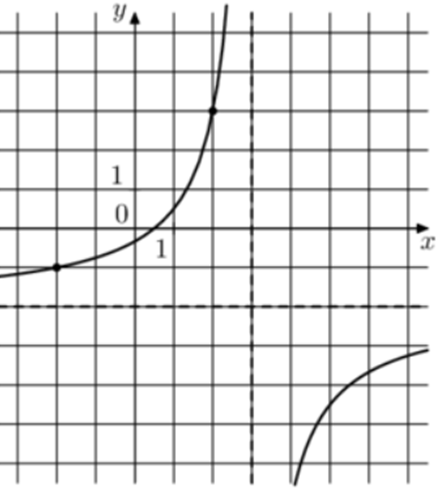
| Задача 20. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: — 2. |
 |
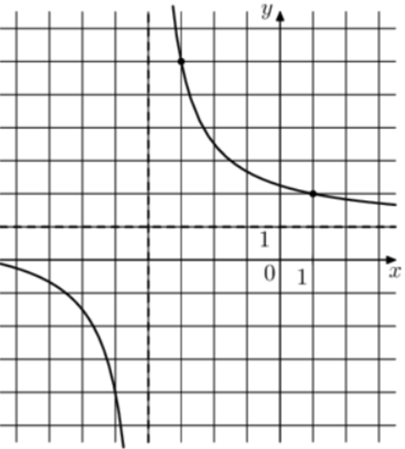
| Задача 21. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 9. |
 |
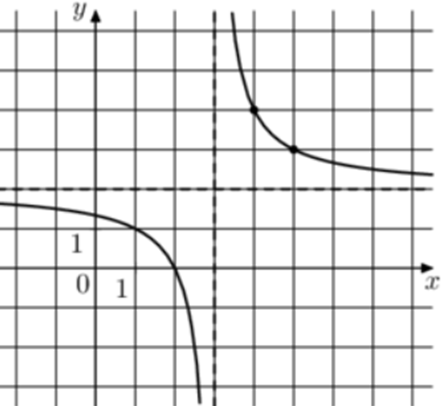
| Задача 22. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 4. |
 |
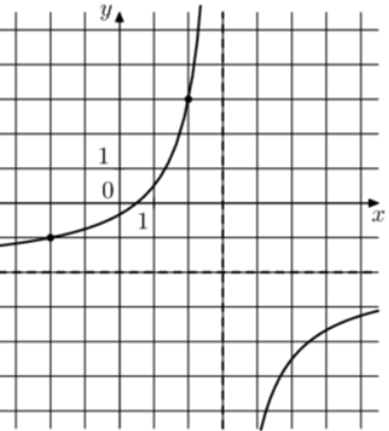
| Задача 23. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 1. |
 |
| Задача 24. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 5. |
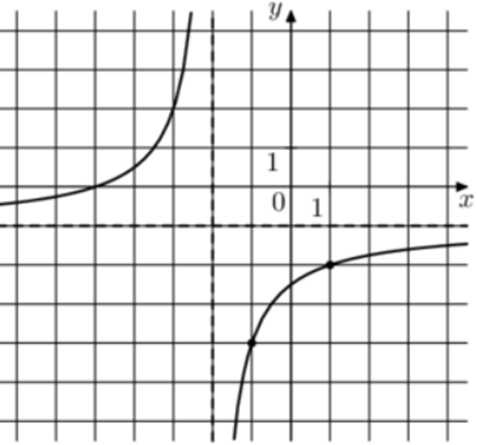 |
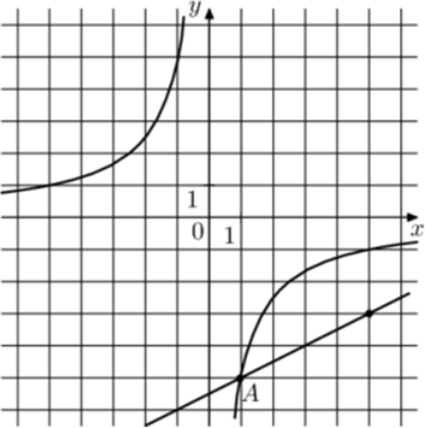
| Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 0,2. |
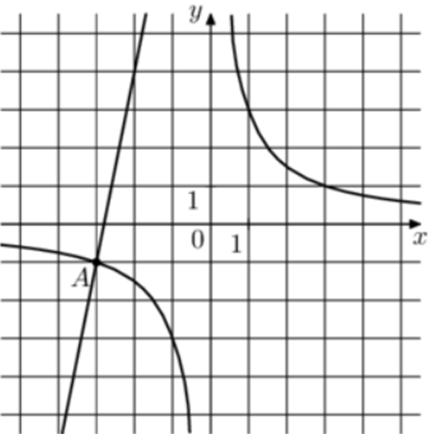 |
| Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6,25. |
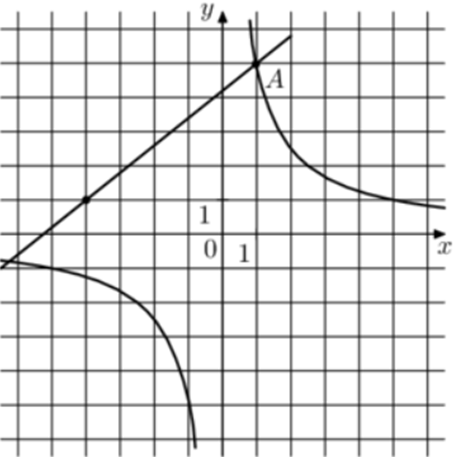 |
| Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 10. |
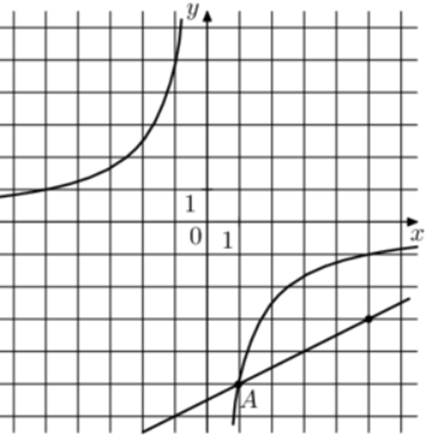 |
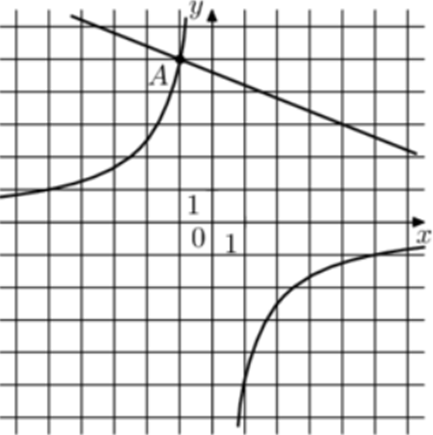
| Задача 28. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 12,5. |
 |
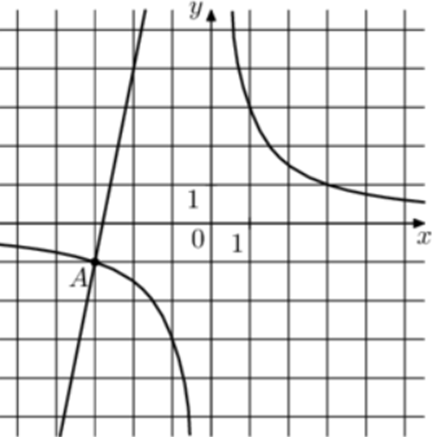
| Задача 29. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 15. |
 |
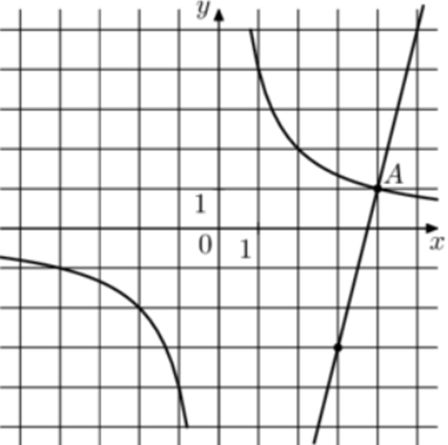
| Задача 30. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
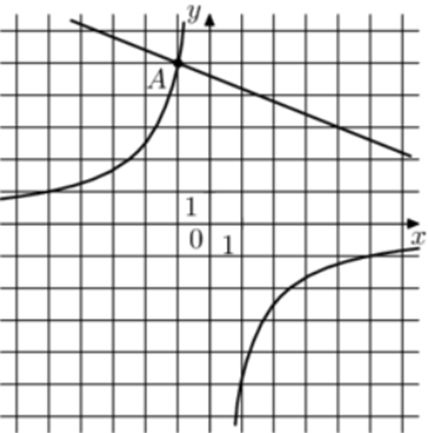
| Задача 31. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,4. |
 |
| Задача 32. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,5. |
 |
09
Янв 2022
Категория: 10 Графики функций
2022-01-09
2022-09-11
Задача 1. На рисунке изображён график функции Найдите
Решение: + показать
Задача 2. На рисунке изображён график функции вида где числа
и
— целые. Найдите значение
, при котором
Решение: + показать
Задача 3. На рисунке изображён график функции вида где
– целые числа. Найдите
Решение: + показать
Задача 4. На рисунке изображён график функции Найдите
Решение: + показать
Задача 5. На рисунке изображены графики функций и
и которые пересекаются в точках
и
. Найдите ординату точки
Решение: + показать
Вы можете пройти тест “Гиперболы”
Автор: egeMax |
Нет комментариев
Задание
№9 «Графики функции»
ЕГЭ
математика профиль
1) Гиперболы
2) Кусочно-линейная функция
3)Параболы
4) Синусоиды
1) Гиперболы
1. 
где числа a, b и c — целые.
Найдите
Решение.
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Асимпто́та, или аси́мптота[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от
точки кривой до этой прямой стремится к нулю при удалении точки вдоль
ветви в бесконечность[2]. Термин впервые появился у Аполлония
Пергского, хотя
асимптоты гиперболы исследовал ещё Архимед[3].
2. 
где числа a, b и c — целые.
Найдите
2. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: −0,75.
3. 
где числа a, b и c — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: 2,875.
2) Кусочно-линейная функция
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
1. 
изображён график функции вида где числа a, b, c и d —
целые. Найдите корень уравнения
Решение.

случаев раскрытия модуля получаем линейную функцию где угловой коэффициент
или
а
свободный член или
Очевидно, что
значит, большему значению
углового коэффициента соответствует а
меньшему — Аналогично большему
значению свободного члена соответствует а
меньшему —
По рисунку определяем, что
Значит,
Решим уравнение
Ответ: 1.
2.
На
рисунке изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 2.
3. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 3.
3)Параболы

где числа a, b и c —
целые. Найдите значение .
Решение.1 способ
По рисунку определяем, что значит,
Тогда
Решение.2 способ
Выбрать три точки . Например (0;-1),
(6,8), (2;4). Подставив координаты первой точки, мы найдем с=-1. Далее
подставив две другие координаты и с, решаем систему уравнений и находим а и в.
4) Синусоиды

изображён график функции вида где числа a, b, c и d — целые.
Найдите
Решение.
По графику
тогда
и
По графику тогда, если
то
— не
имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший
положительный период равен 2, тогда
Таким образом, Найдём
Ответ: −2.
Задание 13539
На рисунке изображён график функции $$y=frac{k}{x}+a$$. Найдите $$f(-8)$$.
Ответ: -0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13557
На рисунке изображён график функции $$f(x)=frac{k}{x}+a$$. Найдите, при каком значении х значение функции равно 7.
Ответ: 0,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14432
На рисунке изображён график функции $$f(x)=frac{k}{x+a}$$.Найдите $$f(-7)$$.
Ответ: -0,4
Скрыть
Точка $$A(-4;1)$$ и $$B(-1;2)$$ принадлежат графику функции. Тогда:
$$left{begin{matrix} -1=frac{k}{-4a}\ 2=frac{k}{-1+a} end{matrix}right.Leftrightarrow left{begin{matrix} 4-a=k\ 2a-2=k end{matrix}right.Leftrightarrow left{begin{matrix} 4-a=2a-2\ k=4-a end{matrix}right.Leftrightarrow left{begin{matrix} a=2\ k=2 end{matrix}right.$$
Получим: $$f(-7)=frac{2}{-7+2}=frac{2}{-5}=-0,4$$
Задание 14449
На рисунке изображён график функции $$f(x)=frac{k}{x+a}.$$ Найдите значение х, при котором $$f(x)=-0,2.$$
Ответ: -13
Скрыть
Вертикальная асимптота графика гиперболы проходит через точку $$x=2,$$ следовательно, параметр $$a=-2.$$
Второй параметр k вычислим из координаты точки $$(-1; -1)$$ на графике:
$$-1=frac{k}{-1-2}Rightarrow k=3$$
Получаем график гиперболы:
$$f(x)=frac{3}{x-2}$$
Найдем точку x, при которой $$f(x)=-0,2:$$
$$-frac{1}{5}=frac{3}{x-2}Rightarrow x=-3cdot5+2=-13$$
Задание 14591
На рисунке изображён график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$k.$$
Ответ: -2
Скрыть
Точки $$(-4;-1)$$ и $$(-2;1)$$ принадлежат графику функции $$f(x).$$ Тогда:
$$left{begin{matrix} -1=frac{a-4k}{b-4}\ 1=frac{a-2k}{b-2} end{matrix}right.Leftrightarrowleft{begin{matrix} a-4k=4-b\ a-2k=-2+b end{matrix}right.Leftrightarrowleft{begin{matrix} 2a-6k=2\ 2k=-6-2b end{matrix}right.Leftrightarrowleft{begin{matrix} a=3k+1\ k=-3-b end{matrix}right.Rightarrow b=-k-3$$
Точка $$(0;5)$$ принадлежит графику функции $$f(x).$$ Тогда:
$$frac{a}{b}=5$$
$$a=5b$$
$$left{begin{matrix} 3k+1=5b\ b=-k-3 end{matrix}right.$$
$$3k+1=5(-k-3)$$
$$8k=-16$$
$$k=-2$$
Задание 14596
На рисунке изображён график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$а.$$
Ответ: 6
Скрыть
$$f(x)=frac{kx+a}{x+b}=k+frac{a-kb}{x+b}$$
При этом $$b=-2,$$ так как вертикальная асимптота сдвинута на 2 единицы вправо.
Получим: $$f(x)=k+frac{a+2k}{x-3}.$$
При этом $$k=-1,$$ так как горизонтальная асимптота сдвинута на 1 единицу вниз.
Получим: $$f(x)=-1+frac{a-2}{x-3}.$$
График проходит через $$(-2;-2).$$
Получим: $$-2=-1+frac{a-2}{-2-2}Leftrightarrow -1=frac{a-2}{-4}Rightarrow a=6.$$
Задание 14621
На рисунке изображен график функции $$y=frac{1}{x+a}+c,$$ где $$a,c$$ ‐ целые числа. Найдите $$c.$$
Ответ: -2
Скрыть
График проходит через $$(4;-1)$$ и $$(2;-3)$$
Получим: $$left{begin{matrix} -1=frac{1}{4+a}+c\ -3=frac{1}{2+a}+c end{matrix}right.Leftrightarrowleft{begin{matrix} -c-1=frac{1}{4+a}\ -c-3=frac{1}{2+a} end{matrix}right.$$
Вычтем из второго уравнения первое:
$$-2=frac{1}{2+a}-frac{1}{4+a}Leftrightarrow -2=frac{4+a-2-a}{(4+a)(2+a)}$$
$$-2(8+6a+a^2)=2Leftrightarrow a^2+6a+8=-1Leftrightarrow a^2+6a+9=0$$
$$Rightarrow a=-3Rightarrow -c-1=frac{1}{4-3}Rightarrow -c=1+1Rightarrow c=-2$$
Задание 14875
На рисунке изображён график функции $$f(x)=frac{k}{x+a}.$$ Найдите $$f(19).$$
Ответ: 0,15
Скрыть
Точки $$(2;1)$$ и $$(-4;-1)$$ принадлежат графику функции. Тогда:
$$left{begin{matrix} frac{k}{2+a}=1\ frac{k}{-4+a}=-1 end{matrix}right.Leftrightarrowleft{begin{matrix} k=2+a\ k=4-a end{matrix}right.$$
$$2+a=4-a$$
$$2a=2$$
$$a=1$$
$$k=4-1=3$$
$$f(x)=frac{3}{x+1}$$
$$f(19)=frac{3}{19+1}=frac{3}{20}=0,15$$
Задание 14894
На рисунке изображен график функции $$f(x)=frac{ax+b}{x+c},$$ где числа $$a, b, c$$ — целые. Найдите значение $$f(29).$$
Ответ: -2,12
Скрыть
График проходит через $$(1;-1); (3;1); (5;-5).$$ Получим:
$$left{begin{matrix} -1=frac{acdot1+b}{1+c}\ 1=frac{3a+b}{3+c}\ -5=frac{5a+b}{5+c} end{matrix}right.Leftrightarrowleft{begin{matrix} -1-c=a+b\ 3+c=3a+b\ -25-5c=5a+b end{matrix}right.Leftrightarrowleft{begin{matrix} 4+2c=2a\ 28+6c=-2a\ 3+c=3a+b end{matrix}right.Leftrightarrowleft{begin{matrix} 32+8c=0\ a=2+c\ b=c+3-3a end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} c=-4\ a=-2\ b=5 end{matrix}right.$$
Получим: $$y=frac{-2x+5}{x-4}.$$ Тогда $$f(29)=frac{-2cdot29+5}{29-4}=frac{-53}{25}=-2,12$$
Задание 15049
На рисунке изображены графики функций $$f(x)=frac{k}{x}$$ и $$g(x)=ax+b,$$ которые пересекаются в точках $$А(-2;3)$$ и $$В(x_0;y_0).$$ Найдите $$x_0.$$
Ответ: 0,75
Скрыть
Прямая проходит через $$(-2;-3)$$ и $$(0;5).$$ Получим:
$$left{begin{matrix} -3=-2k+b\ 5=0k+b end{matrix}right.Leftrightarrowleft{begin{matrix} -2k=-8\ b=5 end{matrix}right.Leftrightarrowleft{begin{matrix} k=4\ b=5 end{matrix}right.$$
Гипербола проходит через $$(-2;-3).$$ Тогда:
$$-3=frac{k}{-2}Rightarrow k=6.$$ Получим $$y=frac{6}{x}.$$
$$frac{6}{x}=4x+5Leftrightarrow 4x^2+5x-6=0$$
$$D=25+96=121$$
$$x_1=frac{-5+11}{2cdot4}=frac{1,5}{2}=0,75$$
$$x_2=frac{-5-11}{2cdot4}=-2$$
Задание 15068
На рисунке изображен график функции $$f(x)=frac{ax+b}{x+c},$$ где a, b и с — целые. Найдите значение f(17).
Ответ: -1,9
Скрыть
График проходит через $$(-1;-1); (-2;0)$$ и $$(-4;-4).$$
Получим:
$$left{begin{matrix} -1=frac{acdot(-1)+b}{-1+c}\ 0=frac{acdot(-2)+b}{-2+c}\ -4=frac{acdot(-4)+b}{-4+c} end{matrix}right.Leftrightarrowleft{begin{matrix} -1=frac{b-a}{c-1}\ 0=frac{b-2a}{c-2}\ -4=frac{b-4a}{c-4} end{matrix}right.Leftrightarrowleft{begin{matrix} 1-c=b-a\ b-2a=0\ 16-4c=b-4a end{matrix}right.Leftrightarrowleft{begin{matrix} 1-c=2a-a\ b=2a\ 16-4c-b=-4a end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} c=1-a\ b=2a\ 16-4+4a-2a=-4a end{matrix}right.Leftrightarrowleft{begin{matrix} a=-2\ b=-4\ c=3 end{matrix}right.$$
Получим:
$$y=frac{-2x-4}{x+3}.$$
$$y(17)=frac{-34-4}{17+3}=frac{-38}{20}=-1,9$$
Задание 15125
На рисунке изображен график функции $$f(x)=frac{k}{x}+a.$$ Найдите $$f(-12).$$
Ответ: 0,75
Скрыть
$$2=frac{k}{3}+a$$
$$−2=frac{k}{-1}+a$$
Решая систему, получаем:
$$f(x)=frac{3}{x}+1$$
$$f(-12)=0,75$$
Задание 15302
На рисунке изображен график функции $$f(x)=frac{kx+a}{x+b}.$$ Найдите $$a.$$
Ответ: 9
Скрыть
График проходит через $$(1;2), (-3;6), (-5;-4).$$ Получим:
$$left{begin{matrix} 2=frac{k+a}{1+b}\ 6=frac{-3k+a}{-3+b}\ -4=frac{-5k+a}{-5+b} end{matrix}right.Leftrightarrowleft{begin{matrix} 2+2b=k+a\ -18+6b=-3k+a\ 20-4b=-5k+a end{matrix}right.$$
Вычтем второе из первого и третьего:
$$left{begin{matrix} 20-4b=4k\ 38-10b=-2k end{matrix}right.Leftrightarrowleft{begin{matrix} 5-b=k\ -19+5b=k end{matrix}right.Leftrightarrowleft{begin{matrix} 24-6b=0\ 5-b=k end{matrix}right.Leftrightarrowleft{begin{matrix} b=4\ k=1 end{matrix}right.$$
Тогда:
$$2+2cdot4=1+aRightarrow a=9$$
Задание 15533
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 15689
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите абсциссу точки пересечения графиков этих функций.
Ответ:
Скрыть
- ЕГЭ по математике профиль
Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.
Для успешного результата необходимо уметь выполнять действия с функциями.
Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы
| Скачать задания | Источник |
| Новые задания 9 | ФИПИ |
| Прототипы задания №9 | vk.com/mathegeexam |
| Скачать задания | vk.com/ekaterina_chekmareva |
| → Теория → Задачи → Шпаргалка |
vk.com/abel_mat |
| Линейная функция | math100.ru |
| Парабола | |
| Гипербола | |
| Логарифмическая и показательная функции | |
| Иррациональные функции | |
| Тригонометрические функции |
Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:
3.3.1 Линейная функция, её график
3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
3.3.3 Квадратичная функция, её график
3.3.4 Степенная функция с натуральным показателем, её график
3.3.5 Тригонометрические функции, их графики
3.3.6 Показательная функция, её график
3.3.7 Логарифмическая функция, её график
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:
При отработке данного задания будут полезны книги:
Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля
Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств
Связанные страницы:
Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты
- Cайты учителей
- Все блоги
- Все файлы
- Все тесты
-
1 - Войти
- Зарегистрироваться / Создать сайт


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 31.01.2022 15:49
Бабошкина Любовь Юрьевна
Учитель математики
66 лет
1 722
23 231
09.11.2021 20:48
В презентации разбирается один из способов решения задания №9 ЕГЭ (гиперболы)
Просмотр содержимого документа
«Графики функции. Задание №9 ЕГЭ-2022»
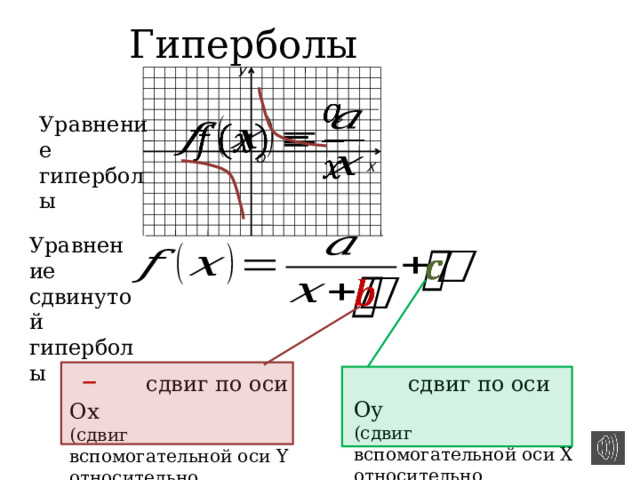
Графики функций
Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама
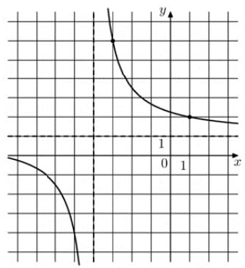
Гиперболы
У
Уравнение гиперболы
О
Х
Уравнение
сдвинутой
гиперболы
– сдвиг по оси Ох
(сдвиг вспомогательной оси Y относительно основной)
сдвиг по оси Оу
(сдвиг вспомогательной оси Х относительно основной)
y 1
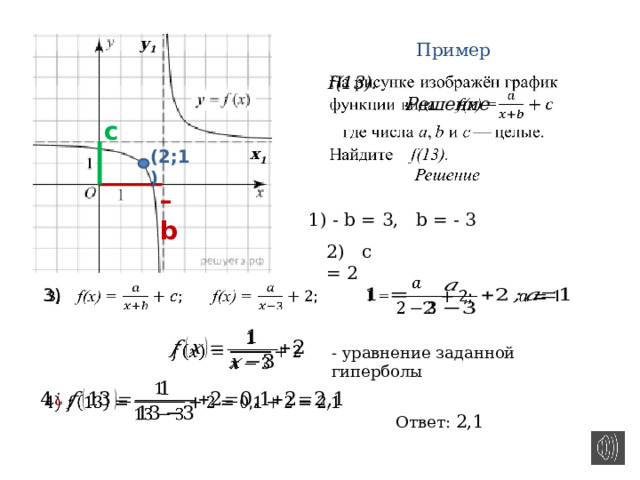
Пример
f(13).
Решение
c
x 1
(2;1)
– b
1) — b = 3, b = — 3
2) c = 2
3)
— уравнение заданной гиперболы
Ответ: 2,1