Егэ математика профиль 9 задание функции - Помощь в подготовке к экзаменам и поступлению

: ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Скачать задания	Источник
Новые задания 9	ФИПИ
Прототипы задания №9	vk.com/mathegeexam
Скачать задания	vk.com/ekaterina_chekmareva
→ Теория → Задачи → Шпаргалка	vk.com/abel_mat
Линейная функция	math100.ru
Парабола
Гипербола
Логарифмическая и показательная функции
Иррациональные функции
Тригонометрические функции

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.

3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10]	Смотреть видеоразбор похожего >>
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74]	Смотреть видеоразбор похожего >>
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19]	Смотреть видеоразбор похожего >>
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49]	Смотреть видеоразбор похожего >>
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29]	Смотреть видеоразбор похожего >>
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17]	Смотреть видеоразбор похожего >>
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5]	Смотреть видеоразбор похожего >>
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6]	Смотреть видеоразбор похожего >>
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6]	Смотреть видеоразбор похожего >>
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1]	Смотреть видеоразбор похожего >>
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3]	Смотреть видеоразбор похожего >>
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64]	Смотреть видеоразбор похожего >>
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2]	Смотреть видеоразбор похожего >>
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82]	Смотреть видеоразбор похожего >>
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22]	Смотреть видеоразбор похожего >>
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4]	Смотреть видеоразбор похожего >>
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9]	Смотреть видеоразбор похожего >>
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8]	Смотреть видеоразбор похожего >>
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7]	Смотреть видеоразбор похожего >>
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29]	Смотреть видеоразбор похожего >>
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9]	Смотреть видеоразбор похожего >>
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38]	Смотреть видеоразбор похожего >>
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2]	Смотреть видеоразбор похожего >>
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20]	Смотреть видеоразбор похожего >>
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08]	Смотреть видеоразбор похожего >>
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4]	Смотреть видеоразбор похожего >>
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3]	Смотреть видеоразбор похожего >>
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8]	Смотреть видеоразбор похожего >>
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9]	Смотреть видеоразбор похожего >>
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13]	Смотреть видеоразбор похожего >>
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24]	Смотреть видеоразбор похожего >>
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9]	Смотреть видеоразбор похожего >>
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5]	Смотреть видеоразбор похожего >>
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5]	Смотреть видеоразбор похожего >>
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1]	Смотреть видеоразбор похожего >>
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5]	Смотреть видеоразбор похожего >>

Источник

Задание
№9 «Графики функции»

ЕГЭ
математика профиль

1) Гиперболы

2) Кусочно-линейная функция

3)Параболы

4) Синусоиды

1) Гиперболы

1. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

Решение.

1. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Асимпто́та, или аси́мптота^[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от
точки кривой до этой прямой стремится к нулю при удалении точки вдоль
ветви в бесконечность^[2]. Термин впервые появился у Аполлония
Пергского, хотя
асимптоты гиперболы исследовал ещё Архимед^[3].

2. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

2. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Ответ: −0,75.

3. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

3. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Ответ: 2,875.

2) Кусочно-линейная функция

1. На рисунке
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения

1. На рисунке
изображён график функции вида где числа a, b, c и d —
целые. Найдите корень уравнения

Решение.

В любом из
случаев раскрытия модуля получаем линейную функцию  где угловой коэффициент  или  а
свободный член  или  Очевидно, что  значит, большему значению
углового коэффициента соответствует  а
меньшему —  Аналогично большему
значению свободного члена соответствует  а
меньшему —

По рисунку определяем, что Значит,

Решим уравнение

Ответ: 1.

На
рисунке изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения

2. На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

Решение.

Заметим, что в точке излома, т.е.
при Значит, корнем уравнения является число 2.

3. На рисунке изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

4. На рисунке изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

4. На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

Решение.

Заметим, что в точке излома, т.е.
при Значит, корнем уравнения является число 3.

3)Параболы

На рисунке изображён график функции вида где числа a, b и c —
целые. Найдите значение .

Решение.1 способ

По рисунку определяем, что значит,

Тогда

Решение.2 способ

Выбрать три точки . Например (0;-1),
(6,8), (2;4). Подставив координаты первой точки, мы найдем с=-1. Далее
подставив две другие координаты и с, решаем систему уравнений и находим а и в.

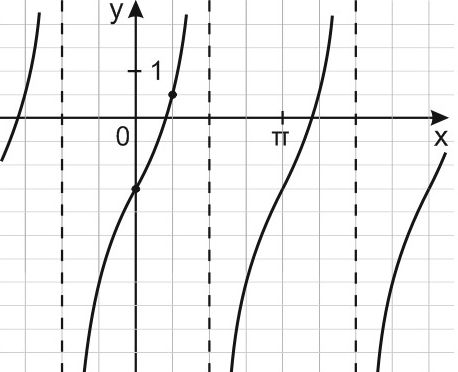
4) Синусоиды

На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите

Решение.

По графику тогда и

По графику тогда, если то

— не
имеет целочисленных решений,

если то

Значит, и

Найдём наименьший положительный период функции

Наименьший положительный период функции равен а по графику наименьший
положительный период равен 2, тогда

Таким образом, Найдём

Ответ: −2.

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №9. Логарифмическая и показательная функции

ЕГЭ Профиль №9. Логарифмическая и показательная функцииadmin2022-08-22T14:16:20+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Логарифмическая и показательная функции

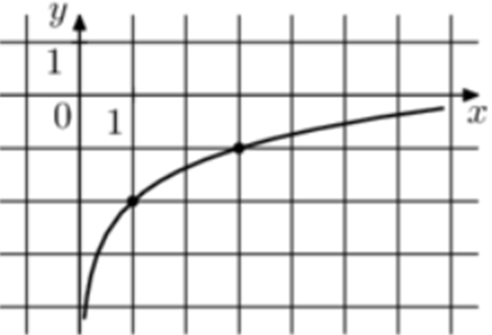
Задача 1. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 1.
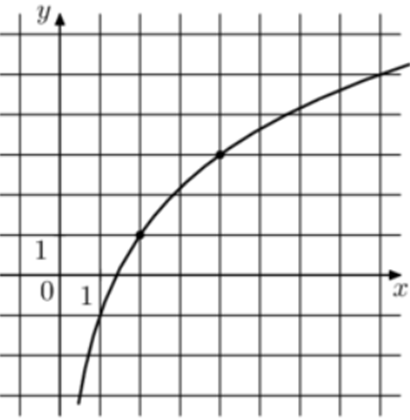
Задача 2. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {16} right).) Ответ ОТВЕТ: 7.
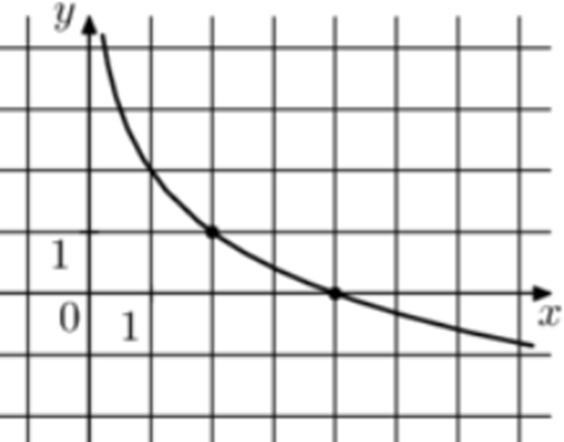
Задача 3. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {128} right).) Ответ ОТВЕТ: — 5.
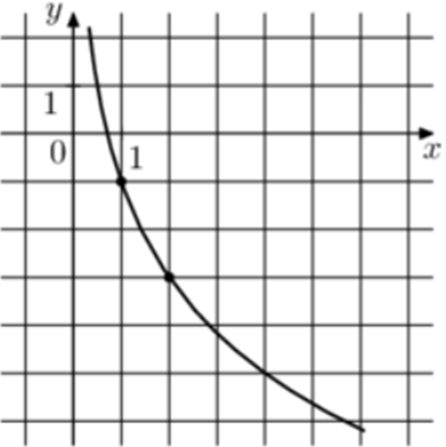
Задача 4. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите (fleft( {0,125} right).) Ответ ОТВЕТ: 5.
Задача 5. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 64.
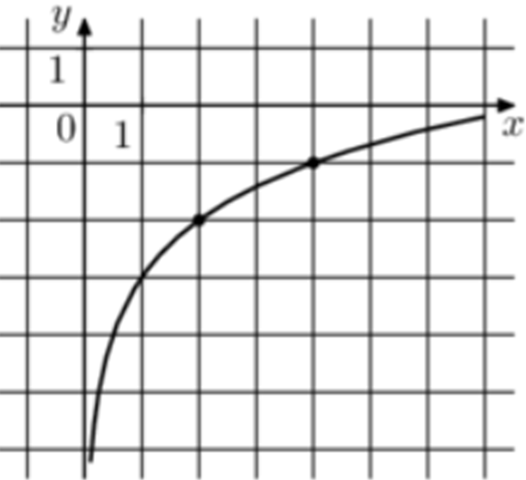Задача 6. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 2.) Ответ ОТВЕТ: 81.
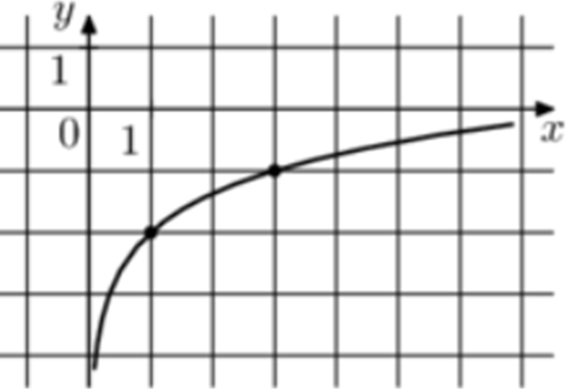Задача 7. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = — 3.) Ответ ОТВЕТ: 32.
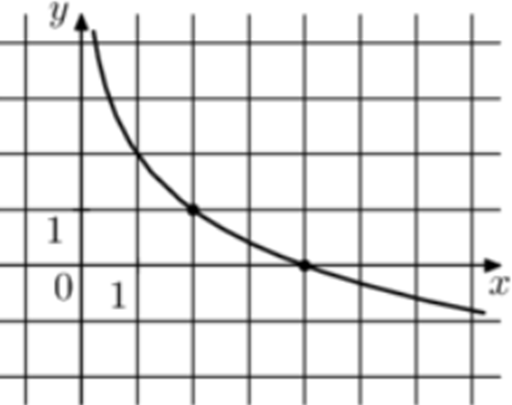Задача 8. На рисунке изображён график функции (fleft( x right) = b + {log _a}x.) Найдите значение x при котором (fleft( x right) = 3.) Ответ ОТВЕТ: 0,25.
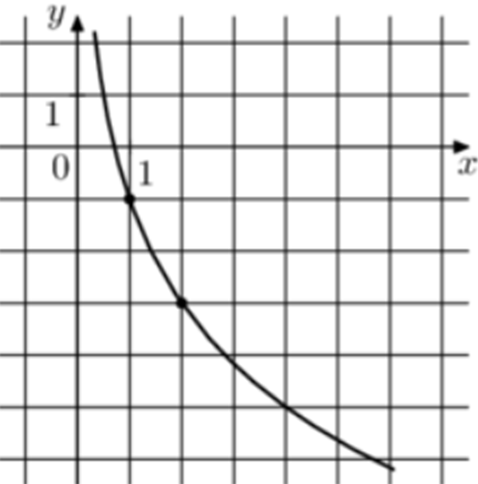Задача 9. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {27} right).) Ответ ОТВЕТ: 5.
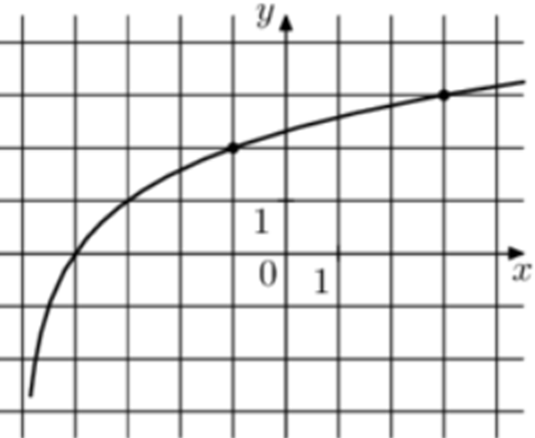Задача 10. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {238} right).) Ответ ОТВЕТ: 5.
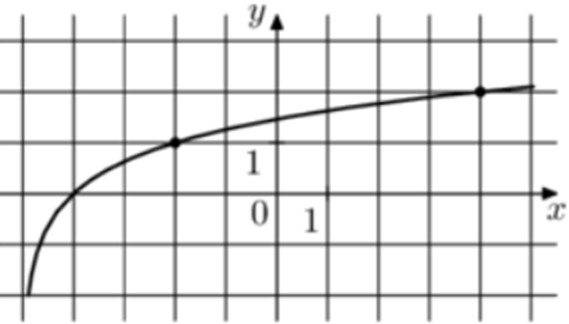Задача 11. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {30} right).) Ответ ОТВЕТ: — 5.
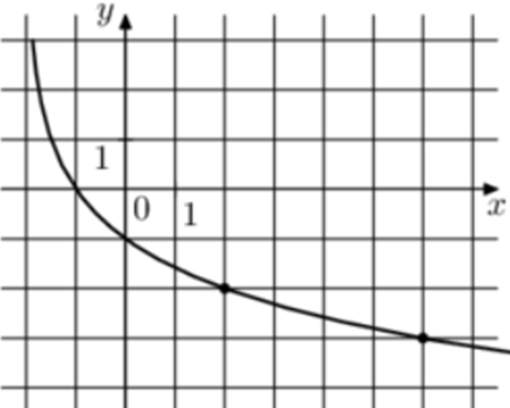Задача 12. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите (fleft( {77} right).) Ответ ОТВЕТ: — 4.
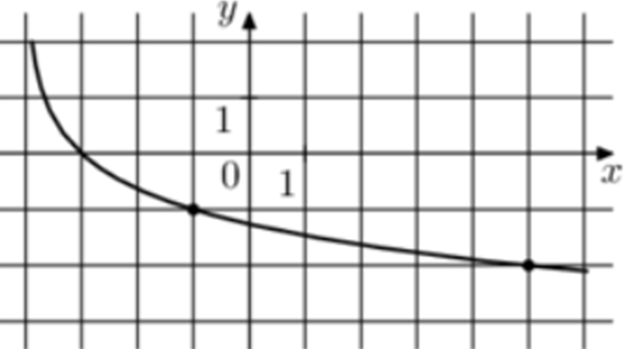Задача 13. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 6.) Ответ ОТВЕТ: 59.
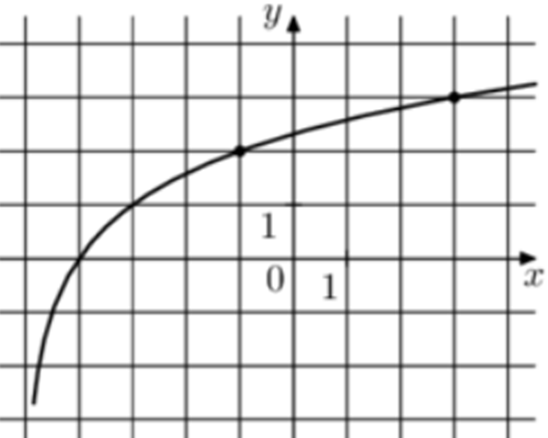Задача 14. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = 5.) Ответ ОТВЕТ: 31.
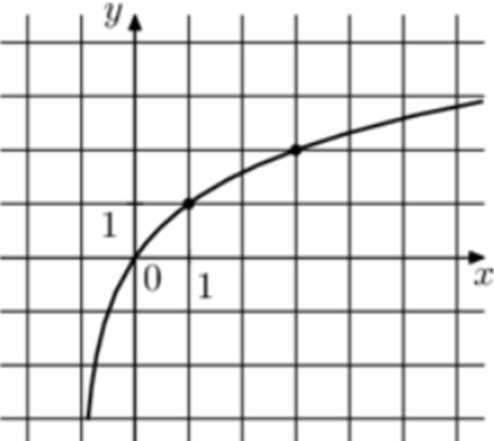Задача 15. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 8.) Ответ ОТВЕТ: 79.
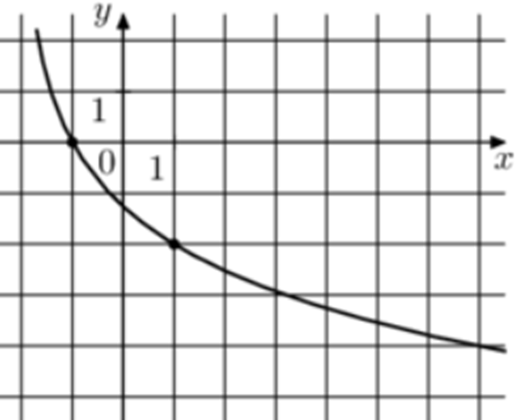Задача 16. На рисунке изображён график функции (fleft( x right) = {log _a}left( {x + b} right).) Найдите значение x, при котором (fleft( x right) = — 5.) Ответ ОТВЕТ: 239.

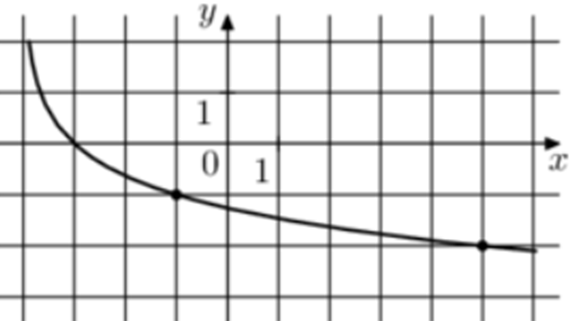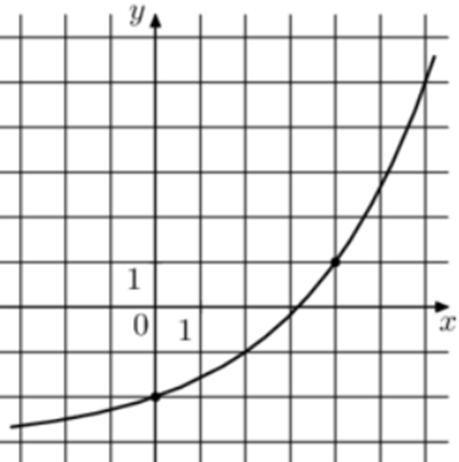
Задача 17. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( {10} right).) Ответ ОТВЕТ: 29.
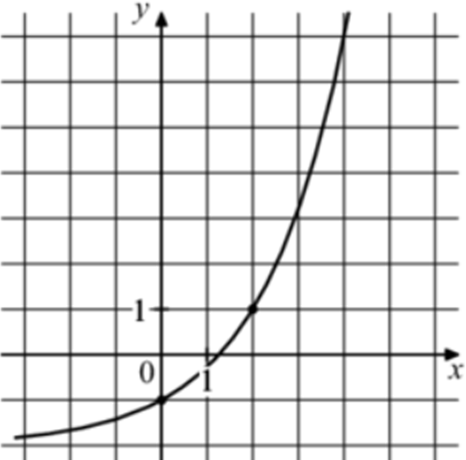
Задача 18. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( 8 right).) Ответ ОТВЕТ: 79.
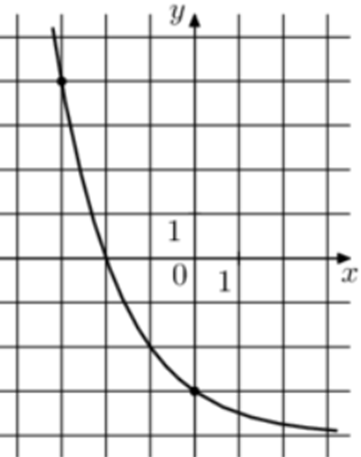
Задача 19. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 28.
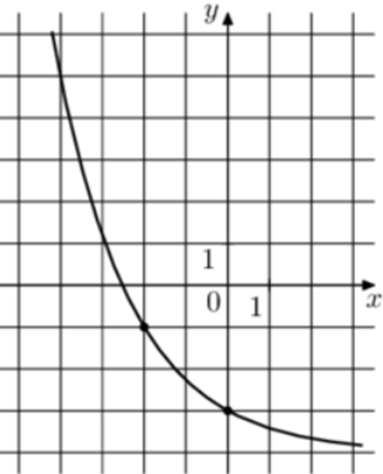
Задача 20. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите (fleft( { — 8} right).) Ответ ОТВЕТ: 77.
Задача 21. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 13.) Ответ ОТВЕТ: 8.
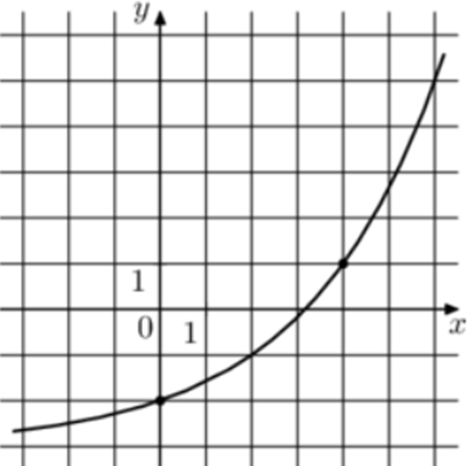Задача 22. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 25.) Ответ ОТВЕТ: 6.
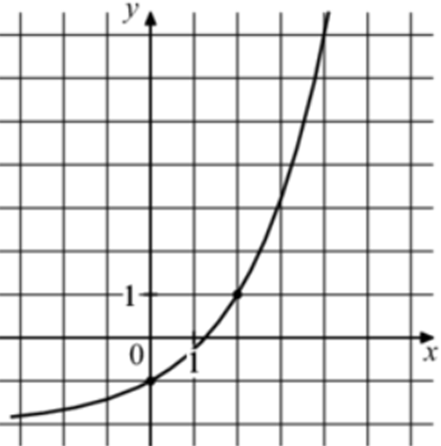Задача 23. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 12.) Ответ ОТВЕТ: — 4.
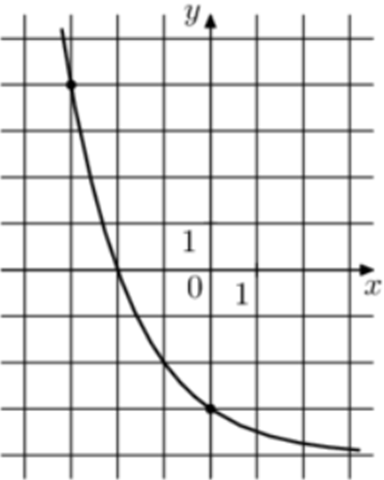Задача 24. На рисунке изображён график функции (fleft( x right) = {a^x} + b.) Найдите значение x, при котором (fleft( x right) = 23.) Ответ ОТВЕТ: — 6.
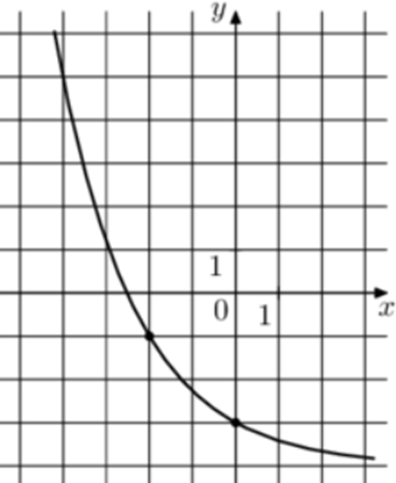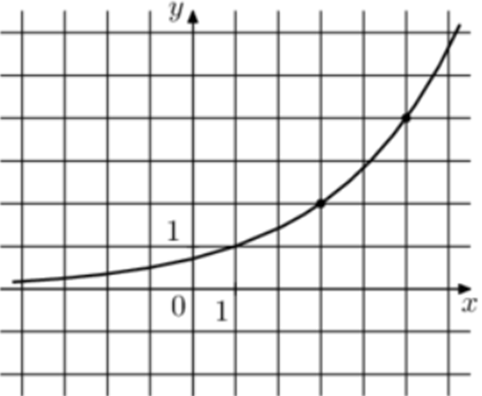
Задача 25. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 0,125.
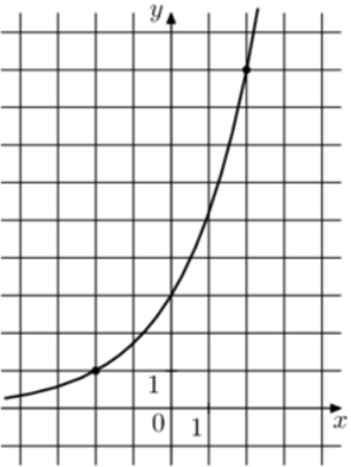
Задача 26. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( 6 right).) Ответ ОТВЕТ: 81.
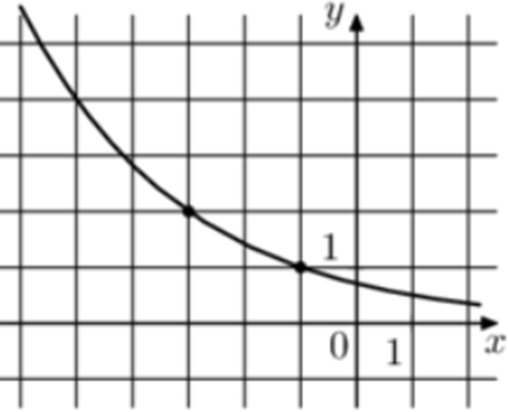
Задача 27. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 9} right).) Ответ ОТВЕТ: 16.
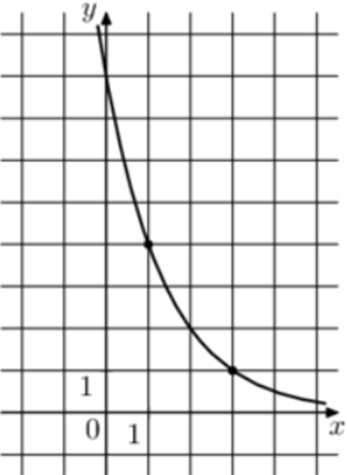
Задача 28. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите (fleft( { — 2} right).) Ответ ОТВЕТ: 32.
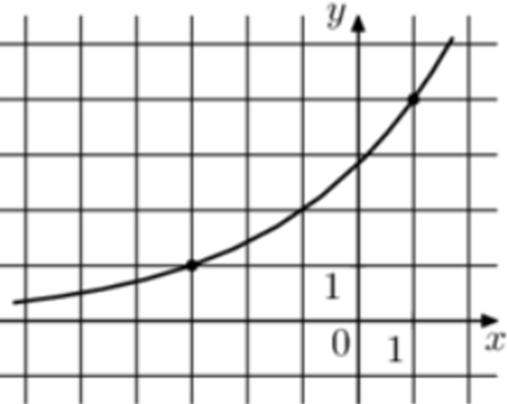
Задача 29. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 16.) Ответ ОТВЕТ: 5.
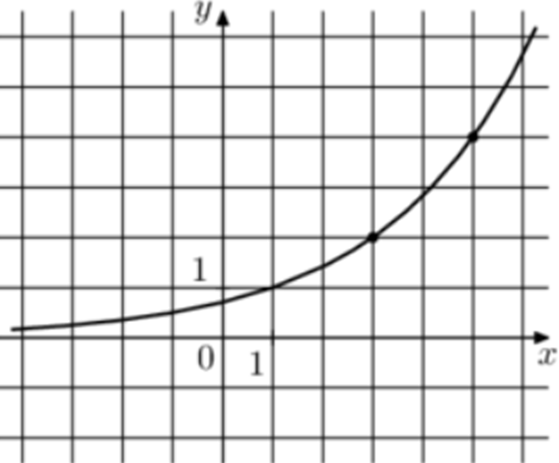
Задача 30. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 0,125.) Ответ ОТВЕТ: — 5.
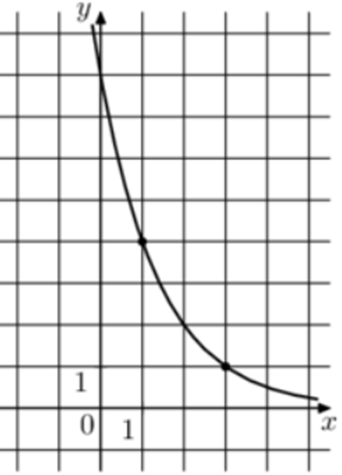
Задача 31. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 64.) Ответ ОТВЕТ: — 3.
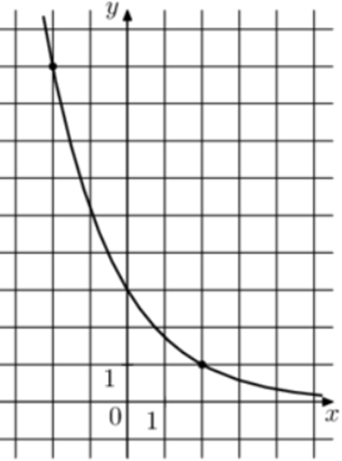
Задача 32. На рисунке изображён график функции (fleft( x right) = {a^{x + b}}.) Найдите значение x, при котором (fleft( x right) = 81.) Ответ ОТВЕТ: — 6.